Gain lifetime characterization through time-resolved stimulated emission in a whispering-gallery mode microresonator

1 Introduction

Optical gain can dramatically modify the response of a system and compensate for the loss of light during communications and information processing. Such gain processes play an important role in various applications [1], including lasers and masers, optical amplifiers, and sensitive detections. The optical gain typically results from the stimulated emission process, which is generated from the recombination of electrons and holes in semiconductors or the coherent amplification through population inversion between different energy levels in gain medium. The lifetime of optical gain, a fundamental parameter and of significant importance for understanding light-matter interaction, determines various properties of a system, for example, the maximum switch speed of the input signal in an active optical switch [2]. The stimulated radiation process corresponds to specific energy level transitions. Therefore, the emission light is considered to have the same properties as those of the input light. By contrast, the luminescence, which results from the spontaneous radiation of excited states and multi-channel transitions, has a wide broadening in spectrum and contains lights in different wavelengths [3]. The lifetime of luminescence can be accurately measured through the changes of its intensity after the pump source is turned off; also, optical gain lifetime needs a simple, effective, and fast method to be characterized precisely.

The whispering-gallery mode (WGM) microresonator [4], [5], [6], which has an ultra-high-quality factor higher than 10⁸ and mode volumes at the cubic micrometer scale, has been widely used in many applications [7], [8], [9], [10], [11], [12], [13], [14]. Moreover, the WGM microresonator serves as a fruitful platform to study various applications of optical gains. Ultra-low-threshold micro-lasers have been implemented using a silica microsphere, microdisk, and microtoroid [15], [16]. Furthermore, sensitive metrology and detection have been realized in active microresonators [17], [18], [19], [20], [21]. WGM microresonators have received strong interest for the realization of cavity quantum electrodynamical systems [7], [8] and the classical analog of quantum systems, such as parity-time optics [22], [23], [24], [25], [26] and electromagnetically induced transparency [27], [28], [29], [30], [31]. To further improve the performance of WGM microresonators, one can decrease their sizes to obtain smaller mode volumes and stronger light-matter interactions; however, this approach can increase bending losses and lower Q values. Another method is to dope rare-earth ions (e.g. Er³⁺, Yb³⁺, or Nd³⁺) [1], [3], [15] or introduce intrinsic Raman gain from the material [18], [19], [32]. For rare-earth ions (e.g. erbium ions), transitions between internal energy levels are stable because these processes which take place in 4f shells are shielded from the interaction with other atoms by the external 5s and 5p electrons. This stability makes rare-earth ions a universal candidate for practical applications, e.g. displays or lighting, performance improvements of magnetic materials, and optical communications. Recently, rare-earth-doped WGM microresonators have been successfully applied in signal amplifiers [33], ultra-long storage of photons [34], and on-demand coupling control [35], [36].

To date, there is no related study that has been conducted to identify optical gain lifetime in microresonators. Here, we present a direct and precise measurement of this lifetime at a specific wavelength through the linewidth changes of an optical mode. An Er³⁺-doped material is taken as an example to demonstrate the feasibility of this method. To enhance the light-matter interaction, we dope erbium ions into WGM microresonators. In our study, a pump laser with a central wavelength of 1430 nm and an input power of 275 μW was coupled into the microtoroid through a tapered fiber to excite erbium ions into intermediate states. Then, this excitation was turned off by optothermal squeezing within 2 μs. Next, another laser in 1550 nm band with a high scanning speed of 4.2 THz/s served as the probe signal. To eliminate the influence of temperature, the thermal relaxation time was also precisely characterized to be 0.33 ms via optothermal spectroscopy. We used six different probe signals with the wavelength scanned over the range from 1528 nm to 1556 nm and wavelength differences of 5.6 nm, which is approximately one free spectral range (FSR). Gain lifetime was measured to be approximately 5.1 ms. Through continually tuning the microresonator, lifetime of optical gains at different resonant wavelengths could also be well measured. Our results precisely show the evolution of optical gain at specific wavelengths, and the lifetime can be characterized simultaneously by measuring the linewidth changes of a probe mode; by contrast, the standard time-resolved photoluminescence (PL) spectroscopy technique, which is based on spontaneous emission of excited states, can just measure the lifetime of fluorescence through its changes of intensity with time. Therefore, the experimental results demonstrated here cannot be achieved by the previous PL technique. Moreover, the use of tapered fiber coupling allows for higher pump and collection efficiencies, thereby greatly decreasing the demand for detectors and measurement techniques.

2 The methods and the evolution of transmission spectra

The experimental configuration is depicted in Figure 1, which shows a silica microtoroidal WGM resonator directly coupled to a tapered fiber. The WGM resonator is an Er³⁺-doped microtoroid, which is fabricated using the sol-gel technique [22], [37]. First, silica layers with a thickness of 2 μm and an ion concentration of 7.4×10²⁴ ions/cm³ are fabricated on the surface of a silicon wafer. Subsequently, photolithography, pattern transfer, dry etching, and reflow are applied to form this surface-tension-induced microtoroid. Figure 1C demonstrates the emission spectum of Er³⁺-doped microtoroid when it is pumped around 1430 nm band. The WGM resonator has intrinsic Q values of 4.2×10⁶ in the 1430 nm pump mode and 5.3×10⁶ in the 1550 nm probe mode. The tapered fiber [38], [39], with a waist diameter of approximately 2 μm, is fabricated through the heat and pull process using a single-mode optical fiber operating in the 1550 nm window. The pump laser and probe signal are provided by two tunable laser diodes with linewidths less than 200 kHz. The central wavelengths and scanning speeds of these laser diodes can be precisely controlled by a computer. The light emitted from laser diodes is coupled into the microtoroid through a coupler and tapered fiber. This tapered fiber has a coupling efficiency exceeding 99%, i.e. the normalized transmission can nearly reach zero and more than 99% of input light can couple into the microtoroid when an optical mode is excited resonantly. Moreover, a three-axis stage with resolution 0.1 μm can continuously tune the coupling strength between this taper fiber and the microtoroid. The light coupled out is divided into two parts. One component (constituting 10%) part is connected with an optical spectrum analyzer (OSA), and the other component (constituting the remaining 90% part) is further divided into 1550 nm and 1430 nm bands after passing through a wavelength division multiplexer (WDM). Finally, the light from these two bands are collected by two photon detectors (PDs) and monitored by an oscilloscope. During the entire process, two variable optical attenuators (VOAs) and polarization controllers (PCs) were used to control the input power and polarization, respectively.

Figure 1:

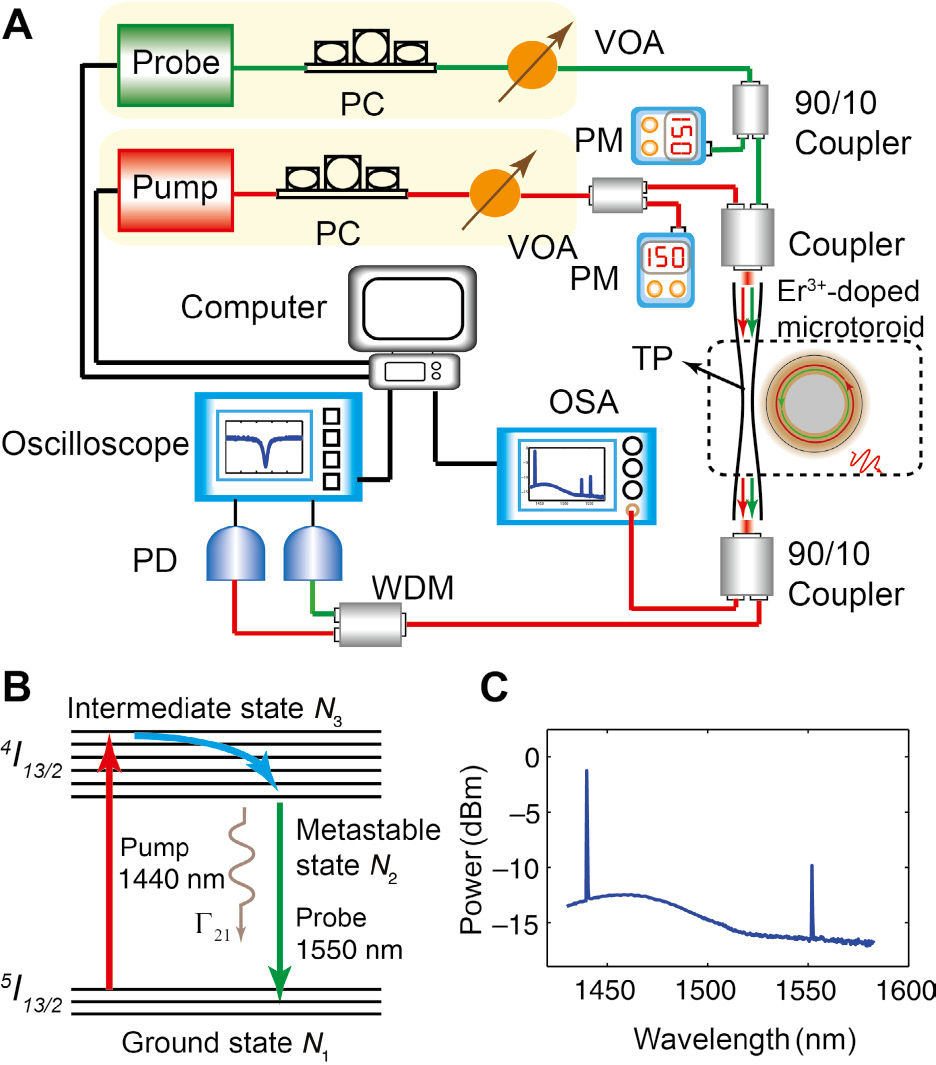
Experimental setup, energy levels and emission spectra of erbium ions.

(A) Experimental configuration for measuring optical gain lifetime. VOA, variable optical attenuator; WDM, wavelength division multiplexer; PD, photodetector; OSA, optical spectrum analyzer; PM, power meter; TP, tapered fiber; PC, polarization controller. (B) The energy levels of erbium ions. Γ₂₁ stands for spontaneous decay rate of erbium ions from metastable states into ground states. (C) Emission spectra of Er³⁺-doped WGM microcavities pumped in the 1430 nm band.

Figure 2 demonstrates the process to measure the lifetime of optical gain. Here, the pump laser in 1430 nm band is linearly modulated at a lower frequency scanning speed 1.2 THz/s, and the frequency scanning speed of the probe signal in 1550 nm band is 4.2 THz/s. The transmission spectrum of this pump laser exhibits triangular broadening due to the optothermal effect, and the probe signal has a standard Lorentz lineshape. Even after being turned off, the pump laser can still provide optical gain for this probe signal after the delay time Δt. Here, we turn off the pump laser within 2 μs through thermal mode squeezing so that the pump laser is off resonance with cavity mode and little light can couple into microtoroid. This mode squeezing is induced by the optothermal effect, where the central wavelength of this pump mode has an opposite shift direction with respect to the input light [30]. As shown in Figure 2A, we continuously tune this probe signal by decreasing. Δt while the pump laser is kept unchanged. The transmission spectra of this probe signal evolve from a Lorentz dip to a Lorentz peak. Note that the measurement in this figure is in the over coupling regime, i.e. the coupling strength between the tapered fiber and microtoroid is greater than the intrinsic dissipation rate of the cavity mode. Figure 2B–I exhibits the changes of these transmission spectra in detail. This process can be divided into three regions: the Lorentz dip region, the transparency region, and the Lorentz peak region. Figure 2B–F corresponds to the Lorentz dip region. In this region, the linewidth of this probe signal becomes increasingly small with the decrease of Δt, and the minimum transmission becomes increasingly high. At the time Δt=2.3 ms, the transmission becomes totally transparent, indicating that the existence of this microtoroid does not cause any loss of the light; that is to say, optical gain provided by erbium ions can completely compensate for the intrinsic loss. The Lorentz peak region is shown in Figure 2H and I, in which this probe signal is amplified, and the transmission is above the normalized line. In this Lorentz peak region, the linewidth of this resonance would continue to decrease, and the peak value becomes increasingly high with the decrease of Δt. The evolution of this probe signal can be described by the differential equation based on the coupled-mode theory [40], [41]:

Figure 2:

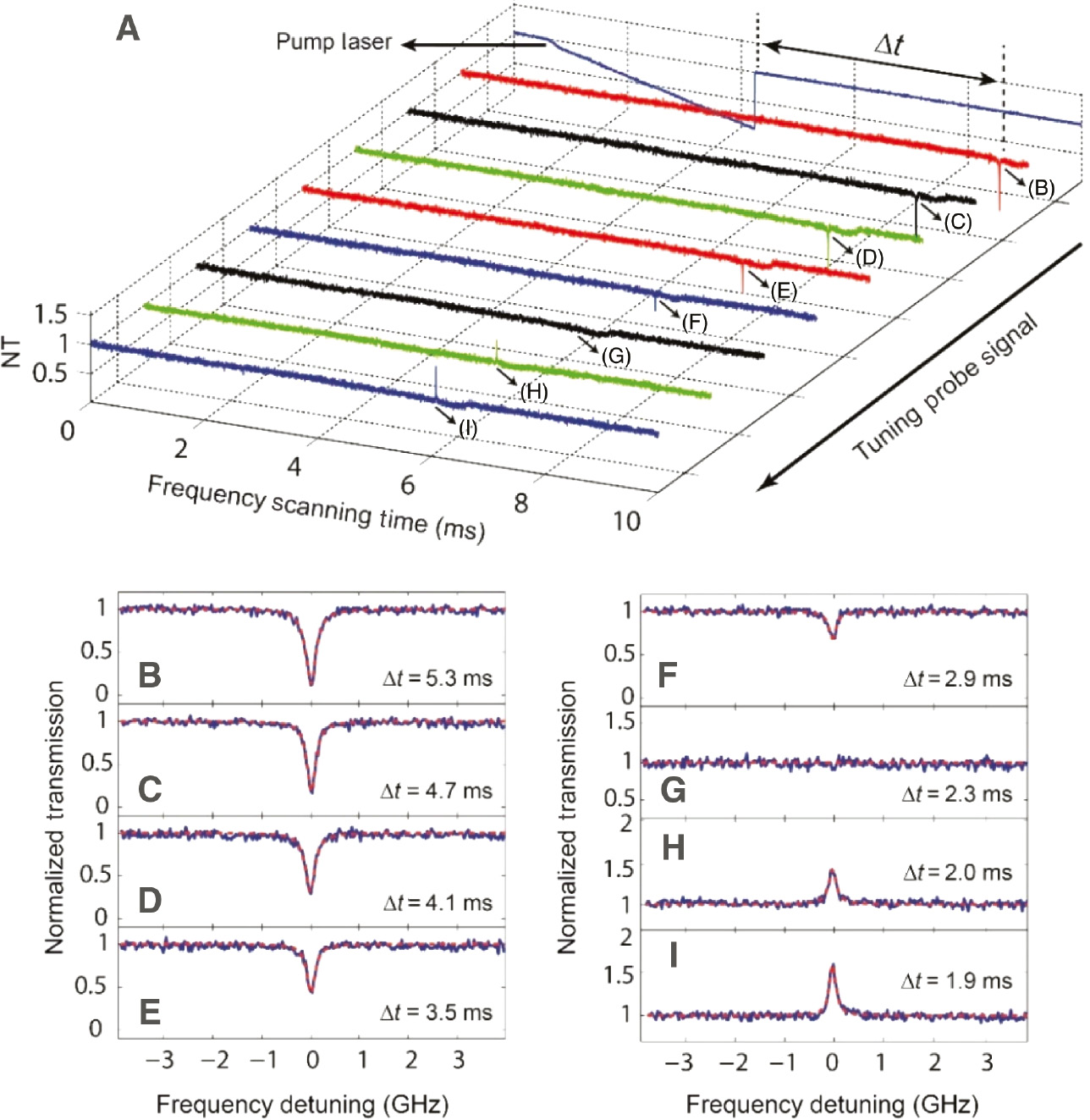
Evolution of the transmission spectra when tuning probe signal.

(A) Evolution of the transmission spectra when measuring the optical gain lifetime. When we decrease the time Δt after the pump laser is turned off, this probe signal become increasingly amplified together with more gains. (B)–(I) Show the details and the fitting curves (red dashed lines) in (A). Note that the horizontal coordinate of (A), i.e. frequency scanning time, has been transformed into frequency detuning in (B)–(I) according to the scanning speed of this probe signal. The pump power here is 275 μW, and the probe signal power is 150 nm. NT denotes normalized transmission.

where a_s describes the amplitude of this probe signal inside the microtoroid, |asin|2 denotes the input power, κs0 is the intrinsic energy decay rate, and κsext represents the coupling strength between microtoroid and taper fiber. g_s is the optical gain provided by the transition of erbium ions from metastable states into ground states. Δω_s(t) is the detuning between the input signal and the central frequency of this probe mode. As this probe signal is linearly modulated at a high scanning speed, g_s can be regarded as a constant when its input power is small enough (Supplementary Figure S6).

Under the steady-state situation, the normalized transmission can be expressed by the following equation using the standard input-output relationship:

Here, κs0−gs can be rewritten as κseff, which denotes the effective energy decay rate after considering the optical gain provided by erbium ions. This transmission is totally transparent under the condition that κs0=gs, while it exhibits a Lorentz dip (or peak) when meeting the condition κs0>gs (or κs0<gs).

Note that when the pump laser is turned off, the temperature of the microtoroid follows an exponential decay. This decay may result in mode squeezing and cause errors in the measurement of optical gains. Therefore, the delay time Δt should be greater than the thermal relaxation time 1/γ_T to avoid this optothermal effect. Here, the thermal relaxation time 1/γ_T of the microtoroid is characterized to be 0.33 ms using the optothermal spectroscopy method (more details are introduced in Supplementary Note 1). During the gain lifetime measurement, the temperature of the microtoroid is always the same as room temperature. Moreover, κsext and κs0 are kept unchanged. Therefore, changes in g_s tend to modify the transmission spectra.

3 Measurement of gain lifetime

Figure 1B shows the energy levels of erbium ions in a standard Λ-type level system. For convenience, the ⁵I_13/2 state is rewritten as the ground state, and the ⁴I_13/2 state consists of both the intermediate state and metastable state. The pump laser in the 1430 nm band excites erbium ions from the ground state into the intermediate state; subsequently, this excitation decays into the metastable state quickly without the emission of photons. In addition, erbium ions in metastable states decay into ground states at a relatively low rate Γ₂₁; the lifetime 1/Γ₂₁ can be as long as several milliseconds [1]. When a rapidly modulated probe signal with scanning speed 4.2 THz/s in the 1550 nm band is coupled into this system, erbium ions in metastable states would jump into ground states and provide optical gain for this probe signal. The gain g_s is determined by the population inversions between these two energy levels [1]:

Here, σse and σsa are the emission and absorption cross sections of a probe signal, respectively; c is the speed of light; n_s denotes the effective refractive index; N₂ and N₁ are the population of erbium ions in the metastable state and ground state within a unit volume, respectively. The condition g_s<0 indicates that the probe signal is absorbed by erbium ions and cannot achieve amplification. If and only if the number of effective erbium ions in the metastable state is greater than that in the ground state, i.e. N2>N1σsa/σse, can the compensation of loss and signal amplification be achieved. Assuming that erbium ions in metastable states decay into ground states at the spontaneous decay rate Γ₂₁, i.e. N2(t)=N2(0)e−Γ21Δt; when the time Δt is infinitely long, then all erbium ions are located in ground states. Moreover, this system satisfies the relationship N₁+N₂=N_total after the pump laser is turned off. Here, the value of N₃ can be regarded as zero when the pump is strong enough. According to Eq. (3), the energy decay rate κEr3+ caused by the absorption of erbium ions if all ions are in ground states could be written as κEr3+=cσsaNtotal/ns.

From Eq. (3) and above analyses, the effective energy decay rate κseff=κs0−gs, which is obtained from the transmission spectrum, can be rewritten as:

In the above expression, κs=κs0+κEr3+, which represents the effective intrinsic losses after considering the absorption of light by erbium ions. gmax=c(σsa+σse)N2(0)/ns, and g_s can be rewritten as gs=gmaxe−Γ21Δt−κEr3+. According to Eq. (2), when we have obtained the transmission spectra of probe signal at different time Δt, the corresponding value of κseff can be read out by fitting these spectra [32], [42]. Meanwhile, it also obeys an exponential decay at the rate of Γ₂₁ through the translation transformation by deleting κ_s, as shown in Eq. (4).

The experimental results are shown in Figure 3. As shown in Figure 3A, gain lifetime at the resonant wavelength 1551 nm is 5.1 ms when the input power of this probe signal is 150 nW; furthermore, if the input power is increased to 230 nW and 310 nW, nearly the same value is obtained (see Supplementary Figure S5). Note that g_s can be regarded as a constant only when the input power is small enough; otherwise, the Fano-like resonance shape may appear [43]. Figure 3B demonstrates experimental results at various resonant wavelengths, which are all around 5.1 ms. From Eq. (4), the lifetime of optical gain is determined only by the spontaneous decay rate from the ⁴I_13/2 state to the ⁵I_13/2 state. Meanwhile, the strength of optical gains is also determined by the absorption and emission cross sections σse and σsa at a specific wavelength. Note that the lifetime of optical gains 1/Γ₂₁ within this ultrahigh Q microresonator is nearly the same as that in free space, i.e. the Purcell factor [44], which describes the enhancement of spontaneous emission inside a resonator, is relatively small. From Fermi’s golden rule, the decay rate Γ₂₁ is determined by the local density of states (LDOS) of ground states. When the transition from ⁴I_13/2 state to ⁵I_13/2 state coincides with one optical mode, the LDOS around this mode is modulated by the microresonator. However, the decay rate caused by total local states within one optical mode after this modulation has slight changes, making the lifetime of optical gains nearly the same as that in free space.

Figure 3:

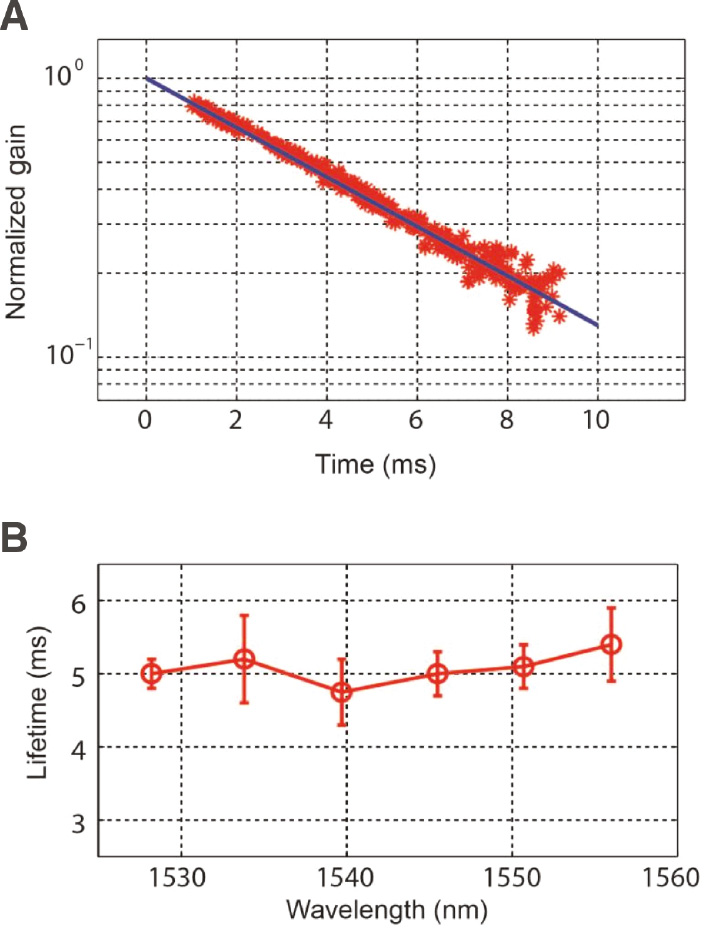
The evolution of gain and gain lifetime at different wavelengths.

(A) Normalized optical gains (κseff−κs)/gmax for a probe signal with input power 150 nW. The parameters after fitting are κ_s=0.189 GHz, and g_max=0.299 GHz. (B) Lifetimes of optical gains at various probe wavelengths.

The population of erbium ions follows a Boltzmann’s distribution when the system is not pumped, i.e. N2/N1=e−ℏωs/kBT, and N3/N1=e−ℏωp/kBT. As the density of erbium ions is fixed, the relationship N₁+N₂+N₃=N_total holds. According to laser rate equations, the evolution is controlled by the following formulas when we consider only the effect of pump laser:

where Γ₃₂ is the transition rate of erbium ions from the intermediate state into the metastable state; this rate is generally larger than Γ₂₁ by three orders of magnitude. ϕ_p is the photon flux, i.e. the number of photons per unit area within a unit time. σpe and σpa are the emission and absorption cross sections of the pump laser, respectively. For WGM microcavities, the photon flux can be expressed as c|a_p|²/(ℏω_pV_pn_p), in which V_p and n_p are the mode volume and refractive index of the pump mode, respectively. For simplicity, we can obtain the behavior of erbium ions quantitatively in steady-state situations by setting the above equations to zero. Furthermore, under the condition Γ₃₂≫Γ₂₁, it is straightforward to determine that N₃/N₂=Γ₂₁/Γ₃₂ and N₂≈N_totalσ_pϕ_p/(Γ₂₁+σ_pϕ_p) (Supplementary Note 2). With increasing pump power, more erbium ions are in the metastable state, and less are in the ground state. As the Q factor of the pump mode is higher than 10⁶, a weak pump can lead to the saturation of the excited states, i.e. N₂≈N_total. This is the origin of many nonlinear behaviors in WGM microcavities.

Figure 4 depicts the behavior of microtoroid and erbium ions using numerical calculations. According to the temperature changes, this figure can be divided into three regions. In Region 1, when little pump laser is coupled into the microtoroid, most erbium ions are in their ground states. Moreover, the temperature remains nearly the same as room temperature. In Region 2, more pump light is coupled into the microtoroid with the decrease of detuning Δω_p, and erbium ions start to make transitions from the ground state into the intermediate state. Furthermore, this region can be divided into saturated and unsaturated areas. In the unsaturated area, population inversions increase sharply. In the saturated area, where the pump is strong enough to satisfy the condition σ_pϕ_p≫Γ₂₁, nearly all the erbium ions are in the metastable state, i.e. N₂≈N_total. In Region 3, when the pump laser is turned off, both the temperature and the number of erbium ions in metastable states exhibit an exponential decay. These two rates obey the relation γ_T/Γ₂₁≈15.45. For N2>N1σsa/σse, optical gain satisfies the condition g_s>0, as shown in blue. In contrast, erbium ions would absorb the input signal when N2<N1σsa/σse and g_s<0; this condition could cause additional losses of light, as shown in gray.

Figure 4:

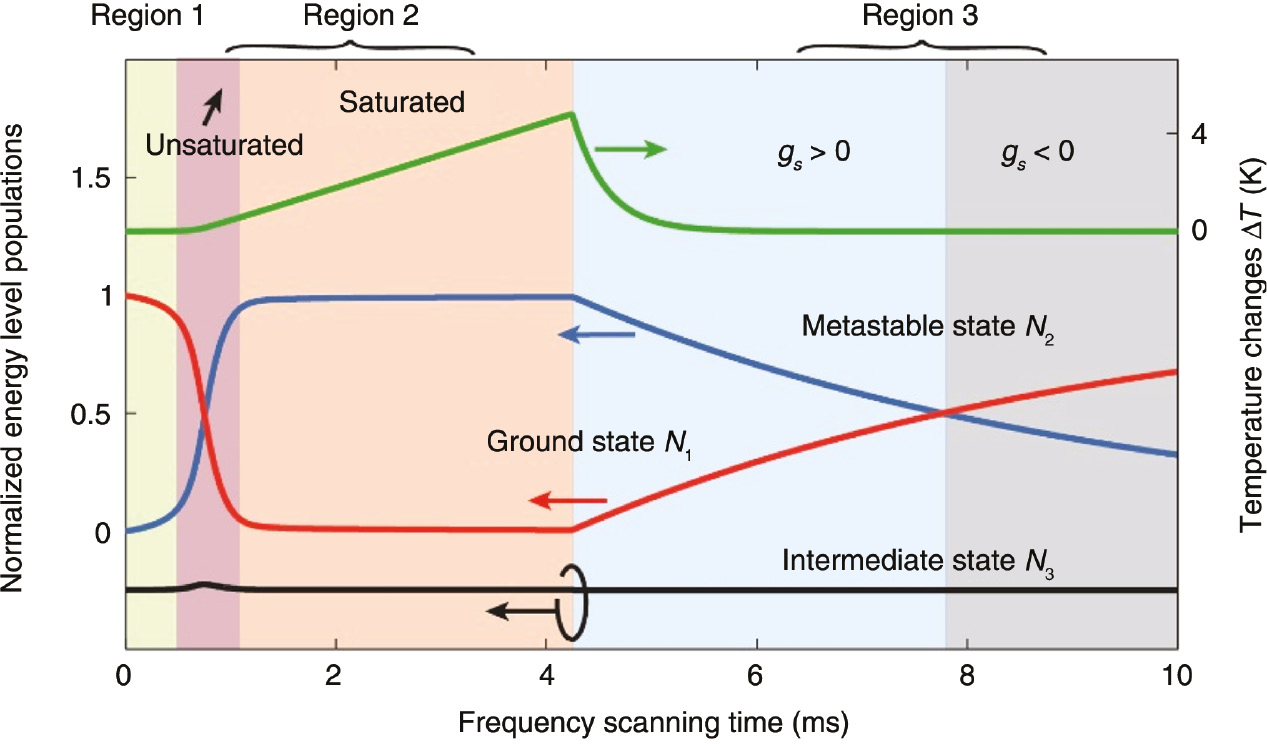
Populations of erbium ions in ground states N₁ (red line), metastable states N₂ (blue line), and intermediate states N₃ (black line), and temperature changes Δt (green line).

Note that the intermediate state population is moved down by 0.25. The parameters are V_mode=367 μm³, σpe=σpa=1.5×10−22cm2, 1/Γ₃₂=9.2 μs, 1/Γ₂₁=5.1 ms, N_total=7.3×10¹⁸ ions/cm³, |apin|2=277 μW,γ_p=1.97×10⁴ W/K, 1/γ_T=0.33 ms, and τ_c=1.17 ps.

As erbium ions are doped into the microresonator, the decay rate Γ₂₁ contains the Purcell effect enhanced spontaneous decay rate F_pΓ_r, the erbium ion energy exchange induced decay rate ΓEr3+, and the non-radiative decay rate Γ_non. Strictly speaking, the lifetime of optical gains and that of fluorescence are different. In this simplified model, we assume that the metastable state is isolated; therefore, they share the same value. However, the metastable state is usually a continuum for real erbium ions, and energy relaxations occur between the internal energy levels. The decay of fluorescence originates from the average transitions from the continuum metastable state into the ground state, and the decay of optical gains corresponds only to the specific transitions between the metastable state and the ground state. Therefore, the lifetime of optical gains and the fluorescence are not exactly the same, although their values may be nearly the same. Our work provides a practical and simple method to precisely measure the lifetime of optical gains at specific wavelengths; such measurements cannot be achieved by the previous PL method. Moreover, this method can reflect the value of the metastable state if neglecting its internal relaxations. Furthermore, when the resonant wavelength of this microtoroid is continuously tuned, the lifetime of optical gain at different wavelengths can also be measured. The tapered fiber coupling used here improves this method’s pump and collection efficiency, which can greatly decrease the demands for detectors and other measurement techniques.

4 Conclusion

In this article, we present the direct measurement of gain lifetime at a specific wavelength through the changes of one optical mode; such a measurement cannot be achieved by the previous PL method. An erbium-doped WGM microresonator was used to show the efficiency of this method. We used six probe signals with the wavelength differences of 5.6 nm (one FSR). All the optical gain lifetime values were found to be approximately 5.1 ms, which is much longer than the thermal relaxation time of 0.33 ms. The method is universal and can be extended to other materials and structures.