Reconfigurable epsilon-near-zero metasurfaces via photonic doping

1 Introduction

Metasurfaces are 2D (flat optics) devices composed of arrays of subwavelength elements with spatially varying phase, magnitude, and polarization responses [1]. They enable the control of the wavefront characteristics, with multiple functionalities including the manipulation of the usual refraction laws [2], [3], focusing [4], [5], cloaking [6], generating optical illusions [7], providing polarization control [8], or even performing mathematical operations [9]. Based on this principle, a number of practical devices have been demonstrated, including metalenses [10], [11], holograms [12], and quarter-wave plates [13], with performance comparable to those of conventional optical components. A more in-depth analysis of metasurfaces and their principle of operation and technological applications can be found in excellent reviews on the topic [1], [14], [15], [16], [17].

Inspired by the success of (passive and static) metasurfaces, the next generation of flat optic devices points toward a dynamic control of the wavefront. If possible, a real-time shaping of the wavefront will have a groundbreaking impact on holography and lidar technologies. For this reason, substantial efforts are being devoted to the development of dynamic metasurfaces, where the properties of their constituent unit cells are reconfigured with the use of electric [18], [19], optical [20], thermal [21], [22], magnetic [23], [24], and mechanical [25] actuators. In analogy with digital electronic systems, further evolutions of this concept might also lead to digital [26] and programmable [27] metamaterials and metasurfaces, into which different functionalities are encoded.

Here, we numerically investigate the potential of epsilon-near-zero (ENZ) media, i.e. a medium with near-zero permittivity [28], [29], [30], [31], for the development of reconfigurable metasurfaces. Previous works on ENZ metasurfaces have exploited their exotic properties to obtain highly directive beams [32], [33], perform beamforming and beamsteering tasks [34], [35], [36], [37], [38], and enhance their nonlinear response [39], [40], [41], [42]. Moreover, electrically tunable ENZ metasurfaces [18] have been demonstrated by exploiting the fact that the ENZ point lies at the transition between metal (opaque) and dielectric (transparent) responses. Here, we adopted a different approach to reconfigurable ENZ metasurfaces, which takes advantage of the peculiar behavior of particles immersed in ENZ media. In fact, we recently demonstrated that 2D particles immersed in a 2D ENZ medium behave as photonic “dopants”, which modify the effective permeability of the host while maintaining a near-zero permittivity [43]. This effect, we labeled as photonic doping, implies that the macroscopic parameters of a body can be reconfigured with a few and arbitrarily located particles.

Several aspects of the photonic doping theory might provide unique opportunities in the design of reconfigurable metasurfaces. (i) The effective medium description holds independently of the size of the unit cell. This implies that the response of a large metasurface can be controlled with one or very few actuators. (ii) The effective medium description also holds independently of the size, number, and/or position of the particles. This freedom in the geometry of the actuators can facilitate their integration. (iii) The effective material description is exact in the sense that it exactly recovers the same external fields at any point of space (even close to the external boundary). Therefore, one can benefit from all the properties of extreme material parameters such as epsilon-and-mu-near-zero (EMNZ) media and perfect magnetic conductor (PMC). (iv) The photonic doping theory is also valid for any shape of the host medium and/or unit cells, which could be exploited in the design of conformal or flexible metasurfaces.

Therefore, there is an obvious synergy between photonic doping and reconfigurable metasurfaces, which is the primary focus of this manuscript. The remainder of the paper is organized as follows: in Section 2, we reviewed the concept of photonic doping and explored its possibilities to modify the transmission spectra of ENZ metasurfaces. Then, the transient analysis of ENZ metasurfaces is carried out in Section 3, which clarifies and highlights the causality aspects related to ENZ media and the theoretical lossless ENZ limit. Then, different reconfigurable mechanisms are investigated in Section 4. To finalize, conclusions and future directions are discussed in Section 5.

2 Photonic doping of ENZ metasurfaces – a brief review

We start our discussion by considering the ENZ metasurface schematically depicted in Figure 1A. In particular, the metasurface is composed of an ENZ (ε_h≈0) slab periodically loaded with (infinitely long) 2D dielectric rods of radius r_p and relative permittivity ε_p, forming unit cells of size L_x×L_y. The photonic doping theory demonstrates that the response of this system can be described via effective permittivity ε_eff and permeability μ_eff regardless of the size of the unit cell and/or the cross-section of the dielectric rods [43]. Specifically, the effective permittivity of the ENZ host continues to be approximately zero ε_eff=ε_h≈0, whereas its effective permeability is given by the addition of the contributions from each of the particle/dopants μ_eff=1+∑_pΔμ_p as if there were no interaction between them [43]. Moreover, the contribution from each particle is independent of its position: Δ μp=1A (∫Apψ(r)dA−Ap), where ψ(r) is a function corresponding the solution to the scalar Helmholtz equation within the particles, subject to the boundary condition ψ(r)=1 (see Ref. [43] for more details and derivation).

Figure 1:

Transmission-reflection spectra of ENZ metasurfaces with photonic doping.

(A) Sketch of the geometry: ENZ metasurface composed of rectangular unit cells of size L_x=1λ_p, L_x=2λ_p containing a 2D dielectric rod of radius r_p=0.122λ_p and relative permittivity ε_p=10. The ENZ slab is modeled using a dispersive Drude model: εh=1−ωp2/(ω2+iωωc) with ω_c=0.03ω_p. (B) Transmission and reflection spectra. Comparison between the results obtained with a full-wave numerical simulation [44] of the ENZ metasurface (solid) and its homogeneous equivalent with effective permittivity ε_eff and permeability μ_eff parameters (dashed). (C) Snapshot of the magnetic field distribution (z-component) at the EMNZ (ω=1.005ω_p) and PMC (ω=0.993ω_p) frequencies.

By definition, the concept of photonic doping operates in a finite bandwidth where the host relative permittivity is sufficiently small (ε_h≈0). However, this bandwidth can be enough to accommodate narrower resonant effects and thus engineer the frequency dispersion of the metasurface. To assess the dispersive response of ENZ metasurfaces, we characterize ENZ host with a Drude-like dispersion model: εh(ω)=1−ωp2/(ω2+iωωc), where ω_p stands for the plasma frequency, at which the ENZ response takes place, and ω_c is the collision frequency, accounting for dissipation losses. Hereafter, we set ω_c=0.03ω_p in accordance with physical realizations of ENZ media in the mid-IR [45], [46]. However, we will also theoretically consider progressively smaller losses to investigate the convergence of the system response toward the theoretical lossless ENZ limit.

It is clear from the aforementioned properties that photonic doping is essentially different from conventional effective medium theories. In addition, the flexibility in geometry it provides (size, shape, and position of the particles and unit cell while allowing for homogenization) might provide new degrees of freedom in the design of metasurfaces. For instance, of particular interest is the case in which the dielectric rods are large enough to be resonant near the ENZ frequency. In this specific case, the response of the ENZ metasurface can be described via dispersive effective material parameters given by

and

It is clear from Equation (2) that doping with resonant dielectric rods results in effective permeability with a Lorentzian dispersion profile, where the resonance frequency corresponds to the rod’s monopolar resonance (ω_0m such that J0(ω0mcεp)=0) and a plasma frequency also determined by the rod geometry ωpm=ω0m2+2πc2Ah−1. Expressions for the effective parameters (1) and (2) and their relevant plasma and resonance frequencies are found by taking Taylor series of Δ μp=1A(∫Apψ(r)dA−Ap) around the rod’s resonance frequency [43]. In addition, we introduce a phenomenological magnetic damping frequency ω_cm to account for dissipation in the ENZ host due to the rod scattered fields and set its value to ω_cm=0.25ω_p to fit the numerical simulations. We emphasize that, in this case, the effective medium description holds in the vicinity and even at the particle resonance.

The transmission and reflection spectra of the proposed configuration were computed with a full-wave numerical solver [44] and it is depicted in Figure 1B. It can be concluded from the figure that the transmission spectrum is characterized by a minimum-maximum sequence. This Fano-like response could be explained as the interference between the broadband response of the ENZ slab and the narrowband response of the rod resonance. However, the transmission spectrum can be more clearly elucidated by means of the effective material parameters obtained in accordance with the photonic doping theory. We emphasize that this description is more comprehensive as it provides an exact representation of the fields external to the metasurface [43]. First, minimum transmission takes place at the resonant frequency ω=ω_0m=0.993ω_p, where the permeability is maximized. Thus, the slab behaves close to a PMC, i.e. a magnetic mirror, opaque to the incident waves, which minimizes the magnetic field (and maximizes the electric field) on its surface (see Figure 1C). Second, the maximum transmission corresponds to the antiresonance frequency ω=ω_pm=1.005ω_p, where the effective permeability approaches zero. Thus, the response of the slab is effectively similar to that of an EMNZ medium. This material is known to exhibit the so-called EMNZ tunneling [47] (in theory, perfect transmission with zero-phase advance), whose signature here is a transmission peak and whose value is determined by the loss of the ENZ host.

As a crosscheck of our effective material parameter description, Figure 2 includes a comparison of the effective material parameters obtained via numerical extraction methods [48] and those predicted by the photonic doping theory. It can be concluded from the figure that there is an excellent agreement between both numerical and theoretical values in a bandwidth around the ENZ frequency before the effective material description breaks down at higher frequencies. In addition, this analysis confirms that the effective permittivity is not changed by the rods, although they induced a Lorentzian effective permeability.

Figure 2:

Comparison between the effective (A) permittivity and (B) permeability, obtained via numerical parameter extraction from the reflection/transmission coefficients (dashed), and their theoretical values (solid).

Numerical values are obtained with the method reported in Ref. [48]. Theoretical values correspond to a permittivity following a Drude model: ε(ω)=1−ωp2/(ω2+iωωc) with ω_c=0.03ω_p, and a permeability following a Lorenztian model: μ(ω)=(ω2−ωpm2+iωωcm)/(ω2−ω0m2+iωωcm) with ω_0m=0.9935ω_p, ω_pm=ω_p, and ω_cm=0.25ω_c. The comparison illustrates how the numerical and theoretical values agree over a bandwidth around the plasma frequency before the effective model description breaks down at higher frequencies.

Thus, we find that doping the ENZ metasurfaces with resonant dielectric rods enables nontrivial modifications of its transmission spectrum, inducing Fano-like resonant response associated with extreme materials responses such as EMNZ and PMC media. This strongly frequency-dependent feature points toward a dynamic and reconfigurable metasurface that switches between opaque and transparent modes. Different strategies for reconfiguring the response of this metasurface are investigated in Section 4. This system might also find applications as a sensing platform, where local small changes on the properties of the dielectric rod results in amplified changes in the macroscopic response of the system (i.e. the transmission coefficient).

3 Transient analysis of ENZ metasurfaces

Exotic wave phenomena related to ENZ media usually raise questions about their causality aspects. After all, how can a zero-phase advance be sustained over arbitrarily long distances? Furthermore, if the response of the system is independent of the position of the particles, could we not move the particles further and further away until the delay becomes significant? If the group velocity is zero in lossless ENZ media [49], how does the wave goes through the material? All these questions and related concerns can be addressed with the same answer: these wave phenomena take place when a finite-size system is in steady state (i.e. after its transient response has passed). In this manner, a given transient time first passes before these steady-state effects are constructed, where all constrains imposed by causality and passivity are satisfied. Naturally, the more extreme the geometry is (e.g. the larger the area of the ENZ medium is or the further way the particles are), the longer it will take for the system to reach steady state. We note that similar questions concerning causality were raised at the beginning of negative-index metamaterial research, which were satisfactorily answered with the analysis of their transient response [50].

Therefore, here we further clarify the causal response of ENZ metasurfaces by carrying out a transient analysis of EMNZ tunneling enabled by photonic doping. To this end, we excite the configuration studied in Figure 1 with an ON-OFF pulse characterized by temporal profile:

with ω₀=ω_p and T_ON=100T₀ and T_ON=1000T₀ with T₀=2π/ω₀. This particular pulse shape has been selected so that our numerical simulations illustrate a complete cycle of interaction in which (i) the incident signal is turned on, (ii) the steady state is reached after a transient time, and (iii) the input signal is turned off and the energy stored in the systems progressively exits it. We numerically compute the transmitted signal by transforming the incident signal, given by Equation (3), into the frequency domain, applying the transmission coefficient obtained with a full-wave numerical solver [44] and applying the inverse Fourier transform. The slab parameters (L_x=1λ_p, L_y=2λ_p, ε_p=0.122λ_p, and r_p=0.122λ_p) are selected so that the system effectively exhibits EMNZ tunneling exactly at its plasma frequency.

Figure 3 depicts the temporal profiles of the incident (blue) and transmitted (red) signals for different amounts of loss as prescribed by the collision frequencies ω_c=0.03ω_p, ω_c=0.01ω_p, ω_c=10⁻⁴ω_p, and ω_c=10⁻⁶ω_p. In doing so, we investigate the response of the system as it theoretically approaches to the lossless ENZ limit. In all these cases, we observe qualitatively similar dynamics. First, the input signal starts around T_ON and the transmitted signal progressively starts to grow and be constructed via multiple reflections. Interestingly, even when dissipation losses approach zero, the response of the system remains overdamped and no oscillations of the envelope are observed in the transmitted signal during transient time. We ascribe this effect to the dampening produced by radiation losses associated with the transmitted and reflected signals. Subsequently, steady state is reached and the amplitude of the transmitted signal stabilizes, so that it approximately behaves as a monochromatic signal. In this interval, the transmission coefficient can be identified based on the magnitude and delay between the incident and transmitted signals. Crucially, as dissipation losses approach zero, the response of the system converges to the same signal, which can be identified as the lossless (in the material sense) response of the system. Interestingly, as shown in the bottom right inset of the figure, the steady-state response of the system in this lossless limit corresponds to unit transmission with zero-phase advance, as expected from EMNZ tunneling. We note that although the group velocity vanishes in the lossless ENZ limit, this quantity plays no significant role in this scenario due to the finite size of the system. Finally, around T_OFF, the incident signal is switched off. In this manner, the transmitted signal decays exponentially as the stored energy (due to the resonant nature of the transmission) leaves the system.

Figure 3:

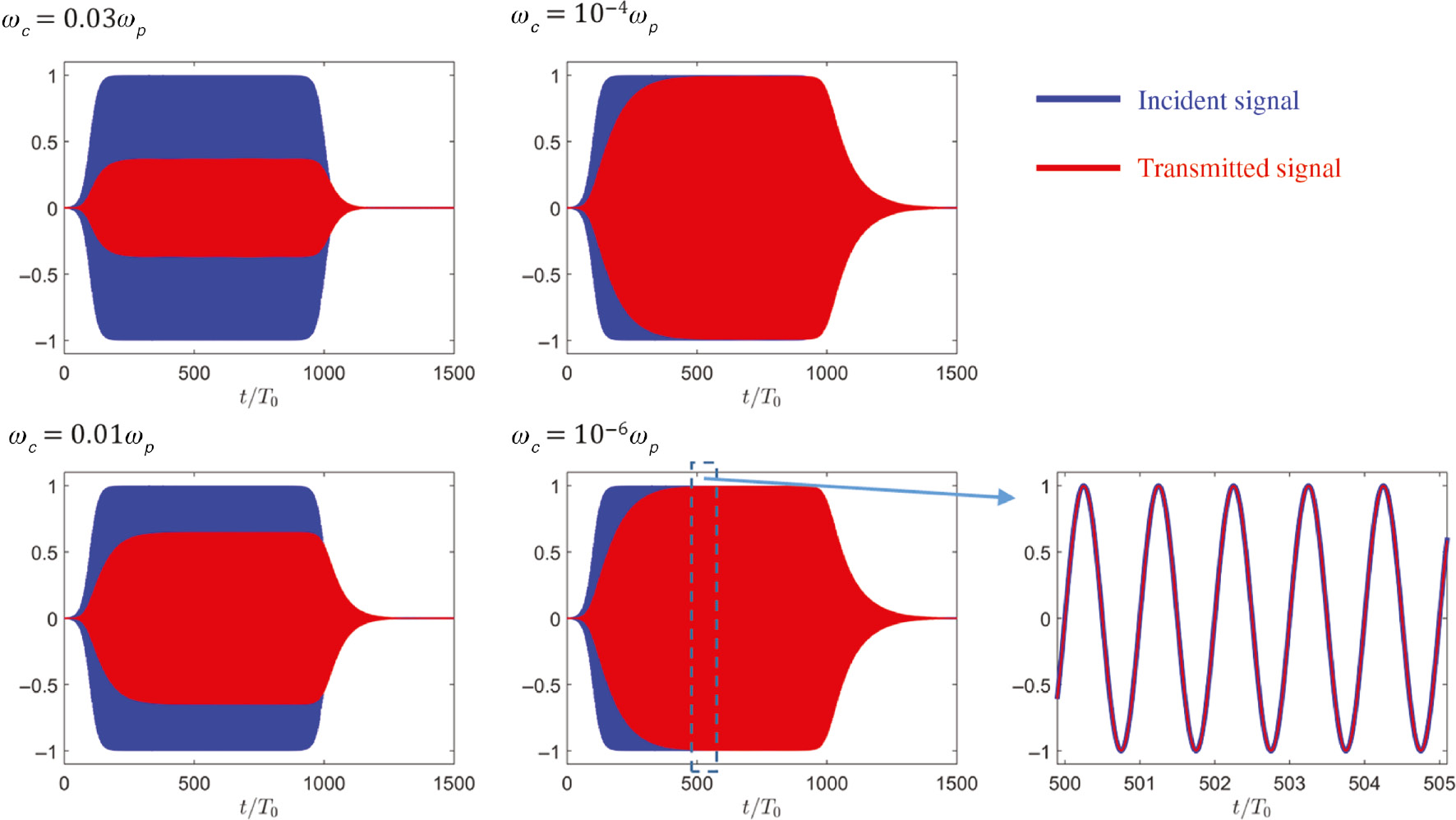
Transient response of ENZ metasurfaces with photonic doping.

Incident (blue) and transmitted (red) signals passing through an ENZ metasurface, photonically doped with a 2D dielectric rod discussed in Figure 1, for four increasingly small amounts of loss as prescribed by the collision frequencies ω_c=0.03ω_p, ω_c=0.01ω_p, ω_c=10⁻⁴ω_p, and ω_c=10⁻⁶ω_p. The incident signal corresponds to the ON-OFF pulse described in Equation (3). Numerical simulations describe how the tunneling effect is established after a transient time is passed once the incident pulse is switched on and how the energy of the system is released after the pulse is switched off. The right bottom inset includes a zoom-in on the incident and transmitted signals once the steady state of the system has been established. The steady-state response of the system is characterized by EMNZ tunneling, i.e. near-unity transmission with zero-phase advance.

Despite its simplicity, our numerical example serves to highlight and clarify the main aspects related to the transient response of ENZ metasurfaces: (i) how an output signal with zero-phase variation is constructed during the transient process, (ii) how energy can be transmitted through a finite-size ENZ body even if the medium exhibits zero group velocity in the lossless limit, and (iii) how the response of the system smoothly converges to the lossless ENZ response as dissipation losses decrease.

4 Reconfigurable mechanisms

The fact that the response of the metasurface can be controlled with a single or a very diluted mixture of randomly located particles suggests exciting possibilities in the development of reconfigurable metasurfaces. First, the fact that the unit cell composing the metasurfaces can span several wavelengths will reduce the number of reconfiguring units. Second, as the particles themselves can be made large too, extra space can be used to include a tuning device. Third, the fact that the response of the system is independent of the position of the particles might ease some potential fabrication constraints and facilitate its integration. In this section, we provide a number of numerical examples to illustrate the potential of different reconfigurable mechanisms for ENZ metasurfaces.

4.1 Dielectric rod actuator

Conceptually, the most straightforward approach to tune the response of the metasurface is to directly change the characteristics of the dielectric rod, i.e. its permittivity ε_p and radius r_p. Figure 4 gathers a parametric analysis of the transmission coefficient as a function of the permittivity and radius of the dielectric rod for the configuration studied in Figure 1, for different amounts of loss characterized by the collision to plasma frequency ratio ω_c/ω_p. Intuitively, increasing the rod permittivity and/or radius (while keeping the operating frequency fixed) is similar to increasing the frequency of operation (for a given rod permittivity and/or radius) in Figure 1B. Therefore, we find from Figure 4 that as the rod permittivity and/or radius is increased, the transmission coefficient undergoes a minimum-maximum transition, associated with the PMC and EMNZ points, similar to what was observed in its spectrum in Figure 1B. More quantitatively, it is found that for low loss it would be possible to switch the metasurface from opaque (T_min=0.002) to transparent (T_max=0.993) configurations with a small percentage change of the rod permittivity, Δεp(%)=2(εp(Tmax)−εp(Tmin))(εp(Tmax)+εp(Tmin))100=1.64%. The same effect is obtained by changing the rod radius, jumping from T_max=0.994 to T_min=0.003 with a Δr_p=0.84% change. Naturally, as dissipation loss in the ENZ host increases, the transmission resonance broadens and the transmission peak value reduces, eventually diminishing the metasurface reconfiguration capabilities. However, our numerical analysis demonstrates that with realistic material parameters (such as ω_c=0.03ω_p for SiC [45], [46]), it is possible to switch the transmission coefficient from T_max=0.427 to T_min=0.081 with a Δε_p=2.62% permittivity change (or switch from T_max=0.428 to T_min=0.082 with a Δr_p=0.31% radius change).

Figure 4:

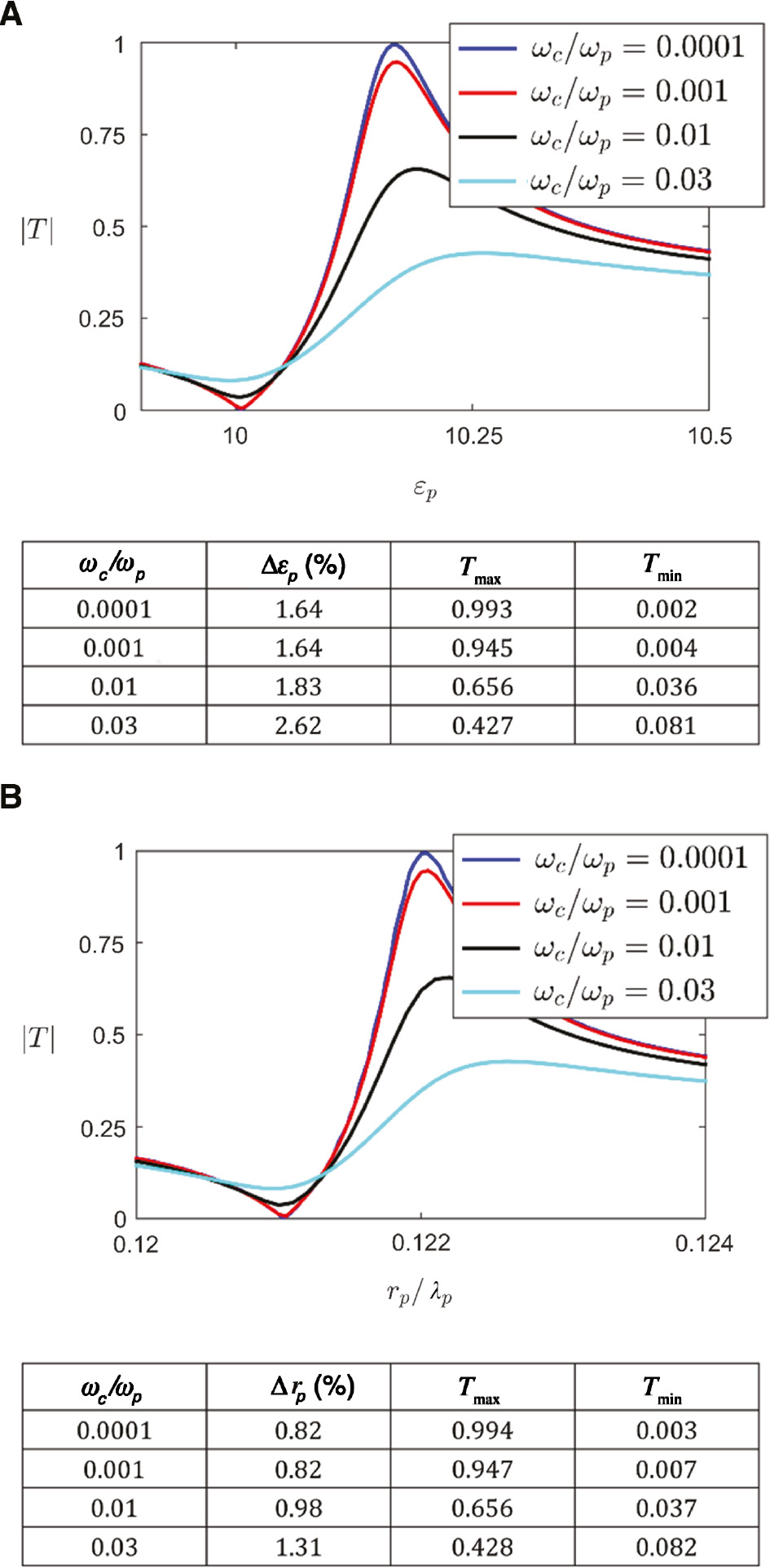
Switching ENZ metasurfaces photonically doped with a single actuator.

Transmission coefficient as a function of variations of the rod (A) permittivity (with r_p=0.121λ_p fixed) and (B) radius (with ε_p=10 fixed) for different amounts of loss. Inset tables include data for the maxima and minima transmission coefficients and the percentage permittivity and radius variation between them. The geometry of the metasurface corresponds to the system analyzed in Figure 1. The numerical simulations illustrate the possibility of switching on and off the transmission through an ENZ metasurface with small percentage variations of the characteristics of the particles.

These numerical results provide a first quantitative estimation of the order of magnitude of the quantities involved. However, these configurations are not optimized and a better performance will be obtained with more sophisticated designs (for example, using a heterogeneous rod or a different rod cross-section). Different strategies could also be used in practice to implement these permittivity and radius changes. On the one hand, nonlinear materials (e.g. Kerr-effect [51] and phase change [21], [52], [53], [54] materials) can provide permittivity changes. Here, a design procedure for the reconfigurable metasurface might include integrating the nonlinear medium in the regions within the dielectric rod where the electric field is maximized (i.e. at the boundary of the dielectric rod), so that the interaction of the nonlinear material with the incoming light is maximized. Interestingly, we note that as the response of the metasurface is independent of the position of the rod, its response will remain reciprocal even if it is nonlinear and with a highly asymmetric geometry. On the other hand, changes in the rod radius could be induced via thermal expansion. Again, one could directly use a homogeneous rod or take advantage of a heterogeneous rod, in which the dielectric rod is covered by a material with a large thermal expansion coefficient. The design of these reconfigurable mechanisms is specific to each one of them and left for future efforts.

4.2 Microfluidics

One can also take advantage of the fact that, within the photonic doping paradigm, the description with effective parameters holds even for particles with a size comparable to the wavelength of operation. This enables the use of low relative permittivity resonators, with potential application in microfluidics. For example, we could consider the extreme case in which the dielectric rod is actually a resonant vacuum (or air) channel (ε_p=1, r_p=0.381λ_p). Then, a liquid could circulate through this channel, increasing the value of ε_p. Ideally, the transmission through the metasurface should be switched from minimum to maximum with small permittivity values. Figure 5B depicts the magnitude of the transmission coefficient as a function of the channel permittivity for this configuration. Again, the response of the system is characterized by a minimum-maximum transition, switching from T_min=0.048 to T_max=0.403 as the permittivity is increased from ε_p=1 (vacuum) to ε_p=1.15. Therefore, these numerical simulations confirm that the ENZ metasurface can operate even when hosting relatively large (r_p=0.381λ_p) and low-permittivity resonators. Interestingly, the system can still be described with effective parameters. This effect is illustrated by the behavior of the transmission coefficient shown in Figure 5B as well as in the field distributions depicted in Figure 5C, corresponding to the (lossy) PMC and EMNZ points.

Figure 5:

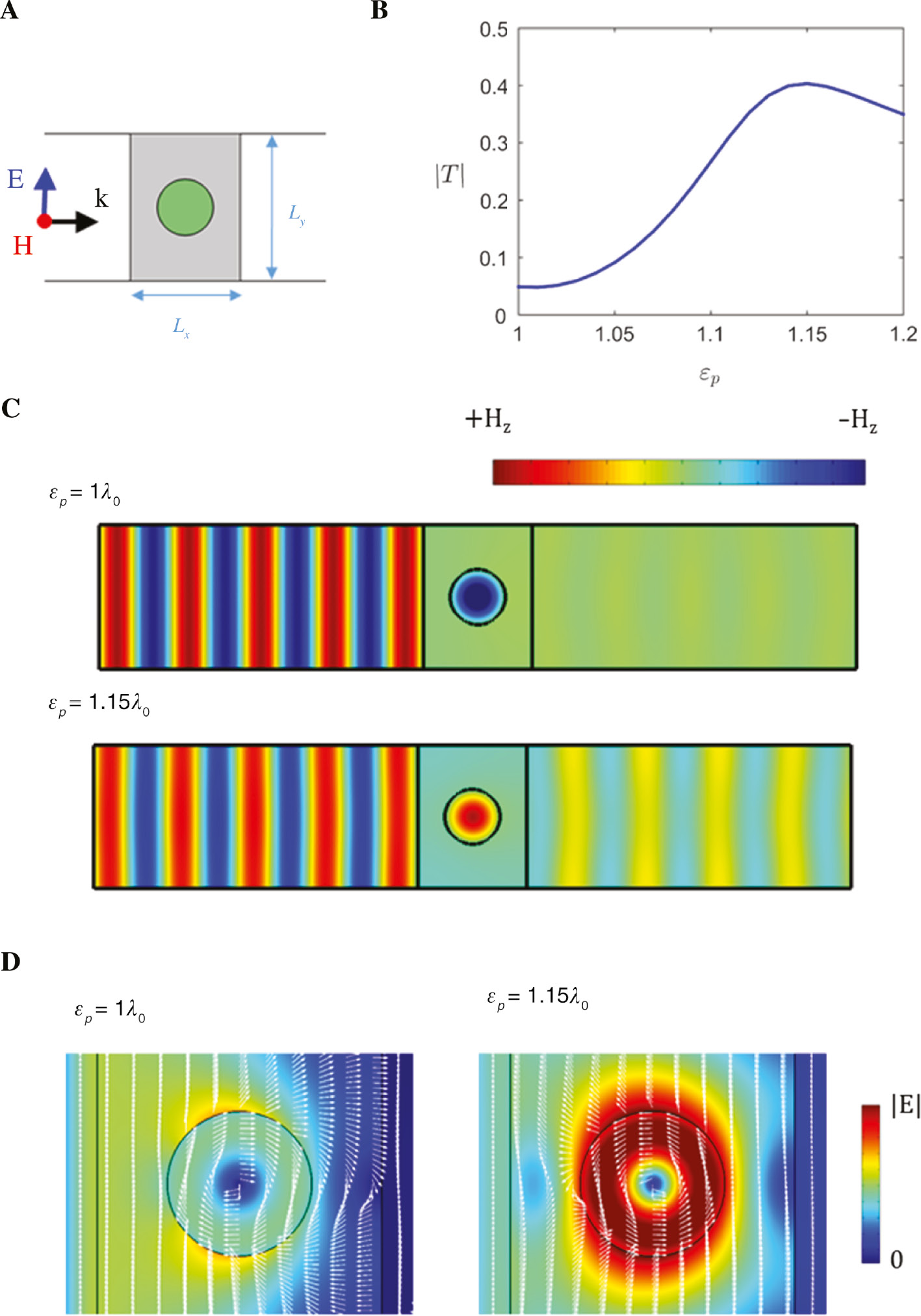
ENZ metasurfaces for microfluidics.

(A) Sketch of the geometry: ENZ metasurface composed of rectangular unit cells of size L_x=1.5λ_p, L_x=2λ_p containing a vacuum (or air) rod of radius r_p=0.381λ_p. We assume that a fluid with low-permittivity ε_p flows along the rod axis facilitating its inspection with an external field. (B) Transmission coefficient as a function of the relative permittivity of the fluid. (C) Snapshot of the magnetic field distribution for ε_p=1 and ε_p=1.15 corresponding to the minimum and maximum of transmission, respectively. (D) Electric field distribution (color map of the field magnitude and normalized vectorial plot) characterized by resonantly enhanced circulating fields within the microfluidic channel.

Other aspects of ENZ metasurfaces might also be of interest for microfluidics. In particular, inspecting the electric field distribution on the channel (see Figure 5D) reveals that it is dominated by a resonantly enhanced and circulating (divergence-free) field distribution. We remark that this effect is qualitatively different from the usual enhancement of localized electric fields (e.g. nanoantennas or plasmonic nanoparticles [55], [56]), which rely on charge accumulation and thus exhibit field lines arising from the boundaries of the particles. In contrast, here we have a localized and enhanced electric field that nevertheless preserves a divergence-free characteristics near the boundary of the channel. This strong circulating electric field could be used to manipulate the particles flowing through the channel with via the optical forces exerted by them. Due to its circulating character, gradient forces would trap the particles within a closed-loop path. One can envision how this effect could be used to link the orbital angular momentum of the particles flowing through the channel to their interaction with the incoming light.

4.3 Mechanical actuators

A dynamic control of the characteristics of the particles within the ENZ metasurface could also be implemented via changes on their geometry induced by mechanical actuators. As an example, we consider the case in which the dielectric rod (ε_p=10, r_p=0.114λ_p) is itself immersed in a vacuum channel of twice its radius (ε_c=1, r_c=2r_p). We assume that a mechanical actuator will allow us to shift the position of the rod from the center to the boundary of the vacuum channel. Due to symmetry considerations and the preferred excitation of the monopole mode, the direction in which the dielectric rod is shifted from the center of the vacuum channel has a negligible impact on the performance of the system. Figure 6 depicts the predicted transmission coefficient as a function of the position of the dielectric rod. It can be concluded from the numerical simulation that switching the rod position from the center (d=0r_p) to the side (d=0.95r_p) of the vacuum channels shifts the transmission coefficient from T_max=0.5 to T_min=0.036.

Figure 6:

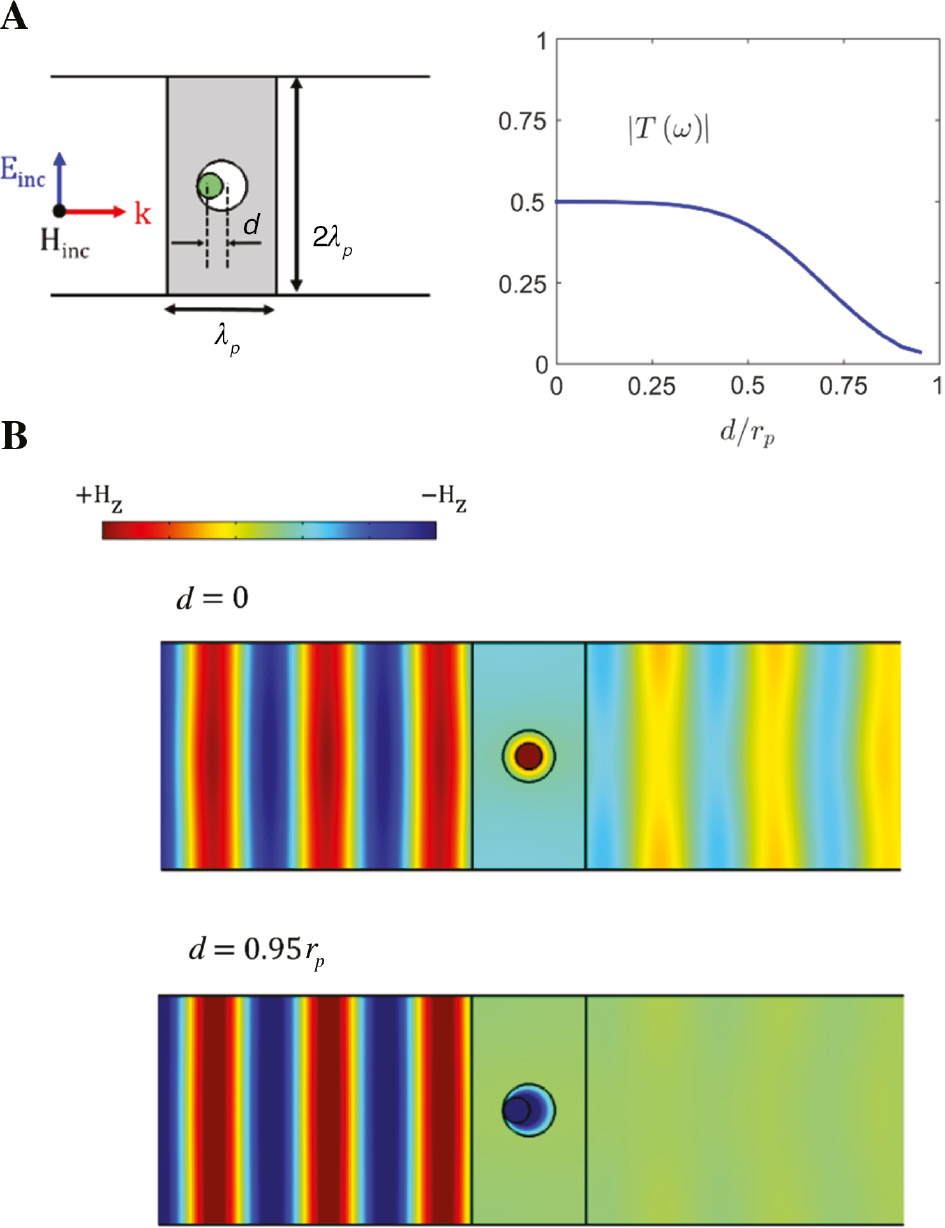
Tuning ENZ metasurfaces photonically doped with mechanical actuators.

(A) Sketch of the geometry: ENZ rectangular unit cell of size 2λ_p×λ_p containing a dielectric rod of radius r_p=0.114λ_p and relative permittivity ε_p=10, which is located within a vacuum rod of radius 2r_p. The transmission of the metasurface is modulated by shifting the position of the dielectric rod a distance d from the center of the vacuum rod. Magnitude of the transmission coefficient as a function of the position of the dielectric rod. (B) Snapshot of the magnetic field distribution at the position for the positions (B-top) d=0 (maximal transmission) and (B-bottom) d=0.95r_p (minimal transmission). The numerical simulations illustrate the possibility of modulating the transmission coefficient from 0.5 to nearly 0 with the use of a mechanical actuator.

Interestingly, the performance in this case is better than that reported in Section 4.1 for the homogeneous dielectric rod. In particular, the top transmission coefficient is 7% larger than in the homogeneous case. This enhancement in the performance can be explained by inspecting the fields excited in the structure (see Figure 6B). It can be concluded from the figure that the air gap around the rod acts as a separation between the resonant cylinder and the dielectric host. This separation enhances the decoupling between the resonator and ENZ host fields, reducing the power dissipated in the ENZ host and increasing the quality factor of the resonant transmission. Overall, this result illustrates the possibility of optimizing the performance of the system with the electromagnetic design of the actuator, which may have potential applications in microelectromechanical and nanoelectromechanical devices.

5 Conclusions

We investigated theoretically the reconfigurable capabilities of ENZ metasurfaces augmented with resonant dielectric rods. Using the photonic doping theory, we showed that the transmission spectrum of this metasurface is characterized by a Fano-like resonance, whose minima and maxima features correspond to PMC and EMNZ material responses. This spectral response can be reconfigured by changing the properties of the particles, which benefit from the rapid spectral variation between opaque (PMC) and transparent (EMNZ) conditions. We analyzed several reconfigurable mechanisms, illustrating how their implementation could benefit from the fact that both the unit cell and the particles can be larger than the wavelength while still preserving the description with effective parameters.

Future investigations might consider doping the metasurface with rods of different sizes and characteristics, which will enable more complex spectral responses that can be harnessed to further enhance the reconfiguration performance. In addition, because photonic doping works independently of the shape of the ENZ host, future investigations could take advantage of this property to develop conformal or even flexible dynamic metasurfaces.