Abstract
This study examines many innovative topological numbers and establishes mathematical interpretations for boron clusters and borophene coverings. The general Randic index, arithmetic index, and Albertson index are discussed in this work for the alpha sheets of boron clusters. Boron cluster sheets are two-dimensional boron atom-based formations called borophene. They are similar to the two-dimensional sheet known as graphene, which is composed of carbon atoms arranged in a hexagonal lattice. The unique electrical, mechanical, and thermal properties of borophene make it a sought-after substance for a variety of uses, such as catalysis, energy storage, and electronics. There are two ways to manufacture borophene: chemical vapour deposition and molecular beam epitaxy. Degree-based topological numbers are a great example of a molecular descriptor that provides information on the connection of atoms in a molecule. These descriptions are based on the notion of a node’s degree in a molecular network, which indicates the number of neighbouring atoms that are directly connected to that node.
1 Introduction
Two-dimensional boron atom-based structures known as borophene include boron cluster sheets. They resemble graphene, a two-dimensional sheet made of carbon atoms that are organised in a hexagonal lattice. Due to its distinctive electrical, mechanical, and thermal characteristics, borophene is a desirable material for a wide range of applications, including catalysis, energy storage, and electronics. Molecular beam epitaxy and chemical vapour deposition are the two methods that can be used to synthesise borophene. Different boron atom layouts, including triangular, honeycomb, and rectangular patterns, can be achieved to produce borophene sheets [1,2,3].
Although there is still much to learn about the characteristics and prospective uses of borophene, several encouraging findings have already been made. For instance, it has been demonstrated that borophene possesses excellent electrical conductivity and may be utilised to make transparent and stretchable conductive films. It might potentially be used as a catalyst for numerous chemical processes and in energy storage systems [4,5,6,7]. Additional information on the boron cluster sheet, known as borophene, may be obtained to gain a more comprehensive understanding of its physical and chemical characteristics, as well as its many uses [8,9,10,11,12,13,14,15].
A prime instance of a molecular descriptor that offers details on the connectivity of atoms in a molecule is degree-based topological numbers. These descriptions are based on the idea of a node’s degree in a molecular network, which denotes how many nearby atoms are directly related to that node [16,17]. There are several types of degree-based topological numbers, including the following:
Vertex degree: The number of edges (bonds) that are connected to a given atom in a molecule.
Average degree: The average number of edges that are connected to all atoms in a molecule.
Eccentricity: The maximum number of edges that must be traversed to reach a given atom from any other atom in the molecule.
Wiener number: The sum of all pairwise distances between all pairs of atoms in a molecule.
Applications for degree-based topological numbers include drug design, modelling of quantitative structure–activity relationships, and molecular similarity analysis. They can offer a rapid and efficient technique to compare the connectivity of atoms in various compounds and are comparatively easy to compute [20,21]. Chemical species and chemical processes may be represented as nodes and edges in a graph, which can then be used to depict a chemical network. Chemical reactions link the reactants and products of the reaction together at their respective nodes. This makes it possible to describe the chemical network as a directed graph, where each node stands for a particular chemical species and each edge for a particular chemical process [22,23].
The transformation of a molecular system into a graph encompasses many distinct stages: It briefly indicates the substance entities that are participating inside the framework. Such a category encompasses several molecular objects, such as ions, molecules, and radicals in the body, as well as similar constituents. It ensures to indicate the molecular processes that establish connections between the various entities within the framework. Such a process might entail the examination and interpretation of empirical information, mathematical formulas, or various kinds of knowledge. Such compound entities should be allocated to individual vertices within the structure of the graph, while each of the chemical responses should be represented by an edge that directly connects the vertices that correspond to the reactants and products involved in the process [24]. Further data are included in visualization pertaining to relevant parameters for the analysis of the molecular system, such as the rate of reaction, concentrations of substances, or thermodynamic characteristics [25]. After the conversion of the molecular system into the form of a graph, a range of networking-theoretic methods and techniques can potentially be used to examine the structure as well as the motion of the system as a whole [26]. One potential implementation of centralization metrics is the identification of significant vertices within a system. Similarly, neighbourhood discovery techniques may be employed to locate clusters of vertices that exhibit high levels of interconnectedness. The use of this methodology could offer valuable observations on the dynamics of intricate molecular infrastructure, hence facilitating the strategic development of novel molecular interactions and procedures [27].
The study by Ajmal et al. [28] provides a comprehensive analysis of toroidal polyhex networks and generalized prisms within the context of our selected subject matter of geometrical numbers. Maji and Ghorai [29] examined the M-polynomials of the improvement networks, and in the study of Balasubramanian [30], Topochemie-2020 is a computer programming application designed for the calculation of structural numbers. In addition to M-polynomials, the introduction and extensive analysis of omega-sine waves have been undertaken for antiepileptic medicines [31]. The significance of uses in this unique notion is shown by the extensive examination of numbering polynomial functions in the field of chemical reactions [32,33], and topological numbers associated with zero-divisor graphs are noted in in the study of Ahmad and Lopez [34]. The comprehensive elucidation of oxide and silicate networks, together with their respective topological numbers, is provided in the study of Javaid and Jung [35]. The study by Ahmad et al. [36] explores the use of optical transposition interconnect systems to analyse switched systems, introducing the innovative notion of structural numbers. In the study of Munir et al. [37], the titania nanotubes; in the study of Siddiqui et al. [38], nanostar dendrimers; and in the study of Gao et al. [39], the notion of reverse degree-based topological numbers is discussed in relation to dendrimers. For further study on the application part of this work, one can refer to previous studies [40,41,42]. Particularly, the work on the Boron cluster, borophene sheet, and other chemical structures that are closely related to this work is given in the study of Zhang et al. [43].
In addition to numerical values, there are many more subjects that are intricately connected to topological numbers and their corresponding literary work, which may be discovered in previous studies [44,45,46,47,48,49,50,51,52,53,54,55,56].
2 Degree-based results of
γ
-sheet of boron clusters
Boron cluster sheets are two-dimensional boron atom-based formations called borophene. They are similar to the two-dimensional sheet known as graphene, which is composed of carbon atoms arranged in a hexagonal lattice. The unique electrical, mechanical, and thermal properties of borophene make it a sought-after substance for a variety of uses, such as catalysis, energy storage, and electronics. There are two ways to manufacture borophene: chemical vapour deposition and molecular beam epitaxy. To create borophene sheets, many arrangements of boron atoms, such as triangular, honeycomb, and rectangular patterns, may be created. Figure 1 shows the graph of

Lemma 2.1
Let
Proof
The graph
This means that the set
as
Let us divide the edges of
Note that
In the following theorems, we determined the degree-based topological indices of
Theorem 2.1
Let
The Randić index is
the second Zagreb index is
the second modified Zagreb index is
the general sum-connectivity index
the sum-connectivity index is
the first Zagreb index is
and the hyper-Zagreb index is
Proof
For the general Randić index
If
If
If
For the general sum-connectivity index
If
If
If
Theorem 2.2
Let
the atom-bond connectivity index
the augmented Zagreb index
the harmonic index
and the symmetric division degree index
Proof
For the geometric-arithmetic index
For the atom-bond connectivity index
For the augmented Zagreb index
For the harmonic index
For the symmetric division degree index
Theorem 2.3
Let
the first redefined Zagreb index
the second redefined Zagreb index
the third redefined Zagreb index
and the variation of the Randić index
Proof
For the Albertson index
For the first redefined Zagreb index
For the second redefined Zagreb index
For the third redefined Zagreb index
For the variation of the Randić index
A comparative study was done and the conclusions are drawn in Figures 2–4. These figures are from the numerical values of Tables 1–3, respectively.

Comparative study for

Comparative study for
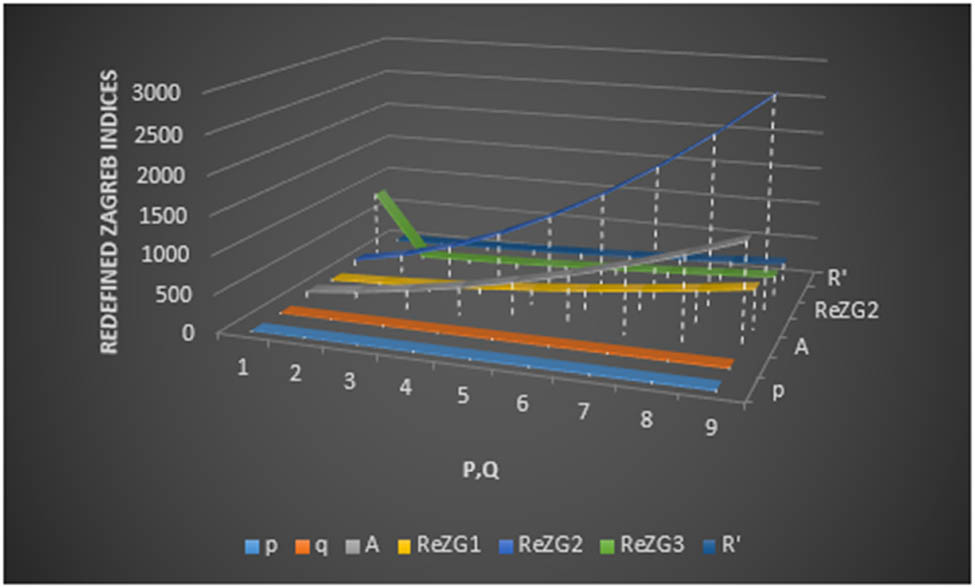
Comparative study for
Numerical behaviour of the
|
|
|
|
|
|
|
|
|---|---|---|---|---|---|---|
| (2,2) | 11.75428 | 1,052 | 2.9939 | 16.54154 | 416 | 3,732 |
| (3,3) | 25.06030 | 2,441 | 6.0261 | 36.31671 | 978 | 9,106 |
| (4,4) | 43.33232 | 4,408 | 10.097 | 63.77488 | 1,776 | 16,824 |
| (5,5) | 66.57034 | 6,953 | 15.206 | 98.91605 | 2,810 | 26,886 |
| (6,6) | 94.77436 | 10,076 | 21.353 | 141.74022 | 4,080 | 39,292 |
| (7,7) | 127.94438 | 13,777 | 28.538 | 192.24739 | 5,586 | 54,042 |
| (8,8) | 166.08040 | 18,056 | 36.762 | 250.43756 | 7,328 | 71,136 |
| (9,9) | 209.18242 | 22,913 | 46.024 | 316.31073 | 9,306 | 90,574 |
| (10,10) | 257.25044 | 28,348 | 56.325 | 389.86690 | 11,520 | 112,356 |
Numerical behaviour of
|
|
|
|
|
|
|
|---|---|---|---|---|---|
| (2,2) | 47.0058 | 29.3423 | 1,009.497 | 11.519777 | 104.53466 |
| (3,3) | 106.1911 | 64.7231 | 2,538.475 | 24.638583 | 231.40299 |
| (4,4) | 89.2124 | 113.8841 | 4,757.293 | 42.689789 | 407.60532 |
| (5,5) | 296.0697 | 176.8253 | 7,665.951 | 65.673395 | 633.14165 |
| (6,6) | 426.7630 | 253.5467 | 11,264.449 | 93.589401 | 908.01198 |
| (7,7) | 581.2923 | 344.0483 | 15,552.787 | 126.437807 | 1,232.21631 |
| (8,8) | 759.6576 | 448.3301 | 20,530.965 | 164.218613 | 1,605.75464 |
| (9,9) | 961.8589 | 566.3921 | 26,198.983 | 206.931819 | 2,028.62697 |
| (10,10) | 1,187.8962 | 698.2343 | 32,556.841 | 254.577425 | 2,500.83330 |
Numerical behaviour of
|
|
|
|
|
|
|
|---|---|---|---|---|---|
| (2,2) | 68 | 24 | 99.66435 | 894 | 10.16667 |
| (3,3) | 142 | 51 | 236.52465 | 2,204 | 21.83334 |
| (4,4) | 240 | 88 | 431.58095 | 4,092 | 38.00001 |
| (5,5) | 362 | 135 | 684.83325 | 6,558 | 58.66668 |
| (6,6) | 508 | 192 | 996.28155 | 9,602 | 83.83335 |
| (7,7) | 678 | 259 | 1,365.92585 | 13,224 | 113.50002 |
| (8,8) | 872 | 336 | 1,793.76615 | 17,424 | 147.66669 |
| (9,9) | 1,090 | 423 | 2,279.80245 | 22,202 | 186.33336 |
| (10,10) | 1,332 | 520 | 2,824.03475 | 27,558 | 229.50003 |
3
α
-Sheets of boron clusters
In this section, we study the

Lemma 3.1
Let
Proof
The graph
This means that the set
as
Note that
In the following theorems, we determine the degree-based topological indices of
Theorem 3.1
Let
The Randić index is
the second Zagreb index is
the second modified Zagreb index is
the general sum-connectivity index
the sum-connectivity index is
the first Zagreb index is
and the hyper-Zagreb index is
Proof
For the general Randić index
If
If
If
For the general sum-connectivity index
If
If
If
Theorem 3.2
Let
the atom-bond connectivity index
the augmented Zagreb index
the harmonic index
and the symmetric division degree index
Proof
For the geometric-arithmetic index
For the atom-bond connectivity index
For the augmented Zagreb index
For the harmonic index
For the symmetric division degree index
Theorem 3.3
Let
the first redefined Zagreb index
the second redefined Zagreb index
the third redefined Zagreb index
and the variation of the Randić index
Proof
For the Albertson index
For the first redefined Zagreb index
For the second redefined Zagreb index
For the third redefined Zagreb index
For the variation of the Randić index
4 Conclusion
In this article, we discussed some novel topological descriptors found in algebraic formulations for the boron cluster or borophene sheets. At the start of the methodology, we defined the graph of boron clusters or borophene sheets in some lemmas for the algebraic properties like how topological indices worked. Later, on behalf of these lemmas, we introduced Randić indices for different parameters such as alpha and geometric arithmetic, atom-bond connectivity, augmented Zagreb, Albertson, and redefined Zagreb indices, which were measured for the borophene sheets.
In this study, we explored the degree-based topological properties of borophene sheets, a novel two-dimensional material with remarkable electrical, mechanical, and thermal properties. By employing graph-theoretical approaches, we derived algebraic formulations for various topological indices, including the Randić index, geometric arithmetic index, atom-bond connectivity index, augmented Zagreb index, Albertson index, and redefined Zagreb indices. These indices serve as powerful tools for understanding the structural and chemical properties of borophene sheets, offering insights into their atomic connectivity and bonding patterns.
Our work began by modelling borophene sheets as molecular graphs, where atoms are represented as nodes and bonds as edges. Through this representation, we established several lemmas and mathematical frameworks to compute topological indices for different configurations of borophene sheets. The results highlight the significance of these indices in predicting the physical and chemical behaviours of borophene, which is crucial for its potential applications in electronics, catalysis, and energy storage.
The findings of this study contribute to the growing body of knowledge on borophene and its topological properties. By providing explicit algebraic expressions for these indices, we have laid the groundwork for further computational and experimental studies. This research not only advances the theoretical understanding of borophene but also paves the way for its practical utilisation in nanotechnology and materials science.
5 Limitations of the work
While this study provides valuable insights into the topological properties of borophene sheets, it is important to acknowledge its limitations in simplified models: The molecular graph representation of borophene sheets assumes idealized structures, which may not fully capture the complexities and defects present in real-world materials. We focus on degree-based indices and experimental validation.
6 Future directions
To build upon this work, future research could focus on the following areas: incorporation of defects and heteroatoms: Real borophene sheets often contain defects or heteroatoms, which can significantly alter their properties. Extending the current framework to account for these factors would enhance its practical relevance. Exploration of other topological indices: Investigating distance-based, eigenvalue-based, or entropy-based indices could provide a more comprehensive understanding of borophene’s properties.
Acknowledgments
The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through the Large Research Project under Grant Number RGP2/339/45.
-
Funding information: The authors extend their appreciation to the Deanship of Research and Graduate Studies at King Khalid University for funding this work through the Large Research Project under Grant Number RGP2/339/45.
-
Author contributions: Conceptualization: Ali Al Khabyah, Ali Ahmad; Methodology: Ali Al Khabyah, Ali Ahmad; Software: Muhammad Azeem, Ali N. A. Koam; Validation: Muhammad Azeem, Ali N. A. Koam; Verification: Ali N. A. Koam; Formal analysis: Ali Ahmad, Muhammad Azeem; Investigation: Ali Al Khabyah, Ali N. A. Koam; Resources: Ali Al Khabyah; Data Curation: Ali Ahmad, Muhammad Azeem; Writing – Original Draft: Ali Al Khabyah, Ali Ahmad, Ali N. A. Koam; Writing – Review & Editing: Ali Al Khabyah, Ali Ahmad, Muhammad Azeem; Visualization: Ali N. A. Koam; Supervision: Ali Ahmad; Project administration: Ali N. A. Koam; Funding acquisition: Ali Al Khabyah.
-
Conflict of interest: Authors state no conflict of interest.
-
Data availability statement: All data generated or analysed during this study are included in this published article.
References
[1] Feng B, Zhang J, Zhong Q, Wenbin L, Shuai L, Hui L, et al. Experimental realization of two-dimensional boron sheets. Nat Chem. 2016;8:563–8. 10.1038/nchem.2491.Search in Google Scholar PubMed
[2] Shabbir A, Azeem M. On the partition dimension of tri-hexagonal alpha-boron nanotube. IEEE Acc. Apr 2021;9:55644–53. 10.1109/ACCESS.2021.3071716.Search in Google Scholar
[3] Zhang Z, Evgeni S, Penev BI. Two-dimensional boron: structures, properties and applications. Chem Soc Rev. 2017;46:6746–63.10.1039/C7CS00261KSearch in Google Scholar
[4] Azeem M, Nadeem MF. Metric-based resolvability of polycyclic aromatic hydrocarbons. Eur Phys J Plus. Jan 2021;136(395). 10.1140/epjp/s13360-021-01399-8.Search in Google Scholar
[5] Xiaojun W, Jun D, Yu Z, Zhiwen Z, Jinlong Y, Xiao Cheng Z. Two-dimensional boron monolayer sheets. ACS Nano. 2012;6(8):7443–53. org/10.1021/nn302696.Search in Google Scholar
[6] Liu Y, Tai G, Hou C, Wu Z, Liang X. Chemical vapor deposition growth of few-layer beta12-borophane on copper foils toward broadband photodetection. ACS Appl Mater Interfaces. 2023;15(11):14566–74. 10.1021/acsami.2c23234.Search in Google Scholar PubMed
[7] Cheng Z, Zhang X, Zhang H, Liu H, Yu X, Dai X, et al. Porous-induced performance enhancement of flat boron sheets for lithium-ion batteries. J Phys Chem C. 2022;126(51):21542–49. 10.1021/acs.jpcc.2c06346.Search in Google Scholar
[8] Xiong Z, Xiao Y, Shen C. Screening of the transition metal single atom anchored on alpha-borophene catalysts as a feasible strategy for electrosynthesis of urea. Chem Mater. 2022;34(21):9402–13. 10.1021/acs.chemmater.2c01572.Search in Google Scholar
[9] Kang Y, Ma X, Fu J, Yang K, Wang Z, Li H, et al. Substrate-mediated borophane polymorphs through hydrogenation of two-dimensional boron sheets. J Phys Chem Lett. 2022;13(43):102220–9. 10.1021/acs.jpclett.2c02417.Search in Google Scholar PubMed
[10] Abdi Y, Mazaheri A, Hajibaba S, Darbari S, Rezvani SJ, Cicco AD, et al. A two-dimensional borophene supercapacitor. ACS Mater Lett. 2022;4(10):1929–36. 10.1021/acsmaterialslett.2c00475.Search in Google Scholar
[11] Chen K, Guo H, Zhang J, Wang L, Wu M. 2D/2D boron/g-C3N4 nanosheet heterojunction boosts photocatalytic hydrogen evolution performance. ACS Appl Energy Mater. 2022;5(9):10657–66. 10.1021/acsaem.2c01370.Search in Google Scholar
[12] Radatovic B, Jadrisko V, Kamal S, Kralj M, Novko D, Vujicic N, et al. Macroscopic single-phase monolayer borophene on arbitrary substrates. ACS Appl Mater Interfaces. 2022;14(18):21727–37. 10.1021/acsami.2c03678.Search in Google Scholar PubMed
[13] Xu Y, Xuan X, Yang T, Zhang Z, Li SD, Guo W. Quasi-freestanding bilayer borophene on Ag(111). Nano Lett. 2022;22(8):3488–94. 10.1021/acs.nanolett.1c05022.Search in Google Scholar PubMed
[14] Li J, An Q, Liu L. A strong two-dimensional semiconductor l-B4C with high carrier mobility. J Phys Chem C. 2022;126(13):6036–46. 10.1021/acs.jpcc.2c00140.Search in Google Scholar
[15] Xu Y, Zhang P, Xuan X, Xue M, Zhang Z, Guo W, et al. Borophane polymorphs. J Phys Chem Lett. 2022;13(4):1107–13. 10.1021/acs.jpclett.1c03827.Search in Google Scholar PubMed
[16] Nadeem MF, Azeem M. The fault-tolerant beacon set of hexagonal mobius ladder network. Math Methods Appl Sci. Jan 2023;46(9):9887–901. 10.1002/mma.9091.Search in Google Scholar
[17] Hayat S, Khan S, Imran M. Quality testing of spectrum-based distance descriptors for polycyclic aromatic hydrocarbons with applications to carbon nanotubes and nanocones. Arab J Chem. 2021;14(3):102994.10.1016/j.arabjc.2021.102994Search in Google Scholar
[18] Hayat S, Khan S, Khan S, Imran M. Distance-based topological descriptors for measuring the pielectronic energy of benzenoid hydrocarbons with applications to carbon nanotubes. Math Methods Appl Sci. 2020. 10.1002/mma.6668.Search in Google Scholar
[19] Malik MYH, Hayat S, Khan S, Binyamin MA. Predictive potential of spectrum-based topological descriptors for measuring the pi-electronic energy of benzenoid hydrocarbons with applications to boron triangular. Math Methods Appl Sci. 2021. 10.1002/mma.7161.Search in Google Scholar
[20] Nadeem MF, Azeem M, Farman I. Comparative study of topological indices for capped and uncapped carbon nanotubes. Polycycl Aromatic Compd. 2020;42(7):4666–83. 10.1080/10406638.2021.1903952.Search in Google Scholar
[21] Nadeem MF, Azeem M, Siddiqui HMA. Comparative study of Zagreb indices for capped, semi-capped and uncapped carbon nanotubes. Polycycl Aromatic Compd. 2021;42(6):3545–62. 10.1080/10406638.2021.1890625.Search in Google Scholar
[22] Hakami KH, Ahmad A, Azeem M, Husain, Koam ANA. A study of two-dimensional coronene fractal structures with M-polynomials. Int J Quantum Chem. 2023;123(13):e27112. 10.1002/qua.27112.Search in Google Scholar
[23] Shanmukha MC, Lee S, Usha A, Shilpa KC, Azeem M. Structural descriptors of anthracene using topological coindices through CoM-polynomial. J Intell Fuzzy Syst. 2023;44(5):8425–36. 10.3233/JIFS-223947.Search in Google Scholar
[24] Bukhari S, Jamil MK, Azeem M, Swaray S. Patched network and its vertex-edge metric-based dimension. IEEE Acc. Jan 2023;11:4478–85. 10.1109/ACCESS.2023.3235398.Search in Google Scholar
[25] Javaid M, Zafar H, Zhu Q, Alanazi AM. Improved lower bound of LFMD with applications of prism-related networks. Math Probl Eng. 2021;2021:9950310.10.1155/2021/9950310Search in Google Scholar
[26] Kulli VR. Reverse zagreb and reverse hyper-Zagreb indices and their polynomials of rhombus silicate networks. Ann Pure Appl Mathematics. 2018;16(1):47–51.10.22457/apam.v16n1a6Search in Google Scholar
[27] Liu J-B, Raza Z, Javaid M. Zagreb connection numbers for cellular neural networks. Discret Dyn Nat Soc. 2020;2020:8038304.10.1155/2020/8038304Search in Google Scholar
[28] Ajmal M, Nazeer W, Munir M, Kang S, Kwun Y. Some algebraic polynomials and topological indices of generalized prism and toroidal polyhex networks. Symmetry. dec 2016;9(1):5.10.3390/sym9010005Search in Google Scholar
[29] Maji D, Ghorai G. Computing F-index, coindex and Zagreb polynomials of the kth generalized transformation graphs. Heliyon. 2020;6(12):e05781.10.1016/j.heliyon.2020.e05781Search in Google Scholar PubMed PubMed Central
[30] Balasubramanian K. TopoChemie-2020. A Fortran 95, 2020.Search in Google Scholar
[31] Huilgol MI, Sriram V, Balasubramanian K. Structure-activity relations for antiepileptic drugs through omega polynomials and topological indices. Mol Phys. 2022;120(3):e1987542. 10.1080/00268976.2021.1987542.Search in Google Scholar
[32] Hosoya H. On some counting polynomials in chemistry. Discret Appl Math. 1988;19(1–3):239–57.10.1016/0166-218X(88)90017-0Search in Google Scholar
[33] Deutsch E, Klavzar S. M-polynomial and degree based topological indices. Iran J Math Chem. 2015;6:93–102.Search in Google Scholar
[34] Ahmad A, Lopez SC. Distance-based topological polynomials associated with zero-divisor graphs. Math Probl Eng. 2021;2021:18.10.1155/2021/4959559Search in Google Scholar
[35] Javaid M, Jung CY. M-polynomials and topological indices of silicate and oxide networks. Int J Pure Appl Math. 2017;115(1):129–52.10.12732/ijpam.v115i1.11Search in Google Scholar
[36] Ahmad A, Hasni R, Elahi K, Asim MA. Polynomials of degree-based indices for swapped networks modeled by optical transpose interconnection system. IEEE Acc. 2020;8:214293–99.10.1109/ACCESS.2020.3039298Search in Google Scholar
[37] Munir M, Nazeer W, Nizami A, Rafique S, Kang S. Mpolynomials and topological indices of titania nanotubes. Symmetry. 2016;8(11):117.10.3390/sym8110117Search in Google Scholar
[38] Siddiqui MK, Imran M, Ahmad A. On zagreb indices, Zagreb polynomials of some nanostar dendrimers. Appl Math Comput. 2016;280:132–9.10.1016/j.amc.2016.01.041Search in Google Scholar
[39] Gao W, Younas M, Farooq A, Virk A, Nazeer W. Some reverse degree-based topological indices and polynomials of dendrimers. Mathematics. 2018;6(10):214.10.3390/math6100214Search in Google Scholar
[40] Noureen S, Ali A, Bhatti AA, Alanazi AM, Shang Y. Predicting enthalpy of formation of benzenoid hydrocarbons and ordering molecular trees using general multiplicative Zagreb indices. Heliyon. 2024;10(10):e30913.10.1016/j.heliyon.2024.e30913Search in Google Scholar PubMed PubMed Central
[41] Raza Z, Akhter S, Shang Y. Expected value of first Zagreb connection index in random cyclooctatetraene chain, random polyphenyls chain, and random chain network. Front Chem. 2023;10:1067874.10.3389/fchem.2022.1067874Search in Google Scholar PubMed PubMed Central
[42] Ismail R, Azeem M, Shang Y, Imran M, Ahmad A. A unified approach for extremal general exponential multiplicative zagreb indices. Axioms. 2023;12(7):675.10.3390/axioms12070675Search in Google Scholar
[43] Zhang Z, Yang Y, Gao G, Yakobson BI. Two-dimensional boron monolayers mediated by metal substrates. Angew Chem. 2015;127(44):13214–8.10.1002/ange.201505425Search in Google Scholar
[44] Abbas G, Ibrahim M, Ahmad A, Azeem M, Elahi K. M-Polynomials of tetra-cyano-benzene transition metal structure. Polycycl Aromatic Compd. 2021;43(1):471–81. 10.1080/10406638.2021.2019797.Search in Google Scholar
[45] Abbas G, Ibrahim M, Ahmad A, Azeem M, Elahi K. M-polynomials and associated topological indices of sodalite materials. Math Probl Eng. Oct. 2021;2021:5924409. 10.1155/2021/5924409.Search in Google Scholar
[46] Zuo X, Nadeem MF, Siddiqui MK, Azeem M. Edge weight based entropy of different topologies of carbon nanotubes. IEEE Access. 2021;9:102019–29. 10.1109/ACCESS.2021.3097905.Search in Google Scholar
[47] Nadeem MF, Imran M, Siddiqui HMA, Azeem M, Khalil A, Ali Y. Topological aspects of metal-organic structure with the help of underlying networks. Arab J Chem. 2021;14(6):103157. 10.1016/j.arabjc.2021.103157.Search in Google Scholar
[48] Raza H, Waheed M, Jamil MK, Azeem M. Structures devised by the generalizations of two graph operations and their topological descriptors. Main Group Met Chem. 2022;45(1):44–56. 10.1515/mgmc-2022-0006.Search in Google Scholar
[49] Ahmad A. Computing the Schultz polynomials and indices for ladder related graphs. Proyecciones (Antofagasta). 2019;38(5):1081–92. 10.22199/issn.0717-6279-2019-05-0070.Search in Google Scholar
[50] Cancan M, Hussain M, Ahmad H. Distance and eccentricity based polynomials and indices of m-level Wheel graph. Proyecciones (Antofagasta). 2020;39(4):869–85. 10.22199/issn.0717-6279-2020-04-0054.Search in Google Scholar
[51] Raza Z, Essa M, Sukaiti K. M-polynomial and degree based topological indices of some nanostructures. Symmetry. 2020;12(5):831. 10.3390/sym12050831.Search in Google Scholar
[52] Liu J-B, Younas M, Habib M, Yousaf M, Nazeer W. M-polynomials and degree-based topological indices of VC5C7[p,q] and HC5C7[p,q] nanotubes. IEEE Acc. 2019;7:41125–32. 10.1109/access.2019.2907667.Search in Google Scholar
[53] Irfan M, Rehman HU, Almusawa H, Rasheed S, Baloch IA. M-polynomials and topological indices for line graphs of chain silicate network and H-naphtalenic nanotubes. J Mathematics. 2021;2021:1–11. 10.1155/2021/5551825.Search in Google Scholar
[54] Riaz M, Gao W, Baig AQ. M-polynomials and degree-based topological indices of some families of convex polytopes. Open J Math Sci. 2018;2(1):18–28. 10.30538/oms2018.0014.Search in Google Scholar
[55] Li C-P, Zhonglin C, Munir M, Yasmin K, Liu J-B. M-polynomials and topological indices of linear chains of benzene, napthalene and anthracene. Math Biosci Eng. 2020;17(3):2384–98. 10.3934/mbe.2020127.Search in Google Scholar PubMed
[56] Baig MNJ, Jung CY, Ahmad N, Kang SM. On the M-polynomials and degree-based topological indices of an important class of graphs. J Discret Math Sci Cryptogr. 2019;22(7):1281–8. 10.1080/09720529.2019.1691327.Search in Google Scholar
© 2025 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Research Articles
- Syntheses, crystal structures, and characterizations of two new Zn(ii)/Ni(ii) coordination polymers constructed by N-donor ligands and sulfate-bridge
- M-polynomial and NM-polynomial indices of camptothecin–polymer conjugate IT-101 structure
- Effects of alkyl size of AlR3 on its reaction with thiophene-2-carbonyl chloride
- Degree-based topological properties of borophene sheets
- A zinc(ii) polymer constructed with 3,5-pyrazoledicarboxylic acid and 1,4-bis(imidazol-1-ylmethyl)butane: Syntheses, crystal structures, and photoluminescence properties
- Study on (r, s)-generalised transformation graphs, a novel perspective based on transformation graphs
- New pyrazole-based Schiff base ligand and its Ni(ii) and Co(iii) complexes as antibacterial and anticancer agents: Synthesis, characterization, and molecular docking studies
- Sombor indices in main group metal chemistry: Computational evaluation of bismuth(iii) iodide, oxide/silicate frameworks, and dendrimers for QSAR applications
- Predictive modeling of physical properties in silane compounds using topological descriptors: A computational approach
- Review Article
- Critical review on the derivative of graphene with binary metal oxide-based nanocomposites for high-performance supercapacitor electrodes
- Retraction
- Retraction of “Synthesis, structure, and in vitro anti-lung cancer activity on an In-based nanoscale coordination polymer”
Articles in the same Issue
- Research Articles
- Syntheses, crystal structures, and characterizations of two new Zn(ii)/Ni(ii) coordination polymers constructed by N-donor ligands and sulfate-bridge
- M-polynomial and NM-polynomial indices of camptothecin–polymer conjugate IT-101 structure
- Effects of alkyl size of AlR3 on its reaction with thiophene-2-carbonyl chloride
- Degree-based topological properties of borophene sheets
- A zinc(ii) polymer constructed with 3,5-pyrazoledicarboxylic acid and 1,4-bis(imidazol-1-ylmethyl)butane: Syntheses, crystal structures, and photoluminescence properties
- Study on (r, s)-generalised transformation graphs, a novel perspective based on transformation graphs
- New pyrazole-based Schiff base ligand and its Ni(ii) and Co(iii) complexes as antibacterial and anticancer agents: Synthesis, characterization, and molecular docking studies
- Sombor indices in main group metal chemistry: Computational evaluation of bismuth(iii) iodide, oxide/silicate frameworks, and dendrimers for QSAR applications
- Predictive modeling of physical properties in silane compounds using topological descriptors: A computational approach
- Review Article
- Critical review on the derivative of graphene with binary metal oxide-based nanocomposites for high-performance supercapacitor electrodes
- Retraction
- Retraction of “Synthesis, structure, and in vitro anti-lung cancer activity on an In-based nanoscale coordination polymer”

