The role of gestures in logic

2.1 16th century

Let us take a typical example of a syllogism that is often found in the early modern period.

All hands belong to the body.

All fingers belong to the hands.

Therefore, all fingers belong to the body.

In every syllogism, we have three judgments or propositions and three terms. In the example given above, the first two judgments, i.e., those that begin with ‘All,’ are called the premises, and the third judgment, which begins with ‘Therefore,’ is called the conclusion.

The three judgments contain exactly three terms. The term ‘hands’ only appears in the premises and is therefore called the middle term (terminus medius). As medius, it connects the other two terms, which are individually connected to the medius in the premises, in such a way that they are related to each other as a conclusion in the last judgement itself. The terms themselves can also be defined according to the set of objects that they name or that the term signifies.

This can also be compared to a real hand: A large hand can grasp more objects of one kind than a small hand that wants to grasp the same kind of objects. It is the same with terms: The largest term is called major term (terminus maior) and in the above given example it is the ‘body’ because it includes many things such as hands or fingers. The smallest or minor term is called terminus minor and is ‘fingers’ in the example given since it is encompassed by the other two terms but does not itself encompass either of them.

In a syllogism, the minor is the subject in question that must be examined. The major is the predicate and says something about the subject in question, i.e., about the minor.

In the 16th century, the Leuven scholar Cornelius Valerius described and visualised the assignment of the three terms with the help of a gesture in his book Tabulae, quibus totius dialecticae praecepta maxime ad usum disserendi. In Figure 1, we see a hand with a splayed thumb, index and middle finger. As the labelling shows, the thumb represents the terminus medius, the index finger the terminus maior and the middle finger the terminus minor. Between the index and middle fingers is written ‘thema[ta simplicia]’ (single words), i.e. maior, minor and middle. The marginal gloss found in some editions of the book states:

It is necessary to be careful at this point not to allow more than three terms, or to avoid any ambiguity of words. We imagine the legitimate dimension of the terms and their arrangement by the three first fingers of the left hand. This makes what is expressed surprisingly simple and expedient. The subject term in question is placed on the middle finger, the predicate of the subject on the index finger, the terminus medius on the thumb. From the middle finger to the index finger, the subject hand shows the argumentative formula of the subject being inferred. (Valerius 1582, p. 79)

Figure 1:

Valerius’ gesture.

Valerius does not elaborate on this gesture in the following. But one can certainly assume that this technique was already known before Valerius and that Valerius and others used it for many purposes in syllogistic. In the context of this gesture, Valerius also discusses so-called Byzantine diagrams, which have triangular or crescent shapes (Bhattacharjee 2024; Cacouros 2001; Panizza 2017; Roberts 2022). Knowing these diagrammatic techniques, one can imagine that Valerius and his contemporaries used gestures that are said to have a similar function to the diagrams from this period. Only through such an extension does it make sense why Valerius depicts such a simple gesture and says that this method of gesture is so easy and convenient. The last sentence in the quote also points to an extended method. So we do not see in Figure 1 everything that the gestures achieve and the quotation itself only indicates a relationship between the gestures and the Byzantine diagrams.

In recent years it has also become known that these Byzantine diagrams had a much higher logical potential than was assumed between the 18th and 21st centuries. We will give an example of how complex such gestures can become at the end of Section 4. However, in order to reinvent such extensions of Valerius’ gestures, it is helpful to look at what other types and techniques of gestures have existed in the history of logic.

2.2 17th century

For our next example, we have chosen the representation of a hand, illustrating various gestures in the area of incipit/desinit logic (Ciola 2017; Uckelman 2018). In doing so, we leave the traditional syllogistic we described earlier and turn to a prefiguration of modern temporal and tense logic. The logic gesture is found in Petrus Tartaretus’ commentary on the logic of Petrus Hispanus (Geudens 2019). The text itself dates back to the Middle Ages, but the rendering relevant to us seems to have been added later. At least, spot checks of medieval text editions of Hispanus have found no illustration of this hand . The relevant edition of this commentary in which a hand is depicted dates from the year 1621 (Tartaret 1621). As Tartaretus was a widely read author, this gesture technique would have been used well into the 17th century.

Other forms of visual communication, such as diagrams, also show the phenomenon that they were either removed from the text at some point or added later by the editor. However, it cannot be ruled out that there are older representations of this gestural technique by Tartaretus or that the gestures were already used in medieval communication. Based on the editions from the early modern period, however, it can be assumed that this technique of visual communication was used in temporal logic for at least more than a century. Here, too, the gesture and the accompanying text actually demand a much more intensive discussion than we are giving here. However, for our purpose of the paper, it should suffice to give an insight into the context and the associated gesture.

The whole section of Tartaretus is about the beginning and ending. He writes:

The first thing to know is that there are some propositions about beginning and ending in which the verb to be or an infinitive verb following beginning or ending remains affirmative […]. Other propositions negate the verb to be or the infinitive verb […]. Note that for the explanation of such propositions it is necessary to take into account that there are two kinds of things: permanent things, which by nature have all their parts simultaneously and adequately for the same time […]. Note, however, that a thing can be successive in two ways. In one way, as far as being is concerned […]. In another way it is called successive as far as production is concerned […]. Note further for the explanation of such propositions that there are four kinds of moments, namely the first moment of a thing’s being, the first moment of a thing’s non-being, the last moment of a thing’s being, the last moment of a thing’s non-being. […] But successive things have two moments, namely the last moment of the non-being of a thing and the first moment of the non-being of a thing. Note further that in addition to the things mentioned, there are also things that last only for a moment […]. (Tartaret 1621, p. 183)

The gesture in Figure 2 illustrate three types of things (R) that are represented by the segments of the thumb: (R1) permanent things, like people, are on the distal phalanx of the thumb, (R2) successive things, like movements, are on the proximal phalanx of the thumb, and (R3) things that last only one instance, like the instance itself, are mapped in the area of the os metacarpale.

Figure 2:

Incipit/desinit gesture (Tartaret 1621, p. 183).

Instances (Instans) or moments are represented on the distal phalanx of the fingers: (I1) the first instance at which a thing exists is represented on the index finger. (I2) the middle finger shows the first instance when a thing ceases to exist. (I3) the ring finger shows the last instance in which a thing exists and (I4) the little finger shows the last instance in which a thing no longer exists. At the proximal phalanx, propositions are then attributed to the instances, which are inferred from them. For (I1), for example, it is true that the thing exists now and it was not immediately before. For (I2) it is true that something is not now, but was before.

The lines and arcs connecting the segments of the thumb with the distal phalanx of the fingers show the possible instances (I) of things (R), i.e. R1(I1, I2); R2(I2, I3); R3(I1, I4). From the example of R1, which is connected to I1 and I2 by the arcs, one can therefore read what applied to a thing like a human being: for a human being like Socrates, it is possible that he is now and was not immediately before, or that he is not now but was immediately before.

At no point does the text refer to the drawing or explain any gestural technique performed by hand. This, too, is a sign that the depiction was added later and stems from a teaching tradition that was only incorporated into the book by the editor. It is striking that the drawings of the hand found within a century contain different assignments of the lines between the finger phalanges and the segments of the thumb. This may be due to the different possibilities of the draughtsman or to the different interpretations of the text by the draughtsman. In our eyes, the drawing shown here corresponds best with the text, but other interpretations are possible.

2.3 18th century

As an example from the 18th century, we have chosen a drawing on syllogistic by Johann Christian Lange. Lange is one of the most important sources for visual communication in logic, mathematics and technology of the early modern period. His works include hundreds of diagrams and drawings, some of which contain logical representations, proof procedures, construction plans for logic machines and didactic diagrams for the philosophy of mathematics. He is also the first currently known author interested in the history of diagrams and has attempted to identify several precursors of his techniques (Barbot et al. 2019; Lemanski 2018).

Lange’s first relevant book with diagrams is the new edition of the Nucleus Logicus written by his teacher Christian Weise. Lange points out that Weise’s approximately 100-page booklet is hardly comprehensible to readers, since the explanatory diagrams to which the metaphors in the text refer may not be familiar to every reader. In this respect, he writes a 700-page commentary on the Nucleus Logicus, which contains countless diagrams and drawings with the corresponding explanations.

Among these diagrams, one also finds a drawing that has a similar function to the drawing we already presented in the 16th century, i.e. Figure 1. In the chapter in which the drawing is found, Lange attempts to explain to the reader that the terminus medius can stand either at the subject or at the predicate position of a proposition. The grammatical subject position is the term before the sentence copula ‘is’, the grammatical predicate follows after. In our example syllogism at the beginning of Section 2.1, the terminus medius ‘hand’ is in the first premise at the subject position and in the second premise at the predicate position. Lange writes:

This particular arrangement of the four figures may also be demonstrated in a pleasant, witty, and still more palpable manner, if we take two gloves, one of which is intended for the right hand, and its shaft represents the major term, while the other is intended for the left hand, and its shaft represents the minor term; then let the fingers adhering or joined to each shaft represent the middle term, which is to be joined to the major and minor terms. Under this assumption, it will be obvious that the position of the two gloves representing the two premises of the syllogism can only vary in four following ways, which shall be represented by this scheme.

Combinatorially, there are only four possible places for the middle term (terminus medius) in the premises. The terminus medius can stand either alternately at the subject and predicate position or only at a unilateral position at both premises. There are two possibilities for both the alternating and unilateral positions. In the alternating position, the terminus medius can stand either in the subject position or in the predicate position of the first premise, which also makes it clear combinatorially that it must change to the other position in the second premise. In the unilateral position, it can be in either the predicate or subject position in both premises.

The four possible combinations are called figures (figura) and to explain these four figures Lange uses both hands or gloves. The terminus medius is represented by the fingers. If the fingers point in two different directions when the hands are parallel, this is an alternating position. If the fingers point only to the left, the terminus medius is at the predicate position; if the fingers point only to the right, the medius is at the subject position. Lange illustrates this in the drawing of Figure 3.

Figure 3:

Lange’s chirotecas (Weise and Lange 1712, p. 176).

Lange announces in his text that he is going to perform a palpable demonstration (palpabiliter demonstrari) with the help of gloves (chirotecas) (Weise and Lange 1712, p. 175f.). In the further course, however, he no longer names the four figures as gloves, but as hands (manus) (Weise and Lange 1712, p. 176). One can assume that Weise and also Lange himself probably did not use gloves when explaining the topic in class, but their own hands. If one imitates the four gestures with the hands, one notices that, for anatomical reasons, Figures 2 and 3 have to be gestured to the side of the body, but Figures 1 and 4 can be represented in front of the body.

2.4 19th century

In the 19th century, logic gestures already become a rarity before they almost died out completely in the 20th century. This is not surprising insofar as diagrams became established in the 19th century through the philosophy of Immanuel Kant (Lemanski 2021, sect. 2.2). Thus, a form of visual communication dominates and logic gestures, which were never very prominent in literature, become a rarity. Nevertheless, two approaches to using gestures to explain the conceptual logic of syllogistics can be found in Aldred James Swinbourne’s Picture Logic from the 1870s.

As already explained on the title page, Swinbourne’s book is an “attempt to popularise the science of reasoning by the combination of humorous pictures” (Swinbourne 1875). The author takes a traditional approach and first presents the concepts, then the judgements and finally the inferences. Among other things, he is guided by the logic of William Stanley Jevons, who is still known in today’s research on visual representation and reasoning for his diagrams and his logical machine. Swinbourne’s chapter on terms is divided into two parts. First, it defines what a term is and the different types of terms, then it introduces the connotation and denotation of terms. In both chapters on term logic, Swinbourne uses a hand to make the differences and types clear. In the following, we will only look at the first chapter, in which the “logical hand” is illustrated.

The term is a metaphor for Swinbourne, as the expression of terminus or boundary is true (Swinbourne 1875, p. 58). This is similar to Zeno or Cicero, as briefly described at the beginning of the chapter. Swinbourne, however, is primarily orientated towards the classification of terms. This is a topic that was not so much mediated by Aristotle between late antiquity and the 20th century, but rather by Porphyry and Boethius. For Swinbourne, a term is anything that can be perceived or imagined and this again breaks down into three areas: An individual is a unit that cannot be further divided. But one can group individuals or one can specify attributes of one or more individuals.

These three areas can be further classified to some extent: Since one cannot divide an individual, the realm of the individual is not further divisible. Socrates would be the singular term indicating such an individual. A group of individuals can now be either collective or general. Swinbourne makes this clear with two terms (Swinbourne 1875, p. 59): ‘black watch’ and ‘horses’. The first term refers to the soldiers of the 3rd Battalion of the Royal Regiment of Scotland and it is not possible to refer to each individual soldier as a ‘black watch’. ‘Horses’, on the other hand, refers to a group of horses and here it makes perfect sense to refer to each individual animal of this group as a horse. A similar distinction can be made with attributes: If an attribute is a noun like ‘whiteness’, then it is an abstract attribute, if it is an adjective like ‘white’, then it is an attributive attribute (Swinbourne 1875, p. 60).

Thus Swinbourne distinguishes five basic types of concepts in logic and assigns them to the hand. The thumb is the individual, as it has a special position among the fingers. The index finger and middle finger introduce the two groups of individuals and the ring finger and little finger the attribute types. Since the middle finger is the longest finger, the most frequently used type of term is assigned to it. This is shown by the logical hand in Figure 4. Swinbourne writes:

Well, then, a term expresses either an individual or group of individuals, or an attribute or group of attributes; and this is as much as to say that terms are an exhaustive enumeration of all that we can see or think of. Take your fingers and thumb, and remember the five terms thus: Figure 4.

Figure 4:

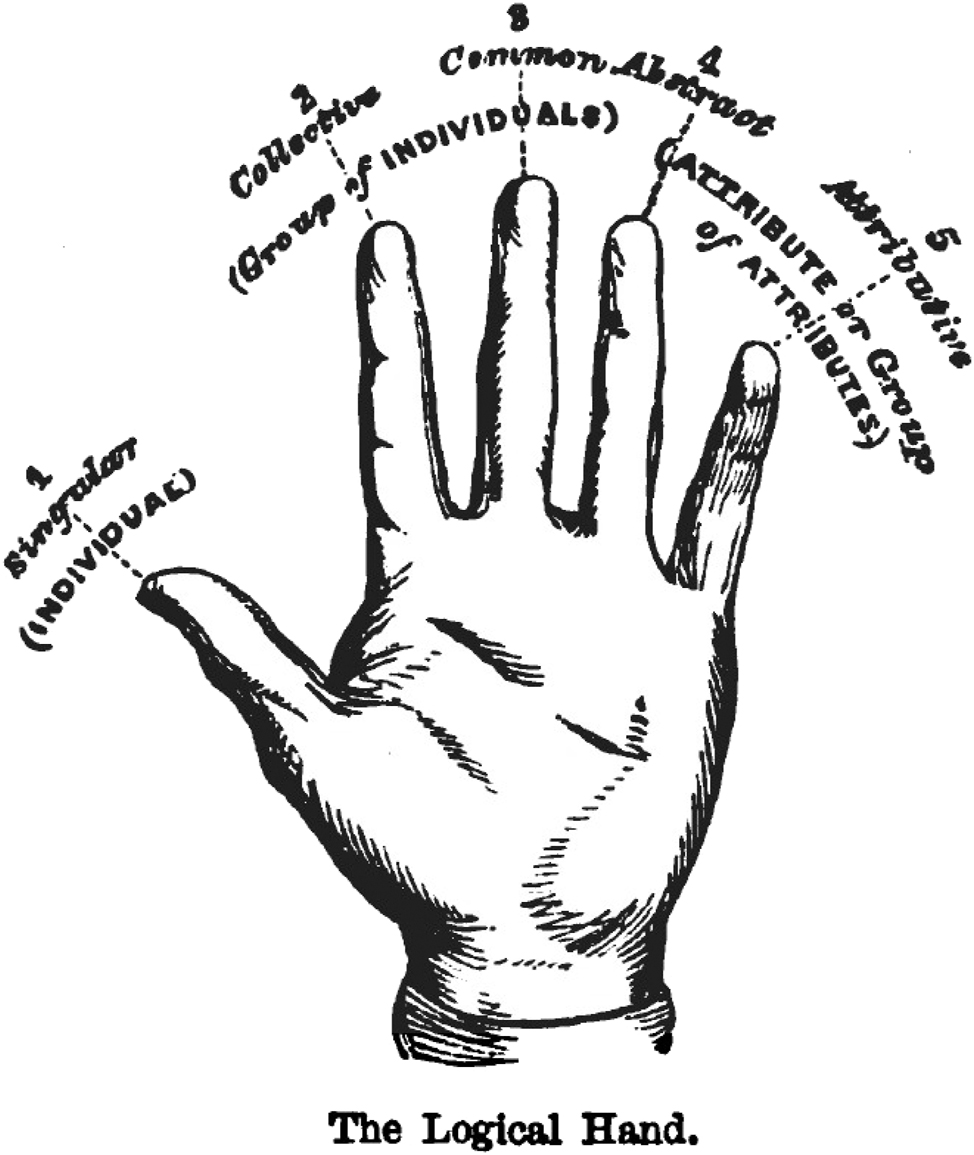
Swinbourne’s logical hand (Swinbourne 1875, p. 60).

Swinbourne admits that there are many more classification possibilities. But the five mentioned are the most important in logic. In addition, this also provides the basis for explaining connotation (intension) and denotation (extension), which are also very important for logic. In this explanation, which follows (Swinbourne 1875, p. 63), Swinbourne also uses a hand and represents groupings of fingers as arcs that represent the movement, similar to Figure 2. In Figure 4, the grouping of the logical hand is not made by the movement, but by the triple classification of the five fingers added in brackets. Here, too, it is conceivable that the five-finger classification of the outstretched hand in Figure 4 is represented by a three-partive classification in the form of a gesture, which would then look similar to the Vulcan salute gesture.

3.1 Representing by means of logic gestures

Let us assume that we do not assign only the middle term, major term and minor term to the fingertips, as Valerius did in Figure 1. Rather, we extend Valerius idea by assuming that the quantitative and qualitative properties of the proposition are also represented. These properties are represented by the four segments per finger, i.e. a for ‘All A is B’, i for ‘Some A is B’, e for ‘No A is B’ and o for ‘Some A is not B’. This information is depicted in Figure 5(a). We consider that the thumb, index and middle fingers represent the properties of the conclusion, major premise and minor premise respectively. Let us further assume that the subject-predicate relationship of a proposition is represented by touching the tip of the fingers. The solid arrows, as shown in Figure 5(b), depict the position of the subject and predicate. For the solid arrow, the arrow tail and head represent the position of the subject and predicate respectively. So, in Figure 5(b), when the tip of the thumb (i.e. the middle term) touches the tip of the index (i.e. the major term) we get the major premise where the subject is the middle term and predicate is the major term. The qualitative and quantitative properties of the major premise are depicted in the segment of the index finger. In this case, it is a universal negative proposition, i.e. e. Similarly, we get the information about the minor premise (represented by the middle finger) by touching the tip of the middle finger (i.e. minor term) with the tip of the thumb. For the conclusion, the subject-predicate relationship is presented by touching the tip of the middle finger with that of the index finger. The properties of the proposition for the conclusion are presented in the section of thumb as shown by the dashed arrow^[1] in Figure 5(b).

Figure 5:

Logic gestures.

If we now use the second hand to help us and tap the respective segment with the congruent fingers, we can already represent entire syllogisms as depicted in Figure 5(c).

A well-formed logic gesture in the reconstructed syllogistic following Valerius thus consists of the three fingers of the left hand, in which one of the four uppermost segments of each finger is touched by the fingertips of the right hand. It can be said that this is the syntax of this type of logic gesture. Figure 5(a), therefore, shows a well-formed logic gesture as an example.

As indicated above, each finger and each segment has a specific meaning, which is illustrated in Figure 5(a). This also gives us a basis for semantics. For example, the well-formed gesture in Figure 5(b) shows e-proposition of the major premise (index finger), a-proposition of the minor premise (middle finger) and the e-proposition in the conclusion (thumb).

The logic gesture in Figure 5(b) thus represents a complete inference. For example, if we take P for the major term, S for the minor term and M for the middle term, Figure 5(b) can be translated into words as follows.

No M is P. All S is M.

Thus, No S is P.

3.2 Reasoning with logic gestures

Those versed in the field of syllogistics will have discerned that the inference represented above is valid. This underscores the necessity of employing logic gestures to identify a methodology for evaluating the validity of inferences. As Valerius asserts, logic gestures are an invaluable tool for such tasks in logical reasoning.

The rules of proof of the syllogism can now be represented by movements. It is then possible to check whether an inference is valid or not (a) by representing the quantitative and qualitative properties of the propositions through the fingers and their segments (Figure 5(b)), (b) by comparing the right hand for syllogisms to be tested with the left hand for axiomatically valid syllogisms (Figure 5(c)), and (c) by indicating the rules of proof through the movement of the fingers (Figure 5(d)).

As mentioned above the movement of the fingers is represented by arrows in Figure 5(b). The left-hand shows the perfect syllogism, and the right hand the imperfect syllogism, the validity of which is to be proven. If the movement of the hands is asynchronous (attributable to their ‘chirality’ or ‘incongruent counterparts’ Bernecker 2012), the validity is not proven. However, if the movements of both hands are synchronised, the imperfect inference has been reduced to the perfect syllogism and the inference is valid. For example, in Figure 5(d), the movement between the thumb and index finger is not synchronised. For the left hand, the movement is from the thumb towards the index finger, whereas this movement is completely reversed for the right hand. The four reduction rules of the syllogism (conversio simplex/per accidens, etc.) are used to check whether synchronicity can be established (Wolff 2023, §§ 53ff.). Each rule changes the movement direction or semantics of the fingers or finger segments.

How exactly this method works has to be explained in detail and with many examples in another technical paper. However, logicians will probably recognize from the information given that Figure 5(d) shows the proof of modus Cesare by modus Celarent. Also, the synchronized movement can be established by revising the movement between the thumb and index finger for the right hand. This entails reversing the subject-predicate relationship for the major premise. This is known as the conversio simplex rule.

4.1 Discussion on the history of logic gestures

The material presented thus far raises a number of questions, some of which relate specifically to the history of logic. These include: Why were logic gestures used at all? Why has so little been handed down about logic gestures, and why is there not much more material about them if they seem to have had certain advantages? Firstly, it should be noted that none of the logic textbooks presented in Section 2 achieved a certain degree of popularity. The most renowned text is Lange’s Nucleus Logicae Weisianae. This book was frequently referenced from the late 18th century onwards, yet few historians of logic have ever had the opportunity to examine it. According to the most recent research, only three copies remain in public libraries or archives worldwide. The book comprises nearly 1,000 pages of numerous innovations, including numerous diagrams and drawings that have not been previously documented. The drawings of the logic gestures are thus simply lost in the sum of information and illustrations given in the amount of material presented. Other illustrations of logic gestures are also printed in non-popular textbooks. To our knowledge, there is no famous logic textbook such as Wolff’s Logica or Kant’s Jäsche Logic that contains illustrations of gestures or more detailed textual descriptions. Therefore, finding references to logic gestures in the 19th century was a matter of chance or the result of extensive research. At present, approximately ten logic gestures are known, all of which date from the period under discussion.

It can be assumed that the use of logic gestures has a longer tradition than is commonly acknowledged. This is evidenced by the examples and metaphors from antiquity that are mentioned at the beginning of Section 2. This is also the case for a great many types of logic diagrams and logical notations, the origin of which is still being discussed in research today (Carrara et al. 2020; Moktefi and Shin 2012). From the Renaissance onwards, for example, a number of schools of thought among logicians have concurred that a significant proportion of logic textbooks from antiquity made reference to the use of visual communication through the medium of metaphor (e.g., ‘figure, ‘concept, ‘containment, etc.). While the metaphors were preserved because the text was copied, the diagrams were not copied and therefore fell into oblivion over the centuries (Wesoły 2012).

It seems plausible to suggest that the textbooks mentioned here were published for a variety of reasons. It seems reasonable to posit that the authors of early modern logic textbooks used them as a kind of mental aid during lectures, given that they were almost always used as the basis for logic lectures. It can be assumed that the logicians who employed these gestures did so with great frequency in logic lessons. An alternative hypothesis is that the gestures were employed as a means of attracting the reader’s attention. Swinbourne’s book is a prime example of a collection of curiosities, a format that was already unusual in the 19th century but became common in the Baroque period, for example. In any case, pupils and students in higher education and universities in the early modern period studied logic for several hours every week for years, so it is probable that they were familiar with and practised different logic gestures. It is therefore probable that graduates of an early modern logic course were also able to communicate with each other using certain gestures.

The use of gestures has the advantage that it does not necessitate the use of any additional resources or apparatus. Notations and diagrams were previously drawn in various media, including sand (‘pulvis eruditus’), on wax tablets (‘tabula cerata’), on laid paper, or carved in stone. In contrast, logic gestures can be performed with only one’s own body. In the Middle Ages and early modern period, this represented a significant advantage over other systems of representation in logic, given that paper was expensive and aids in the form of tablets or sand were not always available. This is exemplified by the use of stone engravings of logic diagrams and notations in European church buildings (O’Meadhra 2012). In contrast to all other media or forms of representation, logic gestures could be employed and conveyed in an ad hoc manner during a lecture.

It is not surprising that there is a paucity of tradition in the use of logic gestures (in contrast to notations and diagrams). The act of drawing three-dimensional logic gestures presents a far greater challenge than the writing of algebraic symbols or the drawing of multi-dimensional logic diagrams. In addition, the available drawings demonstrate that, in contrast to notations and diagrams, there were no established conventions regarding the depiction of logic gestures. Furthermore, it is probable that the production costs of a drawing in book printing were disproportionate to the benefits of the illustration. One might inquire as to the rationale behind the production of a costly drawing of a logic gesture by an early modern logician if the gestures could be demonstrated in class without the need for such an illustration. Consequently, logic gestures were likely to have constituted a living tradition, transmitted from teacher to pupil, and thus did not necessitate documentation in textbooks.

Consequently, there are few incentives for the depiction of gestures, which may explain why they are less well-known than other forms of representation in logic. One potential motivation for the depiction of gestures could have been the desire to visually express school affiliation. It is recognized by those versed in the subject matter and some experts in the field today that the textbook author’s school affiliation can be discerned from notations, from examples, and diagrams (Lemanski 2021, ch. 2.3). This could have been similar to with the depicted or described logic gestures. This would suggest that the depiction of certain logic gestures represents an identity-creating feature that indicates the author’s affiliation to a particular school, region, religion, or culture. A similar phenomenon can be observed in diagrams or notations. For instance, logicians belonging to the Byzantine, Catholic, and Protestant traditions employ disparate example sentences or diagram types (which may vary depending on the region), and they often eschew the utilization of specific formulations or diagrams.

It is possible, however, that certain gestures were not known in other schools, which made it necessary to draw attention to the peculiarity of the gesture by publishing them in textbooks. For example, Lange was a student of a circle of scholars from Zittau and Leipzig who differed significantly from scholars in the neighboring Bohemian countries with regard to the formal presentation of logic (Goebel 2004). There are therefore very strong regional and cultural differences in early modern logic textbooks. Lange’s relocation to Giessen, where the logic textbook in question was produced (Section 2), can therefore be attributed to his desire to familiarize his Giessen students with the techniques employed in Zittau and Leipzig. For instance, he notes that his teacher, Christian Weise, employed a variety of visual communication techniques in Zittau, though these were not included in the textbooks he published. Consequently, he provided annotations and comments to a new edition of his teacher’s textbook, including diagrams and gestures, to facilitate comprehension among his students in Giessen.

The publication of the gestures may have been due to the fact that Lange, as a professor of logic and part of an active circle of famous patrons and colleagues, had greater financial capital and resources at his disposal than his teacher Weise, who was ‘only’ employed at a gymnasium.

It can thus be seen that there were numerous reasons for the use or non-use and for the documentation of logic gestures between the 16th and 19th centuries.

4.2 Discussion on the current status of logic gestures

From the late 18th century onwards, there is a notable decline in the number of references to logic gestures, which ultimately cease to appear entirely from the 19th century onwards. Notwithstanding, Swinbourne’s illustration represents a notable exception. There are a number of potential explanations for this phenomenon. It is important to acknowledge that the advent of rationalism in Central Europe resulted in a notable decline in the utilization of visual communication techniques. This could also include logic gestures. In the first half of the 18th century, algebraic notations and written language were the dominant forms of communication. With the shift from rationalism to Kantianism at the end of the 18th century, logic diagrams came to dominate, and logical algebra declined. Diagrams were relatively simple to draw and increasingly inexpensive to produce in comparison to gesture drawings. From the end of the nineteenth century onwards, a phase known as the ‘crisis in intuition’ set in, during which many forms of visual communication declined in almost all areas of science (Friedman 2022). During this period, a significant number of diagrammatic forms were rendered obsolete, and the already scarce logic gestures became increasingly rare. As logic gestures also relate to syllogistics, which was increasingly replaced by predicate and class logic in the first half of the 20th century (Englebretsen 1990), logic gestures were probably considered obsolete by this time at the latest.

In the early 20th century, gestures and sign language were often regarded as inferior forms of communication within the field of linguistics (Woll 2013). The reasons for this are numerous and complex. For a considerable period in the 20th century, written language was regarded as the primary object of linguistic research. Early structuralist linguists, such as Ferdinand de Saussure, placed emphasis on the systematic nature of written language and focused on the abstract, rule-governed aspects of language that are easier to observe in written texts. Noam Chomsky’s generative grammar, which dominated much of 20th-century linguistic thought, placed emphasis on the formal properties of written or spoken language, particularly syntax. Both Saussure’s Course in General Linguistics and Chomsky’s Syntactic Structures largely ignore the role of gestures and sign language. This is facilitated by the absence of technology, as prior to the advent of video technology, it was challenging to capture and analyze visual communication due to the ephemeral nature of gestures and the dynamic aspects of sign languages. This was further compounded by the fact that sign languages were stigmatised and not recognized as ‘real languages’ with their own grammar and syntax.

This perspective has only rarely been challenged by studies such as Bill Stokoe’s groundbreaking study, Sign Language Structure (Power 2022). A significant shift was initiated by the publication of Per Linell’s The Written Language Bias in Linguistics in 1982, and subsequently reinforced by David McNeill’s Hand and Mind: What Gestures Reveal about Thought. Linell’s work critiques the dominance of written language in linguistic theory, advocating for a more inclusive approach that considers spoken and gestural communication. McNeill’s research further transformed the field by demonstrating that gestures are not merely supplementary to speech but are integral to the cognitive processes underlying communication. He proposed that gestures directly transfer mental images into visible forms, thereby conveying ideas that language alone cannot always express. This insight was first articulated in the early modern period, when gestures and sign language were recognized as a distinct and valid mode of communication. Such evidence can be found in the works of Bacon, Bulwer, and Schopenhauer (Wollock 2002).

The breakthrough for logic also only came in the 1990s when Sun-Joo Shin proved that every form of representation, be it symbolic notations, diagrams, or other forms, can have its own syntax and semantics (Shin 1994). It is not the type of representation but the way in which it is used that determines the status attributed to words, symbols, or schemata. Despite the considerable increase in the use and research of diagrams in logic and mathematics over the past three decades, logic gestures, which have been documented with even less frequency throughout history, remain largely unknown today. The examples presented in Section 2 also show that logicians of the early modern period attributed greater significance to gestures than large parts of the 20th century. Even if they did not define the distinctions between syntax and semantics as clearly as we do today in logic, they knew how to use gestures profitably in logic.

4.3 Discussion on the future of gesture research in logic

Gestures are not a current subject undergoing intense study in logic, neither in teaching nor in research. However, the digital transformation is massively changing the research and teaching landscape in logic, too. Against this background, new possibilities of doing logic and reflecting on logic arise alongside this development. In today’s teaching and research practice, it is becoming increasingly popular to bring highly abstract and formal logical proof steps “to life” by means of computer simulations and animations. The purpose of such dynamic visualizations is to make proof steps, which are statically presented in textbooks, better understandable and more comprehensible. But that’s not all. Additionally, visual proofs and diagrammatic reasoning, which are intuitive to human beings and have many advantages in the communicative practice among logicians and mathematicians, can be translated to computer-readable, formal languages.

Just to give an example: In her book on Gödel’s Theorem’s, Verena Huber-Dyson, a Swiss-American mathematician with a strong research focus on logic and group theory, has described the mathematical proof technique of “diagram chasing” as “a systematic form of hand waving” (Huber-Dyson 1991, p. 98), because it is a technique with one’s hand using arrows. The proof technique of diagram chasing makes it possible to encode a long equation derivation into a dynamic language of diagrams. Insofar as diagrams help conveying proofs otherwise consisting of overly pedestrian chains of equations. This is the reason why Silvia de Toffoli, among others, argues that diagrams are essential and indispensable for the practical performance of diagram chasing, (De Toffoli 2023). What Silvia de Toffoli does not mention, but Verena Huber-Dyson did, is the fact that this diagrammatic technique is profoundly gestural.

This interactive development between visualization and formalization is not only fascinating from a historical point of view. It is also instructive for gesture research in logic and offers a range of new perspectives and challenges. How might gesture research affect the future of logic? Here are some suggestions:

1. Formal semantic analysis of gestures has increasingly become a focal point in linguistics (Ebert 2024). There is also a considerable number of open-source software for gesture-driven programming languages available on the WWW. By contrast, there is practically no research focus on logic with gestures. One might ask how a future logic might look like that uses gestures as a means of representation. We know that diagrammatic reasoning can be formulated as equivalent to first order logic if a calculus for the diagram is defined that allows well-formed formulas to be derived. Developing such a procedure for gesture-based reasoning would be an important step towards multimodal communication and practice of reasoning and proving. In this context, it would be worth exploring the extent to which gesture-based logic is suitable for higher mathematics.

2. Videographic Data Analysis (VDA) is becoming a popular new research method that allows complex communication and action contexts to be explored in mathematics and logic, too. By means of VDA, gestures can be transformed into measurable data. This technological innovation opens up new possibilities to critically reflect on the (own) communicative practice of logical reasoning and raises awareness of the role of gestures and how the use of gestures constitutes the meaning and understanding of logical symbols, notations, proof steps, etc. From this perspective, VDA promises, among other new digital tools, to open up logic for sociological investigation.

3. Gesture research in logic has the potential to critically question and challenge standard narratives in logic that are deeply rooted in the historical-philosophical tradition. Such a standard narrative is, for example, that logic is the art of pure thinking, to paraphrase Antoine Arnauld and Pierre Nicole’s influential Logic or the Art of Thinking, a book that appeared under the French title La Logique ou l’art de penser in 1664, also known as the Port-Royal Logic, because the authors were theologians from the Port-Royal Abbey, a center of the Catholic Jansenist movement in seventeenth-century France and influenced by Cartesianism. The Port Royal Logic is an example of the significant overlap between interpretations of reasoning, rationality and theology. Despite the later separation between science and theology, the rhetoric concerning logic and pure thinking stayed alive, from Immanuel Kant’s characterization of logic as a kind of pure (non-empirical) thinking to Gottlob Frege, who proposed a formal language whose logic is capable of expressing `pure thought.` Such standard narratives are losing their persuasive power in the course of gesture research and the documented embedding of gestures in social communication practices.

4. The current technological developments and innovations are improving the ability to measure, document, record, and store gestures in interpersonal communication practices and human-machine interaction. As always, this research can not only be used but also abused. The digital transformation is even more far-reaching. It is also massively changing the objects of research themselves, their structure, and their content. What this means for our understanding of logic and the history of logic in theory and practice remains to be seen.