Eight-chain and full-network models and their modified versions for rubber hyperelasticity: a comparative study

3.1 Eight-chain model

In this model, the cuboid volume element, cf. Figure 1 is assumed to have edges parallel to the principal directions, which is composed of eight chains (hence the name eight-chain model) oriented in the diagonals from the center of the volume to its corners. The relation between edge length a₀ of the cuboid and the chain length r₀, in the undeformed state, is given by simple geometric relations, a0=23r0, wherein r0=lN is denoted as the end-to-end distance of an unstretched chain. In current deformed state it reads: r=r03-1λ12+λ22+λ32, where λ₁, λ₂, λ₃ are the principal stretches of the right Cauchy-Green tensor C=F^TF, F being the deformation gradient. By defining the mean value of the stretch λ_c, which is required to determine the expression for the macroscopic free energy, we obtain

Figure 1:

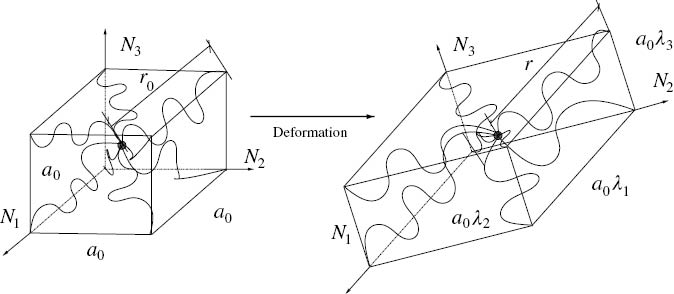
Eight-chain model: initial and deformed chain orientations and stretches.

In Eq. (4), I₁ is the first invariant of C, that is, I₁=trC. Inserting the Langevin statistics of a single chain, the free energy can be obtained as

with the relative chain stretch λc, r=λcN=I13N, where μ, N, γ are the shear modulus, the number of chain segments per chain and the inverse Langevin function, respectively. It is revealed that this model accurately captures the ultimate strain of network deformation while requiring only two material parameters, the shear modulus (μ), and the number of segments per chain (N). Due to the inherent micromechanical explanations in defining these two material parameters, such constitutive framework is often referred a micromechanically motivated model.

The analytical P_i(λ_i)-relations for the three deformation modes UN, EB, and PS, which are required to check the performance of the model on the Treloar data, are obtained from Eq. (1) as

Note that in approximating the inverse Langevin function (γ), the Padé approximation is applied due to its superior performance over other approximation procedures, that is, γ=ℒ  -1(λc, r)≈λc, r3-λc, r21-λc, r2, cf. [11]. By calibrating the UN, EB, and PS equations to the corresponding Treloar data, the optimal material parameters are estimated:

μUN=0.264 MPa,  μEB=0.358 MPa,   μPS=0.311 MPa,NUN=25.60, NEB=30.26, NPS=51.32.

The optimal material parameters obtained by using analytical expressions are utilized to simulate the experimental data of the other two deformation modes and their corresponding errors with respect to the Treloar data are calculated. The results, cf. Figure 2 are obtained by inserting the Padé approximation of the inverse Langevin function in the free energy function. It is clear from the Figure 2 that with a least number of material parameters, that is, two, this model produces better results in all deformation modes.

Figure 2:

Performance of the eight-chain model on the Treloar data. The fittings and simulations in two deformation modes (UN and EB) are good to excellent except in the pure shear case where the prediction fails to reproduce the S-shape of uniaxial case at high strains. Uniaxial simulation and fitting are almost concident (left), whereas equibiaxial simulation overestimates the Treloar data.

3.2 Modified Flory-Erman model

In most of the micromechanically inspired models, authors derive the energy functions by considering only the contributions from the cross-linking of polymer chains, whereas the contributions due to entanglements have been neglected. Boyce and Arruda [8] proposed a modification of their original model by adding a constraint term devised by Flory and Erman [21]. The assumption of Flory and Erman is that a long macromolecule network consists of numerous chain connection points, which are constrained from phantom characteristics due to the presence of neighbouring chains. As a result, the elastic strain energy of the network is originated from two contributions, that is, the phantom (ΨΨ_ph) and the topological constraint (ΨΨ_ct) contributions as

Flory and Erman [21] derived the phantom part of the energy function from the Gaussian chain statistics, equivalent to the Neo-Hookean case, that is, Ψph=∑i=13μ2[1-1ϕ][λi2-1] and the constraint part is obtained from the micromechanics of the chain molecules as

with Bi=κ2[λi2-1][λi2+κ]-2, Di=λi2κ-1Bi. In Eq. (10), the parameter μ represents the shear modulus, ϕ counts the number of chains joining at a junction, and κ measures the strengths of the constraints, respectively. Since the Flory-Erman model at large stretches deviates significantly from the actual response of the networks due to the Gaussian nature of its phantom part, Boyce and Arruda [10] applied their eight-chain energy function for the phantom part to improve the overall response, which, we designate here as the modified Flory-Erman model. Replacing the Neo-Hookean part by the eight-chain energy function, the modified Flory-Erman model yields

where μ, N, γ, λ_c,r are defined in Section 3.1.

The constraint contribution of the stress-stretch relations has to be derived from the single differentiation of the constraint part of the energy function appearing in Eq. (11) and is demonstrated in Appendix A. If the analytical expressions for UN, EB, and PS fit to the corresponding Treloar data, the optimal material parameter sets are found to be

[μUN, NUN, κUN]=[0.251  MPa,  25.46,  2.0][μEB, NEB, κEB]=[0.363 MPa,  37.75,  0.011][μPS, NPS, κPS]=[0.24 MPa,  22.07,  5.323].

Each of the parameter sets is used to simulate the experimental data of other two deformation modes. The results are plotted in Figure 3 as well as the corresponding errors from both fitting and simulation of experiments not used for the parameter identification. In comparison to the original eight-chain model, it is interesting to note that the inclusion of the constraint contribution to the eight-chain energy function improves the simulation for the EB in all three deformation cases as well as the simulations for UN and EB by the PS-fitted parameters, cf. Figure 3 (right). A small drawback of the modified model is that the additional contribution for the topological constraint yields a complicated lengthy expression for the stress-stretch relationships, see Appendix A.

Figure 3:

Performance of the Flory-Erman model modified by the eight-chain energy function on the Treloar data. The fitting quality and predictions are excellent, especially if compared to the similarly structured models, for example, the original eight-chain model or the Gent model, cf. Steinmann et al. [12].

3.3 GD model

To improve the prediction capability in multiaxial loadings for rubber-like materials, very recently Gornet et al. [19] proposed a strain energy function based on the first and second strain invariants of the right Cauchy-Green tensor. The first part is dependent on the first invariant and it corresponds to the Hart-Smith model. The equivalence between the eight-chain model and I₁-dependent part of the Hart-Smith model is established by Chagnon et al. [28]. To enhance the phantom network, that is, the cross-link part expressed by the first invariant I₁, an additional function based on I₂ is added to the energy function. Gornet et al. [19] show that such addition will constrain the eight-chains by a new network of chains on the surfaces of the cube, which mimics the behavior of the constraint contribution. Finally, the energy function of the GD model is expressed as

where h₁, h₂, h₃ are material parameters. Evaluation of Eq. (2) provides the corresponding analytical formulations for the UN, EB, and PS cases:

By calibrating the UN, EB, and PS equations to the corresponding Treloar data, the optimal material parameters are found:

h1UN=0.142MPa,     h1EB=0.194MPa,    h1PS=0.124MPa,h2UN=1.58e−2MPa, h2EB=2.0e−14MPa,h2PS=0.034MPa,h3UN=3.49e−4,         h3EB=2.56e−4,         h3PS=4.94e−4.

For validity of this model, each parameter set obtained from the optimization tool is used to simulate the other two deformation modes. The results are plotted in Figure 4 together with fitting and simulation errors in each case. It can clearly be shown here that the simulations for the EB and PS by the UN-fitted parameters produce results that are quantitatively much more acceptable than any other of the previous models with the same number of parameters, cf. Figures 4 (left and right). The simulations for the EB-fitted parameters overestimate the UN and PS data, cf. Figure 4 (middle), whereas the predictions for the PS-fitted parameters are good to fair, cf. Figure 4 (right).

Figure 4:

Comparison between the GD model and the Treloar data. Fitting to the analytical formulations and model prediction quality are excellent, especially in UN and PS. Only predictions for the EB-fitted parameters overestimate the UN and PS data.

3.4 Bootstrapped eight-chain model

In an attempt to improve the results for the eight-chain model at small strain, a new model called bootstrapped eight-chain model with only two material parameters (same as in the original eight-chain model) is proposed by Miroshnychenko and Green [18, 29]. They further assume that in order to improve results, especially in the biaxial deformation, an additive form of the strain energy function that involves two functions, one depends on the first invariant and the other on the second invariant of a deformation tensor, has to be formulated. Such an assertion is also supported by Pucci and Saccomandi [30], Hart-Smith [31]. The full strain energy function of the bootstrapped eight-chain model is written as:

where i₁=λ₁+λ₂+λ₃ and the definitions of λ_c, N are given in Section 3.1. For the complete expression of the eight-chain model, previous subsection is referred. The energy function from Eq. (16) yields three principal stresses as

Using Eq. (17), the analytical formulations for the three different deformation modes, that is, UN, EB, and PS are derived as

In Eqs. (18–20), λu=i1u3-λcu,  λb=i1b3-λcb,  λp=i1p3-λcp,  i1u=λ+2λ-1/2,  i1b=2λ+λ-2,  i1p=λ+λ-1+1 and λ_cu, λ_cb, λ_cp are defined in Eqs. (6–8).

Fitting the analytical Eqs. (18–20) to Treloar’s data yields the following parameter sets

μUN=0.277MPa,μEB=0.318MPa,μPS=0.322MPa,NUN=26.50,         NEB=30.11,          NPS=72.18.

Figure 5 depicts all fits, the simulations of complementary deformation modes that are not used during optimization and the deviations in comparison to the Treloar’s data. Both fitting quality and validity of the identified parameters are very good to excellent in the UN and EB cases. Optimization with respect to the PS data provides parameter sets that fail to predict the UN data, cf. Figure 5 (right). Similar to the classical eight-chain model, the bootstrapped model also fails to predict the S-shape in the case of UN for PS-fitted parameters. After analyzing the errors, fittings, and the validation results, it can be concluded that with the same number of parameters, the bootstrapped eight-chain model illustrates better performance in all deformation modes than the classical eight-chain model.

Figure 5:

Performance of the bootstrapped eight-chain model on the Treloar data. The fittings and simulations are good to excellent, especially if compared to the similarly structured models, for example, the original eight-chain model or the two-parameter Gent model.

3.5 Meissner-Matějka model

Based on the fact that to cope with the experimental data, not only the contribution from the cross-link part, but also a constraint term in the energy function is essential, Meissner and Matějka [22, 32] proposed an energy function where the cross-link term is derived from the structure-based Arruda-Boyce model and the constraint part is based on the first invariant of the generalized deformation tensor. Note that here the constraint part is exactly same as the constraint part in the extended tube model proposed by Kalikse and Heinrich [33]. Then, the total energy function is expressed:

where μ, N, μ_e, β(0<β≤1) are material parameters. The definitions of λ_c,r, γ are given in Section 3.1. Evaluation of Eq. (1) provides the corresponding analytical formulations for the UN, EB, and PS cases:

where λ_cu, λ_cb, λ_cp are defined in Eqs. (6–8). If one fits the UN, EB, and PS equations to the corresponding Treloar data, the optimal material parameters are found to be:

[μUN, μeUN, NUN]=[0.256 MPa, 0.055 MPa, 25.37][μEB, μeEB, NEB]=[0.270 MPa, 0.095 MPa, 23.47][μPS, μePS, NPS]=[0.217 MPa, 0.146 MPa, 20.37].

Concerning validity of this model, all resulting curves and corresponding errors in comparison with Treloar’s data are summarized in Figure 6. It reveals excellent fitting and validity of the model in all deformation modes. During optimization for the parameter identification, an important parameter, that is, β (0<β≤1) is kept frozen (β=0.2) as suggested by Kaliske and Heinrich [14] for better fitting and simulation of the Treloar data, even if it can be determined during parameter identification. Note that due to the presence of the constraint contribution in the energy function, the simulations for the equibiaxial case are better than the original eight-chain model. The predictions for the UN and PS cases by the EB-fitted parameters slightly overestimate the Treloar data, cf. Figure 6 (middle). In addition, it can be noted that this model captures all deformation mode data excellently if it is compared to the similarly structured three-parameters model, for example, the modified Flory-Erman model or the Gornet-Desmorat (GD) model.

Figure 6:

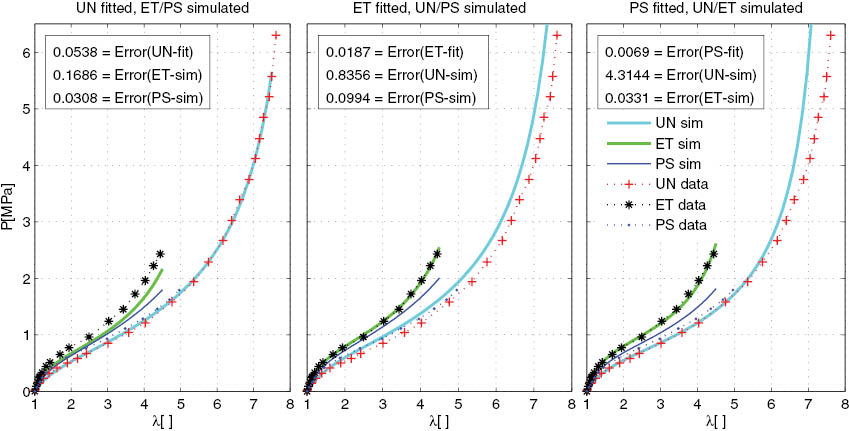
Performance of the Meissner-Matějka model on the Treloar data. The fitting quality and model predictions are excellent in all deformation modes.

3.6 Bechir model

As mentioned earlier, the classical eight-chain model ignores the contribution from the entanglements-like physical cross-links during deformation of the network. To add the effects of the interactions between chains of the cross-linked network, an extra energy function, in addition to the eight-chain energy function, is appended. The free energy of the constraint network is idealized using the standard three-chain energy function and the free energy of the unconstrained idealized network is constructed by means of the eight-chain model. Therefore, according to Bechir et al. [20], the total free energy function of this model is merely a combination of the two chain models, that is,

where β=ℒ  -1(λc,r), λc,r=λ12+λ22+λ323N8 and β¯j=ℒ  -1(λ¯rj), λ¯rj=kλjN3. In Eq. (25), μ_f, μ_c, N₈, N₃, k are shear moduli for the free and constraint parts, numbers of chain segments for the eight- and three-chain functions, and a nonaffine parameter, respectively. Bechir et al. [20] also proposed some relations for the material parameter set, for exampe, μ₀=μ_c+μ_f, where μc=[1-ηαN3]μ0,μ_f=ρλ_γμ₀, and α=+max+(λ̅₁, λ̅₂, λ̅₃). Note that λ̅_i relate to the principal micro-stretches, whereas λ_i are the line stretches (continuum stretches). Evaluation of Eq. (1) provides the corresponding analytical formulations for the UN, EB, and PS cases:

where λk=kλ,  λc,ru=λ2+2/λ3N8,  λc,rb=2λ2+1/λ43N8,  λc,rp=λ2+1+1/λ23N8.

Fitting UN, EB, and PS equations to the corresponding Treloar data, the optimal material parameters are obtained to be

[μUN, ρUN, ηUN, N3UN, N8UN]=[0.296 MPa, 1.28, 1.39, 71.83, 26.01][μEB, ρEB, ηEB, N3EB, N8EB]=[0.251 MPa, 1.46, 1.20, 68.20, 22.02][μPS, ρPS, ηPS, N3PS, N8PS]=[0.201 MPa, 1.26, 1.02, 56.21, 20.21].

To study the model performance, each parameter set obtained from the optimization tool is used to simulate the other two deformation modes. The results are plotted in Figure 7 together with fitting and simulation errors in each case. Although, this model inherits more parameters, that is, five in total, but it can be clearly seen that each set of optimal parameters produces simulation results for the complementary deformation modes that are not quantitatively improved than any other of the previous models of less parameters.

Figure 7:

Performance of the Bechir model on the Treloar data.

3.7 Wu-Giessen model

Several authors [23, 24, 34, 35] coin the term “full-network” where the chains are assumed to be randomly oriented in space for which the strain energy function is derived by integrating the response of all chains over the space. Since the numerical integration for such a full-network model is computationally costly, a weighted average is proposed by combining the three-chain and the eight-chain formulations which might provide better results than the individual three-chain or the eight-chain model [23], that is,

where the parameter ρ is a constant or related to some other physical quantity which is for instance related to the deformation process and Ψ_3c, Ψ_8c are energy functions for the three-chain and eight-chain models, respectively. Such form of the full-network model was proposed by Wu and Giessen [23] to improve the modeling capacity for amorphous glassy polymers, for example, polycarbonate, where the hyperelastic energy function is used for modelling the so-called back stress. Frequently used relation for ρ is ρ=0.85λmax/N, where λ_max=max(λ₁, λ₂, λ₃). The factor 0.85 is chosen to provide the best correlation of Eq. (29) with numerical integration of the full-network equation. The analytical expressions for UN, EB, and PS are obtained according to the idea of the Wu and Giessen [23] model as

where P1,8cUN, P1,8cEB, P1,8cPS and P1,3cUN, P1,3cEB, P1,3cPS are UN, EB, PS stresses for the eight-chain and three-chain models, respectively. For the derivations of P1,3cUN, P1,3cEB, and P1,3cPS, our previous work is referred [12]. To verify the sensitivity of the model with respect to different deformation modes and also with material parameters, if the UN, EB, and PS equations fit to the corresponding Treloar data, the optimal material parameters are identified:

μUN=0.318MPa,   μEB=0.403MPa,    μPS=0.309MPa,NUN=63.69,            NEB=58.00,             NPS=90.53.

Similar to other models, each parameter set of this model obtained from the fitting procedure is used to simulate the other two deformation modes and the corresponding errors are tabulated. The full-network model suggested by Wu and Giessen [23] predicts a biaxial stress-stretch response which falls in between the results predicted by the eight-chain model and that predicted by the three-chain model. Aiming at better performance over the eight-chain model or the three-chain model, the capability of this model to reproduce the experimental data for all deformation modes does not show any significant improvement so far, cf. Figure 8.

Figure 8:

Performance of the full-network model on the Treloar data.

3.8 Zuniga-Beatty model

Zuniga and Beatty [36] at first amend the original eight-chain and three-chain models by using a modified non-Gaussian (Kuhn-Grün) probability function in the case of energy function derivation. Jernigan and Flory [37] show that an amended distribution function, in contrast to the Kuhn-Grün function, provides a much improved approximation to the exact result over the entire range of λ_γ (relative chain stretch) values. Therefore, Zuniga and Beatty [36] rederive the energy functions for the eight-chain and three-chain models using the amended distribution function. Then, a modified full-network model is proposed by combining the amended versions of the eight-chain and three-chain models in the line of Wu and Giessen [23] concept. Wu and Giessen [23] assume the same value for the number of chain segments, that is, N for the eight-chain and three-chain models, which is unjustified due to inherent geometrical considerations of these two models. Hence, Zuniga and Beatty [36] propose separate values for N, that is,. N₃, N₈ for the three-chain and eight-chain models, respectively. Due to the amended form for the probability function, the energy functions of the eight-chain and three-chain models are as follows

and

In Eqs. (31) and (32), λc,r=I13N8, β=ℒ  -1(λc,r), βj=ℒ  -1(λrj), λrj=λjN3, where I₁ and λ_{c, r} are defined in Section 3.1. Hence, the modified form of the full-network energy function proposed by Zuniga and Beatty [36] is

where

In Eq. (34), Λ_L is related to the principal stretches through the state of deformation to which the continuum is subjected so that the greater stretch λ₁=Λ_L and the chain stretch for the eight-chain model is Λc=λ12+λ22+λ323 while a, b are two positive scaling factors. However, for simplicity, they choose to follow a=b=1, see Zuniga and Beatty [36] for details. The analytical formulations for the UN, EB, and PS for this composite model are

where the expressions for P1,3  cmUN, P1,3  cmEB, P1,3  cmPS, P1,8  cmUN, P1,8  cmEB, P1,8  cmPS can be obtained from Appendix B and λ_cu, λ_cb, λ_cp are defined in Eqs. (6–8). The optimal parameter sets for this model are estimated as

μUN=0.27MPa,   μEB=0.48MPa,   μPS=0.45MPa,N3UN=75.13,           N3EB=8.8,               N3PS=6.55,N8UN=25.12,           N8EB=28.55,           N8PS=31.49.

Concerning the validity of the model, the parameter set obtained from the optimization tool in each deformation case is used to simulate the other two deformation modes. The results are plotted in Figure 9 together with fitting and simulation errors in each case. The fittings and simulations for UN- and EB-fitted parameters are good to excellent in predicting the data for other deformation modes except a small overestimation is observed for the PS data. It can be clearly stated here that with an additional parameter, the Zuniga-Beatty version of the full-network shows better performance than the Wu-Giessen version. The reason might be that (i) Zuniga-Beatty used an improved version of the probability function and (ii) the scaling factor (ρ, in the original version of Wu-Giessen model) is replaced by a deformation-dependent stretch, cf. Eq. (34).

Figure 9:

Performance of the Zuniga-Beatty version of the full-network model on the Treloar data. The fitting and simulations in all deformation modes are excellent except an underestimation occurs in the case of UN data for the PS-fitted parameters.