Abstract
Recently, classification systems have received significant attention among researchers due to the important characteristics and behaviors of analysis required in real-time databases. Among the various classification-based methods suitable for real-time databases, fuzzy rule-based classification is effectively used by different researchers in various fields. An important issue in the design of fuzzy rule-based classification is the automatic generation of fuzzy if-then rules and the membership functions. The literature presents different techniques for automatic fuzzy design. Among the different techniques available in the literature, choosing the type, the number of membership functions, and defining parameters of membership function are still challenging tasks. In order to handle these challenges in the fuzzy rule-based classification system, this paper proposes a brain genetic fuzzy system (BGFS) for data classification by newly devising the exponential genetic brain storm optimization. Here, membership functions are optimally devised using exponential genetic brain storm optimization algorithm and rules are derived using the exponential brain storm optimization algorithm. The designed membership function and fuzzy rules are then effectively utilized for data classification. The proposed BGFS is analyzed with four datasets, using sensitivity, specificity, and accuracy. The outcome ensures that the proposed BGFS obtained the maximum accuracy of 88.8%, which is high as compared with the existing adaptive genetic fuzzy system.
1 Introduction
In recent years, substantial attention is paid to computational intelligence techniques such as fuzzy logic, artificial neural network, and genetic algorithm (GA), as they are able to solve complex engineering problems that are not easy to solve by traditional methods. The hybrid approaches are also noticeable in the computational intelligence field. A well-known hybrid approach is the hybridization between fuzzy logic and GA, which results in genetic fuzzy systems [3, 27]. A fuzzy system can be defined as a model structure that has the form of fuzzy rule-based systems (FRBSs) [11]. The fuzzy rule-based classification system (FRBCS) is a famous classification technique that has the ability to create a semantic model to the user. The FRBCS has wide range of applications [4, 14] successfully designed to support the need of intelligent decision support. The real-life problems of varied domains, such as classification, pattern recognition, classical network optimization, travel choice behavior models, pricing prediction system, cross-language question answering, disease prediction, web-based decision support system, behavior-based robotics, identification of quality of rice, and so on, employ FRBCS in order to achieve optimized rule learning [21].
FRBS [5, 6, 17] is one of the categories of fuzzy logic-based classifiers. A major problem in designing fuzzy expert systems is the development of fuzzy if-then rules and the membership functions (knowledge acquisition). Knowledge acquisition for a fuzzy expert system is generalized as a search problem in high-dimensional space in which each point corresponds to a rule set, membership function, and the respective system behavior. The fuzzy relation is a fuzzy set defined on universal sets, which expresses the relation between the input and output [7]. The fuzzy if-then rule is described by the domain experts; in the absence of domain experts, the rules must be taken from the training data space [1, 11, 13].
For generating and learning classification rules from numerical data, various techniques have been proposed, including simple heuristic procedures, clustering methods [13], and GAs [22]. The vast majority of heuristic and meta-heuristic algorithms such as particle swarm optimization [26], simulated annealing, firefly [18], and artificial bee colony optimization are some of the heuristic and meta-heuristic algorithms originated from the behavior of biological systems and physical systems in nature [3]. Several advantages and disadvantages exist for all these algorithms. As an example, simulating annealing can find the optimal solution if the cooling process is slow and the simulation is running long; yet, the fine adjustment in parameters affects the convergence rate of the optimization process [2]. For extracting a compact rule base, a hybrid fuzzy method is proposed in Ref. [23]. The drawback of this model is that it signifies only the rule set in the genetic population and so it does not model the fuzzy system completely. As the membership function and rule set are mutually dependent in a fuzzy system, they need to be developed at the same time [6].
In this paper, a hybrid system called brain genetic fuzzy system (BGFS) is developed for data classification. The proposed hybrid system contains two important phases. In the first phase, exponential brain storm optimization (EBSO) is integrated with GA and then applied to the design process. Here, the type of membership, membership function, and parameters are optimally found out using the proposed algorithm. In the second phase, the rules are optimally found using the EBSO algorithm, which includes three different constraints to find the optimal fuzzy rules. Finally, the classification is performed using the fuzzy inference system, which contains the optimal membership function and fuzzy rule derived through the proposed methods.
The main contributions of the paper are as follows:
A new fuzzy system called BGFS is developed for data classification by combining the traditional fuzzy system with the exponential genetic brain storm optimization (EGBSO) algorithm.
A new algorithm, called EGBSO, is developed for designing fuzzy membership functions by combining the exponential weighted moving average (EWMA) model, brain storm optimization (BSO) algorithm, and GA.
The paper is organized as follows: Section 2 reviews the literature, and Section 3 defines the problem and challenges considered. Section 4 presents the proposed methodology of BGFS for data classification. Section 5 experiments the method, and the conclusion is given in Section 6.
2 Literature Review
The literature presents different approaches for fuzzy rule-based classification, especially in fuzzy rule generation and membership function. GA, apriori algorithm, and ant colony optimization are applied for fuzzy rule extraction recently [5, 12, 15, 17, 27]. For membership function design, ant bee and genetic swarm algorithms are applied [6, 7]. Table 1 details the different methods of fuzzy classifier and their drawbacks along with the purpose.
Literature Survey.
| Authors | Algorithm | Purpose | Disadvantages |
|---|---|---|---|
| Dennis and Muthukrishnan [5] | Adaptive genetic algorithm for rule extraction | Rule generation and optimization | Simple and traditional way of designing membership function |
| Yi and Hullermeier [27] | Apriori-based algorithm | Rule generation and optimization | Many patterns may be uncovered |
| GaneshKumar et al. [6] | Hybrid ant bee algorithm | Membership function designing | Ant colony is not suitable for continuous search |
| GaneshKumar et al. [7] | Genetic swarm algorithm | Optimal rule set and membership function tuning | Genetic algorithm is more sensitive to global search |
| Meng and Pei [17] | Genetic algorithm | Rule extraction | Optimal designing of membership function is required |
| Hu et al. [12] | Genetic algorithm | Rule extraction | Only suitable for small problems because the computational cost is high |
| Juang et al. [15] | Ant colony optimization | Rule extraction | Multiple objectives are required for fuzzy design |
| Binu and Selvi [2] | Bat algorithm | Rule generation and optimization | Intelligence methods for designing the membership function are required |
| Angelov and Buswell [1] | Genetic algorithm | Rule generation | Divergence of the genetic operators is questionable |
| Casillas et al. [3] | Genetic algorithm | Rule generation | Divergence and exploration issues are still there for rule generation |
3 Problem Definition
The fuzzy system is widely applied for classification because it has the capability of providing flexibility and avoiding the learning time as compared with other classifiers like neural network and support vector machine. Even though the fuzzy system comes up with various applications, it found difficulty in designing its components, like rule base and membership function where domain experts’ knowledge is required even though historic data are available. These two important steps should be automatically performed to avoid the requirement of expert knowledge in a fuzzy classification system. This paper considers the challenges in the designing of membership function, and a new methodology is proposed.
Designing of membership function: Designing of membership function is another one important step to be performed in the fuzzy system before performing data classification. The designing of membership function should be done by handling the following challenges.
Challenge 1: How to choose the type and number of membership functions. The fuzzy system has different types of membership function, like Gaussian, triangular, and so on. Based on the data distribution, the type of membership function should be selected; however, identification of the distribution characteristics of data are very difficult manually. So, suggestion of membership function automatically suitable for the data space is a kind of search problem. The second challenge is the number of membership functions to be considered for the input variables. These two searching problems pose the challenging phenomenon in classification rate.
Challenge 2: How to define the parameters of membership function. The definition of range of values for every membership function corresponding to input variables and output variables is important because these two parameters are directly related to the output variable that affects the classification performance. So, rightly finding the parameters of membership function and the range of values is very important in the fuzzy system.
4 Proposed Methodology: BGFS for Data Classification
This paper proposes BGFS for data classification by newly devising the EGBSO algorithm. Here, a hybrid system called BGFS is developed for optimization of membership function. The EBSO is integrated with the GA and then applied to the design process. The type of membership, membership function, and parameters are optimally found out using the proposed algorithm. In the proposed algorithm, solution encoding, objective evaluation, and operations are utilized to easily search through the data space. Figure 1 shows the block diagram of the BGFS. In Figure 1, designing of membership function is carried out using the EGBSO-based algorithm and fuzzy rules are found out using the EBSO-based algorithm from the training data. For the classification phase, the input data are applied to fuzzification to convert the numerical data into linguistic data, and then the linguistic data are matched with the rule base for knowledge inference. After rule inference, the linguistic data are converted into fuzzy score values using the defuzzification phase. Finally, the fuzzy score is used to find the class label of the input data.

Block Diagram of the BGFS.
4.1 Optimal Designing of Fuzzy Membership Function Using EGBSO
The main objective is to design the membership function optimally by deriving the optimal parameters, and selecting the type and number of membership function optimally. The definition of membership function and optimal design process is explained in this section.
4.1.1 Fuzzy Membership Function
A membership function is a curve that provides a measure of the degree of resemblance of an element to a fuzzy set. The membership function fully defines within the fuzzy set. For example, the input database taken for the classification can be indicated as follows:
where m is the number of attributes and n is the number of data objects. Here, attribute is represented as Ai. The aim is to map the attributes to membership function, which can be represented as follows:
where μik is the membership function and p is the number of membership functions considered for an attribute Ai. Here, membership functions can take any structure, but there are some widespread examples that appear in real applications, like “dsigmf” (differential sigmoidal membership function), “gauss2mf” (Gaussian combination membership function), “gaussmf” (Gaussian curve membership function), “gbellmf” (generalized bell-shaped membership function), “pimf” (Π-shaped membership function), “sigmf” (sigmoidal membership function), “smf” (S-shaped membership function), “trapmf” (trapezoidal-shaped membership function), “trimf” (triangular-shaped membership function), and “zmf” (Z-shaped membership function).
Every attribute should be defined with p number of membership functions, and every membership function should be defined with three interval variables, like a, b, c, where a refers to the lower boundary and c defines the upper boundary where the membership degree is zero. b refers to the center having the membership degree of 1. The definition a membership function is given as follows:
So, from the above discussion, we understand that the selection of the shape of curve, the number of membership functions (p), and the interval variables for every membership function is an open challenge for obtaining better results.
4.1.2 Optimal Designing of Membership Function
This section discusses the optimal designing of membership function for fuzzy classification of data samples. Here, solution representation, fitness function, and operations are clearly described for the fuzzy classifier.
4.1.2.1 Solution Representation
Solution representation, or otherwise called as idea encoding, is about encoding of every challenges into a vector element to represent the solution vector. Accordingly, the number of element is 18*m, where m is the number of attributes. Every attribute is represented with eight elements. The 1st element represents the type of membership function, the 2nd element indicates the number of membership functions, and the 3rd–18th elements are encoded with the parametric values of membership function. The type of membership function varies between 1 and 10. The values point to these membership functions, “dsigmf,” “gauss2mf,” “gaussmf,” “gbellmf,” “pimf,” “sigmf,” “smf,” “trapmf,” “trimf,” and “zmf.” The number of membership functions varies between 2 and 4, and the parametric values of every membership function are represented from 3 to 18. If any membership function has only three parameters, then the first three elements of parameters are considered. Figure 2 shows the representation of the solution.
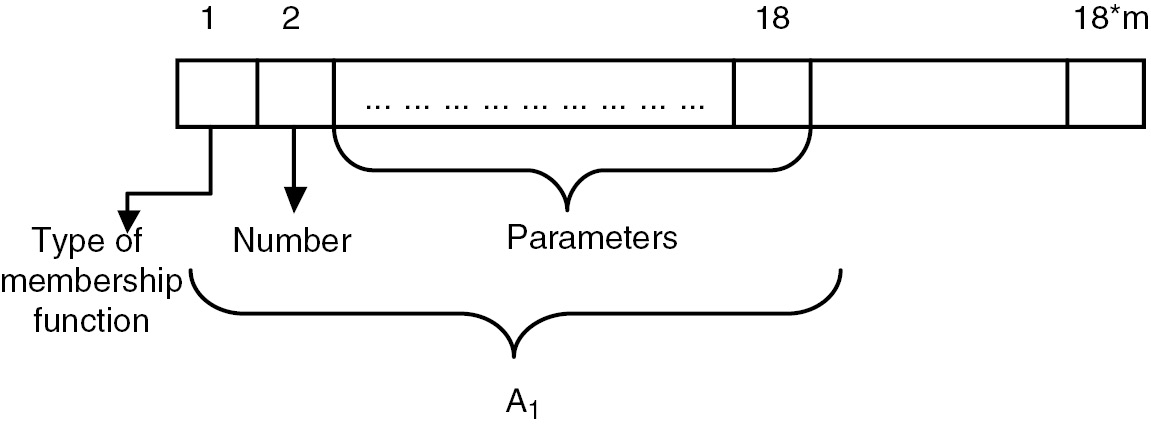
Solution Representation.
4.1.2.2 Fitness Function Formulation
The fitness function is evaluated by applying the membership function designed based on the solution directly to the fuzzy system. Here, rules are found using the EBSO algorithm, which is discussed below. Based on the rule definition and membership function, the fuzzy system is developed and the training data are applied to find the accuracy of the system based on the solution for all the data samples. The accuracy is taken as the fitness of the solution.
where true positive (TP) is correctly identified, false positive (FP) is incorrectly identified, true negative (TN) is correctly rejected, and false negative (FN) is incorrectly rejected.
4.1.2.3 Operations of EGBSO
BSO [24] is modified with mathematical theories called EWMA [9] and GA [18] to improve the design process. In the EGBSO algorithm, ideas are represented as a solution that is updated at every iteration. The advantage of the proposed EGBSO algorithm is better utilization of global information and further improvement of the exploitation and exploration through genetic operators. The pseudo code of the EGBSO algorithm is shown in Figure 3.

Pseudo Code of the EGBSO Algorithm.
Initialization: Assume that q ideas are randomly initialized within the search space, as Ii=⌊Ii1, Ii2, …, Iiq ⌋, where i=1, 2, …, q and d is the dimension of the solution that signifies the variable taken for optimization. In the initialization step, solutions are generated within the lower and upper bound of variables.
Updating ideas using P5a: After initialization, ideas are grouped into two set of ideas based on the k-means clustering algorithm, where k is the number of clusters required. Then, an idea is selected based on the probability and the solution is updated with a cluster center:
where
Updating ideas using P6b: Here, an idea is again selected based on the probability P6b and it is updated by randomly adding the values with a cluster center:
where N(μ, σ) is the random value generated through Gaussian distribution.
Updating ideas using P6bc and genetic operator: The one which is selected based on the P6bc is updated through the use of mutation operator. Mutation is a process of adding the randomly created values to the variables of the ideas.
Updating ideas using P6bc and the EBSO operator: The remaining ideas are updated using the following equation. The equation utilized in BSO algorithm is as follows:
In the EBSO algorithm, the updating of idea is modified using the EWMA model. According to the EWMA model, the prediction of idea can be formulated as
where e is the constant and E(t+1) is the output of the idea for the next iteration using the EWMA model. Et is the output of the pheromone of the last iteration using the EWMA model. The above equation can be rewritten as
where It is idea selected from the last iteration and It+1 is the to be newly generated idea. N(μ, σ) is the Gaussian random value with mean μ and variance σ, and w1, w2 are weight values of the two ideas. ξ is an adjusting factor slowing the convergence speed down as the evolution goes.
where s is a random value between 0 and 1. Ncmax and Nc denote the maximum number of iterations and the current number of iterations, respectively. K adjusts the slope of the logsig function.
Termination: Once all the ideas in the current iteration are completed, the fitness is computed for all the ideas that are generated newly. Then, the fitness is compared with old one and the current to select the ideas for the next iteration. This process is repeated for “t” numbers of iteration and the best idea is output as the optimal solution to the problem.
4.2 Rule Optimization by the EBSO Algorithm
In the proposed BGFS, the rules are optimally found using the EBSO algorithm. At first, ideas are encoded as a vector that contains the 1+m*r element. Here, m is the number of attributes and r is the number of rules. Then, q number of ideas is initialized and grouping is done using k-means clustering. Subsequently, based on the probabilities, the solutions are selected and updating is performed by adding random values with the cluster center. The remaining attributes are updated using the EBSO operator. Then, fitness is computed using the following equation:
where α, β, and γ are weighted constants; Li is the length of the rule; M(ri, D) is the matching count of rule ri and database D; and V(r, c) is the variance function of count of rules from every class.
Then, ideas of current and previous iterations are compared, and the worst one is replaced with the best idea. This process is repeated “t” number of iterations, and the best idea is selected as the fuzzy rule for the proposed BGFS.
4.3 Data Classification Using BGFS
Figure 4 shows the flow of the proposed BGFS for classification. From Figure 4, the classification is performed using the fuzzy inference system, which obtains the input through a fuzzifier. The fuzzifier translates crisp (real-valued) inputs into fuzzy values using the optimal membership function obtained through EGBSO. Then, an inference engine is used to obtain the fuzzy output using the rule inference mechanism. Here, fuzzy rules obtained from EBSO are applied. Then, a defuzzifier is used to translate the fuzzy value into a crisp value. Finally, the decision-making process is performed by the inference engine using the rules contained in the rule base to generate the fuzzy score, which gives the class label of the data sample.

Flow of the Proposed BGFS for Classification.
5 Results and Discussion
The proposed BGFS is analyzed with four datasets using three different metrics, and comparison of performance is also performed to prove the effectiveness of the method.
5.1 Dataset Description
Four datasets, namely PID, Cleveland, Diabetic Retinopathy Debrecen (DRD), and Lung cancer data are taken from UCI machine learning repository [25] for the experimentation. PID [10]: this database contains 768 data objects with eight attributes. This database contains the information of diabetic patients from Pima India. Cleveland [19]: this database contains 303 data objects with 14 attributes. This database contains the information of heart patients from Cleveland. DRD [8]: this dataset contains 1151 data objects with 20 attributes. The attributes are the features extracted from the Messidor image set corresponding to the diabetic patients. Lung cancer data [8, 16]: this dataset contains 32 data objects with 56 attributes. Every datum is related to the patients who are suffering from lung cancer.
5.2 Evaluation Metrics
The performance of the proposed BGFS is validated using three metrics called sensitivity, specificity, and accuracy. The definition of the metrics is given as follows:
where true positive (TP) is correctly identified, false positive (FP) is incorrectly identified, true negative (TN) is correctly rejected, and false negative (FN) is incorrectly rejected.
5.3 Experimental Setup
The proposed BGFS is implemented using MATLAB (R2014a) with fuzzy logic toolbox. The system has an i5 processor of 2.2 GHz CPU clock speed with 4 GB RAM and 64-bit operating system running Windows 8.1. The parameters to be fixed for the proposed BGFS are the constant e and the slope adjustment factor K. These parameters are fixed by analyzing their performance with various values, and the best parameter value is selected for the comparison. The performance is compared with the existing adaptive genetic fuzzy system (AGFS) given in Ref. [5], which is the adaptive GA for fuzzy design.
5.4 Qualitative Evaluation
Qualitative analysis of the fuzzy system refers to the analysis of the fuzzy rules extracted through the EBSO algorithm. The fuzzy rules extracted for the PID data are given in Table 2. From the table, we understand that the number of rules extracted is four and the length of the first and second rule is 9. The first rule says that if A1 is L OR A2 is VL OR A3 is VL OR A4 is H OR A5 is M OR A6 is H OR A7 is VLOR A8 is M THEN CLASS is L. Also, the second rule says that if A1 is H OR A2 is L OR A3 is M OR A4 is VL OR A5 is VL OR A6 is L OR A7is L OR A8 is VL THEN CLASS is H. Figure 5 shows the fuzzy window obtained through fuzzy logic toolbox of DRD data. The first section shows the designing of membership function and its parameters. The second system contains the rule base of the fuzzy Mamdani inference system and the final section is the defuzzifier section.
Rules from PID.
| Number of times pregnant (A1) | Plasma glucose concentration 2 h in an oral glucose tolerance test (A2) | Diastolic blood pressure (mm Hg) (A3) | Triceps skin fold thickness (mm) (A4) | 2-h serum insulin (mu U/ml) (A5) | Body mass index (weight in kg)/ (height in m2) (A6) | Diabetes pedigree function (A7) | Age (years) (A8) | Class variable | Weight | AND/OR method | |
|---|---|---|---|---|---|---|---|---|---|---|---|
| R1 | 2 | 1 | 1 | 4 | 3 | 4 | 1 | 3 | 1 | 0.5 | 1 |
| R2 | 4 | 1 | 3 | 1 | 1 | 2 | 2 | 1 | 2 | 0.5 | 1 |
| R3 | 1 | 2 | 3 | 1 | 2 | 1 | 1 | 4 | 2 | 0.5 | 1 |
| R4 | 2 | 1 | 4 | 1 | 2 | 3 | 3 | 2 | 2 | 0.5 | 1 |

Fuzzy Window of DRD Data.
5.5 Performance Evaluation of the Proposed Algorithm
The performance evaluation of the proposed BGFS is analyzed in this section. Figure 6 shows the parametric values of PID for various e and K values. The performance is almost the same for e constant of 0.3, 0.4, 0.5, and 0.7. The sensitivity, specificity, and accuracy for this e constant are all 88.44%; however, the value of 86.38% is obtained by the proposed system when the e constant value is fixed to 0.6. Also, for K value of 10, 15, and 20, the sensitivity, specificity, and accuracy are all 88.44%; however, 87.15% and 89.88% are obtained when the K value is fixed to 25 and 30. Figure 7 shows the evaluation results of Cleveland for various e and K values. From Figure 7, we understand that the evaluation metrics reached 83.05% for e constant of 0.3. The metric value for e constant of 0.4, 0.5, 0.6, and 0.7 is 87.3%, 88.44%, 86.62%, and 88.44%, respectively. Also, the same performance is obtained for K value of 10, 15, 20, and 25 for the proposed algorithm but the metric values are all 86.62% when the K value is fixed to 30. Figure 8 shows the experimental results of DRD for various e and K values. From Figure 8, we understand that the proposed BGFS obtained the same value of 88. 48% for all the e constants, but the BGFS obtained the accuracy of 88.48%, 88.48%, 86.68%, 87.27%, and 88.69% for the K value of 10, 15, 20, 25, and 30, respectively. Figure 9 shows the performance analysis of the BGFS method in Lung cancer data. From the graph, we understand that the proposed BGFS obtained the maximum accuracy of 85.71% when the e constant is fixed to 0.5. Similarly, for various values of K constant, the proposed BGFS obtained the maximum accuracy of 87.5% when the K value is fixed to 15.

PID for Various e and K Values
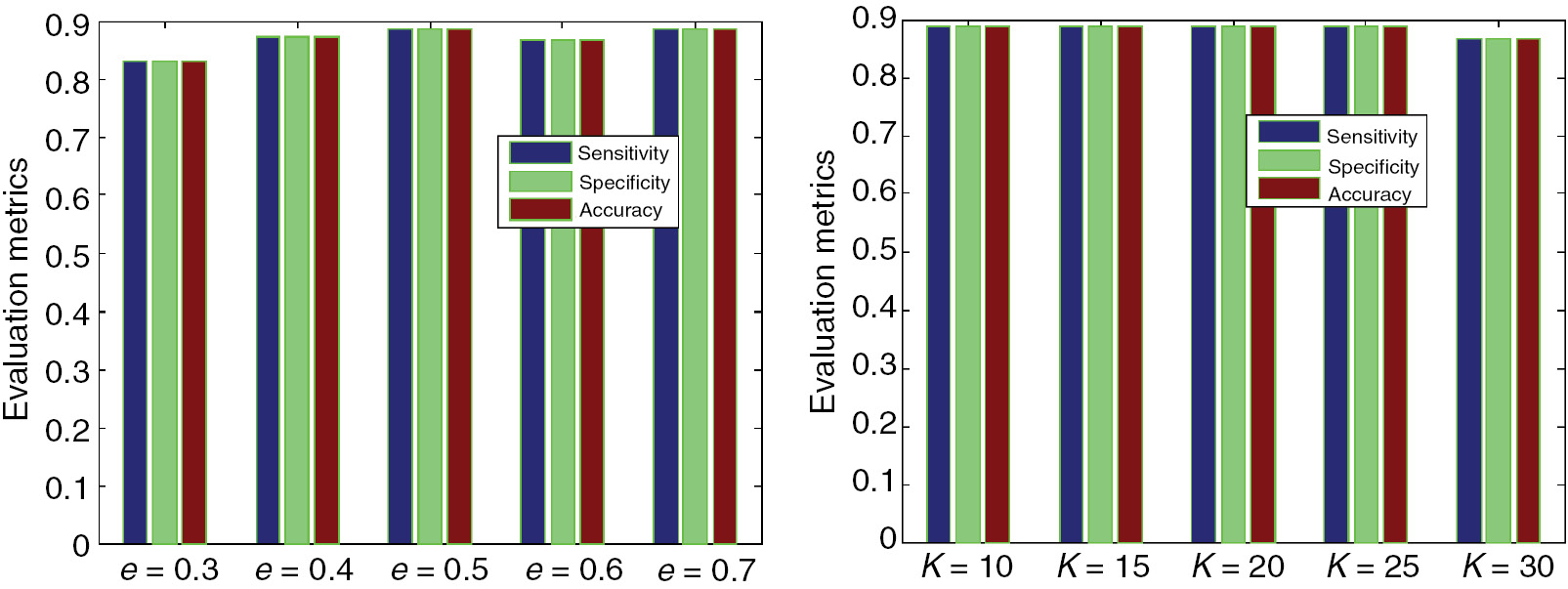
Cleveland for Various e and K Values.

DRD for Various e and K Values.

Lung Cancer Data for Various e and K Values.
5.6 Comparative Analysis
The comparative analysis of the proposed BGFS with the BSFS [20] and AGFS is given in this section. From Table 3, we understand that the accuracy of the BGFS, BSFS, and AGFS is 88.55%, 86.89%, and 86.52%, respectively, for the training data size of 70%. Also, for the training data size of 75%, the proposed BGFS obtained the value of 88%, which is higher than that of the other two existing systems. Similarly, the accuracy of the BGFS, BSFS, and AGFS is 88.4%, 87.01%, and 86.22%, respectively, for the training data size of 80%. Overall, the proposed BGFS outperformed the existing systems by reaching higher values in all the evaluation metrics.
Comparison on PID.
| Metrics | Size | AGFS | BSFS | BGFS |
|---|---|---|---|---|
| Sensitivity | 0.7 | 0.8652 | 0.8689 | 0.8855 |
| 0.75 | 0.8659 | 0.8667 | 0.8809 | |
| 0.8 | 0.8622 | 0.8701 | 0.8840 | |
| 0.85 | 0.8549 | 0.8582 | 0.8721 | |
| 0.9 | 0.8521 | 0.8600 | 0.8630 | |
| Specificity | 0.7 | 0.8652 | 0.8689 | 0.8855 |
| 0.75 | 0.8659 | 0.8667 | 0.8809 | |
| 0.8 | 0.8622 | 0.8701 | 0.8840 | |
| 0.85 | 0.8549 | 0.8582 | 0.8721 | |
| 0.9 | 0.8521 | 0.8600 | 0.8630 | |
| Accuracy | 0.7 | 0.8652 | 0.8689 | 0.8855 |
| 0.75 | 0.8659 | 0.8667 | 0.8809 | |
| 0.8 | 0.8622 | 0.8701 | 0.8840 | |
| 0.85 | 0.8549 | 0.8582 | 0.8721 | |
| 0.9 | 0.8521 | 0.8600 | 0.8630 |
Table 4 shows the performance comparison on Cleveland. When the training data size is fixed to 70%, the proposed BGFS obtained the accuracy of 88.84% but the existing BSFS and AGFS reached the value of 86.85% and 84.69%, respectively. For the training data size of 75%, the accuracy of BGFS, BSFS, and AGFS is 86.74%, 84.95%, and 84.3%, respectively. The performance of the proposed BGFS outperformed the existing systems in all the different samples of testing by reaching the maximum accuracy.
Comparison on Cleveland.
| Metrics | Size | AGFS | BSFS | BGFS |
|---|---|---|---|---|
| Sensitivity | 0.7 | 0.8469 | 0.8685 | 0.8884 |
| 0.75 | 0.8430 | 0.8495 | 0.8674 | |
| 0.8 | 0.8356 | 0.8655 | 0.8794 | |
| 0.85 | 0.8194 | 0.8763 | 0.8313 | |
| 0.9 | 0.7989 | 0.7989 | 0.8571 | |
| Specificity | 0.7 | 0.8469 | 0.8685 | 0.8884 |
| 0.75 | 0.8430 | 0.8495 | 0.8674 | |
| 0.8 | 0.8356 | 0.8655 | 0.8794 | |
| 0.85 | 0.8194 | 0.8763 | 0.8313 | |
| 0.9 | 0.7989 | 0.7989 | 0.8571 | |
| Accuracy | 0.7 | 0.8469 | 0.8685 | 0.8884 |
| 0.75 | 0.8430 | 0.8495 | 0.8674 | |
| 0.8 | 0.8356 | 0.8655 | 0.8794 | |
| 0.85 | 0.8194 | 0.8763 | 0.8313 | |
| 0.9 | 0.7989 | 0.7989 | 0.8571 |
From Table 5, we understand that the accuracy of BGFS, BSFS, and AGFS in DRD datasets is 88.48%, 87.23%, and 86.66%, respectively, for the training data size of 70%. Also, for the training data size of 75%, the proposed BGFS obtained the value of 88.4%, which is higher than that of the other two existing systems. Similarly, the accuracy of BGFS, BSFS, and AGFS is 87.5%, 86.8%, and 86.6%, respectively, for the training data size of 80%.
Comparison on DRD.
| Metrics | Size | AGFS | BSFS | BGFS |
|---|---|---|---|---|
| Sensitivity | 0.7 | 0.8662 | 0.8723 | 0.8848 |
| 0.75 | 0.8683 | 0.8726 | 0.8846 | |
| 0.8 | 0.8667 | 0.8687 | 0.8756 | |
| 0.85 | 0.8702 | 0.8681 | 0.8808 | |
| 0.9 | 0.8601 | 0.8640 | 0.88 | |
| Specificity | 0.7 | 0.8662 | 0.8723 | 0.8848 |
| 0.75 | 0.8683 | 0.8726 | 0.8846 | |
| 0.8 | 0.8667 | 0.8687 | 0.8756 | |
| 0.85 | 0.8702 | 0.8681 | 0.8808 | |
| 0.9 | 0.8601 | 0.8640 | 0.88 | |
| Accuracy | 0.7 | 0.8662 | 0.8723 | 0.8848 |
| 0.75 | 0.8683 | 0.8726 | 0.8846 | |
| 0.8 | 0.8667 | 0.8687 | 0.8756 | |
| 0.85 | 0.8702 | 0.8681 | 0.8808 | |
| 0.9 | 0.8601 | 0.8640 | 0.88 |
Table 6 shows the performance comparison on Lung cancer data. When the training data size is fixed to 70%, the proposed BGFS obtained the accuracy of 84.84% but the existing BSFS and AGFS reached the value of 80.35% and 80.35%, respectively. For the training data size of 75%, the accuracy of BGFS, BSFS, and AGFS is 83.87%, 80.125%, and 80.12%, respectively. The performance of the proposed BGFS outperformed the existing systems in all the different samples of testing by reaching the maximum accuracy. By comparing the overall performance for all the four datasets, the proposed BGFS outperformed the existing systems by reaching higher values in all the evaluation metrics.
Comparison on Lung Cancer Data.
| Metrics | Size | AGFS | BSFS | BGFS |
|---|---|---|---|---|
| Sensitivity | 0.7 | 0.7 | 0.8035 | 0.8035 |
| 0.75 | 0.75 | 0.8012 | 0.8012 | |
| 0.8 | 0.8 | 0.780 | 0.7803 | |
| 0.85 | 0.85 | 0.7888 | 0.8444 | |
| 0.9 | 0.9 | 0.7321 | 0.8035 | |
| Specificity | 0.7 | 0.7 | 0.8035 | 0.8035 |
| 0.75 | 0.75 | 0.8012 | 0.8012 | |
| 0.8 | 0.8 | 0.780 | 0.7803 | |
| 0.85 | 0.85 | 0.7888 | 0.8444 | |
| 0.9 | 0.9 | 0.7321 | 0.8035 | |
| Accuracy | 0.7 | 0.7 | 0.8035 | 0.8035 |
| 0.75 | 0.75 | 0.8012 | 0.8012 | |
| 0.8 | 0.8 | 0.7803 | 0.7803 | |
| 0.85 | 0.85 | 0.7888 | 0.8444 | |
| 0.9 | 0.9 | 0.7321 | 0.8035 |
Figure 10 shows the receiver operating characteristic (ROC) curve for PID and Cleveland data. The ROC curve is plotted in between the true-positive and false-positive rates. From the figure, we understand that the proposed BGFS shows the minimum false-positive rate as compared with AGFS and BSFS. Similarly, Figure 11 shows the ROC curve for DRD and Lung cancer data. This graph also clearly indicates that the proposed BSFS maintain the minimum false-positive rates as compared with AGFS and BSFS.

ROC Curve for PID and Cleveland.

ROC Curve for DRD and Lung Cancer.
6 Conclusion
We have proposed a new fuzzy system called BGFS for data classification. Our aim was to develop an automatic fuzzy genetic classifier with low computational cost. To do this, the traditional Mamdani fuzzy inference system is modified to automatically design the membership function and rules. In membership function design, EGBSO is developed by integrating the exponential model, BSO algorithm, and GA. In the fuzzy rule design, EBSO is applied with three objective constraints. The designed membership function and fuzzy rules are then effectively utilized for data classification. The proposed BGFS is analyzed with existing AGFS in four datasets using sensitivity, specificity, and accuracy. The outcome ensured that the maximum accuracy of 88.8% is obtained by the proposed BGFS as compared with the existing AGFS. Taking into account the results obtained, we can conclude that the proposed BGFS is a solid approach to deal with medical datasets, as it obtained the best accuracy in the experimental study. Future works can be in the direction of devising a single algorithm to design fuzzy membership function and rule definition.
Bibliography
[1] P. P. Angelov and R. A. Buswell, Automatic generation of fuzzy rule-based models from data by genetic algorithms, Inform. Sci.150 (2003), 17–31.10.1016/S0020-0255(02)00367-5Suche in Google Scholar
[2] D. Binu and M. Selvi, BFC: bat algorithm based fuzzy classifier for medical data classification, J. Med. Imaging Health Inform.5 (2015), 599–606.10.1166/jmihi.2015.1428Suche in Google Scholar
[3] J. Casillas, B. Carse and L. Bull, Fuzzy-XCS: a Michigan genetic fuzzy system, IEEE Trans. Fuzzy Syst.15 (2007), 536–550.10.1109/TFUZZ.2007.900904Suche in Google Scholar
[4] W. Combs and J. Andrews, Combinatorial rule explosion eliminated by a fuzzy rule configuration, IEEE Trans. Fuzzy Syst.6 (1998), 1–11.10.1109/91.660804Suche in Google Scholar
[5] B. Dennis and S. Muthukrishnan, AGFS: adaptive genetic fuzzy system for medical data classification, Appl. Soft Comput.25 (2014), 242–252.10.1016/j.asoc.2014.09.032Suche in Google Scholar
[6] P. GaneshKumar, C. Rani, D. Devaraj and T. A. A. Victoire, Hybrid ant bee algorithm for fuzzy expert system based sample classification, IEEE/ACM Trans. Comput. Biol. Bioinform.11 (2014), 347–360.10.1109/TCBB.2014.2307325Suche in Google Scholar PubMed
[7] P. GaneshKumar, T. A. A. Victoire, P. Renukadevi and D. Devaraj, Design of fuzzy expert system for microarray data classification using a novel Genetic Swarm Algorithm, Expert Syst. Appl.39 (2012), 1811–1821.10.1016/j.eswa.2011.08.069Suche in Google Scholar
[8] A. Goel and S. Kr. Srivastava, Role of kernel parameters in performance evaluation of SVM, in: Proceedings of 2016 Second International Conference on Computational Intelligence & Communication Technology (CICT), February 2016.10.1109/CICT.2016.40Suche in Google Scholar
[9] M. A. Grahama, A. Mukherjee and S. Chakraborti, Distribution-free exponentially weighted moving average control charts for monitoring unknown location, Comput. Stat. Data Anal.56 (2012), 2539–2561.10.1016/j.csda.2012.02.010Suche in Google Scholar
[10] Y. Hayashi and S. Yukita, Rule extraction using Recursive-Rule extraction algorithm with J48graft combined with sampling selection techniques for the diagnosis of type 2 diabetes mellitus in the Pima Indian dataset, Inform. Med. Unlocked2 (2016), 92–104.10.1016/j.imu.2016.02.001Suche in Google Scholar
[11] F. Herrera, Genetic fuzzy systems: taxonomy, current research trends and prospects, Evol. Intell.1 (2008), 27–46.10.1007/s12065-007-0001-5Suche in Google Scholar
[12] Y. Hu, R. Chen and G. Tzeng, Finding fuzzy classification rules using data mining techniques, Pattern Recognit. Lett.24 (2003), 509–519.10.1016/S0167-8655(02)00273-8Suche in Google Scholar
[13] I. Jagielska, C. Matthews and T. Whitfort, An investigation into the application of neural networks, fuzzy logic, genetic algorithms, and rough sets to automated knowledge acquisition for classification problems, Neurocomputing24 (1999), 37–54.10.1016/S0925-2312(98)00090-3Suche in Google Scholar
[14] Y. Jin, Fuzzy modeling of high-dimensional systems: complexity reduction and interpretability improvement, IEEE Trans. Fuzzy Syst.8 (2000), 212–221.10.1109/91.842154Suche in Google Scholar
[15] C. F. Juang, C. W. Hung and C. H. Hsu, Rule-based cooperative continuous ant colony optimization to improve the accuracy of fuzzy system design, IEEE Trans. Fuzzy Syst.22 (2014), 723–735.10.1109/TFUZZ.2013.2272480Suche in Google Scholar
[16] H. Liu, A. Gegov and M. Cocea, Complexity control in rule based models for classification in machine learning context, Adv. Comput. Intell. Syst.513 (2016), 125–143.10.1007/978-3-319-46562-3_9Suche in Google Scholar
[17] D. Meng and Z. Pei, Extracting linguistic rules from data sets using fuzzy logic and genetic algorithms, Neurocomputing78 (2012), 48–54.10.1016/j.neucom.2011.05.029Suche in Google Scholar
[18] M. Mitchell, An introduction to genetic algorithms, MIT Press, Cambridge, MA, 1998.10.7551/mitpress/3927.001.0001Suche in Google Scholar
[19] Purushottam, K. Saxena and R. Sharma, Efficient heart disease prediction system using decision tree, in: Proceedings of 2015 International Conference on Computing, Communication & Automation (ICCCA), May 2015.10.1109/CCAA.2015.7148346Suche in Google Scholar
[20] C. Ravi and N. Khare, BSFS: design and development of exponential brain storm fuzzy system for data classification, Int. J. Uncertain. Fuzziness Knowl. Based Syst., accepted.Suche in Google Scholar
[21] C. A. P. Reyes, Evolutionary fuzzy modeling, in: Coevolutionary Fuzzy Modeling, Lecture Notes in Computer Science, 3204, pp. 27–50, 2004.10.1007/978-3-540-30118-9_2Suche in Google Scholar
[22] M. Russo, FuGeNeSys – a fuzzy genetic neural system for fuzzy modeling, IEEE Trans. Fuzzy Syst.6 (1998), 373–388.10.1109/91.705506Suche in Google Scholar
[23] G. Schaefer and T. Nakashima, Data mining of gene expression data by fuzzy and hybrid fuzzy methods, IEEE Trans. Inform. Technol. Biomed.14 (2010), 23–29.10.1109/TITB.2009.2033590Suche in Google Scholar PubMed
[24] Y. Shi, Brain storm optimization algorithm, in: Advances in Swarm Intelligence, LNCS, 6728, pp. 303–309, 2011.10.1007/978-3-642-21515-5_36Suche in Google Scholar
[25] UCI Machine Learning Repository, Available from http://archive.ics.uci.edu/ml/, Accessed 10 October, 2015.Suche in Google Scholar
[26] X. S. Yang, Nature-Inspired Metaheuristic Algorithms, Luniver Press, 2008.Suche in Google Scholar
[27] Y. Yi and E. Hullermeier, Learning complexity-bounded rule-based classifiers by combining association analysis and genetic algorithms, in: Proceedings of the Joint 4th Conference of the European Society for Fuzzy Logic and Technology, pp. 47–52, Barcelona, Spain, September 2005.Suche in Google Scholar
©2018 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Artikel in diesem Heft
- Frontmatter
- Hybrid Weighted K-Means Clustering and Artificial Neural Network for an Anomaly-Based Network Intrusion Detection System
- A Critical Analysis on the Security Architectures of Internet of Things: The Road Ahead
- Double-Valued Neutrosophic Sets, their Minimum Spanning Trees, and Clustering Algorithm
- An Intelligent System for Identifying Influential Words in Real-Estate Classifieds
- Query-Specific Distance and Hybrid Tracking Model for Video Object Retrieval
- A Member Selection Model of Collaboration New Product Development Teams Considering Knowledge and Collaboration
- BGFS: Design and Development of Brain Genetic Fuzzy System for Data Classification
- Utilization of Co-occurrence Pattern Mining with Optimal Fuzzy Classifier for Web Page Personalization
- An Extensive Review on Data Mining Methods and Clustering Models for Intelligent Transportation System
- An Efficient Multiclass Medical Image CBIR System Based on Classification and Clustering
- Prediction Method of Railway Freight Volume Based on Genetic Algorithm Improved General Regression Neural Network
- A Grain Output Combination Forecast Model Modified by Data Fusion Algorithm
Artikel in diesem Heft
- Frontmatter
- Hybrid Weighted K-Means Clustering and Artificial Neural Network for an Anomaly-Based Network Intrusion Detection System
- A Critical Analysis on the Security Architectures of Internet of Things: The Road Ahead
- Double-Valued Neutrosophic Sets, their Minimum Spanning Trees, and Clustering Algorithm
- An Intelligent System for Identifying Influential Words in Real-Estate Classifieds
- Query-Specific Distance and Hybrid Tracking Model for Video Object Retrieval
- A Member Selection Model of Collaboration New Product Development Teams Considering Knowledge and Collaboration
- BGFS: Design and Development of Brain Genetic Fuzzy System for Data Classification
- Utilization of Co-occurrence Pattern Mining with Optimal Fuzzy Classifier for Web Page Personalization
- An Extensive Review on Data Mining Methods and Clustering Models for Intelligent Transportation System
- An Efficient Multiclass Medical Image CBIR System Based on Classification and Clustering
- Prediction Method of Railway Freight Volume Based on Genetic Algorithm Improved General Regression Neural Network
- A Grain Output Combination Forecast Model Modified by Data Fusion Algorithm

