Abstract
In this paper, we will present a novel and the first approach to transforming written Arabic numeral word format into a string of digits according to proposed Arabic numeral rules. In this work, we relied mainly on the Arabic stemmer to determine the digit number, where we proposed a set of stems for the main numbers. The proposed approach covers all problems associated with Arabic numeral texts, including different numeral word shapes and unordered sentences. That is, a textual number could be written in more than one format; moreover, we deal with Arabic accents. In addition, we propose to deal with simple spelling errors and using similarities to find the nearest correct word. The proposed approach covers all possible text numbers in the range of one to millions. Tests have been executed using a possible case from context numeral in the range above, and the experimental results have demonstrated that the proposed approach is promising in the sense that it provides an efficient and error-free transformation. Finally, we built an Android mobile-based application that uses the proposed approach to transform between three different formats: digits, numeral texts, and Abacus.
1 Introduction
As a natural language, Arabic is considered to be one of the most difficult languages to deal with in a localized context. This is because Arabic is rich in syntax, semantics, and morphology. In addition, written letters in Arabic have different shapes according to their position in the word, and accents also play a very important role in the meaning. Therefore, the Arabic language faces many challenges in the field of technology.
Arabic natural language processing has increasing importance, and many systems have been developed for a wide range of applications, including machine translation, information retrieval and extraction, speech synthesis and recognition, localization and multilingual information retrieval systems, text to speech, and tutoring systems. These applications had to deal with several complex problems pertinent to the nature and structure of the Arabic language [7].
In this research, we will focus on the Arabic numerals and how to deal with numbers. Numbers are noted in one or more symbolic formats: as written words (e.g. “one”), or as Arabic digits (e.g. “1”). Writing the numbers as words is a difficult task for a large class of people that have a high probability of errors. They sometimes use one number word in place of another and may write the number with spelling errors. So, we will focus on how to transform written Arabic numeral word format into a string of digits.
In previous works, many approaches and software applications in various languages (such as Swedish, English, French, and German) have been proposed to convert numbers [20].
Regarding the Arabic language, there are few works. For instance, Al-Taani et al. [1] proposed an Arabic Numerals Checker based on finite state transducers (FSTs) to represent numerals and the transformation process. More precisely, the system concentrates only on how to transform a particular number from a string of digits into a multiword format in Arabic language, taking into consideration the gender of the counted object. However, to our knowledge, there is no work for transforming Arabic numerals into digits, which we consider a complex and important point.
Therefore, in this work, we will discuss the difficulties associated with the transformation of Arabic numerals into digits and provide an approach that can deal with them. In fact, there are many problems when writing the numbers as words, especially involving spelling errors; the errors can occur due to deleted, inserted, substituted, and transposed characters, such as “ .” Also, numbers may be written in more than one format representing the same number. For instance, the following two formats “
.” Also, numbers may be written in more than one format representing the same number. For instance, the following two formats “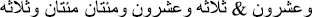 ” represent the number (223).
” represent the number (223).
After that, we will use the proposed approach for building an Android application as an educational Abacus program for children. This application will help children to develop skills about Abacus, numbers, counting, and to have practice in translating abacus configurations into Arabic numerals and vice versa.
There are many fields in which numbers are written as textual numbers. For instance, in the land department, land space and borders on both sides are written as words and as digits. Hence, the proposed work could be used for automatic validation and for checking the mismatch of the entered number as a word and the digit number. The same thing could be applied for financial transactions (such as in the trading business and in banking), when dealing with checks. Other applications can benefit from this work in searching operations by extracting the numbers in a document that are written as a string of words and converting them to digits.
The rest of this paper is organized as follows. Section 2 is dedicated to related works. Section 3 discusses the difficulties in the transformation process and presents the proposed approach. The dataset as well as the experimental results are presented in Section 4. Section 5 introduces the implementation of the Abacus system. We conclude in Section 6.
2 Related Works
Many authors have proposed works for spatial representation and transcoding of numbers. Most of them have focused on out-of-context number conversion; in other words, converting text numbers into digits and vice versa. Some works provide representations and analyses for numerals in various languages (Swedish, English, French, and German), and they suggest “deep structure” rules for converting numerals into digit representation and vice versa. For instance, the following are some of these rules used for English [20]:
Fusion rules: in this step, count the number of digits and divide them into a three-group string from right to left; then, identify the position word as in a hundred that is inserted after position 3.
Lexical rules: identify numerals and substitute the suitable texts for them (e.g. 2→twen/+ty|two).
Other approaches [6, 13, 14, 16, 17, 19] have focused on a model that converts from text format into digit format and vice versa. For example, “six thousand four hundred thirty-five”→6000 400 30 5” or 116→“one hundred plus sixteen.” McCloskey et al. [13, 14] proposed a “numerical transcoding” method based on an “abstract internal representation” of numbers, and it is accomplished by two stages: perception and production. The perception process converts the input form into an internal semantic representation, while the production process converts the semantic representation into numeral form. Both perception and production contain components for lexical and syntactic numerical elements. For example, for the numeral text “nine thousand three hundred ten,” the lexical and semantic numerical element forms are as follows:
nine; thousand; three; hundred; ten
The internal semantic representation is
{9}10EXP3; {3}10EXP2; {10}10EXP1
Then, take the individual numbers:
{9}; {3}; {10}
Finally, produce the result as 9310.
McCloskey et al. [14] proposed a structure for the number-production lexicon called the McCloskey model; this model can be placed within the context of a procedurally explicit model of the number-reading process. When a number is read, a number-production syntax device generates a syntactic frame based on number and digits. For example, for the number 4765, the syntactic frame would take the form
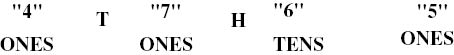
The T and H represent instructions for retrieving the phonological forms and the syntactic value /thousand/ and /hundred/; thereafter, producing a number involves successive retrieval of the phonological forms specified by the filled syntactic frame:
/four/ /thousand/ /seven/ /hundred/ /sixty/ /five/
Deloche and Xavier [6] proposed an alternative model instead of using the McCloskey theory; they provided the asemantic procedure in order to perform the transcoding process. The proposed approach drives a verbal numeral from an Arabic numeral, or vice versa, directly without using an abstract internal representation of the number. This is achieved by tracing the following steps to produce a number in a text format. In the first step, divide the digit number into triples from right to left. In the second step, group the result using punctuation marks, transform the leftmost groups into a three-digit frames, and fill empty positions with zero if the group is filled by one or two digits. In the third step, apply a set of rules to produce the first words of verbal numeral. For instance, the number 11,245 is transformed as follows. First, divide it into two groups, 11 and 245. Second, group them by parenthesis as (011) (245). Then, apply a set of rules that produce the words: (011)→eleven thousand and (245)→two hundred and forty-five. Finally, the produced result is eleven thousand and two hundred and forty-five. This approach did not gain accepted results as it fails to be extended to large numbers.
In Ref. [17], the authors have suggested a set of rules for realizing action expressions in a syntactic form <P> <N> (see Figure 1). Figure 2 shows the use of the proposed rules for the derivation of English numeral number 90,999.

The English Numeral System for Numbers up to 999,999.

Derivation of English Numeral for Number 90,999.
A semantic transcoding procedure has been proposed in Ref. [16] based on the analysis of numerals in Ref. [17] for translating Arabic numbers. This idea was based on subdividing the digit string and separating each part by a suitable multiplicand word. The procedure passes several iterations before arriving to the correct solution. This process takes some time because the most natural fragmentation strategy may yield a wrong subdivision of the digit string.
Seron and Deloche [19] presented a new way of simulating the cognitive processes of numeral transcoding by mapping verbal morphemes to Arabic digits in three layers and different networks. Verbal numbers used as input (number as a word) are represented in seven fields, and the output is represented in four fields, each of them represents a digit (0–9), or “null.”
More recent works [3, 8, 12, 15, 19] provided models of transcoding from digit to sequence words. The work in Ref. [19] depends on general structure parameters based on item length to transcode numbers from the digit form into the text form. The work in Ref. [15] has applied a semantic model, and Cohen et al. [3] applied a multiroute model (semantic and asemantic); in both, the transcoding process occurs in two routes: a “surface” route mapping any digit string into a word sequence according to the language-specific rules and a “deep” semantic route. Macoir et al. [12] suggested semantic and asemantic models of a number processing and transcoding system. The system includes different code-dependent pathways for transcoding spoken verbal numerals and text verbal numerals. The semantic conversion for Arabic digits is too slow to influence naming. The Stroop task [8] has been used in the number processing.
In Refs. [2, 5], the authors have proposed a model that implements a direct conversion from Arabic input to phonological output. Cipolotti and Butterworth [2] added semantic pathways to the semantic processing that is done by the McCloskey model, and they proposed a triple-code model in Ref. [5].
2.1 Researches for Arabic Language
Al-Taani et al. [1] provided an Arabic Numerals Checker that transforms a particular number from a string of digits into a multiword format. The proposed model considers the gender of the counted object. The work is based on FSTs to represent numerals and the transformation process. For example, for the number 783 and the gender male, the output is “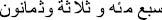 ”; for the number 11 and the gender female, the output is “
”; for the number 11 and the gender female, the output is “ ”. In this approach, the number is divided into a set of blocks that consists of three digits (hundred, tens, ones); each of these blocks are processed according to Arabic numeral rules.
”. In this approach, the number is divided into a set of blocks that consists of three digits (hundred, tens, ones); each of these blocks are processed according to Arabic numeral rules.
Dada [4] provided the details of implementing the Arabic numeral system in grammatical framework. The framework translated words into corresponding words in Arabic depending on the numeral counting (e.g. 1 message→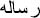 , 2 messages→
, 2 messages→ ).
).
As far as we have read, we did not find any work that translates from a written string of words into a string of digits in Arabic. The following section presents how to deal with Arabic numerals and provide how to transform a particular number from a string of words into a string of digits. For example, input the number is “ ” and the output is 783, and we will deal with any error in spelling of input number and correct it according to Arabic numeral rules.
” and the output is 783, and we will deal with any error in spelling of input number and correct it according to Arabic numeral rules.
3 Proposed Methodology
There are several difficulties in transforming written Arabic numeral word format into a string of digits. These difficulties are divided into two levels: word level and sentence level. At the word level, a number written as a word in Arabic is affected mainly by Arabic accents ( ) and added letters (infix and postfix). For instance, the word “
) and added letters (infix and postfix). For instance, the word “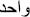 ” without accent is the same as the word “
” without accent is the same as the word “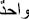 ” with accent. On the other hand, the same word may be written with added letters such as in “
” with accent. On the other hand, the same word may be written with added letters such as in “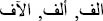 ” or may be in different words such as “
” or may be in different words such as “ ”. Each of these words represents different results, as in “
”. Each of these words represents different results, as in “ ” must be returned as “1,000,000” and “
” must be returned as “1,000,000” and “ ” must be returned as “2,000,000”. In addition, as we mentioned earlier, orthographic errors (errors in spelling) can occur due to inserted characters in the beginning, end, or middle (e.g. “
” must be returned as “2,000,000”. In addition, as we mentioned earlier, orthographic errors (errors in spelling) can occur due to inserted characters in the beginning, end, or middle (e.g. “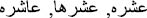 ”); deleted character from the beginning, end, or middle (e.g. “
”); deleted character from the beginning, end, or middle (e.g. “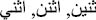 ”); or a substituted character (e.g. “
”); or a substituted character (e.g. “ ”).
”).
At the sentence level, more than one word connected together as a sentence may represent a number. This sentence may contain a composite number such as “ .” Also, it may be included with different orders, such as “
.” Also, it may be included with different orders, such as “ ” or “
” or “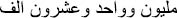 ”. When the sentence includes such different orders, the same number (1,021,000) should be returned.
”. When the sentence includes such different orders, the same number (1,021,000) should be returned.
In general, the flow of the proposed approach includes the following five main phases:
Preprocessing to eliminate the accents from the word (Section 3.1);
Using stemmer to find the roots for the numbers (Section 3.2);
Using the similarity to find the nearest number when the word has been written with spelling errors (Section 3.3);
Rebuilding the sentence to find the correct order if the sentence is unordered (Section 3.4);
Finally, generating the number according proposed Arabic numeral rules (Section 3.5).
3.1 Preprocessing
In this step, we will address problems related to single words including Arabic accent characters ( ) and the different characters such as in “
) and the different characters such as in “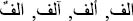 .” Though these words are different from each other, they represent the same number.
.” Though these words are different from each other, they represent the same number.
To solve these problems, we eliminate all extra characters from the word by scanning the word and replacing accented characters (e.g. “ ”) with the same character without accent (“ا”). Besides, the accents “
”) with the same character without accent (“ا”). Besides, the accents “ ” will be replaced by “null.”
” will be replaced by “null.”
For example, the word “ ”
”

However, this was not enough to cover all the preprocessing problems. For instance, writing the character “ ” is different than writing “
” is different than writing “ ,” though they have the same form. To solve this case, we add a new rule, in which any one of these characters “
,” though they have the same form. To solve this case, we add a new rule, in which any one of these characters “ ” will be replaced by “
” will be replaced by “ .”
.”

3.2 Stemming
There are many Arabic stemmers proposed for extracting the root from words [9–11, 18]. However, the Arabic stemmers found in the literature could not be used to directly deal with numbers. This is because several word numbers may have the same stem (such as “ ” and “
” and “ ”). Also, there are some numbers that can be written as a composite number (such as “
”). Also, there are some numbers that can be written as a composite number (such as “ ”). In addition, various words may refer to the same number (such as “
”). In addition, various words may refer to the same number (such as “ ”). Therefore, we build a table (Table 1) consisting of a set of stems for the main numbers.
”). Therefore, we build a table (Table 1) consisting of a set of stems for the main numbers.
Stems for Arabic Numbers.

3.3 Finding Similarity
In this section, we will deal with simple spelling errors and we correct the errors by finding the nearest word using a simple similarity between measures. The similarity measure is defined by the number of characters of the input word to match correctly (in the same order) with the saved word (Table 1) divided by the length of the saved word.
After calculating the similarity between the incorrect word and all the words in the dataset, the word that takes the largest similarity is taken.
For example, if the input word is “ ,” then the following are the similarity values with some words:
,” then the following are the similarity values with some words:

3.4 Ordering
The most important problem that we have faced in our research is related to the structure of the sentences (i.e. unordered forms). For instance, the sentence “ ” is in the correct order because the largest number (million part) comes in the first part then followed by the smaller number (thousand part). However, the sentence “
” is in the correct order because the largest number (million part) comes in the first part then followed by the smaller number (thousand part). However, the sentence “ ” is not in correct order because the smallest number (thousand part) comes in the first part then followed by the largest number (million part). In this case, there will be two different results, although it must be the same result:
” is not in correct order because the smallest number (thousand part) comes in the first part then followed by the largest number (million part). In this case, there will be two different results, although it must be the same result:
“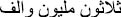 ” is equal to 30,000,100.
” is equal to 30,000,100.
“ ” is equal to 1,030,000,000.
” is equal to 1,030,000,000.
Before addressing this problem, we must initially identify the forms of sentences that could shape the numbers:
<Simple sentence>→

Example:
 .
. .
.
In this case, the order of these sentences does not affect the results, and the result in both sentences will be equal to “121.”
<Complex sentence> →<Simple Sentence>+

→<Simple Sentence>+

→<Simple Sentence>+

→

Case 1: <Simple sentence>+
Example:
“
 ” →The sentence is in order format (121,000,000).
” →The sentence is in order format (121,000,000).“
 ”→The sentence is in order format (1,000,121).
”→The sentence is in order format (1,000,121).“
 ”→The sentence is not in the correct order (1,000,121).
”→The sentence is not in the correct order (1,000,121).
To rebuild the sentence that is not in correct order format, we did the following:
Examine the position of million.
Split the sentence into two sentences (S1 and S2) from the character (“و”+“□”) that is located directly before the million.
Remove the character “و.”
Make swap between S1 and S2, then add (“و”+“□”) between them.

<S2> <و> <S1>………Split the sentence.

<S1> <و> <S2>………Make a swap between S1 and S2.
 .
.
Case 2: <Simple sentence>+
Example:
“
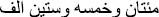 ” →The sentence is in order format (265,000).
” →The sentence is in order format (265,000).“
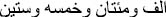 ”→The sentence is in order format (1,265).
”→The sentence is in order format (1,265).“
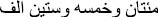 ”→The sentence is not in the correct order (60,205).
”→The sentence is not in the correct order (60,205).
To rebuild the sentence, we follow the same steps as in the case of million; however, this time, we examine the position of thousand.
Case 3: 
Example:
“
 ” →The sentence is in order format (9,071,000).
” →The sentence is in order format (9,071,000).“
 ”→The sentence is not in order format (9,071,000).
”→The sentence is not in order format (9,071,000).
In this case, we will deal with sentences containing million and thousand parts. Thus, we locate the position of million and the position of thousand, and then rebuild the sentence. If the position of million is before the position of thousand, then the sentence is in order form; otherwise, the sentence is in unordered form.
If the sentence is in unordered form, then split the sentence into two parts (S1 and S2) based on the character (“و”+“□”) that is located directly after the thousand part; S1=thousand part and S2=million part. After that, we make a swap between S1 and S2. To illustrate this, consider the following example:


<S2> <و> <S1>………Split the sentence.

<S1> <و> <S2>………Make swap between S1 and S2.
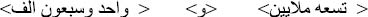
Case 4: <Simple sentence >+
Example:
“
 ” →The sentence is in order format (3,050,020).
” →The sentence is in order format (3,050,020).“
 ”→The sentence is not in order format (3,050,020).
”→The sentence is not in order format (3,050,020).
In this case, we split the sentence into three parts (S1, S2, and S3); S1=the thousand part, S2=the million part, and S3=Simple Sentence. Then, make a swap between S1 and S2. To illustrate this, consider the following example:

<S3> <و> <S2> <و> <S1>………Split the sentence.

<S3> <و> <S2> <و> <S1>………Make swap between S1 and S2.

It should be noticed that there are some ambiguous sentences having different interpretations even for a human. For instance, “ ” – this sentence has three meanings:
” – this sentence has three meanings:
In our approach, we decided to treat such cases as one sentence.
3.5 Generating the Number
In this step, we generate the number from the reordered numeral sentence either by summing or multiplying its parts depending on whether it is simple or complex. To illustrate the above steps, consider the generation of the number from the following complex sentence “ ”:
”:

4 Experiments and Evaluation
In this section, we provide the results of our approach and assess its quality by introducing a set of numeral sentences and converting them to digit numbers. Then, we manually validate the output.
4.1 Dataset
The evaluation has been conducted for two levels: word level and sentence level. For the word level, we have generated “one hundred” numeral words in Arabic that are written correctly without spelling errors (see Table 2). This set represents all the possibilities of single-word digits.
The Results for Level of Word.

Regarding the sentence level, we have written “one hundred and six” sentences that are written properly without spelling errors (see Table 3). Some of them are in correct order, while the rest are not in the correct order (about 16 sentences).
The Results for Level of Sentence.

4.2 Evaluation Results
At the word level, as shown in the results in Table 2, our system addressed all the difficulties. For instance, accent characters are treated properly. In addition, the system was able to treat various words that refer to the same number such as “ .” Finally, for a composite number as a whole word instead of two words such as in “
.” Finally, for a composite number as a whole word instead of two words such as in “ ,” our system will provide the correct digit number “800.”
,” our system will provide the correct digit number “800.”
Also, our system was able to solve all the problems related to the level of sentence regardless whether the sentence is in a correct order or not. The results in Table 3 show that all the sentences have been converted correctly.
5 Implementation
5.1 Tools and Implementation
For the implementation part of the research, the JAVA programming language and the Eclipse tool have been used to build the system, based on an Android application (http://developer.android.com/sdk/index.html). In this application, we relied on API version 17. The resulting system is targeted to any phone that supports Android applications with API version 8 and above.
5.2 Component
The user interface is simple and consists of an abacus panel; two text boxes, one of them used to enter the input number as digit and a second one to enter the number as a text word; and two buttons called “ ” and “
” and “ ” used for conversion and clear contents.
” used for conversion and clear contents.
The abacus panel can be used to represent the input number as the number of beads change. Each column of the abacus can represent numbers from 0 to 9, where the load of each column is different. Each bead in the first column has a weight of one; each bead in the second column has weight of 10, and so on. More precisely, the first three columns from the right represent the ones column, the tens column, and the hundreds column; the second three columns represent the thousands part; and the last three columns represent the millions part.
5.3 Interface
There are three ways to enter a number in the virtual abacus (as shown in Figure 3):
Enter the digit number in the first field. Press the “
 ” button when done. The abacus will update the number as a numeral word in the second field and represent this number in the abacus panel.
” button when done. The abacus will update the number as a numeral word in the second field and represent this number in the abacus panel.Enter the number as a word in the second field. Press the “
 ” button when done. The abacus will update the number as a digit in the first field and representing this number in the abacus panel.
” button when done. The abacus will update the number as a digit in the first field and representing this number in the abacus panel.Change the beads directly by pressing the button increment “+” and the button decrement “–”. Then, the number will be updated automatically as a digit number as well as a numeral word.
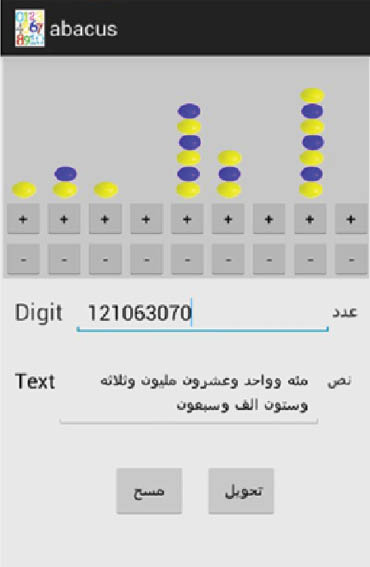
The Abacus Application with a Given Example.
6 Conclusion
The Arabic language is rich in syntax, semantics, and morphology. Among the many languages, there are sets of rules that should be considered during the processing of the Arabic language. Arabic numeral presentation is one of the special concerns. In this research, we have presented an efficient approach that transforms written Arabic numeral texts into a string of digits according to the Arabic numeral rules and vice versa. We developed an automatic application with a set of rules to convert text numbers into a string. The application is useful to many fields especially for banks, post office services, commercial transactions, financial transactions, and land and education departments. Other applications can benefit from this work in searching operations by extracting the numbers in a document written as a string and converting it into digits.
In our proposed approach, we solved all problems associated with the conversion from an Arabic numeral word into digits, and we proposed a set of stems for numbers, to solve the many problems related to the level of words, such as different writings that refer to the same number like in “ ”; additional characters; and accents like in “
”; additional characters; and accents like in “ .” In our work, we distinguished between converged words like in “
.” In our work, we distinguished between converged words like in “ ” and composite numbers like in “
” and composite numbers like in “ .” We presented a technique to solve sentences that are entered in unordered format such as “
.” We presented a technique to solve sentences that are entered in unordered format such as “ ” and “
” and “ .” Our system is able to deal with these problems and return the same number “7,002,000.”
.” Our system is able to deal with these problems and return the same number “7,002,000.”
Tests have been executed using a dataset of numeral texts, where we took a set of Arabic words and sentences that are written properly without spelling errors, and we took all the possibilities of words for the same number and sentences in different order. We entered these words and sentences into our system and obtained the result as digital numbers; we matched them with the supposed results that we obtained manually. The experimental results have demonstrated that the proposed approach is promising in the sense that it provides an efficient and error-free transformation.
The idea of this research was implemented as an educational abacus program for children on Android application in Java programming language and Eclipse environment. This system consists of an abacus panel, two text boxes, and two buttons. This system could be used to convert numbers from abacus to numeral text and digits, and vice versa.
Acknowledgments
This work has been achieved as a graduate research project at the Department of Computer Science/Faculty of Information Technology, Yarmouk University, Jordan, 2015.
Bibliography
[1] A. T. Al-Taani, S. A. Wedian and O. M. Darwish, Arabic numerals checker: checking agreement between numerals and counted objects in the Arabic language, Int. J. Comput. Process. Lang. 22 (2009), 341–357.10.1142/S1793840609002123Suche in Google Scholar
[2] L. Cipolotti and B. Butterworth, Toward a multiroute model of number processing: impaired number transcoding with preserved calculation skills, J. Exp. Psychol. Gen. 124 (1995), 375.10.1037/0096-3445.124.4.375Suche in Google Scholar
[3] L. Cohen, S. Dehaene and P. Verstichel, Number words and number non-words: a case of deep dyslexia extending to Arabic numerals, Brain 117 (1994), 267–279.10.1093/brain/117.2.267Suche in Google Scholar
[4] A. Dada, Implementation of the Arabic numerals and their syntax in GF, in: Proceedings of the 2007 Workshop on Computational Approaches to Semitic Languages: Common Issues and Resources, Association for Computational Linguistics, 2007.10.3115/1654576.1654579Suche in Google Scholar
[5] S. Dehaene, Varieties of numerical abilities, Cognition 44 (1992), 1–42.10.1016/0010-0277(92)90049-NSuche in Google Scholar
[6] G. Deloche and X. Seron, Numerical transcoding: a general production model, Lawrence Erlbaum Associates Inc., Hillsdale, NJ, 1987.Suche in Google Scholar
[7] A. Farghaly and K. Shaalan, Arabic natural language processing: challenges and solutions, ACM Transactions on Asian Language Information Processing (TALIP) 8 (2009), 14.10.1145/1644879.1644881Suche in Google Scholar
[8] W. Fias, B. Reynvoet and M. Brysbaert, Are Arabic numerals processed as pictures in a Stroop interference task? Psychol. Res. 65 (2001), 242–249.10.1007/s004260100064Suche in Google Scholar
[9] I. I. Hmeidi, R. F. Al-Shalabi, A. T. Al-Taani, H. Najadat and S. A. Al-Hazaimeh, A novel approach to the extraction of roots from Arabic words using bigrams, J. Am. Soc. Inf. Sci. Tec. 61 (2010), 583–591.10.1002/asi.21247Suche in Google Scholar
[10] S. Khoja and R. Garside, Stemming Arabic text, Computing Department, Lancaster University, Lancaster, UK, 1999.Suche in Google Scholar
[11] L. S. Larkey, L. Ballesteros and M. E. Connell, Improving stemming for Arabic information retrieval: light stemming and co-occurrence analysis, in: Proceedings of the 25th Annual International ACM SIGIR Conference on Research and Development in Information Retrieval, ACM, 2002.10.1145/564376.564425Suche in Google Scholar
[12] J. Macoir, T. Audet and M. -F. Breton, Code-dependent pathways for number transcoding: evidence from a case of selective impairment in written verbal numeral to Arabic transcoding, Cortex 35 (1999), 629–645.10.1016/S0010-9452(08)70824-4Suche in Google Scholar
[13] M. McCloskey, Cognitive mechanisms in numerical processing: evidence from acquired dyscalculia, Cognition 44 (1992), 107–157.10.1016/0010-0277(92)90052-JSuche in Google Scholar
[14] M. McCloskey, A. Caramazza and A. Basili, Cognitive mechanisms in number processing and calculation: evidence from dyscalculia, Brain Cognition 4 (1985), 171–196.10.1016/0278-2626(85)90069-7Suche in Google Scholar
[15] M. McCloskey, S. M. Sokol and R. A. Goodman, Cognitive processes in verbal-number production: inferences from the performance of brain-damaged subjects, J. Exp. Psychol. Gen. 115 (1986), 307.10.1037/0096-3445.115.4.307Suche in Google Scholar
[16] R. Power and M. F. Dal Martello, From 834 to eighty thirty four: the reading of Arabic numerals by seven-year-old children, Mathematical Cognition 3 (1997), 63–85.10.1080/135467997387489Suche in Google Scholar
[17] R. J. D. Power and H. Christopher Longuet-Higgins, Learning to count: a computational model of language acquisition, in: Proceedings of the Royal Society of London. Series B. Biological Sciences 200 (1978), 391–417.10.1098/rspb.1978.0024Suche in Google Scholar
[18] T. M. T. Sembok, B. M. Abu Ata and Z. A. Bakar, A rule-based Arabic stemming algorithm, in: Proceedings of the 5th European Conference on Computing, World Scientific and Engineering Academy and Society (WSEAS), 2011.Suche in Google Scholar
[19] X. Seron and G. Deloche, From 2 to two: an analysis of a transcoding process by means of neuropsychological evidence, J. Psycholinguist. Res. 13 (1984), 215–236.10.1007/BF01068464Suche in Google Scholar PubMed
[20] B. Sigurd, From numbers to numerals and vice versa, in: Proceedings of the 5th Conference on Computational Linguistics, Volume 2, Association for Computational Linguistics, 1973.10.3115/992567.992600Suche in Google Scholar
©2016 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Artikel in diesem Heft
- Frontmatter
- Low-Cost High-Tech Robotics for Ambient Assisted Living: From Experiments to a Methodology
- Performance Study of Harmony Search Algorithm for Multilevel Thresholding
- Tele-Health Monitoring of Patient Wellness
- An Experimental Comparison of Modeling Techniques and Combination of Speaker – Specific Information from Different Languages for Multilingual Speaker Identification
- Ontology Storage Models and Tools: An Authentic Survey
- SVM–ELM: Pruning of Extreme Learning Machine with Support Vector Machines for Regression
- A Cuckoo Search Algorithm With Elite Opposition-Based Strategy
- Automatic Data Clustering Using Parameter Adaptive Harmony Search Algorithm and Its Application to Image Segmentation
- Developing a System for Converting a Numeral Text into a Digit Number: Abacus Application
- Comparison of Search-Based Software Engineering Algorithms for Resource Allocation Optimization
Artikel in diesem Heft
- Frontmatter
- Low-Cost High-Tech Robotics for Ambient Assisted Living: From Experiments to a Methodology
- Performance Study of Harmony Search Algorithm for Multilevel Thresholding
- Tele-Health Monitoring of Patient Wellness
- An Experimental Comparison of Modeling Techniques and Combination of Speaker – Specific Information from Different Languages for Multilingual Speaker Identification
- Ontology Storage Models and Tools: An Authentic Survey
- SVM–ELM: Pruning of Extreme Learning Machine with Support Vector Machines for Regression
- A Cuckoo Search Algorithm With Elite Opposition-Based Strategy
- Automatic Data Clustering Using Parameter Adaptive Harmony Search Algorithm and Its Application to Image Segmentation
- Developing a System for Converting a Numeral Text into a Digit Number: Abacus Application
- Comparison of Search-Based Software Engineering Algorithms for Resource Allocation Optimization




