Abstract
Proxy signature and group signature are two basic cryptographic primitives. Due to their valuable characteristics, many schemes have been put forward independently and they have been applied in many practical scenarios up to the present. However, with the development of electronic commerce, many special requirements come into being. In this article, we put forward the concept of group–proxy signature, which integrates the merits of proxy signature and group signature for the first time. We also demonstrate how to apply our scheme to construct an electronic cash system. The space, time, and communication complexities of the relevant parameters and processing procedures are independent of group size. Our demonstration of the concrete group–proxy signature scheme shows that the concepts brought forward by us are sure to elicit much consideration in the future.
1 Introduction
In a proxy signature scheme, an original signer can delegate his sign ability to an entity called proxy signer. Then, the proxy signer can sign messages on behalf of the original signer. Since Mambo et al. [18, 19] put forward the concept of proxy signature [18, 19], many proxy signature schemes have been proposed [8, 11, 13, 15, 16, 22, 24–26].
The group signature scheme, introduced by Chaum and van Heyst [10], allows one user from a group to sign messages on behalf of the group without revealing his identity and without allowing the messages to be linkable to other signed messages. Thus, a group signature can be verified with the same and unique public key of the group. There exists an identity called group manager who can “open” particular signatures to revoke the anonymity of the signatures in such schemes. Sometimes a group manager can be divided into an issue manager called issuer and an open manager called opener. This is a desirable property that allows the distribution of trust. Group signatures are among the most important cryptographic primitives for providing privacy and have been used for applications such as anonymous credentials, identity escrow, voting and bidding, electronic cash (e-cash), etc. Many group signature schemes [1–7, 12, 14] have also been put forward as yet.
Let us consider the following scenario. Let O be the root entity of a company or an organization. For some reasons, for instance, it is absent or to improve processing efficiency, the root entity O will delegate his sign ability to its sub-entities similar to the proxy signature scheme. Let P be the set of the sub-entities and Pi be the entity with identity i∈9P. Then, each sub-entity Pi can sign messages on behalf of the original signer O. Under some circumstances, for example, the signer’s privacy needs to be protected, then any verifier can check the validity of the signature similar to the ordinary signature schemes but cannot compromise the real identity corresponding to the signature. Many branch banks who can dispense e-cash on behalf of the country’s central bank can be regarded as the typical application of the above scenario. Such schemes should have the following properties [9, 17]:
No bank should be able to trace any e-cash it issued. Therefore, the consumers can spend their e-cash anonymously.
All the branch banks form a group. Any vendor only needs to invoke a single universal verification procedure, based on the group public key, to ensure the validity of any e-cash he receives.
There is a single public key for the entire group of the branch banks, and the size of this public key should be independent of the number of the branch banks. Therefore, when more branch banks join the group, the public key does not need to be modified.
In case of dispute, there exists some entity in the group formed by the branch banks who can “open” the particular signature and trace the real branch bank who issued the particular e-cash. No one else can determine the identity. No vendor can even determine the bank from which the consumer obtained his e-cash even though the vendor can easily check that the e-cash is valid. This restriction gives an extra layer of anonymity because it conceals both the spender’s identity and the bank who issued the e-cash.
One key point of realizing multibank e-cash system is secure delegation. Concretely, the central bank securely delegates his sign ability to the branch banks. It is similar to the concept of proxy signature. Thus, the concept of proxy signature can be applied to the e-cash system.
Another key point of realizing multibank e-cash system is anonymity. Specifically, after being delegated by the central bank, each branch bank should issue the e-cash anonymously. However, to resist malicious branch banks, there also exists a group manager in the group formed by all the branch banks who can “open” the particular signature and trace the actual issuer. Thus, from this angle, the concept of anonymous e-cash system is similar to the concept of group signature, and the ideas of group signatures can be adopted in e-cash system.
Some scheme [27] just adopts the proxy signature to realize the e-cash system. To prevent the malicious original signer, a third trust party is introduced into the system. Thus, the efficiency is compromised. Furthermore, to satisfy the anonymity requirements, the identity of the branch bank cannot be used to verify the validity of the ultimate signatures. Thus, to satisfy the above requirements, only proxy-unprotected signature can be adopted. That is, all the branch banks use the same secret key delegated jointly by the central bank and the trust party to generate the signatures. Thus, on the one hand, schemes constructed this way cannot resist a frame attack coming from the coalition of the central bank and the third trust party. On the other hand, to resist the coalition attack, the branch bank’s secret key could be additionally required and integrated into the delegation key generated by the central bank and the third party. However, when verifying the ultimate signature, the branch bank’s public key is needed. Thus, a large number of the branch bank’s public key certificates need to be stored, and efficiency declines quickly. Furthermore, the anonymity is difficult to satisfy when the branch bank’s private key and public key are used to generate and verify the signature, respectively.
Lysyanskaya and Ramzan [17] combined the notions of blind signatures and group signatures and presented a group–blind signature and applied it to e-cash system. However, first, their scheme is of low efficiency because the vendor must engage in a protocol with the bank to resist the double spending each time he receives an e-coin from the consumer. Second, the consumer must engage in an expensive several round interactive protocol with the banks each time he wants a new e-coin.
To achieve the requirements of a secure e-cash system listed above, we put forward a novel practical group–proxy signature scheme. Our scheme combines the already existing notions of proxy signatures and group signatures. It is an extension of Miyaji and Umeda’s signature scheme [20] that adds the proxy property. We will show how our scheme can be applied to construct a practical e-cash system where multiple branch banks pertained to the central bank and the branch banks can substitute the central bank to distribute anonymous and untraceable e-cash. Moreover, the identity of the e-cash-issuing bank, i.e., the branch bank, is concealed. All the branch banks form a group, and in case of dispute, the anonymity of the signature can be compromised by the group manager entity in the group.
The rest of the article is organized as follows. In the next section, we describe some preliminaries and the concept and model of the group–proxy signature. Then, our concrete group–proxy signature scheme is presented in Section 3. Some security analysis and performance evaluations are discussed in Sections 4 and 5, respectively. Finally, the conclusions and remarks are made in Section 6.
2 Preliminaries and the Group–Proxy Signature Model
2.1 Notations
For a set A, a ∈RA means that a is chosen randomly and uniformly from A, and A / {a} means that A – {a} = {x ∈ A|x ≠ a}. For a group G = 〈g〉, ord(g) means order of g in G. The bit length of a is denoted by |a|. Let c[j] be the jth bit of a string c. We use ‖ to denote the concatenation of two (binary) strings or of binary representations of integers and group elements.
2.2 Signature Based on Proof of Knowledge
In a signature based on proof of knowledge (SPK), the signer ties his knowledge of a secret to the message to be signed. Thus, a signature of knowledge is used to sign a message and to prove the knowledge of the secret. Without the secret, no one can generate the valid signature. Signatures of knowledge were used by Camenisch and Stadler [6]. Their construction is based on the Schnorr signature scheme [23] to prove knowledge. All the signature of knowledge proposed by Camenisch and Stadler [6] can be proved secure in the random oracle model and their interactive versions are zero-knowledge.
We use several existing protocols of signature of knowledge [6] such as proving the knowledge of double discrete logarithm on a message and proving the knowledge of representations of some elements to the other bases on a message as building blocks in our proposed scheme. Due to space limitation, we omit the details of these protocols here. For more discussions, please refer to Ref. [6].
2.3 The Group–Proxy Signature Model
Our group–proxy signature model extends the group signature over only known-order group [20]. Generally speaking, our proposed group–proxy signature model comes from the basic group signatures [20] and integrates the properties of proxy signatures. Our model allows the member of a group to sign messages anonymously on behalf of some original entity such that the following properties hold for the resulting signature.
Strong unforgeability: Only delegated group members can issue valid signatures on behalf of the original signer.
Signer anonymity and signatures unlinkability: Given a signature, no one except the group manager can determine which group member issued the signature. It is infeasible to determine whether two message–signature pairs were issued by the same group member.
Undeniable signer identity: The identity of the group member who issued the valid signature can always be traced by the entity called group manager.
Secure against framing attacks: Neither the original signer nor the coalition of the original signer and some subset of the delegated group members can generate valid signatures on behalf of other group members.
2.4 Participants and Procedures
Our group–proxy signature scheme consists of a trusted party for the initial setup, the original signer O, two group managers (the issuer and the opener), and group users Pi with unique identities i ∈ N (the set of positive integers). All Pi’s form a group G. Each Pi can join G by its interaction with the issuer. Then, Pi can sign messages anonymously on behalf of O. In case of dispute, the identity of each group–proxy signature can be traced by the opener. Our scheme is specified as a tuple GPS = (Setup, Delegate, Join, Sign, Verify, Open) of polynomial–time algorithms described as follows.
Setup: A probabilistic algorithm that generates the public keys Yo, Yik, Yok and the corresponding private keys xo, xik, xok for the original signer O, the issuer, and the opener.
Delegate: An algorithm that inputs the original signer’s secret key and outputs the proxy signer Pi’s delegation key so.
Join: An interactive protocol between the issuer and the new group member Alice that produces Alice’s secret key x, her membership certificate v, and her public key z.
Sign: An algorithm on input message m, some user’s delegation key so, secret key x, and his membership certificate v produces a signature s on m that satisfies the properties above.
Verify: An algorithm on input (m, s, Yo, Yik, Yok), determines if s is a valid signature for the message m with respect to the corresponding public information.
Open: An algorithm on input (s, xok) returns the identity of the real identity who issued the signature s.
3 Our Proposed Scheme
As shown in the above sections, our proposed group–proxy signature scheme extends the group signature scheme [20] that adds the proxy property. Our scheme allows Pi to prove the knowledge of his delegation key so corresponding to the valid delegation procedures and the original signer’s private key and his membership certificate (Ai, bi) corresponding to his secret key xi. Let P̃ be a prime with P | P̃ - 1, P = pq and q | p – 1. Let g, g1, g2 be the q-order elements in 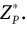 Thus, after obtaining a delegation key so from the original signer O, Pi selects a secret key xi and obtains his membership certificate (Ai, bi), satisfying
Thus, after obtaining a delegation key so from the original signer O, Pi selects a secret key xi and obtains his membership certificate (Ai, bi), satisfying 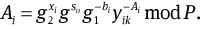 Precisely, our proposed scheme consists of six algorithms as follows.
Precisely, our proposed scheme consists of six algorithms as follows.
3.1 System Setup
Suppose k is a security parameter. To set up the group–proxy signature scheme, similar to Miyaji and Umeda [20], the following procedures are performed:
Suppose H : {0, 1}* → {0, 1}k be the secure, collision resistant, one-way hash function.
Choose a random k-bit prime q and a random prime p, such that q | (p – 1) and set P = pq.
Choose a random prime P/̃ such that P | (P̃ - 1).
Denote cyclic subgroup
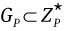 with order q and
with order q and 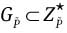 with order P.
with order P.Choose random elements g, h, g1, g2, g3 and g4 ∈RGP / {1} such that the discrete logarithms based on each other elements are unknown.
Choose a random element
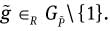
Compute
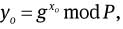
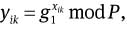 and
and 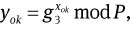 where xo, xik, xok ∈RZq are kept secret by the original signer O, the issuer and the opener, respectively.
where xo, xik, xok ∈RZq are kept secret by the original signer O, the issuer and the opener, respectively.Output the group public key PK =(q, P, P̃, g, h, g1, g2, g3, g4, g̃, yo, yik, yok) and the secret key SK = (xo, xik, xok ∈RZq).
3.2 Generation of the Delegation Key
The original signer O performs the following steps to generate the proxy signing key and delegate his sign ability to the proxy signers:
Generate the warrant mω, which consists of the type of the delegated information, the original and the proxy signers’ identities, the delegation period, etc.
Select ko ∈RZq and compute
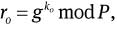
so = xoH(mω ‖ ro) + ko mod q,
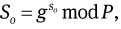
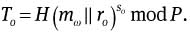
ro, So, To are published by the original signer.
Send (ro, so, mω) to the proxy signer Pi ∈ G via secure channel.
After receiving (ro, so, mω), the proxy signer Pi verifies the validity of the original signer O’s signature by checking
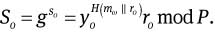
Finally, so is kept secret by the proxy signer Pi, and it will be used to generate the proxy signer’s private signing key in the later sections.
3.3 Registration
In this protocol, after receiving the delegation secret so, user Pi and the issuer jointly perform the following procedures. In the end, Pi obtains a random value xi ∈ Zq satisfying 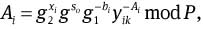 where xi is only known by Pi, and Ai, bi are generated by the issuer manager. The concrete procedures are as follows.
where xi is only known by Pi, and Ai, bi are generated by the issuer manager. The concrete procedures are as follows.
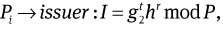 where t, r ∈RZq.
where t, r ∈RZq.Pi ← issuer : u, v ∈RZq.
Pi computes
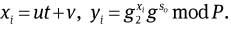
Pi → issuer : yi and a signature on the warrant mω based on the proof of knowledge of (α, β, τ) such that To = H(mω ‖ro)β mod P,
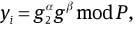 and
and 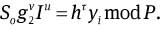 Precisely, Pi executes as follows.
Precisely, Pi executes as follows.
Choose random integers r1, r2, r3 ∈RZq.
Compute
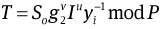 and to = H(mω‖ro) mod P and
and to = H(mω‖ro) mod P and 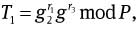
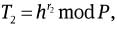
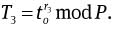
Compute c = H(g2‖g‖h‖to‖yi‖ T‖ To‖ T1‖T2‖ T3‖ro‖mω).
Compute in Zp: s1 = r1 – cxi, s2 = r2 – cur, s3 = r3 – cso.
Send (c, s1, s2, s3) to the issuer.
After receiving (c, s1, s2, s3), the issuer computes
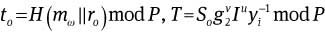
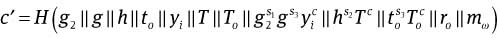
and checks whether c′ = c holds. If not, the protocol aborts.
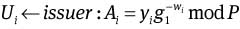 and bi = wi – Aixik mod q, where wi ∈RZq.
and bi = wi – Aixik mod q, where wi ∈RZq.Ui verifies that
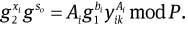
Finally, Pi obtains a membership key (xi, so) and a membership certificate (Ai, bi) ∈ ZP×Zq, and the issuer inserts (IDi, Ai, bi) into the member list ML.
3.4 Signature Generation
To sign a message m, any legitimate Pi executes the following procedures.
Choose a random integer w ∈RZq.
Compute
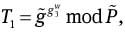
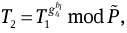
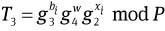 and
and 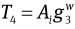
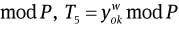 and
and 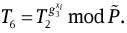
Choose random integers w1j, w2j, w3j ∈RZq, for 1≤j≤k.
Compute
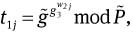 2
2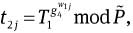
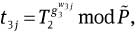 and
and 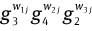 mod P, for 1≤j≤k.
mod P, for 1≤j≤k.Compute c1 = H(g2‖g3‖g4‖‖g̃‖T1‖T2‖T3‖T6‖t11‖…‖t1k‖t21‖…‖t2k‖t31‖…‖t3k‖t41‖…‖t4k‖mω‖m), s1j = w1j – c1[j]bi mod q, s2j = w2j – c1[j]w mod q, and s3j = w3j – c1[j]xi mod q, for 1≤j≤k.
Remark 1. The above protocol is actually the signature of knowledge of
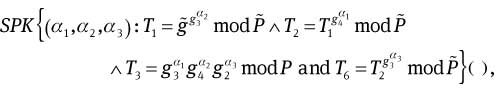
and the set of (c1, s11, . . . , s1k, s21, . . . , s2k, s31, . . . , s3k) ∈ {0, 1}k×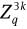 is the corresponding signature.
is the corresponding signature.
Subsequently, Pi executes the following procedures.
Choose random integers w4 ∈RZP, w5, w6, w7, w8 ∈RZP.
Compute to = H(mω‖ro) mod P.
Compute
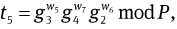
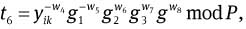
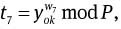
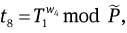 and
and 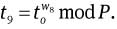
Compute c2 = H( g1‖ g2 ‖ g3 ‖ g4 ‖ g ‖
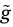 ‖ yik ‖ yok ‖ T1‖T3 ‖ T4 ‖ T5 ‖ To ‖ t5 ‖ t6 ‖ t7 ‖ t8 ‖ t9 ‖ mω‖m), s4 = w4 – c2Ai mod P, s5 = w5 – c2bi mod q, s6 = w6 – c2xi mod q, s7 = w7 – c2w mod q, and s8 = w8 – c2so mod q.
‖ yik ‖ yok ‖ T1‖T3 ‖ T4 ‖ T5 ‖ To ‖ t5 ‖ t6 ‖ t7 ‖ t8 ‖ t9 ‖ mω‖m), s4 = w4 – c2Ai mod P, s5 = w5 – c2bi mod q, s6 = w6 – c2xi mod q, s7 = w7 – c2w mod q, and s8 = w8 – c2so mod q.
Remark 2. The above protocol is actually the signature of knowledge of
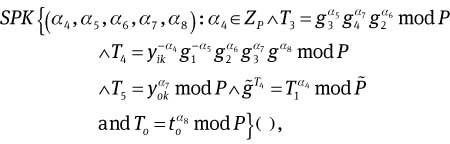
and the set of (c2, s4, s5, s6, s7, s8) ∈ {0, 1}k×Zp×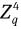 is the corresponding signature.
is the corresponding signature.
3.5 Signature Verification
Any verifier can perform the following procedures to check the validity of the signature.
Compute

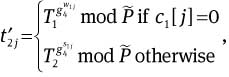
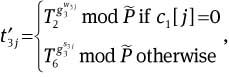
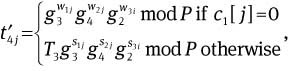
and
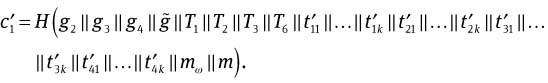
Compute
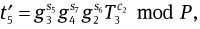
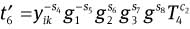 mod P,
mod P, 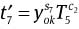 mod P,
mod P, 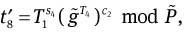
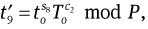 and
and 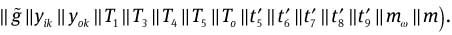
Check whether
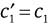 and
and 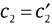 hold. If it does, the signature is valid. Otherwise, it will be rejected.
hold. If it does, the signature is valid. Otherwise, it will be rejected.
3.6 Open
To trace the real identity of a signature on message m, the opener executes as follows.
Check the validity of the signature on message m.
Compute
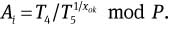
Identify a signer Pi from Ai using the member list ML.
Output the signer’s identity IDi.
4 Security of the Proposed Scheme
Our proposed group–proxy signature scheme extends Miyaji and Umeda’s [20] basic group signature scheme and adds the proxy property. In this section, we will show that our revised group signature part is secure as of old. Furthermore, our security analysis indicates that the added proxy signature part is secure as well.
4.1 Security Proof of the Delegation Phase
As presented in Section 3.2, the proxy signer Pi ∈ G obtains (ro, so, mω) from the original signer O. Actually, (ro, so) is the original signer O’s signature on the warrant mω. The correctness of the signature is obvious. In fact, we use Schnorr-type signature [21], which has been proved secure in the random oracle model, to generate such signature. In general, the warrant mω contains the type of the delegated information, the original and the proxy signers’ identities, the delegation period, etc. Thus, from the angle of the proxy signature, neither can the delegated proxy signer Pi ∈ G abuse the rights delegated by the original signer nor can anyone forge a valid delegation tuple. In the later sections, we will show that any verifier can be convinced that the valid group–proxy signature implies that the proxy signer Pi owns the original signer O’s authorization.
4.2 Security Proof of the Membership Certificate
Similar to Miyaji and Umeda [20], the security of our revised membership certification-generation algorithm is based on the difficulty of the strong multiple discrete logarithm problem (MDLP).
For the security parameter k, let p and q be primes with | q | = k and q | p – 1. Set P = pq, and let g1, g2, g3, g4 ∈ 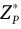 be elements with order q. Define a set
be elements with order q. Define a set 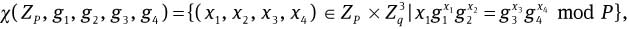 where the discrete logarithms of g1, g2, g3, and g4 based on each other element are not known.
where the discrete logarithms of g1, g2, g3, and g4 based on each other element are not known.
Problem (strong MDLP). Given ZP, g1, g2, g3 and 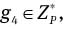 such that the discrete logarithm based on each other element is not known and any subset X ⊂ χ(ZP, g1, g2, g3, g4) with the polynomial order |X|, find a pair (x1, x2, x3, x4) ∈ ZP×
such that the discrete logarithm based on each other element is not known and any subset X ⊂ χ(ZP, g1, g2, g3, g4) with the polynomial order |X|, find a pair (x1, x2, x3, x4) ∈ ZP×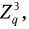 such that
such that 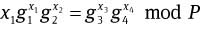 and (x1, x2, x3, x4) ∉ X.
and (x1, x2, x3, x4) ∉ X.
Assumption (strong MDLP assumption). There is no probabilistic polynomial–time algorithm P that can solve the problem above.
Similar to Miyaji and Umeda [20], we have the following theorem to guarantee the security of the certificate-generation algorithm.
Theorem 1.Let A be a polynomial–time adversary who can successfully forge a new certificate, then there exists an adversary B who can attack against the strong MDLP with at least the same advantage.
4.3 Security Proof on the Group Signature
The following theorem shows the security of the group signature generation.
Theorem 2.The interactive version of the group signature generation is an honest-verifier zero-knowledge proof of knowledge of a delegation key authorized by the original signer O and a pair of membership certificate and corresponding membership key obtained by interaction with the issuer. Furthermore, (T4, T5) is the ElGamal ciphertext for A with respect to the public key yok.
Proof sketch. It is easy to prove the completeness and the zero-knowledgeness. The rest is to extract the knowledge. Owing to the knowledge extractor of each SPK, we can extract the values α1, α2, α3, α4, α5, α6, α7 and α8 satisfying
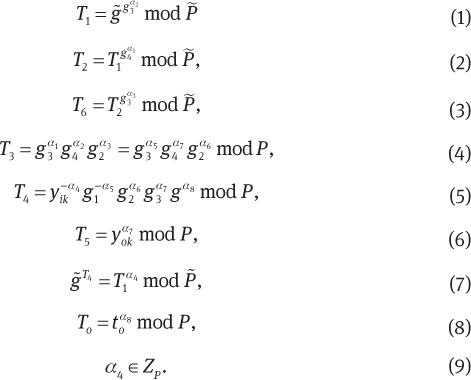
Here, α1 = α5, α2 = α7 and α3 = α6 hold from Eq. (4). Thus, Eqs. (1) and (2) represent

and

From Eqs. (5) and (10), Eq. (7) can be rewritten as
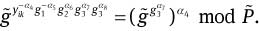
Then

holds.
It is obvious that the tuple {α6, α8, α4, α5} implies a valid delegation key, a membership certificate, and the corresponding membership key.
From Eqs. (8) and (12), the original signer O’s delegation key α8, i.e., so, is extracted. That is to say, our signature proves the knowledge of the delegation key authorized by the original signer O.
From Eq. (12), Eq. (5) represents
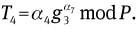
Thus, (T4, T5) is a pair of ElGamal ciphertext, and the ciphertext can be considered as the encryption of α4, i.e., A, with respect to the opener’s public key yok.
Besides, similar to Ref. [20], our proposed scheme satisfies the basic security requirements of the group signature scheme. We omit the proof procedures here. □
5 Efficiency
In this section, we simply analyze the performance of our proposed group–proxy signature-based e-cash system. Based on Miyaji and Umeda’s [20] group signature scheme, the concept of proxy signature is drawn into. Moreover, secure delegation of proxy signature and anonymity of group signature are blended into each other. Here, we first define some notations in Table 1, then the time complexities of each phase of our scheme over Ref. [20] is presented in Table 2. From the comparison, only 9 modular multiplication operations and 17 modular exponentiation operations are increased additionally in one cycle of the procedure. This is much more efficient than “group signature + proxy signature” combined simply. Furthermore, the additional operations are negligible when the system is implemented with the large-scale integrated chip. More specifically, the additional operations over Miyaji and Umeda’s [20] group signature scheme are as follows. In the delegation key generation phase, two modular multiplication operations and four modular exponentiation operations are respectively increased. In registration phase, one modular multiplication operation and one modular exponentiation operation are respectively increased. In the signature generation phase, three modular multiplication operations and six modular exponentiation operations are respectively increased. In the signature verification phase, three modular multiplication operations and six modular exponentiation operations are respectively increased. There is no additional operation increment in the open phase.
Definitions of notations.
| Notation | Definition |
|---|---|
| TMUL | Time for modular multiplication |
| TEXP | Time for modular exponentiation |
Time complexity of the proposed scheme over Ref. [20].
| Phase | TMUL | TEXP |
|---|---|---|
| Delegation key generation | 2 | 4 |
| Registration | 1 | 1 |
| Signature generation | 3 | 6 |
| Signature verification | 3 | 6 |
| Open | 0 | 0 |
From Table 2, we can see that the time complexity of our proposed scheme is almost the same as Miyaji and Umeda’s [20] original scheme, even though the group–proxy property is achieved creatively. Therefore, the implementation of our proposed e-cash system is applicable.
6 Conclusion
We have proposed the group–proxy signature model and presented a concrete scheme. Our scheme is an extension of the group signature scheme proposed by Miyaji and Umeda [20]. The basic group signature scheme is based on only publicly known-order groups. As a result, the ultimate group signature size and the computational amount of the signature generation and verification algorithms are reduced largely. Our security and performance analysis shows that the our proposed scheme is secure and applicable. We also demonstrate how our construction could be applied to set up an e-cash system in which more than one branch banks can be designated by the central bank to dispense anonymous e-cash on behalf of the central bank.
The authors would like to thank the anonymous referees and reviewers for their suggestions to improve this article. This research was supported by the National Natural Science Foundation of China under grant no. 61100214.
Bibliography
[1] M. Abe, J. Groth, K. Haralambiev and M. Ohkubo, Optimal structure-preserving signatures in asymmetric bilinear groups, in: CRYPTO 2011, Lect. Notes Comput. Sci. 6841, pp. 649–666, Springer, Santa Barbara, California, USA, 2011.Search in Google Scholar
[2] G. Ateniese, J. Camenisch, M. Joye and G. Tsudik, A practical and provably secure coalition-resistant group signature scheme, in: Advances in Cryptology – Proceedings of CRYPTO2000, M. Franklin and M. Bellare, eds., Lect. Notes Comput. Sci. 1880, pp. 255–270, Springer, Santa Barbara, California, USA, 2000.Search in Google Scholar
[3] X. Boyen and B. Waters, Full-domain subgroup hiding and constant-size group signatures, in: PKC 2007, A. Yao, T. Okamoto and X. Wang, eds., Lect. Notes Comput. Sci. 4450 (2007), 1C15.Search in Google Scholar
[4] E. Brickell, L. Chen and J. Li, A new direct anonymous attestation scheme from bilinear maps, in: Trust 2008, L. Chen and C. J. Mitchell, eds., Lect. Notes Comput. Sci. 4968 (2008), 1C20.Search in Google Scholar
[5] J. Camenisch and M. Michels, A group signature scheme based on an RSAvariant. Preliminary version, in: Advances in Cryptology – ASIACRYPT‘98, K. Feng, K. Ohta and D. Pei, eds., Tech. Rep. RS-98-27, BRICS, 1998.Search in Google Scholar
[6] J. Camenisch and M. Stadler, Efficient group signatures for large groups, in: Proceedings of CRYPTO ’97, B. Kaliski, ed., Lect. Notes Comput. Sci. 1294, pp. 410–424, Springer-Verlag, Santa Barbara, California, USA, 1997.Search in Google Scholar
[7] J. Camenisch, A. Kiayias and M. Yung, On the portability of generalized schnorr proofs, in: EUROCRYPT 2009, A. Joux, ed., Lect. Notes Comput. Sci. 5479 (2010), 425C442.Search in Google Scholar
[8] F. Cao and Z. F. Cao, A secure identity-based multi-proxy signature scheme, Comput. Elect. Eng.35 (2009), 86–95.10.1016/j.compeleceng.2008.05.005Search in Google Scholar
[9] D. Chaum, Blind signatures for untraceable payments, in: Advances in Cryptology,Proceedings of Crypto ‘82, D. Chaum and R. Rivest, eds., pp. 199–203, Springer, Santa Barbara, California, USA, 1982.10.1007/978-1-4757-0602-4_18Search in Google Scholar
[10] D. Chaum and E. van Heyst, Group signatures, in: Proceedings of EUROCRYPT 91, A. J. Clark and D. W. Davies, eds., Lect. Notes Comput. Sci. 547 (1991), 257–265.10.1007/3-540-46416-6_22Search in Google Scholar
[11] G. Fuchsbauer and D. Pointcheval, Anonymous proxy signatures, in: SCN ‘08, R. Ostrovsky, C. Blundo and X. Boyen, eds., Lect. Notes Comput. Sci. 5229 (2008), 201–217.10.1007/978-3-540-85855-3_14Search in Google Scholar
[12] E. Fujisaki, Sub-linear size traceable ring signatures without random oracles, in: CT-RSA ‘11, G. Ateniese and S. Boldyreva, eds., Lect. Notes Comput. Sci. 6558 (2011), 393–415.10.1007/978-3-642-19074-2_25Search in Google Scholar
[13] S. Hwang and C. Shi, A simple multi-proxy signature scheme, in: Proceedings of the Tenth National Conference on Information Security, D. Wang, ed., pp. 134–138.Search in Google Scholar
[14] N. Lan and S. Rei, Efficient and probably secure trapdoor-free group signature schemes from bilinear pairings, in: ASIACRYPT 2004, K. Kim and P. J. Lee, eds., Lect. Notes Comput. Sci. 3329 (2004), 372–386. http://eprint.iacr.org/2004/104/ [full version].10.1007/978-3-540-30539-2_26Search in Google Scholar
[15] Z. H. Liu, Y. P. Hu and H. Ma, Secure proxy multi-signature scheme in the standard model, in: Proceedings of the Second International Conference, ProvSec 2008, J. Baek, et al., eds., Lect. Notes Comput. Sci. 5324 (2008), 124–140.Search in Google Scholar
[16] Z. H. Liu, Y. P. Hu, X. S. Zhang and H. Ma, Secure proxy signature scheme with fast revocation in the standard model, J. China Univ. Posts Telecomm.16 (2009), 116–124.10.1016/S1005-8885(08)60258-7Search in Google Scholar
[17] A. Lysyanskaya and Z. Ramzan, Group blind digital signatures: a scalable solution to electronic cash, in: Financial Cryptography (FC’98), R. Hirschfeld, ed., Lect. Notes Comput. Sci. 1465 (1998), 184–197.10.1007/BFb0055483Search in Google Scholar
[18] M. Mambo, K. Usuda and E. Okamoto, Proxy signatures for delegation signing operation, in: Proceedings of the Third ACM Conference on Computer and Communication Security, L. Gong, ed., pp. 48–57, 1996.10.1145/238168.238185Search in Google Scholar
[19] M. Mambo, K. Usuda and E. Okamoto, Proxy signatures: delegation of the power to sign message, IEICE Trans. Fundam.E79-A (1996), 1338–1354.Search in Google Scholar
[20] A. Miyaji and K. Umeda, A fully-functional group signature scheme over only known-order group, in: Applied Cryptography and Network Security (ACNS 2004), M. Jakobsson and M. Yung, eds., Lect. Notes Comput. Sci. 3089 (2004), 164–179.10.1007/978-3-540-24852-1_12Search in Google Scholar
[21] D. Pointcheval and J. Stern, Security proofs for signature schemes, in: Proceedings of EUROCRYPT 96, J. Pastor and U. Maur, eds., Lect. Notes Comput. Sci. 1163 (1996), 387–405.10.1007/3-540-68339-9_33Search in Google Scholar
[22] J. C. Schdult, K. Matsuura and K. G. Paterson, Proxy signatures secure against proxy key exposure, in: Public Key Cryptography C PKC 2008, R. Cramer, ed., Lect. Notes Comput. Sci. 4939 (2008), 344–359.10.1007/978-3-540-78440-1_20Search in Google Scholar
[23] C. Schnorr, Efficient identification and signatures for smart cards, in: Proceedings of CRYPTO 89, G. Brassard, ed., Lect. Notes Comput. Sci. 435 (1990), 239–252.10.1007/0-387-34805-0_22Search in Google Scholar
[24] Y. Sun, C. Xu, Y. Yu and B. Yang, Improvement of a proxy multi-signature scheme without random oracles, Comput. Commun. 34 (2011), 257–263.10.1016/j.comcom.2010.02.002Search in Google Scholar
[25] G. K. Verma, A proxy signature scheme over braid groups, Cryptology Eprint Archive Report, 2008. http://www.eprint.iacr.org/2008/160.Search in Google Scholar
[26] L. Yi, G. Bai and G. Xiao, Proxy multi-signature scheme, Electron. Lett.36 (2000), 527–528.10.1049/el:20000422Search in Google Scholar
[27] H. Zhou, B. Wang, L. Tie and J. Li, An electronic sash system with multiple banks based on proxy signature scheme, J. Shanghai Jiao Tong Univ.38 (2004), 79–82 [in Chinese].Search in Google Scholar
©2013 by Walter de Gruyter Berlin Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Articles in the same Issue
- Masthead
- Masthead
- Review
- Single-Channel Speech Enhancement Techniques for Distant Speech Recognition
- Research Articles
- Group–Proxy Signature Scheme: A Novel Solution to Electronic Cash
- Vowel Phoneme Segmentation for Speaker Identification Using an ANN-Based Framework
- Four-Area Load Frequency Control of an Interconnected Power System Using Neuro-Fuzzy Hybrid Intelligent Proportional and Integral Control Approach
- A Novel Full-Reference Color Image Quality Assessment Based on Energy Computation in the Wavelet Domain
- Machine Vision Approach for Automating Vegetation Detection on Railway Tracks
- An Intelligent Fused Approach for Face Recognition
Articles in the same Issue
- Masthead
- Masthead
- Review
- Single-Channel Speech Enhancement Techniques for Distant Speech Recognition
- Research Articles
- Group–Proxy Signature Scheme: A Novel Solution to Electronic Cash
- Vowel Phoneme Segmentation for Speaker Identification Using an ANN-Based Framework
- Four-Area Load Frequency Control of an Interconnected Power System Using Neuro-Fuzzy Hybrid Intelligent Proportional and Integral Control Approach
- A Novel Full-Reference Color Image Quality Assessment Based on Energy Computation in the Wavelet Domain
- Machine Vision Approach for Automating Vegetation Detection on Railway Tracks
- An Intelligent Fused Approach for Face Recognition

