Algebraic groups over finite fields: Connections between subgroups and isogenies

The image ϕ ⁢ ( G ′ ⁢ ( F q n ) ) has index | Ker ⁡ ϕ ⁢ ( F q n ) | in G ⁢ ( F q n ) .

Proof

Since G ′ and 𝐺 are isogenous over F q , in particular, they are isogenous over F q n . Two groups isogenous over F q n have the same number of F q n -rational points [1, Proposition 16.8]. Therefore, the cardinality of the kernel is equal to the index of the image. ∎

Let G ′ and 𝐺 be two connected linear algebraic groups defined over F q . Let ϕ : G ′ → G be an isogeny of order 𝑘 defined over F q . Then, for infinitely many 𝑛, the group of rational points G ⁢ ( F q n ) has a subgroup of index 𝑘. The set of integers for which this happens contains an arithmetic progression.

Proof

Since Ker ⁡ ϕ is finite, we have Ker ⁡ ϕ = Ker ⁡ ϕ ⁢ ( F q m ) for some 𝑚. It follows that Ker ⁡ ϕ = Ker ⁡ ϕ ⁢ ( F q n ) for every multiple 𝑛 of 𝑚. By Lemma 2.1, the group G ⁢ ( F q n ) has a subgroup of index 𝑘 for every 𝑛 multiple of 𝑚. ∎

The following group isomorphism holds:

In particular, ϕ ⁢ ( G ′ ⁢ ( F q n ) ) is a normal subgroup of G ⁢ ( F q n ) .

Proof

Take x ∈ G ⁢ ( F q n ) . Since ϕ : G ′ → G is surjective, there is y ∈ G ′ such that ϕ ⁢ ( y ) = x . Since 𝜙 commutes with σ q n and σ q n ⁢ ( x ) = x , we have

Consider the map

First of all, we need to check that μ q n is well defined. If a different 𝑦 is chosen, say z ∈ G ′ such that ϕ ⁢ ( z ) = x , then y ⁢ z − 1 ∈ Ker ⁡ ϕ , and so

which is equivalent to ( z − 1 ⁢ σ q n ⁢ ( z ) ) − 1 ⁢ y − 1 ⁢ σ q n ⁢ ( y ) ∈ λ q n ⁢ ( Ker ⁡ ϕ ) since λ q n ⁢ ( Ker ⁡ ϕ ) is central.

Now we prove that μ q n is surjective. Let a ∈ Ker ⁡ ϕ . By Lang’s Theorem, there is y ∈ G ′ such that y − 1 ⁢ σ q n ⁢ ( y ) = a . Let x = ϕ ⁢ ( y ) . Since ϕ ⁢ ( y − 1 ⁢ σ q n ⁢ ( y ) ) = 1 , we have σ q n ⁢ ( x ) = x , and so x ∈ G ⁢ ( F q n ) . By definition, 𝑥 is mapped to y − 1 ⁢ σ q n ⁢ ( y ) by μ q n , which is equal to 𝑎.

Next, we prove that μ q n is a homomorphism. Take any x , w ∈ G ⁢ ( F q n ) ; let ϕ ⁢ ( y ) = x and ϕ ⁢ ( z ) = w . We need to show that ( y ⁢ z ) − 1 ⁢ σ q n ⁢ ( y ⁢ z ) is equal to

This is the same as

which holds since y − 1 ⁢ σ q n ⁢ ( y ) ∈ Ker ⁡ ϕ is central.

Finally, we prove that the kernel of μ q n is ϕ ⁢ ( G ′ ⁢ ( F q n ) ) . Let x = ϕ ⁢ ( y ) be an element of G ⁢ ( F q n ) such that y − 1 ⁢ σ q n ⁢ ( y ) belongs to λ q n ⁢ ( Ker ⁡ ϕ ) . Then

for some a ∈ Ker ⁡ ϕ . Since Ker ⁡ ϕ is central and y − 1 ⁢ σ q n ⁢ ( y ) = a − 1 ⁢ σ q n ⁢ ( a ) , it follows that

and so a − 1 ⁢ y ∈ G ′ ⁢ ( F q n ) . Therefore, x = ϕ ⁢ ( y ) = ϕ ⁢ ( a − 1 ⁢ y ) belongs to ϕ ⁢ ( G ′ ⁢ ( F q n ) ) . ∎

Let G ′ , 𝐺 and ϕ : G ′ → G be two connected linear algebraic groups and an isogeny defined over F q n . Let 𝐻 be a subgroup of G ⁢ ( F q n ) containing ϕ ⁢ ( G ′ ⁢ ( F q n ) ) . Let 𝐾 be the subgroup of Ker ⁡ ϕ containing λ q n ⁢ ( Ker ⁡ ϕ ) and satisfying

Then G ′′ = G ′ / K is a connected linear algebraic group defined over F q n ; the induced isogeny ϕ ′′ : G ′′ → G reaches 𝐻.

Proof

The group 𝐾 is defined over F q n : since λ q n ⁢ ( Ker ⁡ ϕ ) ⊆ K ⊆ Ker ⁡ ϕ , in particular, λ q n ⁢ ( K ) ⊆ K , and so 𝐾 is σ q n -invariant. Therefore, the quotient group G ′′ = G ′ / K is defined over F q n . Its group of F q n -rational points is

Since K ⊆ Ker ⁡ ϕ holds, the isogeny ϕ : G ′ → G induces a well defined isogeny ϕ ′′ : G ′′ → G . We claim that the image

is equal to 𝐻, completing the proof.

Let x ∈ H . Then x = ϕ ⁢ ( y ) for some y ∈ G ′ . Since x ∈ G ⁢ ( F q n ) , then

By hypothesis, 𝐾 contains λ q n ⁢ ( Ker ⁡ ϕ ) , and therefore, λ q n ⁢ ( y ) ∈ K . This proves that 𝑥 is an element of (3.1).

Conversely, let 𝑥 be an element of (3.1). Then x = ϕ ⁢ ( y ) for some y ∈ G ′ satisfying λ q n ⁢ ( y ) ∈ K . It follows that x − 1 ⁢ σ q n ⁢ ( x ) = ϕ ⁢ ( λ q n ⁢ ( y ) ) = 1 , and therefore, x ∈ G ⁢ ( F q n ) . By definition of μ q n , the coset x ⁢ ϕ ⁢ ( G ′ ⁢ ( F q n ) ) is mapped to the coset λ q n ⁢ ( y ) ⁢ λ q n ⁢ ( Ker ⁡ ϕ ) . Since μ q n induces an isomorphism between the quotients, the coset x ⁢ ϕ ⁢ ( G ′ ⁢ ( F q n ) ) is an element of H / ϕ ⁢ ( G ′ ⁢ ( F q n ) ) . By hypothesis, 𝐻 contains ϕ ⁢ ( G ′ ⁢ ( F q n ) ) , and therefore, x ∈ H . ∎

Let G ′ , G and ϕ : G ′ → G be two connected linear algebraic groups and an isogeny defined over F q . For infinitely many 𝑛, let H n be a subgroup of G ⁢ ( F q n ) containing ϕ ⁢ ( G ′ ⁢ ( F q n ) ) . Then there are finitely many isogenies reaching all H n .

Proof

Fix any 𝑛 for which H n is defined. Since G , G ′ and 𝜙 are defined over F q , in particular, they are defined over F q n , so Lemma 3.2 applies.

Now let 𝑛 vary. Since K n ⊆ Ker ⁡ ϕ and Ker ⁡ ϕ is finite, there are only finitely many possibilities for ϕ ′′ : G ′′ → G . ∎

In Lemma 3.2, the subgroup K = K n contains λ q n ⁢ ( Ker ⁡ ϕ ) ; this implies that the isogeny ϕ ′′ : G ′′ → G is defined over F q n . In general, the isogenies of Corollary 3.3 are defined over any field F q m for which Z ⁢ ( G ⁢ ( F q m ) ) = Z ⁢ G since, in this case, λ q m ⁢ ( Ker ⁡ ϕ ) = { 1 } . If, for every 𝑛, the subgroup K n contains λ q ⁢ ( Ker ⁡ ϕ ) , then the isogenies are all defined over F q .

Let 𝐺 be a finite group. Let 𝑁 and 𝐻 be two subgroups. Suppose that 𝑁 is normal. Then

Let 𝐺 be a reductive linear algebraic group defined over F q . Fix k ≥ 1 and suppose that, for infinitely many 𝑛, the group of rational points G ⁢ ( F q n ) contains a subgroup H n of index 𝑘. Then there are finitely many isogenies from linear algebraic groups onto 𝐺 such that all but finitely many of the H n are reached by at least one of these.

Proof

Reductive groups can be obtained from simple groups and tori by taking products and isogenies. The proof of the theorem, which consists of several steps, shows that the class of algebraic groups satisfying the statement contains simple groups and tori and is closed under the formation of reductive groups.

Step 1: If 𝐺 is simple, simply connected, then k = 1 . Let 𝐺 be simple, simply connected and suppose k > 1 . Choose 𝑛 such that H n is defined. Since H n has index 𝑘, its normalizer has index at most 𝑘; therefore, H n has at most 𝑘 conjugates. Each of them has index 𝑘, so their intersection

is a normal subgroup of index between 𝑘 and k k . Since k > 1 , for 𝑛 large enough, Tits’ Theorem implies

This is a contradiction since | G ⁢ ( F q n ) | grows as 𝑛 grows (see [8, Table 24.1]), while the size of the center | Z ⁢ ( G ⁢ ( F q n ) ) | is bounded by | Z ⁢ G | , which is finite by hypothesis. We conclude that k = 1 . The statement is trivially satisfied by the identity map G → G .

Step 2: If 𝐺 is semisimple, simply connected, then k = 1 . Let 𝐺 be semisimple, simply connected. Then 𝐺 is direct product of its minimal connected normal subgroups which are simple, simply connected and defined over F q (see [10, Paragraphs 17.22, 17.24]). We proceed by induction on the number of simple components. Let 𝑁 be one simple component. By Step 1, applied to 𝑁, the intersection H n ∩ N ⁢ ( F q n ) must be equal to N ⁢ ( F q n ) for 𝑛 large enough. By Lemma 3.5, the index k = [ G ( F q n ) : H n ] must be equal to the index of H n / N ⁢ ( F q n ) in the quotient G ⁢ ( F q n ) / N ⁢ ( F q n ) . Since 𝑁 is connected, we have ( G / N ) ⁢ ( F q n ) = G ⁢ ( F q n ) / N ⁢ ( F q n ) by [1, Corollary 16.5 (ii)] and induction applies to G / N .

Step 3: The statement is true if 𝐺 is semisimple. Let 𝐺 be semisimple. Then it admits a universal covering ϕ : G ′ → G , where G ′ is simply connected and 𝜙 is an isogeny, both defined over F q (see [10, Paragraph 16.21]). Note that, since 𝐺 is semisimple, the group G ′ is semisimple, and so Step 2 applies to G ′ . The preimages of ϕ ⁢ ( G ⁢ ( F q n ) ) ∩ H n with respect to 𝜙 have index bounded by 𝑘, and so, by Step 2, they coincide with G ′ ⁢ ( F q n ) for 𝑛 large enough. This means that ϕ ⁢ ( G ′ ⁢ ( F q n ) ) ⊆ H n . Corollary 3.3 applies.

Step 4: The statement is true if 𝐺 is a torus. Let 𝐺 be a torus. Since G ⁢ ( F q n ) is isomorphic to a subgroup of ( F q m * ) d for some 𝑚 and 𝑑, the integers 𝑘 and 𝑞 must be coprime. Consider the homomorphism G → G sending g ↦ g k ; it is defined over F q . Since 𝑘 and 𝑞 are coprime, this morphism is an isogeny. Since G ⁢ ( F q n ) / H n has 𝑘 elements, we have G ⁢ ( F q n ) k ⊆ H n . Corollary 3.3 applies.

Step 5: The statement is true if 𝐺 is the direct product of a torus and a semisimple group, both defined over F q . Let G = T × S , where 𝑇 is a torus and 𝑆 is semisimple. The integers [ T ⁢ ( F q n ) : H n ∩ T ⁢ ( F q n ) ] and [ S ⁢ ( F q n ) : H n ∩ S ⁢ ( F q n ) ] are divisors of [ G ( F q n ) : H n ] = k . Since the divisors of 𝑘 are finite in number, we reduce to finitely many cases, so by Step 3 and Step 4, we find finitely many isogenies ϕ × ψ reaching ( H n ∩ T ⁢ ( F q n ) ) × ( H n ∩ S ⁢ ( F q n ) ) , which is a subgroup of H n . Once more, Corollary 3.3 applies.

Step 6: The statement is true if 𝐺 is reductive. Let 𝐺 be reductive. Let 𝑇 be the identity component of Z ⁢ G and S = [ G , G ] the derived subgroup. Since F q is perfect, 𝑇 and 𝑆 are defined over F q (see [12, Section 12.1.7]). The group 𝑇 is a torus, the group 𝑆 is semisimple and the product map π : T × S → G is an isogeny [8, Proposition 6.20, Corollary 8.22].

By Lemma 3.5, the index of

in T ⁢ ( F q n ) ⁢ S ⁢ ( F q n ) divides 𝑘, so there are only finitely many possibilities and hence finitely many possibilities for the index of π − 1 ⁢ ( H n ) in T ⁢ ( F q n ) × S ⁢ ( F q n ) . By Step 5, for every π − 1 ⁢ ( H n ) , we find an isogeny ϕ : G ′ → T × S defined over F q n reaching ϕ ⁢ ( G ′ ⁢ ( F q n ) ) = π − 1 ⁢ ( H n ) , and finitely many isogenies are enough to reach all π − 1 ⁢ ( H n ) . For every 𝜙, the composition π ∘ ϕ : G ′ → G is an isogeny defined over F q n , and the image π ( ϕ ( G ′ ( F q n ) ) is contained in H n . Lemma 3.2 applies to each 𝜙, giving finitely many isogenies reaching all H n . ∎

Let 𝐺 be semisimple, simply connected and k > 1 . Then, for 𝑛 sufficiently large, the group G ⁢ ( F q n ) contains no subgroups of index 𝑘. In particular, the minimal indices of proper subgroups of G ⁢ ( F q n ) diverge to infinity.

Proof

Fix h > 1 . For every k ∈ { 2 , … , h } , there is n k such that, for every n > n k , the group G ⁢ ( F q n ) contains no subgroups of index 𝑘. For every 𝑛 larger than max ⁡ { n 2 , … , n h } , the minimal index of proper subgroups of the group G ⁢ ( F q n ) is larger than ℎ. ∎

Let 𝐺 be semisimple and let 𝑑 be the order of its universal covering ϕ : G ′ → G . Let H n ⊆ G ⁢ ( F q n ) be an infinite sequence of subgroups of fixed index 𝑘. Then, for every 𝑛 large enough, the group H n contains the image of the universal covering ϕ ⁢ ( G ′ ⁢ ( F q n ) ) . In particular, k ≤ d .

Let 𝐺 be a linear algebraic group defined over F q . Let k ≥ 1 such that 𝑘 and 𝑞 are coprime and, for infinitely many 𝑛, the group of rational points G ⁢ ( F q n ) contains a subgroup H n of index 𝑘. Then there are finitely many linear algebraic groups G ′ and isogenies G ′ → G such that, except for finitely many 𝑛, every H n is reached by one of them.

Proof

Let 𝑈 be the unipotent radical of 𝐺. As F q is perfect, 𝑈 is defined over F q (see [12, Section 12.1.7]). Since U ⁢ ( F q n ) is a 𝑝-group, the index of U ⁢ ( F q n ) ∩ H n in U ⁢ ( F q n ) divides both 𝑞 and 𝑘, so it must be 1, and hence U ⁢ ( F q n ) ⊆ H n . Theorem 3.6 applied to the quotient G / U gives finitely many isogenies ϕ : G ′ → G / U reaching H n / U ⁢ ( F q n ) for 𝑛 large.

Fix 𝑛 and one isogeny ϕ : G ′ → G / U reaching H n / U ⁢ ( F q n ) . We want to lift 𝜙 to 𝐺. Consider the fiber product G ′ × G / U G whose elements are the pairs ( g ′ , g ) ∈ G ′ × G satisfying ϕ ⁢ ( g ′ ) = π ⁢ ( g ) , where π : G → G / U is the canonical projection. We have the following commutative diagram:

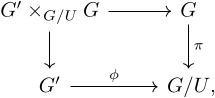
where the unlabelled arrows are the canonical projections.

For now, suppose that G ′ × G / U G is connected. The top arrow

is an isogeny since its kernel is Ker ⁡ ( ϕ ) × 1 . Since 𝜙, 𝜋 and 𝑈 are defined over F q and 𝑈 is connected, we have

and by commutativity of the diagram, we have

where the right-hand side equals H n / U ⁢ ( F q n ) . We conclude that

Finally, if G ′ × G / U G is not connected, replace it by its identity component: since 𝐺 and G ′ are connected, the projections remain surjective, and the same argument applies. ∎

Let k ≥ 1 , and assume that either 𝐺 is reductive or 𝑘 is prime to 𝑞. The set of 𝑛 such that G ⁢ ( F q n ) contains a subgroup of fixed index 𝑘 is either finite, or it contains an arithmetic progression.

Lemma 3.1 can be generalized to Steinberg endomorphisms; see [5, Proposition 1.4.13] and [13, Proposition 4.5]. Indeed, if F : G → G , F ′ : G ′ → G ′ are Steinberg endomorphisms satisfying ϕ ∘ F ′ = F ∘ ϕ , the groups G F / ϕ ⁢ ( G ′ ⁣ F ′ ) and Ker ⁡ ϕ / L ⁢ ( Ker ⁡ ϕ ) are isomorphic, where G F and G ′ ⁣ F ′ denote the fixed point subgroups and L ⁢ ( y ) = y − 1 ⁢ F ′ ⁢ ( y ) . This suggests a generalization of Theorem 3.6 and Theorem 4.1 to groups arising as fixed points of Steinberg endomorphisms. However, it is not clear to the author how to generalize Steps 2 and 3 of the proof of Theorem 3.6.

Let 𝐺 be a semisimple, simply connected linear algebraic group defined over ℚ. Let k > 1 . Then, for 𝑝 sufficiently large, the group G ⁢ ( F p ) contains no subgroup of index 𝑘.

Proof

Suppose that 𝐺 is simple and simply connected; the general case follows by induction on the number of simple factors.

Suppose that, for infinitely many 𝑝, the group G ⁢ ( F p ) contains a subgroup of index k > 1 . Then, as in the proof of Theorem 3.6, for 𝑝 large enough, we obtain

This is a contradiction since G ⁢ ( F p ) grows as 𝑝 grows (see [8, Table 24.1]), while the size of the center | Z ⁢ ( G ⁢ ( F p ) ) | is bounded by | Z ⁢ G | , which is finite by hypothesis. We conclude that k = 1 . ∎