Conditioning on Post-treatment Variables

Answer-1

Yes, something is wrong here, but not with Rule-2. It has to do with the interpretation of P(y|do(x),z), which will become clear when we prove the validity of Rule-2 in our graph

Rule-2 says:

Indeed, if we go to the definition of P(y|do(x),z), we obtain:

which proves Rule-2.

The same result obtains whenever Z blocks all back-door paths from X to Y, as in the canonical confounding model (Figure 1(a)), as well as in the typical selection-bias model (Figure 1(b)). P(y|do(x),z) is identified (by P(y|x,z)) in both models, despite the fact that in Figure 1(b)Z is a descendant of both treatment and outcome, in double violation of the back-door criterion. P(y|do(x),z) is no longer estimable when conditioning on Z opens a back-door path from X to Y as in Figure 2(a), because the condition (X⊥⊥Y|Z)GX_ is violated. It is identified in Figure 2(b), where the condition is satisfied.

Figure 1:

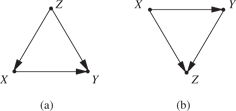
Two models in which P(y|do(x),z)=P(y|x,z) because Zd-separates X from Y once we remove arrows emanating from X.

Figure 2:

In Model (a), P(y|do(x),z) is not identified (when U is unobserved) since Rule-2 in inapplicable. It is identified in Model (b) since X and Y are separated in GX_.

Answer-2

The two are not contradictory. Rule-2 is always valid, regardless if Z is pre-treatment or post-treatment. At the same time, the prohibition imposed by the back-door cannot be dismissed, it needs to be considered on two occasions. First, whenever we seek a license to use the adjustment formula and write:

Second, whenever we seek to estimate causal effects in a specific group of units characterized by Z=z. Contrary to syntactic appearance, the expression P(y|do(x),z) in Rule-2, does not represent such effects when Z is post-treatment.

Let us deal with these two cases separately.

2.1 License to adjust

Consider the adjustment formula of eq. (1). This formula is not valid when Z is Y-dependent, as in our causal chain

If we apply it blindly, we get the sum in (eq. (1)), instead of the correct answer, which is P(y|do(x))=P(y|x).

To see what goes wrong with blind adjustment, let us trace its derivation, for a pre-treatment Z:

This works fine when we can substitute P(z|do(x)) with P(z), but not when Z is post-treatment and P(z|do(x)) depends on x. Thus, Rule-2 in itself is not sufficient for adjustment; blind adjustment will produce erroneous estimands.

If we avoid the substitution P(z|do(x))=P(z|x) and proceed cautiously in G1, we get

which is the correct answer for G1. But this is obtained though careful derivation, not by blind adjustment.

Blind adjustment is valid, however, when Z is pure descendant ^[1] of X, as in Figure 3. We know that the back-door prohibition against post-treatment covariates is lifted in this case [1, p. 339, 2] and, indeed, if we take Z as a covariate and blindly apply the adjustment formula to G2, we get the correct result:

Figure 3:

A model in which Z is a pure descendant of X, thus satisfying the (extended) back-door condition and permitting adjustment for Z.

The latter equality is obtained through the conditional independence P(y|x,z)=P(y|x) which holds in G2.

2.2 Identifying unit-specific effects

We are now ready to discuss the second task for which back-door admissibility is needed: estimating unit-specific effects.

In many applications, the query of interest is not to find Qdo=P(y|do(x),z), but to find Qc=P(yx|z), where yx is short for the counterfactual statement Yx=y. Back-door admissibility gives us the license to equate the two queries, and get

By the counterfactual query Qc we mean: Take all units which are currently at level Z=z, and ask what their Y would be had they been exposed to treatment X=x. This is different from Qdo=P(y|do(x),z)), which means: Expose the whole population to treatment X=x, take all units which attained level Z=z (post exposure) and report their Y′ s.

We call Qc‘‘unit-specific’’ because, as x varies, Qc remains focused on the same set of units (i.e. those that are currently at Z=z), with (hypothetical) histories that vary with x. Some of these units may not have experienced any of those histories and would have attained different levels of Z if they did. In contrast, Qdo focusses on one stratum, Z=z, and, as x varies, it allows different units to enter and leave that stratum.

Obviously, when Z is a pre-treatment covariate, we have Qdo=Qc, but when Z is post-treatment, the most common question we ask is Qc: find P(yx|z), not Qdo: find P(y|do(x),z)). The back-door criterion gives us a license to equate both queries with P(y|x,z). Here is why: If Z satisfies the back-door condition, the First Law of causal inference ^[2] dictates the conditional independence Yx⊥⊥X|Z, also known as ‘‘conditional ignorability’’ [3], so

This license is similar to Rule-2, but it is applied to a different expression; whereas ignorability allows us to remove a subscript, Rule-2 allows us to remove a do-operator.

We can see the difference in graph G2 of Figure 3. Here Z satisfies the (extended) back-door condition, so we can write

Rule-2 in itself does not give us this license because it is applicable to a different query P(y|do(x),z) and cannot handle counterfactual expressions.

Answer-3

We certainly should, because the two questions have different semantics and deliver different answers, whenever Z does not satisfy the back-door condition. This can be demonstrated in graph G3.^[3]

In this graph, Qdo gives:

While Qc gives:

which is totally alien to Qdo=P(y|z).

Intuition supports this inequality. If we let X be education, Z be skill and Y be salary, Qdo looks at people assigned to x years of education who subsequently achieved skill level z, and asks how would their salary Y depend on x, assuming that they end up with the same skill Z=z. The graph states that skill alone determines salary, not how it was acquired, therefore Qdo evaluates to: P(y|do(x),z))=P(y|z) namely, education has no effect on salary, once we know z, as shown in the graph. ^[4] In contrast, Qc asks for the role that education plays in the salary of one specific group of units, those at skill Z=z. In other words, we look at those who are currently at skill Z=z and ask, counterfactually: what their salary would be like had they received x years of schooling. Since some of those at skill Z=z had no schooling, their skill level would be greater than z had they received schooling, and so would their salary. This explains the inequality Qdo≠Qc.

Answer-4

Qdo is rarely posed as a research question of interest, probably because it lacks immediate causal interpretation. It serves primarily as an auxiliary mathematical object in the service of other research questions. One such research question is the unconditional causal effect of X on Y, denoted P(y|do(x)), which is fully analyzed using the do-calculus [4], namely, using Qdo. Another research question benefitting from Qdo occurs in transportability problems [5, 6], where the target query is P∗(y|do(x)) (the causal effect in a new population), and has been fully analyzed in do-calculus, again, using Qdo. I have not seen Qdo presented as a target query on its own right.

Answer-5

If we aim at estimating P(y|do(x)) from selection biased data under S=1, we are not asking for Qdo nor for Qdo. Rather, we are asking for P(y|do(x)) and we are allowed to use all means available, including the rules of do-calculus (which invoke P(y|do(x),z)) as long as we can recover P(y|do(x)) from selection biased data [7].

To demonstrate, assume that variable Z in Figure 3 stands for ‘‘selection’’ to the data, and our task is to recover the causal effect P(y|do(x)). Applying Rule-2 (on the null set) we can write

which established the recovery of the target effect from the biased data P(y|x,Z=1).

As another example, consider the following model (after [8]) X→Y←L→S where L is unobserved and S=1 represents selection. Since S is not separable from Y, P(y|do(x)) is not recoverable from the data P(x,y|S=1). (For intuition, imagine the confounder L being sex, in a study that excludes girls from participation. Surely, the average treatment effect is not recoverable from male-only data.) Assume moreover that only few cases drop from the study, i.e. P(S=0) is small and estimable. We can then write

and obtain a lower bound

Two points are worth noting (1): the lower bound has the form of Qdo:P(y|do(x),z) and (2) the lower bound is estimable from the data available, giving P(y|x)P(S=1|do(x)).

This bounding method does not work for the graph X→Y→S. Writing:

we see that, even if we are given the last term, P(S=1|do(x)), we cannot estimate the first.

It is important to note that, if we set out to estimate this bound, our target of identification would be a Qdo-type expression P(y|do(x),S=1) where S is a descendant of X and we could unleash the full power of do-calculus, ignoring the fact that we are only in possession of biased data, conditioned on S=1.