Quantifying an Agreement Study

1 Introduction

The agreement problem has a long history starting with the correlation coefficient for agreement over 100 years ago and it covers a broad range of data with applications arising from many different fields. In medical and other related sciences, clinical or experimental measurements usually serve as a basis for diagnostic, prognostic, therapeutic, and performance evaluations. Examples can be found for assessing the reliability of multiple raters (or measurement methods), assessing the suitability for tumor evaluation of using a local laboratory or a central laboratory in a randomized clinical trial (RCT), assessing the agreement of the clinical trial assay (CTA) and the in vitro diagnostic device (IVD) in the companion diagnostics (CDx) development for developing a personalized medicine, assessing the reliability of the inclusion criteria for entry into an RCT, validating surrogate endpoints in a study, determining that the important outcome measurements are interchangeable among the evaluators in an RCT. Any elegant study design cannot overcome the damage by unreliable measurement [1]. A good measurement agreement is very important and crucial for a study investigator.

There are many methods developed to assess the agreement of two measurement methods. According to Liao and Capen [2], the existing approaches can be classified into three categories. The first category is the hypothesis testing approach, which tests the departure from the perfect agreement (i.e. the intercept equals to 0 and the slope equals to 1). The second category is an index approach which includes the first commonly used correlation coefficient, the intraclass correlation coefficient (ICC), the concordance correlation coefficient (CCC) [3], and the improved CCC [4], and many more. The improved concordance coefficient also takes the variability from each individual measurement method into consideration in assessing the agreement between the two measurement methods. The third category is an interval approach. The earliest approach in this category is the Bland-Altman [5] approach using an approximate 95% confidence interval for the difference as the limit of agreement with a supplemental mean difference plot. The limits of agreement are directly linked to practitioners’ subject knowledge. This approach is simple and intuitive to implement and has generated many applications as a favorite for medical researchers. However, there are some concerns when applying for this approach in real examples with difficulty in interpretation such as the validity of the assumptions, the artifactual bias and trend, etc. [6–12]. More detail can be found in Liao and Capen [9]. To overcome the limitations observed for Bland-Altman approach, Liao and Capen [9] proposed an interval approach to handle more complicated scenarios in practice and provide more information. This new approach includes Bland-Altman’s approach as its special case and evaluates concordance by defining an agreement interval for each individual paired observation and assessing the overall concordance (an R-coded function has been developed to implement these interval approaches).

There seems a consensus in the agreement community that the hypothesis testing approach is definitely not appropriate for assessing the agreement since it heavily depends on the residual variance and can lead to rejecting a reasonably good agreement when this variance is small, but fail to reject a poor agreement when this variance is large. There are many critiques in the literature about using an index in assessing agreement. Major concerns about using an index approach are (1) it assumes an often violated bivariate distribution with a fixed mean and constant covariance; (2) it is very sensitive to the range of the measurements available in the sample and sensitive to sample heterogeneity – the greater this range, the higher the index; (3) it is not related to the actual scale of measurement or to the size of error which might be scientifically allowable; (4) the same index value has different meanings in different experiments. There are still many existing or newly developed index applications. However, there is a trending toward using the interval approaches preferably. The interval approach works on the actual scale of the measurements and links the subject knowledge to the agreement limits without the concerns from the index approaches and provides more useful and informative information.

Many papers have been published to explore ways to measure the agreement of two measurements. However, all these methods do not link the conclusion with the size of the experiment. The conclusion for an agreement study from a large size experiment should be more convincing than the conclusion from a smaller size experiment. There has been relatively little attention on this kind of assessment to quantify how good the agreement is. In Section 2, a quantification method is described. The method is based on two rates: the discordance rate and tolerance probability. Two examples are used in Section 3 to illustrate the agreement quantification method. Summary follows in Section 4.

2 Quantifying an agreement

Different metrics can be defined to measure the agreement in theory. However, in practice, a simple and intuitive measure of agreement for each individual pair (X, Y) (i.e. within-individual between methods) is preferred, where the measurement X(Y) is the reportable value and it can be transformation of the original readout, such as the log-scaled observation. An obvious simple and intuitive starting point and commonly accepted metric is the difference between measurements for each pair and then make an agreement statement by comparing the difference to a specified interval Δ. If the difference of paired measurements falls within a specified interval Δ, then the paired measurements are considered to agree with each other.

Given this specified interval Δ and the assumption that the two measurement methods agree, there always exists a discordance rate α such that P(Y−X∈Δ)=1−α. Thus, there is a one-to-one relationship between the discordance rate α and the agreement interval Δ. The agreement assessment can be well described in Figure 1 [9]. When the differences for all the paired observations from the two measurement methods fall within the agreement interval Δ or no more than specified k paired differences fall outside of the agreement interval Δ, then the two measurement methods are claimed having good agreement between the two measurement methods.

Figure 1

Graphic illustration of agreement assessment [9]

The agreement interval Δ can be constructed in different ways. Liao and Capen [9] described a method constructing the agreement interval Δ with many good features using the linear measurement error model. Consider the linear measurement error model [13, 14] as follows:

where (X0,Y0) are the unobserved (fixed) true values, ε and δ are independently normally distributed with zero means and equal variance σ2. The agreement interval Δ is defined as (−t1−α/2,n−12σ,+t1−α/2,n−12σ). For a given data set with a fixed sample size n and the agreement interval Δ, a conclusion can be drawn no matter how big the sample size n is. However, the conclusion for an agreement study from a large size experiment is more convincing than the conclusion from a smaller size experiment. Thus, to be more descriptive and meaningful, any agreement conclusion should be always linked with sample size n. There has been relatively little attention on this kind of assessment to quantify how good the agreement is. Toward this, the final conclusion should be directly linked to sample size n and this kind of approach is described as follows.

For each paired observation, there are only two scenarios: the difference either falls within or falls outside of the agreement interval Δ. If the difference falls outside of the agreement interval Δ, then this pair is called a discordance pair, meanwhile, if the difference falls inside the agreement interval Δ, then this pair is called a concordance pair. Given a data set with n paired observations, the number of discordance pairs and the number of concordance pairs can be determined. The goal is to report that the two measurement methods are either concordant or discordant in a specific level based on the number of discordance pairs and the number of concordance pairs. If the discordant is labeled as “diseased” and the concordance is labeled as “non-diseased,” then the receiver operating characteristic (ROC) curve for a medical test in classification [15] can be borrowed for this goal.

For a specific false positive fraction (FPF), say, p0, the corresponding true positive fraction (TPF) value, ROC(p0), can provide a relevant summary index, but the partial area under the curve, pAUC(p0)=∫0p0ROC(p)dp, is a recommended summary index that restricts attention to FPFs at and below p0, which uses all points on the ROC curve in the range (0, p0) of FPFs. Note that pAUC(p0) is the average of the TPF across FPFs in (0, p0) and pAUC(p0)≤p0, where equality occurs when the test is a perfect one, which completely separates “diseased” and “non-diseased” subjects [15].

Given a data set with n paired observations and the agreement interval Δ (thus, the discordance rate α), let k be the number of discordance pairs. Then there are n – k concordance pairs. Define the tolerance probability β to be the largest value such that the following inequality is true:

Comparing this definition in inequality eq. (1) with the ROC concept and results in previous paragraph, the left side of inequality eq. (1) defines the FPF and the tolerance probability β is the average of TPFs over the range of the FPF. When the equality occurs in inequality eq. (1), then the procedure is a perfect one, which completely separates “diseased” and “non-diseased” subjects, i.e. the agreement assessment procedure perfectly identifies the discordance and concordance pairs. Thus, an agreement assessment can be quantified based on the discordance rate α and the tolerance probability β using the observed numbers of discordance pairs and the concordance pairs observed from the data set.

As demonstrated in Liao [16], the sample size is an increasing function of the tolerance probability β but a decreasing function of the discordance rate α. The discordance rate and tolerance probability play similar roles as the significant level and the power in a hypothesis testing setting from the Neyman–Pearson framework. More samples are needed in k > 0 than k = 0 to claim the same tolerance probability. For example, when k = 0 and with the sample size n = 59, the agreement conclusion can be quantified at the discordance rate α = 0.05 with a tolerance probability β = 0.95. However, when k = 1 (i.e. there is a discordance pair) and with the sample size n = 59, the agreement conclusion can be quantified at the discordance rate α = 0.05 with a tolerance probability β = 0.80 only. In order to have the same tolerance probability β = 0.95, a large sample size n = 93 is needed in this case.

3 Illustrations

3.1 An assay bridging study

Consider an assay bridging study, where a new assay was developed to replace the current assay used for a marketed product. Agreement was to be assessed by having each assay to test a common sample set ranging in concentration from 10 to 800 U/mL with one of three different matrices. For this purpose, 32 paired samples across the entire selected potency range were tested. It was therefore important to know how the concordance of these two assays should be determined. The data are plotted in a log scale in Figure 2.

Figure 2

Raw data. The solid line is the perfect agreement line (log(New Assay) = log(Current Assay)). The dotted line is the regression line from the measurement error model

If Lin’s CCC index is used, the estimated CCC is 0.9989 with the 95% confidence interval as (0.9977, 0.9994), which indicates an excellent agreement. The Bland–Altman’s limit of agreement is (–0.1338, 0.0929). Following Liao and Capen [9], a linear measurement error model is used to model the relationship between the measurement in the log-scale from the new assay and the measurement in the log-scale from the current assay:

log(new)=a+b×log(current)0+ε

log(current)=log(current)0+δ

At the discordance rate α = 0.05, the agreement interval Δ is (–0.1036, +0.1036), which is about (–9.84, 10.92)% difference in the raw scale. To virtually check the agreement between the new assay and the current assay, the difference between the log-new assay and the log-current assay is plotted against the sample number in Figure 3.

Figure 3 clearly shows that all the 32 paired differences are inside the agreement interval limits at the discordance rate α = 0.05, i.e. all the 32 pairs are the concordance pairs. Thus, the agreement between the new assay and the current assay for measuring the potency can be quantified at the discordance rate α = 0.05 with a tolerance probability β = 0.80. A useful interpretation of an analysis of agreement must lay explicitly its dependence upon clinical/scientific limits of tolerance. If, for example, any difference between these two assays is not over 12% difference in the raw scale, then it is considered no clinical impact or scientific difference. Thus, the clinically acceptable agreement interval Δ should be (–0.1133, +0.1133) which corresponds to a discordance rate of 0.034. The agreement assessment based on this clinically based agreement interval is also shown in Figure 3, which shows that all the paired differences are inside the clinically acceptable agreement interval limits. With this clinically acceptable agreement interval, the discordance rate is α = 0.034 and no paired difference falls outside of the clinically defined agreement interval, then the agreement between the new assay and the current assay for measuring the potency can be quantified with a tolerance probability β = 0.66 at the discordance rate α = 0.034. Note that the tolerance probability β using the clinically accepted agreement interval is smaller than that from the agreement interval determined at discordance rate α = 0.05 since a smaller discordance rate α = 0.034 is used. Again, this mirrors the similar relationship between the significant level and the power in a hypothesis testing setting.

Figure 3

Agreement assessment. The dotted line at the discordance rate α = 0.05; the solid line at the clinically meaningful limit, allowing up to 12% potency difference

3.2 Inferior pelvic infundibular angle measurement

Consider the data set from Luiz et al. [17]. For convenience, the data are reproduced in Table 1. The data include registers the inferior pelvic infundibular angle (IPIA) for 52 kidneys, evaluated by means of computerized tomography (T) and urography (U). Due to the financial costs of a tomography, obtaining reliable results through urography would be convenient for the diagnoses and treatment of renal lithiasis. Thus, it is important to understand how good the measurement from the less expensive urography agrees with the measurement from the expensive tomography. Before the analysis, the data are plotted in Figure 4. It is possible to detect some discrepancy between these two methods. This disagreement should be evaluated through the incorporation of some clinical information to answer if the difference between the methods actually does or does not have any relevance, from the clinical standpoint.

Figure 4

Raw data. The solid line is the perfect agreement line (U = T). The dotted line is the regression line from the measurement error model

Table 1

Inferior pelvic infundibular angle (IPIA), in degrees, by urography and tomography (n = 52 kidneys) [17]

Kidney	Method		Kidney	Method
	Urography	Tomography		Urography	Tomography
1	100°	97°	27	40°	45°
2	58°	77°	28	70°	60°
3	95°	74°	29	63°	50°
4	55°	59°	30	103°	94°
5	79°	79°	31	95°	91°
6	95°	85°	32	80°	66°
7	60°	78°	33	72°	63°
8	88°	78°	34	68°	65°
9	68°	68°	35	48°	58°
10	94°	96°	36	70°	75°
11	60°	74°	37	90°	105°
12	64°	64°	38	60°	65°
13	88°	76°	39	80°	80°
14	57°	60°	40	96°	90°
15	66°	78°	41	54°	58°
16	67°	71°	42	80°	75°
17	76°	67°	43	88°	83°
18	95°	103°	44	70°	78°
19	85°	95°	45	90°	85°
20	105°	78°	46	79°	65°
21	80°	70°	47	100°	90°
22	85°	80°	48	85°	76°
23	82°	78°	49	108°	100°
24	102°	102°	50	53°	65°
25	100°	102°	51	58°	40°
26	75°	77°	52	49°	53°

If using Lin’s CCC index, the estimated CCC is 0.810 with the 95% confidence interval as (0.693, 0.885), which indicates a very good agreement. The Bland–Altman’s limit of agreement is (–17.752, 21.098). Following Liao and Capen [9], a linear measurement error model is used to model the relationship between the measurement from urography and the measurement from tomography:

U=a+b×T0+ε

T=T0+δ

At the discordance rate α = 0.05, the agreement interval Δ is (–19.275, +19.275). To virtually check the agreement between urography and tomography, the difference between urography and tomography is plotted against the sample number in Figure 5.

Figure 5

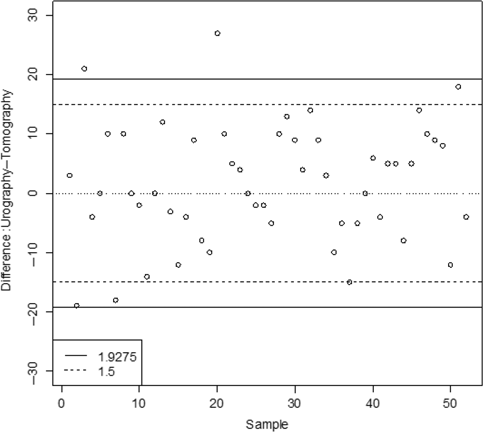
Agreement assessment. The solid line at the discordance rate α = 0.05; the dotted line at the clinically meaningful limit is (–15, +15)

Figure 5 clearly shows that two paired differences are outside of the agreement interval limits, i.e. there are 2 discordance pairs and 50 concordance pairs in the experiment. Thus, the agreement between the urography and the tomography for measuring the IPIA can be quantified at the discordance rate α = 0.05 with a tolerance probability β = 0.48. Note that if no paired difference falls outside of the agreement limits at the discordance rate α = 0.05, the sample size 52 would give a tolerance probability β = 0.93.

As pointed out in Luiz et al. [17], a useful interpretation of an analysis of agreement must clearly demonstrate its dependence upon clinical limits of tolerance. Any measurement of agreement thus would be calculated through the difference and would be represented in the graphic. For example, a difference not inferior to 15° is needed for urography method to be clinically meaningfully suitable for use. The agreement assessment using this clinically meaningful agreement interval is also plotted in Figure 5. Figure 5 indicates that there are five paired differences outside the clinically meaningful limit (–15, +15), which represents a discordance rate α = 0.125. Thus, the agreement between urography and the tomography for measuring the IPIA can be quantified at the discordance rate α = 0.125, with a tolerance probability β = 0.64. Note that the tolerance probability β using the clinically accepted agreement interval is larger than that from the agreement interval determined at discordance rate α = 0.05 since a larger discordance rate α = 0.125 is used.

4 Summary

Agreement assessment comes from many different medicinal and scientific areas. Many statistical methods have been proposed to assess the agreement. However, no method exists to quantify how good the agreement of two measurement methods is. The conclusion for an agreement study from a large size experiment should be more convincing than the conclusion from a smaller size experiment. The difference between measurements for each pair is a very intuitive and attractive metric to measuring the agreement. In this paper, the discordance rate α and the tolerance probability β are used to quantify the agreement assessment. The two rates play similar roles as the significant level and the power in the hypothesis testing setting. In this quantification approach, the sample size is directly linked into the final conclusion with these two rates based on the numbers of discordance pairs and concordance pairs. The sample size is an increasing function of the tolerance probability β but a decreasing function of the discordance rate α. This proposed agreement quantification approach was illustrated through two examples with information from clinical/scientific judgment incorporated into the agreement assessment. It demonstrated that this proposed agreement quantification is a very feasible approach and we expect more this kind of agreement assessment in the near future.

As illustrated in the two examples, it is recommended to quantify the agreement study using both the variability-based agreement interval Δ such as that at the discordance rate α = 0.05 level and the clinical/scientific-based agreement interval Δ such as that the clinical/scientific judgment incorporated into the agreement assessment. Similar to the choice of the significant level and the power in the hypothesis testing setting, the choice of an appropriate value for the discordance rate and the tolerance probability for the agreement quantification should be discussed before designing the agreement study.