Maslov index, lagrangians, mapping class groups and TQFT
-
Patrick M. Gilmer
und
Gregor Masbaum
Abstract.
Given a mapping class f of an oriented
surface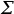 
and a
lagrangian λ in the first homology of 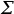, we define an
integer
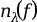. We use
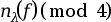to describe
a
universal central extension of the
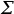mapping class group of as an index-four subgroup of the
extension constructed from the Maslov index of triples of lagrangian subspaces in the homology of
the surface. We give two
descriptions of this subgroup.
One is
topological using surgery, the other is homological and builds on
work of Turaev and work of Walker. Some applications to TQFT are
discussed. They are based on the fact that our construction allows one to precisely describe how the phase
factors that arise in the skein theory approach to TQFT-representations of the mapping class group depend on the choice of a
lagrangian on the surface.
© 2013 by Walter de Gruyter Berlin Boston
Artikel in diesem Heft
- Masthead
- Morrey regularity for almost minimizers of asymptotically convex functionals with nonstandard growth
- Splitting-up scheme for nonlinear stochastic hyperbolic equations
- Pcf and abelian groups
- Cropping Euler factors of modular L-functions
- Maslov index, lagrangians, mapping class groups and TQFT
- Erratum [0.1mm] Use of reproducing kernels and Berezin symbols technique in some questions of operator theory [Forum Math., DOI 10.1515/FORM.2011.073]
Artikel in diesem Heft
- Masthead
- Morrey regularity for almost minimizers of asymptotically convex functionals with nonstandard growth
- Splitting-up scheme for nonlinear stochastic hyperbolic equations
- Pcf and abelian groups
- Cropping Euler factors of modular L-functions
- Maslov index, lagrangians, mapping class groups and TQFT
- Erratum [0.1mm] Use of reproducing kernels and Berezin symbols technique in some questions of operator theory [Forum Math., DOI 10.1515/FORM.2011.073]
