Abstract
Dissipative particle dynamics and molecular simulations were carried out to investigate the phase behaviors of glycidyl azide polymer (GAP)/hydroxyl-terminated polybutadiene (HTPB) polymer blend in dioctyl sebacate (DOS), and mixture of DOS and bis(2,2-dinitropropyl)formal/acetal (A3), respectively. The rheology of GAP/HTPB propellant slurry plasticized by A3/DOS was studied. First, single-phase aggregations of GAP and HTPB appear slightly in A3/DOS whereas it is conspicuous in DOS, which results from the small surface tension between the GAP/HTPB plasticized by A3/DOS and the weak thermal diffusion of this blend. Furthermore, with the plasticizing ratio (po/pl) increasing to 1.2, the GAP/HTPB propellant slurry plasticized by A3/DOS exhibits small viscosity and yield stress, and the Newtonian-like behavior of slurry improves its manufacturability. Finally, integral GAP/HTPB-based propellant can be obtained using A3/DOS as plasticizers.
1 Introduction
Solid propellants lay the main foundation for rockets and missiles. Propellants generally consist of polymer binders, plasticizers, energetic particles and metal fuel agent. Energy efficiency is of vital importance to the propellant and is a topic of concern for researchers in the aerospace or defense industries (1), (2). However, further improvement for conventional propellants has been limited due to the low energy of the polymer binders and the plasticizers. For example, the hydroxyl-terminated polybutadiene (HTPB)-based propellant uses a binder (HTPB) and plasticizers [dioctyl sebacate (DOS), generally] with low enthalpies of formation (ΔHf) and the low density (3), (4). Therefore, some new energetic binders and plasticizers were recently developed (5), (6), (7), (8), and their applications in propellants remedied the shortage of energy performance. Among them, glycidyl azide polymer (GAP) has drawn tremendous attention due to its high formation enthalpy, high density and low sensitivity. It is a promising energetic binder of advanced propellants. Bis(2,2-dinitropropyl) formal/acetal (A3) was developed as an insensitive energetic plasticizer for the azido-propellant formulations (9), (10), (11). GAP-based propellants are expected to achieve excellent energetic characteristics and insensitivity by the addition of A3.
However, the steric hindrance of azide groups (-N3) greatly limits the mobility of the chains, resulting in poor mechanical properties of GAP (12), (13), (14). Compared with GAP, HTPB presents excellent mechanical and low temperature properties (15), (16). Introducing GAP into HTPB through blending is expected to increase both the energetic and mechanical properties. However, the immiscibility of GAP/HTPB blend prevents its practical application in propellants (17), (18). In fact, the large surface tension between GAP and HTPB facilitates phase separation during blending, which also limits its application. This pendent problem is expected to be solved through our new approach.
From an application perspective, it is desirable to introduce GAP and the energetic plasticizer (A3) simultaneously into HTPB systems (including DOS); in this way, the energy characteristics of propellant can be significantly improved, and the surface tension between GAP and HTPB may be decreased under the influence of plasticizers. Miscibility of the liquid phase in propellant has significant effect on the fluidity, molding quality and mechanical properties of solid propellant. Then the relevant studies not only can provide guidance to our experiments but also are useful for understanding the mechanism of phase behaviors among these polymer binders and plasticizers. Moreover, considering the economic costs of energetic materials (especially GAP and A3), before experiments, we need effective means to validate the feasibility of this method (introducing GAP and A3 into HTPB). Therefore, it is necessary to investigate the miscibility of the systems in which the energetic polymer and plasticizer are introduced.
Dissipative particle dynamics (DPD) and molecular dynamics (MD) provide effective ways to study the micromorphology and phase behaviors. By these techniques, we investigated the thermodynamic evolution of GAP/HTPB blend plasticized by A3/DOS and DOS, respectively. Based on simulation results, the polymer blend with best miscibility was used in solid propellant for a rheology study.
2 Simulation and experimental details
2.1 Theory of DPD
A mesoscale simulation program, dissipative particle dynamic (DPD), provides a dynamic algorithm that incorporates hydrodynamics for studying coarse-grained systems over long length and time scales (19), (20), (21). This technique is frequently used to simulate the phase behavior of polymer blends. For the coarse-grained particle (DPD bead) i and j, the interactions fi between them can be mainly divided into five terms (22), (23): conservative force
The terms in the bracket describing the bond or non-bond interaction of the bead i with its neighbor j are given by
where rij is the distance between beads i and j; eij is the unit vector (ri−rj)/rij; ω(r) is a function that determines the radial dependence of the force; aij is the repulsion amplitude that reflects the chemical characteristics of the interacting particles; γij and σij are the friction coefficient and the amplitude of the noise, respectively; Δt is the time step; and ξij is a random number with zero mean and unit variance. It is noteworthy that aij has relation with Flory-Huggins parameter χij, aij=aii+3.27χij(ρ=3), where aii has the value of 25kBT. Total bond and angle potential energy can be expressed as
where C and k are the coefficient describing the strength of the bond and angle potential, respectively; r0 and θ0 are the equilibrium bond length and angle, respectively; and r and θ are the bond length and angle, respectively.
2.2 Theory of MD
Molecular dynamic (MD) is generally used to simulate the motions of atoms or molecules. It is also adopted in this article to investigate the thermal diffusion in the blends of polymers and plasticizers. In MD simulations, Newton’s equation of motion (24) is used to calculate the force of atom i:
where Fi is the force, mi is the mass and ai is the acceleration of atom i. The force on atom i can be computed directly from the derivative of the potential energy V with respect to the coordinate ri:
where t is the simulation time. A classical algorithm named as Verlet velocity algorithm (25) can solve the equation of motion. It overcomes the out-of-synchrony shortcoming of the Verlet leapfrog method. The Verlet velocity algorithm is as follows:
where r(t), v(t) and a(t) are respectively the position, velocity and acceleration at time t. This algorithm was adopted in our MD simulations.
For a simulation system at equilibrium, atoms tend to diffuse away from their original location. The mean square displacement (MSD) of these atoms with respect to their original position is obtained as the second moment of their distribution at t>0 and is related to the diffusion coefficient as follows:
where ri denotes the position vector of ith atom, and angular brackets denote an ensemble average. Then the limiting slope of the mean square displacement as a function of time can be used to evaluate the self-diffusion coefficient of an atom undergoing random Brownian motion in three dimensions.
2.3 Simulations method
2.3.1 DPD method
In our research, two kinds of polymers GAP (X̅n=37) and HTPB (X̅n=56), which adopted as the propellant binders, were utilized to simulate their phase behaviors in the presence of DOS or A3/DOS plasticizers. By means of the DPD code in Material Studio 7.0 software (26), we first presented the molecular structures and coarse-grained models of the polymers (Figure 1) and plasticizers (Figure 2). HTPB chains contain different configurations of trans-2,3-butadiene (l), cis-2,3-butadiene (m) and vinyl-1,2-butadiene (n). All of these groups can be represented by H1, H2 and H3 beads (l+m+n=55), respectively. In the case of GAP, the ether and the side azidomethyl groups are the significant difference from HTPB. Soft polyether segments (-OCHCH2-) make the chains flexible, and therefore we simplified them with G1 coarse grain. However, the rigid azidomethyl groups (-CH2N3) in the side chain decreases the flexibility and weight percentage of the main chains (27); thus, the G2 bead was used to characterize it. The coarse-grained models of GAP and HTPB are linear and branched, respectively.
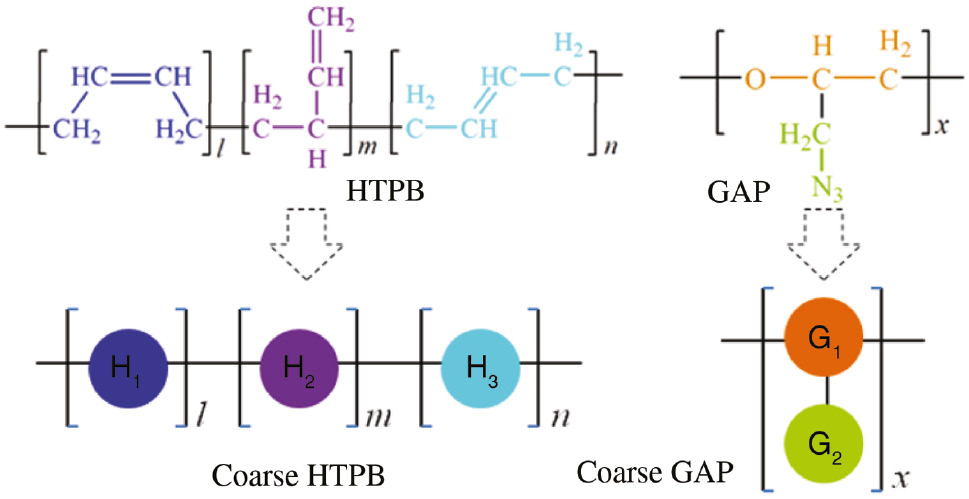
Coarse-grained modeling of GAP and HTPB in DPD simulations.

Coarse-grained modeling of DOS and A3 in DPD simulations.
A3 is the blend of BDNPF/BDNPA with the mole ratio of 1:1.
The coarse graining method of plasticizers (DOS and A3) follows the similar principle that distinguishes the characteristic groups and general groups. Ester groups in the DOS molecule have relatively stronger polarity and, thus, were simplified as bead D2. Two kinds of nonpolar alkyl groups in the middle or end site of DOS molecules were represented as D3 and D1 beads respectively. A3 is a eutectic mixture of BDNPF and BDNPA. The characteristic groups in A3 are energetic (-NO2), ether bond (-O-CH2-O-) and (-O-CHCH3-O-). Because the coarse grain beads of plasticizers share a similar volume with GAP or HTPB unit beads, we modeled the coarse grains of the nitro and methyl end groups in BDNPF/A as B2. Lastly, the groups contain ether bond on the middle site in BDNPF and BDNPA were respectively represented as B2 and B3.
After the coarse grain models were completely built, the interaction (or repulsion) parameter aij, which contribute mainly to the conservative force
Calculated repulsion parameter matrix for different beads.
| aij | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| G1 | G2 | H1 | H2 | H3 | B1 | B2 | B3 | D1 | D2 | D3 | |
| G1 | 25.0 | ||||||||||
| G2 | 26.1 | 25.0 | |||||||||
| H1 | 32.8 | 31.4 | 25.0 | Symmetry | |||||||
| H2 | 33.6 | 32.2 | 25.1 | 25.0 | |||||||
| H3 | 33.8 | 32.3 | 25.0 | 25.2 | 25.0 | ||||||
| B1 | 35.3 | 31.0 | 28.4 | 29.4 | 28.4 | 25.0 | |||||
| B2 | 25.4 | 27.5 | 34.5 | 35.3 | 35.1 | 37.3 | 25.0 | ||||
| B3 | 25.2 | 26.7 | 32.0 | 32.7 | 32.6 | 34.5 | 25.1 | 25.0 | |||
| D1 | 36.4 | 34.4 | 25.9 | 25.9 | 25.7 | 26.3 | 38.7 | 35.4 | 25.0 | ||
| D2 | 34.1 | 40.4 | 56.9 | 58.5 | 57.9 | 56.2 | 33.5 | 34.6 | 62.1 | 25.0 | |
| D3 | 37.7 | 35.7 | 26.9 | 27.1 | 26.7 | 27.1 | 40.0 | 36.6 | 25.5 | 63.2 | 25.0 |
Next, in order to explore the phase aggregation or separation behavior of propellant binders in different plasticizers, two periodic cells with a volume of 30×30×30 Å3 were constructed to pack the binders and different plasticizers for DPD dynamics. For comparison with the experiments, the mass fraction of these binders and plasticizers in our simulations was in conformity with that used in experiments. One cell was filled with GAP, HTPB and DOS with the mass ratio of 0.5:0.5:1.2. The mass ratio of the system containing mixed plasticizers was GAP/HTPB/A3/DOS=0.5:0.5:0.6:0.6. It is worth noting that two types of compounds, BDNPF and BDNPA, account for the same mass fraction in the blend. A time step Δt of 0.05 was used; the rc and grid spacing were respectively determined as 4.64 Å and 1.0. One hundred and five DPD steps were exerted to relax the coarse grain configurations. At the end of simulations, no fluctuation in pressure or temperature occurred, which means that the systems reached equilibrium. Then the analysis can be performed.
2.3.2 MD method
Thermal diffusion, which is related to the free volume of molecules, also has an influence on the phase behaviors of blends. Thermal diffusion could accelerate the process of phase separation; that is, higher diffusion rate of molecules makes blend get to phase equilibrium faster, or vice versa. We therefore also performed all atom molecular dynamics (MD) simulations (29) to study the diffusion of HTPB and GAP in the blend of GAP/HTPB/DOS and GAP/HTPB/A3/DOS using Forcite code in Material Studio 7.0 (26). To be specific, first, GAP, HTPB, A3 and DOS molecules were separately constructed and relaxed using COMPASS forcefield. Then two amorphous cells (50×50×50 Å3) with periodic boundary conditions were built, one was filled with GAP, HTPB and DOS, another one was filled with GAP, HTPB, A3 and DOS. The densities of these cells containing GAP/HTPB/DOS and GAP/HTPB/A3/DOS were 0.99 g·cm−3 and 1.13 g·cm−3 (practical case). The percentage content of each molecule was the same as the DPD beads. Modeling procedures for MD simulations are given in Figure 3.
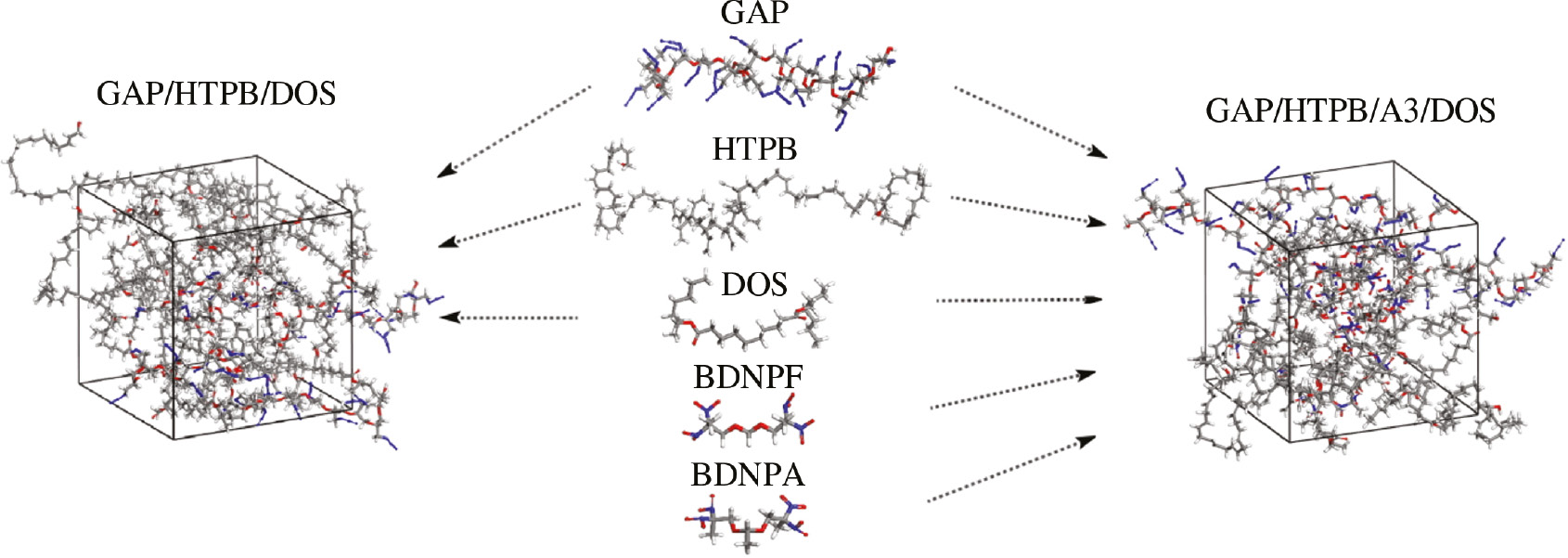
Modeling for the amorphous cells of GAP/HTPB/DOS and GAP/HTPB/A3/DOS in MD simulations.
After the models were built completely, energy minimization was performed to relax the molecular structures by Smart algorithm, the maximal iteration step was 5000. Subsequently, annealing simulations including five cycles between 300 and 500 K for the relaxed structures were carried to overcome energy barriers, and the obtained configuration with the lowest energy was used to execute a 40 ps NVT dynamic process. During the process, the initial velocities of atoms followed Maxwell distributions and were calculated by velocity Verlet algorithm, Coulombic and van der Waals interactions were calculated by Atom based method (30) and Nosé thermostat (31) was used to control the temperature. Once the systems were at equilibrium, the final 12 frames of the results were extracted to calculate the mean square displacement (MSD) curves of HTPB and GAP in two cells.
2.4 Materials and experiments
GAP prepolymer has a hydroxyl group content of 0.55 mmol·g−1 and an average molecular weight of 3700 g·mol−1. HTPB prepolymer has a hydroxyl group content of 0.75 mmol·g−1 and an average molecular weight of 3000 g·mol−1. Desmodur N100 (curing agent I) has an average molecular weight of 728 g·mol−1 and an average functionality of 3.87. The geminal dinitro energetic plasticizer A3 (BDNPF/A) has an acid value of 3.93×10−5 mmol·g−1 and 0.04% wt. H2O content, and ester plasticizer DOS has a purity of 99.6%. All the reagents above were purchased from Liming Research Institute of Chemical Industry in China. Toluene diisocyanate (TDI, curing agent II) with a molecular weight of 174 g·mol−1 and functionality of 2, curing catalysts dibutyltin dilaurate (DBTDL) and triphenyl bismuth (TPB), DOS and catalysts were purchased from the Institute of Chemistry Chinese Academy of Sciences in Shanghai China. Cyclotrimethylenetrinitramine (RDX), ammonium perchlorate (AP) with average particle size of 180 μm and 130 μm, respectively, were produced from Xing’an Chemical Industry Co., Ltd., Shanxi. Aluminum (Al) with average particle size of 13.7±3 μm was purchased from Ansteel Group Corp., Liaoning. Binder and plasticizers were dried in vacuum oven for 8 h at 60–80°C before use. A mixture of DBTDL (dissolved in DOS, 0.5% wt.) and TPB (dissolved in DOS, 0.5% wt.) with ratio of 1:2 was used as the curing catalyst. Details of the propellant formulations in our experiments are listed in Table 2.
Propellant formulations in experiments.
| No. | Formulation I | Formulation II | ||
|---|---|---|---|---|
| Ingredients | Content, wt.% | Ingredients | Content, wt.% | |
| Role | ||||
| Binders | GAP/HTPB | 3.17/3.17 | GAP/HTPB | 3.17/3.17 |
| Plasticizers | DOS | 8.72 | A3/DOS | 4.36/4.36 |
| Curing agents | N100/TDI | 0.44/0.30 | N100/TDI | 0.44/0.30 |
| Solid particles | AP/RDX/Al | 48/18/18 | AP/RDX/Al | 48/18/18 |
| Curing catalysts | DBTDL/TPB | 0.07/0.13 | DBTDL/TPB | 0.07/0.13 |
All the experimental composite propellant mixtures were prepared in 400 g batches in a vertical mixer. The liquid ingredients (except curing agents and catalysts) were charged and stirred for 30 min followed by vacuum mixing for another 30 min to remove entrapped air or moisture. Subsequently, the Al power, RDX and AP were respectively added into the mixture with a time interval of 20 min, followed by vacuum mixing. N100 and TDI were added simultaneously with further mixing of 20 min. Lastly, the catalysts DBTDL and TPB were dropped slowly to the slurry, and then a 10-min mixing was required. A small amount of slurry (40 g) was taken for rheological measurements, which were carried out under 60°C. The remaining slurry was cast into a mold and cured at 60°C for 6 days to obtain a propellant grain.
3 Results and analysis
3.1 Phase behavior of binders/plasticizers
The miscibility or the aggregation morphology of the liquid components has a dramatic effect on the fluidity of the propellant slurry and the molding quality of the propellant grains, whereas the liquid microarea among solid particles determines the momentum transfer efficiency in the two-phase flow process and the distribution of components (27). For instance, if phase separation occurs in the liquid phase of propellant slurry, the fluidity of the slurry may be insufficient for casting (32), and also, molding defects may appear after curing. Therefore, we explored the phase behaviors of the GAP/HTPB binder in different plasticizers using DPD technique and selected the optimal plasticizer for this binder. First, the morphology of GAP (red beads) and HTPB (blue beads) bulks with energy evolution are illustrated in Figure 4.

Morphology of GAP/HTPB/DOS (A) and GAP/HTPB/A3/DOS (B) blend in DPD simulations.
Beads of A3 and DOS are hidden to facilitate the observation.
As can be seen from Figure 4, the GAP and HTPB beads tend to aggregate as spheres when the DPD cells relax to equilibrium. This aggregation behavior mainly proceeds before 6.7×104 steps. From the view of thermodynamics, the aggregation of the same beads is proved to be a spontaneous process. The spheroidal profile [especially in (B)] may decrease the surface tension between binders and plasticizers. However, the aggregation morphology of GAP and HTPB beads in the two figures shows distinct characteristics. Particularly, two kinds of beads have a more uniform dispersion in A3/DOS than in DOS plasticizer. For quantitative analysis, the concentration of GAP and HTPB beads in the cells is extracted and subsequently plotted in Figure 5.

Density profiles of GAP and HTPB beads in GAP/HTPB/DOS (A) and GAP/HTPB/A3/DOS (B) in DPD simulations.
The density distribution is counted along the x-axis of cells.
The concentration profiles in Figure 5A and B correspond to the equilibrium condition of the systems in Figure 4A and B, separately. There are some similarities between the two plots in that both the density of GAP and HTPB beads presents a gradient distribution. Specifically, GAP beads aggregate at the distance of about 8 Å and 22 Å, whereas the HTPB beads concentration peaks appear at the distance of about 5 Å, 15 Å or 24 Å, where the content of GAP beads is small.
The reason for distinct density difference between GAP and HTPB in Figure 5A can be attributed to the pairwise miscibility between binders and plasticizers. The high repulsion parameters (aij) between the GAP beads (G1 and G2) and the HTPB units (H1, H2 and H3) in Table 1 reveal weak interactions between polar groups (azido methyl and polyether units) and non-polar groups (unsaturated alkene groups). In the case of DOS, two kinds of alkyl groups have similar chemical characteristics to alkene groups. As a result, there is strong affinity between them. However, despite the strong polarity of ester group on DOS molecules and azido methyl groups on GAP chains, the mobility of the electronegative azide groups (-N3) is limited due to its steric hindrance, thus leading to weaker interactions and a higher value of aij (40.4) between them. Therefore, phase separation of GAP/HTPB binders plasticized by DOS occurs distinctly.
By contrast, the bead density of two binders exhibits a more uniform distribution in Figure 5B than that in Figure 5A, which indicates that the addition of A3 can enhance the miscibility of GAP and HTPB by a certain degree. Both A3 and GAP molecules contain ether (or similar) groups. In addition, the azido methyl groups interact strongly with ether groups. This results in a good miscibility between GAP and A3; that is, GAP can be dissolved with A3 in any proportion, that is the reason why GAP is generally plasticized by A3 (33), (34). It should be emphasized that although the end of A3 (BDNPF/A) molecules contains polar nitro groups, the symmetry of -NO2 substitution sites and methyl groups in the ends may enhance the affinity of A3 molecules and the cis- and trans-1, 4-butadiene units on HTPB chains (aij of 28.4 in Table 1). In addition, A3 and DOS liquid in our experiments are mutually miscible due to the compatibilizing effect of B1 units in A3 molecules. As a result, the distribution of GAP and HTPB chains in A3/DOS is more uniform than that in DOS.
Next, we will analyze the effect of thermal diffusion on the phase behaviors of GAP/HTPB/ DOS and GAP/HTPB/A3/DOS blends. Based on the MD simulation results, MSD profiles of GAP and HTPB in the two blends are plotted in Figure 6, and the diffusion coefficient (k) of two polymers can be obtained through linear regressions.

MSD profiles of GAP (A) and HTPB (B) in two blends in MD simulations.
As can be seen obviously from Figure 6, the diffusion of GAP and HTPB in GAP/HTPB/DOS is faster than in GAP/HTPB/A3/DOS, resulting in a higher k value in the former blend. It indicates that the required time for phase separation between GAP and HTPB in GAP/HTPB/DOS is shorter than that in GAP/HTPB/A3/DOS, and two reasons account for this phenomenon. First internal friction and viscosity of A3 molecules are higher than that of DOS; therefore, polymer diffusion in the blend becomes difficult upon addition of A3. Second, as we discussed above, A3 improves the compatibility of the blend, and the surface tension between GAP and HTPB tends to decrease. The conclusion drawn here is consistent with the result of the DPD simulation. Additionally, compared with the blend plasticized by DOS, the blend plasticized by A3/DOS shows potential applications in solid propellant. GAP/HTPB-based propellants using A3/DOS as plasticizers will therefore be prepared in the next section.
3.2 Rheological study of propellant slurry
Miscibility of liquid phase has a significant influence on the fluidity (or rheology) of propellant slurry; moreover, better fluidity of slurry in the mixing and casting (preparation) process is critical to the molding quality of propellant grains. It is therefore necessary to study the rheological behavior of propellant slurry. In Section 2.1, the advantage of A3/DOS blend in plasticizing GAP/HTPB binders has been corroborated through DPD and MD techniques. In this section, we prepared the propellant slurry plasticized by DOS and A3/DOS for confirming the simulation results and selecting the optimal plasticizer for the GAP/HTPB based propellant. According to formulations listed in Table 2, two propellant slurries were mixed under the same conditions as described in Section 1.3, then slurry samples 1 and 2 were obtained. For convenience of investigation and comparison, the pictures of two slurries are shown in Figure 7.

Flow behavior of propellant slurry plasticized by DOS (A) and A3/DOS (B).
As can be seen in Figure 7, the solid particles in the slurry plasticized by DOS cluster together. The mixture has poor fluidity and leveling in the PTFE mold until it is under forced vibration. This mixture exhibits a low viscosity but inconsecutive state; that is, solid particles, especially AP and RDX, cannot efficiently adhere to the binders so that the slurry presents a lumpy appearance. This phenomenon can be attributed to the poor physical compatibility between the pairwise units on GAP and DOS. The G2/D2 and G1/D3 sets exhibit higher repulsion parameters aij in Table 1, which leads to the obvious phase separation between GAP and HTPB (Figure 4A) and thus inconsecutive state (Figure 7A). As far as the application is concerned, it is difficult to guarantee a better molding quality of the propellant plasticized by DOS after curing.
By contrast, the fluidity and the leveling property of slurry plasticized by A3/DOS are far superior than that of the former. This can be mainly attributed to the better compatibility between polymers plasticized by A3/DOS as shown in Figure 4B. Thus, GAP chains get more disperse in plasticizers A3/DOS than that in DOS, further leading to a continuous state of slurry in Figure 7B. Therefore, compatibility between the liquid components is demonstrated to have a significant effect on the rheology or processing properties of propellant. Based on the results, the slurry containing A3/DOS was used for a further study in the next section.
3.3 Influence of po/pl on the rheology
In Section 2.2, A3/DOS was determined as the promising plasticizers of GAP/HTPB-based propellant; therefore, high-energy GAP/HTPB-based propellant can be prepared for some further studies. However, before preparation, a quantitative rheological study of this propellant should be implemented to provide rheological parameters for the mixing and casting (or preparation) process. Because the molding quality of propellant depends on its rheological properties, integral propellant grain can be obtained with better rheological properties, but poor rheological properties may lead to some defects in the propellant. Therefore, appropriate rheological parameters are generally required for preparation processes.
As reported in some literature (35), (36), (37), (38), viscosity and flow curves are the most essential graphs to understand the rheological behaviors of a liquid. Slurries with different plasticizing ratio (po/pl) were investigated and presented in Figure 8A and B.
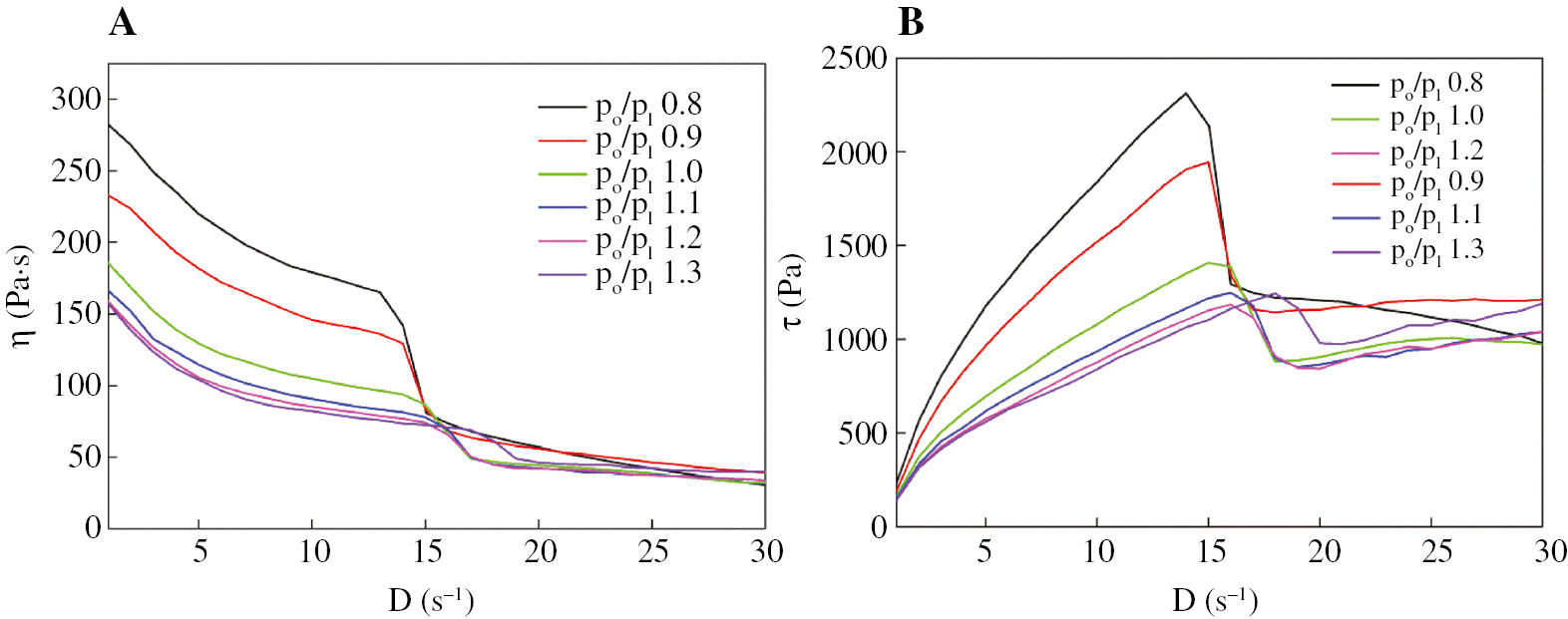
Viscosity curves (A) and flow curves (B) of slurry with varied po/pl.
It can be seen from Figure 8A that in the shear rate range of 0 s−1 to 30 s−1, the viscosity (η) values on these curves decrease sharply, which resulted from the pseudoplastic and shear-thinning characteristics. However, the variation trend of these curves is different from that of the common pseudoplastic fluid (39), (40). There are step changes on these curves. Initially, the viscosities of these slurries decrease sharply with the increment of the shear rate because the reorientation of polymer chains occurs and the physical entanglements weaken under the shear force, then the η decreases sharply. In this stage, there is a stable momentum transfer in the solid-liquid two-phase flow. With the increasing shearing speed, η of the slurry remarkably decreased with the shear rate ranging from 13 s−1 to 17 s−1, which indicates that distortional flow occurs in slurry. This is mainly due to the asynchrony of liquid flow and solid flow. In addition, the blend cannot be completely compatible (but better than GAP/HTPB/DOS blend). This may result in the discontinuity of the slurry at higher rate. Figure 8B shows the corresponding shear stress with the increase in shear rate. Initially, for each curve, the shear stress increases to its peak because the entanglement and the interactions between molecular chains are weakened by the rotor. Then the stress decreases sharply with the distortional flow.
Moreover, the po/pl has a significant influence on η. A dramatic decrease in η can be seen with the po/pl increasing from 0.8 to 1.1, indicating that the increasing A3 and DOS content can dilute the GAP and HTPB chains. The entanglement and interactions between chains are weakened, but the variation amplitude of η tends to decrease when the po/pl is greater than 1.1 because the intermolecular distance of polymers is long enough.
However, the viscosity (η) itself is not the only influencing factor for the rheology of the propellant slurry. Some other rheological parameters should be considered before casting, such as the non-Newtonian index (n) and yield stress (τy). For a comprehensive analysis of the slurry, we also calculated or captured them from the experimental data as presented in Figure 9, noting that the apparent viscosity is extracted from Figure 8A with a shear rate of 1 s−1.

Rheological parameters of propellant slurry with the variation of po/pl.
(A) Non-Newtonian index (n), (B) viscosity (η) and (C) yield stress (τy).
Figure 9 shows a stronger dependence of rheological parameters on the plasticization. With the po/pl increasing from 0.8 to 1.3, the n ascends from 0.31 to 0.45, indicating that the slurry becomes more similar to the Newtonian fluid, which has less dependence on the shear rate. It is noteworthy that the non-Newtonian characteristics are presented by polymers in this blend. A greater po/pl Newtonian fluid is desired in the casting process of the propellant. For the case of η, the variation trend has been discussed above. Here, we are concerned about the value of η, which is an essential parameter for casting, with the po/pl increasing above 1.1, the η ranges from 157 Pa·s to 167 Pa·s, compared to the η of HTPB propellant slurry reported in literature (40), the η of GAP/HTPB propellant slurry at 60°C is small enough for mixing and casting, see Table 3, and is also beneficial to the dispersal and wetting of solid particles. A po/pl range of 1.1 to 1.3 seems to be more appropriate. The last parameter τy is obtained from the Casson rheological model (41), (42), revealing the leveling property of the slurry; a smaller value of τy causes the slurry to flow under the static pressure itself, i.e. the blend tends to flow spontaneously. As can be seen from Figure 9C, the τy decreases dramatically as the po/pl varies from 0.8 to 1.3. τy fluctuates with a po/pl range of 1.1 to 1.3 and reaches the minimum 55.23 Pa with the po/pl of 1.2, meaning a better leveling property can be obtained here.
The viscosity (η) of GAP/HTPB and HTPB propellant.
| Propellant | T (°C) | po/pl | η/Pa·s (1 s−1) |
|---|---|---|---|
| GAP/HTPB | 60 | 1.1∼1.3 | 157∼167 |
| HTPB (40) | 60 | 0 | 570 |
3.4 Molding quality of GAP/HTPB propellant
Based on the rheological study above, a conclusion can be drawn that a po/pl of 1.2 facilitates the mixing and casting process of the propellant slurry. Then we prepared propellant samples using this parameter. After the preparation and curing process, the propellant was sliced for observation as shown in Figure 10.

Samples of GAP/HTPB propellant after curing.
It can be observed from Figure 10 that the cured samples exhibit a compact characteristic. No defects exist inside the slices, indicating a better molding quality of the propellant plasticized by A3/DOS. This demonstrates that the A3/DOS plasticizer is suitable for the GAP/HTPB propellant. There are many reasons that contribute to this. First, compared to GAP/HTPB/DOS, the GAP/HTPB/A3/DOS blend shows a better compatibility. Next, the blend has a weakened diffusion due to A3, and the required time for phase separation becomes longer. Lastly, a po/pl of 1.2 facilitates the mixing and casting process.
4 Conclusion
In this study, by means of DPD and molecular dynamics, we demonstrated a better miscibility and a weaker diffusion of GAP/HTPB/A3/DOS blend compared to GAP/HTPB/DOS. We conducted a rheology study on the propellant slurry and prepared the GAP/HTPB propellant successfully.
The A3/DOS blend decreases the surface tension between the polymers and the plasticizers more than DOS due to the terminal region of BDNPF/A (two substances of A3). As a result, the GAP/HTPB/A3/DOS blend shows an improved miscibility. Moreover, the thermal diffusion of the GAP or HTPB is remarkably weakened by A3/DOS. In our experiments, the propellant slurry plasticized by A3/DOS shows better fluidity and leveling. With the po/pl increasing to 1.2, the viscosity and yield stress of the slurry are at or near its minimum. Moreover, it exhibits Newtonian-like behavior. Finally, the GAP/HTPB propellant plasticized by A3/DOS could be prepared without defects.
Funding: NSAF, Grant Number: No. U1630142.
References
1. Yaman H, Çelik V, Değirmenci E. Experimental investigation of the factors affecting the burning rate of solid rocket propellants. Fuel. 2014;115:794–803.10.1016/j.fuel.2013.05.033Suche in Google Scholar
2. Arkhipov VA, Kiskin AB, Zarko VE, Korotkikh AG. Laboratory method for measurement of the specific impulse of solid propellants. Combust Explos Shock. 2014;50(5):622–4.10.1134/S0010508214050177Suche in Google Scholar
3. Dey A, Sikder AK, Talawar MB, Chottopadhyay S. Towards new directions in oxidizers/energetic fillers for composite propellants: an overview. Cent Eur J Energ Mater. 2015;12(2):377–99.Suche in Google Scholar
4. Jawalkar SN, Ramesh K, Radhakrishnan KK, Bhattacharya B. Studies on the effect of plasticiser and addition of toluene diisocyanate at different temperatures in composite propellant formulations. J Hazard Mater. 2009;164(2):549–54.10.1016/j.jhazmat.2008.08.064Suche in Google Scholar PubMed
5. Gaur B, Lochab B, Choudhary V, Varma IK. Azido polymers-energetic binders for solid rocket propellants. J Macromol Sci C. 2003;43(4):505–45.10.1081/MC-120025976Suche in Google Scholar
6. Babuk VA, Dolotkazin IN, Glebov AA. Burning mechanism of aluminized solid rocket propellants based on energetic binders. Propell Explos Pyrot. 2005;30(4):281–90.10.1002/prep.200500012Suche in Google Scholar
7. Menke K, Heintz T, Schweikert W, Keicher T, Krause H. Formulation and properties of ADN/GAP propellants. Propell Explos Pyrot. 2009;34(3):218–30.10.1002/prep.200900013Suche in Google Scholar
8. Badgujar DM, Talawar MB, Asthana SN, Mahulikar PP. Advances in science and technology of modern energetic materials: an overview. J Hazard Mater. 2008;151(2):289–305.10.1016/j.jhazmat.2007.10.039Suche in Google Scholar PubMed
9. Gore GM, Tipare KR, Divekar CN, Bhatewara RG, Asthana SN. Studies on effect of incorporation of BDNPF/A on burning rates of RDX/AP/AI filled CMDB propellants. J Energ Mater. 2002;20(3):255–78.10.1080/07370650208244824Suche in Google Scholar
10. Talawar MB, Sivabalan R, Anniyappan M, Gore GM, Asthana SN, Gandhe BR. Emerging trends in advanced high energy materials. Combust Explo Shock. 2007;43(1):62–72.10.1007/s10573-007-0010-9Suche in Google Scholar
11. Cho JR, Kim JS, Lee KD, Cheun YG, Park BS. Energetic plasticizer comprising eutetic mixture of bis(2, 2-dinitropropyl) formal, 2, 2-dinitropropyl 2, 2-dinitrobutyl formal and bis(2, 2-dinitrobutyl) formal, and preparation method. U S Patent 6,620,268. 2003-9–16.Suche in Google Scholar
12. Min BS, Park YC, Yoo JC. A study on the triazole crosslinked polymeric binder based on glycidyl azide polymer and dipolarophile curing agents. Propell Explos Pyrot. 2012;37(1):59–68.10.1002/prep.201000127Suche in Google Scholar
13. Hu C, Guo X, Jing Y, Chen J, Zhang C, Huang J. Structure and mechanical properties of crosslinked glycidyl azide polymers via click chemistry as potential binder of solid propellant. J Appl Polym Sci. 2014;131(16):318–23.10.1002/app.40636Suche in Google Scholar
14. Ding Y, Hu C, Guo X, Che Y, Huang J. Structure and mechanical properties of novel composites based on glycidyl azide polymer and propargyl-terminated polybutadiene as potential binder of solid propellant. J Appl Polym Sci. 2014;131(7):40007.10.1002/app.40007Suche in Google Scholar
15. Wingborg N. Increasing the tensile strength of HTPB with different isocyanates and chain extenders. Polym Test. 2002;21(3):283–7.10.1016/S0142-9418(01)00083-6Suche in Google Scholar
16. Deluca LT, Galfetti L, Maggi F, Colombo G, Merotto L, Boiocchi M, Paravan C, Reina A, Tadini P, Fanton L. Characterization of HTPB-based solid fuel formulations: performance, mechanical properties, and pollution. Acta Astronaut. 2013;92(2):150–62.10.1016/j.actaastro.2012.05.002Suche in Google Scholar
17. Zhou Y, Long XP, Zeng QX. Simulation studies of the interfaces of incompatible glycidyl azide polymer/hydroxyl-terminated polybutadiene blends by dissipative particle dynamics. I. The effect of block copolymers and plasticizers. J Appl Polym Sci. 2012;125(2):1530–7.10.1002/app.36370Suche in Google Scholar
18. Gottlieb L, Greenfeld H, Blumer-Ganon B. In-situ compatibilization of an immiscible liquid hydroxyl-terminated polymer pair by rate controlled reactions with a diisocyanate. Polymer. 2018;138(5):320–8.10.1016/j.polymer.2018.01.012Suche in Google Scholar
19. Luo Z, Jiang J. Molecular dynamics and dissipative particle dynamics simulations for the miscibility of poly (ethylene oxide)/poly (vinyl chloride) blends. Polymer. 2010;51(1):291–9.10.1016/j.polymer.2009.11.024Suche in Google Scholar
20. Zhao Y, You LY, Lu ZY, Sun CC. Dissipative particle dynamics study on the multicompartment micelles self-assembled from the mixture of diblock copolymer poly (ethyl ethylene)-block-poly (ethylene oxide) and homopolymer poly (propylene oxide) in aqueous solution. Polymer. 2009;50(22):5333–40.10.1016/j.polymer.2009.09.014Suche in Google Scholar
21. Chatterjee A, Wu LM. Predicting rheology of suspensions of spherical and non-spherical particles using dissipative particle dynamics (DPD): methodology and experimental validation. Mol Simul. 2008;34(3):243–50.10.1080/08927020801957748Suche in Google Scholar
22. Fedosov DA, Pivkin IV, Karniadakis GE. Velocity limit in DPD simulations of wall-bounded flows. J Comput Phys. 2008;227(4):2540–59.10.1016/j.jcp.2007.11.009Suche in Google Scholar
23. Centeno RC, Bustamante-Rendón RA, Hernández-Fragoso JS, Arroyo-Ordoñez I, Pérez E, Alas SJ, Goicochea AG. Surfactant chain length and concentration influence on the interfacial tension of two immiscible model liquids: a coarse-grained approach. J Mol Model. 2017;23(11):306.10.1007/s00894-017-3474-xSuche in Google Scholar PubMed
24. Brázdová V, Bowler DR. Molecular dynamics and Monte Carlo. J Chem Phys. 2002;116(22):9616–9.10.1002/9783527671816.ch6Suche in Google Scholar
25. Spreiter Q, Walter M. Classical molecular dynamics simulation with the velocity Verlet algorithm at strong external magnetic fields. J Comput Phys. 1998;152(1):102–19.10.1006/jcph.1999.6237Suche in Google Scholar
26. Acceryls Inc (2013) Material Studio 7.0. Acceryls Inc, San Diego.Suche in Google Scholar
27. Li Y, Li C, Chen E, Ying Y. Pressure wave propagation characteristics in a two-phase flow pipeline for liquid-propellant rocket. Aerosp Sci Technol. 2011;15(6):453–64.10.1016/j.ast.2010.09.011Suche in Google Scholar
28. Groot RD, Warren PB. Dissipative particle dynamics: bridging the gap between atomistic and mesoscopic simulation. J Chem Phys. 1997;107(11):4423–35.10.1063/1.474784Suche in Google Scholar
29. Zhan X, Xin Y, Zhao K, Wang S, Chen J, Zhang Y, Mao Z. Synthesis, characterization and molecular dynamics simulation of the polyacrylates membranes. E-Polymers. 2016;16(1):83–9.10.1515/epoly-2015-0211Suche in Google Scholar
30. Karasawa N, Goddard WAI. Force fields, structures, and properties of poly(vinylidene fluoride) crystals. Macromolecules. 1992;25(25):7268–81.10.1021/ma00052a031Suche in Google Scholar
31. Evans DJ, Holian BL. The Nosé–Hoover thermostat. J Chem Phys. 1985;83(8):4069–74.10.1063/1.449071Suche in Google Scholar
32. Manu SK, Varghese TL, Mathew S, Ninan KN. Compatibility of glycidyl azide polymer with hydroxyl terminated polybutadiene and plasticizers. J Propul Power. 2009;25(2):533–6.10.2514/1.38145Suche in Google Scholar
33. Nair UR, Asthana SN, Rao AS, Gandhe BR. Advances in high energy materials. Defense Sci J. 2010;60(2):137–51.10.14429/dsj.60.327Suche in Google Scholar
34. Reed R, Chan ML. Insensitive high energetic explosive formulations. US Patent 5061330[P]. 1991.Suche in Google Scholar
35. Heywood NI, Alderman NJ. Improving slurry viscosity and flow-curve measurements. Chem Eng Prog. 2004;100(4):27–34.Suche in Google Scholar
36. Firth BA. Flow properties of coagulated colloidal suspensions II. Experimental properties of the flow curve parameters. J Colloid Interface Sci. 1976;57(2):248–56.10.1016/0021-9797(76)90200-9Suche in Google Scholar
37. Mahanta AK, Dharmsaktu I, Pattnayak PK. Rheological behaviour of HTPB-based composite propellant: effect of temperature and pot life on casting rate. Defence Sci J. 2007;57(4):581–8.10.14429/dsj.57.1791Suche in Google Scholar
38. Mei R, Grosso M, Tronci S, Barattia R, Corominasb F. Real-time control of viscosity curve for a continuous production process of a non-Newtonian fluid. 13th International Conference on Chemical and Process Engineering. 2017, Milano.10.3390/pr6020012Suche in Google Scholar
39. Madlener K, Ciezki HK. Some aspects of rheological and flow characteristics of gel fuels with regard to propulsion application. 45th AIAA Joint Propulsion Conference and Exhibit. 2009; Denver, Colorado.10.2514/6.2009-5240Suche in Google Scholar
40. Mahanta AK, Dharmsaktu I, Pattnayak PK. Rheological behaviour of HTPB-based composite propellant: effect of temperature and pot life on casting rate. Defence Sci J. 2007;57(4):435–42.10.14429/dsj.57.1791Suche in Google Scholar
41. Kelessidis VC, Maglione R. Modeling rheological behavior of bentonite suspensions as Casson and Robertson-Stiff fluids using Newtonian and true shear rates in Couette viscometry. Powder Technol. 2006;168(3):134–47.10.1016/j.powtec.2006.07.011Suche in Google Scholar
42. Castro MA, Olivares MCA, Putman CM, Cebral JR. Unsteady wall shear stress analysis from image-based computational fluid dynamic aneurysm models under Newtonian and Casson rheological models. Med Biol Eng Comput. 2014;52(10): 827–39.10.1007/s11517-014-1189-zSuche in Google Scholar PubMed
©2018 Walter de Gruyter GmbH, Berlin/Boston
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Artikel in diesem Heft
- Frontmatter
- In this Issue
- Full length articles
- Polyaniline-based cadaverine sensor through digital image colorimetry
- Lignin linked to slow biodegradability of urea-crosslinked starch in an anaerobic soil environment
- Controlling stereocomplexation, heat resistance and mechanical properties of stereocomplex polylactide films by using mixtures of low and high molecular weight poly(D-lactide)s
- Effects of zinc acetate and cucurbit[6]uril on PP composites: crystallization behavior, foaming performance and mechanical properties
- Titanium dioxide-benzophenone hybrid as an effective catalyst for enhanced photochemical degradation of low density polyethylene
- Morphology and micromechanics of liquid rubber toughened epoxies
- Simulation of GAP/HTPB phase behaviors in plasticizers and its application in composite solid propellant
- Promotion of poly(vinylidene fluoride) on thermal stability and rheological property of ethylene-tetrafluoroethylene copolymer
- Poly(N-octyl-4-vinylpyridinium bromide) copolymers in aqueous solutions: potentiometric and thermodynamic studies
- Synthesis of miktoarm star-shaped and inverse star-block copolymers by a combination of ring-opening polymerization and click chemistry
- Communication
- Synthesis of polyacrylonitrile and mechanical properties of its electrospun nanofibers
Artikel in diesem Heft
- Frontmatter
- In this Issue
- Full length articles
- Polyaniline-based cadaverine sensor through digital image colorimetry
- Lignin linked to slow biodegradability of urea-crosslinked starch in an anaerobic soil environment
- Controlling stereocomplexation, heat resistance and mechanical properties of stereocomplex polylactide films by using mixtures of low and high molecular weight poly(D-lactide)s
- Effects of zinc acetate and cucurbit[6]uril on PP composites: crystallization behavior, foaming performance and mechanical properties
- Titanium dioxide-benzophenone hybrid as an effective catalyst for enhanced photochemical degradation of low density polyethylene
- Morphology and micromechanics of liquid rubber toughened epoxies
- Simulation of GAP/HTPB phase behaviors in plasticizers and its application in composite solid propellant
- Promotion of poly(vinylidene fluoride) on thermal stability and rheological property of ethylene-tetrafluoroethylene copolymer
- Poly(N-octyl-4-vinylpyridinium bromide) copolymers in aqueous solutions: potentiometric and thermodynamic studies
- Synthesis of miktoarm star-shaped and inverse star-block copolymers by a combination of ring-opening polymerization and click chemistry
- Communication
- Synthesis of polyacrylonitrile and mechanical properties of its electrospun nanofibers

