Abstract
Epoxy acrylate (EA) and tripropylene glycol diacrylate (TPGDA) are two main components of ultraviolet-curable coatings. In this study, the viscosity of EA-TPGDA binary mixtures at various mass ratios was measured by a rotational viscometer at temperatures between 298.15 and 313.15 K. The temperature dependence of the viscosity of the mixtures is discussed. An empirical correlation between the viscosity and the temperature was obtained based on the Andrade equation. The results indicated that the calculated viscosity values show a good agreement with experimental data. This will contribute to the evaluation of the rheological properties and provide a theoretical basis for the industrial application of coatings.
1 Introduction
In recent years, ultraviolet (UV)-curable coatings have received great interest owing to both technological advances and the increasing environmental pressure to reduce the emission of volatile organic compounds (VOC) (1–9). In comparison with conventional solvent-based coatings, UV-curable coatings offer the advantage of low VOC emission, rapid curing at ambient temperature, low energy consumption, high productivity and high degrees of cross-linking (giving rise to outstanding scratch, chemical and stain resistance). Therefore, such coatings provide a wide range of economic and ecological benefits.
UV-curable coatings usually contain four main components (10): the oligomer, the reactive diluent, the photoinitiator and various additives. Epoxy acrylate (EA) is a common oligomer in UV-curable coatings, which is the most principal component for film formation. Tripropylene glycol diacrylate (TPGDA), as the reactive diluent, not only can dissolve the oligomer to adjust the viscosity of the curing system but also can participate in the reaction in photo-initiation polymerization. The viscosity of UV-curable coatings is an important physical property, which is related to the adhesion to the substrates and to the thickness and quality of the cured films. The viscosity of the coating is mainly dependent on the oligomer and reactive diluent owing to their large proportion in compositions. Meanwhile, the influence of temperature on it is also remarkable.
In the present study, we measured the temperature-dependent viscosity of EA-TPGDA binary mixtures at various proportions using a rotational viscometer to develop an empirical correlation for predicting the experimental data. This will contribute to the evaluation of the rheological properties and provide a theoretical basis for the industrial application of coatings.
2 Experimental section
EA was purchased from Jiangmen Ever-Ray New Material Co. Ltd., Jiangmen, China. TPGDA was purchased from Tianjin Institute of Chemical Reagent, Tianjin, China. The molecular structures of EA and TPGDA are shown in Figure 1. The reagents were used without further treatment. A series of mixtures with different mass ratios of EA and TPGDA (3:7, 4:6, 5:5, 6:4 and 7:3) were prepared. Each mixture was mixed intensively using a magnetic stirrer. The viscosity data were measured and recorded by a rotational viscometer (HX-905, designed by Northeastern University, Shenyang, China) at a rotational speed of 200 rpm. The temperatures of the samples were controlled using a constant temperature water bath (with an uncertainty of ±0.5 K). Each viscosity value was obtained by computing the mean value of three measurements. MATLAB 7.0 (The MathWorks, Inc., Natick, USA) was used for fitting the temperature decadence of viscosity.

Molecular structures of EA and TPGDA.
3 Results and discussion
The viscosities of the mixtures at different temperatures from 298.15 to 323.15 K were investigated. The results are shown in Table 1. The results indicate that the viscosity increased with increasing concentration of EA at a specific temperature. The viscosity of a mixture decreased with increasing temperature. To estimate the relationship between viscosity and temperature or the composition of a binary system intuitively, a plot of the temperature dependence of the viscosity of EA-TPGDA binary mixtures with different compositions was made using the MATLAB software based on a cubic spline interpolation method, as shown in Figure 2. The area with the more intensive isoviscous curve indicates greater influence on the viscosity. Therefore, from Figure 2, it can be observed that the temperature dependence of the viscosity of EA-TPGDA binary mixtures became more significant with increasing concentration of EA.
Viscosity of EA-TPGDA binary mixtures at different temperatures.
| Sample no. | Mass ratio (EA/TPGDA) | Viscosity (Pa s) | |||||
|---|---|---|---|---|---|---|---|
| 298.15 K | 303.15 K | 308.15 K | 313.15 K | 318.15 K | 323.15 K | ||
| EA-3 | 3:7 | 0.0743 | 0.0643 | 0.0401 | 0.0304 | 0.0234 | 0.0182 |
| EA-4 | 4:6 | 0.0953 | 0.0844 | 0.0738 | 0.0626 | 0.0424 | 0.0324 |
| EA-5 | 5:5 | 0.2009 | 0.1646 | 0.1172 | 0.1051 | 0.0689 | 0.0519 |
| EA-6 | 6:4 | 0.3873 | 0.3194 | 0.2046 | 0.1644 | 0.1110 | 0.0848 |
| EA-7 | 7:3 | 0.9441 | 0.8145 | 0.5682 | 0.3883 | 0.2705 | 0.1868 |
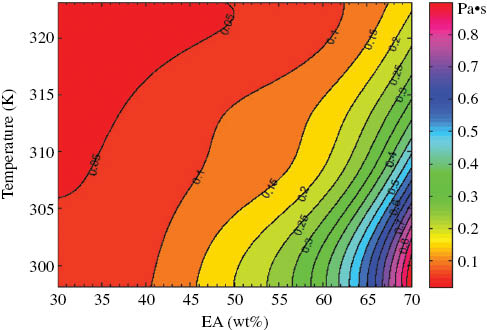
Temperature dependence of the viscosity of EA-TPGDA binary mixtures.
So far, numerous research studies on the temperature dependence of viscosity have been reported. Some empirical and theoretical equations have also been formulated (11–15). However, the theory of Kincaid et al. (16) has played an important role in the research on liquid transport property, which applied the transition state theory of reaction rate to the liquid transport phenomenon. And a notable empirical equation on the relationship between viscosity and temperature is presented by means of the Arrhenius-type equation as follows:
where A is the pre-exponential factor, R is the perfect gas constant and E is the apparent activation energy of the viscous flow. This equation was obtained by combining Newton’s laws of motion and the liquid structure. It is assumed that the macromolecule is in a certain position in space like a crystal. When a macromolecule transfers to a nearby vacancy, an energy barrier (E) needs be tunneled through. The rate of tunneling through the energy barrier for the molecule is similar to the reaction rate. According to a report by Sastry and Patel (17), the apparent activation energy of the viscous flow in a polymer solution is dependent on the solvent and polymer, and on the molecular weight of the polymer and its concentration. The variety of pre-exponential factor A is related to the flexible and stiff chains of the solvent and polymer. According to the Andrade equation, the Napierian logarithm of the viscosity (lnη) has a linear relation with the reciprocal of the temperature (T-1), as shown in Figure 3.

Linear relation between lnη and T-1 of the mixtures.
The correlated data were compared with the corresponding experimental data by computing the average absolute relative deviation (ARD):
where N is the number of data points in each set. The fitting parameters and the ARD are reported in Table 2. The results indicate that the calculated viscosity values based on the Andrade equation show a good agreement with the experimental data. Although the shear-rate dependence on coating viscosity was not considered, we could use the Andrade equation to determine the effect of temperature on the viscosity of EA-TPGDA binary mixtures at a certain shear rate. It is helpful for evaluating the rheological properties and for predicting an applicable viscosity for a coating in the coating industry.
Fitting parameters and average absolute relative deviation (ARD) of EA-TPGDA binary mixtures at temperatures between 298.15 and 313.15 K.
| Sample no. | E (J/mol) | A | ARD (%) |
|---|---|---|---|
| EA-3 | 47,356.54 | 3.96×10-10 | 4.61 |
| EA-4 | 34,719.26 | 8.76×10-8 | 8.03 |
| EA-5 | 43,349.2 | 5.38×10-9 | 5.35 |
| EA-6 | 50,249.82 | 6.46×10-10 | 4.69 |
| EA-7 | 53,833.15 | 3.96×10-10 | 6.47 |
4 Conclusions
The viscosity of EA-TPGDA binary mixtures at various mass ratios was measured at temperatures between 298.15 and 313.15 K. The temperature dependence of the viscosity of the mixtures became more significant with increasing concentration of EA. An empirical correlation between the viscosity and the temperature was obtained based on the Andrade equation. The results indicate that the calculated viscosity shows a good agreement with the experimental data.
Acknowledgments
This work is financially supported by the National Natural Science Foundation of China (no. 51074053) and the Fundamental Research Funds for the Central Universities (no. N090602012).
References
1. Chittavanich P, Miller K, Soucek MD. A photo-curing study of a pigmented UV-curable alkyd. Prog Org Coat. 2012;73:392–400.10.1016/j.porgcoat.2011.02.005Search in Google Scholar
2. Aerykssen JH, Khudyakov IV. New acrylated oligomers with a sulfide group for radiation-curable coatings. Ind Eng Chem Res. 2011;50:1523–9.10.1021/ie101816bSearch in Google Scholar
3. Yu YY, Chien WC, Chen SY. Preparation and optical properties of organic/inorganic nanocomposite materials by UV curing process. Mater Des. 2010;31:2061–70.10.1016/j.matdes.2009.10.013Search in Google Scholar
4. Chemtob A, Versace DL, Belon C, Céline CB, Rigolet S. Concomitant organic-inorganic UV-curing catalyzed by photoacids. Macromolecules 2008;41:7390–8.10.1021/ma801017kSearch in Google Scholar
5. Hwang HD, Park CH, Moon JI, Kim HJ, Masubuchi T. UV-curing behavior and physical properties of waterborne UV-curable polycarbonate-based polyurethane dispersion. Prog Org Coat. 2011;72:663–75.10.1016/j.porgcoat.2011.07.009Search in Google Scholar
6. Xiao X, Hao C. Preparation of waterborne epoxy acrylate/ silica sol hybrid materials and study of their UV curing behavior. Colloids Surf A: Physicochem Eng Aspects 2010;59:82–7.10.1016/j.colsurfa.2010.01.067Search in Google Scholar
7. Wang Y, Liu F, Xue X. Synthesis and characterization of UV-cured epoxy acrylate/POSS nanocomposites. Prog Org Coat. 2013;76:863–9.10.1016/j.porgcoat.2013.02.007Search in Google Scholar
8. Yu B, Wang X, Xing W, Yang H, Song L, Hu Y. UV-curable functionalized graphene oxide/polyurethane acrylate nanocomposite coatings with enhanced thermal stability and mechanical properties. Ind Eng Chem Res. 2012;51:14629–36.10.1021/ie3013852Search in Google Scholar
9. Mishra RS, Mishra AK, Raju KV. Synthesis and property study of UV-curable hyperbranched polyurethane acrylate/ZnO hybrid coatings. Eur Polym J. 2009;45:960–6.10.1016/j.eurpolymj.2008.11.023Search in Google Scholar
10. Decker C. Kinetic study and new applications of UV radiation curing. Macromol Rapid Commun. 2002;23:1067–93.10.1002/marc.200290014Search in Google Scholar
11. Xu HN, Ma SF. Effect of temperature on viscosity of aqueous Triton X-114 solution. J Chem Eng Data 2011;56:2677–9.10.1021/je100775eSearch in Google Scholar
12. Ghasem NM, Al-Marzouqi MH, El-Naas MH. Effect of temperature, composition, and shear rate on polyvinylidene fluoride/dimethylacetamide solution viscosity. J Chem Eng Data 2009;54:3276–80.10.1021/je900248aSearch in Google Scholar
13. Wang Z, Fu L, Xu H, Shang Y, Zhang L, Zhang J. Density, viscosity, and conductivity for the binary systems of water+dual amino-functionalized ionic liquids. J Chem Eng Data 2012;57:1057–63.10.1021/je2007549Search in Google Scholar
14. Larriba M, García S, Navarro P, García J, Rodríguez F. Physical properties of n-butylpyridinium tetrafluoroborate and n-butylpyridinium bis(trifluoromethylsulfonyl)imide binary ionic liquid mixtures. J Chem Eng Data 2012;57:1318–25.10.1021/je300093rSearch in Google Scholar
15. Domanska U, Zawadzki M, Lewandrowska A. Effect of temperature and composition on the density, viscosity, surface tension, and thermodynamic properties of binary mixtures of n-octylisoquinolinium bis{(trifluoromethyl)sulfonyl}imide with alcohols. J Chem Thermodyn. 2012;48:101–11.10.1016/j.jct.2011.12.003Search in Google Scholar
16. Kincaid JF, Eyring H, Stearn AE. The theory of absolute reaction rates and its applications to viscosity and diffusion in the liquid state. Chem Rev. 1941;28:301–65.10.1021/cr60090a005Search in Google Scholar
17. Sastry KS, Patel RD. Temperature dependence of solution viscosity of polymer in solvent-nonsolvent systems. Die Makromol Chem. 1969;128:166–75.10.1002/macp.1969.021280115Search in Google Scholar
©2015 by De Gruyter
This article is distributed under the terms of the Creative Commons Attribution Non-Commercial License, which permits unrestricted non-commercial use, distribution, and reproduction in any medium, provided the original work is properly cited.
Articles in the same Issue
- Frontmatter
- In this Issue
- Full length articles
- Carbon fiber-reinforced plastics based on epoxy resin toughened with core shell rubber impact modifiers
- Microencapsulation of diglycidyl 1,2-cyclohexanedicarboxylate by in situ polymerization: preparation and characterization
- Reactions taking place during molecular chlorine impact on monomers in a wide range of temperatures
- Composition-dependent depression of the glass transition temperature of the rubber phase in a PE-SBR blend
- Thermochemical and mechanical properties of tea tree (Melaleuca alternifolia) fibre reinforced tapioca starch composites
- Hydrogel beads from sugar cane bagasse and palm kernel cake, and the viability of encapsulated Lactobacillus acidophilus
- Composite materials derived from biodegradable starch polymer and Atriplex halimus fibers
- Simultaneous utilization of soju industrial waste for silica production and its residue ash as effective cationic dye adsorbent
- Enhancement of the dielectric performance of PA11/PVDF blends by a solution method with dimethyl sulfoxide
- Communication
- Temperature dependence of the viscosity of epoxy acrylate-tripropylene glycol diacrylate binary mixtures
Articles in the same Issue
- Frontmatter
- In this Issue
- Full length articles
- Carbon fiber-reinforced plastics based on epoxy resin toughened with core shell rubber impact modifiers
- Microencapsulation of diglycidyl 1,2-cyclohexanedicarboxylate by in situ polymerization: preparation and characterization
- Reactions taking place during molecular chlorine impact on monomers in a wide range of temperatures
- Composition-dependent depression of the glass transition temperature of the rubber phase in a PE-SBR blend
- Thermochemical and mechanical properties of tea tree (Melaleuca alternifolia) fibre reinforced tapioca starch composites
- Hydrogel beads from sugar cane bagasse and palm kernel cake, and the viability of encapsulated Lactobacillus acidophilus
- Composite materials derived from biodegradable starch polymer and Atriplex halimus fibers
- Simultaneous utilization of soju industrial waste for silica production and its residue ash as effective cationic dye adsorbent
- Enhancement of the dielectric performance of PA11/PVDF blends by a solution method with dimethyl sulfoxide
- Communication
- Temperature dependence of the viscosity of epoxy acrylate-tripropylene glycol diacrylate binary mixtures

