Home Posterior predictive treatment assignment methods for causal inference in the context of time-varying treatments
Article
Licensed
Unlicensed Requires Authentication

Posterior predictive treatment assignment methods for causal inference in the context of time-varying treatments

  • Shirley X. Liao EMAIL logo , Lucas Henneman and Cory Zigler
Published/Copyright: October 1, 2020
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Epidemiologic Methods
From the journal Epidemiologic Methods Volume 9 Issue 1

Abstract

Marginal structural models (MSM) with inverse probability weighting (IPW) are used to estimate causal effects of time-varying treatments, but can result in erratic finite-sample performance when there is low overlap in covariate distributions across different treatment patterns. Modifications to IPW which target the average treatment effect (ATE) estimand either introduce bias or rely on unverifiable parametric assumptions and extrapolation. This paper extends an alternate estimand, the ATE on the overlap population (ATO) which is estimated on a sub-population with a reasonable probability of receiving alternate treatment patterns in time-varying treatment settings. To estimate the ATO within an MSM framework, this paper extends a stochastic pruning method based on the posterior predictive treatment assignment (PPTA) (Zigler, C. M., and M. Cefalu. 2017. “Posterior Predictive Treatment Assignment for Estimating Causal Effects with Limited Overlap.” eprint arXiv:1710.08749.) as well as a weighting analog (Li, F., K. L. Morgan, and A. M. Zaslavsky. 2018. “Balancing Covariates via Propensity Score Weighting.” Journal of the American Statistical Association 113: 390–400, https://doi.org/10.1080/01621459.2016.1260466.) to the time-varying treatment setting. Simulations demonstrate the performance of these extensions compared against IPW and stabilized weighting with regard to bias, efficiency, and coverage. Finally, an analysis using these methods is performed on Medicare beneficiaries residing across 18,480 ZIP codes in the U.S. to evaluate the effect of coal-fired power plant emissions exposure on ischemic heart disease (IHD) hospitalization, accounting for seasonal patterns that lead to change in treatment over time.

Keywords: Bayesian inference; causal inference; marginal structural models; time-varying treatments
Corresponding author: Shirley X. Liao, Biostatistics, Harvard University, Boston, MA, USA, E-mail:

  1. Research funding: This work was supported by research funding from NIHR01ES026217, NIHR01GM111339 and EPA 83587201. Its contents are solely the responsibility of the grantee and do not necessarily represent the official views of the USEPA. Furthermore, USEPA does not endorse the purchase of any commercial products or services mentioned in the publication.

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Competing interests: Authors state no conflict of interest.

Appendix

A. Observations highly weighted under IPW and OW

Closer examination of both OW and IPW reveals differences in what each weighting scheme prioritizes and which observations receive are up-weighted and down-weighted under each procedure.

Figure 6 plots the log of IP-weights against OW calculated on a single data set simulated as described in Section “Heterogeneous exposure effect simulation” under each of the three and five time points settings. For reference, observations are colored by the number of times they appear in DGCOP.

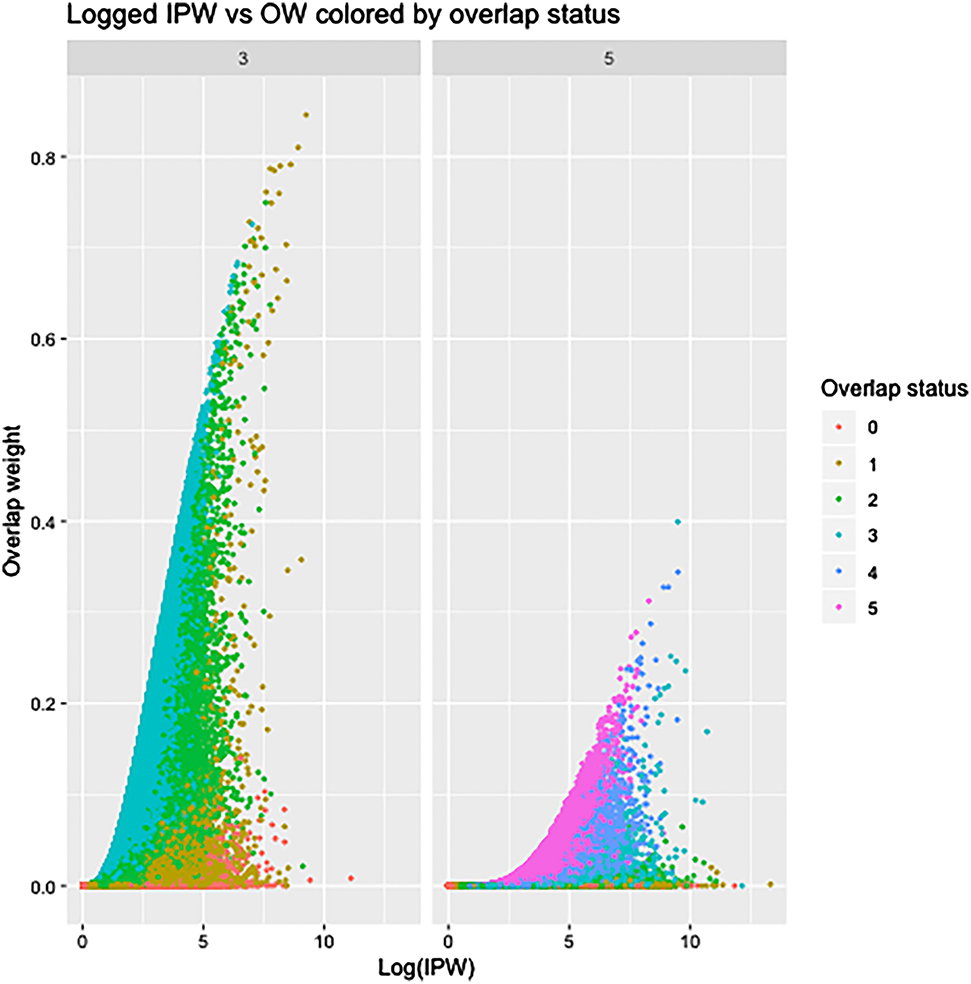
Figure 6: Logged IPW weights vs. OW weights calculated in the heterogeneous exposure effect setting, colored by cumulative overlap state.
Figure 6:

Logged IPW weights vs. OW weights calculated in the heterogeneous exposure effect setting, colored by cumulative overlap state.

Both IPW and OW are alike in that they down-weight observations with a high probability of receiving the observed exposure pattern. An observation with a low IPW would never have a high OW. However, observations with a low OW and high IPW are common.

In order for an observation to have a high OW, it must consistently display a high to moderate probability of receiving the opposite exposure than observed at each time point. This is due to the restricted range of OW, which severely penalizes observations which have a near-zero probability of observing the opposite exposure at any time point. As seen on Figure 6, observations with high OW tend to exist in an area of covariate overlap in the PS distribution at most of the time points, though are not necessarily all members of the DGCOP.

IPW performs differently to OW in two key ways. First, an observation does not have to exhibit consistently high probability of receiving the opposite exposure to be assigned an extreme IPW. Rather, due to the lack of upper bound on IPWs, an observation may receive such an extreme weight at one time point that its behavior at other time points has little effect on its final weight. Second, observations which receive extreme weights under IPW are in fact often in areas of low covariate overlap. IPW highly up-weights observations which, at any time point, are one of a few representing its own exposure group in an area of the PS distribution overwhelmingly populated by members of the opposite exposure group. As evidenced in Figure 6, observations which receive extreme IPWs are often not in the DGCOP.

References

Abel, D., T. Holloway, R. Kladar, P. Meier, D. Ahl, M. Harkey, and J. Patz. 2017. “Response of Power Plant Emissions to Ambient Temperature in the Eastern united states.” Environmental Science & Technology 51: 5838–46, https://doi.org/10.1021/acs.est.6b06201.10.1021/acs.est.6b06201Search in Google Scholar PubMed

Austin, P. C. 2016. “Variance Estimation when Using Inverse Probability of Treatment Weighting (Iptw) with Survival Analysis.” Statistics in Medicine 35: 5642–55, https://doi.org/10.1002/sim.7084.10.1002/sim.7084Search in Google Scholar PubMed PubMed Central

Cole, S. R., and M. A. Hernan. 2008. “Constructing Inverse Probability Weights for Marginal Structural Models.” American Journal of Epidemiology 168: 656–64. Also available at https://academic.oup.com/aje/article/168/6/656/88658/Constructing-Inverse-Probability-Weights-for.10.1093/aje/kwn164Search in Google Scholar PubMed PubMed Central

Crump, R., V. Hotz, G. Imbens, and O. Mitnik. 2009. “Dealing with Limited Overlap in Estimation of Average Treatment Effects.” Biometrika 96: 187–99, https://doi.org/10.1093/biomet/asn055.10.1093/biomet/asn055Search in Google Scholar

Cummiskey, K., C. Kim, C. Choirat, L. Henneman, J. Schwartz, and C. Zigler. 2019. “A Source-Oriented Approach to Coal Power Plant Emissions Health Effects.” arXiv:1902.09703 [stat].Search in Google Scholar

Dockery, D. W., C. A. PopeIII, X. Xu, J. D. Spengler, J. H. Ware, M. E. Fay, B. G. Ferris, and F. E. Speizer. 1993. “An Association between Air Pollution and Mortality in Six US Cities.” New England Journal of Medicine 329: 1753–9, https://doi.org/10.1056/nejm199312093292401.10.1056/NEJM199312093292401Search in Google Scholar PubMed

Dominici, F., M. Greenstone, and C. R. Sunstein. 2014. “Particulate Matter Matters.” Science 344: 257–9. Also available at https://science.sciencemag.org/content/344/6181/257.10.1126/science.1247348Search in Google Scholar PubMed PubMed Central

Dwyer-Lindgren, L., A. H. Mokdad, T. Srebotnjak, A. D. Flaxman, G. M. Hansen, and C. J. Murray. 2014. “Cigarette Smoking Prevalence in US Counties: 1996-2012.” Population Health Metrics 12: 5, https://doi.org/10.1186/1478-7954-12-5.10.1186/1478-7954-12-5Search in Google Scholar PubMed PubMed Central

Elliott, M. R. 2009. “Model Averaging Methods for Weight Trimming in Generalized Linear Regression Models.” Journal of Official Statistics 25: 1–20.Search in Google Scholar

Fitzmaurice, G., M. Davidian, G. Verbeke, and G. E. Molenberghs. 2008. Longitudinal Data Analysis. Cleveland, OH: CRC Press.10.1201/9781420011579Search in Google Scholar

Henneman, L., C. Choirat, C. Ivey, K. Cummiskey, and C. M. Zigler. 2019a. “Characterizing Population Exposure to Coal Emissions Sources in the united states Using the Hyads Model.” Atmospheric Environment 203: 271–80, https://doi.org/10.1016/j.atmosenv.2019.01.043.10.1016/j.atmosenv.2019.01.043Search in Google Scholar PubMed PubMed Central

Henneman, L., C. Choirat, and C. Zigler. 2019b. “Accountability Assessment of Health Improvements in the united states Associated with Reduced Coal Emissions between 2005 and 2012.” Epidemiology 30: 477–85, https://doi.org/10.1097/ede.0000000000001024.10.1097/EDE.0000000000001024Search in Google Scholar PubMed PubMed Central

Hernan, M., and J. Robins. 2018. Causal Inference. Boca Raton: Chapman and Hall/CRC.Search in Google Scholar

Kalnay, E., M. Kanamitsu, R. Kistler, W. Collins, D. Deaven, L. Gandin, M. Iredell, S. Saha, G. White, J. Woollen, Y. Zhu, M. Chelliah, W. Ebisuzaki, W. Higgins, J. Janowiak, K. C. Mo, C. Ropelewski, J. Wang, A. Leetmaa, R. Reynolds, R. Jenne, and D. Joseph. 1996. “The Ncep/ncar 40-year Reanalysis Project.” Bulletin of the American Meterological Society 77: 437–71, https://doi.org/10.1175/1520-0477(1996)077<0437:tnyrp>2.0.co;2.10.4324/9781315793245-16Search in Google Scholar

Li, F., K. L. Morgan, and A. M. Zaslavsky. 2018. “Balancing Covariates via Propensity Score Weighting.” Journal of the American Statistical Association 113: 390–400, https://doi.org/10.1080/01621459.2016.1260466.10.1080/01621459.2016.1260466Search in Google Scholar

Liao, S. 2020 “Uncertainty in the Design Stage of Two-Stage Bayesian Propensity Score Analysis.” Statistics in Medicine, https://doi.org/10.1002/sim.8486.10.1002/sim.8486Search in Google Scholar

Lippmann, M. 2014. “Toxicological and Epidemiological Studies of Cardiovascular Effects of Ambient Air Fine Particulate Matter (pm2.5) and its Chemical Components: Coherence and Public Health Implications.” Critical Reviews in Toxicology 44: 299–347, https://doi.org/10.3109/10408444.2013.861796.10.3109/10408444.2013.861796Search in Google Scholar

Moore, K., R. Neugebauer, F. Lurmann, J. Hall, V. Brajer, S. Alcorn, and I. Tager. 2010. “Ambient Ozone Concentrations and Cardiac Mortality in Southern California 1983–2000: Application of a New Marginal Structural Model Approach.” American Journal of Epidemiology 171: 1233–43. Also available at http://aje.oxfordjournals.org/content/171/11/1233.abstract.10.1093/aje/kwq064Search in Google Scholar

Moore, K. L., R. S. Neugebauer, M. J. van der Laan, and I. B. Tager. 2012. “Causal Inference in Epidemiological Studies with Strong Confounding.” Statistics in Medicine 31: 1380–404, https://doi.org/10.1002/sim.4469.10.1002/sim.4469Search in Google Scholar

Mortality, G., and C. of Death Collaborators. 2014. “Global, Regional, and National Age-Sex Specific All-Cause and Cause-specific Mortality for 240 Causes of Death, 1990–2013: A Systematic Analysis for the Global Burden of Disease Study 2013.” Lancet 385: 117–71.10.1016/S0140-6736(14)61682-2Search in Google Scholar

Petersen, M. L., K. E. Porter, S. Gruber, Y. Wang, and M. J. van der Laan. 2010. “Diagnosing and Responding to Violations in the Positivity Assumption.” Statistical Methods in Medical Research 21: 31–54, https://doi.org/10.1177/0962280210386207.10.1177/0962280210386207Search in Google Scholar

Pope, C. A., R. T. Burnett, G. D. Thurston, M. J. Thun, E. E. Calle, D. Krewski, and J. J. Goldleski. 2004. “Cardiovascular Mortality and Long-Term Exposure to Particulate Air Pollution Epidemiological Evidence of General Pathopysiological Pathways of Disease.” Circulation 109: 71–7, https://doi.org/10.1161/01.cir.0000108927.80044.7f.10.1161/01.CIR.0000108927.80044.7FSearch in Google Scholar

Pope, C. A.III, R. T. Burnett, M. J. Thun, E. E. Calle, D. Krewski, K. Ito, and G. Thurston. 2002. “Lung Cancer, Cardiopulmonary Mortality, and Long-Term Exposure to Fine Particulate Air Pollution.” Journal of the American Medical Association 287: 1132–41.https://doi.org/10.1001/jama.287.9.1132.10.1001/jama.287.9.1132Search in Google Scholar

Robins, J. 1986. “A New Approach to Causal Inference in Mortality Studies with a Sustained Exposure Periodapplication to Control of the Healthy Worker Survivor Effect.” Mathematical Modelling 7: 1393–512, https://doi.org/10.1016/0270-0255(86)90088-6.10.1016/0270-0255(86)90088-6Search in Google Scholar

Robins, J. 2000. Marginal Structural Models versus Structural Nested Models as Tools for Causal Inference. New York, NY: Springer.10.1007/978-1-4612-1284-3_2Search in Google Scholar

Robins, J. M., M. Hernan, and B. Brumback. 2000. “Marginal Structural Models and Causal Inference in Epidemiology.” Epidemiology 11: 550, https://doi.org/10.1097/00001648-200009000-00011.10.1097/00001648-200009000-00011Search in Google Scholar PubMed

Seidel, D., Y. Zhang, A. Beljaars, J.-C. Golaz, A. Jacobson, B. Medeiros, C. Seidel, Y. Zhang, A. Beljaars, J.-C. Golaz, A. Jacobson, and B. Medeiros. 2012. “Climatology of the Planetary Boundary Layer over the Continental United States and Europe.” Journal of Geophysical Research 117: 17106, https://doi.org/10.1029/2012JD018143.10.1029/2012JD018143Search in Google Scholar

Thurston, G. D., R. T. Burnett, M. C. Turner, Y. Shi, D. Krewski, R. Lall, K. Ito, M. Jerrett, S. M. Gapstur, W. Ryan Diver, and C. Arden Pope. 2016. “Ischemic Heart Disease Mortality and Long-Term Exposure to Source-Related Components of US Fine Particle Air Pollution.” Environmental Health Perspectives 124: 785–94, https://doi.org/10.1289/ehp.1509777.10.1289/ehp.1509777Search in Google Scholar PubMed PubMed Central

Tsiatis, A. 2006. Semiparametric Theory and Missing Data. New York: Springer Series in Statistics.Search in Google Scholar

van der Laan, M. J., and J. M. Robins. 2003. Unified Methods for Censored Longitudinal Data and Causality. New York: Springer Series in Statistics.10.1007/978-0-387-21700-0Search in Google Scholar

van der Laan, M. J., and D. Rubin. 2006. “Targeted Maximum Likelihood Learning.” International Journal of Biostatistics 2, https://doi.org/10.2202/1557-4679.1043.10.2202/1557-4679.1043Search in Google Scholar

Xiao, Y., E. E. Moodie, and M. Abrahamowicz. 2013. “Comparison of Approaches to Weight Truncation for Marginal Structural Cox Models.” Epidemiologic Methods 2: 1–20. Also available at https://www.degruyter.com/view/j/em.2013.2.issue-1/em-2012-0006/em-2012-0006.xml.10.1515/em-2012-0006Search in Google Scholar

Zigler, C. M., and M. Cefalu. 2017. “Posterior Predictive Treatment Assignment for Estimating Causal Effects with Limited Overlap.” eprint arXiv:1710.08749.Search in Google Scholar

Received: 2019-11-28
Accepted: 2020-09-04
Published Online: 2020-10-01

© 2020 Walter de Gruyter GmbH, Berlin/Boston

Articles in the same Issue

  1. Editorial
  2. The mean prevalence
  3. Research Articles
  4. Heterogeneous indirect effects for multiple mediators using interventional effect models
  5. Sleep habits and their association with daytime sleepiness among medical students of Tanta University, Egypt
  6. Population attributable fractions for continuously distributed exposures
  7. A real-time search strategy for finding urban disease vector infestations
  8. Disease mapping models for data with weak spatial dependence or spatial discontinuities
  9. A comparison of cause-specific and competing risk models to assess risk factors for dementia
  10. A simple index of prediction accuracy in multiple regression analysis
  11. A comparison of approaches for estimating combined population attributable risks (PARs) for multiple risk factors
  12. Posterior predictive treatment assignment methods for causal inference in the context of time-varying treatments
  13. Random effects tumour growth models for identifying image markers of mammography screening sensitivity
  14. Extrapolating sparse gold standard cause of death designations to characterize broader catchment areas
  15. Extending balance assessment for the generalized propensity score under multiple imputation
  16. Regression analysis of unmeasured confounding
  17. The Use of Logic Regression in Epidemiologic Studies to Investigate Multiple Binary Exposures: An Example of Occupation History and Amyotrophic Lateral Sclerosis
  18. Meeting the Assumptions of Inverse-Intensity Weighting for Longitudinal Data Subject to Irregular Follow-Up: Suggestions for the Design and Analysis of Clinic-Based Cohort Studies
https://doi.org/10.1515/em-2019-0024
Keywords for this article
Bayesian inference; causal inference; marginal structural models; time-varying treatments

Articles in the same Issue

  1. Editorial
  2. The mean prevalence
  3. Research Articles
  4. Heterogeneous indirect effects for multiple mediators using interventional effect models
  5. Sleep habits and their association with daytime sleepiness among medical students of Tanta University, Egypt
  6. Population attributable fractions for continuously distributed exposures
  7. A real-time search strategy for finding urban disease vector infestations
  8. Disease mapping models for data with weak spatial dependence or spatial discontinuities
  9. A comparison of cause-specific and competing risk models to assess risk factors for dementia
  10. A simple index of prediction accuracy in multiple regression analysis
  11. A comparison of approaches for estimating combined population attributable risks (PARs) for multiple risk factors
  12. Posterior predictive treatment assignment methods for causal inference in the context of time-varying treatments
  13. Random effects tumour growth models for identifying image markers of mammography screening sensitivity
  14. Extrapolating sparse gold standard cause of death designations to characterize broader catchment areas
  15. Extending balance assessment for the generalized propensity score under multiple imputation
  16. Regression analysis of unmeasured confounding
  17. The Use of Logic Regression in Epidemiologic Studies to Investigate Multiple Binary Exposures: An Example of Occupation History and Amyotrophic Lateral Sclerosis
  18. Meeting the Assumptions of Inverse-Intensity Weighting for Longitudinal Data Subject to Irregular Follow-Up: Suggestions for the Design and Analysis of Clinic-Based Cohort Studies
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 29.10.2025 from https://www.degruyterbrill.com/document/doi/10.1515/em-2019-0024/html
Scroll to top button