Abstract
The oxidation number and number of transferred electrons are two paramount parameters in the study of redox reactions. Their calculations are both important and challenging. The oxidation number of organic carbons is used in organic chemistry, biochemistry, and applied chemistry. Combustion reaction is a classical type of redox reaction, in which the oxygen molecule (O2) is the oxidizing agent. In this article, the integration of three sets of relations is explored by using the method of balancing organic combustion: (i) number of transferred electrons and oxidation number of organic carbons, (ii) mole of oxygen molecule and number of transferred electrons, and (iii) oxidative ratio, oxidation number of organic carbons, and number of transferred electrons. This method can also establish the relationships among the stoichiometric coefficients, mole of oxygen molecule, oxidative ratio, number of transferred electrons, and oxidation number of organic carbons. Furthermore, the oxidation number of organic carbons and the number of transferred electrons of a given organic compound can be determined by the derived mathematical equations.
Introduction
The balancing of chemical equations, stoichiometry, and redox reactions are some of the basic contents in chemistry curriculum (Chang & Goldsby, 2013; Tro, 2020). Redox reaction is an electron-transfer reaction, and it emerges with the oxidation number change (∆ON). The oxidation number (ON) and the number of transferred electrons (Te−) are two paramount parameters in the study of redox reactions (IUPAC, 2019). The oxidation number of organic carbons (ONC) is widely used in the fields of organic and biological chemistry (Bentley, Franzen, & Chasteen, 2002; Hanson, 1990; Halkides, 2000; Yuen & Lau, 2022a), environmental chemistry (Kroll et al., 2011; Kroll, Lim, Kessler, & Wilson, 2015), and biogeochemistry (Chadwick, Masiello, Baldock, Smernik, & Randerson, 2007; Chadwick, Masiello, Baldock, Smernik, & Randerson, 2007; Dick, Yu, Tan, & Lu, 2019; Masiello, Hockaday, & Gallagher, 2007).
The net primary production (NPP) reactions and combustion reactions are two opposite redox reactions. Examples are shown as follows:
Net primary production reaction: CO2 + H2O + N-resource → C x H y O z N v + O2
Combustion reaction: C x H y O z N v + O2 → CO2 + H2O + N-product
The oxidative ratio (OR) is defined as the ratio of moles of O2 to moles of CO2 in NPP and combustion reactions (Gallagher et al., 2014; Randerson et al., 2006; Worrall, Clay, Masiello, & Mynheer, 2013). The relationship between OR and ONC has been established in the study of NPP reactions (Hockaday et al., 2009, 2015; Masiello, Gallagher, Randerson, Deco, & Chadwick, 2008), and the relationships among OR, ONC, and Te− have been found in the study of organic combustion reactions (Yuen & Lau, 2022b). Although the stoichiometric amount of oxygen molecule (nO2) plays a significant role in NPP and combustion reactions, the relationships among nO2, OR, Te−, and ONC have not been revealed.
Assigning ON and counting Te− are important tasks in the study of redox reactions and they often pose difficulties for teachers and students (Brandriet & Bretz, 2014; De Jong, Acampo, & Verdonk, 1995; Garnett & Treagust, 1992). The purpose of this article is to explore a method which can solve the aforesaid problems. A combustion model is established to understand the relationships among ONC, Te−, nO2, and OR. Three pillars are needed. First, an organic combustion reaction acts as a model reaction. Second, the method of balancing and deducting chemical equations is used as a tool. Third, the stoichiometric coefficients (SC) in the balanced combustion reaction are used as connectors. Three sets of relations: (i) OR, ONC, and Te−; (ii) ONC and Te−; and (iii) nO2 and Te− are integrated. Consequently, new interrelationships among nO2, OR, Te−, and ONC are established. The Te− and ONC of organic compounds can also be determined by the derived mathematical equations.
Procedures for counting OR, Te−, and ONC of organic molecules
The ONC of organonitrogen are seldom studied (Kauffman, 1986; Jurowski, Krzeczkowska, & Jurowska, 2015; Yuen & Lau, 2022c). The general formula of organonitrogen compound, C
x
H
y
O
z
N
v
, is chosen as an example. Even though  ,
,  ,
,  , and
, and  have the same molecular formula of C3H7O3N, these four structural formulas have different ONN.
have the same molecular formula of C3H7O3N, these four structural formulas have different ONN.
Example 1. Balancing the combustion reaction of C3H7O3N.
Step 1: Starting from the structural formula of C3H7O3N.

Counting ON for non-carbon atoms:
All hydrogen atoms: ONH = +1.
All oxygen atoms: ONO = −2.
One nitrogen atom: ONN = −3.
Step 2: Setting up the combustion reaction.
The N-product plays a critical role in understanding the stoichiometric relationship in a combustion reaction. The ONN of the reactant ( ) is identified as −3, and the NH3 (ONN = −3) is selected as the N-product accordingly.
) is identified as −3, and the NH3 (ONN = −3) is selected as the N-product accordingly.
The combustion reaction is shown as: C3H7O3N → CO2 + H2O + NH3.
Step 3: Balancing the combustion reaction.
The combustion reaction is balanced by balancing atoms in the sequence from C atoms to N atoms to H atoms to O atoms.
Step 4: Identifying the stoichiometric coefficients of nO2 and nCO2.
Based on the balanced combustion reaction, the coefficients of nO2 =
Step 5: Counting OR from the ratio of nO2 to nCO2.
Based on the ratio of nO2 to nCO2
Step 6: Counting Te− from nO2.
O2 is the oxidizing agent in the combustion reactions. Each O atom gains 2 electrons (O + 2e− → O−2) and each O2 molecule gains 4 electrons (O2 + 4e− → 2O−2).
Step 7: Counting ONC from Te−.
The relationship between Te− and ∆ONC has been established in the half redox reactions (Yuen & Lau, 2022d). The mathematical equations and calculation are shown as follows:
The mean ONC of  (C3H7O3N) equals to +
(C3H7O3N) equals to +
Balancing combustion reactions: counting nO2, nCO2, OR, Te−, and ONC
Nitrogen atoms have nine oxidation numbers (ONN), the values of which lie between −3 to +5. By using the same procedure as shown in Example 1 (ONN = −3), different N-products are assigned by different ONN. The chemical formulas of N-products are combined with H-atom, O-atom, or both O-atom and H-atom. The resulted values of nO2, nCO2, OR, Te−, and ONC are given in Table 1.
Parameters of ONN, nO2, nCO2, OR, Te−, and ONC in the balancing combustion reactions of C3H7O3N molecules.
| Equation # | Balancing the combustion reaction | ONN | nO2 | nCO2 | OR | Te− | ONc |
|---|---|---|---|---|---|---|---|
| 1 | C3H7O3N +
|
−3 |
|
3 |
|
10 | +
|
| 2 | C3H7O3N +
|
−2 |
|
3 |
|
11 | +
|
| 3a | C3H7O3N + 3O2 → 3CO2 + 3H2O +
|
−1 | 3 | 3 | 1 | 12 | 0 |
| 3b | C3H7O3N + 3O2 → 3CO2 + 2H2O + NH2OH | −1 | 3 | 3 | 1 | 12 | 0 |
| 4 | C3H7O3N +
|
0 |
|
3 |
|
13 | −
|
| 5 | C3H7O3N +
|
+1 |
|
3 |
|
14 | −
|
| 6 | C3H7O3N +
|
+2 |
|
3 |
|
15 | 1 |
| 7a | C3H7O3N + 4O2 → 3CO2 + 3H2O + HNO2 | +3 | 4 | 3 |
|
16 | −
|
| 7b | C3H7O3N + 4O2 → 3CO2 +
|
+3 | 4 | 3 |
|
16 | −
|
| 8 | C3H7O3N +
|
+4 |
|
3 |
|
17 | −
|
| 9a | C3H7O3N +
|
+5 |
|
3 |
|
18 | −2 |
| 9b | C3H7O3N +
|
+5 |
|
3 |
|
18 | −2 |
When Equations (1) and (2) are compared, NH3 and N2H4 are found to have different ONN, and they produce different nO2, OR, and Te−.
When Equations (3) and (4) are compared, N-products of HNO3 and N2O5 are found to contain the same ONN even though they have different chemical formulas. Their nO2, OR, and Te− remain the same.
Balancing general combustion reactions: counting nO2, nCO2, OR, Te−, and ONC by using SC
C x H y O z N v is used for balancing and deducting the combustion equation. NH3 (ONN = −3) is chosen as a N-product in Example 2.
Example 2. Balancing the general combustion reaction of C x H y O z N v .
Balancing the combustion reaction: C x H y O z N v + O2 → CO2 + H2O + NH3 .
Expressing nO2, nCO2, OR, Te−, and ONC by using SC.
By using the same procedure shown in Example 2, different N-products are assigned by different ONN. Their values of ONN, nO2, OR, Te−, and ONC are given in Table 2.
Stoichiometric coefficients and parameters of ONN, nO2, OR, Te−, and ONC in the balancing combustion reactions of C x H y O z N v molecules.
| Balancing the combustion reaction | ONN | nO2 | OR | Te− | ONC |
|---|---|---|---|---|---|
| C
x
H
y
O
z
N
v
+
|
−3 |
|
|
4x + y − 2z − 3v |
|
| C
x
H
y
O
z
N
v
+
|
−2 |
|
|
4x + y − 2z − 2v |
|
| C
x
H
y
O
z
N
v
+
|
−1 |
|
|
4x + y − 2z − v |
|
| C
x
H
y
O
z
N
v
+
|
−1 |
|
|
4x + y − 2z − v |
|
| C
x
H
y
O
z
N
v
+
|
0 |
|
|
4x + y − 2z |
|
| C
x
H
y
O
z
N
v
+
|
+1 |
|
|
4x + y − 2z + v |
|
| C
x
H
y
O
z
N
v
+
|
+2 |
|
|
4x + y − 2z + 2v |
|
| C
x
H
y
O
z
N
v
+
|
+3 |
|
|
4x + y − 2z + 3v |
|
| C
x
H
y
O
z
N
v
+
|
+3 |
|
|
4x + y − 2z + 3v |
|
| C
x
H
y
O
z
N
v
+
|
+4 |
|
|
4x + y − 2z + 4v |
|
| C
x
H
y
O
z
N
v
+
|
+5 |
|
|
4x + y − 2z + 5v |
|
| C
x
H
y
O
z
N
v
+
|
+5 |
|
|
4x + y − 2z + 5v |
|
Formulating nO2, nCO2, OR, Te−, and ONC of C x H y O z N v molecule
Any non-carbon ON (ONH, ONO, ONN) of C x H y O z N v can be determined by its structural formula (Yuen & Lau, 2022c). Its atomic coefficients can also be identified.
non-carbon ON: ONH, ONO, ONN.
atomic coefficient: x for carbon, y for hydrogen, z for oxygen, v for nitrogen.
| Atom | C | H | O | N |
| ON | – | ONH | ONO | ONN |
| Atomic coefficient | x | y | z | v |
By balancing the combustion reaction of C x H y O z N v + O2 → CO2 + H2O + [N-product], the general mathematical equations of C x H y O z N v molecules are given as follows:
The values of nO2, Te−, nCO2, OR, and ONC can be calculated by using non-carbon ON of ONH, ONO, and ONN, and atomic coefficients of x, y, z, and v.
Procedures for determining Te−, nO2, nCO2, OR, and ONC of C x H y O z N v molecule and balancing its corresponding combustion reaction
Example 3. Given methyl red,  .
.
Determining all non-carbon ON and atomic coefficients from the structural formula.
| Atom | C | H | O | N | N |
| ON | – | +1 | −2 | −1 | −3 |
| Atomic coefficient | 15 | 15 | 2 | 2 | 1 |
Calculating Te−, nO2, nCO2, OR, and ONC by using mathematical equations.
| Mathematical equation | Calculation |
|---|---|
| Te− = 4x + ONH(y) + ONO(z) + ONN(v 1) + ONN(v 2) | Te− = 4(15) + (+1)(15) + (−2)(2) + (−1)(2) + (−3)(1) = 66 |
| nO2 =
|
nO2 =
|
| nCO2 = nC = x | nCO2 = 15 |
| OR =
|
OR =
|
| ONC = 4 −
|
ONc = 4 −
|
Balancing the combustion reaction by using the SC of nO2 and nCO2.
The unbalanced combustion reaction of “C15H15O2N3 + O2 → CO2 + H2O + N2H2 + NH3” can be set up and balanced as follows:
Using the calculated SC of nO2 and nCO2:
Balancing N2H2 and NH3:
Balancing H2O:
In Example 3, the values of Te−, nO2, OR, and ONC can be calculated by the derived mathematical equations, which are based on the balanced organic combustion reactions. Reversely, the combustion reaction of C x H y O z N v molecules can also be balanced by the resulted nO2 and nCO2.
Interrelationships among Te−, nO2, OR, and ONC in C x H y O z X w N v S u P t molecule
The strategy, which is used for balancing and deducting C x H y O z N v , can be extended to work on C x H y O z X w N v S u P t molecule (X, N, S, P stand for halogen, nitrogen, sulfur, and phosphorus respectively). For C x H y O z XwN v S u P t , all possible non-carbon ON are shown as: ONH = +1, ONO = −1 to −2, ONX = −1 to +7, ONN = −3 to +5, ONS = −2 to +6, and ONP = −3 to +5.
The general combustion reaction:
ON and atomic coefficients for calculating Te−, nO2, nCO2, OR, and ONC.
non-carbon ON: ONH, ONO, ONX, ONN, ONS, ONP.
atomic coefficients: x, y, z, w, v, u, t.
| Atom | C | H | O | X | N | S | P |
| ON | ONH | ONO | ONX | ONN | ONS | ONP | |
| Atomic coefficient | x | y | z | w | v | u | t |
The derived general mathematical equations for C x H y O z X w N v S u P t are shown as follows:
Relationships among SC, nO2, OR, Te−, and ONC.
By using combustion reactions as models, the relationships among nO2, OR, Te−, and ONC are derived. The tetrahedral model with SC in the center as connectors can be established and is shown in Figure 1.

Tetrahedral relationships among nO2, OR, Te−, and ONC with SC in the center.
By integrating three sets of relationships of (i) OR and Te−; (ii) ONC and Te−; and (iii) nO2 and Te−, the interrelationships among four parameters of nO2, OR, Te−, and ONC are established. As a result, there are six sets of relationships among four parameters: nO2, OR, Te−, and ONC, which are derived and summarized in Table 3.
Triangular relationships among Te−, OR, and ONC.
Interrelationships among four parameters: nO2, OR, Te−, and ONC.
| Relationship | Mathematical equation | |
|---|---|---|
| Te− and nO2 | Te− = 4 nO2 | nO2 =
|
| Te− and OR | Te− = 4 x OR | OR =
|
| Te− and ONc | Te− = x (4 − ONC) | ONC = 4 −
|
| ONC and nO2 | ONC = 4 (1 −
|
nO2 =
|
| ONC and OR | ONC = 4 (1 − OR) | OR = 1 −
|
| nO2 and OR | nO2 = x OR | OR =
|
-
x = nC = atomic coefficient of organi c carbons in C x H y O z X w N v S u Pt molecule.
The Te−, OR, or ONC can be determined by nO2. The triangular relationship among Te−, OR, and ONC with nO2 in the center is shown in Figure 2.
Triangular relationships among nO2, ONC, and Te−.

Triangular relationships among Te−, OR, and ONC with nO2 in the center.
The nO2, ONC, and Te− can be determined by OR. The triangular relationship among nO2, ONC, and Te− with OR in the center is shown in Figure 3.
Equivalence between the gain of electrons and the loss of electrons.
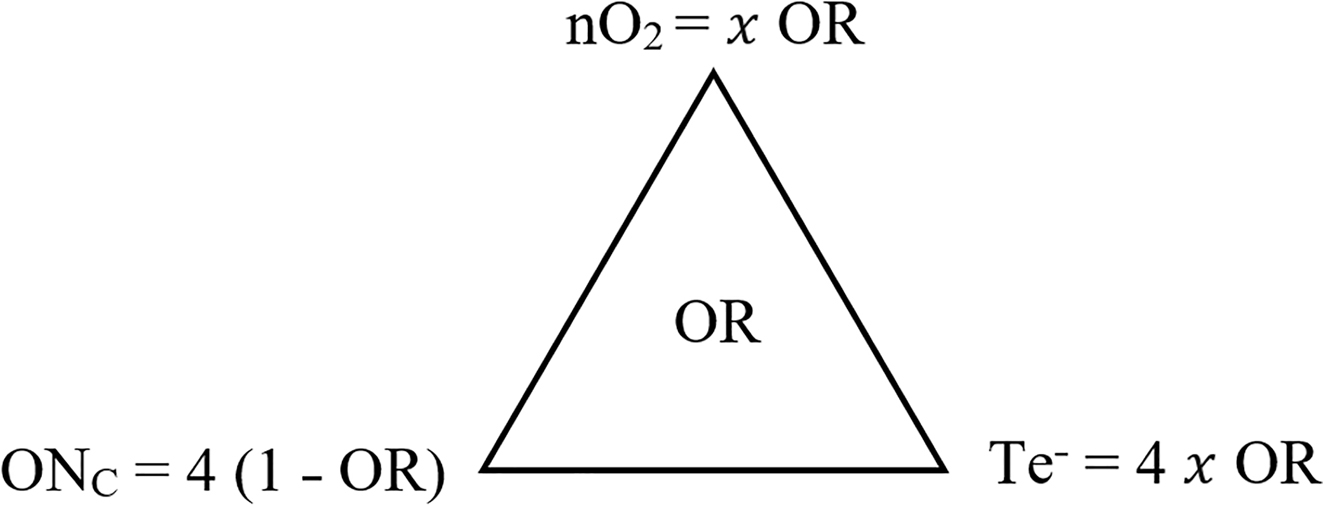
Triangular relationships among nO2, ONC, and Te− with OR in the center.
By using the combustion model, the gain of electrons from oxygen molecules (O2) and the loss of electrons from carbon atoms of C x H y O z X w N v S u P t molecule must be equal. It means that for all other atoms, their ON do not change in the combustion reaction.
Determining Te−, nO2, OR, and ONC of C x H y O z X w N v S u P t molecule by using mathematical equations
Example 4. Given Celecoxib,  .
.
C x H y O z X w N v S u = C17H14O2F3N3S.
ONH = +1, ONO = −2, ONF = −1, ONN = −3, ONN = −2, ONS = +4
x = 17, y = 14, z = 2, w = 3, v 1 = 1, v 2 = 2, u = 1
| Atom | C | H | O | F | N | N | S |
| ON | – | +1 | −2 | −1 | −3 | −2 | +4 |
| Atomic coefficient | 17 | 14 | 2 | 3 | 1 | 2 | 1 |
| Mathematical equation | Calculation |
|---|---|
| Te− = 4x + ONH(y) + ONO(z) + ONX(w) + ONN(v1) + ONN(v2) + ONS(u) nO2 =
|
Te− = 4(17) + (+1)(14) + (−2)(2) + (−1)(3) + (−3)(1) + (−2)2 + (+4)(1) = 72 nO2 =
|
| nCO2 = nC = x | nCO2 = 17 |
| OR =
|
OR =
|
| ONC = 4 −
|
ONC = 4 −
|
Example 5. Given Cangrelor,  .
.
C x H y O z X w N v S u Pt = C17H25O12Cl2F3N5S2P3
ONH = +1, ONO = −2, ONF = −1, ONCl = −1, ONN = −3, ONS = −2, ONP = +5
x = 17, y = 25, z = 12, w 1 = 2, w 2 = 3, v = 5, u = 2, t = 3
| Atom | C | H | O | Cl | F | N | S | P |
| ON | – | +1 | −2 | −1 | −1 | −3 | −2 | +5 |
| Atomic coefficient | 17 | 25 | 12 | 2 | 3 | 5 | 2 | 3 |
| Mathematical equation | Calculation | |||||||
|---|---|---|---|---|---|---|---|---|
| Te− = 4x + ONH(y) + ONO(z) + ONCl(w 1) + ONF(w 2) + ONN(v) + ONS(u) + ONP(t) | Te− = 4(17) + (+1)(25) + (−2)(12) + (−1)(2) + (−1)(3) + (−3)(5) + (−2)2 + (+5)(3) = 60 | |||||||
| nO2 =
|
nO2 =
|
|||||||
| nCO2 = nC = x | nCO2 = 17 | |||||||
| OR =
|
OR =
|
|||||||
| ONC = 4 −
|
ONC = 4 −
|
|||||||
In Examples 4 and 5, the mathematical equation for counting Te− of organic compounds in the general chemical formula of C x H y O z X w N v S u Pt is used and then nO2, OR, and ONC can be calculated consequently.
Procedures for balancing combustion reactions of C x H y O z X w N v S u Pt molecule and determining its corresponding Te− and ONC from nO2 or OR
Example 6. Given Celecoxib,  , C17H14O2F3N3S.
, C17H14O2F3N3S.
Determining all non-carbon ON and all atomic coefficients.
| Atom | C | H | O | F | N | N | S |
| ON | – | +1 | −2 | −1 | −2 | −3 | +4 |
| Atomic coefficient | 17 | 14 | 2 | 3 | 2 | 1 | 1 |
Balancing the combustion reaction
The unbalanced combustion reaction of “C17H14O2F3N3S + O2 → CO2 + H2O + HF + H2NNH2 + NH3 + SO2” can be set up and balanced as follows:
Using the coefficient of nCO2 (nC = nCO2):
Balancing HF:
Balancing H2NNH2 and NH3:
Balancing SO2:
Balancing H2O:
Balancing O2:
| nO2 = 18 | nCO2 = 17 | OR =
|
Calculating Te− and ONC from nO2 or OR
| Calculating Te− and ONc | |||
|---|---|---|---|
| From nO2 | From OR | ||
| Mathematical equation | Calculation | Mathematical equation | Calculation |
| Te− = 4 nO2 | Te− = 4 (18) = 72 | Te− = 4 x OR | Te− = 4 (17)(
|
| ONC = 4 (1 −
|
ONC = 4 (1 −
|
ONC = 4 (1 − OR) | ONC = 4 (1 −
|
Example 7. Given Cangrelor,  , C17H25O12Cl2F3N5S2P3.
, C17H25O12Cl2F3N5S2P3.
Determining all non-carbon ON and all atomic coefficients.
| Atom | C | H | O | Cl | F | N | S | P |
| ON | – | +1 | −2 | −1 | −1 | −3 | −2 | +5 |
| Atomic coefficient | 17 | 25 | 12 | 2 | 3 | 5 | 2 | 3 |
Balancing the combustion reaction.
The unbalanced combustion reaction of “C17H25O12Cl2F3N5S2P3 + O2 → 17CO2 + H2O + HCl + HF + NH3+H2S + H3PO4” can be set up and balanced as follows:
Using atomic coefficient nC = nCO2:
Balancing HCl:
Balancing HF:
Balancing NH3:
Balancing H2S:
Balancing H3PO4:
Balancing H2O:
Balancing O2:
| nO2 = 15 | nCO2 = 17 | OR =
|
Calculating Te− and ONC from nO2 or OR.
| Calculating Te− and ONc | |||
|---|---|---|---|
| From nO2 | From OR | ||
| Mathematical equation | Calculation | Mathematical equation | Calculation |
| Te− = 4 nO2 | Te− = 4 (15) = 60 | Te− = 4 x OR | Te− = 4 (17) (
|
| ONC = 4 (1 −
|
ONC = 4 (1 −
|
ONC = 4 (1 − OR) | ONC = 4 (1 −
|
In Examples 6 and 7, firstly the combustion reactions of C x H y O z X w N v S u Pt molecules are balanced; secondly the nO2, and nCO2 can be identified; and thirdly their corresponding Te− and ONC can be determined by using nO2 or OR.
Conclusions
The concepts of ONC and Te− play significant roles in both pure and applied chemistry. However, the tasks of assigning ONC and counting Te− are challenging. In this article, the interrelationships among nO2, OR, Te−, and ONC are established by using an organic combustion reaction as a model. Consequently, six sets of mathematical equations among these four parameters of organic compounds in the general chemical formula of C x H y O z X w N v S u Pt are formulated. Furthermore, ONC and Te− of a given organic compound can be determined by the derived mathematical equations.
-
Author contributions: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.
-
Research funding: None declared.
-
Conflict of interest statement: The authors declare no conflicts of interest regarding this article.
References
Bentley, R., Franzen, J., & Chasteen, T. G. (2002). Oxidation numbers in the study of metabolism. Biochemistry and Molecular Biology Education, 30, 288–292. https://doi.org/10.1002/bmb.2002.494030050114.Search in Google Scholar
Brandriet, A. R., & Bretz, S. L. (2014). Measuring meta-ignorance through the lens of confidence: Examining students’ redox misconceptions about oxidation numbers, charge, and electron transfer. Chemistry Education Research and Practice, 15(4), 729–746. https://doi.org/10.1039/c4rp00129j.Search in Google Scholar
Chadwick, O. A., Masiello, C. A., Baldock, J., Smernik, R., & Randerson, J. (2007). The oxidation state of soil organic carbon: A new proxy for carbon storage mechanisms and land use change. In Kearney Foundation of Soil Science Soil Carbon and California’s Terrestrial Ecosystems Final Report: 2002020, 1/1/2003-12/31/2004. Retrieved from http://kearney.ucdavis.edu/OLD%20MISSION/2002_Final_Reports/2002020Chadwick_FINALkms.pdf.Search in Google Scholar
Chang, R., & Goldsby, K. A. (2013). Chemistry (11th ed.). USA: McGraw-Hill International Edition.Search in Google Scholar
De Jong, O., Acampo, J., & Verdonk, A. (1995). Problems in teaching the topic of redox reactions: Actions and conceptions of chemistry teachers. Journal of Research in Science Teaching, 32(10), 1097–1110. https://doi.org/10.1002/tea.3660321008.Search in Google Scholar
Dick, J. M., Yu, M., Tan, J., & Lu, A. (2019). Changes in carbon oxidation state of metagenomes along geochemical redox gradients. Frontiers in Microbiology, 10, 120. https://doi.org/10.3389/fmicb.2019.00120.Search in Google Scholar PubMed PubMed Central
Gallagher, M. E., Masiello, C. A., Hockaday, W. C., Baldock, J. A., Snapp, S., & McSwiney, C. P. (2014). Controls on the oxidative ratio of net primary production in agricultural ecosystems. Biogeochemistry, 121, 581–594.https://doi.org/10.1007/s10533-014-0024-9.Search in Google Scholar
Garnett, P., & Treagust, D. F. (1992). Conceptual difficulties experienced by senior high school students of electrochemistry: Electric circuits and oxidation-reduction equations. Journal of Research in Science Teaching, 29(2), 121–142. https://doi.org/10.1002/tea.3660290204.Search in Google Scholar
Halkides, C. J. (2000). Assigning and using oxidation numbers in biochemistry lectures courses. Journal of Chemical Education, 77, 1428–1432. https://doi.org/10.1021/ed077p1428.Search in Google Scholar
Hanson, R. W. (1990). Oxidation states of carbon as aids to understanding oxidative pathways in metabolism. Biochemical Education, 18(40), 194–196.https://doi.org/10.1016/0307-4412(90)90132-8.Search in Google Scholar
Hockaday, W. C., Gallagher, M. E., Masiello, C. A., Baldock, J. A., Iversen, C. M., & Norby, R. J. (2015). Forest soil carbon oxidation state and oxidative ratio responses to elevated CO2. Journal of Geophysical Research Biogeosciences, 120, 1797–1811. https://doi.org/10.1002/2015jg003010.Search in Google Scholar
Hockaday, W. C., Masiello, C. A., Randerson, J. T., Smernik, R. J., Baldock, J. A., & Chadwick, O. A. (2009). Measurement of soil carbon oxidation state and oxidative ratio by 13C nuclear magnetic resonance. Journal of Geophysical Research Biogeosciences, 114, G02014. https://doi.org/10.1029/2008jg000803.Search in Google Scholar
IUPAC (2019). In Compendium of Chemical Terminology, (the “Gold Book”). Compiled by McNaught, A. D., & Wilkinson, A. D. (2nd ed.). Oxford: Blackwell Scientific Publications. Online version (2019-) created by S. J. Chalk.Search in Google Scholar
Jurowski, K., Krzeczkowska, M. K., & Jurowska, A. (2015). Approaches to determining the oxidation state of nitrogen and carbon atoms in organic compounds for high school students. Journal of Chemical Education, 92, 1645–1652. https://doi.org/10.1021/ed500645v.Search in Google Scholar
Kauffman, J. M. (1986). Simple method for determination of oxidation numbers of atoms in compounds. Journal of Chemical Education, 63, 474–475. https://doi.org/10.1021/ed063p474.Search in Google Scholar
Kroll, J. H., Donahue, N. M., Jimenez, J. L., Kessler, S. H., Canagaratna, M. R., Wilson, K. R. …Worsnop, D. R. (2011). Carbon oxidation state as a metric for describing the chemistry of atmospheric organic aerosol. Nature Chemistry, 3, 133–139. https://doi.org/10.1038/nchem.948.Search in Google Scholar PubMed
Kroll, J. H., Lim, C. Y., Kessler, S. H., & Wilson, K. R. (2015). Heterogeneous oxidation of atmospheric organic aerosol: Kinetics of changes to the amount and oxidation state of particle-phase organic carbon. The Journal of Physical Chemistry. A., 119, 10767–10783. https://doi.org/10.1021/acs.jpca.5b06946.Search in Google Scholar PubMed
Masiello, C. A., Gallagher, M. E., Randerson, J. T., Deco, R. M., & Chadwick, O. A. (2008). Evaluating two experimental approaches for measuring ecosystem carbon oxidation state and oxidative ratio. J. Geophys. Res. Biogeosci., 113, G03010. https://doi.org/10.1029/2007jg000534.Search in Google Scholar
Masiello, C. A., Hockaday, W. C., & Gallagher, M. E. (2007) Organic carbon oxidation state (Cox): A new proxy for the earth’s C and O cycles. In Goldschmidt Conference Abstracts. A633. Retrieved from https://www.researchgate.net/publication/267787476_Organic_Carbon_Oxidation_State_C_ox_A_new_proxy_for_the_Earth’s_C_and_O_cycles.confproc.Search in Google Scholar
Randerson, J. T., Masiello, C. A., Still, C. J., Rahn, T., Poorter, H., & Field, C. B. (2006). Is carbon within the global terrestrial biosphere becoming more oxidized? Implications for trends in atmospheric O2. Global Change Biology, 12, 260–271. https://doi.org/10.1111/j.1365-2486.2006.01099.x.Search in Google Scholar
Tro, N. J. (2020). Chemistry—A Molecular Approach (5th ed.). USA: Pearson.Search in Google Scholar
Worrall, F., Clay, G. D., Masiello, C. A., & Mynheer, G. (2013). Estimating the oxidative ratio of the global terrestrial biosphere carbon. Biogeochemistry, 115, 23–32. https://doi.org/10.1007/s10533-013-9877-6.Search in Google Scholar
Yuen, P. K., & Lau, C. M. D. (2022a). Fragmentation method for assigning oxidation numbers in organic and bioorganic compounds. Biochemistry and Molecular Biology Education, 50, 29–43. https://doi.org/10.1002/bmb.21582.Search in Google Scholar PubMed
Yuen, P. K., & Lau, C. M. D. (2022b). Exploring the relationships among stoichiometric coefficients, number of transferred electrons, mean oxidation number of carbons, and oxidative ratio in organic combustion reactions. Chemistry Teacher International, 4(1), 39–46. https://doi.org/10.1515/cti-2021-0020.Search in Google Scholar
Yuen, P. K., & Lau, C. M. D. (2022c). New approach for assigning mean oxidation number of carbons to organonitrogen and organosulfur compounds. Chemistry Teacher International, 4(1), 1–13. https://doi.org/10.1515/cti-2021-0015.Search in Google Scholar
Yuen, P. K., & Lau, C. M. D. (2022d). From balancing redox reactions to determining change of oxidation number. Journal of College Science Teaching, 51(3), 22–26.10.1080/0047231X.2022.12290556Search in Google Scholar
© 2023 the author(s), published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution-NonCommercial-NoDerivatives 4.0 International License.
Articles in the same Issue
- Frontmatter
- Special Issue Papers
- High performance liquid chromatography as a micro-destructive technique for the identification of anthraquinone red dyestuffs in cultural heritage objects
- Assessing strategies for enhancing the integration of cultural practices in teaching and learning of chemistry in secondary schools
- Pre-service teachers’ views on chemistry of fine art materials of cultural heritage
- Elements of Country: a First Nations-first approach to chemistry
- Integrating expertise for teaching conservation science to cultural heritage conservation students – A closer look at radiation, colour and museum lighting topics
- Research Articles
- Simple mathematical equations for calculating oxidation number of organic carbons, number of transferred electrons, oxidative ratio, and mole of oxygen molecule in combustion reactions
- How do students apply the octet rule and how do they justify this application?
- Good Practice Reports
- A simple pedagogical limiting reactant kitchenette experiment including a simple algorithm
- Studying the nomenclature of dioxins using a structure model kit based on electronic components linked with plastic tubes
- Review Article
- Confinement of ozone hole mainly in the Antarctic stratosphere to protect the living kingdom on the earth: chemistry behind this Nature’s unique gift
Articles in the same Issue
- Frontmatter
- Special Issue Papers
- High performance liquid chromatography as a micro-destructive technique for the identification of anthraquinone red dyestuffs in cultural heritage objects
- Assessing strategies for enhancing the integration of cultural practices in teaching and learning of chemistry in secondary schools
- Pre-service teachers’ views on chemistry of fine art materials of cultural heritage
- Elements of Country: a First Nations-first approach to chemistry
- Integrating expertise for teaching conservation science to cultural heritage conservation students – A closer look at radiation, colour and museum lighting topics
- Research Articles
- Simple mathematical equations for calculating oxidation number of organic carbons, number of transferred electrons, oxidative ratio, and mole of oxygen molecule in combustion reactions
- How do students apply the octet rule and how do they justify this application?
- Good Practice Reports
- A simple pedagogical limiting reactant kitchenette experiment including a simple algorithm
- Studying the nomenclature of dioxins using a structure model kit based on electronic components linked with plastic tubes
- Review Article
- Confinement of ozone hole mainly in the Antarctic stratosphere to protect the living kingdom on the earth: chemistry behind this Nature’s unique gift

