Computational analysis of nanoparticles and waste discharge concentration past a rotating sphere with Lorentz forces

Pullare Nimmy; Adebowale Martins Obalalu; Kallur Venkat Nagaraja; Javali Kotresh Madhukesh; Umair Khan; Anuar Ishak; Devanathan Sriram; Syed Modassir Hussain; Raman Kumar; Ahmed M. Abed

doi:10.1515/arh-2024-0012

Article Open Access

Computational analysis of nanoparticles and waste discharge concentration past a rotating sphere with Lorentz forces

Pullare Nimmy , Adebowale Martins Obalalu , Kallur Venkat Nagaraja , Javali Kotresh Madhukesh , Umair Khan , Anuar Ishak , Devanathan Sriram , Syed Modassir Hussain , Raman Kumar and Ahmed M. Abed

Published/Copyright: August 6, 2024

Published by

Become an author with De Gruyter Brill

Author Information

From the journal Applied Rheology Volume 34 Issue 1

Abstract

As industries rely more and more on magnetohydrodynamic (MHD) systems for different uses in power, production, and management of the environment, it becomes essential to optimize these operations. The study seeks to improve the effectiveness and productivity of cooling structures, chemical reaction reactors, and contaminant control methods by investigating these intricate interconnections. Because of this, the work scrutinizes the endothermic/exothermic (EN/EX) chemical processes, convective boundary conditions, and pollutant concentration impacts on MHD nanofluid circulation around a rotating sphere. The governing equations based on the above assumptions are reduced into a system of ordinary differential equations and solved numerically with Runge–Kutta Fehlberg’s fourth- and fifth- order schemes. The obtained numerical outcomes from the numerical scheme are presented with the aid of graphs, and the results show that the rate of mass transfer decreases with an increase in the external pollutant local source and solid volume percentage. For changes in the values of the activation energy parameter and solid fraction, the rate of thermal dispersion drops for the EN case and upsurges for the EX case. The concentration profile shows increment with the addition of the external pollutant source variation parameter and local pollutant external source parameter. The outcomes of the present work can be helpful in cooling equipment, developing advanced methods for controlling pollution, environmental management, MHD generators, and various industrial contexts.

Keywords: rotating sphere; magnetic field; endothermic–exothermic chemical reactions; pollutant concentration; nanofluid

1 Introduction

The study of fluid flow around a rotating sphere has been the focused of a plethora of researchers owing to the numerous applications it has in practical engineering domains, such as chemical and food processing, thermal and nuclear plants, conveying of sediments in rivers, and combustion systems. For a while, there has been much research on spherical geometry owing to its dynamic flow characteristics and useful applications. Recently, the natural convection over a sphere placed in a porous medium was analyzed by Chamkha et al. [1]. The nonlinear convective flow of a Williamson nanoliquid past a revolving sphere was investigated by Patil and Benawadi [2]. The magnetohydrodynamic (MHD) flow and thermal transport of a Casson hybrid nanofluid (HNF) along a spinning sphere were discussed by Singla et al. [3]. Ahmad et al. [4] considered the stagnation point movement of an HNF stream around a rotating sphere. The Oldroyd-B NF path around a rotating sphere under convective heat conditions was assessed by Kenea and Ibrahim [5]. Nimmy et al. [6] discussed the effects of a chemical reaction on an MHD NF flow on a rotating sphere.

An alternative approach is to use active heat sources for the convective heat transfer process, which can influence both flow characteristics and help with temperature. The fluid motion under a magnetic field (called magnetohydrodynamics, MHD) analyzes and describes the dynamics of electrically conductive fluids that move. In recent years, scientists and engineers have been interested in MHD because it is relevant to many applications: transformers, generators, flow control, accelerators, and heating and cooling plants. Modification of a fluid’s thermophysical properties, like thermal conductivity and viscosity, can be brought about by introducing a magnetic field into the gas. Its magnetic field causes the flow rate, pressure, speed, and temperature of the fluid to change. So, one might ask what happens when a magnetic field is placed within that. The results of this question are truly remarkable in flow control applications. This has presented increased significance in thermal power and other industrial fields. So, we now use magnetically driven heat piping for cooling electronic devices and secondary circulation for liquid handling in pipes in the metallurgical industry to be vaporized and fed into solidification hearths where it may then solidify as a plate product of nuclear power water heater. Over a cone, the unsteady mass and heat transfer of fluid under the impact of the magnetic field were scrutinized by Chamkha and Rashad [7]. Under the influence of the magnetic field, the Maxwell NF movement across a rotating disk was investigated by Srilatha et al. [8]. With the influence of gyrotactic microorganisms and a magnetic dipole, the 3D flow of a non-Newtonian fluid was studied by Madhu et al. [9]. The influence of the magnetic field on the mass and heat transfer of an HNF flow along a porous medium was investigated by Sharma et al. [10]. The effect of a magnetic field on the stabilization of triple component magneto-convection for porous fluid systems was considered by Manjunatha et al. [11]. The MHD flow of hybrid ferroparticles accompanied by thermal radiation was studied by Gherieb et al. [12]. Additional significant research on magnetic fields is presented in the studies of Krishna et al., Kumar et al., Manjunatha et al., Khan et al., and Alharbi et al. [13–17].

Studies on convective heat transmission are essential for processes requiring extremely high temperatures, such as those in nuclear power plants and thermal energy storage. Because of its extensive application in manufacturing and technical industries, as well as its power supply to electronic devices and computer gadgets, the study of boundary layer problems with convective boundary conditions (BCs) has recently caught the attention of academics. Recently, the effect of convective heat transfer in a Maxwell NF stream was elucidated by Algehyne et al. [18]. The analysis of heat transfer of an HNF flow over a cone together with the convective BC was elucidated by Yahaya et al. [19]. The motion of NF along the surface of a cone with convective BCs was deliberated by Francis et al. [20]. Incorporated with the convective BCs, the mass and heat transfer enhancement of a Maxwell NF was probed by Hussain et al. [21]. Over a stretching sheet embedded in a porous medium, the HNF flow with convective conditions was simulated by Akbar et al. [22].

Energy is transported through and out of the environment during a chemical reaction, causing an increase or decrease in the temperature profile. The chemical reaction where energy is discharged into the surrounding environment is termed an exothermic chemical reaction (EX CR), and the process in which energy is extracted from the external medium is described as the endothermic chemical reaction (EN CR). The most prevalent kind of energy transfer is heat energy, which heats the surrounding environment. Hydrogen ions are released when an acid ionizes and dissolves in water. As a result, heat is released into the air. As a result, EX reactions include the burning of firewood, rusting of iron, and reactions of an acid with water. The EN CR produces a cooling effect and lowers the temperature in that vicinity. An example of an EN reaction is when the ice cube melts in water by receiving heat energy from the surroundings into the liquid. Ambient temperature increases after an EX process and decreases in the case of an EN reaction. A large number of investigators have studied the mass and heat transfer flow by using endothermic–exothermic chemical reactions (EN-EX CRs) near different geometries. Chu et al. [23] conducted a study on the HNF flow over a parabolic stretching surface with the CR and activation energy. Madhukesh et al. [24] investigated the impact of EN-EX CRs on NF transportation in a microchannel. In light of the results obtained for EN-EX CRs and activation energy, Singh et al. [25] inspected the transport of tri-hybrid NF flow past a wedge-cone surface.

The number of contaminants existing in soil, water, or air is referred to as the pollutant concentration. The globe has been worried about the unchecked rise in pollutants in recent years because of the expansion in industrial facilities, vehicles, and industrial waste, as well as the release of various hazardous gases into the atmosphere and a rise in the disposal of trash into water bodies. The health of humans, animals, and other living beings is more significantly impacted by pollutants. Nanoparticles exhibit a variety of properties that facilitate the removal of contaminants and can increase heat transfer. To determine the wide range of flow and concentrations of pollutant dispersion, experimental approaches based on field measurements are frequently employed. Elattar et al. [26] scrutinized the pollutant concentration in an NF stream past a plane surface. With the presence of waste discharge concentration, the HNF over an elongating surface was deliberated by Yaseen et al. [27]. Over a surface with varying thicknesses, Ramesh et al. [28] explored the impact of EN-EX CR and waste discharge concentration. Over a Riga plate, the effects of pollutant concentration on non-Newtonian NF movement were explored by Xin et al. [29].

Nanotechnology which is technically developed and deals with certain types of nanomaterials has been widely utilized to improve the characteristics of heat transfer in numerous fluids. The low thermal conductivity of many liquids is the main obstacle to boosting heat transmission in the electrical and mechanical approaches. It thus needs fluids with better thermal characteristics. Hence, in 1995, Choi and Eastman developed a suspension called “Nanofluid” by incorporating nanoparticles into the base fluid comprising ethylene glycol, oil, kerosene, and water. Compared to base fluids, nanofluids (NFs) possess higher thermal properties and better thermal conductivity. Applications for the superior properties of NFs may be found in a wide range of industries, such as food processing, heat exchangers, nuclear reactors, cooling appliances, medicinal equipment, and thermal management systems. Concerning these applications, the boundary layer flow past a porous medium saturated with an NF was studied by Chamkha and Rashad [30]. Over a stretching sheet, the unsteady flow of Maxwell NF was investigated by Madhu et al. [31]. The effects of ion and Hall slip on MHD flow across a vertical plate were examined by Krishna and Chamkha [32]. The thermal transport of a non-Newtonian NF over a stretching surface was elucidated by Sohail et al. [33]. Using finite element method, Liu et al. [34] investigated the thermal transport of HNF in the Prandtl fluid structure along a porous sheet. Under the influence of thermal radiation, Madhu et al. [35] probed the HNF flow over a cylinder. The impact of thermal radiation and thermophoretic effects on an NF along a microchannel was investigated by Nimmy et al. [36]. Works of Takhar et al., Sohail and Abbas, and Bai et al. [37–39] also contain some relevant studies on NFs.

Several studies have been published on the individual effects such as EN-EX CRs, convective BCs, and pollutant concentrations, but very few research articles are available regarding these aspects for the orientational flow of MHD NFs across a rotating sphere. The research void would allow us to explore a new and undiscovered area of study. This study could provide valuable information on the collective effects and interaction of NF circulation in these circumstances. Understanding these dynamics matters a lot, as they affect different engineering aspects that are responsible for the success of industries and production processes. This research could improve industrial processes and help planning for environmental preservation. By investigating these parameters, this research is aimed at enhancing the efficiency and sustainability of industrial applications with less environmental negative side effects.

2 Mathematical background of the flow problem

In the current work, an incompressible boundary layer circulation of NFs (a water and titanium oxide mixture) in a forward stagnation point with a constant temperature is examined around a rotating sphere object in the presence of an external pollutant concentration, a magnetic field, and the thermal radiation effect (Figure 1). Therefore, x ˆ , y ˆ , and z ˆ denote the coordinate surface, the direction normal to the sphere, and the axis in the direction of rotation, respectively. Let Ω ( t ) = B 1 ⁎ t , B 1 ⁎ > 0 be the angular velocity of the spherical object revolving around its diameter and parallel to the far-field velocity. There is no angular motion of the sphere experienced in the liquid at t = 0 . Around the sphere surface, the temperature is considered to be constant. The angular and free stream velocities which depend upon time are given by u ˆ e ( x ˆ , t ) = A 1 ⁎ x ˆ t , A 1 ⁎ > 0 . Furthermore, the implications of EX-EN CRs on the thermal equation are addressed. C and T denote the concentration and temperature of the sphere, respectively, and C ∞ and T ∞ demonstrate the far-field concentration and ambient temperature, respectively. These assumptions serve as the basis for the governing equations, which are given below [40,41].

(1) ∂ ( r ˆ u ˆ ) ∂ x ˆ + ∂ ( r ˆ v ˆ ) ∂ y ˆ = 0 ,

(2) ∂ u ˆ ∂ t + u ˆ ∂ u ˆ ∂ x ˆ + v ˆ ∂ u ˆ ∂ y ˆ = w ˆ 2 r ˆ d r ˆ d x ˆ + ∂ u ˆ e ∂ t + υ nf ∂ 2 u ˆ ∂ y ˆ 2 + u ˆ e ∂ u ˆ e ∂ x ˆ − σ nf ρ nf B 0 2 ( u ˆ − u ˆ e ) ,

(3) ∂ w ˆ ∂ t + u ˆ ∂ w ˆ ∂ x ˆ + v ˆ ∂ w ˆ ∂ y ˆ = υ nf ∂ 2 w ˆ ∂ y ˆ 2 − u ˆ w ˆ r ˆ d r ˆ d x ˆ − σ nf ρ nf B 0 2 w ˆ ,

(4) ∂ T ∂ t + u ˆ ∂ T ∂ x ˆ + v ˆ ∂ T ∂ y ˆ = k nf ( ρ C p ) nf ∂ 2 T ∂ y ˆ 2 + ρ f ( ρ C p ) nf β 1 × K r 2 T T ∞ n exp − E a K T ( C − C ∞ ) ︸ Endothermic / exothermic chemical reaction ,

(5) ∂ C ∂ t + u ˆ ∂ C ∂ x ˆ + v ˆ ∂ C ∂ y ˆ = D f ∂ 2 C ∂ y ˆ 2 − K r 2 T T ∞ n exp − E a K T ( C − C ∞ ) ︸ Activation energy + P ( C ) ︸ pollutant source .

Figure 1

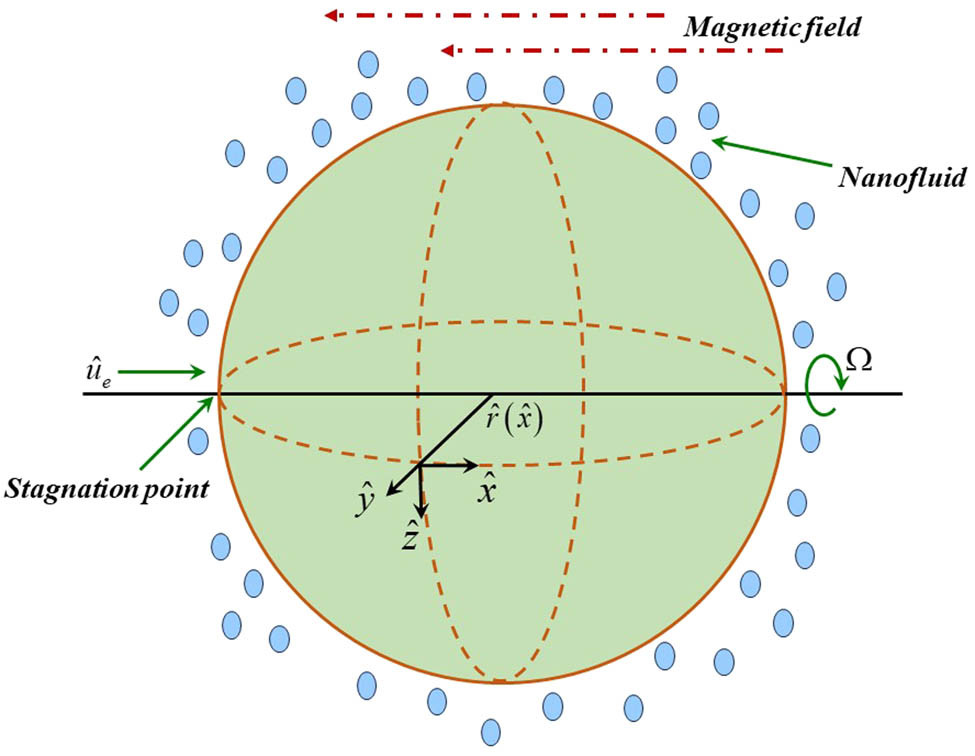
Flow geometry of the problem.

The appropriate initial and BCs are as follows:

(6) u ˆ ( 0 , x ˆ , y ˆ ) = u ˆ i ( x ˆ , y ˆ ) , v ˆ ( 0 , x ˆ , y ˆ ) = v ˆ i ( x ˆ , y ˆ ) , w ˆ ( 0 , x ˆ , y ˆ ) = w ˆ i ( x ˆ , y ˆ ) , T ( 0 , x ˆ , y ˆ ) = T i ( x ˆ , y ˆ ) , C ( 0 , x ˆ , y ˆ ) = C i ( x ˆ , y ˆ ) ,

(7) u ˆ ( t , x ˆ , 0 ) = 0 , v ˆ ( t , x ˆ , 0 ) = 0 , w ˆ ( t , x ˆ , 0 ) = Ω ( t ) r ˆ , − k nf ∂ T ∂ y ˆ = h f ⁎ ( T w − T ) ( t , x ˆ , 0 ) , C ( t , x ˆ , 0 ) = C w , u ˆ ( t , x ˆ , w ˆ ) = u ˆ e ( x ˆ , t ) = A 1 ⁎ x ˆ t , w ˆ ( t , x ˆ , ∞ ) = 0 , T ( t , x ˆ , ∞ ) = T ∞ , C ( t , x ˆ , ∞ ) = C ∞ .

Here, u ˆ , v ˆ , and w ˆ represent the velocity components in the x ˆ , y ˆ , and z ˆ directions, respectively. Also, t denotes the time, B 0 quantifies the magnetic field strength, β 1 ⁎ is the EN/EX factor, K r 2 designates the parameter for the chemical reaction, E a symbolizes the activation energy, ρ is the density, D f defines the diffusivity, k denotes the thermal conductivity, r ˆ is the radial distance measured between the axis of symmetry and the surface element, υ expresses the kinematic viscosity, σ demonstrates the electrical conductivity, K denotes the Boltzmann constant, C p represents the specific heat, h f ⁎ describes the heat transfer coefficient, nf , f denote the NF and the base fluid, respectively, and i is the subscript which denotes the initial condition. According to Xin et al. [29], the exterior pollutant source function P ( C ) is defined as P ( C ) = λ 2 exp ( Q 1 ( C − C ∞ ) ) , where λ 2 is the external pollutant concentration and Q 1 is the external source variation factor.

Furthermore, to ease the analysis of the problem, we need to introduce the following similarity variables such as:

(8) ψ = A 1 ⁎ x ˆ υ f t f ( η ) , u ˆ = A 1 ⁎ x ˆ f ′ ( η ) t , v ˆ = − A 1 ⁎ υ f t f ( η ) , η = 1 υ f t y ˆ , w ˆ = B 1 ⁎ x ˆ g ( η ) t , θ = T − T ∞ T w − T ∞ , r ˆ ≈ x ˆ , u ˆ e = x ˆ A 1 ⁎ t , χ = C − C ∞ C w − C ∞ , d r ˆ d x ˆ = 1 .

Using equation (8), the governing equations (1)–(5) are converted into the requisite posited ODEs, which are displayed as follows:

(9) f ‴ + D 1 D 2 f ″ η 2 + f A 1 ⁎ − A 1 ⁎ ( f ′ ) 2 + f ′ + A 1 ⁎ ( λ g 2 + 1 ) − 1 − σ nf σ f M F D 2 ( f ′ − 1 ) = 0 ,

(10) g ″ + D 1 D 2 g ′ η 2 + A 1 ⁎ f + g 1 − 2 A 1 ⁎ f ′ − σ nf σ f M F D 2 = 0 ,

(11) 1 Pr D 3 k nf k f θ ″ + θ ′ η 2 + f A 1 ⁎ + λ 1 σ ⁎ A 1 ⁎ D 3 × [ ( T r ⁎ − 1 ) θ + 1 ] n exp − E ( T r ⁎ − 1 ) θ + 1 χ = 0 ,

(12) χ ″ + Sc χ ′ η 2 + f A 1 ⁎ − Sc σ ⁎ A 1 ⁎ [ ( T r ⁎ − 1 ) θ + 1 ] n exp − E ( T r ⁎ − 1 ) θ + 1 χ + Sc β e B χ = 0 .

The simplified BCs are as follows:

(13) g = 1 , f ′ = 0 , f = 0 , θ ′ = − Bi ( 1 − θ ) , χ = 1 at η = 0 ,

(14) f ′ = 1 , g = 0 , θ = 0 , χ = 0 as η → ∞ .

In equations (9)–(11),

D 1 = ( 1 − φ ⁎ ) 2.5 , D 2 = 1 − φ ⁎ + φ ⁎ ρ s ρ f , and D 3 = 1 − φ ⁎ + φ ⁎ ( ρ C p ) s ( ρ C p ) f .

The above-stated equations comprise distinct influential parameters. The corresponding nondimensional parameters are mathematically defined in Table 1 along with the name of the parameters.

Table 1

Non-dimensional parameters

Formula	Name of the parameter
A 1 ⁎	Acceleration parameter
λ = B 1 ⁎ A 1 ⁎ 2	Rotation parameter
Pr = μ f C p k f	Prandtl number
T r ⁎ = T w T ∞	Temperature ratio parameter
Sc = υ f D f	Schmidt number
σ ⁎ = K r 2 A 1 ⁎	Chemical reaction rate
E = E a K T ∞	Activation energy
λ 1 = β 1 ⁎ ( C p ) f C w ‒ C ∞ T w ‒ T ∞	EN-EX reaction constraint
β = λ 2 t C w ‒ C ∞	Local pollutant external source parameter
B = Q 1 ( C w ‒ C ∞ )	External pollutant source variation parameter

The engineering physical quantities of interest are the coefficients of skin friction C f along the x and z directions, local Nusselt number Nu , and local Sherwood number Sh . Mathematically, they are defined as follows [42]:

(15) C fx = μ nf ρ f u ˆ e 2 ∂ u ˆ ∂ y ˆ y ˆ = 0 C fz = − μ nf ρ f u ˆ e 2 ∂ w ˆ ∂ y ˆ y ˆ = 0 Nu = − x ˆ k nf ∂ T ∂ y ˆ y ˆ = 0 k f ( T w − T ∞ ) Sh = − x ˆ D f ∂ C ∂ y ˆ y ˆ = 0 D f ( C w − C ∞ ) .

The reduced engineering coefficients are given as follows:

(16) Re C fx = f ″ ( 0 ) D 1 A 1 ⁎ , Re C fz = − λ g ′ ( 0 ) D 1 A 1 ⁎ .

(17) Nu Re = − k nf k f θ ′ ( 0 ) A 1 ⁎ ,

(18) Sh Re = − χ ′ ( 0 ) A 1 ⁎ ,

where Re = A 1 ⁎ x ˆ 2 υ f t characterizes the local Reynolds number. Moreover, Table 2 demonstrates the correlations of the thermophysical properties of the NF. Therefore, the experimental data of the base fluid (water) and the titania nanoparticles are highlighted in Table 3.

Table 2

Thermophysical properties of the NF [43]

Properties	Correlations
Density	ρ nf = ρ f 1 ‒ φ ⁎ + φ ⁎ ρ s ρ f
Heat capacity	( ρ C p ) nf = ( ρ C p ) f 1 ‒ φ ⁎ + φ ⁎ ( ρ C p ) s ( ρ C p ) f
Dynamic viscosity	μ nf = μ f ( 1 ‒ φ ⁎ ) 2.5
Thermal conductivity	k nf = k f k s + 2 k f ‒ φ ⁎ 2 ( k f ‒ k s ) k s + 2 k f + φ ⁎ ( k f ‒ k s )
Electrical conductivity	σ nf σ f = 3 σ s σ f ‒ 1 φ ⁎ σ s σ f + 2 ‒ σ s σ f ‒ 1 φ ⁎ + 1

Table 3

Thermophysical properties of the base fluid and nanoparticles [44]

Properties	ρ	C p	k	σ	Pr
TiO₂	4,250	686.2	8.9538	2.38 × 10 6	—
H₂O	997.1	4,179	0.613	5.5 × 10 6	6.2

3 Methodology

In scientific and engineering problems, ordinary differential equations are commonly encountered and are usually solved via the Runge–Kutta technique. The integrated method RKF-45 originates from the Runge–Kutta domain, where techniques with similar errors and distinct orders are created by merging identical functions. This strategy, which combines the fifth-order scheme with the fourth-order Runge–Kutta scheme, aids in the very accurate approximation of ODE solutions as compared to lower-order approaches. The ability of the RKF-45 technique to adaptively vary the step size during integration is one of its key advantages. This helps to maintain the accuracy and capture variations in the associated solution. RKF-45 is advantageous for solving ODEs in a range of scientific and engineering applications because of the fifth-order component’s contribution in improving the accuracy and the fourth-order component’s computing efficiency.

The following is the RKF-45 method’s algorithm:

(19) y i + 1 = y i + 25 216 R 1 + 1 , 408 2 , 565 R 3 + 2 , 197 4 , 104 R 4 − 1 5 R 5 ,

(20) z i + 1 = y i + 16 135 R 1 + 6 , 656 12 , 825 R 3 + 28 , 561 56 , 430 R 4 − 9 50 R 5 + 2 55 R 6 .

The following lists the six steps in the approach.

(21) R 1 = hf ( x i , y i ) ,

(22) R 2 = hf x i + 1 4 h , y i + 1 4 R 1 ,

(23) R 3 = hf x i + 3 8 h , y i + 3 32 R 1 + 9 32 R 2 ,

(24) R 4 = hf x i + 12 13 h , y i + 1 , 932 2 , 147 R 1 − 7 , 200 2 , 147 R 2 + 7 , 296 2 , 147 R 3 ,

(25) R 5 = hf x i + h , y i + 439 216 R 1 − 8 R 2 + 3 , 680 513 R 3 − 845 4 , 104 R 4 ,

(26) R 6 = hf x i + 1 2 h , y i − 8 27 R 1 + 2 R 2 − 3 , 544 2 , 565 R 3 − 1 , 859 4 , 104 R 4 − 11 40 R 5 .

As the generated equations (9)–(12) and BCs (13) and (14) are very challenging to solve analytically, the resultant equations are reduced to the first order in order to determine the numerical solution. This approach can break down the problem and facilitate a solution. For this, the following substitutions are employed.

f , f ′ , f ″ g , g ′ θ , θ ′ χ , χ ′ = Λ 1 , Λ 2 , Λ 3 Λ 4 , Λ 5 Λ 6 , Λ 7 Λ 8 , Λ 9 .

Thus, the equations in (9)–(12) are transformed into

(27) f ‴ = − D 1 D 2 Λ 3 η 2 + Λ 1 A 1 ⁎ − A 1 ⁎ ( Λ 2 ) 2 + Λ 2 + A 1 ⁎ ( λ ( Λ 4 ) 2 + 1 ) − 1 − σ nf σ f M F D 2 ( Λ 2 − 1 ) ,

(28) g ″ = − D 1 D 2 Λ 5 η 2 + A 1 ⁎ Λ 1 + Λ 4 1 − 2 A 1 ⁎ Λ 2 − σ nf σ f M F D 2 ,

(29) θ ″ = − 1 Pr D 3 k nf k f − 1 Λ 7 η 2 + Λ 1 A 1 ⁎ + λ 1 σ ⁎ A 1 ⁎ D 3 [ ( T r ⁎ − 1 ) Λ 6 + 1 ] n exp − E ( T r ⁎ − 1 ) Λ 6 + 1 Λ 8 ,

(30) χ ″ = − Sc Λ 9 η 2 + Λ 1 A 1 ⁎ − Sc σ ⁎ A 1 ⁎ [ ( T r ⁎ − 1 ) Λ 6 + 1 ] n exp − E ( T r ⁎ − 1 ) Λ 6 + 1 Λ 8 + Sc β e B Λ 8 .

The boundary constraints are transformed into

(31) Λ 4 = 1 , Λ 2 = 0 , Λ 1 = 0 , Λ 7 = − Bi ( 1 − Λ 6 ) , Λ 8 = 1 at η = 0 ,

(32) Λ 2 = 1 , Λ 4 = 0 , Λ 6 = 0 , Λ 8 = 0 as η → ∞ .

The transformed equations are solved via the RKF-45 approach. Since the BCs include unknowns, a shooting technique is being implemented to identify the solution that meets the conditions at infinity. This is accomplished by giving the parameter values, choosing an error tolerance of around 10⁻⁶ and a step size of 0.01. Using the thermophysical properties of the NF given in Table 3 and setting the default values for every parameter, that is, A 1 ⁎ = 1 , σ ⁎ = 0.1 , M F = 1 , λ = 1 , E = 0.1 , Bi = 0.5 , T r ⁎ = 0.1 , Sc = 0.8 , and λ 1 = ± 1 , solutions are found. Here, θ ′ = − Bi ( 1 − θ ) is replaced by θ ( 0 ) = 1 . The results of the current numerical approach have been verified by comparison with earlier research in the literature and are given in Table 4.

Table 4

Validation of code with the work of Malvandi [45] for some limiting cases ( M F = λ 1 = 0 , D 1 = D 2 = 1 )

A 1 ⁎ →		0.5	1	2
Malvandi [45]	‒ θ ′ ( 0 )	0.467648	0.589527	0.779526
Current study	‒ θ ′ ( 0 )	0.467643	0.589532	0.779529
Malvandi [45]	f ″ ( 0 )	0.79913	1.2828	1.9172
Current study	f ″ ( 0 )	0.79915	1.2842	1.9175
Malvandi [45]	‒ g ′ ( 0 )	0.30339	0.64579	1.05415
Current study	‒ g ′ ( 0 )	0.30341	0.64586	1.05416

4 Analysis of results

This section presents the results of the study derived from the numerical analysis. The influence of distinct dimensionless constraints and how they affect various profiles are further elaborated upon in detail. This section provides detailed explanations of the key physical variables and various limitations that affect the rates of heat transfer, mass transfer, and surface drag force.

The influence of λ on the velocity profiles f ′ ( η ) and g ( η ) is depicted in Figure 2. For higher values of λ , the f ′ ( η ) profile is found to be increasing, while a reverse trend is experienced for g ( η ) . The presence of a rotation parameter causes forces to act on the liquid, accelerating the flow of fluid. The sphere rotates over its coordinate quicker and more vigorously with the augmenting values of λ enhancing the flow characteristics of the NF. This process leads to an upgrade in f ′ ( η ) . As λ grows, the amplitude of g ( η ) drastically decreases, especially in the vicinity of the sphere’s outermost layer, where radial forces are most pronounced. The strong radial outflow fundamentally opposes and suppresses the fluid’s capacity to sustain swirling emotions. With the influence of the increased rotation of the sphere, the g ( η ) profile declines, respectively.

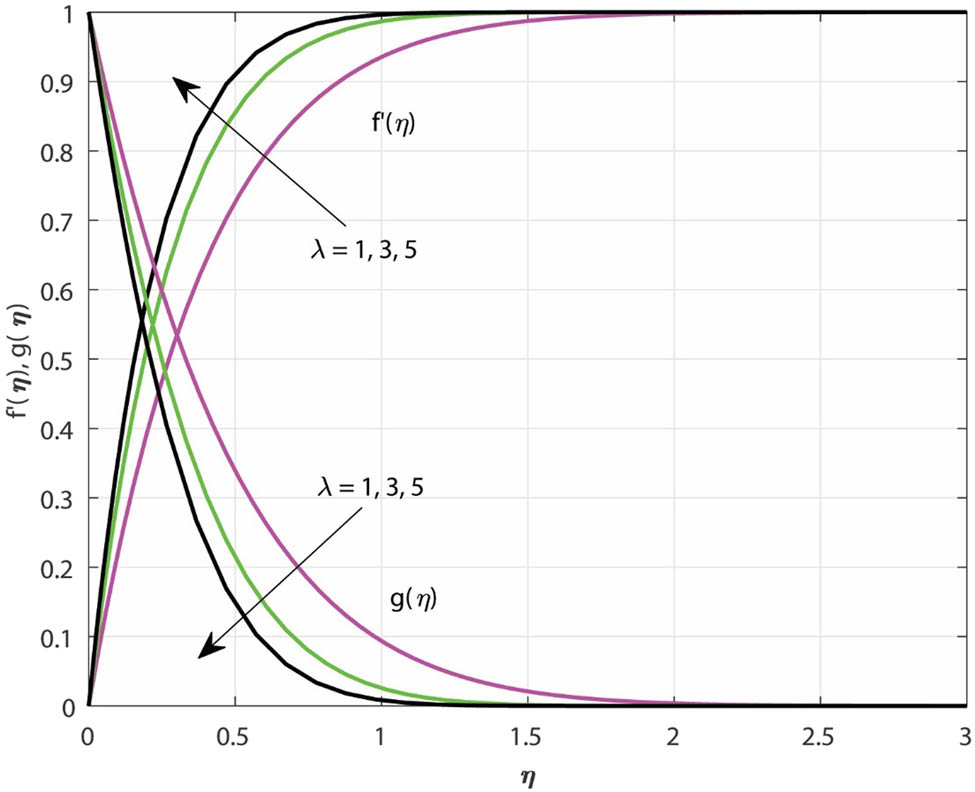
$Figure 2 Variations in f ′ ( η ) f^{\prime} (\eta ) and g ( η ) g(\eta ) due to the change in λ \lambda .$

Figure 2

Variations in f ′ ( η ) and g ( η ) due to the change in λ .

The impact of A 1 ⁎ on f ′ ( η ) and g ( η ) is displayed in Figure 3. From the figure, it is clear that for increasing values of A 1 ⁎ , the f ′ ( η ) profile upsurges while g ( η ) declines. This is because when the acceleration increases, the fluid gains more radial momentum due to the outer centrifugal inertia. Higher acceleration increases the movement of liquid molecules and elevates the sphere’s rotational forces increasing the primary velocity f ′ ( η ) . A centrifugal force orthogonal to the primary flow direction is produced by the curvature of the fluid flow which resists the motion of fluid in the rotating axis. When the acceleration increases due to the quicker revolution of the sphere, the tremendous centrifugal inertia produces a significant radial outflow close to the outer boundary. This radial flow suppresses and disturbs the formation of coherent tangential whirling movements, resulting in a decrement in g ( η ) .

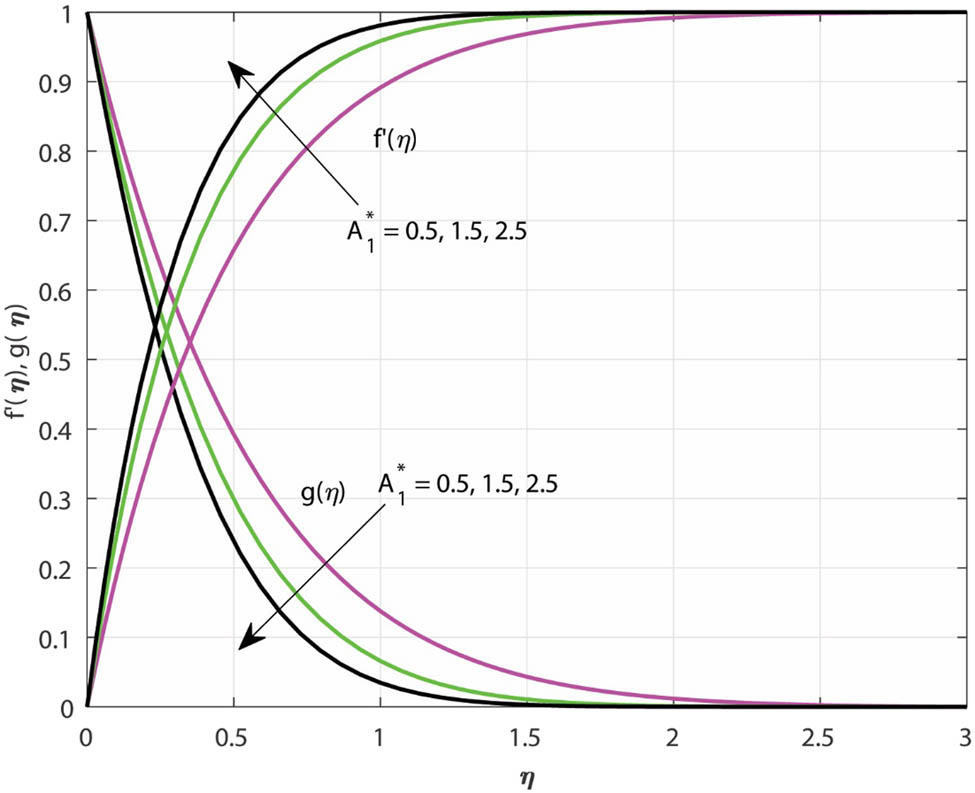
$Figure 3 Variations in f ′ ( η ) f^{\prime} (\eta ) and g ( η ) g(\eta ) due to the change in A 1 ⁎ {A}_{1}^{\ast } .$

Figure 3

Variations in f ′ ( η ) and g ( η ) due to the change in A 1 ⁎ .

The variations in f ′ ( η ) and g ( η ) concerning the magnetic parameter M F are shown in Figure 4. For elevated values of M F , f ′ ( η ) increases and g ( η ) decreases. The reason for this is that a higher M F symbolizes a stronger Lorentz force and a strong bond between the magnetic field and the liquid surrounding the spinning sphere. Furthermore, the stronger primary rotation which is governed by forces applied by M F and keeps the secondary rotating components from forming in the liquid movement can account for the decrease in secondary velocity g ( η ) .

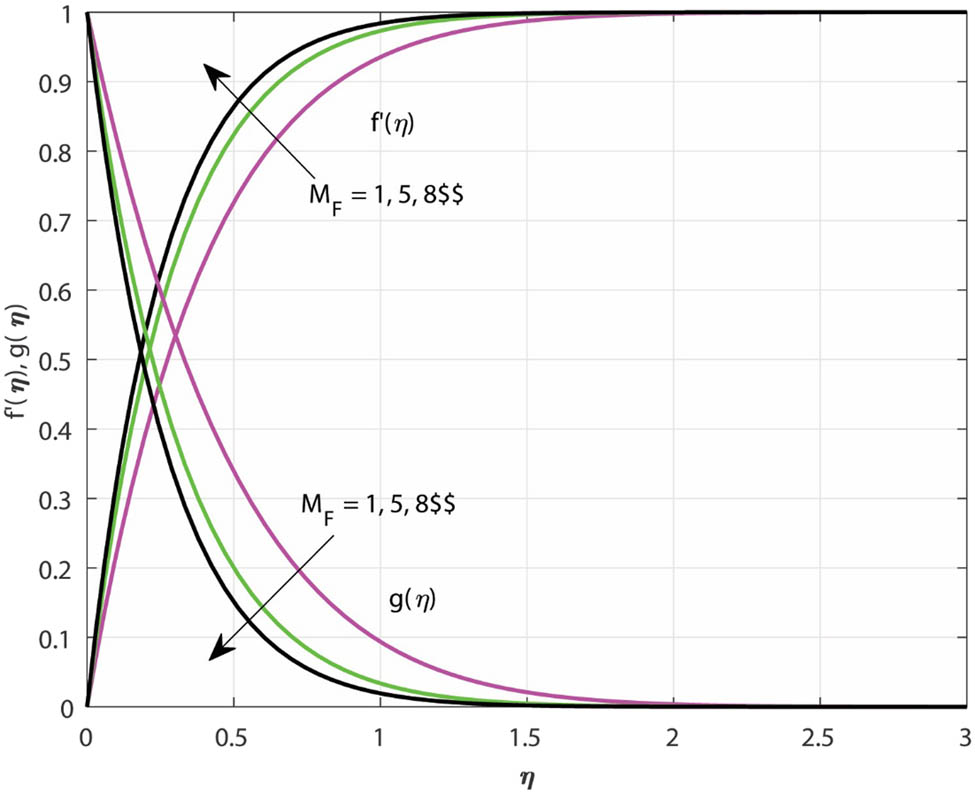
$Figure 4 Variations in f ′ ( η ) f^{\prime} (\eta ) and g ( η ) g(\eta ) due to the change in M F {M}_{\text{F}} .$

Figure 4

Variations in f ′ ( η ) and g ( η ) due to the change in M F .

For EN ( λ 1 = − 1 ) and EX ( λ 1 = 1 ) CRs, the change in the temperature profile θ ( η ) for increased values of E is depicted in Figure 5. The least amount of energy needed to initiate a chemical reaction is known as the activation energy. This energy prevents the EN-EX CR from proceeding by acting as a barrier. In the EX case, for higher values of E , θ ( η ) decreases and is increased in the case of EN CR. Increasing the activation energy in the EX CR scenario increases the energy barrier that prevents the process from producing heat. Consequently, the reaction rate decreases, leading to a reduction in the thermal profile as a result of a drop in temperature production. On the other hand, in the EN CR process, when E increases, the system’s reaction rates slow down and the need for heat absorption declines. In this situation, this leads to a more advantageous balance between heat generation and absorption, which raises the temperature and produces an improved thermal profile.

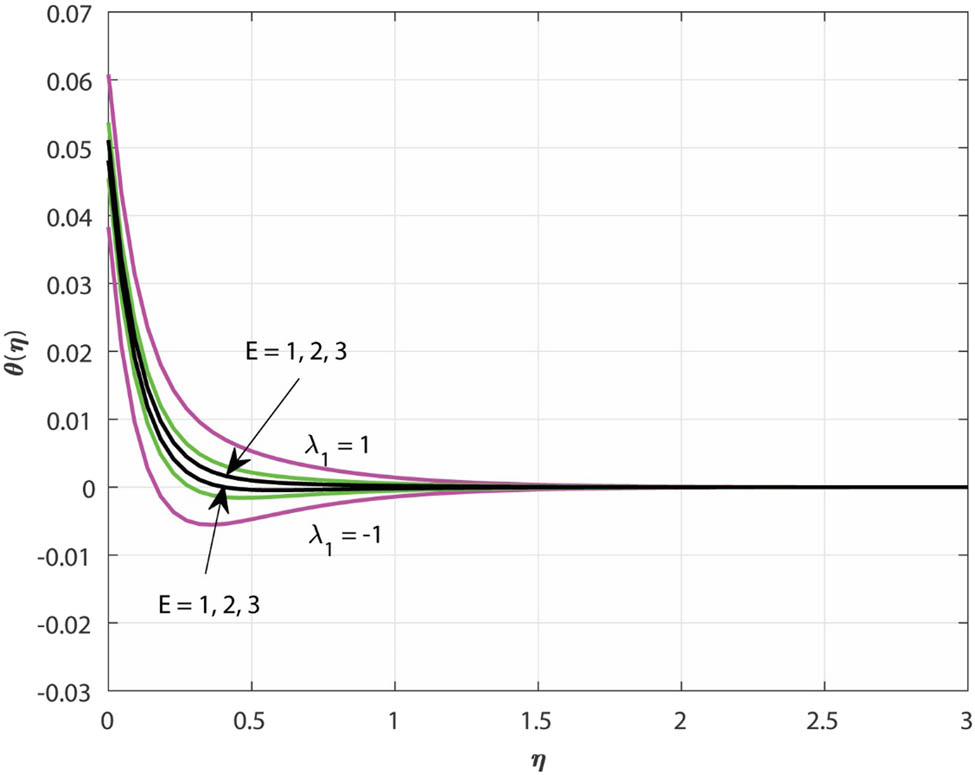
$Figure 5 Variations in θ ( η ) \theta (\eta ) due to changes in E E and λ 1 {\lambda }_{1} .$

Figure 5

Variations in θ ( η ) due to changes in E and λ 1 .

The impact of Biot number Bi on the temperature profile for both the EN ( λ 1 = − 1 ) and EX ( λ 1 = 1 ) reactions is portrayed in Figure 6. From the figure, it is evident that as Bi increases, θ ( η ) increases for both EN-EX CRs. In an EN CR, the heat is absorbed from the surroundings. The higher values of Bi indicate that the convective heat transfer coefficient is inclined and that the thermal resistance is skewed, which increase the rate of heat transmission. The temperature profile may rise as a result of the increased heat available to drive the EN process. In an EX CR, the heat is emitted into the surroundings. Improved convective heat transport is implied by a higher Bi. This indicates that heat produced by EX CRs may be removed from the reaction site more effectively. It may, however, initially let the reaction site attain a greater temperature before the heat dissipates if the external thermal resistance is much decreased for increasing Bi .

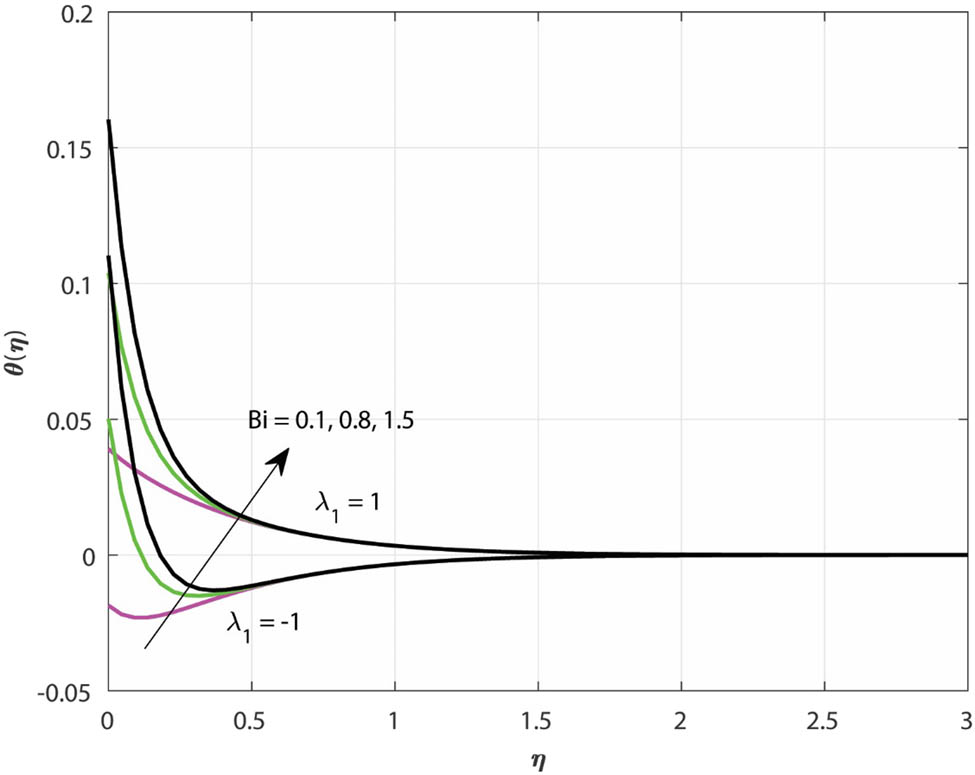
$Figure 6 Variations in θ ( η ) \theta (\eta ) due to changes in Bi \text{Bi} and λ 1 {\lambda }_{1} .$

Figure 6

Variations in θ ( η ) due to changes in Bi and λ 1 .

The variation in θ ( η ) for increased values of σ ⁎ for both EN-EX CRs is depicted in Figure 7. From the figure, it is clear that for EN reactions ( λ 1 = − 1 ), the θ ( η ) profile decreases while it is increased for the EX case ( λ 1 = 1 ). During chemical reactions, heat is produced at a higher rate. Hence, an increase in heat energy causes an increase in the temperature profile in the case of EX CR. The growing values of the chemical reaction parameter in an EN CR process indicate that the system on the whole has a substantial need for heat absorption. As a result, in the EN CR, using more heat, the temperature drops, lowering the thermal profile.

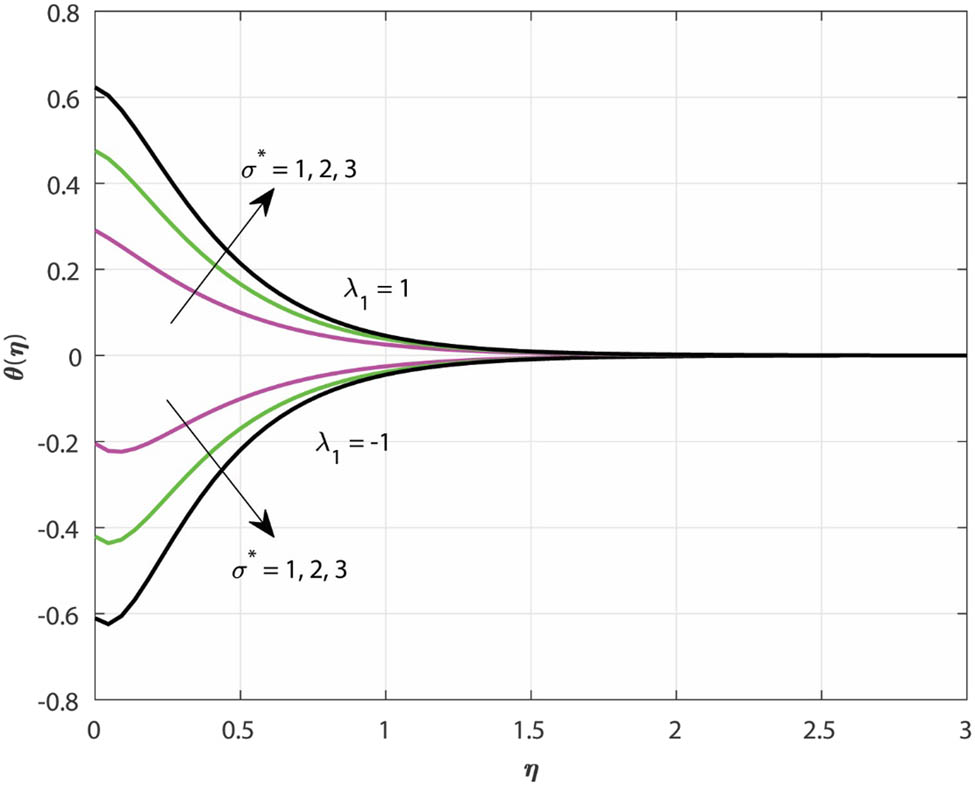
$Figure 7 Variations in θ ( η ) \theta (\eta ) due to changes in σ ⁎ \sigma \ast and λ 1 {\lambda }_{1} .$

Figure 7

Variations in θ ( η ) due to changes in σ ⁎ and λ 1 .

The nature of the concentration profile χ ( η ) for increased values of B and β is illustrated in Figures 8 and 9, respectively. The concentration profile increases with an increase in both B and β . These parameters describe the extent to which the flow system is impacted by external sources of pollution. As a result of the external BCs, the rate at which the pollutant species penetrates the system is measured by the external pollutant source parameter. The upsurge values of B and β indicate the boosting of pollutants in the fluid system. The concentration profiles additionally increase in magnitude as this parameter increases, indicating a greater amount of polluting material from external sources.

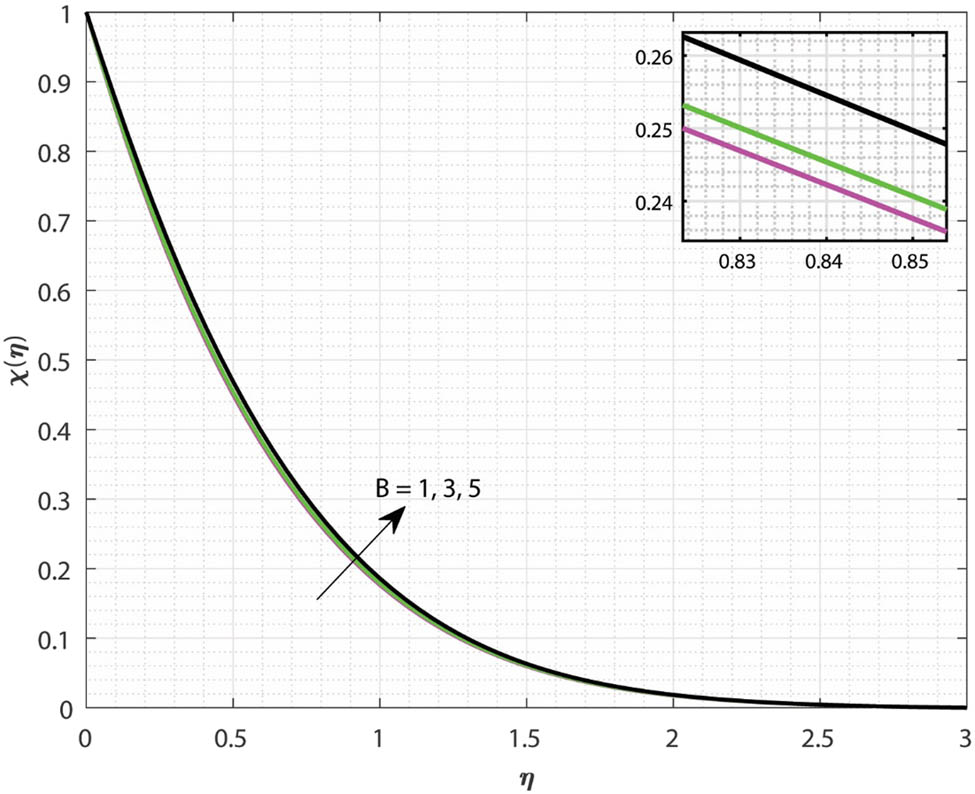
$Figure 8 Variations in χ ( η ) \chi (\eta ) due to the change in B B .$

Figure 8

Variations in χ ( η ) due to the change in B .

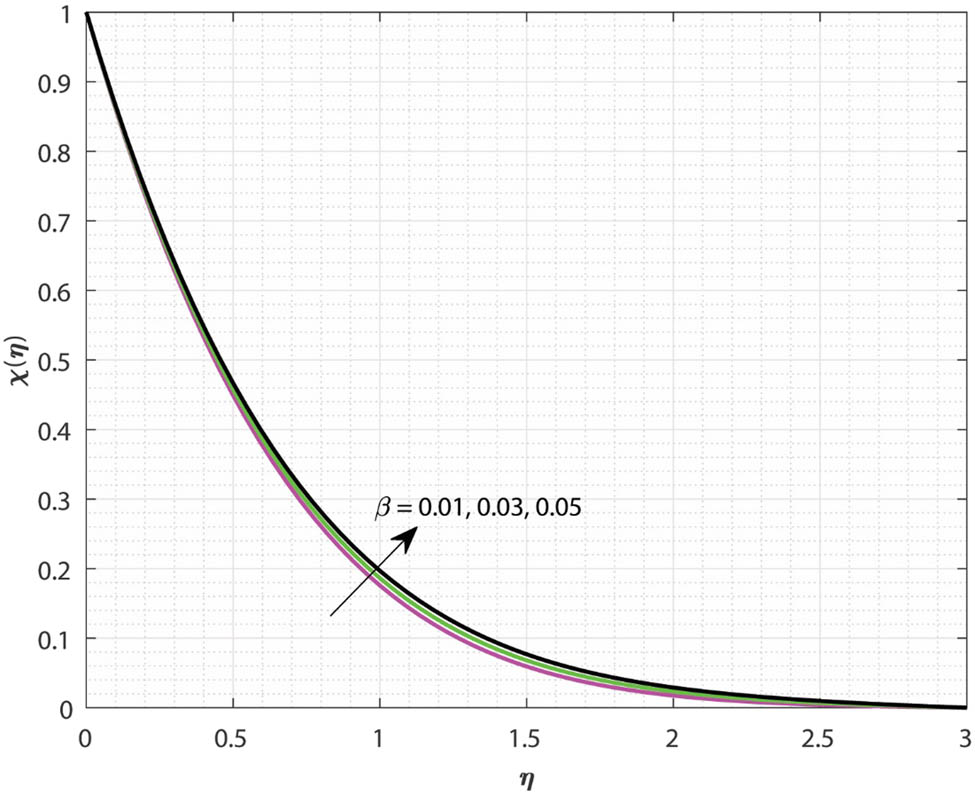
$Figure 9 Variations in χ ( η ) \chi (\eta ) due to the change in β \beta .$

Figure 9

Variations in χ ( η ) due to the change in β .

The influence of σ ⁎ on the concentration profile is depicted in Figure 10. An augmentation in σ ⁎ decreases the concentration profile. This is because the reactant molecules are often consumed in chemical processes. The concentration of these reactants decreases as the reaction continues. The higher values of σ ⁎ indicate that there are more molecules in the reaction, which causes the reactants to be consumed more quickly and lowers the system’s concentration.

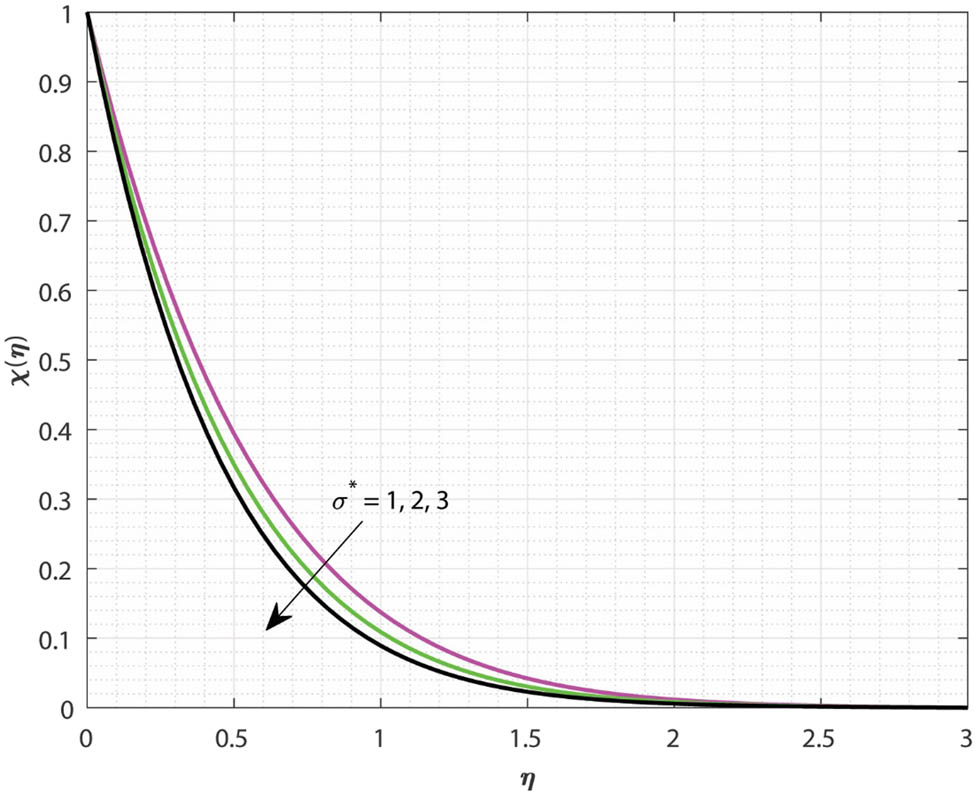
$Figure 10 Variations in χ ( η ) \chi (\eta ) due to the change in σ ⁎ \sigma \ast .$

Figure 10

Variations in χ ( η ) due to the change in σ ⁎ .

Figure 11 presents the impact of E on the concentration profile χ ( η ) . From the figure, it is clear that as the activation energy increases, the concentration profile upsurges. This is an observation caused by an Arrhenius function. The quantity of generative chemical reaction increases, leading to a decrease in the modified Arrhenius function and an enhancement of χ ( η ) is experienced.

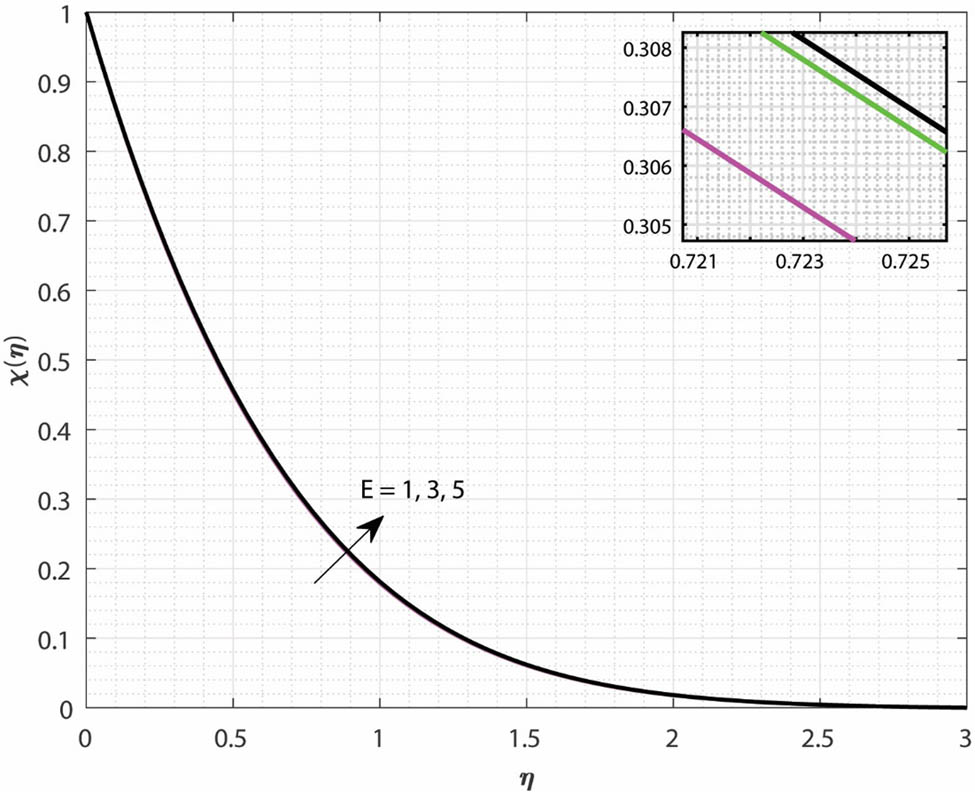
$Figure 11 Variations in χ ( η ) \chi (\eta ) due to the change in E E .$

Figure 11

Variations in χ ( η ) due to the change in E .

Figures 12 and 13 display the variations of the skin friction coefficient C f x and C f z on the magnetic parameter M F for increasing values of φ ⁎ . The improved values of M F and φ ⁎ lead to an increase in both C f x and C f z . This is because when both M F and φ ⁎ are increased concurrently, the effective viscosity of the fluid is enhanced due to the combined effects of the solid particles and magnetic field interactions. The Lorentz force and the enhanced momentum transfer from the suspended particles together increase the flow resistance close to the wall, which increases the skin friction coefficient. A further increase of values of M F elevates the interaction between the liquid and the sphere influencing the circulatory motion, and an increment in φ ⁎ results in an increased concentration of particles inside the pathway of the liquid which intensifies the force on the spherical object thereby increasing the C f x . Increased values of M F also cause the contact between the liquid and the sphere to intensify along the z-axis, changing the fluid flow pattern. Thus, the combined effect of M F and the upsurged values of φ ⁎ , which acts as a barrier for the fluid motion, will lead to an increment in C f z .

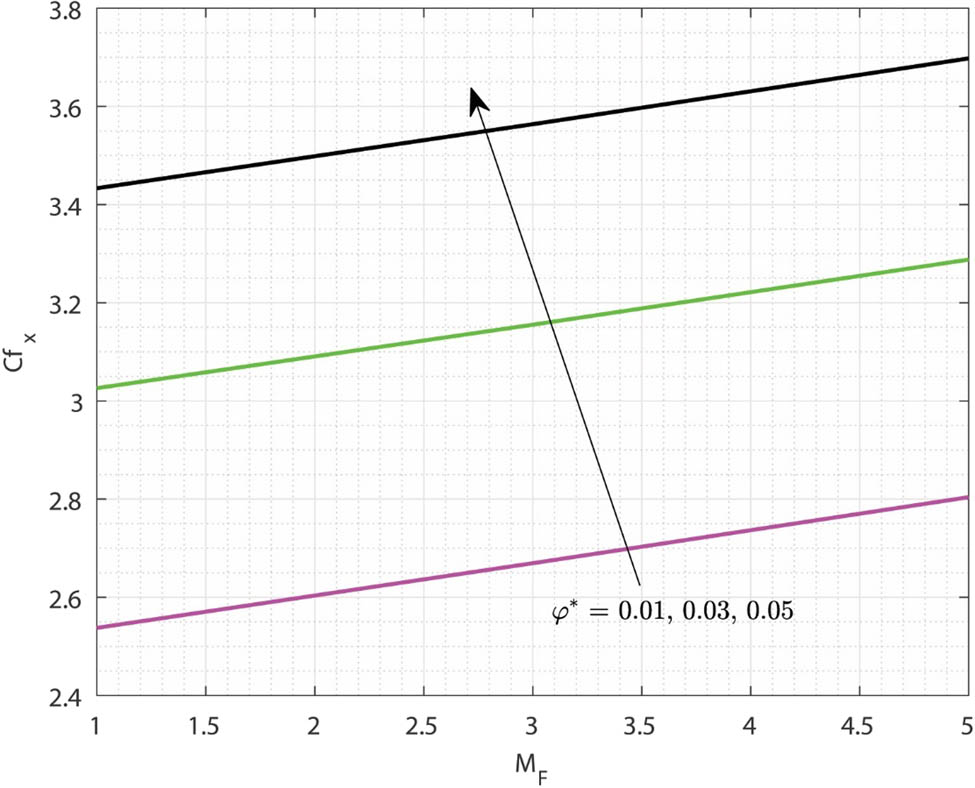
$Figure 12 Variations in C f x C{f}_{x} due to the change in M F {M}_{\text{F}} for varying values of φ ⁎ \varphi \ast .$

Figure 12

Variations in C f x due to the change in M F for varying values of φ ⁎ .

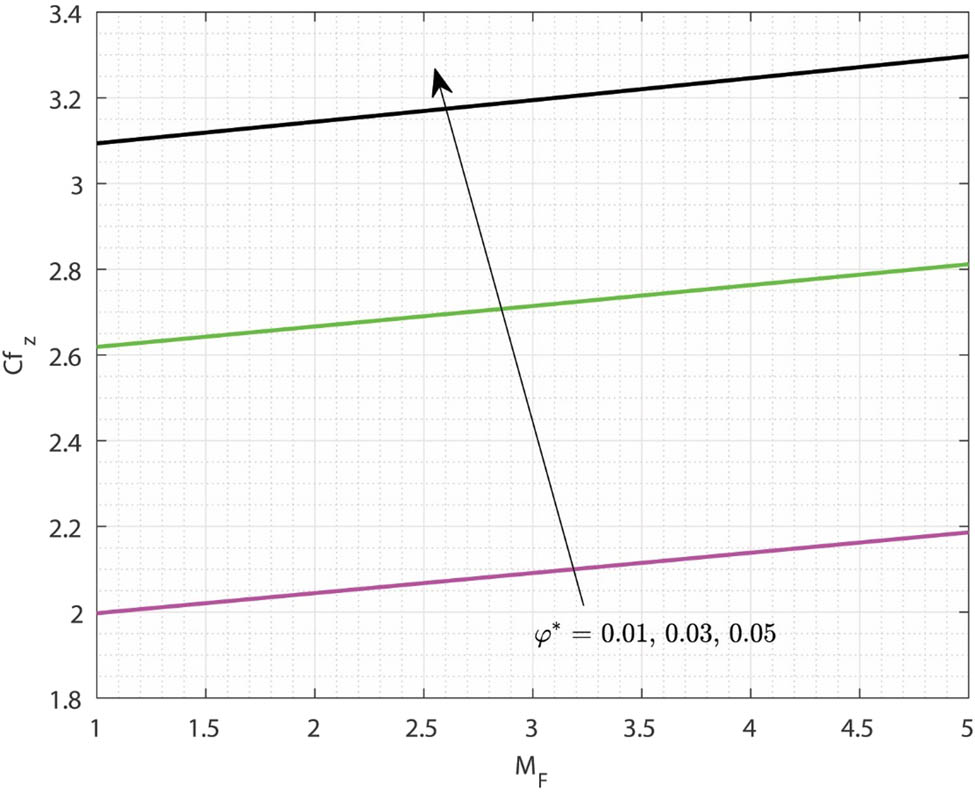
$Figure 13 Variations in C f z C{f}_{z} due to the change in M F {M}_{\text{F}} for varying values of φ ⁎ \varphi \ast .$

Figure 13

Variations in C f z due to the change in M F for varying values of φ ⁎ .

The impact of E on Nu for increased values of φ ⁎ for both the EN ( λ 1 = − 1 ) and EX ( λ 1 = 1 ) reactions is depicted in Figure 14. For the EN process, increasing values of E and φ ⁎ decrease Nu , but a reverse trend is experienced for the EX case. A higher activation energy indicates a more temperature-sensitive CR rate. For the increased activation energy rate, the release of heat is enhanced due to the reaction which leads to a greater temperature differential between the wall and the fluid which facilitates convective heat transfer. For an EX CR process, the higher values of activation energy will lead to a stronger temperature gradient close to the reactive surface. Moreover, with an increase in the solid volume fraction, the surface area for the transmission of heat and the thermal conductivity of the mixture increased resulting in a higher rate of heat transfer. In the case of an EN CR, heat is absorbed from the environment, which may lower the temperature between the fluid and the wall diminishing convective heat transfer. The higher solid volume fraction not only reduced convective heat transmission but also thickened the mixture and may cause the fluid velocity near the spherical wall to slow down. Since they enhanced heat absorption and viscosity and minimized temperature gradients – all of which diminish the convective heat transfer efficiency – increasing the activation energy and solid volume percentage of particles can typically lower the Nu for an EN CR.

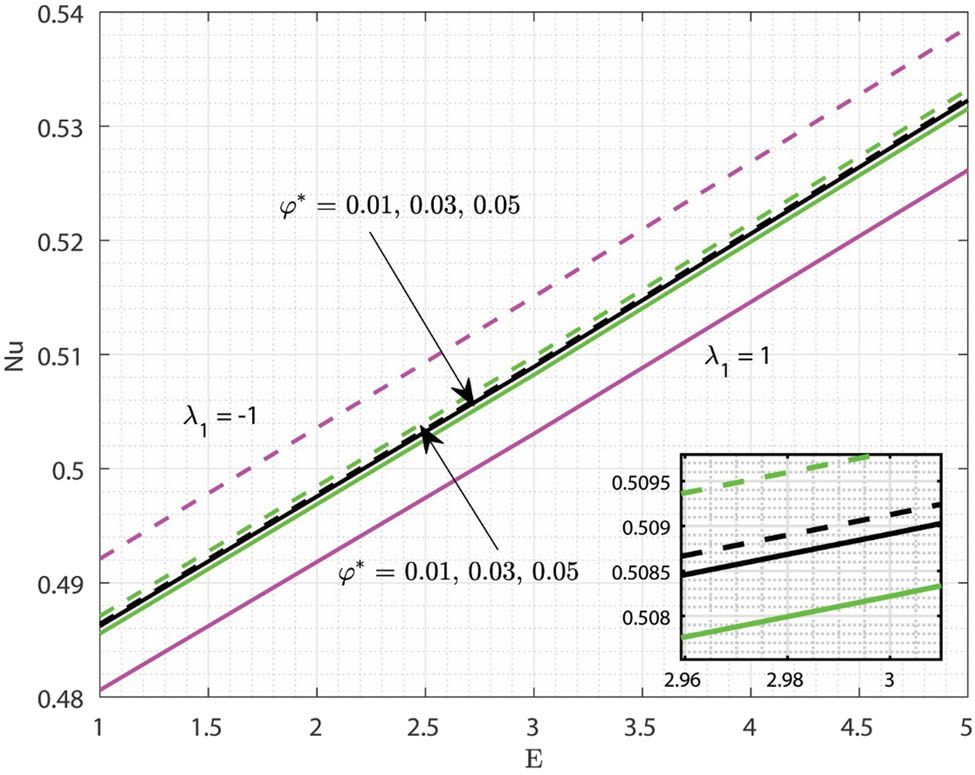
$Figure 14 Variations in Nu \text{Nu} due to the change in E E for varying values of φ ⁎ \varphi \ast and λ 1 {\lambda }_{1} .$

Figure 14

Variations in Nu due to the change in E for varying values of φ ⁎ and λ 1 .

Figure 15 demonstrates the influence of mass transfer on the local pollutant external source β for increased values of φ ⁎ . For augmenting values of β and φ ⁎ , a decrement in Sh is experienced. A considerable increase in the local pollution source may cause the surrounding fluid to become saturated with the pollutant. As the concentration gradient approaches equilibrium, the mass transfer driving force diminishes, hence reducing the convective mass transfer rate. Moreover, a larger solid volume percentage makes the mixture more viscous, which might obstruct the fluid motion and convective mass transfer. Increased viscosity thickens the boundary layer, reducing the Sh and impeding the mass movement.

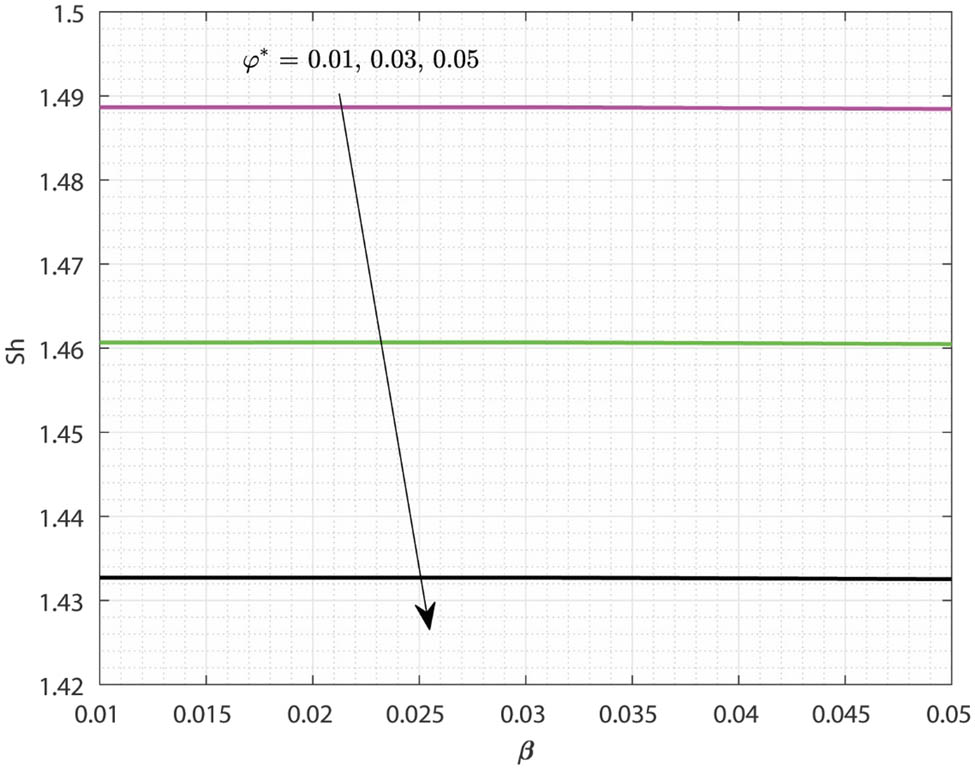
$Figure 15 Variations in Sh \text{Sh} due to the change in β \beta for varying values of φ ⁎ \varphi \ast .$

Figure 15

Variations in Sh due to the change in β for varying values of φ ⁎ .

5 Final remarks

The current research investigates the thermodynamic properties of chemical reactions, the influence of convective BCs, and the effect of pollutant concentration on the circulation of MHD NFs around a spinning sphere. The numerical results of simplified equations are obtained using a highly efficient numerical method, and these results are thoroughly analyzed and discussed. The study yielded the following novel findings.

The primary velocity increases for enhanced values of magnetic, rotation, and acceleration constraints, while a reverse behavior is seen for the secondary velocity.
The temperature decreases in the EX case and increases in the EN case for increasing values of activation energy constraint, while an opposite behavior is observed in the case of chemical reaction constraint.
In both EN/EX cases, temperature increases for Bi values.
Concentration profile shows improvement for increased values of local pollutant source and external pollutant source parameters.
The rate of thermal distribution decreases for an EN case and enhances for an EX case for changes in the values of solid fraction and activation energy parameter.
The rate of mass transfer decreases with an increase in the external pollutant local source and solid volume percentage.

The outcomes of this study have several practical implications in the real world. It can optimize thermal management, hence enhancing cooling systems in power plants and electronic gadgets. Chemical reactors can enhance the reaction efficiency and performance. The study’s findings on the impacts of pollutants are helpful for the development of sophisticated contaminant management and environmental protection measures. Furthermore, it has the potential to enhance the functionality of energy production systems, such as MHD generators, by improving their operations. In summary, the results enhance the development of more efficient and long-lasting solutions in many commercial and ecological contexts.

ahmed-abed@zu.edu.eg

Acknowledgements

This work was funded by the Universiti Kebangsaan Malaysia project number “DIP-2023-005.” The authors thank the Deanship of Scientific Research, Islamic University of Madinah, Madinah, Saudi Arabia, for supporting this research work. In addition, this study was supported via funding from the Prince Sattam bin Abdulaziz University project number (PSAU/2024/R/1445).

Funding information: This work was funded by the Universiti Kebangsaan Malaysia project number “DIP-2023-005.” The authors thank the Deanship of Scientific Research, Islamic University of Madinah, Madinah, Saudi Arabia, for supporting this research work. In addition, this study was supported via funding from the Prince Sattam bin Abdulaziz University project number (PSAU/2024/R/1445).
Author contributions: P.N., A.M.O., and K.V.N: conceptualization, methodology, software, formal analysis, validation, and writing – original draft. J.K.M. and U.K.: Writing – original draft, data curation, investigation, visualization, software, and validation. A.I.: conceptualization, writing – review & editing, supervision, resources, and writing – original draft. D.S. and R.K.: validation, writing – review & editing, software, and writing – original draft. S.M.H. and A.M.A.: validation, writing – review & editing, software, provided significant feedback, and assisted in the revised version of the manuscript. Further, they have also supported revising the manuscript critically for important intellectual content.
Conflict of interest: The authors declare that they have no conflict of interest.
Data availability statement: The datasets used and/or analyzed during the current study are available from the corresponding author upon reasonable request.

References

[1] Chamkha A, Gorla RSR, Ghodeswar K. Non-similar solution for natural convective boundary layer flow over a sphere embedded in a porous medium saturated with a nanofluid. Transp Porous Med. 2011;86:13–22. 10.1007/s11242-010-9601-0.Search in Google Scholar

[2] Patil PM, Benawadi S. The mixed convection flow of a Williamson nanoliquid over a rotating sphere with the aspects of activation energy. Int J Model Simul. 2024;44:31–43. 10.1080/02286203.2022.2151965.Search in Google Scholar

[3] Singla T, Kumar B, Sharma S. Mixed convective viscous dissipative flow of Casson hybrid nanofluid with variable thermal conductivity at the stagnation zone of a rotating sphere. Can J Chem Eng. 2024. 10.1002/cjce.25352.Search in Google Scholar

[4] Ahmad H, Alnahdi AS, Bilal M, Albalwi MD, Faqihi AA. Energy and mass transmission through hybrid nanofluid flow passing over a spinning sphere with magnetic effect and heat source/sink. Nanotechnol Rev. 2024;13. 10.1515/ntrev-2023-0194.Search in Google Scholar

[5] Kenea G, Ibrahim W. Nonlinear convection stagnation point flow of Oldroyd-B nanofluid with non-Fourier heat and non-Fick’s mass flux over a spinning sphere. Sci Rep. 2024;14:841. 10.1038/s41598-024-51475-z.Search in Google Scholar PubMed PubMed Central

[6] Nimmy P, Obalalu AM, Nagaraja KV, Madhukesh JK, Khan U, Ishak A, et al. Thermal scrutinization of time-dependent flow of nanoparticles over a rotating sphere with autocatalytic chemical reaction. Eur Phys J Plus. 2024;139:291. 10.1140/epjp/s13360-024-05081-7.Search in Google Scholar

[7] Chamkha AJ, Rashad AM. Unsteady heat and mass transfer by MHD mixed convection flow from a rotating vertical cone with chemical reaction and Soret and Dufour effects. Can J Chem Eng. 2014;92:758–67. 10.1002/cjce.21894.Search in Google Scholar

[8] Srilatha P, Madhu J, Khan U, Kumar RN, Gowda RP, Ahmed SB, et al. Heat transfer analysis in magnetohydrodynamic nanofluid flow induced by a rotating rough disk with non-Fourier heat flux: aspects of modified Maxwell–Bruggeman and Krieger–Dougherty models. Nanoscale Adv. 2023;5:5941–51. 10.1039/D3NA00711A.Search in Google Scholar

[9] Madhu J, Baili J, Kumar RN, Prasannakumara BC, Gowda RJP. Multilayer neural networks for studying three-dimensional flow of non-Newtonian fluid flow with the impact of magnetic dipole and gyrotactic microorganisms. Phys Scr. 2023;98:115228. 10.1088/1402-4896/acfe5e.Search in Google Scholar

[10] Sharma G, Hanumagowda BN, Varma SVK, Kumar RN, Alqahtani AS, Malik MY. Impact of magnetic field and nonlinear radiation on the flow of Brinkmann-type chemically reactive hybrid nanofluid: a numerical study. J Therm Anal Calorim. 2024;149:745–59. 10.1007/s10973-023-12720-1.Search in Google Scholar

[11] Manjunatha N, Yellamma, Sumithra R, Verma A, Gowda RP, Madhu J. The impact of the heat source/sink on triple component magneto-convection in superposed porous and fluid system. Mod Phys Lett B. 2024;38:2450020. 10.1142/S0217984924500209.Search in Google Scholar

[12] Gherieb S, Kezzar M, Ayub A, Sari MR, Khan U, Muhammad T, et al. Insight into the dynamics of slip and radiative effect on magnetohydrodynamic flow of hybrid ferroparticles over a porous deformable sheet. ZAMM – J Appl Math Mech/Z Für Angew Math Und Mech. 2024;104:e202300729. 10.1002/zamm.202300729.Search in Google Scholar

[13] Krishna MV, Swarnalathamma BV, Chamkha AJ. Investigations of Soret, Joule and Hall effects on MHD rotating mixed convective flow past an infinite vertical porous plate. J Ocean Eng Sci. 2019;4:263–75. 10.1016/j.joes.2019.05.002.Search in Google Scholar

[14] Kumar B, Seth GS, Nandkeolyar R, Chamkha AJ. Outlining the impact of induced magnetic field and thermal radiation on magneto-convection flow of dissipative fluid. Int J Therm Sci. 2019;146:106101. 10.1016/j.ijthermalsci.2019.106101.Search in Google Scholar

[15] Manjunatha S, Kuttan BA, Jayanthi S, Chamkha A, Gireesha BJ. Heat transfer enhancement in the boundary layer flow of hybrid nanofluids due to variable viscosity and natural convection. Heliyon. 2019;5:e01469. 10.1016/j.heliyon.2019.e01469.Search in Google Scholar PubMed PubMed Central

[16] Khan U, Zaib A, Ishak A, Sherif E-SM, Wróblewski P. Unsteady slip flow of special second-grade fluid induced by Fe3O4 particles past a movable sheet with magnetic and nonlinear heat source/sink. Int J Numer Methods Heat Fluid Flow. 2024;34:2321–44. 10.1108/HFF-01-2024-0030.Search in Google Scholar

[17] Alharbi LF, Khan U, Zaib A, Ishak A. Analyzing the impact of thermophoresis particle deposition and magnetohydrodynamic cross-flow of Williamson hybrid nanofluids across a permeable deformable surface. ZAMM – J Appl Math Mech/Z Für Angew Math Und Mech. 2024;104:e202300947. 10.1002/zamm.202300947.Search in Google Scholar

[18] Algehyne EA, Abdelmohsen SAM, Gowda RJP, Kumar RN, Abdelbacki AMM, Gorji MR, et al. Mathematical modeling of magnetic dipole effect on convective heat transfer in Maxwell nanofluid flow: single and multi-walled carbon nanotubes. Waves Random Complex Media. 2023;33:489–504. 10.1080/17455030.2022.2125598.Search in Google Scholar

[19] Yahaya RI, Mustafa MS, Arifin NM, Pop I, Wahid NS, Ali FM, et al. Mixed convection hybrid nanofluid flow over a stationary permeable vertical cone with thermal radiation and convective boundary condition. ZAMM – J Appl Math Mech/Z Für Angew Math Und Mech. 2024;104:e202300428. 10.1002/zamm.202300428.Search in Google Scholar

[20] Francis P, Sambath P, Fernandez-Gamiz U, Noeiaghdam S, Dinarvand S. Computational analysis of bio-convective Eyring-Powell nanofluid flow with magneto-hydrodynamic effects over an isothermal cone surface with convective boundary condition. Heliyon. 2024;10:e25088. 10.1016/j.heliyon.2024.e25088.Search in Google Scholar PubMed PubMed Central

[21] Hussain Z, Aljuaydi F, Ayaz M, Islam S. Enhancing thermal efficiency in MHD kerosene oil-based ternary hybrid nanofluid flow over a stretching sheet with convective boundary conditions. Results Eng. 2024;22:102151. 10.1016/j.rineng.2024.102151.Search in Google Scholar

[22] Akbar NS, Zamir T, Akram J, Noor T, Muhammad T. Simulation of hybrid boiling nano fluid flow with convective boundary conditions through a porous stretching sheet through Levenberg Marquardt artificial neural networks approach. Int J Heat Mass Transf. 2024;228:125615. 10.1016/j.ijheatmasstransfer.2024.125615.Search in Google Scholar

[23] Chu Y-M, Nazir U, Sohail M, Selim M, Lee J-R. Enhancement in thermal energy and solute particles using hybrid nanoparticles by engaging activation energy and chemical reaction over a parabolic surface via finite element approach. Fractal Fract. 2021;5:119. 10.3390/fractalfract5030119.Search in Google Scholar

[24] Madhukesh JK, Prasannakumara BC, Shehzad SA, Anwar MI, Nasir S. Endothermic and exothermic chemical reactions’ influences on a nanofluid flow across a permeable microchannel with a porous medium. Int J Ambient Energy. 2024;45:2325515. 10.1080/01430750.2024.2325515.Search in Google Scholar

[25] Singh V, Naduvinamani NB, Vinutha K, Prasannakumara BC, Madhukesh JK, Abdulrahman A. Sodium alginate-based MHD ternary nanofluid flow across a cone and wedge with exothermic/endothermic chemical reactions: A numerical study. Numer Heat Transfer, Part A: Appl. 2024;1–20. 10.1080/10407782.2024.2355520.Search in Google Scholar

[26] Elattar S, Khan U, Zaib A, Ishak A, Saleh W, Abed AM. Scrutinization of waste discharge concentrations in Eyring-Powell nanofluid past a deformable horizontal plane surface. Water. 2023;15:3419. 10.3390/w15193419.Search in Google Scholar

[27] Yaseen M, Rawat SK, Khan U, Sarris IE, Khan H, Negi AS, et al. Computational analysis of heat and mass transfer flow of wall jet hybrid nanofluid with irregular heat source/sink effects and waste discharge concentration. J Magn Magn Mater. 2023;588:171434. 10.1016/j.jmmm.2023.171434.Search in Google Scholar

[28] Ramesh GK, Madhukesh JK, Aly EH, Gireesha BJ. Endothermic and exothermic chemical reaction on MHD ternary (Fe2O4–TiO2–Ag/H2O) nanofluid flow over a variable thickness surface. J Therm Anal Calorim. 2024;149:6503–15. 10.1007/s10973-024-13013-x.Search in Google Scholar

[29] Xin X, Ganie AH, Alwuthaynani M, Bonyah E, El-Wahed Khalifa HA, Fathima D, et al. Parametric analysis of pollutant discharge concentration in non-Newtonian nanofluid flow across a permeable Riga sheet with thermal radiation. AIP Adv. 2024;14:045018. 10.1063/5.0200401.Search in Google Scholar

[30] Chamkha AJ, Rashad AM. Natural convection from a vertical permeable cone in a nanofluid saturated porous media for uniform heat and nanoparticles volume fraction fluxes. Int J Numer Methods Heat Fluid Flow. 2012;22:1073–85. 10.1108/09615531211271871.Search in Google Scholar

[31] Madhu M, Kishan N, Chamkha AJ. Unsteady flow of a Maxwell nanofluid over a stretching surface in the presence of magnetohydrodynamic and thermal radiation effects. Propuls Power Res. 2017;6:31–40. 10.1016/j.jppr.2017.01.002.Search in Google Scholar

[32] Krishna MV, Chamkha AJ. Hall and ion slip effects on unsteady MHD convective rotating flow of nanofluids – Application in biomedical engineering. J Egypt Math Soc. 2020;28:1. 10.1186/s42787-019-0065-2.Search in Google Scholar

[33] Sohail M, Alrabaiah H, Nazir U. Radiative flow of MHD non-Newtonian fluid by utilizing the updated version of heat flux model under Joule heating. Heat Transf. 2021;50:3407–25. 10.1002/htj.22034.Search in Google Scholar

[34] Liu J, Nazir U, Sohail M, Mukdasai K, Singh A, Alanazi M, et al. Numerical investigation of thermal enhancement using MoS2–Ag/C2H6O2 in Prandtl fluid with Soret and Dufour effects across a vertical sheet. AIP Adv. 2023;13:075112. 10.1063/5.0152262.Search in Google Scholar

[35] Madhu J, Madhukesh JK, Sarris I, Prasannakumara BC, Ramesh GK, Shah NA, et al. Influence of quadratic thermal radiation and activation energy impacts over oblique stagnation point hybrid nanofluid flow across a cylinder. Case Stud Therm Eng. 2024;60:104624. 10.1016/j.csite.2024.104624.Search in Google Scholar

[36] Nimmy P, Kumar RN, Madhukesh JK, Khan U, Ishak A, Nagaraja KV, et al. The significance of quadratic thermal radiative scrutinization of a nanofluid flow across a microchannel with thermophoretic particle deposition effects. Nanotechnol Rev. 2024;13. 10.1515/ntrev-2024-0045.Search in Google Scholar

[37] Takhar HS, Chamkha AJ, Nath G. Combined heat and mass transfer along a vertical moving cylinder with a free stream. Heat Mass Transf. 2000;36:237–46. 10.1007/s002310050391.Search in Google Scholar

[38] Sohail M, Abbas ST. Utilization of variable thermal conductivity and diffusion coefficient on non-Newtonian Prandtl model with modified heat and mass fluxes. Multidiscip Model Mater Struct. 2024;20:317–40. 10.1108/MMMS-10-2023-0328.Search in Google Scholar

[39] Bai D, Muhammad N, Shah NA, Ali B, Raju CSK, Wakif A, et al. OpenFOAM simulation of turbulent flow in a complex dam structure. Indian J Phys. 2024;98:3277–86. 10.1007/s12648-024-03085-8.Search in Google Scholar

[40] Madhukesh JK, Sahar F, Prasannakumara BC, Shehzad SA. Waste discharge concentration and quadratic thermal radiation influences on time-dependent nanofluid flow over a porous rotating sphere. Numer Heat Transfer, Part B: Fundam. 2024;1–19. 10.1080/10407790.2024.2336205.Search in Google Scholar

[41] Karthik K, Srilatha P, Madhukesh JK, Khan U, Prasannakumara BC, Kumar R, et al. Computational examination of heat and mass transfer of nanofluid flow across an inclined cylinder with endothermic/exothermic chemical reaction. Case Stud Therm Eng. 2024;57:104336. 10.1016/j.csite.2024.104336.Search in Google Scholar

[42] Ramesh GK, Madhukesh JK, Ali Shah N, Yook S-J. Flow of hybrid CNTs past a rotating sphere subjected to thermal radiation and thermophoretic particle deposition. Alex Eng J. 2023;64:969–79. 10.1016/j.aej.2022.09.026.Search in Google Scholar

[43] Devi SPA, Devi SSU. Numerical investigation of hydromagnetic hybrid Cu – Al2O3/water nanofluid flow over a permeable stretching sheet with suction. Int J Nonlinear Sci Numer Simul. 2016;17:249–57. 10.1515/ijnsns-2016-0037.Search in Google Scholar

[44] Waini I, Khan U, Zaib A, Ishak A, Pop I. Inspection of TiO2-CoFe2O4 nanoparticles on MHD flow toward a shrinking cylinder with radiative heat transfer. J Mol Liq. 2022;361:119615. 10.1016/j.molliq.2022.119615.Search in Google Scholar

[45] Malvandi A. The unsteady flow of a nanofluid in the stagnation point region of a time-dependent rotating sphere. Therm Sci. 2015;19:1603–12. 10.2298/TSCI121020079M.Search in Google Scholar

Received: 2024-01-30

Revised: 2024-07-02

Accepted: 2024-07-16

Published Online: 2024-08-06

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

https://doi.org/10.1515/arh-2024-0012

Keywords for this article

rotating sphere; magnetic field; endothermic–exothermic chemical reactions; pollutant concentration; nanofluid

Creative Commons

BY 4.0