Home A method for the use of ellipticities and spot diameters for the measurement of aberrations in wide-field telescopes
Article
Licensed
Unlicensed Requires Authentication

A method for the use of ellipticities and spot diameters for the measurement of aberrations in wide-field telescopes

  • Lothar Noethe EMAIL logo , Pietro Schipani , Ronald Holzlöhner and Andrew Rakich
Published/Copyright: June 7, 2014
Become an author with De Gruyter Brill
Author Information
Advanced Optical Technologies
From the journal Advanced Optical Technologies Volume 3 Issue 3

Abstract

In wide-field survey telescopes, the patterns of spot sizes and ellipticities can be used to determine wavefront aberrations generated by the telescope. The calculation of spot sizes and ellipticities generated by telescope aberrations is most conveniently done if the aberrations are expressed in terms of Zernike-type polynomials whose derivatives are orthonormal. The field dependence of the spot sizes and ellipticities generated by the telescope can conveniently be expressed by low-order Zernike polynomials. Because the exposure times in astronomical survey work are typically rather short, this information may be used for a quasi-closed loop control of the telescope optics. The ability to accurately subtract ellipticities generated by telescope errors could also be useful for observations such as gravitational lensing surveys.

Keywords: active optics; ellipticities; telescope aberrations; wide-field telescopes.
Corresponding author: Lothar Noethe, ESO, Karl-Schwarzschild Strasse 2, Garching 85748, Germany, e-mail:

7 Appendix

7.1 Notations used for Zernike polynomials Zm, j and slope Zernike polynomials Sm, j

Table 4

Correspondence between indices m, j, the Noll notation and commonly used names for Zernike polynomials.

mjNoll notationName
01Z1Piston
02Z4Defocus
03Z11Spherical aberration
11Z2, Z3Tilt
22Z7, Z8Third-order coma
33Z16, Z17Fifth-order coma
21Z5, Z6Third-order astigmatism
22Z12, Z13Fifth-order astigmatism
31Z9, Z10Trefoil

7.2 Relationships between normalized and non-normalized Zernike and slope Zernike polynomials

If modified radial components Rm,j(r) and Bm,j(r) are defined by:

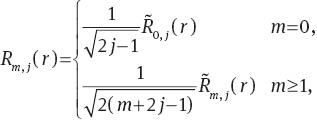
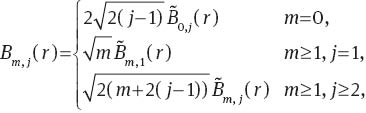
(62)Rm, j(r)={12j−1 R˜0, j(r)m=0,12(m+2j−1) R˜m, j(r)m≥1, (62)
(63)Bm, j(r)={22(j−1) B˜0,j(r)m=0,m B˜m, 1(r)m≥1, j=1,2(m+2(j−1)) B˜m, j(r)m≥1, j≥2, (63)

the relationships between Zernike and slope Zernike polynomials are given by:

(64)Rm, j(r)=∑i=1j Bm, i (64)
(65)Bm, j(r)=Rm, j(r)−Rm, j−1(r). (65)

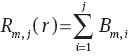
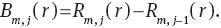
With n=m+2(j–1), the functions Rm,j(r) and Bm,j(r) are identical to the functions Rnm(r) and Bmn(r) in [11].

7.3 Expression of the derivatives of slope Zernike polynomials in terms of Zernike polynomials

The derivative of a slope Zernike polynomial Sm,j,a(r, φ) with respect to x and y can be expressed as a single Zernike polynomial Z1,j,a(r, φ) for m=0 or as a sum of two Zernike polynomials Zm,j,b(r, φ) and Zm+1,j-1,b(r, φ) for m>0, with a, b∈{c, s}.

(66)∂∂xS0, j(r)=+a0, jZ1, j−1, c(r, φ), (66)
(67)∂∂yS0, j(r)=+a0, jZ1, j−1, s(r, φ) (67)
(68)∂∂xSm, j, c(r, φ)=+am, jZm+1, j−1, c(r, φ)+bm, jZm−1, j, c(r, φ), (68)
(69)∂∂ySm, j, c(r, φ)=+am, jZm+1, j−1, s(r, φ)−bm, jZm−1, j, s(r, φ), (69)
(70)∂∂xSm, j, s(r, φ)=+am, jZm+1, j−1, s(r, φ)+bm, jZm−1, j, s(r, φ), (70)
(71)∂∂ySm, j, s(r, φ)=−am, jZm+1, j−1, c(r, φ)+bm, jZm−1, j, c(r, φ). (71)

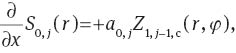
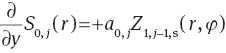
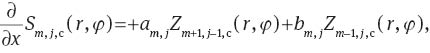
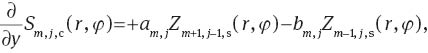
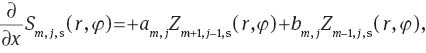
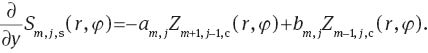
The values for the coefficients am,j and bm,j are shown in Table 5.

Table 5

Coefficients used in Eqs. (66) to (71).

mc, sj∂/∂x, ∂/∂yam,jbm,j
0c, s>1∂/∂x, ∂/∂y1/20
1c1∂/∂x01
1∂/∂y00
>1∂/∂x1/21/2
>1∂/∂x1/20
1s1∂/∂x00
1∂/∂y01
>1∂/∂x1/20
>1∂/∂y1/21/2
>1c, s1∂/∂x, ∂/∂y01/2
>1∂/∂x, ∂/∂y1/21/2

7.4 Examples of ellipticity patterns due to telescope aberrations

7.4.1 Linear astigmatism and defocus due to tilt of focal plane

A linear astigmatism that is symmetric to the x-axis and a linear defocus generated by a tilt of the focal plane around the y-axis are described by:

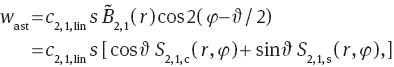
(72)wast=c2, 1, lin s B˜2, 1(r) cos2(φ−ϑ/2)=c2, 1, lin s [cosϑ S2, 1, c(r, φ)+ sinϑ S2, 1, s(r, φ),] (72)

and by Eq. (29) with ϑ0,2=0, respectively. Similarly to Section 4.7 one obtains the following expressions:

(73)ϵ=2rp2 c0, 2, lin c2, 1, lin s2 cosϑ, (73)
(74)α=ϑ2, (74)
(75)ϵx=1rp2 c0, 2, lin c2, 1, lin s2 (1+cos2ϑ), (75)
(76)ϵy=1rp2 c0, 2, lin c2, 1, lin s2 sin2ϑ. (76)

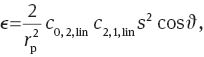
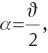
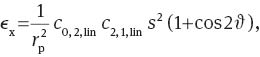
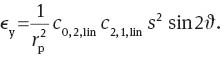
Because the dependence on the radial field variable s is proportional to s2, the field dependencies can be expressed in terms of Zernike polynomials Z0,1,c(s), Z0,2,c(s) and Z2, 1, c(s, ϑ) for ϵx and Z2,1,s(s, ϑ) for ϵy.

7.4.2 Linear astigmatism and nominal defocus

A linear astigmatism that is symmetric to the x-axis is described in Eq. (72) and a rotationally symmetric nominal defocus by:

(77)w0, 2(s, ϑ, r)=F0, 2(s) S0, 2(r). (77)

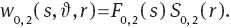
Then,

(78)ϵ=2rp2 c2, 1, lin s F0, 2(s), (78)
(79)α=ϑ2, (79)
(80)ϵx=1rp2 c2, 1, lin s F0, 2(s) cosϑ, (80)
(81)ϵy=1rp2 c2, 1, lin s F0, 2(s) sinϑ. (81)

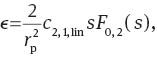
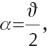
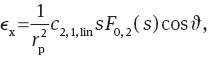
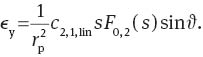
The dependencies of the expressions on the field radius s can be expressed as polynomials with odd powers of s. Therefore, the field dependencies of the x- and y-components of ϵ→ contain the Zernike polynomials Z1,j(s, ϑ) with j≥1.

7.4.3 Trefoil and coma

In the VST, nominal trefoil is negligible. However, the coefficient c3,1,c of field-constant S3,1,c(r, φ) in the VST may be of the order of 300 nm. Together with nominal third-order coma S1,2(r, φ), it may generate ellipticities of the order of 8ϵWL with the field dependencies:

(82)ϵ=2rp2 c3, 1, c F1, 2(s), (82)
(83)α=ϑ2, (83)
(84)ϵx=2rp2 c3, 1, c F1, 2(s) cosϑ, (84)
(85)ϵy=2rp2 c3, 1, c F1, 2(s) sinϑ. (85)

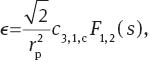
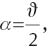
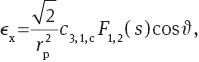
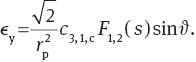
Because F1,2(s) is a polynomial in s with only odd powers, ϵx can be expressed by Zernike polynomials Z1,j,c(s, ϑ) and ϵy by Zernike polynomials Z1,j,s(s, ϑ).

References

[1] M. Liang, V. Krabbendam, C. F. Claver, S. Chandrasekharan and B. Xin, Proc. SPIE 8444, Q8444Q-1-13 (2012).Search in Google Scholar

[2] M. Jarvis and B. Jain, arXiv:astro-ph/0412234 (2004).Search in Google Scholar

[3] M. Jarvis, P. Schechter and B. Jain, arXiv:astro-ph/0810.0027 (2008).Search in Google Scholar

[4] Z. Ma, G. Bernstein, A. Weinstein and M. Sholl, Publ. Astron. Soc. Pac., 120, 1307–1317 (2008).Search in Google Scholar

[5] L. B. Moore, A. M. Hvisc and J. Sasian, Opt. Exp. 20, 15655–15670 (2008).Search in Google Scholar

[6] A. Manuel and J. Burge, Proc. SPIE 7433, 7433A (2009).Search in Google Scholar

[7] P. Schechter and R. Levinson, PASP 123, 812 (2011).10.1086/661111Search in Google Scholar

[8] K. Thompson, Adv. Opt. Techn. 2, 89–95 (2013).Search in Google Scholar

[9] C. A. Laury-Micoulout, A&A 51, 343 (1976).10.1007/BF02568162Search in Google Scholar

[10] W. Lukosz, Opt. Acta 10, 1–19 (1963).Search in Google Scholar

[11] J. Braat, J. Opt. Soc. Am. 4, 643–650 (1987).Search in Google Scholar

[12] I. W. Kwee and J. J. M. Braat, Pure Appl. Opt. 2, 21–32 (1993).Search in Google Scholar

[13] P. Schipani, M. Capaccioli, C. Arcidiacono, J. Argomedo, M. Dall’Ora, et al., Proc. SPIE 8444, 84441C (2012).Search in Google Scholar

[14] L. Noethe, Prog. Opt. 43, 1–69 (2002).Search in Google Scholar

[15] P. Schipani, L. Noethe, C. Arcidiacono, J. Argomedo, M. Dall’Ora, et al., J. Opt. Soc. Am. A29, 1359 (2012).10.1364/JOSAA.29.001359Search in Google Scholar PubMed

Received: 2014-3-21
Accepted: 2014-5-9
Published Online: 2014-6-7
Published in Print: 2014-6-1

©2014 THOSS Media & De Gruyter Berlin/Boston

Articles in the same Issue

  1. Frontmatter
  2. Community
  3. News from the European Optical Society
  4. Conference Notes
  5. Conference Calendar
  6. Topical Issue: Optics for Astronomy / Guest Editors: Jan Burke, Andrew Rakich and Jim Burge
  7. Editorial
  8. Optics for astronomy – Editorial
  9. Review Articles
  10. Active optics with a minimum number of actuators
  11. Highly sensitive telescope designs for higher contrast observations
  12. Replicated spectrographs in astronomy
  13. Ultra-smooth finishing of aspheric surfaces using CAST technology
  14. Hydroxide catalysis bonding for astronomical instruments
  15. Research Articles
  16. Fabrication and metrology of lithium niobate narrowband optical filters for the solar orbiter
  17. A method for the use of ellipticities and spot diameters for the measurement of aberrations in wide-field telescopes
  18. Deflectometric measurement of large mirrors
  19. The Four-Laser Guide Star Facility: Design considerations and system implementation
https://doi.org/10.1515/aot-2014-0024
Keywords for this article
active optics; ellipticities; telescope aberrations; wide-field telescopes.

Articles in the same Issue

  1. Frontmatter
  2. Community
  3. News from the European Optical Society
  4. Conference Notes
  5. Conference Calendar
  6. Topical Issue: Optics for Astronomy / Guest Editors: Jan Burke, Andrew Rakich and Jim Burge
  7. Editorial
  8. Optics for astronomy – Editorial
  9. Review Articles
  10. Active optics with a minimum number of actuators
  11. Highly sensitive telescope designs for higher contrast observations
  12. Replicated spectrographs in astronomy
  13. Ultra-smooth finishing of aspheric surfaces using CAST technology
  14. Hydroxide catalysis bonding for astronomical instruments
  15. Research Articles
  16. Fabrication and metrology of lithium niobate narrowband optical filters for the solar orbiter
  17. A method for the use of ellipticities and spot diameters for the measurement of aberrations in wide-field telescopes
  18. Deflectometric measurement of large mirrors
  19. The Four-Laser Guide Star Facility: Design considerations and system implementation
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 15.11.2025 from https://www.degruyterbrill.com/document/doi/10.1515/aot-2014-0024/html
Scroll to top button