Abstract
Taking the special nonlinear characteristics of the domestic and international gold price into account, this paper systematically analyzed its nonlinearity by the methods of BDS test, R/S analysis and improved largest Lyapunov exponent. We find three main results: (1) ARMA-GARCH model could adequately explain the linear and nonlinear dependence of gold price series; (2) long-memory does not exist anymore in price series explained by ARMA-GARCH model; (3) chaos phenomenon which is sensitive to the initial value does not exist either in the residuals of regression model. Therefore, we believe that the nonlinearity of gold price is mainly characterized in conditional heteroscedasticity rather than chaos.
1 Introduction
With the fluctuations of the global economy and the depression of expectation in recent years, the international price of gold reached one after another peak. As a symbol of the precious metal prices, the nonlinear characteristics of the changes of the prices of gold reflect the characteristics of the changes of the macroeconomic. Whether the nonlinearity of the gold price is chaotic or not affects the judgment of the characteristics of the macroeconomic. Many scholars have found nonlinear features in commercial price such as conditional heteroscedasticity. But it is hard to observe directly whether there is chaos behind the superficial price fluctuation.
The characteristic of the nonlinearity of the price of gold is essential. If the nonlinear fluctuation shows only in conditional heteroscedasticity, it is safe and proper to follow the EMH framework to analyze the macroeconomic and the financial market, and it is still reasonable to hold the points that the yield follows a martingale process and the prices of the assets can be predicted. But if the nonlinearity of the price is chaos, suggesting that it is a deterministic low-dimension dynamic system, the randomness of asset prices then comes from their sensitivity to the initial state mostly rather than the turbulence outside. The abnormal yield produced by a chaotic dynamic system happens to explain the extremely negative yield of the capital market, such as the stock disaster in 1987, the so-called “six sigma event”. If it is really chaotic, the supervisor should change the methods they use to regulate the market.
The common tests for randomness cannot distinguish the chaos in the financial time series data with so much noise. The most effective way nowadays for testing chaos phenomenon are the followings: BDS test, R/S test and the largest Lyapunov test. The three methods are not contradictory, they are testing the chaos phenomenon from different perspectives, that is, nonlinear dependence, long memory and sensitivity of initial conditions. Firstly, BDS test is a nonparametric test designed to test if there is nonlinear dependence, whose result is sensitive to the choice of embedding dimension and proximity parameters. Secondly, R/S test is capable of testing the long-term memory in the data, judging whether the reverting phenomenon is negative or positive and finding the average period of the data. Thirdly, largest Lyapunov exponent describes the sensitivity of the motion to its initial conditions quantitatively and reflecting its chaotic characteristic.
Most of the methods testing chaos have some relationship with correlation integral. Grassberger and Pocaccia[5] proposed the correlation integral and correlation dimension test to test the dimension of a chaotic system. Since the existence of nonlinear dependence is a prerequisite of the existence of chaos, Brock, Dechert and Scheinkman proposed the BDS test based on the correlation integral to test the nonlinear dependence of financial series data. Similarly, with a basis of the correlation integral, Kim et al.[7] proposed CC phase space reconstruction algorithm, which, relying on Takens’ theorem, is the basis for calculating Lyapunov exponents. The largest Lyapunov exponent gives a chaotic system a quantitative description on its sensitivity to the initial state of the system. Aimed at the largest Lyapunov exponent, Rostentein et al.[12] proposed the small-amount-data algorithm that is not only simple and direct but also more accurate than the previous algorithms.
Frank and Stengos[4] estimated the correlation dimensions and Kolmogorov entropy of gold and silver spot prices, finding chaotic characteristics. DeCoster et al.[3] calculated the correlation dimensions of the futures of sugar, silver, copper and coffee, in which evidence for the existence of chaos had been found. By calculating correlation integral and carrying out BDS test, Yang and Brorsen[15] analyzed prices of several future products and pointed out that chaos existed in prices of commodity futures. Arjun et al. (2001), however, found nonlinear dependence instead of chaos existed in series by calculating correlation integral and Kolmogorov entropy and testing residuals of ARMA-GARCH model. Also, Andres et al. (2002) discovered through BDS and Kaplan tests that nonlinear characteristics existed in foreign exchange rates series. Wang et al.[13] calculated the correlation dimensions d of Shanghai Composite Index using G-P algorithm, and Lyapunov exponent using Wolf method and reached a conclusion that chaos existed in Chinese stock market.
By reviewing the recent literatures, we found that direct test of nonlinearity without delinearizing series, i.e. filtering the series by ARMA model, would lead to a conclusion that chaos existed in series. The reason for the conclusion is that current BDS and R/S analytical method both rejected i.i.d.[1] assumption in testing linear, nonlinear and chaos characteristics. Besides, the adoption of low order ARCH model[2] in filtering the nonlinear characteristics of series frequently leads to wrong conclusion that chaos exists in series. So far there is no widely accepted conclusion on whether nonlinear characteristics of financial time series are results of low dimension chaos or conditional heteroscedasticity. Considering the robustness of the empirical results and the principle of “test test and test”, we determinate the nonlinear characteristics of gold price series by carrying out BDS test and R/S analysis and calculating largest Lyapunov exponent respectively in these papers.
2 BDS tests of gold prices in home and abroad
BDS test is usually used to detect nonlinear dependence structure of series, popular among researches because of its non-substitutability. Our BDS test idea is as follows:
Pre-process data by converting price series {XN} to log return series {RN–1}, carry out descriptive statistical analysis and test whether the series are weak stationary by ADF unit root tests.
Test the hypothesis that return series are i.i.d. by BDS test. The rejection of i.i.d. hypothesis means linear of nonlinear dependence exists in series.
Eliminate the linear dependence of series. We choose BIC information criteria and parameters t-test to choose the proper ARMA model for each series thus to filter the linear structure, followed by BDS test on residuals. The failure of BDS test illustrated nonlinear dependence of series, thus we should consider whether it results from characteristics in various time periods.
Due to the long time span of data collection[3], it is possible that characteristics of series in different time periods cause series’ failure to be i.i.d.. In order to exclude this possibility, we divide return series into two sample intervals of the same length, filter respectively with optimal linear model and carry out BDS tests on their residuals. If test results are significantly different from those of entire population, then the reason why population fails BDS test might be the structural change of population series; if test results are not distinct different, then time-varying variance should be considered as a cause.
Exclude the time-varying variance in series. Xie and Yang[14] standardized series with standard error in current month, paving the way for such a practice. More specifically, we use GARCH model to filter the time-varying variance, and then choose the optimal linear model under BIC information criteria. After excluding the effects of time-varying variance, we conduct BDS test again. If BDS test is passed, we can conclude that ARMA-GARCH model can explain the characteristics of series effectively, and that chaos doesn’t exist in series. Otherwise nonlinear structure such as chaotic systems exists in series, which can not be detected by AMRA-GARCH model.
2.1 BDS test
BDS test is based on a basic idea that, if a series {Xn} is i.i.d., then ∀i ≠ j, ∀ε, ∀m, we have
where ε shows the approaching level (often called approach parameter) of status in the series, m shows the dimension of reconstructed phase space (often called embedding dimension). The equations above are established if and approximately only if time series {Xn} is i.i.d.. Thus by selecting any of the equations as null hypothesis we can test whether {Xn} is i.i.d.. In practice, Brock et al. (1987) calculated correlation integral Cm,n(ε) and Pm acquired, based on which later scholars made much generalization and improvements. In this paper we choose Kanzler’s[6] method, a practical generalization in 1999 based on Brock’s achievements that can be described as follows. First we define indicative function
For finite time series {Xn}, proper proximity parameter ε and embedding dimension m, we define correlation integral revised by Kanzler as follows:
If {Xn} ~ i.i.d., correlation integral Cm,n(ε) approximately equals to [C1,n–m+1(ε)]m and we could use [C1,n–m+1(ε)]m to estimate the mean of Cm,n(ε). After standardizing Cm,n(ε) we could get statistic W:
where
Brock et al.[2] demonstrated that under the assumption of {Xn} ~ i.i.d., the limiting distribution of Wm,n(ε) is standard norm distribution. When
Two important parameters should be set before BDS test: proximity parameter ε and embedding dimension m (see Table 1 for a summary on parameter choice). In theory, we need only to satisfy 0 < ε < max(Xn) – min(Xn) to choose proximity parameter ε. However, Kočendal[8] pointed out that the result of BDS test is quite sensitive to the choice of ε, and during practice we also found that as long as slight difference exists in proximity parameter, the calculated correlation integral varies greatly and thus causes the result of BDS test to be entirely different. In actual testing practice, it often occurs that the results contradict each other under different proximity parameter ε. Improper proximity parameter could incorrectly measure the closeness between data, which is the same as using a too-long or too-short ruler to measure the length of an object, causing relatively large errors.
A summary on worldwide scholar’s choice of proximity parameter
| Year | Scholar Name | ε (multiple of series standard error σ) |
|---|---|---|
| 1992 | Rothman | 0.50, 1.00, 1.25, 1.50, 2.00 |
| 1993 | Kugler and Lenz | 1 |
| 1993 | Hsieh | 0.50, 1.00, 1.50, 2.00 |
| 1993 | Brock, Hsieh, and LeBaron | 0.50, 0.75, 1.00, 1.25, 1.50 |
| 1996 | Cecen and Erkal | 0.5 |
| 1996 | de Lima | 1.00, 1.25 |
| 1996 | Chappell, Padmore, and Ellis | 0.40, 0.625, 1.00, 1.60 |
| 1997 | Serletis and Gogas | 0.50, 1.00, 1.50, 2.00 |
| 2000 | Brooks and Henry | 1.00, 1.50 |
| 2000 | Aguirre and Aguirre | 0.65, 0.70, 0.75, 0.80, 0.85, 0.90 |
| 2002 | Chen and Kuan | 0.75, 1.00 |
| 2003 | Panagiotidis | 0.50, 1.00, 2.00 |
| 2004 | Kočenda and Briatka | 0.6 to 1.9 |
Through empirical study, Kanzler discovered that under the condition of smaller embedding dimensions m, BDS statistic Wm,n(ε*) is optimal if we choose proximity parameter ε which makes single dimension correlation integral C1,n(ε) near 0.7. The algorithm’s complexity in time and space is rather high and, as Jorge et al. (2002) mentioned, computer capacity in the past could hardly satisfy its requirement. However, with the significant improvement of computer performance and algorithm, optimizing proximity parameter ε becomes feasible and easy. In this paper we adopt Kanzler’s method, for each embedding dimension m, choose an optimal proximity parameter ε on conditions that single dimension correlation integral C1,n(ε) is fixed to 0.7, and thus obtain the optimal BDS statistic Wm,n(ε*). In terms of choosing the embedding dimension, Brock et al.[2] suggested that, on the premise of ensuring
2.2 Data sample selection
During the century before the end of The Bretton Woods System, gold underlies the currencies of the world. It makes little sense to study the ‘fixed’ gold price. In 1997 America ended the convertibility of gold into US dollars, terminating the gold standard that had lasted for more than a century. Since then, gold has faded from the currency scene and evolved into a commodity with price attribute. London Gold Market and COMEX, with their long history, have been the largest spots and futures market, and therefore data from the two exchanges are representative. We choose daily London Gold Fixing in London Gold Market and closing price of dominant futures of gold in COMEX from 2nd Jan. 1975 to 19th Apr. 2011[4]. For domestic data, we choose daily closing price of spot Gold AU9995 in Shanghai Gold Exchange from 31st Oct. 2002 to 20th Apr. 2011[5]. After the founding of New China, the purchasing, marketing and pricing of gold has been monopolized. The trading price of gold hasn’t come out until the opening of Shanghai Gold Exchange in Oct. 2002. Gold AU9995 indicates gold with purity above 99.95%. Its spot trading has been active, and it has been the settlement for gold futures in major future exchanges home and abroad. Consider that Chinese future market of gold wasn’t formally formed until 2008, the data volume is limited, and thus we don’t use domestic gold future data.
In this paper we converted gold prices of London spot, COMEX futures and Shanghai futures into logarithmic return series, conducting unit root test and obtained the stationary, descriptive statistics and unit-root test results of series (see Table 2 and Table 3).
Descriptive statistics and normality test
| Mean | SD | Skewness | Kurtosis | JB statistic | P-value | |
|---|---|---|---|---|---|---|
| London spot price | 0.0002 | 0.0126 | 0.0027 | 14.17 | 47693.79 | 0.0000 |
| COMEX future price | 0.0002 | 0.0126 | 0.0084 | 10.07 | 18845.71 | 0.0000 |
| Shanghai spot price | 0.00065 | 0.0113 | –0.2563 | 9.221 | 3369.85 | 0.0000 |
Unit root test
| ADF test | Philips-Perron test | |||
|---|---|---|---|---|
| T statistic | P value | Adjusted t statistic | P value | |
| London spot price | –14.93347 | 0.0000 | –100.0707 | 0.0001 |
| COMEX future price | –15.30907 | 0.0000 | –96.68592 | 0.0001 |
| Shanghai spot price | –31.0917 | 0.0000 | –47.94408 | 0.0001 |
2.3 Results of BDS tests
2.3.1 BDS test of the original series
In order to test the existence of dependence in original series, we first carry out BDS test on original return series. Here we choose the proximity parameter ε* which makes the single dimensional correlation integral C1,n(ε) approximate 0.7, and we choose the embedding dimension m between 2 to 10. BDS test results of original series are in Table 4. As the table shows, test results in all embedding dimensions reject in 1% significance level the hypothesis that original return series is i.i.d., but we cannot decide the existence of nonlinear dependence in the series.
BDS test of original series
| m | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| London spot price | 25.8 | 32.3 | 37.4 | 42.1 | 47.1 | 52.2 | 58.1 | 64.7 | 72.5 |
| COMEX future price | 22.9 | 28.2 | 31.9 | 35.2 | 38.8 | 42.9 | 47.6 | 52.8 | 59.0 |
| Shanghai spot price | 9.32 | 12.1 | 14.1 | 15.8 | 17.4 | 19.1 | 21.2 | 23.5 | 25.9 |
Note: All test results rejected the null hypothesis of i.i.d..
2.3.2 BDS test after linear model filtration
Based on the results that hypothesis of i.i.d. are all rejected in original series, we choose the optimal ARMA model under BIC information criteria and t-test of auto-regression parameters to filter and eliminate the linear dependence of return series, and then test the residuals of ARMA model to decide whether nonlinear dependence existed in series. For London spot return series we choose ARMA(3,3) as linear model, for COMEX future return ARMA(3,3), and for Shanghai spot return MA(2)(see Table 5 for detailed results). After eliminating the linear dependence with optimal linear model, we test the residuals of the three return series respectively (see Table 6 for test results).
Parameters in ARMA-GARCH model of London gold spots
| Mean Equation | Variance Equation | ||
|---|---|---|---|
| c | 1.50 × 10–5 (0.175055) | ω | 7.13 × 10–7*** (10.69556) |
| θ1 | –0.031518** (–2.892106) | α1 | 0.083008*** (32.95886) |
| θ2 | 0.017221* (1.657169) | β1 | 0.917649*** (405.1998) |
| θ3 | 0.016047* (1.479584) | ||
| R-squared | 0.002467 | Durbin-Watson stat | 2.026494 |
| Loglikelihood | 29263.06 | Akaike info criterion | –6.378732 |
| F-statistic | 3.777334 | Schwarz criterion | –6.373296 |
BDS statistic for residuals of ARMA model
| m | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| London spot price | 24.9 | 31.5 | 36.6 | 42.2 | 46.1 | 51.1 | 56.7 | 36.1 | 70.5 |
| COMEX future price | 22.6 | 27.8 | 31.5 | 34.7 | 38.1 | 42.0 | 46.6 | 51.7 | 57.7 |
| Shanghai spot price | 9.27 | 11.9 | 13.9 | 15.5 | 17.2 | 18.9 | 20.9 | 32.2 | 25.7 |
Note: All test results rejected the null hypothesis of i.i.d..
The ARMA model residuals of London spot return, COMEX future return and Shanghai spot return all reject the i.i.d. hypothesis in 1% significance level. This indicates that ARMA model cannot effectively explain the dependent characteristic, which is the nonlinear dependence, in gold return series. To further determine whether the cause is the characteristics that vary with different time period, we divide gold return series into two parts of the same length, and filter with proper ARMA model respectively. Here we filter with ARMA model series from London, New York and Shanghai, which add up to 6 subsample intervals, and conduct BDS test on obtained residuals. In view of the short length of Shanghai spot return series, the embedding dimension m were chose between 2 to 6 (see detailed results in Table 7).
BDS tests of ARMA model residuals on subsample intervals
| London spot price | COMEX future price | Shanghai spot price | ||||
|---|---|---|---|---|---|---|
| m | 1975–1993 ARMA(3,3) | 1993–2011 ARMA(3,3) | 1975–1993 ARMA(3,3) | 1993–2011 ARMA(2,2) | 2002–2007 ARMA(4,4) | 2007–2011 ARMA(3,1) |
| 2 | 20.99 | 10.82 | 18.45 | 9.90 | 7.30 | 4.68 |
| 3 | 25.88 | 15.14 | 21.71 | 13.73 | 9.43 | 5.68 |
| 4 | 29.86 | 18.33 | 24.35 | 16.34 | 10.54 | 7.09 |
| 5 | 33.27 | 21.31 | 26.68 | 18.69 | 11.31 | 8.10 |
| 6 | 37.04 | 24.30 | 29.27 | 21.17 | 12.01 | 9.13 |
| 7 | 40.93 | 27.38 | 32.17 | 23.95 | ||
| 8 | 45.38 | 30.78 | 35.51 | 26.99 | ||
| 9 | 50.30 | 34.53 | 39.11 | 30.36 | ||
| 10 | 56.00 | 39.09 | 43.48 | 34.18 | ||
Note: All test results rejected the null hypothesis of i.i.d..
The test results agree on different subsample intervals. Residuals of ARMA model all reject the i.i.d. hypothesis. Although BDS statistic varies with different intervals, the i.i.d. hypothesis are all rejected in minuscule significant level. According to this, we find that the nonlinear dependence in series is not caused by the different characteristic in different time period.
2.3.3 Test after conditional heteroscedasticity model filtration
Here we test whether the nonlinear dependence is caused by time-varying variance of the return series. We choose ARMA-GARCH model to eliminate the time-varying variance and obtain the MA(3)-GARCH(1,1) model for London spot, ARMA(5,5)-GARCH(4,4) model for COMEX future and MA(2)-GARCH(1,1) model for Shanghai spot, and then carry out BDS test on standardized residuals(see results in Table 8).
BDS tests on residuals of fitting models
| Subintervals | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|
| London spot price | 0.45 | 0.26 | 0.61 | 0.92 | 1.34 | 1.47 | 1.56 | 1.53 | 1.63 |
| COMEX future price | –0.11 | –0.49 | –0.63 | –0.92 | –0.97 | –0.85 | –0.74 | –0.70 | –0.54 |
| Shanghai spot price | –0.33 | –0.24 | –0.34 | –0.15 | –0.14 | –0.18 | –0.15 | –0.09 | –0.09 |
Note: all test results accepted the null hypothesis of i.i.d..
Almost all test results accept the i.i.d. hypothesis[6], which showed the nonlinear dependence of gold return series could be fully described with GARCH model. In other words, from the aspects of BDS tests, nonlinear dependence beyond ARMA-GARCH model doesn’t exist in the daily gold price series, i.e., chaos doesn’t exist.
3 R/S analysis on gold price at home and abroad
Hurst discovered the durability of water level when studying the Niles River and calculated Hurst index through rescaled range analysis, which quantified the characteristic. Peters[10, 11] pointed out that R/S analysis was an effective tool in discriminating fractional noise (random sequence) and chaotic noise series, and could observe the series’ average period of non-periodic cycle. An evidence for the existence of chaotic attractor is the characteristic of infinite period. As a result R/S analysis can be an effective judgment on the existence of chaos. Lo (1991) proposed revised R/S analysis method and can eliminate the disturbance of short-term memory and heteroscedasticity.
Here we hope to determine the nonlinear attributes of series by R/S analysis and we divide the empirical method into two aspects: On one hand, since the standardized residuals (hereinafter ‘fitting model residuals’) we use where the short-term memory and heteroscedasticity in series have been removed by ARMA-GARCH models[7], we can employ directly the classic R/S analysis. In this paper we employ R/S analysis on original gold price series and fitting model residuals respectively, and by comparing these empirical study results we can determine the nonlinear attributes of series. On the other hand, according to the parameters in fitting models, we employ R/S analysis on a generated series, which uses random numbers as residuals and has same characteristics with the original series, and study the difference between two analysis results. No difference between them indicates that simple ARMA-GARCH model can generate same characteristics with original series, which means no characteristics beyond ARMA-GARCH model exist in original series.
3.1 R/S analysis method
For sequence {Xn}, n = 1, 2, · · ·, N, · · ·, 2N, · · ·, 3N, · · ·, the length for each subsequence is N. Here we divide the sequence to several nonintersecting N-length subsequences, and calculate the accumulative deviation for each subsequence
where MN is mean of Xn. The difference between maximum and minimum cumulative deviation is regarded as the range of N-length subsequence of series {Xn}
To eliminate the effect of dimension and ensure the scale invariance of statistics, Hurst introduced rescaled range
Hurst discovered that rescaled range was a power function of observation time N, satisfying
where a is constant and H is Hurst index. In practice we often convert the above equation to logarithmic form
For each observation time N, we obtain different rescaled range
There are three possible values for Hurst index: 1) H = 0.5, which means the sequence is random and independent; 2) 0 ≤ H < 0.5, which means the system is ergodic or antipersistant; 3) 0.5 < H < 1.00, which means the sequence is persistence. In fact, since the length of sequences is finite, the Hurst index of randomly generated sequence with complete i.i.d. does not equal to 0.5. As a result, based on previous study results, Peters (1994) obtained the expectation of
Similarly, through LS regression we can obtain an estimation of Hurst index expectation. By comparing analysis results of time series
3.2 Analysis results of R/S
3.2.1 R/S analysis on empirical data
We carry out R/S analysis on series of spot price in London and Shanghai[9]. In Figure 1, the steep curve is
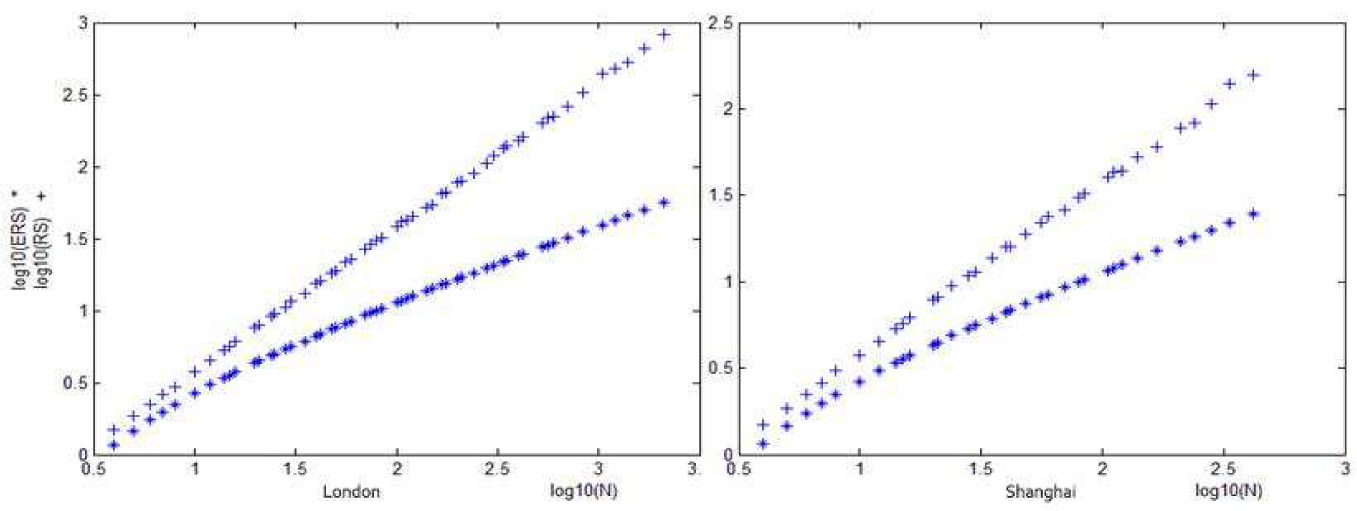
R/S analysis on original gold price data in London and Shanghai
Hurst index of gold data under different processing at home and abroad
| Gold in London | Gold in Shanghai | |
|---|---|---|
| Hurst index of original price series | 1.0091 | 0.9997 |
| Hurst index of residuals of ARMA-GARCH model | 0.5921 | 0.6225 |
| Expectation of Hurst index under i.i.d. | 0.5897 | 0.6301 |
However, after converting gold price series into logarithmic return series and filtering with ARMA-GARCH model, we obtain a significantly different result (see Figure 2 for details): No difference exists between fitting model residuals of gold price and expectations of i.i.d. series, which means that in the series, long-term memory beyond the ARMA-GARCH process does not exist in series. According to Fig. 2,
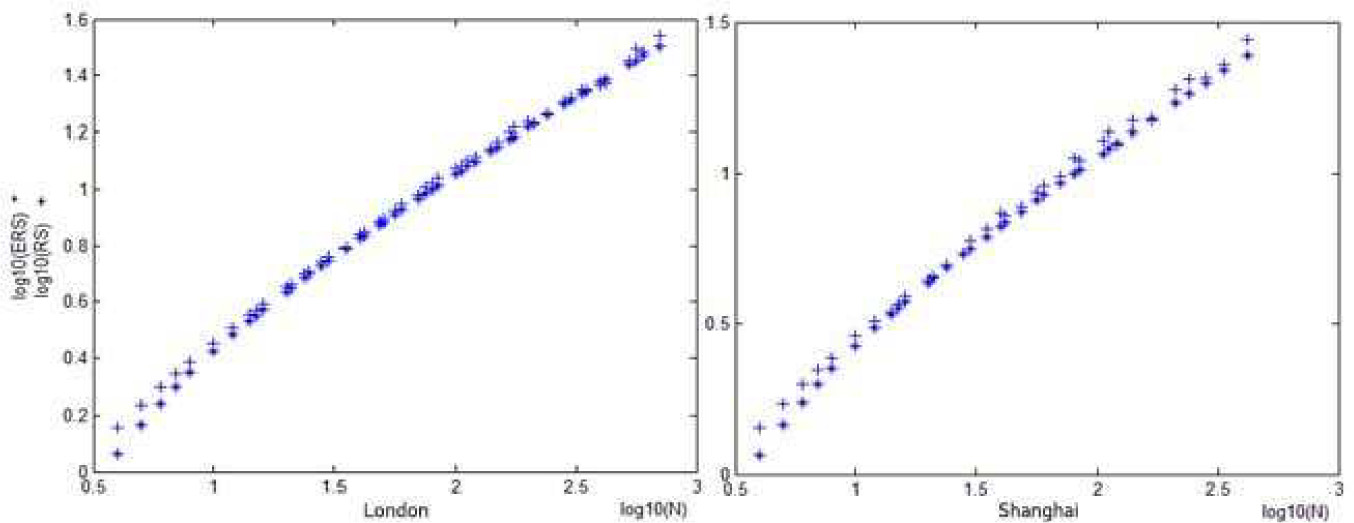
R/S analysis on fitting model residuals of gold return series in London and Shanghai
3.2.2 R/S contrastive analysis of surrogate data
To further verify our assumption (i.e. the absense of deterministic process beyond ARMA-GARCH in series[10]), we generate a simulated ARMA-GARCH process which shares the same parameters with London gold price process[11]. Through R/S contrastive analysis and comparison with results of R/S analysis original gold price series in London and Shanghai, we discover from Figure 3 that the linear and nonlinear dependence of gold price series in London and Shanghai can be perfectly described by corresponding ARMA-GARCH model. There is little difference between original series and simulated series, suggesting that ARMA-GARCH process can discribe effectively the characteristics of series.
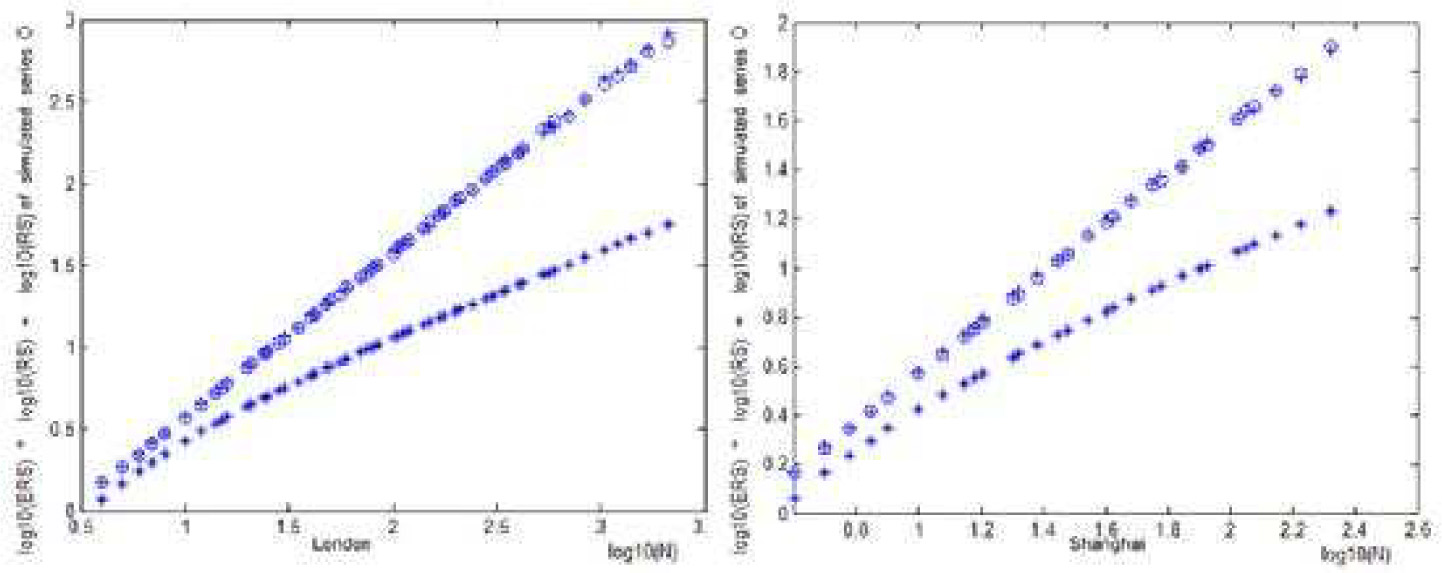
A comparison of R/S analysis on gold original price series in London and Shanghai
Through R/S test on gold price series, we find the long-term memory existing in original price series rather than in residual series filtered with ARMA-GARCH models. Besides, by simply simulating series with ARMA-GARCH model (same parameters with original series), we can obtain identical characteristics in R/S analysis. This further illustrates that the nonlinear characteristics can be effectively discribed with ARMA-GARCH model, and long-term memory beyond ARMA-GARCH model does not exist in gold price series. The nonlinear characteristic of gold price series is conditional heteroscedasticity, instead of chaos.
4 Revised Lyapunov exponent analysis
A system with chaotic structure has an important feature-extreme sensitivity on initial condition, i.e. subtle change in initial value will cause unpredictable enormous variation in the future. The sensitivity can be discribed quantitatively by Lyapunov exponent. Different axis in phase space has different Lyapunov exponent. A negative Lyapunov exponent of a certain axis means that, measured by this axis, two adjacent points tend to approach fixed point and periodic attractors over time, while a positive Lyapunov exponent means the seperation of two adjacent points. This phenomenon is the result of sensitivity on initial condition and thus corresponds with chaotic motion. The zero Lyapunov exponent represents a critical status between stable mode and chaotic mode. It can be viewed either as an end of periodic motion or as the beginning of chaotic motion, but is random in nature.
The study of chaotic characteristics in time series begins with the proposal of theory of reconstructed phase space by Packard et al. in 1980. Due to the nonlinear interaction between all degrees of freedom in the system, the evolution of each independent variable over time contains information about long-term evolution of all other variables in system. As a result, we could study the chaotic behavior of whole nonlinear system through time series of a certain variable. The calculation of Lyapunov exponent based on reconstructed phase space of time series is of significance for determinating whether chaotic behavior exists in a dynamic system that cannot be discribed with differential equation.
4.1 Reconstructing phase space with C-C algorithm
To reconstruct phase space, we need two parameters: delay time Td and embedding dimension m. Chinese scholar Lü[9] discovered that, the result of Lyapunov exponent calculation is sensitive to the choice of parameters in reconstruction of phase space. Current methods to choose reconstruction parameters are: methods of autocorrelation, multiple autocorrelation, mutual information and C-C algorithm. To begin with, since the series to be calculated in the paper are residuals of ARMA-GARCH models which have no obvious autocorrelation characteristic, and no smooth and meaningful autocorrelation or multiple autocorrelation curves can be generated, as a result methods of autocorrelation and multiple autocorrelation cannot be used in this paper. Besides, due to the large data volumn in this paper[12], the mutual information method which requires high computation cannot be realized in short period of time.
In an overall consideration of mutual information method’s power and computation speed, we choose C-C algorithm in this paper. The idea of C-C algorithm, as well as BDS tests, is based on correlation integral using the following relationship
where r stands for correlation radius (same meaning with the proximity parameters in BDS tests). Brock et al. assumed that, given an i.i.d. series, for any m and r, C(m, N, r, t) approximately equals to Cm(1, N, r, t) at all time, which can be regarded as a measure of nonlinear dependence. Based on this assumption, we could search for delay time Td by using the figure of S(m, N, r, t) varying with time under nonlinear dependence. The figure can also be viewed as the meaning of changes in autocorrelation function with time under linear dependence.
In order to analyze the nonlinear dependence of series and eliminate short-term spurious correlation, we divide series into t nonintersecting series by time interval t, calculate
Whent = 2, {Xi} is divided into {X1, X3, ···, XN–1} and {X2, X4, · · ·, XN}
For general t, the series is divided into t nonintersecting series, having
Suppose that the time series subjects to i.i.d., for a given m and r, when N approximates infinite, for all r we have
Although actual series might be quite long, it cannot be treated as infinite, and thus S(m, N, r, t) generally does not equal to zero. As a result, the local largest time interval can be chosen as either null point of
4.2 The calculation of Lyapunov exponent
The major calculation methods of Lyapunov exponent are: defination, Wolf method, Jacobian method, P-norm method and Rosenstein method. To employ defination method we need original differential equations that generate dynamic system, which, unfortunately, we cannot obtain. Wolf method is suitable for small sample and low noise time series, which cannot be adopted in this paper because the sample data (daily trading data over 30 years) are large and noisy. Jacobian method, suitable for large and noisy sample, seems adoptable here, but we find that in this method, Lyapunov exponent is calculated using the speed tangent vector evloves with time, and the tangent vector in reconstructed phase space, which consists of ARMA-GARCH model residuals, shakes violently. As a result, the employment of Jacobian method becomes quite difficult.
In the study of chaos, we can determine a system’s chaotic characteristics simply by calculating the largest Lyapunov exponent. Based on that consideration, we choose the Rosenstein method (also called small data set arithmetic), which only calculates the largest Lyapunov exponent. However, traditional Rosenstein method determines delay time Td by autocorrelation method, while here we use C-C algorithm instead. Besides, to employ Rosenstein method we need to determine the average period[13]. Here we choose Fast Foourier Transform.
4.3 Lyapunov exponents of gold price abroad
In this paper we use Rosenstein method to calculate largest Lyapunov exponent based on phase space reconstruction by C-C algorithm. Although C-C algorithm can reduce both the time spent in iterative operation and the space complexity, to determine the real minimal value of ρS, the total length of series has to be as large as possible. For price series in London and New York, we make use of all 9000 samples from ARMA-GARCH model residuals, while for those in Shanghai, the data amount is too limited to search for smallest value of ρS, thus we fail to determine the embedding dimension and reconstruct the phase space. As a result, in this chapter we only listed empirical results of gold data in London and New York.
First we determine the parameters in phase space reconstruction-delay time Td and embedding dimension m (see results Figure 3 and Figure 5). Fig. 4 shows that ∆S reaches the first minimal value when T = 2. We choose Td = 2 as the actual delay for model residual series of London spot. ρS reaches its minimal value when t = 10, i.e. Tw = (m – 1)Td = 10, from which we obtain embedding dimension m = 6.
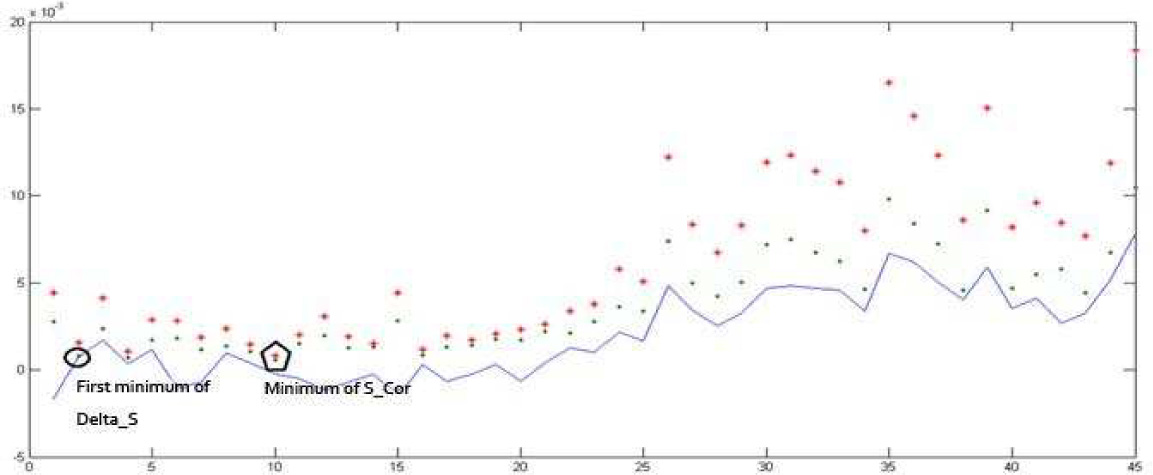
Delay time Td and embedding dimension m for model residuals of London spot
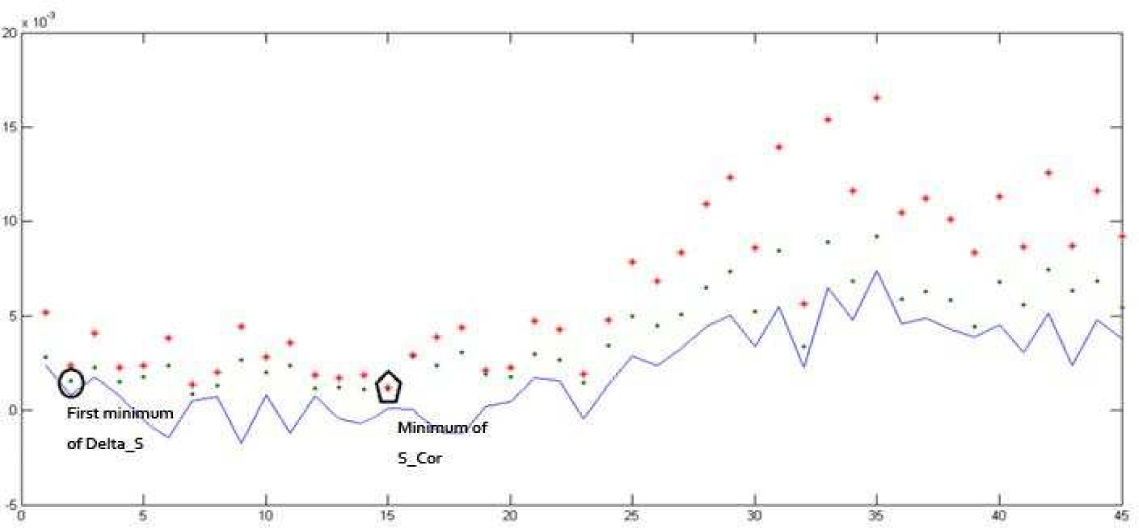
Delay time Td and embedding dimension m for model residuals of New York futures
According to Figure 5, ∆S reaches its first minimal value at T = 2. As a result, we choose Td = 2 as actual delay for gold residual series. The minimum of ρS is reached at t = 15, i.e. Tw = (m – 1)Td = 15 from which we obtain embedding dimension m = 8.
In this paper we determine the average period with Fast Foourier Transform (FFT), which is a fast algorithm to calculate discrete Foourier Transform. Using this algorithm, the multiplication number required by calculation reduce significantly. The larger the transformed sampling point number N is, the more it saves on calculation cost. By FFT calculation, the average period of fitting model residual series in London and New York is 20.0893 and 34.8231.
Finally, we reconstruct phase space using C-C algorithm, and obtained Lyapunov exponents figure of ARMA-GARCH model residuals with revised Rosenstein method. In Figure 6 (upper one), the slope of line stands for the largest Lyapunov exponents of fitting model residuals in New York. As is obvious, although the slope is negative, it approximates zero (–5.113574144831425E–04). This illustrates that fitting model residuals of New York gold futures are random rather than chaotic. According to Figure 6 (lower one) the slope of line is the largest Lyapunov exponent of fitting model residuals in London. From the figure we can clearly see that the slope of the curve approximates zero (0.0062). This illustrates that fitting model residuals of London gold spots are random instead of chaotic.
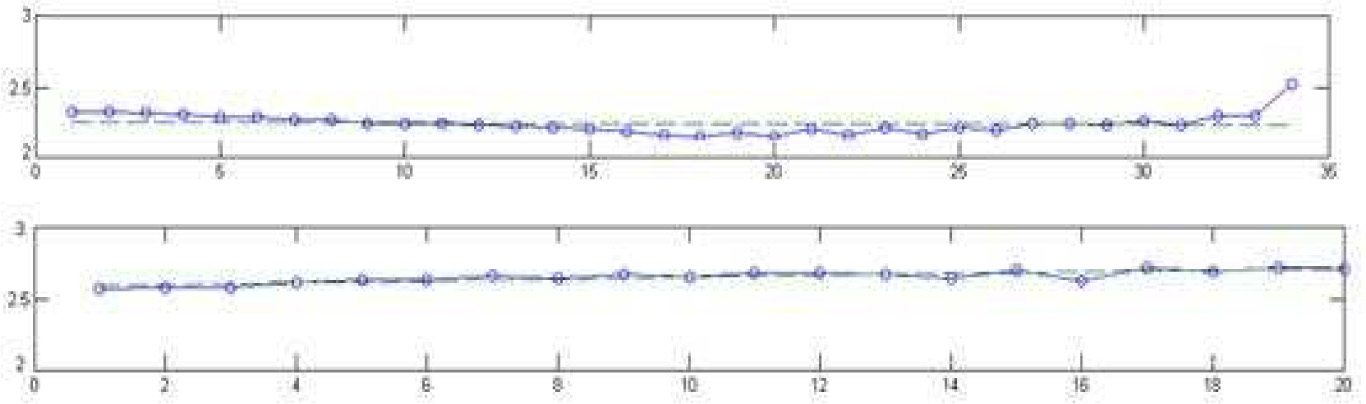
Largest Lyapunov exponents of model residuals in New York (upper) & London (lower)
5 Conclusion
In this paper we employed BDS test, rescaled range (R/S) analysis and revised largest Lyapunov exponents on gold price data at home and abroad, and analyzed the nonlinear attribute of gold price.
First, we discovered that ARMA model residuals of gold price return series could not pass the BDS test, while standardized residuals of ARMA-GARCH model could pass the BDS test. This suggests that the nonlinear dependence of gold series can be discribed perfectly with GARCH model. Thus, nonlinear dependence beyond ARMA-GARCH model in daily gold price series does not exist, i.e. chaos doesn’t exist.
Second, we employed R/S test on original gold price series and discovered strong long-term memory, which did not exist in fitting model residuals. According to the phenomenon that simulated data exhibited same characteristic with original series, we conclude that long-term memory beyond ARMA-GARCH model does not exist in gold price series, and that the nonlinear characteristic of gold price is conditional heteroscedasticity.
Third, we reconstructed phase space according to C-C algorithm and discovered that the largest Lyapunov exponent of ARMA-GARCH model residuals approximated zero, which means that chaotic phenomenon, characterized by initial value sensitivity does not exist in fitting model residuals of gold series.
In conclusion, all linear and nonlinear dependence can be effectively discribed by ARMA-GARCH model. Long term memory beyond ARMA-GARCH model does not exist in series. Chaotic phenomenon characterized by initial value sensitivity does not exist in fitting model residuals. As a result, the nonlinear characteristic in gold price series is conditional heteroscedasticity instead of chaos[14].
References
[1] Barnett W A, Gallant A R, Hinich M J, et al. A single-blind controlled competition among tests for nonlinearity and chaos. Journal of Econometrics, 1997, 82(1): 157–19210.1108/S0573-8555(2004)0000261033Search in Google Scholar
[2] Brock W A, Scheinkman J A, Dechert W D, et al. A test for independence based on the correlation dimension. Econometric Reviews, 1996, 15(3): 197–23510.1080/07474939608800353Search in Google Scholar
[3] DeCoster G P, Labys W C, Mitchell D W. Evidence of chaos in commodity futures prices. Journal of Futures Markets, 1992, 12(3): 291–30510.1002/fut.3990120305Search in Google Scholar
[4] Frank M, Stengos T. Measuring the strangeness of gold and silver rates of return. Review of Economic Studies, 1989, 56(4): 553–56710.2307/2297500Search in Google Scholar
[5] Grassberger P, Procaccia I. Measuring the strangeness of strange attractors. Physica D: Nonlinear Phenomena, 1983, 9(1): 189–20810.1007/978-0-387-21830-4_12Search in Google Scholar
[6] Kanzler L. Very fast and correctly sized estimation of the BDS statistic. Christ Church and Department of Economics, University of Oxford, 199910.2139/ssrn.151669Search in Google Scholar
[7] Kim H S, Eykholt R, Salasc J D. Nonlinear dynamics, delay times, and embedding windows. Physica D: Nonlinear Phenomena, 1999, 127(1): 48–6010.1016/S0167-2789(98)00240-1Search in Google Scholar
[8] Kčcenda E, Briatka L’. Optimal range for the iid test based on integration across the correlation integral. Econometric Reviews, 2005, 24(3): 265–29610.1080/07474930500243001Search in Google Scholar
[9] Lü J H, Lu J A, Chen S H. Chaotic time series analysis and application. Wuhan University Press, 2002Search in Google Scholar
[10] Peters E E. Fractal market analysis: Applying chaos theory to investment and economics. John Wiley and Sons, New York, 1994Search in Google Scholar
[11] Peters E E. Chaos and order in the capital markets: A new view of cycles, prices, and market volatility. John Wiley and Sons, New York, Second edition, 1996Search in Google Scholar
[12] Rosenstein M T, Collins J J, De Luca C J. A practical method for calculating largest Lyapunov exponents from small data sets. Physica D: Nonlinear Phenomena, 1992, 65(1): 117–13410.1016/0167-2789(93)90009-PSearch in Google Scholar
[13] Wang W N, Wang B H, Chen X. The statistic analysis of the index of Shanghai securities. Operations Research and Management Science, 2003, 12(4): 85–90Search in Google Scholar
[14] Xie C, Yang N, Sun B. Empirical research on the chaotic dynamical features of exchange rate time series. Systems Engineering — Theory & Practice, 2008, 2008(8): 118–122Search in Google Scholar
[15] Yang S R, Brorsen B W. Nonlinear dynamics of daily futures prices: Conditional heteroskedasticity or chaos? The Journal of Futures Markets, 1993, 13(2): 175–19110.1002/fut.3990130205Search in Google Scholar
© 2014 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Spatial Dynamics, Vocational Education and Chinese Economic Growth
- The Differential Algorithm for American Put Option with Transaction Costs under CEV Model
- Nonlinear Dynamics of International Gold Prices: Conditional Heteroskedasticity or Chaos?
- Design and Pricing of Chinese Contingent Convertible Bonds
- A Robust Factor Analysis Model for Dichotomous Data
- Non-linear Integer Programming Model and Algorithms for Connected p-facility Location Problem
- Uncertain Comprehensive Evaluation Method Based on Expected Value
- MSVM Recognition Model for Dynamic Process Abnormal Pattern Based on Multi-Kernel Functions
Articles in the same Issue
- Spatial Dynamics, Vocational Education and Chinese Economic Growth
- The Differential Algorithm for American Put Option with Transaction Costs under CEV Model
- Nonlinear Dynamics of International Gold Prices: Conditional Heteroskedasticity or Chaos?
- Design and Pricing of Chinese Contingent Convertible Bonds
- A Robust Factor Analysis Model for Dichotomous Data
- Non-linear Integer Programming Model and Algorithms for Connected p-facility Location Problem
- Uncertain Comprehensive Evaluation Method Based on Expected Value
- MSVM Recognition Model for Dynamic Process Abnormal Pattern Based on Multi-Kernel Functions


