Permutation tests for analyzing cospeciation in multiple phylogenies: applications in tri-trophic ecology
-
Lazarus K. Mramba
, Stuart Barber
Abstract
There is a need for a reliable statistical test which is appropriate for assessing cospeciation of more than two phylogenies. We have developed an algorithm using a permutation method that can be used to test for and infer tri-trophic evolutionary relationships of organisms given both their phylogenies and pairwise interactions. An overall statistic has been developed based on the dominant eigenvalue of a covariance matrix, and compared to values of the statistic computed when tree labels are permuted. The resulting overall p-value is used to test for the presence or absence of cospeciation in a tri-trophic system. If cospeciation is detected, we propose new test statistics based on partial correlations to uncover more details about the relationships between multiple phylogenies. One of the strengths of our method is that it allows more parasites than hosts or more hosts than parasites, with multiple associations and more than one parasite attached to a host (or one parasite attached to multiple hosts). The new method does not require any parametric assumptions of the distribution of the data, and unlike the old methods, which utilize several pairwise steps, the overall statistic used is obtained in one step. We have applied our method to two published datasets where we obtained detailed information about the strength of associations among species with calculated partial p-values and one overall p-value from the dominant eigenvalue test statistic. Our permutation method produces reliable results with a clear procedure and statistics applied in an intuitive manner. Our algorithm is useful in testing evidence for three-way cospeciation in multiple phylogenies with tri-trophic associations and determining which phylogenies are involved in cospeciation.
The authors would like to thank the editor and referees whose comments have substantially improved this paper. LKM gratefully acknowledges Kenya Medical Research Institute (KEMRI) Kilifi, Kenya, for funding his masters research studies. The Dyer and Forister labs acknowledge support from the United States National Science Foundation, awards DEB 1020509 and DEB 1145609.
Appendix A: Example datasets
The phylogenetic trees simulated for Sections 3.1–3.3 are shown in Figure A1(A–C) respectively and their corresponding triangular interaction matrices T(a)–T(c) are given in (2). Here, (A) refers to the example with no cospeciation; (B) refers to strong cospeciation betweeen X and Y while Z is independent of both; and (C) refers to the example where all three trees are strongly cospeciated.
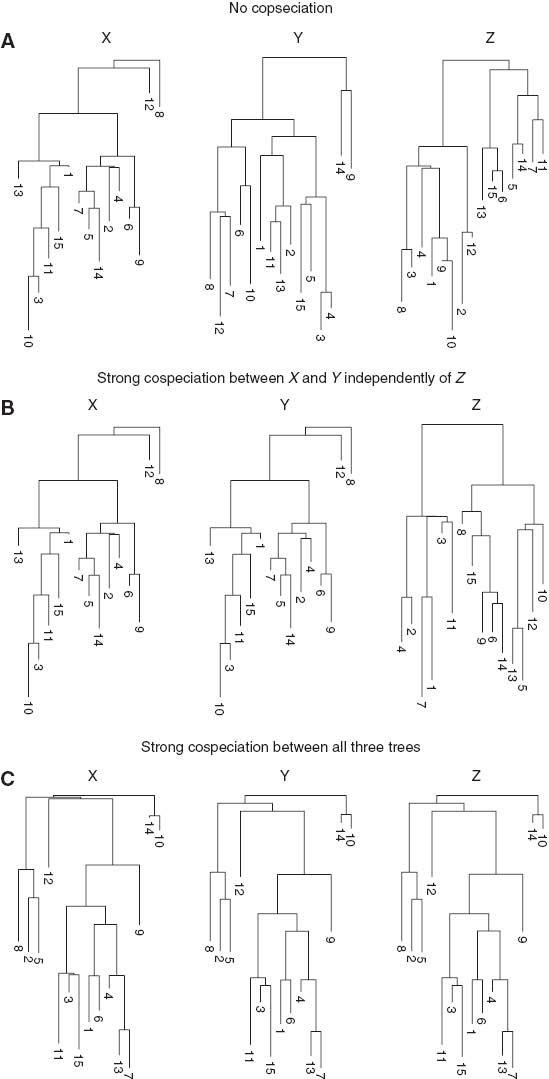
Trees generated with varying degrees of cospeciation.
Appendix B: Labels for the termite-bacteria-protist dataset
Termite labels, X.
| 1 | Rhinotermes_marginalis |
| 2 | Rhinotermes_hispidus |
| 3 | Schedorhinotermes_sp_Australia |
| 4 | Parrhinotermes_sp |
| 5 | Schedorhinotermes_sp_Laos |
| 6 | Termitogeton_planus |
| 7 | Psammotermes_allocerus |
| 8 | Heterotermes_longiceps |
| 9 | Heterotermes_tenuis |
| 10 | Coptotermes_formosanus_japan |
| 11 | Coptotermes_formosanus_china |
| 12 | Coptotermes_sp_Malaysia |
| 13 | Coptotermes_sp_Laos |
| 14 | Coptotermes_testaceus |
Protist labels, Y.
| 1 | AB262494_Psudotrichonympha_sp |
| 2 | AB262495_Psudotrichonympha_sp |
| 3 | AB262496_Psudotrichonympha_sp |
| 4 | AB262497_Psudotrichonympha_sp |
| 5 | AB262498_Psudotrichonympha_sp |
| 6 | AB032211_Psudotrichonympha_sp |
| 7 | AB262486_Psudotrichonympha_sp |
| 8 | AB262487_Psudotrichonympha_sp |
| 9 | AB262488_Psudotrichonympha_sp |
| 10 | AB262489_Psudotrichonympha_sp |
| 11 | AB262490_Psudotrichonympha_sp |
| 12 | AB262491_Psudotrichonympha_sp |
| 13 | AB262492_Psudotrichonympha_sp |
| 14 | AB262493_Psudotrichonympha_sp |
Bacteria labels, Z.
| 1 | AB262559_Br02Htl_S4 |
| 2 | AB262560_Br78HtT_S1 |
| 3 | AB218918_CfPt1_2 |
| 4 | AB262555_CNCpF_S1 |
| 5 | AB262556_Ma79Cp_S1 |
| 6 | AB262557_La10Cp_S3 |
| 7 | AB262558_Br75CpT_S1 |
| 8 | AB218919_TpPtN_4 |
| 9 | AB262562_Br84RhM_S5 |
| 10 | AB262563_Br76RhH_S1 |
| 11 | AB262564_La19Sc_S1 |
| 12 | AB262566_My26Pa_S1 |
| 13 | AB262565_Au05Sc_S1 |
| 14 | AB262561_SA16PsA_S4 |
Appendix C: Labels and interaction matrix for the tree-moth-wasp dataset
Tree labels, X.
| 1 | Viburnum |
| 2 | Acer |
| 3 | Salix |
| 4 | Trifolium |
| 5 | Medicago |
| 6 | Ulmus |
| 7 | Prunus |
| 8 | Crataegus |
| 9 | Malus |
| 10 | Sorbus |
| 11 | Fagus |
| 12 | Quercus_robur |
| 13 | Alnus |
| 14 | Betula |
| 15 | Corylus |
| 16 | Carpinus |
Moth labels, Y.
| 1 | Paronix_carpinella |
| 2 | P_schreberella |
| 3 | P_harrisella |
| 4 | P_nicellii |
| 5 | P_cavella |
| 6 | P_froelichiella |
| 7 | P_lautella |
| 8 | P_insignitella |
| 9 | P_roboris |
| 10 | P_spinicolella |
| 11 | P_viminiella |
| 12 | P_salicicolella |
| 13 | P_rajella |
| 14 | P_ulmifoliella |
| 15 | P_geniculella |
| 16 | P_platanoidella |
| 17 | P_sylvella |
| 18 | P_quercifoliella |
| 19 | P_lantanella |
| 20 | P_maestingella |
| 21 | P_sorbi |
| 22 | P_corylifoliella |
| 23 | P_coryli |
| 24 | P_esperella |
| 25 | P_cydoniella |
| 26 | P_oxyacanthae |
| 27 | P_mespilella |
| 28 | P_blancardella |
Wasp labels Z.
| 1 | insignitellae |
| 2 | carpini |
| 3 | zwoelferi |
| 4 | niveipes |
| 5 | atys |
| 6 | suprafolius |
| 7 | Cila_ex_Quercus |
| 8 | splendens |
| 9 | cila_ex_Viburnum |
| 10 | cila_ex_Corylus |
| 11 | buekkensis |
| 12 | pseudoplatanus |
| 13 | acerianus |
| 14 | latreillii |
| 15 | butus |
References
Ahmad, F., M. Aslam and M. Razaq (2004): “Chemical ecology of insects and tritrophic interactions,” Research (Science), 15, 181–190.Search in Google Scholar
Campbell, V., P. Legendre and F. J. Lapointe (2011): “The performance of the congruency among distance matrices(CADM) test in phylogenetic analysis,” BMC Evol. Biol., 11, 64.Search in Google Scholar
Charleston, M. and R. D. M. Page (2002): Tree Map 2.0b A Macintosh program for the analysis of how dependent phylogenies are related, by co-phylogeny mapping, Division of Environmental Evolutionary Biology, Institute of Biomedical Life Sciences, University of Glasgow, Glasgow, UK, Availble at: http://www.it.usyd.edu.au/mcharles/software/treemap/treemap.html.Search in Google Scholar
Choi, K. and S. M. Gomez (2009): “Comparison of phylogenetic trees through alignment of embedded evolutionary distances,” BMC Bioinformatics, 10, 423.10.1186/1471-2105-10-423Search in Google Scholar PubMed PubMed Central
Drummond, A. J. and A. Rambaut (2007): “BEAST: Bayesian evolutionary analysis by sampling trees,” BMC Evol. Biol., 7, 214.Search in Google Scholar
Ewens, W. J. and G. R. Grant (2001): Statistical Methods in Bioinformatics, Statistics for Biology and Health, Springer Science, New York, USA.10.1007/978-1-4757-3247-4Search in Google Scholar
Fahrenholz, H. (1913): “Ectoparasiten und Abstmmungslehre,” Zoology, 41, 371–374.Search in Google Scholar
Forister, M. L. and C. R. Feldman (2010): “Phylogenetic cascades and the origins of tropical diversity,” Trop. Biol. Conservation, 1–9.Search in Google Scholar
Fourment, M. and M. J. Gibbs (2006): “Patristic: a program of calculating patristic distances and graphically comparing the components of genetic changes,” BMC Evol. Biol., 6, 1.Search in Google Scholar
Hommola, K., J. E. Smith, Y. Qiu and W. R. Gilks (2009): “A permutation test of host-parasite cospeciation,” Mol. Biol. Evol., 26, 1457–1468.Search in Google Scholar
Huelsenbeck, J. P., B. Rannala and B. Larget (2000): “A Bayesian framework for the analysis of cospeciation,” Evolution, 54, 352–364.10.1111/j.0014-3820.2000.tb00039.xSearch in Google Scholar PubMed
Klassen, G. J. (1992): “A history of the macroevolutionary approach to studying host-parasite associations,” Parasitology, 78, 573–587.10.2307/3283532Search in Google Scholar
Lapointe, F.-J. and P. Legendre (1990): “A statistical framework to test the consensus of two nested classifications,” Syst. Zool., 39, 1–13.Search in Google Scholar
Lapointe, F.-J. and P. Legendre (1992a): “A statistical framework to test the consensus among additive trees (cladograms),” Syst. Biol., 41, 158–171.10.1093/sysbio/41.2.158Search in Google Scholar
Lapointe, F.-J. and P. Legendre (1992b): “Statistical significance of the matrix correlation coefficient for comparing independent phylogenetic trees,” Syst. Biol., 41, 378–384.10.1093/sysbio/41.3.378Search in Google Scholar
Legendre, P. and F.-J. Lapointe (2004): “Assessing congruence among distance matrices: single-male Scotch whiskies revisited,” Aust. NZ J. Stat., 46, 615–629.Search in Google Scholar
Legendre, P., Y. Desdevies and E. Bazin (2002): “A statistical test for host-parasite coevolution,” Syst. Biol., 51, 217–234.Search in Google Scholar
Lopez-Vaamonde, C., H. C. J. Godfray, S. A. West, C. Hansson and J. M. Cook (2005): “The evolution of host use and unusual reproductive strategies in Achrysocharoides parasitoid wasps,” Evol. Biol., 18, 1029–1041.Search in Google Scholar
Merkle, D. M. and N. Wieseke (2010): “A parameter-adaptive dynamic programming approach for inferring co-phylogenies,” BMC Bioinformatics, 11, S60.10.1186/1471-2105-11-S1-S60Search in Google Scholar PubMed PubMed Central
Micha, S. G., S. Kistenmacher, G. Mölck and U. Wyss (2000): “Tritrophic interactions between cereals, aphids and parasitoids: discrimination of different plant-host complexes by Aphidius Rhopalosiphi,” Eur. J. Entomol., 97, 539–543.Search in Google Scholar
Noda, S., O. Kitade, T. Inoue, M. Kawai, M. K. K. Hiroshima, Y. Hongoh, R. Constantino, V. Uys, J. Zhong, T. Kudo and M. Ohkuma (2007): “Cospeciation in the triplex symbiosis of termite gut protists (Pseudotrichonympha spp.), their hosts, and their bacterial endosymbionts,” Mol. Ecol., 16, 1257–1266.Search in Google Scholar
Page, R. D. M. (1990): “Temporal congruence and cladistic analysis of biogeography and cospeciation,” Syst. Zool., 39, 205–26.Search in Google Scholar
Page, R. D. M. (1994a): “Parallel phylogenies: Reconstructing the history of host-parasite assemblages,” Cladistics Int. J., 10, 155–173.10.1111/j.1096-0031.1994.tb00170.xSearch in Google Scholar
Page, R. D. M. (1994b): “Maps between trees and cladistic analysis of historical associations among genes, organisms and areas,” Syst. Biol., 43, 58–77.10.1093/sysbio/43.1.58Search in Google Scholar
Page, R. D. M. (1995): Tree Map. Division of Environmental Evolutionary Biology, Institute of Biomedical Life Sciences, Glasgow, UK: University of Glasgow.Search in Google Scholar
Page, R. D. M. (1996): “Temporal congruence revisited: Comparison of mitochondrial DNA sequence divergence in cospeciating pocket gophers and their chewing lice,” Syst. Biol., 45, 151–67.Search in Google Scholar
Page, R. D. M. (2003): Tangled trees: Phylogeny, cospeciation, and coevolution, Chicago and London: The University of Chicago Press.Search in Google Scholar
Paradis, E. (2006): Analysis of Phylogenetics and Evolution with R, Use R, New York: Springer.10.1007/978-0-387-35100-1Search in Google Scholar
Paradis, E., J. Claude and K. Strimmer (2004): “APE: analyses of phylogenetics and evolution in R language,” Bioinformatics, 20, 289–290.10.1093/bioinformatics/btg412Search in Google Scholar PubMed
Paterson, A. M. and R. D. Gray (1997): Host-parasite cospeciation, host switching and missing the boat. In: Clayton, D. H., Moore, J. (Eds.), Host-Parasite Evolution: General Principles and Avian Models, Oxford: Oxford University Press, pp. 236–250.Search in Google Scholar
Paterson, A. M., R. L. Palma and R. D. Gray (1999): “How frequently do avian lice miss the boat?” Syst. Biol., 48, 214–223.Search in Google Scholar
Percey, D. M., R. D. Page and Q. C. B. Cronk (2004): “Plant-insect interactions: double-dating associated insect and plant lineages reveals asynchronous radiations,” Syst. Biol., 53, 120–127.Search in Google Scholar
Planet, P. J. (2006): “Tree disagreement: Measuring and testing incongruence in phylogenies,” Biomed. Informatics, 39, 86–102.Search in Google Scholar
R Development Core Team (2012): R: A Language and Environment for Statistical Computing, R Foundation for Statistical Computing, Vienna, Austria, Available at: http://www.R-project.org/, ISBN 3-900051-07-0.Search in Google Scholar
Ronquist, F. and J. P. Huelsenbeck (2003): “MrBayes 3: Bayesian phylogenetic inference under mixed models,” Bioinformatics, 19, 1572–1574.10.1093/bioinformatics/btg180Search in Google Scholar PubMed
Siddall, M. E. (1996): “Phylogenetic covariance probability: confidence and historical associations,” Syst. Biol., 45, 48–66.Search in Google Scholar
Siddall, M. E. (2001): “Computer-intensive randomization in systematics,” Cladistics, 17, 35–52.10.1111/j.1096-0031.2001.tb00103.xSearch in Google Scholar
©2013 by Walter de Gruyter Berlin Boston
Articles in the same Issue
- Masthead
- Masthead
- Research Articles
- A new variance stabilizing transformation for gene expression data analysis
- Kernel approximate Bayesian computation in population genetic inferences
- Permutation tests for analyzing cospeciation in multiple phylogenies: applications in tri-trophic ecology
- Accounting for undetected compounds in statistical analyses of mass spectrometry ‘omic studies
- Modeling, simulation and analysis of methylation profiles from reduced representation bisulfite sequencing experiments
- Estimation of weighted log partial area under the ROC curve and its application to MicroRNA expression data
- Random forests on distance matrices for imaging genetics studies
Articles in the same Issue
- Masthead
- Masthead
- Research Articles
- A new variance stabilizing transformation for gene expression data analysis
- Kernel approximate Bayesian computation in population genetic inferences
- Permutation tests for analyzing cospeciation in multiple phylogenies: applications in tri-trophic ecology
- Accounting for undetected compounds in statistical analyses of mass spectrometry ‘omic studies
- Modeling, simulation and analysis of methylation profiles from reduced representation bisulfite sequencing experiments
- Estimation of weighted log partial area under the ROC curve and its application to MicroRNA expression data
- Random forests on distance matrices for imaging genetics studies


