Abstract
Given the solubilities of non-ionic organic solutes in water, their solubilities in seawater are obtained by correlation expressions involving two descriptors for the constituent ions (or salts) of seawater and two descriptors of the solutes. The former are the standard partial molar volumes and the intrinsic molar volumes and the latter are the molar volume (the Le Bas variant of it) and either the Hildebrand solubility parameter δH or the Kamlet–Taft solvatochromic π*.
Introduction
The solubility of an non-ionic organic solute (subscript N) in water, sN0/mol L–1, can be estimated by means of several well-known linear solvation energy relationships (LSERs). An examples of such an LSER is that of Kamlet et al. [1, 2] for 25 °C:
where VNI is the computer-generated intrinsic molar volume of the solute [3], π* is its solvatochromic polarity/polarizability index, β is its solvatochromic electron pair donicity index, and tF is the fusion/melting temperature of the solute (if it is solid at the relevant temperature for the solubility). Another example is the general solubility equation of Yalkowski et al. [4, 5]:
where PoW is the logarithm of the 1-octanol/water partition coefficient of the solute [6]. A further example is the LSER of Abraham and Le [7]:
where VX is the McGowan molar volume of the solute [8], α is its solvatochromic hydrogen bond donicity [with β and π* as in eq. (1)], and RS is the excess molar refraction [7].
Given the solubility of a solute in pure water, the question now arises: what would be its solubility in an electrolyte solution (subscript E) of molar concentration cE/mol L–1, and specifically, what would be its solubility in seawater? The latter question is of environmental importance and it should be useful if this solubility could be estimated within reasonable limits.
The general description of the effect of an electrolyte on the solubility of a solute is in terms of the Setchenow expression, relating the solubility in the presence of the electrolyte, sNE/mol L–1, to that in its absence:
This proportionality with the concentration of the electrolyte is generally valid up to 1 mol L–1, and the proportionality coefficient kNE is called the Setchenow constant. It is depends on the natures of both the solute and the electrolyte. The latter may also be a mixture as is seawater, and because of the proportionality that holds down to infinite dilution of the electrolyte, kNE should be additive in the values of the constituent ions of the electrolyte.
This paper presents correlation expressions that permit the estimation of the solubility of non-ionic organic solutes in seawater, given their solubilities in pure water [either experimental values or estimated by expressions such as (1)–(4)] following the principles in a previous paper by the author discussed below.
The database
The composition of seawater in terms of its ionic or salt constituents depends to some extent on the location, salinity, temperature and other conditions of sampling, but Table 1 lists a representative recent set of values for salinity 3.5 % at 25 °C. The ionic composition (subscrtipt I), cI/mol L–1, is from Gros et al. [9] and the salt composition, cE/mol L–1, is from Mistry et al. [10]. Note that the ionic composition lacks an entry for the hydrogencarbonate anion present in the salt composition, but its presence is very minor and it has practically no effect on the salting out ability by the constituents of seawater regarding non-ionic organic solutes.
The composition and volumetric properties of the constituents of seawater in terms of the ions [9] and of the salts [10].
| Ion | c I/mol dm–3 | ν I | V I ∞ conv/cm3 mol–1 | V I intr/cm3 mol–1 | ΔVIconv/cm3 mol–1 | ν IΔVIconv/cm3 mol–1 |
|---|---|---|---|---|---|---|
| Na+ | 0.4767 | 0.4186 | –1.21 | 4.78 | 5.99 | 2.52 |
| K+ | 0.0100 | 0.0087 | 9.02 | 11.83 | 2.81 | 0.02 |
| Mg2+ | 0.0560 | 0.0492 | –21.17 | 1.68 | 22.85 | 1.13 |
| Ca2+ | 0.0090 | 0.0079 | –17.85 | 4.50 | 22.35 | 0.18 |
| Cl– | 0.5585 | 0.4903 | 17.83 | 26.69 | 8.86 | 4.37 |
| Br– | 0.0009 | 0.0008 | 24.71 | 33.89 | 9.18 | 0.01 |
| SO42– | 0.0280 | 0.0245 | 13.98 | 30.69 | 16.71 | 0.35 |
| Sum | 1.1391 | 1.0000 | 8.58 | |||
|
|
||||||
| Salt | c E/mol dm–3 | ν E | V E ∞/cm3 mol–1 | V E intr/cm3 mol–1 | ΔVE/cm3 mol–1 | ν EΔVE/cm3 mol–1 |
|
|
||||||
| NaCl | 0.4197 | 0.8100 | 16.62 | 31.47 | 14.85 | 6.01 |
| MgCl2 | 0.0456 | 0.1053 | 14.49 | 55.06 | 40.57 | 2.14 |
| Na2SO4 | 0.0288 | 0.0556 | 11.56 | 40.25 | 28.69 | 0.80 |
| CaCl2 | 0.0105 | 0.0203 | 17.81 | 57.88 | 40.07 | 0.41 |
| KCl | 0.0009 | 0.0017 | 26.87 | 38.52 | 11.67 | 0.01 |
| NaHCO3 | 0.0024 | 0.0046 | 22.19 | 21.87 | –0.32 | 0.00 |
| KBr | 0.0013 | 0.0025 | 33.73 | 45.72 | 11.99 | 0.01 |
| Sum | 0.5182 | 1.0000 | 9.38 | |||
The solubility of hydrocarbons with ≥5 carbon atoms in water and seawater was critically examined by Shaw et al. [11] in 1989 and their solubility in water was re-examined by Maczynski and Shaw et al. [12] in 2005. A review of the effects of salts on the solubility of non-ionic organic compounds in seawater was published by Xie et al. [13] in 1997, including also several compounds other than hydrocarbons. A few more recent references have also solubility data for seawater [14–17].
The combined list of for 25 °C is shown in Table 2 as log(sN0/sNE) values, whether originally each solubility datum is presented as mol L–1, mg L–1, Henry’s law constant for volatile solutes, etc. Solubility values expressed as g (100 g solution)–1 [11] cannot be compared directly between pure and seawater and the data should be multiplied by the densities of the solutions to convert them eventually to the common mol L–1 scale. Since those solubilities expressed as g (100 g solution)–1 are very small, the densities of pure water, 997.045 kg m–3 and of mean seawater, 1023.3 kg m–3 (salinity 3.5 %) [30] at 25 °C may be employed for this purpose.
Solubility ratios in water and seawater of non-ionic organic compounds at 25 °C and their relevant properties.
| Solute | Ref. | log(sN0/sNE) | V LB [13] | δ H [ref] | π* [ref] |
|---|---|---|---|---|---|
| Benzene | [11, 13] | 0.095, 0.097 | 96.0 | 18.8 [18] | 0.55 [18] |
| Toluene | [11, 13] | 0.129, 0.083 | 111.2 | 18.8 [18] | 0.49 [18] |
| Ethylbenzene | [11, 13] | 0.150, 0.162 | 140.4 | 18.0 [18] | 0.53 [18] |
| o-Xylene | [11, 13] | 0.115, 0.118 | 140.4 | 18.0 [18] | 0.51 [18] |
| m-Xylene | [11, 13] | 0.127, 0.139 | 140.4 | 18.0 [18] | 0.47 [18] |
| p-Xylene | [11, 13] | 0.136, 0.148 | 140.4 | 18.1 [18] | 0.45 [18] |
| Cumene | [11, 13] | 0.175, 0.183 | 170.0 | 17.6 [18] | 0.41 [18] |
| 1,2,3-Trimethylbenzene | [13] | 0.173 | 162.6 | 18.6 [19] | 0.47 [20] |
| 1,2,4-Trimethylbenzene | [11, 13] | 0.161, 0.190 | 162.6 | 18.2 [19] | 0.47 [20] |
| Mesitylene | [11, 13] | 0.176, 0.188 | 162.6 | 18.1 [18] | 0.45 [18] |
| n-Butylbenzene | [13] | 0.231 | 184.8 | 17.6 [21] | 0.49 [20] |
| s-Butylbenzene | [13] | 0.180 | 184.8 | 17.1 [21] | (0.45) |
| t-Butylbenzene | [13] | 0.153 | 184.8 | 17.1 [21] | 0.42 [22] |
| Naphthalene | [11, 13] | 0.155, 0.149 | 147.6 | 20.3 [23] | 0.70 [24] |
| Biphenyl | [13] | 0.211 | 185 | 17.0 [23] | 0.54 [25] |
| Acenaphthene | [13] | 0.129 | 173 | 18.9 [26] | 0.62 [20] |
| Phenanthrene | [13] | 0.184 | 199 | 20.0 [23] | 0.80 [24] |
| Anthracene | [13] | 0.149 | 197 | 20.3 [23] | 0.80 [24] |
| Phenol | [13] | 0.074 | 103.4 | 25.1 [18] | 0.72 [18] |
| o-Nitrophenol | [13] | 0.097 | 131.9 | 27.0 [27, 28] | |
| m-Nitrophenol | [13] | 0.107 | 131.9 | 30.9 [27, 28] | |
| p-Nitrophenol | [13] | 0.079 | 131.9 | 31.3 [27, 28] | 1.15 [20] |
| Nitrobenzene | [14] | 0.087 | 124.5 | 21.3 [18] | 1.01 [20] |
| o-Nitrotoluene | [14] | 0.104 | 146.7 | 21.9 [29] | 0.90 [22] |
| m-Nitrotoluene | [14] | 0.097 | 146.7 | 21.3 [21] | |
| p-Nitrotoluene | [13] | 0.060 | 153.0 | 22.2 [29] | 0.97 [20] |
| p-Toluidine | [13] | 0.103 | 132.4 | 19.4 [21] | 0.69 [24] |
| 2,4-Dinitrobenzaldehyde | [16] | 0.082 | 165 | ||
| 2,6-Dinitrobenzaldehyde | [16] | 0.077 | 165 | ||
| Acetaldehyde | [15, 17] | 0.067, 0.086 | (47) | 20.2 [18] | (0.67) |
| Propanal | [17] | 0.101 | (66) | 20.1 [18] | 0.65 [18] |
| Butanal | [17] | 0.140 | (84) | 20.0 [18] | 0.63 [18] |
| Pentanal | [17] | 0.133 | (102) | (19.9) | (0.61) |
| Acetone | [15, 17] | 0.112, 0.053 | 74.0 | 22.1 [18] | 0.62 [18] |
| 2-Butanone | [17] | 0.115 | (92) | 18.7 [18] | 0.60 [18] |
The accuracy of the listed log(sN0/sNE) values depends on those of the individual solubilities in the two media. The reported uncertainties of the ‘recommended’ or ‘tentative’ solubility values [10, 11] in pure water range from ±2.3 % for benzene and o-xylene to ±12.5 % for m-xylene and cumene, and those for seawater should be at least as large, because fewer determinations have been made of them. Solubilities <0.2 g (kg solution)–1 are too uncertain to be included in the present evaluation and are not shown in Table 2.
Correlations of the relative solubilities
The author has shown [31] that two descriptors of the salts and two of the solutes are sufficient for the correlation and eventual prediction of the relative solubilities in salt solutions and pure water, log(sN0/sNE). The descriptors for the salts are the conventional standard molar volumes of the constituent ions VI∞ conv [32] (and their fractional concentrations of the total ions νI [9]) and their intrinsic molar volumes VI,intr = (4πNA/3)(krI)3, where k = 1.213 [31, 33], taking care of voids around the ions (except for sulfate, where k = 1 was used), and rI are the ionic radii [31]. The values at 25 °C for seawater are shown in Table 1. Also shown there are the values for the constituent salts, the fractional concentrations νE [10], their standard molar volumes VE∞, and the corresponding intrinsic volumes VEintr. The VE∞ are the sums of the stoichiometrically weighted VI∞ conv and the VEintr = ΣνIVI,intr. The small differences between the ionic and salt concentrations in the two references employed [9, 10] cause the quantities ΣνIΔVI∞ conv = ΣνI(VIintr – VI∞ conv) and ΣνEΔVE∞ = ΣνE(VEintr – VE∞) to differ somewhat, and their average, 9.0 ± 0.4 cm3 mol–1 is used henceforth.
The descriptors of the solutes are their molar volumes (the Le Bas values, VLB/cm3 mol–1 [13], are used) and either the Hildebrand solubility parameter δH/MPa0.5 or the Kamlet–Taft polarity/polarizability index π*, with values shown in Table 2. Both these quantities were taken from [18] for liquid solutes where available. Solubility parameters δH had to be calculated for solid solutes from the molar enthalpies of formation of their crystals and those of their gaseous forms [27, 29] and the molar volumes [28] of the solutes. Other values of δH were obtained from data in [19, 21, 23, 26]. Polarity/polarizability index, π*, values for the nitroaromatic and some other solutes were taken from [20, 22, 24, 25]. Values in parenthesis were estimated.
Most of the relative solubility data, log(sN0/sNE), where subscript E pertains to seawater, are for aromatic solutes. The solubilities of aliphatic hydrocarbons in pure water and seawater were too small to yield reliable log(sN0/sNE) data. The few available values of this variable pertain to carbonyl compounds: aldehydes and ketones, but the variability of the δH and π* descriptors cover a too narrow range (7.4 % and 11.0 %) to make them necessary for the correlations of the relative solubilities, for which the solute molar volume descriptor, VLB, suffices. The correlation expressions according to [31] then become for both aliphatic and aromatic solutes:
where the term 2.0 δH does not apply to aliphatic solutes, Fig. 1, and:
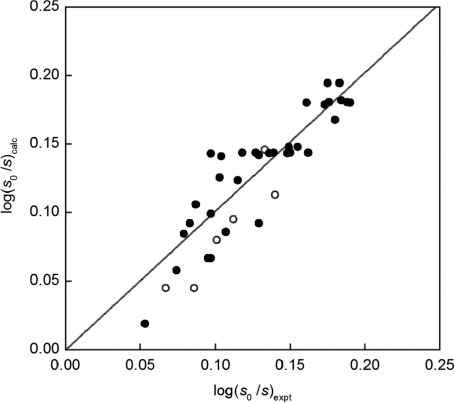
Calculated, eq. (6) with the δH descriptor, vs. experimental solubilities of solutes in seawater and pure water at 25 °C, log(s0/s), for aromatic solutes (•) and aliphatic ones (○).
where the term 68π* does not apply to aliphatic solutes, Fig. 2.
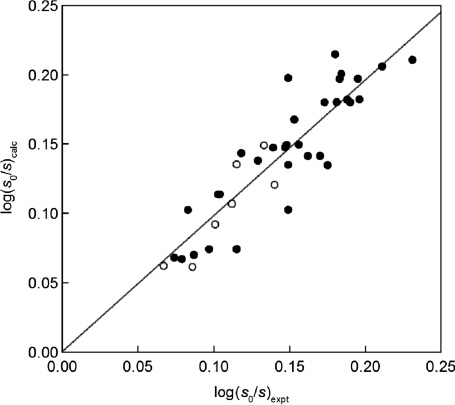
Calculated, eq. (7) with the π* descriptor, vs. experimental solubilities of solutes in seawater and pure water at 25 °C, log(s0/s), for aromatic solutes (•) and aliphatic ones (○).
Discussion
The overall span of the available log(sN0/sNE) data of the aromatic solutes is not large (about 0.2 units) and the average deviations with the δH descriptor (0.025 units, Fig. 1) is somewhat larger than with the π* descriptor (0.020 units, Fig. 2), but the overall agreement of the calculated and the experimental values is satisfactory. The low log(sN0/sNE) value for acetone, 0.053, and that for toluene, 0.083, are obviously outliers and were not included in the correlation expression. The agreement in Figs. 1 and 2 of the present paper is better than that achieved for the salting out constant of sodium chloride shown in Fig. 2 of [31], for the data from Xie et al. [13] and of Ni and Yalkowski [34], involving both aromatic and aliphatic solutes.
Although seawater consists mainly of aqueous sodium chloride, the presence of the other salts does have an effect on the solubility of non-ionic organic solutes as is seen, e.g., in the review [13]. Therefore, the correlation expression (6) differs somewhat from the general expression, eq. (12) in terms of the π* descriptor in [31]. The variety of aliphatic solutes that could be considered here is too small to warrant a reliable prediction for other aliphatic solutes, but in the case of aromatic solutes this should be possible by means of eqs. (6) or (7), depending on whether δH or π* values for solutes not included in the present set are available or can be estimated.
Article note
A collection of invited papers based on presentations at the 16th International Symposium on Solubility Phenomena and Related Equilibrium Processes (ISSP-16), Karlsruhe, Germany, July 21–25 2014.
References
[1] M. J. Kamlet, R. M. Doherty, M. H. Abraham, P. W. Carr, F. Doherty, R. W. Taft. J. Phys. Chem.91, 1996 (1987).10.1021/j100291a062Search in Google Scholar
[2] M. J. Kamlet, R. M. Doherty, M. H. Abraham, Y. Marcus, R. W. Taft. J. Phys. Chem.92, 5244 (1988).10.1021/j100329a035Search in Google Scholar
[3] D. J. Leahy. Pharm. Sci.75, 629 (1986).10.1002/jps.2600750702Search in Google Scholar
[4] N. Jain, S. H. Yalkowsky. J. Pharm. Sci.90, 234 (2001).10.1002/1520-6017(200102)90:2<234::AID-JPS14>3.0.CO;2-VSearch in Google Scholar
[5] G. Yang, Y. Ran, S. H. Yalkowsky. J. Pharm. Sci.91, 517 (2002).10.1002/jps.10022Search in Google Scholar
[6] C. Hansch, A. Leo. Substituent Constants for Correlation Analysis in Chemistry and Biology. Wiley, New York (1979).Search in Google Scholar
[7] M. H. Abraham, J. Le. J. Pharm. Sci.88, 858 (1999).10.1021/js9901007Search in Google Scholar
[8] M. H. Abraham, J. C. McGowan. Chromatographia23, 243 (1987).10.1007/BF02311772Search in Google Scholar
[9] N. Gros, M. F. Camoes, C. Oliviera, M. C. R. Silva. J Chromatogr. A1210, 92 (2008).Search in Google Scholar
[10] K. H. Mistry, H. A. Hunter, J. H. Lienhard V. Desalination318, 34 (2013).10.1016/j.desal.2013.03.015Search in Google Scholar
[11] D. G. Shaw, M.-C. Haulait-Pirson, G. T. Hefter, A. Maczynski, Eds. IUPAC Solubility Data Series. Vol. 37, 38, Hydrocarbons with Water and Seawater. Pergamon Press, New York (1989).Search in Google Scholar
[12] A. Maczynski, D. G. Shaw, M. Goral, B. Wisniewska-Goclowska, A. Skrzecz, Z. Maczynska, I. Owczarek, K. Blazej, M.-C. Haulait-Pirson, F. Kapuku, G. T. Hefter, A. Szafranski. J. Phys. Chem. Ref. Data34, 441 (2005).10.1063/1.1790005Search in Google Scholar
[13] W.-H. Xie, W.-Y. Shiu, D. Mackay. Marine Envir. Res.44, 429 (1997).10.1016/S0141-1136(97)00017-2Search in Google Scholar
[14] D. J. L. Prak, D. W. O’Sullivan. J. Chem. Eng. Data54, 1231 (2009).10.1021/je800624cSearch in Google Scholar
[15] H.-J. Benkelberg, S. Hamm, P. Warneck. J. Atmos. Chem.20, 17 (1995).10.1007/BF01099916Search in Google Scholar
[16] D. J. L. Prak, D. W. O’Sullivan. J. Chem. Eng. Data56, 2630 (2011).Search in Google Scholar
[17] X. Zhou, K. Mopper. Environ. Sci. Technol.24, 1864 (1990).10.1021/es00082a013Search in Google Scholar
[18] Y. Marcus. The properties of Solvents, Wiley, Chichester (1997).Search in Google Scholar
[19] D. R. Lide, ed. Handbook of Chemistry and Physics, 82nd ed. CRC Press, Baton Rouge (2001–2002).Search in Google Scholar
[20] F. Xu, X. Liang, B. Lin, F. Su, K.-W. Schramm, A. Kettrup. Chemosphere48, 553 (2002).10.1016/S0045-6535(02)00100-5Search in Google Scholar
[21] W. V. Steele, R. D. Chirico, S. E. Knipmeyer, A. Nguyen. J. Chem. Eng. Data47, 648 (2002).10.1021/je0100847Search in Google Scholar
[22] M. J. Kamlet, R. M. Doherty, R. W. Taft, M. H. Abraham, G. D. Veith, D. J. Abraham. Environ. Sci. Technol.21, 149 (1987).10.1021/es00156a004Search in Google Scholar
[23] Y.-P. Chin, W. J. Weber Jr. Environ. Sci. Technol.23 978 (1989).10.1021/es00066a008Search in Google Scholar
[24] M. J. Kamlet, M. H. Abraham, P. W. Carr, R. M. Doherty, R. W. Taft. J. Chem. Soc., Perkin Trans. II, 2087 (1988).10.1039/P29880002087Search in Google Scholar
[25] G. Geblewicz, D. J. Schiffrin. J. Chem. Soc., Faraday Trans. 184, 561 (1988).10.1039/f19888400561Search in Google Scholar
[26] N. M. Djordjevic. Thermochim. Acta177, 109 (1991).10.1016/0040-6031(91)80089-2Search in Google Scholar
[27] A. Heintz, S. Kapteina, S. P. Verevkin. J. Phys. Chem. A111, 6552 (2007).10.1021/jp0730388Search in Google Scholar
[28] L. K. Schnackenberg, R. D. Berger. J. Chem. Inf. Model.45, 360 (2005).10.1021/ci049643eSearch in Google Scholar
[29] J. A. Widegren, T. J. Bruno. J. Chem. Eng. Data55, 159 (2010).10.1021/je900293jSearch in Google Scholar
[30] A. Poisson, C. Brunet, J. C. Brun-Cottan. Deep-Sea Res.27A, 1013 (1980).10.1016/0198-0149(80)90062-XSearch in Google Scholar
[31] Y. Marcus. J. Mol. Liq.177, 7 (2013).10.1016/j.molliq.2012.09.007Search in Google Scholar
[32] F. J. Millero. Chem Rev.71, 147 (1971).10.1021/cr60270a001Search in Google Scholar
[33] P. Mukerjee. J. Phys. Chem.65, 740 (1961).10.1021/j100823a009Search in Google Scholar
[34] N. Ni, S. H. Yalkowski. Intl. J. Pharm.254, 167 (2003).10.1016/S0378-5173(03)00008-5Search in Google Scholar
©2015 IUPAC & De Gruyter
Articles in the same Issue
- Frontmatter
- Preface
- 16th International Symposium on Solubility Phenomena and Related Equilibrium Processes (ISSP-16)
- Conference papers
- On the crystallization kinetics of highly soluble salts
- Solid–liquid equilibria in systems [Cxmim][Tf2N] with diethylamine
- Thermodynamic properties of molybdate ion: reaction cycles and experiments
- Solubility and the periodic table of elements
- Solubility and spectroscopic study of AnIII/LnIII in dilute to concentrated Na–Mg–Ca–Cl–NO3 solutions
- On the solubility of non-ionic organic solutes in seawater
Articles in the same Issue
- Frontmatter
- Preface
- 16th International Symposium on Solubility Phenomena and Related Equilibrium Processes (ISSP-16)
- Conference papers
- On the crystallization kinetics of highly soluble salts
- Solid–liquid equilibria in systems [Cxmim][Tf2N] with diethylamine
- Thermodynamic properties of molybdate ion: reaction cycles and experiments
- Solubility and the periodic table of elements
- Solubility and spectroscopic study of AnIII/LnIII in dilute to concentrated Na–Mg–Ca–Cl–NO3 solutions
- On the solubility of non-ionic organic solutes in seawater

