Abstract
In this article, we present the Laguerre wavelet exact Parseval frame method (LWPM) for the two-dimensional flow of a rotating micropolar fluid in a porous channel with huge mass transfer. This flow is governed by highly nonlinear coupled partial differential equations (PDEs) are reduced to the nonlinear coupled ordinary differential equations (ODEs) using Berman's similarity transformation before being solved numerically by a Laguerre wavelet exact Parseval frame method. We also compared this work with the other methods in the literature available. Moreover, in the graphs of the velocity distribution and microrotation, we shown that the proposed scheme's solutions are more accurate and applicable than other existing methods in the literature. Numerical results explaining the effects of various physical parameters connected with the flow are discussed.
1 Introduction
The examinations on the liquid stream with a high mass transfer in a permeable channel are generally listening cautiously on Newtonian fluids, and an equivalent difficulty for non-Newtonian fluids is in the lot to-be preferred situation. Various kinds of non-Newtonian fluids are couple-stress fluids, viscoelastic fluids, micropolar fluids, power-law fluids, etc. In the current paper, we have considered a micropolar liquid, a non-Newtonian fluid, as the working fluid. The hypothesis of micropolar fluids was first determined by Eringen [1, 2].
In the soul, the pivoting non-Newtonian progression of fluids consists of micro constituents gave the original incentive to the development of the theory; however, the succeeding study has fruitfully useful the model to a wide scope of zones composites, microemulsions, polymer blends, permeable rocks, etc. Broad utilizations of the micropolar liquid hypothesis specified in the books of Eringen [3] and Lukaszewicz [4].
Micropolar flow in a permeable can althrough bulky mass transferis studied using the perturbation analysis [5] and Homotopy analysis method [6]. Idris [7] considered the importance of a non-uniform temperature gradient on micropolar fluids under convective heat transfer. Sajid et al. [8] felt the boundary layer flow of a micropolar fluid in a permeable channel by Homotopy analysis. Joneidi et al. [9] obtained numerical solutions and Homotopy analysis for micropolar fluid flow in a porous channel. They brought the velocities and rotation results for different values of well-known physical parameters. Recently, Sobamowo et al. [10] studied the micropolar fluid flow with high mass transfer in a porous channel driven by suction/injection. Sreenivasulu et al. [11] examined the combined effects of viscous dissipation and Joule heating on MHD three-dimensional laminar flow of a viscous incompressible nonlinear radiating Casson nanofluid past a nonlinear stretching porous sheet. Gireesha and Sindhu [12] studied the natural convection flow of Casson fluid through an annular microchannel formed by two cylinders in the presence of the magnetic field. Khan et al. [13] introduced a new Haar wavelet method to solve Jeffery-Hamel flow and heat transfer in Eyring-Powell fluid in the presence of an external magnetic field. Khan and Razzaq [14] explained that the Legendre wavelet method to reduce the fuzzy differential equations to the fuzzy algebraic equations system made the problem easily computable to attain the solutions more rapidly than the other existing methods in the literature. Khan et al. [15] investigate the three-dimensional axisymmetric steady flow of micropolar fluid over a rotating disk in a slip-flow regime. Zhang et al. [16] studied the blood flow's entropy analysis through an anisotropically tapered artery under the suspension of magnetic Zinc-oxide nanoparticles.
Nonlinear marvel plays an essential part in material science, applied arithmetic, and design issues. A few of the appropriate territories to wave marvels encase liquid mechanics, optical filaments, plasma, versatile media, and so forth. What's more, getting precise answers to these issues is genuinely safe. Regardless, in current years, mathematical strategies radically have been urbanized to be utilized for a nonlinear coupled system of equations. A few of them are solved using numerical methods Murthy and Singh [17], and some are solved via the perturbation method Magyari and Keller [18].
Wavelets are special functions in a restricted domain; that is, a wave function, instead of oscillating everlastingly, drops to zero. Newly, we have been facing various kinds of wavelets with two parameters such as, k is the translation parameter and n is dilation parameter. The hypothesis and uses of wavelets is a reasonably youthful new branch in the signal processing and numerical analysis. It has been functional in engineering applications, such as signal analysis, time-frequency analysis, and engineering mathematics. A wavelet is a powerful tool in the field of numerical methods which helps to find the numerical solutions for the various forms of the differential equations such as, Laguerre wavelet method, Hermite wavelet method, Cardinal B-spline wavelet-based numerical method, CAS wavelets analytic solutions by Shiralashetti and Kumbinarasaiah [19, 20, 21, 22], Chebyshev wavelets approach Biazar and Ebrahimi [23]. Berman [24] studied the Laminar flow in channels with porous walls. Preliminaries of Laguerre wavelets and frames are given in [25]. Recently, very attractive fluid flow problems are solved by using wavelet technique [26, 27, 28].
To the best of our konwledge, no one solved this type of problem using the Laguerre wavelet exact Parseval frame in the view of literature. This impetus us to solve such equations via the Laguerre wavelet exact Parseval frame. The present work's interest is to solve the coupled nonlinear ordinary differential equations governing micropolar fluid flow in a porous channel with high mass transfer by using the Laguerre wavelet exact Parseval frame method, and the results have a comparison with solutions of Joneidi et al. [9]. We wish to establish how the extra material constants of the micropolar fluid influence the flow for large mass transfer through the channel walls.
This article's motivation is to illustrate the present algorithm in solving some following systems of two highly nonlinear ODEs. The proposed algorithm is useful for obtaining numerical solutions of the system of nonlinear differential equations. Significantly, this algorithm yields an exact solution for a system of ordinary differential equations which are having solutions as a polynomial of finite degree [25]. The obtained results are compared with the Optimal Homotopy Asymptotic method (OHAM), Runge-Kutta solutions Joneidi et al. [9].
2 Problem formulation
The highly nonlinear coupledordinary differential equations which explain the Micropolar boundary layer fluid flow in a porous channel with high mass transfer can be summarized as introduced by Joneidi et al. [9]:
The boundary conditions are
or the flow is symmetric about the channel
where the prime (′) denotes differentiation concerning η. The non-dimension Reynolds number
3 Laguerre wavelet exact Parseval frame method
The Laguerre wavelet exact Parseval frame method is used to solve Eq. (1) subjected to the boundary conditions given in Eq. (2). First, assume the solution in the following form:
F (η) and G (η) are truncated as
where
Discrete each of the above equations using the following collection points
which leads to (2k−1 M − 4) + (2k−1 M − 2) number of equations. But, by data 6 equations are furnished by boundary conditions. On solving this system containing 2 (2k−1 M) number of nonlinear algebraic equations by the suitable solver, we get 2 (2k−1 M) Laguerre wavelet exact Parseval frame coefficients then substitute these coefficients in Eq. (5) leads the Laguerre wavelet exact Parseval frame numerical solution for Eq. (1).
4 Results and discussion
In organize to authenticate the computer code urbanized in this study, the outcomes for various values of η for unchanging values of N1 = N2 = 1, N3 = 0.1 and Re = −1 are compared with the consequences of Joneidi et al. [9] in Tables 1–2 and Figures 1–3. This accuracy gives us high confidence in the validity of this problem and reveals an excellent engineering accuracy agreement. This investigation is completed by depicting the effects of some important parameters to evaluate how these parameters influence this fluid. The velocities F (η), F′ (η) and rotation G (η) profiles for various parameters Re, N1, N2 and N3 by Laguerre wavelet exact Parseval frame method are shown in Figures 4–9. In these figures, we removed comparing our results with the analytical/numerical solution because of having an excellent agreement.
The results of LWPM, OHAM, and numerical solution for F (η) when N1 = N2 = 1, N3 = 0.1 and Re = −1.
| η | LWPM | OHAM | RKM |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0.05 | 0.07571249476 | 0.0751848245 | 0.07518206173 |
| 0.10 | 0.15101759237 | 0.1499912277 | 0.14998590360 |
| 0.15 | 0.22551218925 | 0.2240404899 | 0.22403298656 |
| 0.20 | 0.29879786577 | 0.2969533656 | 0.29694421863 |
| 0.25 | 0.37048088622 | 0.3683499493 | 0.36833980248 |
| 0.30 | 0.44017219883 | 0.4378496438 | 0.43783919066 |
| 0.35 | 0.50748743573 | 0.5050712335 | 0.50506115802 |
| 0.40 | 0.57204691299 | 0.5696330849 | 0.56962399728 |
| 0.45 | 0.63347563063 | 0.6311534657 | 0.63114584762 |
| 0.50 | 0.69140327256 | 0.6892510064 | 0.68924516577 |
| 0.55 | 0.74546420665 | 0.7435452985 | 0.74354134489 |
| 0.60 | 0.79529748466 | 0.7936576481 | 0.79365548778 |
| 0.65 | 0.84054684231 | 0.8392119830 | 0.83921133966 |
| 0.70 | 0.88086069924 | 0.8798359223 | 0.87983638200 |
| 0.75 | 0.91589215901 | 0.9151620112 | 0.91516309029 |
| 0.80 | 0.94529900911 | 0.9448291282 | 0.94483035438 |
| 0.85 | 0.96874372094 | 0.9684840590 | 0.96848505804 |
| 0.90 | 0.98589344987 | 0.9857832407 | 0.98578381378 |
| 0.95 | 0.99642003515 | 0.9963946743 | 0.99639484474 |
| 1.00 | 1.00000000000 | 0.9999999999 | 1.00000000000 |
The results of LWPM, OHAM, and numerical solution for G (η) when N1 = N2 = 1, N3 = 0.1 and Re = −1.
| η | LWPM | OHAM | RKM |
|---|---|---|---|
| 0 | 0 | 0 | 0 |
| 0.05 | −0.020717786 | −0.020190420 | −0.020190328 |
| 0.10 | −0.041053555 | −0.040103456 | −0.040103308 |
| 0.15 | −0.0607462855 | −0.059460171 | −0.059460011 |
| 0.20 | −0.079525826 | −0.077978581 | −0.077978446 |
| 0.25 | −0.097112907 | −0.095372231 | −0.095372128 |
| 0.30 | −0.113219132 | −0.111348866 | −0.111348747 |
| 0.35 | −0.127546982 | −0.125609174 | −0.125608933 |
| 0.40 | −0.139789812 | −0.137845643 | −0.137845116 |
| 0.45 | −0.149631855 | −0.147741505 | −0.147740487 |
| 0.50 | −0.156748221 | −0.154969796 | −0.154968072 |
| 0.55 | −0.160804894 | −0.159192523 | −0.159189909 |
| 0.60 | −0.161458736 | −0.160059942 | −0.160056339 |
| 0.65 | −0.158357483 | −0.157209965 | −0.157205409 |
| 0.70 | −0.151139750 | −0.150267674 | −0.150262384 |
| 0.75 | −0.139435025 | −0.138844967 | −0.138839370 |
| 0.80 | −0.122863675 | −0.122540328 | −0.122535036 |
| 0.85 | −0.101036941 | −0.100938713 | −0.100934437 |
| 0.90 | −0.073556942 | −0.073611577 | −0.073608923 |
| 0.95 | −0.040016671 | −0.040117008 | −0.040116126 |
| 1.00 | 0.000000000 | 0.00000000 | 0.0000000000 |

Comparison between the solutions of OHAM, numerical solution, and Laguerre wavelet exact Parseval frame method for F (η) when N1 = N2 = 1, N3 = 0.1 and Re = −1.

Comparison between the solutions of OHAM, numerical solution, and Laguerre wavelet exact Parseval frame method for G (η) when N1 = N2 = 1, N3 = 0.1 and Re = −1.

Comparison between the solutions of OHAM, numerical solution, and Laguerre wavelet exact Parseval frame method for F′ (η) when N1 = N2 = 1, N3 = 0.1 and Re = −1.
Figure 4 shows the rotation G (η) profile of the fluid for different values of the Reynolds number. The rotation profile curves in the (η, G (η))-plane show an upward concave shape and G (η) increases with a decrease in the Reynolds number's values. For an unchanging value of the Reynolds number, the rotation profile G (η) decreases with increasing η, up to around 0.6, and subsequently increases with increasing η. Also, from these figures, we observe that with an increase in the Reynolds number, the point at which minimum rotation occurs does not move away from the origin of the channel.

Rotation profile, G (η) via Laguerre wavelet exact Parseval frame method for different Reynolds number values when N1 = N2 = 1, N3 = 0.1.
Figure 5 shows the velocity F (η) curve of the fluid for a variety of values of the Reynolds number. The velocity F (η) curve decreases with decreasing the values of Reynolds number and η. But when suction occurs, as is shown in this figure, inverse results are obtained.

Velocity profile, F (η) via Laguerre wavelet exact Parseval frame method for different Reynolds number values when N1 = N2 = 1, N3 = 0.1.
Figure 6 shows the velocity distribution F′ (η) profile of the fluid for various values of the Reynolds number Re. The velocity distribution F′ (η) profile decreases with increasing the value of η. The velocity distribution F′ (η) increases with increasing the value of the Reynolds number. All the above results are obtained when N1 = N2 = 1, N3 = 0.1.

Velocity profile, F′ (η) via Laguerre wavelet exact Parseval frame method for different values of Reynolds number when N1 = N2 = 1, N3 = 0.1.
Figures 7 and 8 show the rotation G (η) curve for various values of N1 and N2. The behavior of the rotation profile is similar to Figure 4. For a fixed value of N1 (Figure 7) or N2 (Figure 8), the rotation G (η)attains a minimum value concerningη. The rotation G (η) increases with increasing the value of N2, but the opposite trend is noticed with increasing N1. Figure 9 shows the rotation G (η) profile for different values of N3. The rotation G (η) profile increases with decreasing the value of N3. Moreover, micropolar parameters have no vital role in the velocity profiles and are not given in this paper.

Effects of different values of (a) N1 and (b) N2 on G (η) when Re = 1, N1 = 1, N3 = 0.1.
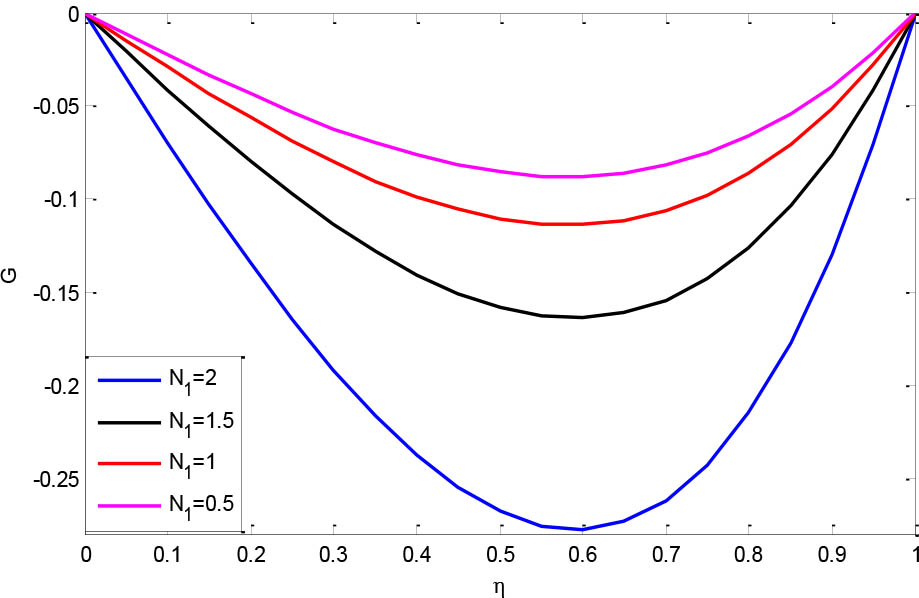
Effects of different values of (a) N1 and (b) N2 on G (η) when Re = 1, N2 = 1, N3 = 0.1.

Effects of different values of N3 on G (η) when N1 = N2 = 1, and Re = 1.
5 Conclusions
In this paper, we functional the Laguerre wavelet exact Parseval frame method to solve coupled nonlinear ODEs from the Berman's similarity solution of micropolar fluid flow in a permeable canalbulky mass transfer. This method is easy to apply and yields the preferred accuracy. It has seemed that increasing the value of Re leads to an increase in the velocities F (η) and F′ (η). However, Micropolar parameters have no critical role in the velocities profiles. For each value of the Reynolds number, rotation G (η) attains the smallest value does not go away from the center of the channel. The rotation G (η) decreases with decreasing the value of N2, but the opposite trend is noticed with increasing N1 and N3. Further the comparisons between the OHAM, Runge-Kutta solutions Joneidi et al. [9] and the present work, it was shown that the current work provided a promising approach for this type of equations. While the Laguerre wavelet exact Parseval frame leads to more accurate results, it seems that the accuracy and rapidity of the Laguerre wavelet exact Parseval frame method (LWPM) are higher than that of the OHAM method in this problem. This method is an extension work of [25]. The process in [25] applied only to initial valued problems. But, in the present approach, we extended for boundary value problems. As per the literature survey, we have not found any article of frames applied to micropolar fluid flow problems. So, this is the first paper on micropolar fluid flow problems via wavelet frames.
Acknowledgments
The authors wish to thank the reviewer for useful comments which helped in improving the paper considerably.
Funding information: The authors state no funding involved.
Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.
Conflict of interest: The authors state no conflict of interest.
References
[1] Eringen AC. Simple micropolar fluids. Int. J. Eng. Sci. 1964;2:205–217.10.1016/0020-7225(64)90005-9Search in Google Scholar
[2] Eringen AC. Theory of micropolar fluids. Journal of Mathematics and Mechanics. 1966;16:1–18.10.21236/AD0469176Search in Google Scholar
[3] Eringen AC. Micro continum field theories. II. Fluentmedia, NewYork, Springer, 2001.Search in Google Scholar
[4] Lukaszewicz G. Micropolar fluids: Theory and applications. Basel, Brikhauser, 1999.10.1007/978-1-4612-0641-5Search in Google Scholar
[5] Kelson NA, Desseaux A, Farrell TW. Micropolar flow in a porous channel with high mass transfer. ANZIAM Journal. 2002;44:479–495.10.21914/anziamj.v44i0.692Search in Google Scholar
[6] Ziabakhsh Z, Domairry G. Homotopy analysis solution of micro-polar flow in a porous channel with high mass transfer. Advances in Theoretical and Applied Mechanics. 2008;1:79–94.Search in Google Scholar
[7] Idris R, Othman H, Hashim I. On the effect of non-uniform basic temperature gradient on Benard–Marangoni convection in micropolar fluids. Int Commun Heat Mass. 2009;36:203–209.10.1016/j.icheatmasstransfer.2008.11.009Search in Google Scholar
[8] Sajid M, Abbas Z, Hayat T. Homotopy analysis for boundary layer flow of a micropolar fluid through a porous channel. Appl. Math. Model. 2009;33:4120–4125.10.1016/j.apm.2009.02.006Search in Google Scholar
[9] Joneidi AA, Ganji DD, Babaelahi M. Micropolar flow in a porous channel with high mass transfer. Int Commun Heat Mass. 2009;36:1082–1088.10.1016/j.icheatmasstransfer.2009.06.021Search in Google Scholar
[10] Sobamowo GM., Akinshilo AT, Jayesimi LO. Analysis of micropolar fluid flow through a porous channel driven by suction/injection with high mass transfer. International Journal of Thermal Energy and Applications. 2019;5:67–77.Search in Google Scholar
[11] Khan NA, Razzaq OA. An efficient computer based wavelets approximation method to solve Fuzzy boundary value differential equations. Nonlinear Eng. 2016;5(1):1–6.10.1515/nleng-2015-0021Search in Google Scholar
[12] Khan NA, Sultan F, Shaikh A, Ara A, Rubbab Q. Haar wavelet solution of the MHD Jeffery-Hamel flow and heat transfer in Eyring-Powell fluid. AIP Advances. 2016;6(11):115102.10.1063/1.4967212Search in Google Scholar
[13] Khan NA, Naz F, Sultan F. Entropy generation analysis and effects of slip conditions on micropolar fluid flow due to a rotating disk. Open Eng. 2017;7(1):185–198.10.1515/eng-2017-0025Search in Google Scholar
[14] Sreenivasulu P, Poornima T, Reddy NB. Influence of joule heating and non-linear radiation on mhd 3d dissipating flow of casson nanofluid past a nonlinear stretching sheet. Nonlinear Eng. 2019;8(1):661–672.10.1515/nleng-2017-0143Search in Google Scholar
[15] Zhang L, Bhatti MM, Marin M, Mekheimer KS. Entropy analysis on the blood flow through anisotropically tapered arteries filled with magnetic zinc-oxide (ZnO) nanoparticles. Entropy. 2020;22(10):1070.10.3390/e22101070Search in Google Scholar
[16] Gireesh BJ, Sindhu S. MHD natural convection flow of Casson fluid in an annular microchannel containing porous medium with heat generation/absorption, Nonlinear Eng. 2020;9(1):223–232.10.1515/nleng-2020-0010Search in Google Scholar
[17] Murthy PVSN, Singh P. Thermal dispersion effects on non-Darcy natural convection over horizontal plate with surface mass flux. Arch. Appl. Mech. 1997;67:487–495.10.1007/s004190050133Search in Google Scholar
[18] Magyari E, Keller B. Exact solutions for self-similar boundary-layer flows induced by permeable stretching walls. Eur. J. Mech. B Fluids. 2000;19:109–122.10.1016/S0997-7546(00)00104-7Search in Google Scholar
[19] Shiralashetti SC, Kumbinarasaiah S. Theoretical study on continuous polynomial wavelet bases through wavelet series collocation method for nonlinear Lane–Emden type equations. Appl. Math. Comput. 2017;315:591–602.10.1016/j.amc.2017.07.071Search in Google Scholar
[20] Shiralashetti SC, Kumbinarasaiah S. Hermite wavelets operational matrix of integration for the numerical solution of nonlinear singular initial value problems. Alex. Eng. J. 2018;57:2591–2600.10.1016/j.aej.2017.07.014Search in Google Scholar
[21] Shiralashetti SC, Kumbinarasaiah S. Cardinal b-spline wavelet based numerical method for the solution of generalized Burgers–Huxley equation. Int. J. Appl. Math. Comput. Sci. 2018;4:73.10.1007/s40819-018-0505-ySearch in Google Scholar
[22] Shiralashetti SC, Kumbinarasaiah S. CAS wavelets analytic solution and Genocchi polynomials numerical solutions for the integral and integro-differential equations. J. Interdiscip. Math. 2019;1–18.10.1080/09720502.2019.1602354Search in Google Scholar
[23] Biazar J, Ebrahimi H. Chebyshev wavelets approach for nonlinear systems of Volterra integral equations. Comput. Math. with Appl. 2012;63:608–616.10.1016/j.camwa.2011.09.059Search in Google Scholar
[24] Berman AS. Laminar flow in channels with porous walls. Int. J. Appl. Phys. 1953;24:1232–1235.10.1063/1.1721476Search in Google Scholar
[25] Shiralashetti SC, Kumbinarasaiah S. Laguerre wavelets exact parseval frame-based numerical method for the solution of system of differential equations. Int. J. Appl. Comput. Math. 2020;6:101.10.1007/s40819-020-00848-9Search in Google Scholar
[26] Kumbinarasaiah S, Ramane HS, Pise, KS, Harihara G. numerical-solution-for-nonlinear-klein–gordon equation via operational-matrix by clique polynomial of complete graphs. Int. J. Appl. Comput. Math, 2021;7:12.10.1007/s40819-020-00943-xSearch in Google Scholar
[27] Kumbinarasaiah S, Mundewadi RA. The new operational matrix of integration for the numerical solution of integrodifferential equations via Hermite wavelet. SeMA (2021), 10.1007/s40324-020-00237-8Search in Google Scholar
[28] Kumbinarasaiah S, Raghunatha KR. The applications of hermite wavelet method to nonlinear differential equations arising in heat transfer. International Journal of Thermofluids. 2021;9:100066.10.1016/j.ijft.2021.100066Search in Google Scholar
© 2021 S. Kumbinarasaiah et al., published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Nonlinear absolute sea-level patterns in the long-term-trend tide gauges of the East Coast of North America
- Insight into the significance of Joule dissipation, thermal jump and partial slip: Dynamics of unsteady ethelene glycol conveying graphene nanoparticles through porous medium
- Numerical results for influence the flow of MHD nanofluids on heat and mass transfer past a stretched surface
- A novel approach on micropolar fluid flow in a porous channel with high mass transfer via wavelet frames
- On the exact and numerical solutions to a new (2 + 1)-dimensional Korteweg-de Vries equation with conformable derivative
- On free vibration of laminated skew sandwich plates: A finite element analysis
- Numerical simulations of stochastic conformable space–time fractional Korteweg-de Vries and Benjamin–Bona–Mahony equations
- Dynamical aspects of smoking model with cravings to smoke
- Analysis of the ROA of an anaerobic digestion process via data-driven Koopman operator
- Lie symmetry analysis, optimal system, and new exact solutions of a (3 + 1) dimensional nonlinear evolution equation
- Extraction of optical solitons in birefringent fibers for Biswas-Arshed equation via extended trial equation method
- Numerical study of radiative non-Darcy nanofluid flow over a stretching sheet with a convective Nield conditions and energy activation
- A fractional study of generalized Oldroyd-B fluid with ramped conditions via local & non-local kernels
- Analytical and numerical treatment to the (2+1)-dimensional Date-Jimbo-Kashiwara-Miwa equation
- Gyrotactic microorganism and bio-convection during flow of Prandtl-Eyring nanomaterial
- Insight into the significance of ramped wall temperature and ramped surface concentration: The case of Casson fluid flow on an inclined Riga plate with heat absorption and chemical reaction
- Dynamical behavior of fractionalized simply supported beam: An application of fractional operators to Bernoulli-Euler theory
- Mechanical performance of aerated concrete and its bonding performance with glass fiber grille
- Impact of temperature dependent viscosity and thermal conductivity on MHD blood flow through a stretching surface with ohmic effect and chemical reaction
- Computational and traveling wave analysis of Tzitzéica and Dodd-Bullough-Mikhailov equations: An exact and analytical study
- Combination of Laplace transform and residual power series techniques to solve autonomous n-dimensional fractional nonlinear systems
- Investigating the effects of sudden column removal in steel structures
- Investigation of thermo-elastic characteristics in functionally graded rotating disk using finite element method
- New Aspects of Bloch Model Associated with Fractal Fractional Derivatives
- Magnetized couple stress fluid flow past a vertical cylinder under thermal radiation and viscous dissipation effects
- New Soliton Solutions for the Higher-Dimensional Non-Local Ito Equation
- Role of shallow water waves generated by modified Camassa-Holm equation: A comparative analysis for traveling wave solutions
- Study on vibration monitoring and anti-vibration of overhead transmission line
- Vibration signal diagnosis and analysis of rotating machine by utilizing cloud computing
- Hybrid of differential quadrature and sub-gradients methods for solving the system of Eikonal equations
- Developing a model to determine the number of vehicles lane changing on freeways by Brownian motion method
- Finite element method for stress and strain analysis of FGM hollow cylinder under effect of temperature profiles and inhomogeneity parameter
- Novel solitons solutions of two different nonlinear PDEs appear in engineering and physics
- Optimum research on the temperature of the ship stern-shaft mechanical seal end faces based on finite element coupled analysis
- Numerical and experimental analysis of the cavitation and study of flow characteristics in ball valve
- Role of distinct buffers for maintaining urban-fringes and controlling urbanization: A case study through ANOVA and SPSS
- Significance of magnetic field and chemical reaction on the natural convective flow of hybrid nanofluid by a sphere with viscous dissipation: A statistical approach
- Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications
- Research on vibration monitoring and fault diagnosis of rotating machinery based on internet of things technology
- An improved image processing algorithm for automatic defect inspection in TFT-LCD TCON
- Research on speed sensor fusion of urban rail transit train speed ranging based on deep learning
- A Generalized ML-Hyers-Ulam Stability of Quadratic Fractional Integral Equation
- Study on vibration and noise influence for optimization of garden mower
- Relay vibration protection simulation experimental platform based on signal reconstruction of MATLAB software
- Research on online calibration of lidar and camera for intelligent connected vehicles based on depth-edge matching
- Study on fault identification of mechanical dynamic nonlinear transmission system
- Research on logistics management layout optimization and real-time application based on nonlinear programming
- Complex circuit simulation and nonlinear characteristics analysis of GaN power switching device
- Seismic nonlinear vibration control algorithm for high-rise buildings
- Parameter simulation of multidimensional urban landscape design based on nonlinear theory
- Research on frequency parameter detection of frequency shifted track circuit based on nonlinear algorithm
Articles in the same Issue
- Nonlinear absolute sea-level patterns in the long-term-trend tide gauges of the East Coast of North America
- Insight into the significance of Joule dissipation, thermal jump and partial slip: Dynamics of unsteady ethelene glycol conveying graphene nanoparticles through porous medium
- Numerical results for influence the flow of MHD nanofluids on heat and mass transfer past a stretched surface
- A novel approach on micropolar fluid flow in a porous channel with high mass transfer via wavelet frames
- On the exact and numerical solutions to a new (2 + 1)-dimensional Korteweg-de Vries equation with conformable derivative
- On free vibration of laminated skew sandwich plates: A finite element analysis
- Numerical simulations of stochastic conformable space–time fractional Korteweg-de Vries and Benjamin–Bona–Mahony equations
- Dynamical aspects of smoking model with cravings to smoke
- Analysis of the ROA of an anaerobic digestion process via data-driven Koopman operator
- Lie symmetry analysis, optimal system, and new exact solutions of a (3 + 1) dimensional nonlinear evolution equation
- Extraction of optical solitons in birefringent fibers for Biswas-Arshed equation via extended trial equation method
- Numerical study of radiative non-Darcy nanofluid flow over a stretching sheet with a convective Nield conditions and energy activation
- A fractional study of generalized Oldroyd-B fluid with ramped conditions via local & non-local kernels
- Analytical and numerical treatment to the (2+1)-dimensional Date-Jimbo-Kashiwara-Miwa equation
- Gyrotactic microorganism and bio-convection during flow of Prandtl-Eyring nanomaterial
- Insight into the significance of ramped wall temperature and ramped surface concentration: The case of Casson fluid flow on an inclined Riga plate with heat absorption and chemical reaction
- Dynamical behavior of fractionalized simply supported beam: An application of fractional operators to Bernoulli-Euler theory
- Mechanical performance of aerated concrete and its bonding performance with glass fiber grille
- Impact of temperature dependent viscosity and thermal conductivity on MHD blood flow through a stretching surface with ohmic effect and chemical reaction
- Computational and traveling wave analysis of Tzitzéica and Dodd-Bullough-Mikhailov equations: An exact and analytical study
- Combination of Laplace transform and residual power series techniques to solve autonomous n-dimensional fractional nonlinear systems
- Investigating the effects of sudden column removal in steel structures
- Investigation of thermo-elastic characteristics in functionally graded rotating disk using finite element method
- New Aspects of Bloch Model Associated with Fractal Fractional Derivatives
- Magnetized couple stress fluid flow past a vertical cylinder under thermal radiation and viscous dissipation effects
- New Soliton Solutions for the Higher-Dimensional Non-Local Ito Equation
- Role of shallow water waves generated by modified Camassa-Holm equation: A comparative analysis for traveling wave solutions
- Study on vibration monitoring and anti-vibration of overhead transmission line
- Vibration signal diagnosis and analysis of rotating machine by utilizing cloud computing
- Hybrid of differential quadrature and sub-gradients methods for solving the system of Eikonal equations
- Developing a model to determine the number of vehicles lane changing on freeways by Brownian motion method
- Finite element method for stress and strain analysis of FGM hollow cylinder under effect of temperature profiles and inhomogeneity parameter
- Novel solitons solutions of two different nonlinear PDEs appear in engineering and physics
- Optimum research on the temperature of the ship stern-shaft mechanical seal end faces based on finite element coupled analysis
- Numerical and experimental analysis of the cavitation and study of flow characteristics in ball valve
- Role of distinct buffers for maintaining urban-fringes and controlling urbanization: A case study through ANOVA and SPSS
- Significance of magnetic field and chemical reaction on the natural convective flow of hybrid nanofluid by a sphere with viscous dissipation: A statistical approach
- Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications
- Research on vibration monitoring and fault diagnosis of rotating machinery based on internet of things technology
- An improved image processing algorithm for automatic defect inspection in TFT-LCD TCON
- Research on speed sensor fusion of urban rail transit train speed ranging based on deep learning
- A Generalized ML-Hyers-Ulam Stability of Quadratic Fractional Integral Equation
- Study on vibration and noise influence for optimization of garden mower
- Relay vibration protection simulation experimental platform based on signal reconstruction of MATLAB software
- Research on online calibration of lidar and camera for intelligent connected vehicles based on depth-edge matching
- Study on fault identification of mechanical dynamic nonlinear transmission system
- Research on logistics management layout optimization and real-time application based on nonlinear programming
- Complex circuit simulation and nonlinear characteristics analysis of GaN power switching device
- Seismic nonlinear vibration control algorithm for high-rise buildings
- Parameter simulation of multidimensional urban landscape design based on nonlinear theory
- Research on frequency parameter detection of frequency shifted track circuit based on nonlinear algorithm

