Abstract
Information borrowing from historical data is gaining increasing attention in clinical trials for rare and pediatric diseases, where small sample sizes may lead to insufficient statistical power for confirming efficacy. While Bayesian information borrowing methods are well established, recent frequentist approaches, such as the test-then-pool and equivalence-based test-then-pool methods, have been proposed to determine whether historical data should be incorporated into statistical hypothesis testing. Depending on the outcome of these hypothesis tests, historical data may or may not be utilized. This paper introduces a dynamic borrowing method for leveraging historical information based on the similarity between current and historical data. Similar to Bayesian dynamic borrowing, our proposed method adjusts the degree of information borrowing dynamically, ranging from 0 to 100 %. We present two approaches to measure similarity: one using the density function of the t-distribution and the other employing a logistic function. The performance of the proposed methods is evaluated through Monte Carlo simulations. Additionally, we demonstrate the utility of dynamic information borrowing by reanalyzing data from an actual clinical trial.
Acknowledgements
We are grateful to the editor, associate editor, and reviewers for their valuable comments and helpful suggestions.
-
Research ethics: Not applicable.
-
Informed consent: Not applicable.
-
Author contributions: The authors have accepted responsibility for the entire content of thismanuscript and approved its submission.
-
Use of Large Language Models, AI and Machine Learning Tools: None declared.
-
Conflict of interest: The authors state no conflict of interest.
-
Research funding: Nothing to declare.
-
Data availability: Not applicable.
A Appendix
A.1 Sensitivity analysis simulations
We performed the supplemental simulations according to Table 3. The number of simulations in each scenario was 10,000. The number of bootstrap sets was 5,000 due to the computing cost (Figures 5–9).
Parameter setting for supplemental simulation.
| Scenario | n t | n c | n h | μ t | μ c | μ h | σ t = σ c = σ h |
|---|---|---|---|---|---|---|---|
| S1 | 50 | 25 | 25 | 0 | 0 | −1 | 5 |
| S2 | 50 | 50 | 50 | 0 | 0 | −1 | 5 |
| S3 | 100 | 50 | 50 | 0 | 0 | −1 | 5 |
| S4 | 100 | 100 | 100 | 0 | 0 | −1 | 5 |
| S5 | 50 | 25 | 25 | 2 | 0 | 0 | 8 |
| S6 | 50 | 50 | 50 | 2 | 0 | 0 | 8 |
| S7 | 100 | 50 | 50 | 2 | 0 | 0 | 8 |
| S8 | 100 | 100 | 100 | 2 | 0 | 0 | 8 |
| S9 | 50 | 25 | 25 | 2 | 0 | 1 | 8 |
| S10 | 50 | 50 | 50 | 2 | 0 | 1 | 8 |
| S11 | 100 | 50 | 50 | 2 | 0 | 1 | 8 |
| S12 | 100 | 100 | 100 | 2 | 0 | 1 | 8 |
| S13 | 50 | 25 | 25 | 2 | 0 | −1 | 8 |
| S14 | 50 | 50 | 50 | 2 | 0 | −1 | 8 |
| S15 | 100 | 50 | 50 | 2 | 0 | −1 | 8 |
| S16 | 100 | 100 | 100 | 2 | 0 | −1 | 8 |
| S17 | 50 | 25 | 25 | 2 | −1 | 0 | 8 |
| S18 | 50 | 50 | 50 | 2 | −1 | 0 | 8 |
| S19 | 100 | 50 | 50 | 2 | −1 | 0 | 8 |
| S20 | 100 | 100 | 100 | 2 | −1 | 0 | 8 |
-
The type-1 error rates and powers are shown below.
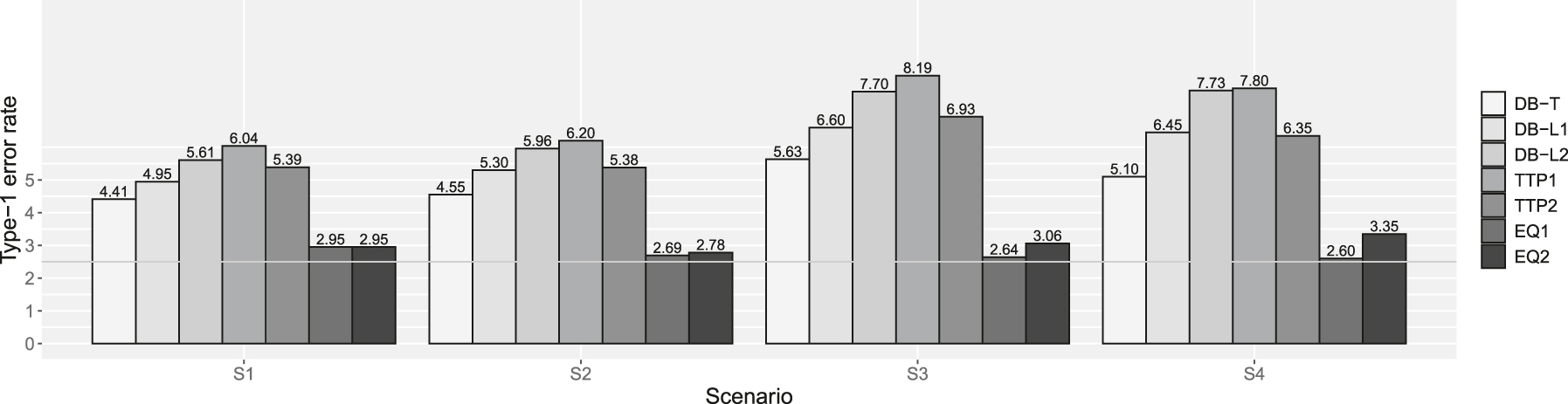
Type-1 error rates in supplemental simulation. DB-T is the dynamic borrowing method based on the density function of the t-distribution, DB-L1 is the dynamic borrowing based on the logistic function with β0 = −7.379 and β1 = 4.472, DB-L2 is the dynamic borrowing based on the logistic function with β0 = −7.374 and β1 = 3.747, TTP1 is the original TTP (test-then-pool) method under αh1 = 0.05, TTP2 is the original TTP (test-then-pool) method under αh1 = 0.10, EQ1 is the equivalence-based TTP (test-then-pool) method under αh2 = 0.05, and EQ2 is the equivalence-based TTP (test-then-pool) method under αh2 = 0.10, Gray line is 2.5 %.
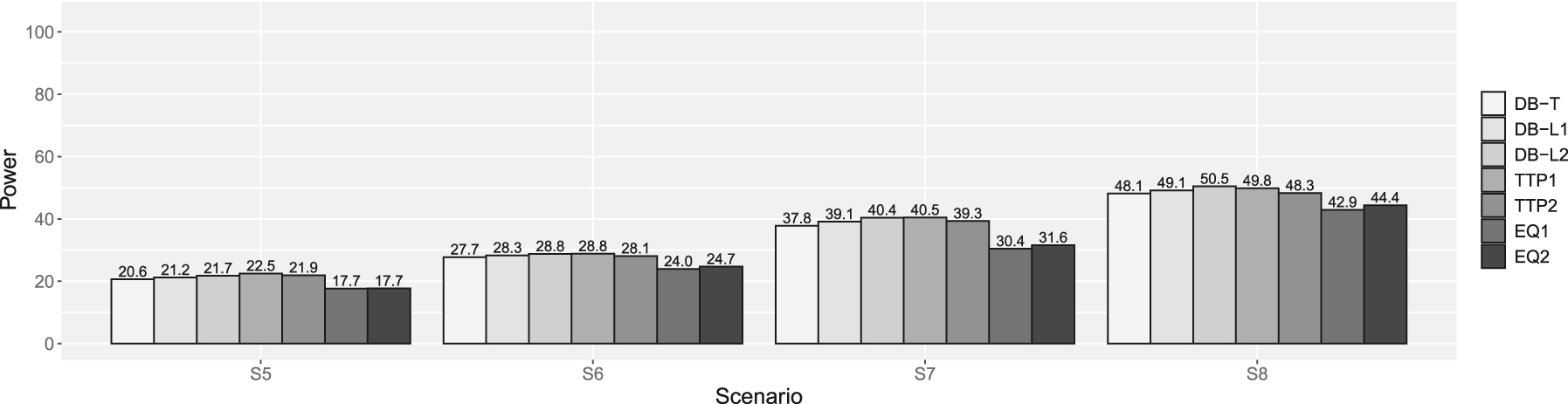
Powers of scenarios 5–8 in supplemental simulation. DB-T is the dynamic borrowing method based on the density function of the t-distribution, DB-L1 is the dynamic borrowing based on the logistic function with β0 = −7.379 and β1 = 4.472, DB-L2 is the dynamic borrowing based on the logistic function with β0 = −7.374 and β1 = 3.747, TTP1 is the original TTP (test-then-pool) method under αh1 = 0.05, TTP2 is the original TTP (test-then-pool) method under αh1 = 0.10, EQ1 is the equivalence-based TTP (test-then-pool) method under αh2 = 0.05, and EQ2 is the equivalence-based TTP (test-then-pool) method under αh2 = 0.10, Gray line is 2.5 %.
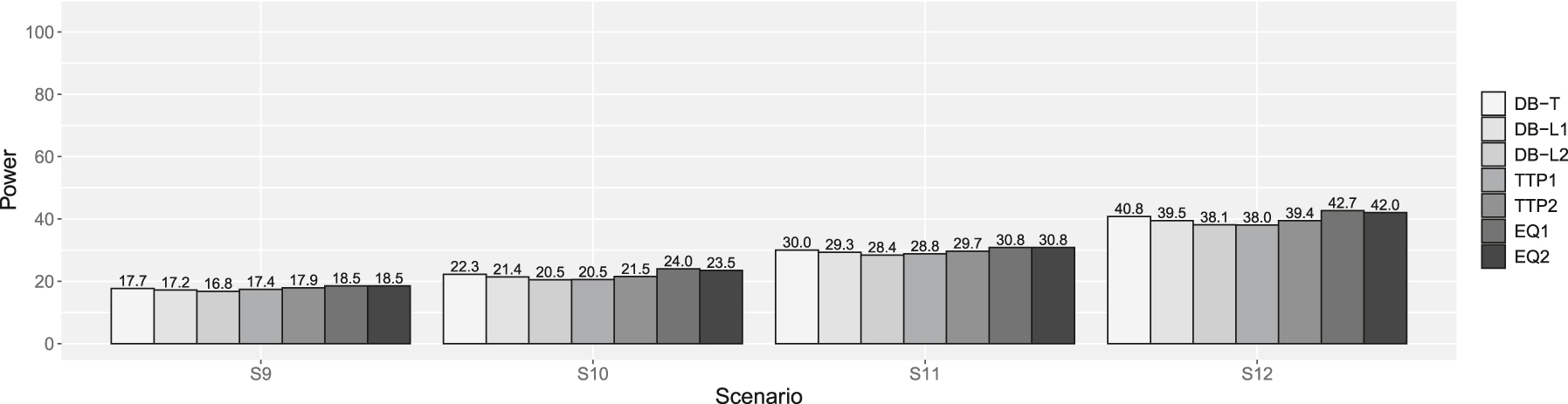
Powers of scenarios 9–12 in supplemental simulation. DB-T is the dynamic borrowing method based on the density function of the t-distribution, DB-L1 is the dynamic borrowing based on the logistic function with β0 = −7.379 and β1 = 4.472, DB-L2 is the dynamic borrowing based on the logistic function with β0 = −7.374 and β1 = 3.747, TTP1 is the original TTP (test-then-pool) method under αh1 = 0.05, TTP2 is the original TTP (test-then-pool) method under αh1 = 0.10, EQ1 is the equivalence-based TTP (test-then-pool) method under αh2 = 0.05, and EQ2 is the equivalence-based TTP (test-then-pool) method under αh2 = 0.10, Gray line is 2.5 %.
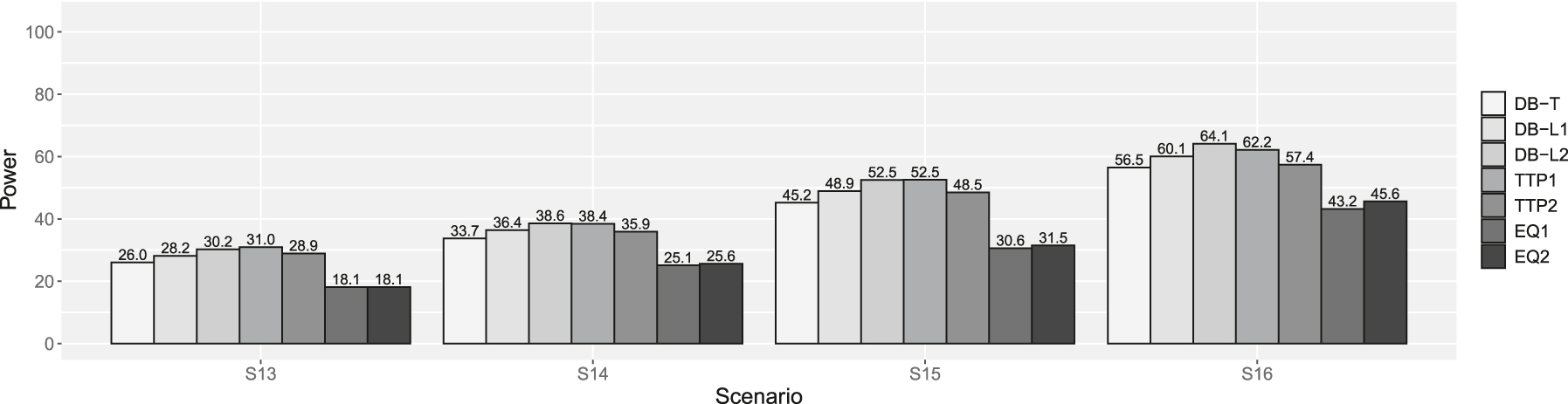
Powers of scenarios 13–16 in supplemental simulation. DB-T is the dynamic borrowing method based on the density function of the t-distribution, DB-L1 is the dynamic borrowing based on the logistic function with β0 = −7.379 and β1 = 4.472, DB-L2 is the dynamic borrowing based on the logistic function with β0 = −7.374 and β1 = 3.747, TTP1 is the original TTP (test-then-pool) method under αh1 = 0.05, TTP2 is the original TTP (test-then-pool) method under αh1 = 0.10, EQ1 is the equivalence-based TTP (test-then-pool) method under αh2 = 0.05, and EQ2 is the equivalence-based TTP (test-then-pool) method under αh2 = 0.10, Gray line is 2.5 %.
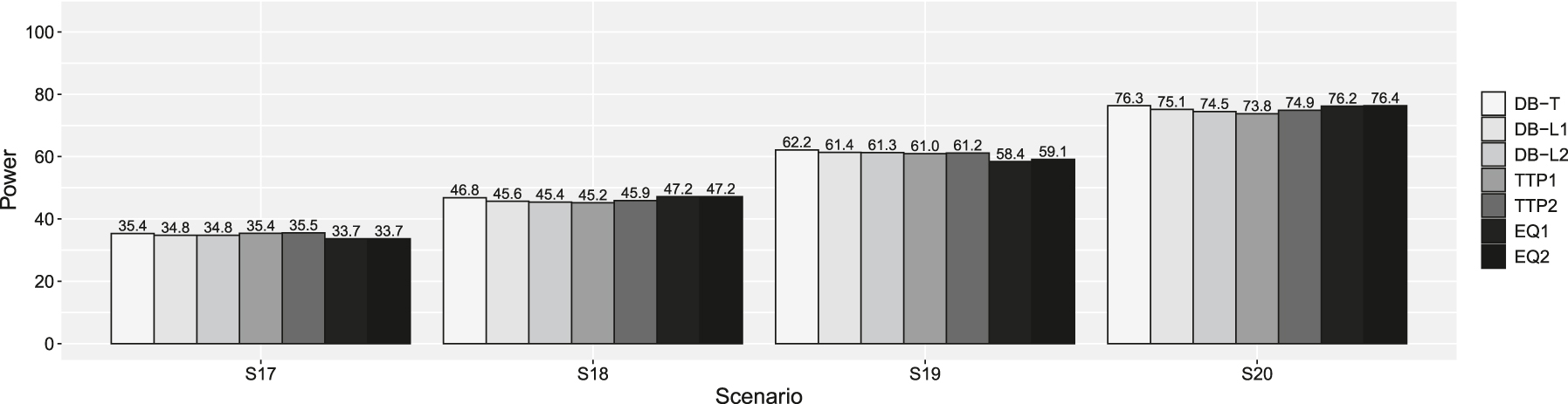
Powers of scenarios 17–20 in supplemental simulation. DB-T is the dynamic borrowing method based on the density function of the t-distribution, DB-L1 is the dynamic borrowing based on the logistic function with β0 = −7.379 and β1 = 4.472, DB-L2 is the dynamic borrowing based on the logistic function with β0 = −7.374 and β1 = 3.747, TTP1 is the original TTP (test-then-pool) method under αh1 = 0.05, TTP2 is the original TTP (test-then-pool) method under αh1 = 0.10, EQ1 is the equivalence-based TTP (test-then-pool) method under αh2 = 0.05, and EQ2 is the equivalence-based TTP (test-then-pool) method under αh2 = 0.10, Gray line is 2.5 %.
References
1. U.S. Food and Drug Administration. Considerations for the design and conduct of externally controlled trials for drug and biological products 2023. Available from: https://www.fda.gov/regulatory-information/search-fda-guidance-documents/considerations-design-and-conduct-externally-controlled-trials-drug-and-biological-products.Search in Google Scholar
2. Pocock, SJ. The combination of randomized and historical controls in clinical trials. J Chron Dis 1976;29:175–88. https://doi.org/10.1016/0021-9681(76)90044-8.Search in Google Scholar PubMed
3. Hobbs, BP, Carlin, BP, Mandrekar, SJ, Sargent, DJ. Hierarchical commensurate and power prior models for adaptive incorporation of historical information in clinical trials. Biometrics 2011;67:1047–56. https://doi.org/10.1111/j.1541-0420.2011.01564.x.Search in Google Scholar PubMed PubMed Central
4. Zhu, M, Sridhar, S, Hollingsworth, R, Chit, A, Kimball, T, Murmello, K, et al.. Hybrid clinical trials to generate real-world evidence: design considerations from a sponsor’s perspective. Contemp Clin Trials 2020;94:105856. https://doi.org/10.1016/j.cct.2019.105856.Search in Google Scholar PubMed
5. Ibrahim, JG, Chen, M-H, Gwon, Y, Chen, F. The power prior: theory and applications. Stat Med 2015;34:3724–49. https://doi.org/10.1002/sim.6728.Search in Google Scholar PubMed PubMed Central
6. Ibrahim, JG, Chen, MH. Power prior distributions for regression models. Stat Sci 2000:46–60. https://doi.org/10.1214/ss/1009212673.Search in Google Scholar
7. Duan, Y, Ye, K, Smith, EP. Evaluating water quality using power priors to incorporate historical information. Environmetrics: Off J Int Environmetrics Society 2006;17:95–106. https://doi.org/10.1002/env.752.Search in Google Scholar
8. Neuenschwander, B, Branson, M, Spiegelhalter, DJ. A note on the power prior. Stat Med 2009;28:3562–6. https://doi.org/10.1002/sim.3722.Search in Google Scholar PubMed
9. Neuenschwander, B, Capkun-Niggli, G, Branson, M, Spiegelhalter, DJ. Summarizing historical information on controls in clinical trials. Clin Trials 2010;7:5–18. https://doi.org/10.1177/1740774509356002.Search in Google Scholar PubMed
10. Schmidli, H, Gsteiger, S, Roychoudhury, S, O’Hagan, A, Spiegelhalter, D, Neuenschwander, B. Robust meta-analytic-predictive priors in clinical trials with historical control information. Biometrics 2014;70:1023–32. https://doi.org/10.1111/biom.12242.Search in Google Scholar PubMed
11. Viele, K, Berry, S, Neuenschwander, B, Amzal, B, Chen, F, Enas, N, et al.. Use of historical control data for assessing treatment effects in clinical trials. Pharm Stat 2014;13:41–54. https://doi.org/10.1002/pst.1589.Search in Google Scholar PubMed PubMed Central
12. Wen, L, Liu, F, Snavely, D. Revisit of test-then-pool methods and some practical considerations. Pharm Stat 2020;19:498–517. https://doi.org/10.1002/pst.2009.Search in Google Scholar PubMed
13. Li, R, Lin, R, Huang, J, Lu, T, Zhu, J. A frequentist approach to dynamic borrowing. Biom J 2023:2100406. https://doi.org/10.1002/bimj.202100406.Search in Google Scholar PubMed
14. Jiang, L, Nie, L, Yuan, Y. Elastic priors to dynamically borrow information from historical data in clinical trials. Biometrics 2023;79:49–60. https://doi.org/10.1111/biom.13551.Search in Google Scholar PubMed PubMed Central
15. Keller, M, Montgomery, S, Ball, W, Morrison, M, Snavely, D, Liu, G, et al.. Lack of efficacy of the substance p (neurokinin1 receptor) antagonist aprepitant in the treatment of major depressive disorder. Biol Psychiatry 2006;59:216–23. https://doi.org/10.1016/j.biopsych.2005.07.013.Search in Google Scholar PubMed
Supplementary Material
This article contains supplementary material (https://doi.org/10.1515/ijb-2024-0051).
© 2025 Walter de Gruyter GmbH, Berlin/Boston

