Investigation of Twist Waves Distribution along Structurally Nonuniform Yarn

1 Introduction

Analysis of research literature indicates that the structure of yarn depends on technological and kinematic factors. Structure control, i.e., ways to reduce twist loss and twist distribution along the yarn, and the methods of density regulation are not considered. It is a big problem as characteristics and quality of yarn depend on it. We consider the change in torsion quantity on a ring spinning machine. Formed yarn gets one twist per one turn of the runner. The number of coiled yarn twists changes depending on coil diameter. So, with an increase in diameter of winding, a larger twist occurred. Practice has shown that when twisting the yarn into a coil with a larger and smaller diameters, the difference is about 1% [1]. Twist unevenness also occurs due to vertical movement of the ring bar at a certain distance. So, for example, when lowering the ring strip, a shorter yarn is wound on the package because a part of its length is not wound due to increasing cylinder height. Therefore, in practice, it is used the average twist obtained when the number of torsions in any section of yarn divided by its length. In this case, appearance of twist irregularities is not taken into account, as it is very important for uniform yarn structure. In well-known papers [2,3,4,5,6,7,8,9,10,11,12,13,14,15,16,17], the roughness in twist is not analyzed, i.e., the conditions for formation of structure, on which the quality indicators of yarn obtained by the spinning machine are largely dependent, are not taken into account. As noted above, the difference in the number of yarn twist segments leads to appearance of twists in short sections when the annular strip moves up and down. Uniformity of twist distribution in this case depends on the spinning method, i.e., a twist along the yarn is distributed differently. Investigations of these issues are described in papers [2, 5,6,7,8,9,10]. On yarn twist distribution at different spinning methods, the positive results were obtained. A number of works are about the study of twist distribution in OE yarn [11,12,13,14,15]. The issue of twist distribution in the modified yarn was also studied [7]. In all papers, the process of twist wave distribution along the yarn is considered. In this case, the distribution of shear deformations occurs both along the axis of the yarn and along the radial direction. For twist distribution along the yarn, the structural unevenness is important. Twist distribution has been sufficiently investigated, but, as a rule, a structurally uniform and homogeneous product is considered, while the structure of the product is not considered. Therefore, twist distribution with such shortcomings is investigated in this paper.

2 Theory

In paper [5, 6] considered twist distribution of the yarn with structural unevenness where applied the generalized law for Hooke's anisotropic medium, according to which the correspondences between the components of the stress and strain tensors in ax symmetric coordinates are represented by five elastic constants [7].

where σ_rr, σ_zz, σ_θθ, σ_rz, σ_zθ, and σ_rθ are axial, radial, ring, and shear stresses and ɛ_rr, ɛ_zz, ɛ_θθ, ɛ_rz, ɛ_zθ, and ɛ_rθ are corresponding deformations in coordinates r0z, where axis 0z is directed along the axis of the yarn, and axis 0r is perpendicular to it, and the origin of coordinates is at point O (0,0) (Figure 1). Moreover, E₁ and E₂ correspond the Young's modulus along axial directions 0z and 0r, respectively, and υ₁₂ and υ₃₂ are corresponding Poisson's ratios, characterized by a change in yarn thickness and twist due to axial deformation G-modulus of planar rigidity (zθ).

Figure 1

Scheme of the yarn twisting process.

We denote the angular displacement of yarn arbitrary section by u_θ = u(r, z, t) = rθ (r, z, t) and consider the remaining components of the displacement vector to be equal to zero.

We denote the angular displacement of yarn arbitrary section by uθ = u(r, z, t) –, and the remaining components of the displacement vector are assumed to be zero; then, the components of the strain tensor will be expressed by using the following equation:

In Eq. (2), we see that deformation shifts ɛ_θz and ɛ_rθ are linearly depend on displacement u(r, z, t) and its derivative. In an adopted scheme, the motion equation is as follows:

after substitution of σ_zθ and σ_rθ from Eq. (1), the Eq. (3) takes the following form:

Eq. (4) describes the distribution of twisting waves along the yarn with a structurally heterogeneous property. In this case, the twist changes both along the axis of the yarn and along the radial direction. We consider a yarn with radius r₀ and final length l, sliding at constant speed ν on positive direction of axis 0z. It is more convenient to study the dynamics of a moving yarn in Euler variables. Therefore, passing from total time derivatives to a local one, we obtain the following equation:

where a2=E2r is the speed of cylindrical wave distribution and b=Gρ is the speed of twist wave distribution. We consider the process of formation and propagation of stationary wave processes in a yarn, a side surface that is free from tangential forces:

For yarn axis, the displacement roundedness condition is applied:

Yarn initial cross section A in Euler's variable is inactive, i.e.,

Full angular speed of the yarn in a cross section B will be equal to the following equation:

where ω_* is the angular speed of the twisting part.

The solution for Eq. (5) satisfying the boundary conditions of Eqs (6) and (7) can be represented as follows:

where function R_n(r) satisfied the following equation

and according to Eqs (9) and (10) the boundary conditions are

The solution of Eq. (11) is represented through the first-order Bessel function, R_n = J₁(λ_nx) λ_n – equation roots: J0(λnr0)(λn2r02−1)−λnr0J1(λnr0)=0 , where J₀ (x) is the zero order of Bessel function. Putting the expression u(r, z, t) from Eq. (10) to Eq. (5) and taking into consideration Eq. (11), we obtain the following equation:

Using the condition of orthogonality ∫0r0rRn(r)Rk(r)dr=0 at n ≠ k, we obtain the following equation:

where a=E2/ρ(1+υ32) .

Eq. (12) for known values of characteristic numbers λn describes the process of monochromatic twist wave distribution along the yarn. The matter of no twist change in a radial direction corresponding to a zero form of fluctuations with λ₁ = 0 is considered in the paper [11].

The solution of Eq. (14) is represented as follows:

Function u(r, z, t) has the following form:

where functions y_z(z) satisfy the equations

and according to Eqs (7) and (9) satisfy the following conditions

where pn=∫0r0rJ1(λnr)dr∫0r0rJ12(λnr)dr

We consider the case ν > b and solution for Eq. (16). Taking Eq. (17) into consideration, it will be represented as follows:

where α1n=b2ω2+a2λn2(ν2−b2)−νων2−b2 ,

A_n = A_1n + iA_2n is a complex constant, the component of which is determined from conditions of Eq. (18)

Thus, the angular movement of the yarn between sections A and B can be represented as follows:

where

As seen in Eq. (19), the values α_1n and α_2n are positive (α_1n > 0) and negative (α_2n < 0) numbers accordingly. They are the wave numbers corresponding to various forms of fluctuations on variable r and describing the wave distribution along positive and negative directions of axis 0z with speeds c_1n = − ω / α_2n (ω) and c_2n = − ω / α_1n (ω) accordingly. Here, the speeds of waves depend on frequency ω, which indicates the presence of wave dispersion.

If we do not take into account the twist changes in radial direction, then from Eq. (14), we obtain the expressions for the wave numbers as given in the study by Xu et al [10].

Moreover, the wave numbers k₁ and k₂ indicate the wave distribution along positive and negative directions of axis 0z, with the speeds b + ν and ν − b, associated with Doppler effect accordingly. From Eq. (19), it is seen that each eigen value λ_n corresponds to the distribution speeds c_1n (ω) and c_2n (ω), which depend on frequency ω, i.e., as the wave dispersion effect occurs. For wave distribution speeds, using the dimensionless values χ =ωr₀ / b, λ¯n=λnr0 , ν¯=ν/b , and σ = a / b, we obtain the following equation:

Figure 2 presented the curves of V_1n and V_2n speed dependence (referred to shear wave speed b) on dimensionless frequency χ = ωr₀ / b. The calculations were performed for the following values:

Figure 2

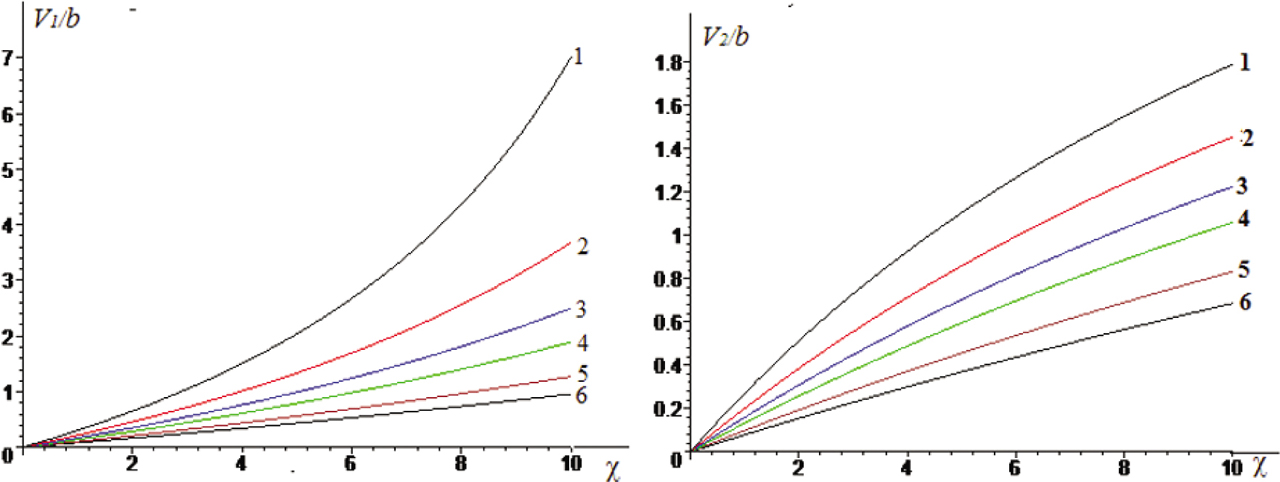
Dependences of backward (a) and direct (b) wave distribution speed on reduced frequency χ at different forms of fluctuations. 1− n = 3, 2 − n = 4, 3− n = 5, 4 − n = 6, 5 − n = 8, 6 − n =10.

The analysis of curves shows that Doppler effect for waves distributing along the yarns is held for each fluctuation form of the yarn by its thickness. In this case, the Doppler effect for the backward wave is stronger than that for the direct one. This is due to the processes of wave's reflection from the axis of the yarn.

4 Conclusion

The conditions for distribution of twist waves for a moving yarn with a constant speed are studied, and the parameters of Doppler effect for waves that are distributed along the yarn are determined. It was found that the Doppler effect for the backward wave is stronger than that for the direct one for 3.5 times. This is due to the processes of wave's reflection from yarn axis.