Different substituent effects on the supramolecular arrays in some (E)-halo- and nitro-benzaldehyde oximes: confirmation of attractive π(C=N)···π(phenyl) interactions

2.1 General

The asymmetric unit of each compound, 1–4, contains a single molecule. All four compounds crystallize in the monoclinic system: compounds 1, 2 and 4 in space group P2₁/c and compound 3 in P2₁/n, all with Z=4. The geometry around the oxime moieties is (E) in all four molecules. Figure 2 illustrates the atom arrangements and numbering schemes. The interplanar angles between the substituents and their attached phenyl group are all less than 10° in compounds 1, 2 and 4, but in the ortho-substituted compound, 3, all such angles are greater than 26°, due to steric hindrance between the nitro and oxime groups (Table 1). Details of the hydrogen bonding and other intermolecular interactions are provided in Table 2. The major intermolecular interactions in 1–4 involve the O13–H13···N12 hydrogen bonds. In 1 these generate C(3) chains which run parallel to the b axis formed by the action of the screw axis at (1/2, y, 1/4) (Fig. 3), whilst in 2–4, the O13–H13···N12 hydrogen bonds form R22(6) dimers across the centres of symmetry at (1/2, 0, 1/2), (1, 1/2, 1/2) and (1, 1̅, 1), respectively. Within the R22(6) dimers of compounds 2–4 there are O13–H13···O13 hydrogen bonds, with longer than usual H13···O13 distances, of 2.585(19), 2.636(18) and 2.59(2) Å, respectively, and small O13–H13···O13 angles, near 120°, see (Table 2). The involvement of pairs of the O13–H13···O13 hydrogen bonds subdivides the R22(6) dimers into three rings – two R12(3) rings and one R22(4) ring. Such R12(3) and centrosymmetric R22(4) rings have been variously reported for organic molecules. Indeed a recent CCDC data base search revealed more than 500 entries of non-solvated structures having centrosymmetric H₂O₂ rings with H–O–H angles of 120° or less and H–O distances up to the sum of the contact radii, 2.72 Å, of oxygen and hydrogen. In particular, the literature search indicated that various aldoximes, but not all, possess similar sub-divided R22(6) rings, with much smaller H–O distances, e.g., less than 2.60 Å: examples include 4-Me₂NC₆H₄CH=NOH from room temperature data [CCDC codes MABZOX and 1208893: ref 26] and more from data at low temperatures [e.g. 2,3-Me₂-4-MeOC₆H₂CH=NOH: CCDC codes OKUHAD and 161452; ref 27]: 4-BrC₆H₄CH=NOH: CCDC codes BAGWOW and 181389: ref 28]. The data for compounds 2–4 are thus not unusual and do suggest that the O13–H13···O13 hydrogen bonds can be considered as contributing to the overall stability of the R22(6) dimers. Two views of each of the R22(6) dimers are shown in Fig. 4, one looking face-on and the other side-on to the parallel phenyl rings. The perpendicular distances between the parallel phenyl rings in the R22(6) dimers are 0.955, 2.609 and 0.751 Å, respectively in 2–4 (Fig. 4): the greater distance in compound 3 reflects the greater deviation of its oxime unit from the plane of its attached phenyl group as a consequence of steric hindrance between its groups in ortho-position.

Fig. 2:

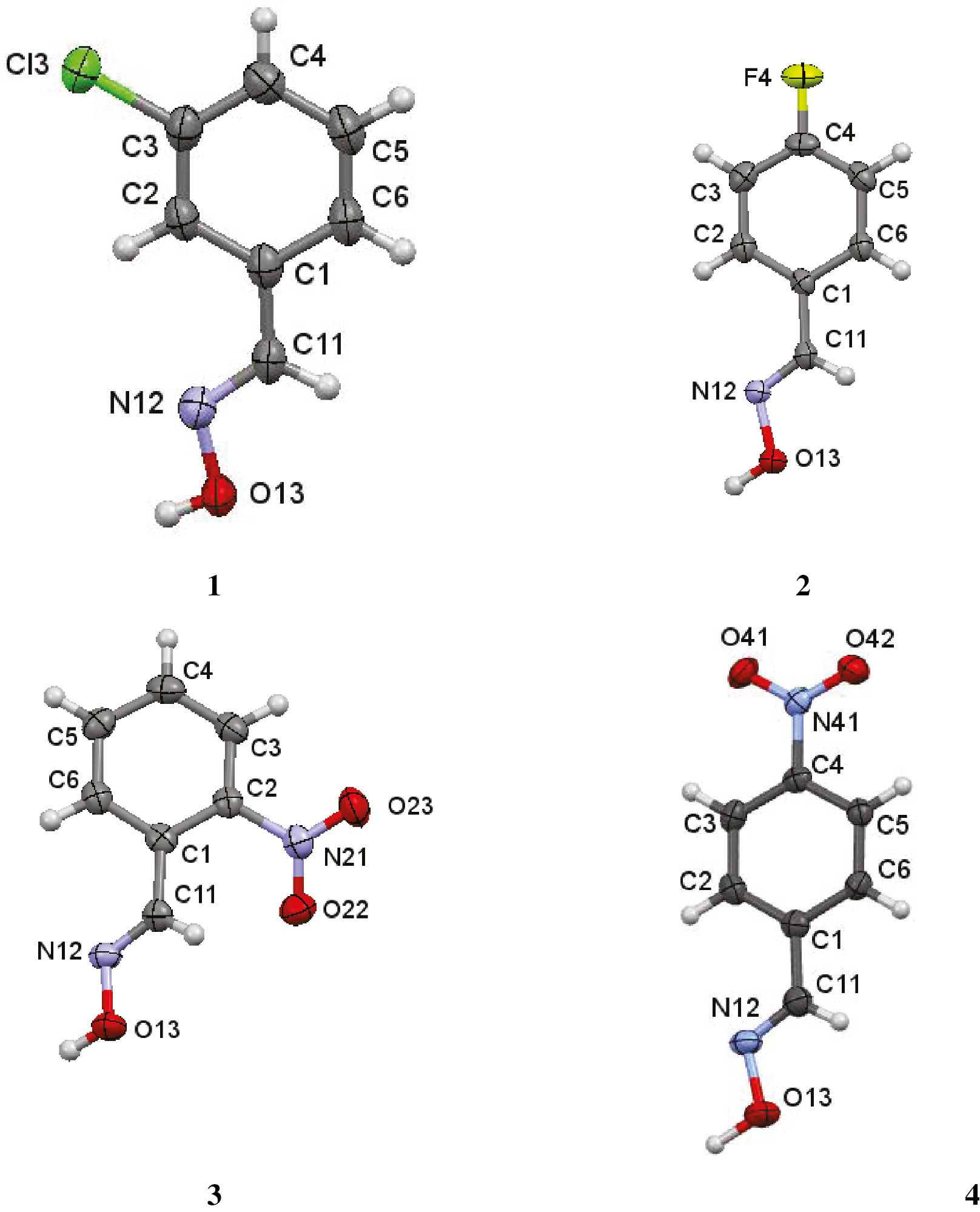
Views of the asymmetric units of 1–4 with the atom numbering schemes. Displacement ellipsoids are drawn at the 80% probability level, hydrogen atoms as spheres with arbitrary radii.

Fig. 3:

The C3 chain in compound 1, formed from C13–H13···N12 hydrogen bonds. Table 3 lists the symmetry operations.

Fig. 4:

Two views of the R22(6) dimers for compounds 2, 3 and 4.

Table 3 lists the percentage atom-atom contacts for all compounds.

2.2 Other intermolecular interactions in individual compounds

2.2.1 The chain-forming compound 1

Interactions in 1, in addition to the C(3) chain forming O13–H13···N12 hydrogen bond, are (i) short Cl···Clⁱ intermolecular contacts, which link the C3 chains: the Cl···Cl distance is 3.418(6) Å, just within the sum of the contact radii of 3.50 Å (symmetry code: i=–x, –y, –z), and (ii) π(C=N)···π(phenyl) interactions, with a Cg(C=N)···Cg(phenyl)ⁱⁱ distance of 3.290(1) Å (Cg being the center of gravity of the phenyl ring): symmetry code: ii=x, −1+y, z) (Fig. 5). The π(C=N)···π(phenyl) interaction is more fully discussed in the Section: π(C=N)···π(phenyl) contacts below.

Fig. 5:

Compound 1. (a) Part of a stack of molecules formed from π(C=N) ···π(phenyl) interactions. The Cg(C=N)···Cgⁱ (phenyl) distance is 3.290(1) Å (symmetry code: i=x, –1+y, z; (b) the overlap of the C=N and phenyl π systems in successive rows of the π(C=N)···π(phenyl).

The Hirshfeld surface and Fingerprint (FP) plots [29], [30] for compound 1 are shown in Fig. 6. The C···C, Cl···Cl and N···H close contacts are designated as are the site of the π···π contacts. In the FP plot, the two spikes pointing southwest relate to N···H contacts including those making the C(3) chains; the high density of pixels near d_i≈d_e≈1.8 Å is due to C···C contacts, and that close to the d_i≈d_e≈1.8–2.0 Å region is due to Cl···Cl contacts, and the wings ending approximately at (d_i; d_e)≈(1.2; 1.8) Å are due to H···Cl contacts.

Fig. 6:

Compound 1. (a) View of the Hirshfeld surface mapped over d_norm: the set of two intense red area spots relate to N···H close contacts in forming the C3 chain; also designated are the sites of the C···C and π···π contacts; (b) the FP plot, the two spikes pointing southwest relate to N···H contacts including those making the C(3) chains; the high density of pixels near d_i≅d_e≅1.8 Å are due to C···C and those close to d_i≅d_e≅1.8–2.0 Å interval are due to Cl···Cl contacts, wings ending approximately at (d_i; d_e)≅(1.2; 1.8) Å are due to H···Cl contacts.

Compound 1 has the highest percentage of H···C/C···H contacts and the lowest percentage of H···H and H···O/O···H contacts of all four compounds studied here, see Table 3. There is also a high percentage of H···Cl/Cl···H contacts in compound 1

2.3 The compounds forming R22(6) dimers

2.3.1 Compound 2

In 2, in addition to the O13–H13···N12 and O13–H13···O13 hydrogen bonds, there are weaker C11–H11···O13, C3–H3···F4 and C5–H5···F4 hydrogen bonds, and π···π interactions. The overall structure can be conveniently considered to be formed from two sub-structures. Firstly, the R22(6) dimers are linked by the C5–H5···F4 hydrogen bonds into chains, which are further linked by the π···π interactions into sheets, as illustrated in Fig. 7a. Within the sheets are R22(8) rings, arising from the C–H···F hydrogen bonds, as well as the R22(6) rings. The overlap of the π systems in successive layers of the π···π stacks is illustrated in Fig. 7b: the Cg···Cgⁱ distance is 3.7672 (7) Å, and the perpendicular distance between the planes is 3.4186(5) Å with a slippage of 1.583 Å (symmetry code: i=x, −1+y, z). The second sub-structure in compound 2 is a further sheet formed from combinations of C11–H11···O13 and C3–H3···F4 hydrogen bonds. Each of these hydrogen bonds individually generates C4 spiral chains, which run parallel to the b axis, formed by the action of the screw axis at (1/2, y, 1/4). Within this sheet is a network of R44(22) rings (Fig. 7c). Combination of the two different sheets generates a three-dimensional array.

Fig. 7:

Compound 2. (a) Part of a sheet formed from linking the R22(6) dimers with C5–H5···F4 hydrogen bonds and π···π interactions; (b) the overlap of the π systems in successive layers of the π···π stack, shown in Fig. 7a; (c) part of a sheet formed from linkages using C11–H11···O13 and C3–H3···F4 hydrogen bonds. Details of the intermolecular interactions are displayed in Table 3.

Compound 2 has the highest percentage of H···H contacts, 32.0%, significantly higher than the sum, 21.8%, of fluorine contacts (H···F/F···H, F···C/C···F and F···F). The H···O/O···H, H···C/C···H, and H···N/N···H contacts all are ca 10%.

The three other 4-halobenzaldehyde oximes, (E)-4-XC₆H₄CH=N–OH (X=Cl [31], Br [28] and I [20]) were also shown to form R22(6) dimers.

2.3.2 Compound 3

The intermolecular interactions in compound 3, in addition to the dimer forming O13–H13···N12 and C3–H3···O13 hydrogen bonds, are C6–H6···O23(nitro) hydrogen bonds and π···π interactions. The R²₂(6) dimers are linked by the C3–H3···O13 and C6–H6···O23 hydrogen bonds into sheets. These sheets are composed of a network of R33(12) and R44(26) rings, complemented by R22(6) rings (Fig. 8a). The sub-structure generated from linking the R22(6) dimers with the π···π interactions is illustrated in Fig. 8b. The overlap of the π systems in successive layers of the stack is shown in Fig. 8c: the Cg···Cgⁱ distance is 3.6405(7) Å, the perpendicular distance between the planes is 3.5064 (5)Å and the slippage is 0.979 Å (symmetry code: −1+x, y, z). The distance between N21(nitro group) and O22ⁱ (nitro group) in successive layers of the stack is 3.0658(13) Å, which is at the sum of the contact radii and thus does not suggest any significant nitro group – nitro group interaction. There is however a short O13(hydroxyl)···O23ⁱⁱ(nitro) separation of 2.928(13) Å, well within the sum of the contact radii of 3.04 Å (symmetry code: ii=3/2–x, 1/2+y, 1/2–z).

Fig. 8:

Compound 3. (a) Part of a sheet of molecules formed from combination of O13–H13···N12, C3–H3···O13 and C6–H6···O23 hydrogen bonds; (b) part of a double π···π stack, formed from the R22(6) dimers; (c) the overlap of the π systems in the stacks shown in Fig. 8b. Details of the intermolecular interactions are displayed in Table 3.

2.3.3 Compound 4

There are major differences between the contacts found in compounds 3 and 4, which are both nitro phenyl derivatives. In compound, 4, in addition to the O13–H13···N12 and C3–H3···O13 hydrogen bonds, which form the R22(6) dimers, there are other intermolecular interactions solely involving the nitro group atoms. Three distinct types of nitro group interactions are found in compound 4, all of which link the R22(6) dimers into more elaborate sub-structures: (i) the nitro group oxygen atom, O41, acts as the acceptor in C6–H6···O41ⁱ and C11–H11···O41ⁱⁱ hydrogen bonds (Table 2). (ii) nitro···nitro group interactions [32], with a O42···N41ⁱⁱⁱ separation of 2.8641(13) Å (symmetry code: iii=–x, 1/2+y, 1/2–z), and (iii) both the oxygen atoms of the nitro group are used in N41–O41···πⁱⁱⁱ and N41–O42···πⁱⁱⁱ, with O41···πⁱⁱⁱ and O42···πⁱⁱⁱ distances of 3.8471(10) and 3.3858(10) Å, respectively (symmetry code iii=x, 1+y, z). The first of these interactions, involving the C6–H6···O41 and C11–H11···O41 hydrogen bonds, link the dimers into tilted two-molecule wide columns as illustrated in Fig. 9a. Within the columns are R22(6) and R44(26), as well as R22(6) rings. The nitro groups at the ends of the R22(6) dimers are involved in the nitro···nitro group contacts with O41···O42^v and O42···N41^vi distances of 2.9294(11) and 2.8641(13) Å, respectively, both within the appropriate sums of the contact radii of 3.04 and 3.07 Å, respectively (symmetry codes: v=–x, −1/2+y, 1/2–z; vi=–x, 1/2+y, 1/2–z). These nitro···nitro group interactions, which provide a Chevron-type arrangement, are illustrated in Fig. 9b. Figure 9c shows the arrangement obtained from linking the R22(6) dimers by N41–O41···π, N41–O42···π and the nitro···nitro interactions. Within this arrangement are layers of R22(6) dimers in which the C=N unit of the oxime in one layer sits above a phenyl ring in a successive layer, with a Cg(C=N) ···Cg(phenyl) distance of 3.406 Å, which suggests a π(C=N)···π(phenyl) interaction (Fig. 9d and e). This is longer than the equivalent distance found in compound 1 and, in addition, this positioning of the C=N unit may be serendipitous and a consequence of the other interactions in the column, for example the N41–O41···π, N41–O42···π interactions (Fig. 9d). However, while it is not so clear cut as the situation in compound 1, such a π(C=N) ···π(phenyl) interaction is stabilizing as discussed below in the chapter on π(C=N) ···π(phenyl) interactions.

Fig. 9:

Compound 4. (a) Part of a two-molecular wide tilted sheet formed from linking the R22(6) dimers by C6–H6···O41 and C11–H11···O41 hydrogen bonds; (b) the Chevron style arrangement arising from the nitro-nitro group interactions; (c) a part of the arrangement generated from linking the R22(6) dimers by N41–O41···π, N21–O42···π and the nitro-nitro interaction; (d) part of the stack obtained from combination of the N41–O41···π, N21–O42···π and π (C=N) ···π(phenyl) interactions; (e) the overlap of molecules in the stack shown in Fig. 9d. Details of the intermolecular interactions are displayed in Table 3.

2.4 Comparison of the structures of the three isomeric nitrobenzaldehyde oximes

Comparisons of the structures of the three isomeric mono-nitrobenzaldehyde oximes can be made, as the structure of 3-nitrobenzaldehyde oxime, 5, has been briefly reported from data collected at room temperature [33]. The ortho- and meta-isomers, compounds 3 and 5, have similar sets of intermolecular interactions, which are significantly different from those of the para-isomer, 4. While only the classical hydrogen bonds forming the R22(6) dimers were mentioned in the published report on 4 [33], a deeper analysis of the structure has indicated a strong π···π interaction, with a Cg···Cg distance of 3.7738(14) Å, a distance between parallel phenyl rings of 3.4677(10) Å and a slippage of 1.489 Å, similar to the situation in the ortho-isomer, 3. Also as in compound 3, the nitro group atoms are only involved in C–H···O hydrogen bonds, but rather than the sheet found in compound, 3, only a two-molecule wide column is generated from the R22(6) dimers and the available C–H···O hydrogen bonds in 5.

No π(C=N)···π(phenyl) interaction is apparent in 5, as the relevant Cg···Cg distance is >4.4 Å.

2.5 Hirshfeld surfaces and FP plots for compounds, 2–4

Views of the Hirshfeld surface [29], [30] for compounds, 2–4, which form R22(6) dimers, are illustrated in Fig. 10. For each compound, red areas are designated corresponding to O–H···N and N···H–O and other contacts, including the O···O and N···O close contacts found in compound 4. The FP plots for these three compounds are illustrated in Fig. 11. The similarity of the three FP plots is apparent: any differences between the plots arise from the different percentages of H···X (X=H, O, N, Cl or F) contacts for each molecule. The N···H close contacts are responsible for the pair of sharp spikes ending at d_e/d_i ca 1.2 Å (d_e and d_i are the axes of the FP plots). Close to these spikes are other, less-sharp, peaks, which correspond to O···H contacts, and the area within the spikes appearing as the comb-like teeth is due to H···H close contacts involving the hydroxyl group of the oxime. The small teeth-like peaks shown in Fig. 11 for the R22(6) dimer-forming compounds and their absence in the FP plot for the C3 chain-forming compound 2, shown in Fig. 6, clearly point to major differences in the structures. A breakdown of the H···X (X=H, O, N, and F) contacts in compound 2, is illustrated in Fig. 12. The percentage atom···atom contacts in 2–4 are shown in Table 3. As expected for the two nitro derivatives, 3 and 4, the combined percentages of close contacts involving oxygen are high.

Fig. 10:

Views of the Hirshfeld surface mapped over d_norm for compounds (a) 2, (b) 3 and (c) 4, forming R22(6) rings. In each compound, red areas relating to O–H···N and N···H–O and other contacts are designated.

Fig. 11:

FP plots for compounds (a) 2, (b) 3 and (c) 4, which form the R22(6) dimers. The N···H close contacts result in the pair of sharp spikes in the FP plot, ending at d_e/d_i ca.1.2 Å. Very close to those spikes are other, less-sharp, peaks which arise from O···H contacts. The area within the spikes appearing as “teeth of a comb” is due to H···H close contacts involving the H atoms of the hydroxyl group of the oxime. The higher percentage of C···C contacts in compound 3 are indicated by the higher pixel frequency at d_e / d_i≅1.8 Å as shown by the light green and red areas.

Fig. 12:

Partial FP plots for 2 showing pixels due to (a) F···H, (b) H···H, (c) N···H and (d) O···H contacts.

2.6 π(C=N)···π(phenyl) interactions

The clear indication of a π(C=N)···π(phenyl) interaction in compound 1, and the less clear indication in compound 4, led to an investigation of similar interactions in other oximes with Cg(C=N)···Cg(phenyl) distances up to 3.30 Å. Among the compounds found were the high pressure P2₁/n phase of salicylaldoxime [SALOXM-08] [34], the high pressure I2/a phase of 3-t-butylsalicylaldoxime [NIRJII-07] [35] and benzene-1,3,5-tris(N-hydroxy-methanimine) [ADOJEK] [36]. Oxime ethers, such as, 1-(salicylidene-oxy)-2-(3-methoxysalicylidenesmino-oxy)ethane [FOJROM] [37] were also found with short Cg(C=N)···Cg((phenyl) distances. A search on 12-06-2018 of the CCDC data base of compounds possessing C=N–X fragments (X=OH, OR, NR¹R² etc) with Cg(C=N)···Cg(phenyl) distances less than 3.30 Å, revealed more than 80 hits. Extending the Cg(C=N)···Cg(phenyl) distance beyond 3.30 to 4.0 Å brought in many more compounds. Short Cg(C=N)···Cg(phenyl) distances were found to be very much less common for compounds with -CH=N–OR (R=H or organyl) fragments, compared to compounds with C=N–NXY fragments.

2.6.1 Theoretical calculations on the potential of π(C=N) ···π(phenyl) interactions in compound 1

A theoretical study of the potential π(C=N) ···π(phenyl) interactions was carried out on compound 1, using initially a stacked dimer, extracted from the CIF (structure A in Fig. 13). Figure 13 shows the various structures and sub-structures, and their associated calculated interaction energies. To separate the two possible intermolecular interactions in the dimer A – the π(CN)···π(phenyl) interaction and the OH···N hydrogen bond – two additional dimers were constructed: replacement of the CH=N(OH) moiety by a hydrogen atom in the upper molecule removes the OH···N interaction (structure B) and replacement of the chlorophenyl unit by a hydrogen atom in both molecules removes the potential π(CN) ···π(phenyl) interaction (structure C). The interaction energy of structure A (−22.9 kJ mol⁻¹) shows that there is a considerable and attractive interaction between the two molecules at the experimental geometry. However, only part of this attraction can be attributed to the π(CN)···π(phenyl) interaction, as there is also an OH···N interaction in the dimer. When optimizing the geometry (structure D), this interaction makes the structure less parallel. Structure E, where one of the molecules is rotated to avoid this OH···N interaction, remains parallel and has an interaction energy of −29.6 kJ mol⁻¹. Assuming that this interaction energy results from two CN···π interactions, one such interaction is estimated to be −14.8 kJ mol⁻¹.

Fig. 13:

Stuctures, used in the theoretical calculations on the π(CN)···π(phenyl) interaction in compound 1, and their energies.

Structures B and C aim to eliminate the π(CN)···π(phenyl) and OH···N interactions. The sum of the interaction energies of B and C (−23.9 kJ mol⁻¹) is not far off from that of the full dimer (−22.9 kJ mol⁻¹), so it seems reasonable to assume that the interaction energy of the full dimer is a sum of the π(CN)···π(phenyl) and OH···N interactions. These results suggest that the π(CN)···π(phenyl) interaction accounts for −19.3 kJ mol⁻¹. This is a bit higher than the −14.8 kJ mol⁻¹ estimated above, but is probably an overestimation, as there are more attractive interactions in this dimer than just the π(CN)···π(phenyl) interaction (for example, with the hydrogen atom of the upper molecule above the ring of the lower molecule in structures A and B). In summary, the calculations support that the CN···π interaction is attractive, with a considerable magnitude estimated to be in the range of −15 to −18 kJ mol⁻¹.

Table 4 shows a breakdown of the interaction energy into separate contributions using sSAPTO. The sSAPT0 interaction energies are in reasonable agreement with the PBE0 values. The results show that dispersion is relatively more important in A and B compared to C, and electrostatics are more important in C.

Table 4:

Crystal data.

	1	2	3	4
Crystal data
Chemical formula	C7H6ClNO	C7H6FNO	C7H6N2O3	C7H6N2O3
Mr	155.58	139.13	166.14	166.14
Crystal system, space group	Monoclinic, P21/c	Monoclinic, P21/c	Monoclinic, P21/n	Monoclinic, P21/c
Temperature, K	100	100	100	100
a, b, c, Å	12.1214(7), 4.4332(2), 13.6946(8)	14.2137(5), 3.7672(1), 11.9364(4)	3.6405(1), 13.4466(6), 14.8993(7)	6.2083(2), 4.8431(2), 24.3013(8)
β, deg	109.283(6)	99.210(3)	95.086(4)	94.986(3)
V, Å3	694.62(7)	630.90(4)	726.48(5)	727.91(5)
Z	4	4	4	4
Radiation type	MoKα	MoKα	MoKα	MoKα
μ, mm−1	0.5	0.1	0.1	0.1
Crystal size, mm3	0.20×0.05×0.03	0.20×0.10×0.02	0.15×0.05×0.03	0.06×0.05×0.01
Data collection
Diffractometer	(a)	(a)	(a)	(b)
Absorption correction	(c)	(c)	(c)	(c)
No. of measured/independent/observed [I>2 σ(I)] reflections	14977/1591/1381	13530/1443/1349	16152/1669/1549	8656/1670/1462
Rint	0.068	0.029	0.064	0.021
(sin θ/λ)max, Å––1	0.649	0.649	0.649	0.649
Refinement
No. of reflections	1591	1443	1669	1670
No. of parameters	95	95	113	113
No. of restraints	0	0	0	1
H atom treatment	(d)	(d)	(d)	(d)
R[F2>2 σ(F2)], wR(F2), S	0.041, 0.118, 1.08	0.033, 0.101, 1.09	0.033, 0.089, 1.07	0.036, 0.102, 1.08
Δρmax/min, e Å–3	0.53, –0.37	0.35, –0.21	0.31, –0.16	0.38, –0.23
CCDC No	1846653	1846654	1846655	1856711

1. (a) Rigaku FRE+equipped with VHF Varimax confocal mirrors and an AFC12 goniometer and HyPix 6000 detector diffractometer; (b) XtaLAB AFC12 (RCD3): Kappa single diffractometer; (c) Multi-scan CrysAlis Pro 1.171.39.30d (Rigaku Oxford Diffraction, 2017) Empirical absorption correction using spherical harmonics, implemented in SCALE3 ABSPACK scaling algorithm; (d) H atoms treated by a mixture of independent and constrained refinement. Computer programs used: CrysAlis PRO 1.171.39.30d [38], Oscail [39], Shelxt [40], ShelXle [41], Shelxl2017/1 [42], Mercury [43], Platon [44].

3.1 Synthesis and crystallization

The compounds, 1–4, were prepared by refluxing the corresponding aldehyde with hydroxyamine in an aqueous solution containing potassium carbonate, rather than pyridine, following a published procedure [45]. They were purified by recrystallization from methanol solutions.

3-Chlorobenzaldehyde oxime, 1: m.p. 64–65°C [46]. 4-Fluorobenzaldehyde oxime, 2:. m.p. 85–87°C (lit [http://synquestlabs.com/product/id/53507.html]: m.p. 85–86°C). 2-Nitrobenzaldehyde oxime, 3: m.p. 97–98°C (lit. [https://www.alfa.com/en/catalog/A14565/]: m.p. 98–102°C). 4-Nitrobenzaldehyde oxime, 4: m.p. 123–124°C (lit. [https://www.alfa.com/en/catalog/L09144/]: m.p. 122–125°C).

3.2 Crystallography

Crystal data, data collection and structure refinement details are summarized in Table 5 [38], [39], [40], [41], [42], [43], [44]. In each case the oxime group has an (E) geometry. In all compounds the oxime hydroxyl hydrogen atoms were refined and their positions checked on a final difference map where all atom positions lie within the maximum contour level. All other hydrogen atoms were refined as riding atoms at a distance of 0.95Å.

The Hirshfeld surfaces and two-dimensional fingerprint (FP) plots [29], [30] were generated using Crystal Explorer 3.1 [29], [30]. The Hirshfeld surface mapped over d_norm is scaled in the range −0.68 to 1.17.

3.3 Theoretical study of the π(C=N)···π(phenyl) interaction in compound 1

Hydrogen geometries were optimised with the BLYP-D3 density functional (BLYP [47], [48] augmented with Grimme’s D3 dispersion correction [49] in conjunction with the def2-SVP basis set [50] using Orca [51], keeping all other atoms at the experimental geometry. Interaction energies were computed with PBE0-D3 (the hybrid PBE0 functional [52] augmented with D3) and the ma-def2-TZVP basis set [50], [53]. The counterpoise procedure [54] was used to eliminate BSSE. As the heavy atoms are at the crystallographic positions, deformation energies were omitted. The interaction energies were thus computed as follows:

Here, the superscript {AB} denotes that all calculations employ the dimer basis set, and the attributes in round brackets, (AB), denote that all calculations employ the dimer geometry.

Additional calculations at the PBE0-D3/ma-def2-TZVP level employing the counterpoise procedure. The structures were additionally analyzed with Symmetry-Adapted Perturbation Theory (SAPT) [55], which calculates the interaction energy directly without computing the dimer and monomer energies. We employed a scaled version, sSAPT0 [56], of the simplest truncation of the SAPT expansion (SAPT0), with a truncated aug-cc-pVDZ basis set labelled jun-cc-pVDZ (previously called aug-cc-pVDZ’ [57]), using Psi4 [58]. This level of theory was recommended as a good-performing, efficient level of SAPT [56].