Abstract
Three series of rare earth-transition metal-indides RE3T2In4 (RE=Y, Gd–Tm, Lu; T=Ni, Ru, Rh) were synthesized from arc-melted RE3T2 precursor compounds and indium tear shot in sealed niobium ampoules using different annealing sequences. The new indides crystallize with the hexagonal Lu3Co2In4-type structure, space group P6̅. All samples were characterized on the basis of Guinier powder patterns and six structures were refined from single crystal X-ray diffractometer data. The RE3T2In4 structures are derived from the ZrNiAl type through RE/In ordering, paralleled by a symmetry reduction from P6̅2m to P6̅. This induces twinning for some of the investigated crystals. The main crystal chemical motifs of the RE3T2In4 structures are trigonal prisms of rare earth, respectively indium atoms that are filled by the transition metals.
1 Introduction
The ZrNiAl structure [1], [2], [3], a ternary ordered version of the Fe2P type [4] is one of the basic structure types for equiatomic intermetallic compounds RETX and TT′X (RE=rare earth element, T=transition metal; X=element of the 3rd, 4th, or 5th main group). More than 1300 representatives are listed in the Pearson Data Base [5]. This structure type allows for a broad range of element combinations, variations of the valence electron count and certain differences in the atomic radii. Especially the cerium [6], [7], ytterbium [7], [8], and uranium [9], [10], [11] containing phases have been studied with respect to their greatly varying magnetic ground states and valence changes. If the geometrical requests for a given element combination cannot be fulfilled, superstructure formation along with small distortions (and thinning of the subcell symmetry) is a way out [12], [13].
Besides distortions, the ZrNiAl structure also allows for coloring on the four crystallographically independent sites, leading to other ordering variants with distinctly different bonding patterns. Typical compositions are Ni6BSi2, Zr6CoGa2, Lu3CoGa5, Zr3Cu4Si2, or Y3NiAl3Ge2 [14], all keeping the subcell structure, space group P6̅2m. This is different for the structures of Ti4Ni2Ga3 [15] and the series RE3Co2In4 (RE=Ho, Er, Tm, Lu) with the Lu3Co2In4 type [16]. The Ti4Ni2Ga3 type shows a doubling of the subcell c axis and substantial shifts of several atoms off the subcell mirror planes. The 1:1 Co/In coloring within the trigonal rare earth prisms in the Lu3Co2In4 type series deserves a symmetry reduction to space group P6̅. Phase analytical studies in the gadolinium–rhodium–indium systems led to the isotypic compound Gd3Rh1.94In4 [17]. As an example we present the coloring variants for HoRhIn [18] and Ho3Rh2In4 in Fig. 1.
![Fig. 1: Projection of the HoRhIn [18] and Ho3Rh2In4 structures onto the crystallographic xy planes. Holmium, rhodium and indium atoms are drawn as medium grey, blue, and magenta circles, respectively. The trigonal prismatic units and the two-dimensional [RhIn], respectively [Rh2In4] networks are emphasized. Atom designations and relevant interatomic distances are given.](/document/doi/10.1515/znb-2016-0167/asset/graphic/j_znb-2016-0167_fig_001.jpg)
Projection of the HoRhIn [18] and Ho3Rh2In4 structures onto the crystallographic xy planes. Holmium, rhodium and indium atoms are drawn as medium grey, blue, and magenta circles, respectively. The trigonal prismatic units and the two-dimensional [RhIn], respectively [Rh2In4] networks are emphasized. Atom designations and relevant interatomic distances are given.
The ordering pattern is even more complex for the scandium compounds Sc3Ni2.10In3.60, Sc3Ni2.14In3.76, ScPd0.981In and Sc3Rh1.594In4 [19]. The palladium compound crystallizes with the subcell structure with small defects on the transition metal site. The coloring in the nickel compounds deserves the same symmetry reduction as reported for the Lu3Co2In4 series and Gd3Rh1.94In4. The ordering variant with the lowest space group symmetry is Sc3Rh1.594In4, which crystallizes with a translationengleiche subgroup of Ti4Ni2Ga3.
In continuation of our studies on coloring variants of the ZrNiAl type [3], [6], [12], [13], [17], [19] we systematically investigated the existence range for the Lu3Co2In4 type. These phases are formed only with the smaller (late) rare earth elements. Herein we report on the synthesis, the solid solution behavior and the crystal chemistry of the three series RE3T2In4 with RE=Y, Gd–Tm, Lu and T=Ni, Ru, Rh.
2 Experimental
2.1 Synthesis
Starting materials for the syntheses of the RE3T2In4 samples were sublimed ingots of the rare earth elements (Smart Elements, >99.9%), nickel wire (Alpha Aesar, ∅ 1 mm, >99.5%), ruthenium and rhodium powder (Agosi, >99.9%), and indium tear shot (ChemPur, >99.9%). The samples were synthesized in three steps. First pieces of the rare earth elements were mixed with the transition metal (ruthenium and rhodium powder were previously cold-pressed to pellets) in the ideal 3:2 atomic ratio and arc-melted [20] under an argon atmosphere of ca. 700 mbar. Argon was purified with titanium sponge (900 K), silica gel, and molecular sieves. The buttons were re-melted three times to ensure homogeneity. For the second step, the arc-melted RE3T2 buttons were crushed, mixed with the appropriate amount of indium and arc-welded in a niobium tube under an argon pressure of ca. 800 mbar. The filled containers were subsequently placed in the water-cooled sample chamber of an induction furnace (Hüttinger Elektronik, Freiburg, Germany, Typ TIG 2.5/300) [21] and the following annealing sequence was applied: (i) rapid heating to 1470 K and keeping this temperature for 2 min, (ii) cooling to 1220 K within 5 min and keeping for 10 min (iii) cooling to 870 K within 30 min and keeping for 150 min, and (iv) switching off the power supply. The temperature was controlled by a Sensor Therm Methis MS09 pyrometer with an accuracy of ±30 K. The polycrystalline samples could easily be mechanically separated from the ampoules. They were crushed in a mortar, pressed to pellets, placed in small open niobium crucibles and sealed in evacuated silica ampoules for oxidation protection. In this last step the samples were annealed at 1020 K for another 10 days. Most samples were obtained in X-ray pure form after this heat treatment. The silvery RE3T2In4 samples are stable in air.
2.2 X-ray diffraction
The polycrystalline RE3T2In4 samples were characterized by X-ray powder diffraction using a Guinier camera (Enraf-Nonius, type FR 552) equipped with an imaging plate detector (Fujifilm BAS-1800), CuKα1 radiation, and α-quartz (a=491.30, c=540.46 pm) as an internal standard. The hexagonal lattice parameters (Table 1) were refined by a least-squares routine. Correct indexing was ensured with the help of calculated patterns using the LazyPulverix routine [22].
Lattice parameters (Guinier powder data) of hexagonal RE3T2In4 phases.
| Compound | a (pm) | c (pm) | V (nm3) |
|---|---|---|---|
| RE3Ni2In4 series | |||
| Y3Ni2In4 | 769.9(2) | 376.6(1) | 0.1933 |
| Gd3Ni2In4 | 769.8(2) | 380.68(9) | 0.1954 |
| Gd3Ni2.26In3.74* | 770.25(3) | 380.01(2) | 0.1952 |
| Tb3Ni2In4 | 770.4(2) | 377.16(7) | 0.1939 |
| Dy3Ni2In4 | 769.9(2) | 374.49(9) | 0.1922 |
| Ho3Ni2.20In3.80* | 766.99(2) | 371.26(1) | 0.1891 |
| Ho3Ni2In4 | 768.6(2) | 372.4(1) | 0.1905 |
| Er3Ni2In4 | 767.9(3) | 370.3(1) | 0.1891 |
| Tm3Ni2In4 | 766.8(2) | 368.08(7) | 0.1874 |
| Lu3Ni2In4 | 765.2(1) | 365.09(8) | 0.1851 |
| RE3Ru2In4 series | |||
| Y3Ru2In4 | 803.0(1) | 366.45(6) | 0.2046 |
| Gd3Ru2In4 | 798.3(2) | 375.2(1) | 0.2071 |
| Tb3Ru2In4 | 799.5(2) | 369.1(1) | 0.2043 |
| Dy3Ru2In4 | 798.2(2) | 366.0(1) | 0.2019 |
| Ho3Ru2In4 | 800.4(2) | 362.1(1) | 0.2009 |
| Er3Ru2In4 | 800.8(2) | 358.8(1) | 0.1993 |
| Tm3Ru2In4 | 799.0(3) | 356.3(1) | 0.1970 |
| Lu3Ru2In4 | 798.4(1) | 352.51(6) | 0.1946 |
| RE3Rh2In4 series | |||
| Y3Rh2In4 | 780.4(1) | 378.36(8) | 0.1996 |
| Gd3Rh2In4 | 777.3(3) | 384.9(1) | 0.2014 |
| Gd3Rh1.94In4 [17] | 781.4(5) | 383.8(3) | 0.2029 |
| Tb3Rh2In4 | 778.8(2) | 380.2(1) | 0.1997 |
| Dy3Rh2In4 | 780.0(2) | 375.8(1) | 0.1980 |
| Ho3Rh2In4 | 780.5(2) | 373.6(1) | 0.1971 |
| Ho3Rh2.39In3.61* | 768.48(4) | 377.49(2) | 0.1931 |
| HoRhIn [18] | 747.21(6) | 385.72(3) | 0.1865 |
| Er3Rh2In4 | 781.2(2) | 370.2(1) | 0.1956 |
| Tm3Rh2In4 | 781.6(2) | 367.0(1) | 0.1942 |
| Lu3Rh2In4 | 779.9(2) | 363.3(1) | 0.1914 |
Data determined for the single crystals (marked with an asterisk) are listed for comparison. Standard deviations are given in parentheses.
Small irregularly shaped single crystals were selected from several of the crushed samples. These crystal fragments were glued to thin quartz fibers using bees wax and studied on a Buerger camera (using white Mo radiation) to check their quality. Intensity data were collected at room temperature on a Stoe IPDS-II image plate system (graphite-monochromatized Mo radiation; λ=71.073 pm) in oscillation mode or on a STOE StadiVari diffractometer equipped with a Mo micro focus source and a Pilatus detection system. Numerical absorption corrections were applied to the data sets. Due to a Gaussian-shaped profile of the micro focus X-ray source scaling was applied along with numerical absorption corrections to the StadiVari data sets. Details of the data collections and the crystallographic parameters are summarized in Tables 2 and 3.
Crystal data and structure refinement results for Gd3Ni2.26(4)In3.74(4), Ho3Ni2.20(2)In3.80(2) and Gd3Ru2In4; Lu3Co1.87In4 type, space group P6̅, Z=1.
| Compound | Gd3Ni2.26(4)In3.74(4) | Ho3Ni2.20(2)In3.80(2) | Gd3Ru2In4 |
| Molar mass, g mol−1 | 1033.86 | 1060.27 | 1133.17 |
| Lattice parameters | Table 1 | Table 1 | Table 1 |
| Calculated density, g cm−3 | 8.79 | 9.31 | 9.09 |
| Absorption coefficient, mm−1 | 41.1 | 47.6 | 38.0 |
| F(000), e | 439 | 449 | 476 |
| Crystal size, μm3 | 30×30×40 | 20×30×60 | 10×20×40 |
| Transm. ratio (min /max) | 0.230/0.465 | 0.176/0.509 | 0.237/0.741 |
| θ range, deg | 3–35 | 3–34 | 3–33 |
| Range in hkl | ±12, ±12, ±6 | ±11, ±11, ±5 | ±12, ±12, ±5 |
| Total no. reflections | 2983 | 2713 | 2760 |
| Independent reflections/Rint | 643/0.0290 | 556/0.0200 | 573/0.0333 |
| Reflections with I>2 σ(I) /Rσ | 619/0.0248 | 553/0.0131 | 535/0.0345 |
| Data/parameters | 643/22 | 556/22 | 573/20 |
| Goodness-of-fit on F2 | 1.159 | 1.124 | 0.721 |
| R1/wR2 for I>2 σ(I) | 0.0246/0.0471 | 0.0108/0.0255 | 0.0136/0.0221 |
| R1/wR2 for all data | 0.0261/0.0474 | 0.0116/0.0271 | 0.0148/0.0221 |
| Twinning matrix | (0 1 0/1 0 0/0 0 −1) | (0 1 0/1 0 0/0 0 −1) | – |
| Twin fraction | 0.506(2) | 0.388(1) | – |
| Flack parameter | −0.03(3) | −0.018(14) | −0.011(14) |
| Extinction coefficient | 0.0125(5) | 0.0151(6) | 0.0048(2) |
| Largest diff. peak/hole, e Å−3 | 1.86/−2.12 | 2.11/−1.65 | 0.71/−0.79 |
Crystal data and structure refinement results for Ho3Ru2In4, Ho3Rh2In4 and Ho3Rh2.39(1)In3.61(1); Lu3Co1.87In4 type, space group P6̅, Z=1.
| Compound | Ho3Ru2In4 | Ho3Rh2In4 | Ho3Rh2.39(1)In3.61(1) |
| Molar mass, g mol−1 | 1156.21 | 1159.89 | 1155.25 |
| Lattice parameters | Table 1 | Table 1 | Table 1 |
| Calculated density, g cm−3 | 9.56 | 9.77 | 9.94 |
| Absorption coefficient, mm−1 | 44.0 | 45.2 | 45.8 |
| F(000), e | 485 | 487 | 485 |
| Crystal size, μm3 | 20×20×40 | 20×20×40 | 20×20×20 |
| Transm. ratio (min/max) | 0.281/0.537 | 0.135/0.330 | 0.360/0.483 |
| θ range, deg | 3–32 | 3–35 | 3–35 |
| Range in hkl | ±12, ±12, ±5 | ±12, ±12, ±5 | ±12, ±12, ±6 |
| Total no. reflections | 2385 | 3106 | 2847 |
| Independent reflections/Rint | 520/0.0278 | 641/0.0243 | 633/0.0290 |
| Reflections with I>2 σ(I)/Rσ | 506/0.0187 | 613/0.0204 | 597/0.0234 |
| Data/parameters | 520/20 | 641/20 | 633/22 |
| Goodness-of-fit on F2 | 1.149 | 0.952 | 1.095 |
| R1/wR2 for I>2 σ(I) | 0.0202/0.0434 | 0.0128/0.0221 | 0.0241/0.0536 |
| R1/wR2 for all data | 0.0215/0.0437 | 0.0147/0.0224 | 0.0269/0.0544 |
| Twinning matrix | – | – | (0 1 0/1 0 0/0 0 −1) |
| Twin fraction | – | – | 0.356(3) |
| Flack parameter | −0.003(19) | −0.021(9) | 0.00(2) |
| Extinction coefficient | 0.0052(4) | 0.0152(4) | 0.0119(9) |
| Largest diff. peak/hole, e Å−3 | 1.94/−1.55 | 0.87/−0.81 | 2.14/−2.12 |
2.3 Structure refinements
Isotypism of the RE3T2In4 indides with Lu3Co2In4 [16] and Gd3Rh1.94In4 [17] was already evident from the Guinier powder patterns. All data sets were compatible with space group P6̅. The atomic positions of Gd3Rh1.94In4 were taken as starting values and the structures were refined using Shelxl-97 [23] (full-matrix least-squares on F2) with anisotropic atomic displacement parameters for all atoms. Some of the crystals showed twinning, a consequence of the symmetry reduction towards low Laue symmetry. Refinement of the correct absolute structure was ensured through calculation of the Flack parameters [24], [25]. Since we observed mixed occupancies and defect formation for the series of Sc3Ni2.10In3.60, Sc3Ni2.14In3.76, ScPd0.981In and Sc3Rh1.594In4 compounds [19], all occupancy parameters were refined in separate series of least-squares cycles. Three of the crystals showed transition metal indium mixing and these mixed occupancies were refined as least-squares variables. The final difference Fourier syntheses revealed no residual peaks. The refined atomic positions, displacement parameters, and interatomic distances are given in Tables 4 and 5.
Atomic coordinates and isotropic displacement parameters (pm2) of RE3T2In4 (RE=Gd, Ho; T=Ni, Rh and Rh).
| Atom | Wyck. | Occupancy | x | y | z | U11 | U22 | U33 | U12 | Ueq |
|---|---|---|---|---|---|---|---|---|---|---|
| Gd3Ni2.26(4)In3.74(4) | ||||||||||
| Gd | 3k | 100 | 0.58269(11) | 0.97389(11) | 1/2 | 125(3) | 179(4) | 115(2) | 79(3) | 138(2) |
| Ni1 | 1b | 100 | 0 | 0 | 1/2 | 137(7) | U11 | 138(13) | 69(4) | 138(5) |
| Ni2 | 1c | 100 | 1/3 | 2/3 | 0 | 95(9) | U11 | 128(18) | 48(5) | 106(7) |
| In1/Ni3 | 1e | 74(4)/26(4) | 2/3 | 1/3 | 0 | 67(9) | U11 | 223(15) | 34(4) | 119(8) |
| In2 | 3j | 100 | 0.24835(15) | 0.9987(2) | 0 | 113(4) | 125(4) | 141(4) | 64(4) | 125(2) |
| Ho3Ni2.20(2)In3.80(2) | ||||||||||
| Ho | 3k | 100 | 0.58310(5) | 0.97072(4) | 1/2 | 97(1) | 138(2) | 72(1) | 57(1) | 103(1) |
| Ni1 | 1b | 100 | 0 | 0 | 1/2 | 107(4) | U11 | 112(6) | 53(2) | 109(3) |
| Ni2 | 1c | 100 | 1/3 | 2/3 | 0 | 92(5) | U11 | 93(7) | 46(2) | 92(3) |
| In1 | 1e | 85(2)/15(2) | 2/3 | 1/3 | 0 | 57(4) | U11 | 188(6) | 28(2) | 100(4) |
| In2 | 3j | 100 | 0.25102(7) | 0.99947(9) | 0 | 92(2) | 90(2) | 111(2) | 51(1) | 95(1) |
| Gd3Ru2In4 | ||||||||||
| Gd | 3k | 100 | 0.41250(5) | 0.03372(5) | 1/2 | 241(2) | 184(2) | 163(1) | 109(1) | 195(1) |
| Ru1 | 1b | 100 | 0 | 0 | 1/2 | 164(2) | U11 | 481(7) | 82(1) | 269(2) |
| Ru2 | 1e | 100 | 2/3 | 1/3 | 0 | 157(2) | U11 | 178(4) | 78(1) | 164(2) |
| In1 | 1c | 100 | 1/3 | 2/3 | 0 | 153(2) | U11 | 318(5) | 77(1) | 208(2) |
| In2 | 3j | 100 | 0.73524(7) | 0.00077(7) | 0 | 213(2) | 168(2) | 370(4) | 79(2) | 258(1) |
| Ho3Ru2In4 | ||||||||||
| Ho | 3k | 100 | 0.58994(8) | 0.96427(7) | 1/2 | 177(3) | 120(2) | 103(2) | 71(2) | 135(1) |
| Ru1 | 1b | 100 | 0 | 0 | 1/2 | 118(4) | U11 | 329(10) | 59(2) | 188(4) |
| Ru2 | 1c | 100 | 1/3 | 2/3 | 0 | 107(4) | U11 | 110(7) | 53(2) | 108(3) |
| In1 | 1e | 100 | 2/3 | 1/3 | 0 | 91(4) | U11 | 254(8) | 45(2) | 145(3) |
| In2 | 3j | 100 | 0.26941(13) | 0.00129(12) | 0 | 158(4) | 116(4) | 270(5) | 54(3) | 188(2) |
| Ho3Rh2In4 | ||||||||||
| Ho | 3k | 100 | 0.41353(4) | 0.03276(3) | 1/2 | 129(1) | 104(1) | 93(1) | 55(1) | 110(1) |
| Rh1 | 1b | 100 | 0 | 0 | 1/2 | 109(2) | U11 | 199(4) | 54(1) | 139(1) |
| Rh2 | 1e | 100 | 2/3 | 1/3 | 0 | 91(2) | U11 | 100(4) | 46(1) | 94(1) |
| In1 | 1c | 100 | 1/3 | 2/3 | 0 | 85(2) | U11 | 221(4) | 43(1) | 130(1) |
| In2 | 3j | 100 | 0.74142(6) | 0.99979(6) | 0 | 115(2) | 98(2) | 167(2) | 48(1) | 129(1) |
| Ho3Rh2.39(1)In3.61(1) | ||||||||||
| Ho | 3k | 100 | 0.41122(11) | 0.02043(14) | 1/2 | 167(4) | 326(4) | 92(2) | 135(3) | 190(2) |
| Rh1 | 1b | 100 | 0 | 0 | 1/2 | 151(4) | U11 | 197(8) | 76(2) | 166(3) |
| Rh2 | 1e | 100 | 2/3 | 1/3 | 0 | 108(5) | U11 | 124(10) | 54(3) | 114(4) |
| In1/Rh3 | 1c | 62(1)/38(1) | 1/3 | 2/3 | 0 | 122(7) | U11 | 216(12) | 61(4) | 153(6) |
| In2 | 3j | 100 | 0.74320(15) | 0.0000(2) | 0 | 158(5) | 136(3) | 150(4) | 87(4) | 142(2) |
Coefficients Uij of the anisotropic displacement factor tensor of the atoms are defined by: −2π2[(ha*)2U11+…+2hka*b*U12]. U13=U23=0.
Interatomic distances (pm) of Ho3Rh2In4, Ho3Rh2.38(1)In3.62(1) and HoRhIn [18].
| Ho3Rh2In4 | Ho3Rh2.38In3.62 | HoRhIn | ||||||
|---|---|---|---|---|---|---|---|---|
| Ho: | 2 | Rh2 | 287.4 | 291.2 | 4 | Rh2 | 297.7 | |
| 1 | Rh1 | 310.8 | 308.5 | 1 | Rh2 | 303.4 | ||
| 2 | In2 | 319.3 | 311.2 | 2 | In | 317.0 | ||
| 2 | In1 | 320.2 | 322.9 | 4 | In | 328.4 | ||
| 2 | In2 | 328.1 | 324.0 | 2 | Ho | 385.7 | ||
| 2 | In2 | 342.5 | 337.0 | 4 | Ho | 392.9 | ||
| 2 | Ho | 373.6 | 377.5 | |||||
| 2 | Ho | 378.4 | 384.0 | |||||
| 2 | Ho | 450.6 | 428.6 | |||||
| Rh1: | 6 | In2 | 274.9 | 273.1 | 6 | In | 272.3 | |
| 3 | Ho | 310.8 | 308.5 | 3 | Ho | 303.4 | ||
| Rh2: | 6 | Ho | 287.4 | 291.2 | 3 | In | 281.8 | |
| 3 | In2 | 293.9 | 290.1 | 6 | Ho | 297.7 | ||
| In1/Rh3: | 3 | In2 | 293.7 | 290.1 | ||||
| 6 | Ho | 320.3 | 311.2 | |||||
| In2: | 2 | Rh1 | 274.9 | 273.1 | 2 | Rh1 | 272.3 | |
| 1 | In1 | 293.7 | 290.0 | 2 | Rh2 | 281.8 | ||
| 1 | Rh2 | 293.8 | 290.1 | 2 | Ho | 317.0 | ||
| 2 | Ho | 319.3 | 322.9 | 4 | Ho | 328.4 | ||
| 2 | Ho | 328.1 | 324.0 | 2 | In | 333.0 | ||
| 2 | Ho | 342.5 | 337.0 | |||||
| 2 | In2 | 349.4 | 341.8 | |||||
| 2 | In2 | 373.6 | 377.5 | |||||
All distances within the first coordination spheres are listed. Standard deviations are all equal or <0.3 pm.
Further details of the crystal structure investigations may be obtained from Fachinformationszentrum Karlsruhe, 76344 Eggenstein-Leopoldshafen, Germany (fax: +49-7247-808-666; e-mail: crysdata@fiz-karlsruhe.de, http://www.fiz-karlsruhe.de/request_for_deposited_data.html) on quoting the deposition numbers CSD-431660 (Gd3Ni2.26In3.74), CSD-431659 (Ho3Ni2.20In3.80), CSD-431664 (Gd3 Ru2In4), CSD-431663 (Ho3Ru2In4), CSD-431662 (Ho3Rh2In4), and CSD-431661 (Ho3Rh2.39In3.61).
2.4 EDX data
The six crystals studied on the diffractometers were semiquantitatively analyzed by EDX using a Zeiss EVO® MA10 scanning electron microscope in variable pressure mode. GdF3, HoF3, Ni, Ru, Rh, and InAs were used as standards. The experimentally observed compositions were close to the ones refined from the single crystal X-ray data. No impurity elements (especially from the container material) were detected.
3 Crystal chemistry
The indides RE3T2In4 (RE=Y, Gd–Tm, Lu; T=Ni, Ru, Rh) crystallize with the hexagonal Lu3Co2In4 structure [16] and extend significantly the number of representatives for this type. The four series (with T=Co, Ni, Ru, Rh) only exist for the smaller (late) rare earth elements. The cell volumes decrease from the gadolinium to the lutetium compound (Fig. 2) as a consequence of the lanthanide contraction. The three yttrium compounds fit in these series in between the volumes of the terbium and dysprosium compounds, similar to many other series of rare earth-transition metal-indides [26]. Small deviations in the volume plot are a consequence of the solid solutions.
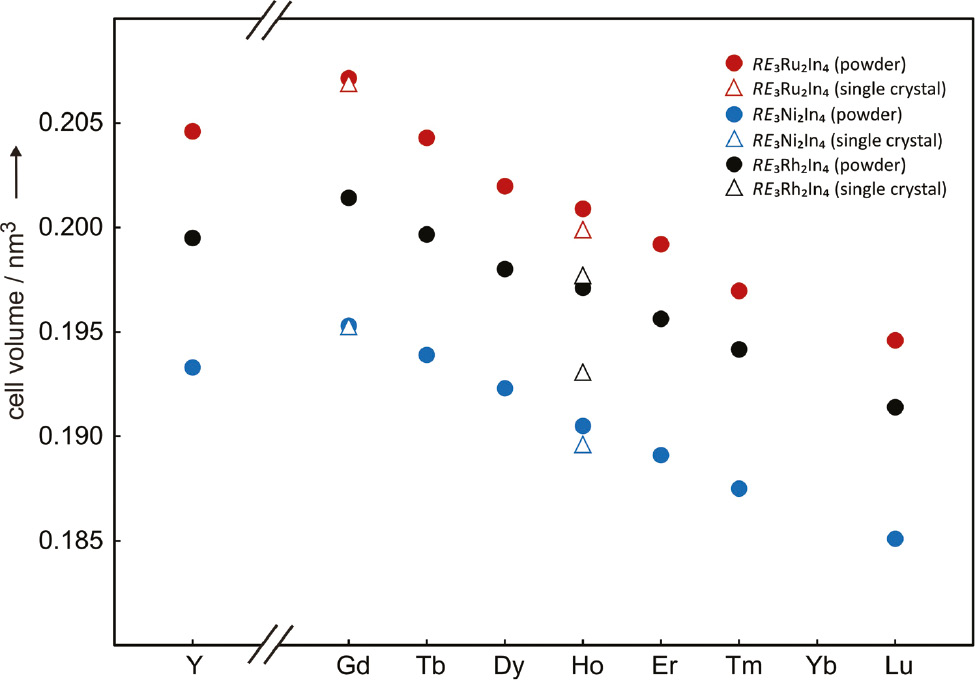
Course of the cell volumes of the series of hexagonal RE3T2In4 compounds.
Interestingly no ytterbium-based compound was obtained for any of these series. This seems to correlate with the existence range of the equiatomic compounds RETIn. With cobalt and ruthenium no equiatomic RETIn phases exist and within the RENiIn series no ytterbium compound has been reported [26], whereas YbRhIn [18] adopts the orthorhombic TiNiSi type with completely different crystal chemistry. This might be a consequence of the ytterbium valence (tendency towards divalent ytterbium).
In the following discussion we exemplarily focus on the three indides HoRhIn [18], Ho3Rh2In4 and Ho3Rh2.39In3.61. The complete list of interatomic distances is given in Table 5. The striking difference between HoRhIn (a=747.21(6), c=385.72(3) pm, c/a=0.516) and Ho3Rh2In4 (a=780.5(2), c=373.6(1) pm, c/a=0.479) is the course of the lattice parameters influenced by the Rh/In substitution. Since the covalent radius [27] of indium (150 pm) is significantly larger than that of rhodium (125 pm), we observe a drastic widening of those trigonal holmium prisms that are filled with indium. This leads to the strong increase of the lattice parameter a. In parallel, for keeping the overall bonding, the c parameter decreases. This anisotropic behavior occurs for all 3-2-4 phases that have a 1-1-1 counterpart. The cell parameters of the mixed occupied phase Ho3Rh2.39In3.61 fit in between the data for HoRhIn and Ho3Rh2In4.
The ordered Rh/In substitution has consequences on the individual atom coordinations. First of all one observes a lowering of the space group symmetry from P6̅2m to P6̅ (translationengleiche symmetry reduction of index 2; splitting of the 2c subcell site into two one-fold sites). The corresponding group-subgroup relation has been published in [17]. The changes of the interatomic distances are readily visible from Table 5 and Fig. 1. The distances for the partially substituted phase Ho3Rh2.38In3.62 are between those of HoRhIn and Ho3Rh2In4. The Rh/In ordering leads to Ho6 prisms with smaller (378 pm; filled with rhodium) and longer edges (451 pm, filled with indium).
The shortest interatomic distances in the three phases occur for Rh–In (272–275 pm), in close agreement with the sum of the covalent radii [27] for Rh+In of 275 pm. This underlines the importance of Rh–In bonding as a stabilizing parameter. Similar ranges of Rh–In distances occur in many ternary alkaline earth and rare earth based indides [28], [29]. Filling half of the Ho6 prisms with indium (this is the situation in Ho3Rh2In4) leads to substantial In–In bonding. Each of these indium atoms binds to three In3 triangles (349 pm In–In) with In–In distances of 294 pm, somewhat shorter than the In–In distances in indium metal (4×325 and 8×338 pm) [30].
A final question concerns the stability range for these hexagonal RETIn (≡RE3T3In3) and RE3T2In4 phases. A first approach might be the valence electron count (VEC). Since the 3-2-4 phases exist with Ru, Rh, and Ni as transition metal component, the VEC ranges from 37 to 41 per formula unit. Equiatomic hexagonal indides are known with T=Rh, Ni, Pd, Pt, Cu, Au. This corresponds to a VEC range from 45 to 51 (three formula units are calculated for better comparison with the 3-2-4 phases). Increasing or decreasing the VEC out of these small ranges may destabilize such a structural arrangement. This might be the reason for the non-existence of RERuIn phases. However, VEC cannot be the only determining parameter since also no RECoIn phases exist that would formally be isotypic with the RERhIn series. More detailed phase analytical studies along with electronic structure calculations are needed in future in order to fully understand this structural family.
Acknowledgments
This work was supported by the Deutsche Forschungsgemeinschaft. We thank BSc Martha Sieg for experimental help. O.N. is indebted to the NRW Forschungsschule Molecules and Materials – A Common Design Principle for a PhD fellowship.
References
[1] P. I. Krypyakevich, V. Ya. Markiv, E. V. Melnyk, Dopov. Akad. Nauk. Ukr. RSR, Ser. A. 1967, 750.Search in Google Scholar
[2] A. E. Dwight, M. H. Mueller, R. A. Conner, Jr., J. W. Downey, H. Knott, Trans. Met. Soc. AIME1968, 242, 2075.Search in Google Scholar
[3] M. F. Zumdick, R.-D. Hoffmann, R. Pöttgen, Z. Naturforsch. 1999, 54b, 45.10.1515/znb-1999-0111Search in Google Scholar
[4] S. Rundqvist, F. Jellinek, Acta Chem. Scand. 1959, 13, 425.10.3891/acta.chem.scand.13-0425Search in Google Scholar
[5] P. Villars, K. Cenzual, Pearson’s Crystal Data: Crystal Structure Database for Inorganic Compounds (release 2015/16), ASM International®, Materials Park, OH (USA) 2015.Search in Google Scholar
[6] R. Pöttgen, B. Chevalier, Z. Naturforsch. 2015, 70b, 289.10.1515/znb-2015-0018Search in Google Scholar
[7] S. Gupta, K. G. Suresh, J. Alloys Compd. 2015, 618, 562.10.1016/j.jallcom.2014.08.079Search in Google Scholar
[8] R. Pöttgen, D. Johrendt, D. Kußmann, in Handbook on the Physics and Chemistry of Rare Earths, Vol. 32 (Eds.: K. A. Gschneidner Jr., J.-C. Bünzli), North-Holland/Elsevier, Amsterdam, 2001, chapter 207, p. 453.Search in Google Scholar
[9] H. Fujii, T. Takabatake, Y. Andoh, J. Alloys Compd. 1992, 181, 111.10.1016/0925-8388(92)90303-QSearch in Google Scholar
[10] R. A. Robinson, A. C. Lawson, V. Sechovsky, L. Havela, Y. Kergadallan, H. Nakotte, F. R. de Boer, Actinides ‘93 Conference, Santa Fe, NM USA, 19–24 Sept. 1993; Abstract: LA-UR--93-2739.Search in Google Scholar
[11] Ł. Gondek, A. Szytuła, J. Alloys Compd. 2007, 442, 111.10.1016/j.jallcom.2006.07.136Search in Google Scholar
[12] M. F. Zumdick, R. Pöttgen, Z. Kristallogr. 1999, 214, 90.10.1524/zkri.1999.214.2.90Search in Google Scholar
[13] R. Pöttgen, Z. Anorg. Allg. Chem. 2014, 640, 869.10.1002/zaac.201400023Search in Google Scholar
[14] E. Parthé, L. Gelato, B. Chabot, M. Penzo, K. Cenzual, R. Gladyshevskii, TYPIX–Standardized Data and Crystal Chemical Characterization of Inorganic Structure Types, Gmelin Handbook of Inorganic and Organometallic Chemistry, 8th edition, Springer, Berlin 1993.10.1007/978-3-662-10641-9Search in Google Scholar
[15] V. Ja. Markiv, N. N. Beljavina, A. A. L’isenko, A. A. Babenko, Dopov. Akad. Nauk Ukr. RSR, Ser. B1983, 34.Search in Google Scholar
[16] V. I. Zaremba, Y. M. Kalychak, P. Y. Zavalii, A. N. Sobolev, Dopov. Akad. Nauk Ukr. RSR, Ser. B1989, 37.Search in Google Scholar
[17] U. Ch. Rodewald, M. Lukachuk, R.-D. Hoffmann, R. Pöttgen, Monatsh. Chem. 2005, 136, 1985.10.1007/s00706-005-0375-ySearch in Google Scholar
[18] M. Lukachuk, V. I. Zaremba, R. Pöttgen, Intermetallics2003, 11, 581.10.1016/S0966-9795(03)00042-6Search in Google Scholar
[19] M. Lukachuk, V. I. Zaremba, R.-D. Hoffmann, R. Pöttgen, Z. Naturforsch. 2004, 59b, 182.10.1515/znb-2004-0210Search in Google Scholar
[20] R. Pöttgen, T. Gulden, A. Simon, GIT Labor-Fachzeitschrift1999, 43, 133.Search in Google Scholar
[21] D. Kußmann, R.-D. Hoffmann, R. Pöttgen, Z. Anorg. Allg. Chem. 1998, 624, 1727.10.1002/(SICI)1521-3749(1998110)624:11<1727::AID-ZAAC1727>3.0.CO;2-0Search in Google Scholar
[22] K. Yvon, W. Jeitschko, E. Parthé, J. Appl. Crystallogr.1977, 10, 73.10.1107/S0021889877012898Search in Google Scholar
[23] G. M. Sheldrick, Acta Crystallogr.2008, A64, 112.10.1107/S0108767307043930Search in Google Scholar
[24] H. D. Flack, G. Bernadinelli, Acta Crystallogr.1999, A55, 908.10.1107/S0108767399004262Search in Google Scholar
[25] H. D. Flack, G. Bernadinelli, J. Appl. Crystallogr. 2000, 33, 1143.10.1107/S0021889800007184Search in Google Scholar
[26] Ya. M. Kalychak, V. I. Zaremba, R. Pöttgen, M. Lukachuk, R.-D. Hoffmann, in Handbook on the Physics and Chemistry of Rare Earths, Vol. 34 (Eds.: K. A. Gschneider Jr., V. K. Pecharsky, J.-C. Bünzli), Elsevier, Amsterdam, 2005, chapter 218, p. 1.10.1016/S0168-1273(04)34001-8Search in Google Scholar
[27] J. Emsley, The Elements, Oxford University Press, Oxford 1999.Search in Google Scholar
[28] R.-D. Hoffmann, U. Ch. Rodewald, R. Pöttgen, Z. Naturforsch. 1999, 54b, 38.10.1515/znb-1999-0110Search in Google Scholar
[29] R.-D. Hoffmann, R. Pöttgen, V. I. Zaremba, Ya. M. Kalychak, Z. Naturforsch. 2000, 55b, 834.10.1515/znb-2000-0907Search in Google Scholar
[30] J. Donohue, The Structures of the Elements, Wiley, New York 1974.Search in Google Scholar
©2016 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Frontmatter
- In this Issue
- Synthesis, crystal and electronic structure of the new sodium chain sulfido cobaltates(II), Na3CoS3 and Na5[CoS2]2(Br)
- Structure elucidation and synthesis of hydroxylated isatins from Streptomycetes
- Synthesis and characterization of allyl- and vinyl-substituted 1,2-bis(tetrazolo)ethanes as polymeric precursors
- Unusual pyranosyl cembranoid diterpene from Sarcophyton trocheliophorum
- The chemical behavior of the silaoxine C22H34OSi3 and silaazetidine C25H43NSi4 towards CO2
- Synthesis and structural characterization of BaSr2Ge3O9
- Hydrothermal synthesis of a new lead(II) borate (Pb4O)Pb2B6O14-II
- The quaternary arsenide oxides Ce9Au5–xAs8O6 and Pr9Au5–xAs8O6
- Structure and bonding of 2,2,2-trichloroethylacetate: An experimental gas phase and computational study
- Indides RE3T2In4 (RE = Y, Gd–Tm, Lu; T = Ni, Ru, Rh) with a ZrNiAl superstructure
- Synthesis, crystal structures and blue emission of zinc(II) halide complexes of 1-alkyl-imidazole and (–)-nicotine
- Die Lanthanoid(III)-Oxid-Oxoselenate(IV) Ln2O[SeO3]2 (Ln=Sm–Tm)
- Photoreactivity of monofluorinated 2-azidobenzimidazoles towards carboxylic acids
Articles in the same Issue
- Frontmatter
- In this Issue
- Synthesis, crystal and electronic structure of the new sodium chain sulfido cobaltates(II), Na3CoS3 and Na5[CoS2]2(Br)
- Structure elucidation and synthesis of hydroxylated isatins from Streptomycetes
- Synthesis and characterization of allyl- and vinyl-substituted 1,2-bis(tetrazolo)ethanes as polymeric precursors
- Unusual pyranosyl cembranoid diterpene from Sarcophyton trocheliophorum
- The chemical behavior of the silaoxine C22H34OSi3 and silaazetidine C25H43NSi4 towards CO2
- Synthesis and structural characterization of BaSr2Ge3O9
- Hydrothermal synthesis of a new lead(II) borate (Pb4O)Pb2B6O14-II
- The quaternary arsenide oxides Ce9Au5–xAs8O6 and Pr9Au5–xAs8O6
- Structure and bonding of 2,2,2-trichloroethylacetate: An experimental gas phase and computational study
- Indides RE3T2In4 (RE = Y, Gd–Tm, Lu; T = Ni, Ru, Rh) with a ZrNiAl superstructure
- Synthesis, crystal structures and blue emission of zinc(II) halide complexes of 1-alkyl-imidazole and (–)-nicotine
- Die Lanthanoid(III)-Oxid-Oxoselenate(IV) Ln2O[SeO3]2 (Ln=Sm–Tm)
- Photoreactivity of monofluorinated 2-azidobenzimidazoles towards carboxylic acids

