Nonlinear rarefactive isothermal ion acoustic waves in magnetized ultrarelativistic degenerate plasmas

1 Introduction

The enormous areas of quantum degenerate plasma particles in astrophysical regions like compact objects (i.e., white dwarfs, neutron stars and pulsar magnetosphere) and laboratory (such as semiconductor plasma, laser compressed plasma and nanostructures) have attracted the researchers of all over the world to study in the field of dense plasmas [1], [2], [3], [4], [5], [6], [7], [8], [9], [10], [11], [12], [13], [14], [15]. Indeed, the quantum degeneracy effects in the system start playing an important role when the de Broglie thermal wavelengths  λB(=(ℏ/2πjkBTj )1/2) for degenerate particles (e.g., electrons and positrons, where j = e and p for the electron and for the positron, respectively) are similar to/larger than the average interfermionic distance nj−1/3 (i.e., when  njλB3≳1). In such situation, plasma temperature T_j (i.e., the electron and positron temperatures ) approaches the Fermi temperature TFj(=EFj/kB) (i.e., the electron and positron Fermi temperatures) and follows the Fermi–Dirac statistical distribution [16], [17], [18], [19], [20], where EFj(=(ℏ2/2mj)(3π2nj)2/3) is the Fermi energy of degenerate particles, n_j is the number density of fermions, ℏ is the Planck constant divided by 2π, m_j is the rest mass of a degenerate particle and k_B is the Boltzmann constant. A matter of importance in compact objects, in which the number densities of particles are enormous, is that when the electron and positron thermal energies become slight compared to electron and positron Fermi energies, then the electron and positron degeneracy pressures can be dominant over the electron and positron thermal pressures. Therefore, the lower energy state is filled with electrons so additional electrons can generate degeneracy pressure. In the case of white dwarfs, the average density could be changed from 10⁶ to 10⁸ g.cm⁻³, the degenerate electron number can be of the order of 10²⁹ cm⁻³ and the average interparticle distance is in the range of 10⁻¹⁰ cm. Thus, the light nuclei can be considered inertial, while both electrons and positrons are taken to obey the degeneracy pressure to prevent the gravitational collapse of compact objects. Moreover, the basic constituents of white dwarfs are mainly positively and negatively charged heavy elements (such as carbon, oxygen, helium with an envelope of hydrogen gas). The presence of heavy elements is found to form in a prestellar stage of the universe’s evolution when all matter was compressed to extremely high densities. For white dwarfs, the average number density of heavy particles is in the range of 10²⁹ cm⁻³, with the distance between heavy particles being in the range of 10⁻¹⁰ cm [21], [22], [23]. It is well known that Chandrasekhar obtained the mathematical standard model for white dwarfs by using the Fermi–Dirac statistics for fermions [24], [25], [26]. In the last few decades, most previous investigations have been assumed that degenerate particles are completely degenerate and cold (i.e., T_j = 0) []. For example, Mamun and his research group [29], [30], [31], [32], [33], [34] discussed that the modification of nonlinear waves due to the existence of heavy negative ions in degenerate plasmas. They [34] found that the existence of the ultrarelativistic degenerate electrons, as well as positrons and stationary heavy negative ions, play a significant role in the basic features of the nonlinear ion-acoustic solitary waves and double layers. Furthermore, they [34] demonstrated that the presence of stationary heavy negative ions provides the possibility of the co-existence of both compressive and rarefactive nonlinear ion-acoustic solitary waves. It is important to mention here that the temperature T_j is utilized to define the energy spread for a classical ideal gas physically. The energy distribution of a degenerate particle gas is determined by the Fermi energy E_Fj at zero temperature (or the chemical potentialµ_j) and temperature T_j. As a result, the study of degenerate particles at nonzero temperature (i.e., Tj≠0) has engendered a lot of interest, and several types of research have recently been made to examine the linear and nonlinear waves in a degenerate plasma system, which corresponds to the Fermi gas and provides the possibility of examining how the nonlinear wave structures depend on the physical parameters μ_j and T_j [41], [42], [43], [44], [45], [46], [47], [48], [49], [50], [51]. The equation of state for a degenerate gas in such situation has been discussed analytically by many investigators. In particular, Dubinov and his research group applied the analytical formula of the state equation for degenerate plasmas to investigate the propagation of nonlinear waves [44], [45], [46], [47], [48], [49]. Dubinov and Kitaev [49], for example, examined the Langmuir waves in warm quantum electron-ion plasmas. They [49] demonstrated that the equation’s numerical solutions reveal the small scale quantum Langmuir oscillations attributed to the Bohm quantum force. El-Shamy et al. [50] illustrated that the amplitude and the width of compressive isothermal ion-acoustic solitary waves increase as the chemical potential of electrons increases. El-Shamy et al. [51] stated that the amplitude and the steepness of the monotonic isothermal ion-acoustic shock waves slightly decrease due to the increase in the Fermi temperature ratio of the low temperature of electrons. Nevertheless, most previous studies [41], [42], [43], [44], [45], [46], [47], [48], [49], [50], [51] focused on studying solitary waves, except for the work done by Dubinov and Sazonkin [45]. They [45] have determined the domains of the presence of solitary and periodic ionic sound waves in unmagnetized nonrelativistic degenerate electron–positron–ion plasma. They [45] illustrated that these domains do not intersect. However, the studies of features of nonlinear rarefactive isothermal ion-acoustic solitary and periodic travelling waves in magnetized ultrarelativistic degenerate plasmas are still lacking. In this context, the well-known bifurcation analysis is important in many theoretical physics areas for investigating the dynamical behavior; hence, it is important to study nonlinear acoustic periodic travelling waves for different plasma models in laboratories and astrophysical situations [52]. Over the last few years, the bifurcation theory has been extensively employed to study nonlinear waves’ physical nature in various plasma models due to its significant applications in different plasma situations [53], [54], [55], [56], [57], [58], [59], [60], [61]. For example, El-Shamy et al. [57] examined the features of electrostatic travelling waves in degenerate dense magnetoplasmas consisting of nondegenerate inertial cold ions and relativistic degenerate inertialess electrons and positrons. They [57] found that the amplitude and the width of the electrostatic periodic travelling wave increase with the decrease in the concentration of positrons. Very recently, Mandi et al. [61] investigated the dynamics of ion-acoustic waves in Thomas–Fermi plasmas with source term, which consist of electrons and positrons, following zero-temperature Fermi-gas statistics and ions behave as a classical fluid. They [61] demonstrated that the concentration of positrons has a vital role in forming and the transition of periodic ion-acoustic waves. However, the effects of ultrarelativistic degenerate inertialess electrons and positrons and immobile heavy negative ions have been paid less attention. Therefore, the main objective of this study is to investigate the influence of chemical potentials of fermions and the concentration of heavy negative ions on the nonlinear rarefactive isothermal ion-acoustic solitary and periodic travelling waves in ultrarelativistic degenerate magnetoplasmas by using the bifurcation analysis of the planar dynamical systems. It is important to mention here that this investigation is closely related to compact objects, such as white dwarf stars, where many previous studies have predicted the existence of acoustic-modes [62], [,63], in which ions provide the inertia and degenerate electrons, as well as positrons supply restoring forces to support ion-acoustic mode.

The manuscript is structured as follows. In Section 2, we recall the basic equations and derive then the linear dispersion relation and the nonlinear Zakharov–Kuznetsov (ZK) equation that governs the dynamics of nonlinear waves propagating in the present model. In Section 3, the bifurcation analysis is applied to study the possibility of the existence of the rarefactive isothermal ion-acoustic solitary wave and periodic travelling wave solutions. Numerical analysis, simulation and results are finally discussed in Section 4.

2 Model equations

A magnetized ultrarelativistic degenerate plasma system composed of warm fluid ions and ultrarelativistic degenerate inertialess electrons and positrons in the presence of an external static magnetic field  B→=B0eˆz , where eˆz  is the unit vector along the Z-axis. Propagation of nonlinear isothermal ion-acoustic waves (IIAWs) is described by the following normalized basic equations [36], [50]:

The number densities of ultrarelativistic degenerate electrons and positrons are given, respectively, by (see Refs. [50], [51]).

The physical quantities ni, u→i (uiX,uiY,uiZ)  and ϕ are the number density and the velocity of warm ions, and the electrostatic wave potential, respectively. Further, T is the time and ∇→ (=(∂/∂X, ∂/∂Y, ∂/∂Z)) ,  where X, Yand Z are space coordinates. Here Ωi(=eB0/mic)  is the ion cyclotron frequency. Now, let us consider the following normalization: ni→ni ni(0), ne→ne ne(0),  np→nenp(0),u→i→u→iCF,ϕ→eϕεFe,  ∇→→∇→λF,T→Tωi,and  Ω→Ωωi, ni(0) is the unperturbed number density of ions,  ne(0) is the unperturbed number density of electrons,  np(0) is the unperturbed number density of positrons,  CF(=εFe/mi) is the ion Fermi acoustic speed, λF(=εFe/4πe2 ni(0)) is the Debye radius, ωi−1(=mi/4πe2 ni(0)) is the plasma period. It should be mentioned here that the detailed derivation of Eqs. (3) and (4) is provided in Ref. [50]. Now, we define the following notations: σ(=53TiTFe),Ω(=eB0mic),β(=ne(0)ni(0)),α(=np(0)ni(0)),γ(=Zhnh(0)ni(0)), β1(=C2eC1e),β2(=μ0eC1e),β3(=13C1e), α1(=C2pσFC1p), α2(=μ0p σF 2C1p),α3(=σF33C1p),σF(=TFeTFp), C1j(=(μ0j33+μ0j(π23σj2−12mj2c4εFj2))),C2j(=μ0j2+(π23σj2−mj2c42εFj2)) and σj(=TFjTj)εFj=(3π2 nj(0))13 ℏc. Here nh(0) is the number density of static negative heavy ions, Z_his the charged state of immobile heavy negative ions, c is the speed of light in vacuum, e is the magnitude of the electric charge, µ_0e and µ_0p are the chemical potentials (or the Fermi energies at zero temperatures) of electrons and positrons at ϕ=0, respectively, m_i is the ion mass, T_i is the ion temperature. C_1j and C_2j contain the effect of degeneracy. Later, C_1j and C_2j will be encountered as the effect of degeneracy on the nonlinear structures.

Now, we study the dispersion characteristics of propagating electrostatic mode (ω, k) in magnetized ultrarelativistic degenerate plasmas with static heavy negative ions for several physical parameters. By utilizing Fourier transform, one can examine the dispersion law for linear modes described by Eqs. (1)–(5). Thus, the dispersion relation can be written as

Therefore, one can rearrange Eq. (6) to become

where Q1=(Ω2+k2σ+k2k2+(ββ1+αα1)) and Q2=(σ+1k2+(ββ1+αα1))k∥2Ω2. Here, ω and k are wave frequency and wave number, respectively, k2=k∥2+k⊥2, k∥2=kz2=k2cos2(θ)=ℓz2k2, k⊥2=kx2+ky2=k2(ℓx2+ℓy2), where ℓ_x, ℓ_y, and ℓ_z are the directional cosines of the wave vector k→ along the x, y, and z axes, respectively, so that ℓx2+ℓy2+ℓz2=1.

Indeed, the upper and lower signs (i.e.,  ω=ω+ and  ω−) correspond to the propagating isothermal ion-cyclotron and isothermal ion-acoustic waves, respectively. Let us now focus on the ion-acoustic waves for a dispersion correction of order k³ and small wave numbers (i.e., long wavelengths); Eq. (8) can be approximated to the lowest order as an acoustic-like dispersion law [64], [65], [66], [67], [68], [69]

where ρ=1(ββ1+αα1) , and for the limit of a weak dispersion the phase velocity V of long-wavelength (low-frequency) ion-acoustic waves becomes

Finally, we can obtain

where the coefficients B and C are given by (=(V2−σ)22V) and (=(1+V4Ω2(V2−σ)2)), respectively. Later, B and C will be encountered as the coefficients of the dispersive terms in a nonlinear ZK equation. For numerical illustrations, [22], [,] we can take some physical parameters that find in compact astrophysical objects, such as white dwarfs  ne(0)≅1029 cm−3,  np(0)≅1029 cm−3 , and  ni(0)≅1029 cm-3, and the average number density of heavy negative particles is of the order of 10²⁹ cm⁻³, which satisfy the quasineutrality condition. Furthermore, the corresponding Fermi temperatures of the electron and positron are rewritten as follows: TFe≅ 6.4×(106−108) K, and TFp≅ 6×(106−108) K. Furthermore, B0≅109−1011 G  and Te,p≅6x106 K. It is observed here that the electron/positron Fermi temperature is of the same order as that of the system temperature T_e,p, but  TFe,p> Te,p. Moreover, the ion temperature is given by Ti≅0.2×(104−106) K [72]. The characteristics of the linear isothermal ion-acoustic waves (IIAWs) are shown in Figures 1–4. It is clear that the chemical potentials of fermions, μ_0e and μ_0p , the thermal effect of warm ions, σ and the concentration of static heavy negative ions, γ, basically modify the angular wave frequency, ω. Clearly, when the angular wave frequency, ω, approaches the ion cyclotron frequency, Ω, for large wavenumber k, the modifications are observed significantly. As shown in Figures 1–4, the increase in μ_0e, μ_0p, σ, and γ lead to an increase in the angular wave frequency, ω, respectively. The figures show that the lowest increase in ω occurs with σ, while the highest increase occurs with γ.

Figure 1:

The ω − k relation for the isothermal ion-acoustic waves in a magnetized ultrarelativistic degenerate plasma for Ω = 0.5, α = 0.11, γ = 0.77, µ_0p = 0.3,σ_e = 30, σ_p = 30, σ = 0.005, µ_0e = 0.4 (red solid curve) and µ_0e = 0.5 (blue dashed curve).

Figure 2:

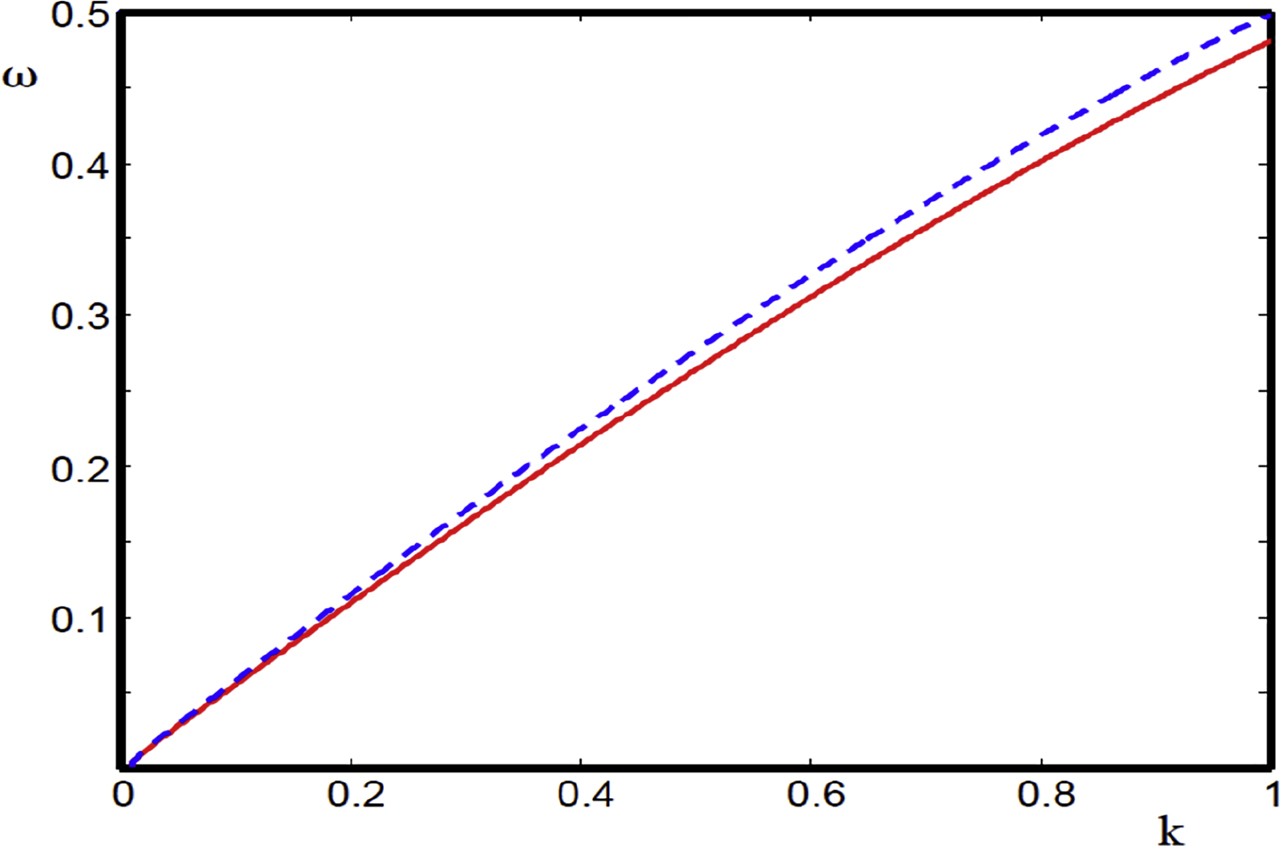
The ω − k relation for the isothermal ion-acoustic waves in a magnetized ultrarelativistic degenerate plasma for Ω = 0.5, α = 0.11, γ = 0.77, µ_0e = 0.5,σ_e = 30, σ_p = 30, σ = 0.005, µ_0p = 0.3 (red solid curve) and µ_0p = 0.4 (blue dashed curve).

Figure 3:

The ω − k relation for the isothermal ion-acoustic waves in a magnetized ultrarelativistic degenerate plasma for Ω = 0.5, α = 0.11, γ = 0.77, µ_0e = 0.5, µ_0p = 0.3, σ_e = 30, σ_p = 30, σ = 0.005 (red solid curve) and σ = 0.001 (blue dashed curve).

Figure 4:

The ω − k relation for the isothermal ion-acoustic waves in a magnetized ultrarelativistic degenerate plasma for Ω = 0.5, µ_0e = 0.5, µ_0p = 0.3, σ_e = 30, σ_p = 30, σ = 0.005, β = 0.33, γ = 0.77 (red solid curve) and β = 0.22, γ = 0.88 (blue dashed curve).

We shall examine the physical nature of nonlinear isothermal ion acoustic waves in magnetized ultrarelativistic degenerate plasmas. Based on the characteristic of the linear dispersion law for small wavenumber k, one can introduce the following stretched coordinates [].

where ε is a real and small parameter measuring the strength of nonlinearity and V is the phase velocity normalized by the ion Fermi acoustic speed. Furthermore, the dependent variables are expanded as

where

Putting Eqs. (12)–(14) into Eqs. (1)–(5), and collecting the terms in different powers of ε, the lowest-order in ε gives

Following the same strategy, one can obtain the second-order in ε, and hence, one can eliminate the second-order terms of the velocities and the number densities, and with the help of the first order, we finally obtain the ZK equation as follows:

where V, B, and C have the same forms as before and  A(=(3(V2−σ9)(V2−σ)3+2(αα2−ββ2))) is the nonlinear coefficient. Since B is always positive, the physical nature of the nonlinear ion-acoustic waves depends on the sign of the nonlinear coefficient A; the positive and the negative values of the nonlinear coefficient, A, will be related to compressive and rarefactive nonlinear ion acoustic waves, respectively. In the Sections 3 and 4, as mentioned earlier, we will focus our work on the properties of nonlinear rarefactive isothermal ion-acoustic solitary and periodic travelling waves in magnetized ultrarelativistic degenerate plasmas (i.e., A < 0). As displayed in Figure 5, the nonlinearity coefficient, A, has been varied from a positive sign (A > 0) to a negative sign (A < 0) due to the variation in μ_0e for different values of physical parameters β, α, and γ.

Figure 5:

The change of the nonlinear coefficient, A, against µ_0e for µ_0p = 0.3, σ_e = 30, σ_p = 30, σ = 0.005, Ω = 0.5, γ = 0.77, α = 0.11, β = 0.33 (red solid curve) and γ = 0.87, α = 0.25, β = 0.37 (blue dashed curve).

3 Nonlinear RIIASW and RIIAPTW solutions of the ZK equation

In this part, we use the bifurcation analysis to discuss the possibility of the existence of rarefactive isothermal ion acoustic solitary wave (RIIASW) and rarefactive isothermal ion acoustic periodic travelling wave (RIIAPTW) solutions. Also, we introduce the following independent variables:

where v₀ denotes the constant speed of the reference frame. Now, we apply the transformation Eq. (20) to Eq. (19) with  ϕ(1)(x,y,z,t)=ϕ(η), we obtain

integrating Eq. (21) with respect to η, we obtain

where the coefficients δ₁, δ₂, and δ₃ are defined by A2((ℓz2+(1−ℓz2) C)),  −v0ℓzB(ℓz2+(1−ℓz2) C) and DℓzB(ℓz2+(1−ℓz2) C) , respectively, and D is an integration constant. It is crucial to note that D>v02/2AB ℓz. Putting Φ=ϕ(η) and dΦ/dη=Ψ, then Eq. (22) can be expressed as a dynamical system of first-order differential equations (i.e., the planar Hamiltonian system).

It is worth noticing that the Hamiltonian system depends on the proposed plasma model’s physical parameters. Furthermore, the dynamical system Eq. (23) is a conservative Hamiltonian system that governs a particle of unit mass’s motion of under the effect of the potential forces. The Hamiltonian function (total energy) can be written as

where h is an arbitrary constant that determines the value of the energy. It is instructive at this point to describe all the possible nonlinear wave solutions for Eq. (19) by applying the phase portrait (i.e., the (Φ,Ψ) phase plane) of the Hamiltonian system Eq. (23). Of interest is to note that, at δ1≠0, δ2≠0 and δ3≠0, Eq. (23) has two equilibrium points Θ0(Φ0,0) and Θ1(Φ1,0) where Φ0=−δ2−Δ/2δ1 and Φ1=−δ2+Δ/2δ1  , where Δ=δ22−4δ1δ3>0. We assume that M(Φi,0) is the coefficient matrix of the linearized system of Eq. (23) at an equilibrium point Θi(Φi,0), where i = 0, 1. Applying the concept of dynamical systems, an equilibrium point Θ0(Φ0,0) of Eq. (23) is a saddle point when J=det M(Φ0,0)≅−v0ℓzB((ℓz2+(1−ℓz2) C))<0. On the other hand, at Θ1(Φ1,0), J=det  M(Φ1,0)≅v0ℓzB((ℓz2+(1−ℓz2) C))>0, the planar Hamiltonian system is a center point. The values of the energy h at the equilibrium points Θ0(Φ0,0) and Θ1(Φ1,0) are, respectively,  H(Φ0,0)=h=(δ23−6δ1δ2δ3−Δ3)/12δ12  is approximately equal to zero and  H(Φ1,0)=h=(δ23−6δ1δ2δ3+Δ3)/12δ12≅−4v03/6A2B3ℓz3((ℓz2+(1−ℓz2) C))<0. In this situation, where B and ℓz (i.e., 0<ℓz<1) are always positive, it is crucial to note that h > 0, except v₀ < 0 that corresponds physically to a nonlinear wave travelling towards negative η. Therefore, we will focus on analytical solutions and numerical simulations of the dynamical system for two energy values h, when h≅0 and h < 0.

Now, we utilize the energy integral Eq. (24) to find RIIASW and RIIAPTW solutions. It is given by

where P(Φ) is a polynomial of degree three in Φ, and it takes the following form

Figure 6:

Phase portrait of the dynamical system Eq. (23) with µ_0e = 0.3, µ_0p = 0.3 α = 0.11, γ = 0.77, σ_e = 30, σ_p = 30, σ = 0.005, Ω = 0.5 and ℓz=0.7.

On the level of the energy h < 0, there is a family of periodic orbits around the center point Θ1(Φ1,0) and it is demonstrated in Figure 6 by red color. A nonlinear RIIAPTW solution to Eq. (19) in terms of Jacobian elliptic functions is given by [59].

with the periodic τ=96 |δ1|(ϕ3−ϕ1) K(k), where K(k) is a complete elliptic integral with the modulus k=(ϕ2−ϕ1)(ϕ3−ϕ1), which is the measure of nonlinearity, where 0 < k ≤ 1 and ϕ1<ϕ2<ϕ3 are the three real roots of the following equation: h−δ13 Φ3−δ22 Φ2−δ3Φ=0 .

4 Numerical analysis, simulation and results

In this section, we will investigate numerically the RIIASW and RIIAPTW solutions to Eq. (19) in the fluctuations of physical parameters µ_0e, µ_0p, σ, ℓ_z,  γ and Ω. Figure 7(a) and (b) illustrate the variety of nonlinear rarefactive isothermal ion-acoustic solitary waves (RIIASWs) and rarefactive isothermal ion-acoustic periodic travelling waves (RIIAPTWs), respectively, in a certain range of the space coordinate η for two different values µ_0e = 0.4 and 0.5, viz., keeping all the other parameters fixed. Obviously, the electrostatic potentials of RIIASWs and RIIAPTWs are amplified (i.e., the amplitude becomes deeper), as the chemical potential of electrons is decreased (i.e., for lower µ_0e). It is well known physically that an increase in the chemical potential of electrons/positrons means that the electrons/positrons’ background density increases. As shown in Figure 5, an increase in the density of background electrons manifested through increasing µ_0e, leads to an increase in the absolute value of the nonlinear coefficient, A, (i.e., |A|) that can physically decrease the excitations of RIIASWs and RIIAPTWs. The other important parameter in this plasma system that needs attention is µ_0p. Figure 8(a) and (b) explore, respectively, the effects of µ_0p on the electrostatic potentials of RIIASW and RIIAPTW solutions. The electrostatic potentials become more profound and broader as µ_0p decreases. We note that the increase in the concentration of positive ions manifested through decreasing µ_0p to keep the quasi-neutrality condition in the plasma system leads to an increase in the driving force that is provided by positive ion inertia of the RIIASWs and RIIAPTWs; hence, the absolute values of the pulse amplitude and the width increase. Figure 9(a) and (b) demonstrate the variation of RIIASW and RIIAPTW profiles with the direction cosine ℓz, respectively. The excitations of RIIASWs and RIIAPTWs increase for lower ℓz, implying an amplification of the electrostatic potential disturbance as the RIIASW and RIIAPTW propagate away from the external static magnetic field. It should be mentioned here that at  ℓz→0, the amplitudes of the RIIASWs and RIIAPTWs increase to infinity and the widths tend to decrease zero. This means that, physically, we have to assume larger ℓz (i.e., smaller θ, where θ is the angle that the propagation vector of RIIASWs and RIIAPTWs makes with the magnetic field, 0 < θ < 45°) to preserve the validity of the electrostatic approximation in numerical analysis. Figure 10(a) and (b) display the RIIASW and RIIAPTW modes’ physical behavior for different values of γ. It is observed that the absolute value of electrostatic pulse amplitude (the width) increases (decreases) for lower γ. This means physically that an increase in the background density of electrons, manifested through decreasing γ, leads to an increase in the restoring force that can physically increase the excitations of RIIASWs and RIIAPTWs. It is also worth observing that the electron concentration effect to form the restoring force is more pronounced than its influence on the nonlinear coefficient to form RIIASW and RIIAPTW profiles. Figure 11(a) and (b) give, respectively, the RIIASW and RIIAPTW structures for two different values of σ = 0.001 and 0.005. The absolute values of the pulse amplitude and the width slightly increase for larger σ. The slight amplification of the amplitude is due to an increase in the fraction of thermal ions, which are the source of energy for RIIASWs and RIIAPTWs. Finally, in Figure 12(a) and (b), we have plotted the electrostatic potentials of RIIASW and RIIAPTW solutions as a function of Ω(=0.5–0.3). It is clear that the amplitudes remain unchanged and the widths become wider as the ion cyclotron frequency Ω decrease. This means that an increase in the magnitude value of the external static magnetic field leads to an increase in the ion cyclotron frequency and a decrease in the dispersion of the system. Therefore, the static magnetic field acts to restrict the charged particles of fluid elements tightly to the force lines so that the transverse motion of these particles is forced within the fluid element, a situation referred to as magnetic confinement. Thus, the uniform external magnetic field makes the RIIASWs and RIIAPTWs profiles more spiky. In fact, it is helpful to compare our results with the findings of El-Shamy et al. [50]. Without immobile heavy negative ions, the present study agrees exactly with the earlier work by El-Shamy et al. [50]. However, it is worth noting here that El-Shamy et al. [50] have focused only on studying compressive IIASWs, while in this investigation we were interested in studying the features of RIIASWs and RIIAPTWs.

Figure 7:

Variation of nonlinear rarefactive isothermal ion-acoustic waves for µ_0p = 0.3 α = 0.11, γ = 0.77, σ_e = 30, σ_p = 30, σ = 0.005, Ω = 0.5, ℓz=0.8, µ_0e = 0.4 (red solid curve) and µ_0e = 0.5 (blue dashed curve). (a) RIIASW and (b) RIIAPTW.

Figure 8:

Variation of nonlinear rarefactive isothermal ion-acoustic waves for µ_0e = 0.5, α = 0.11, γ = 0.77, σ_e = 30, σ_p = 30, σ = 0.005, Ω = 0.5, ℓz=0.8, µ_0p = 0.3 (red solid curve) and µ_0p = 0.4 (blue dashed curve). (a) RIIASW and (b) RIIAPTW.

Figure 9:

Variation of nonlinear rarefactive isothermal ion-acoustic waves for µ_0e = 0.5, µ_0p = 0.3, α = 0.11, γ = 0.77, σ_e = 30, σ_p = 30, σ = 0.005, Ω = 0.5, ℓz=0.8  (red solid curve) and ℓz=0.9  (blue dashed curve). (a) RIIASW and (b) RIIAPTW.

Figure 10:

Variation of nonlinear rarefactive isothermal ion-acoustic waves for µ_0e = 0.5, µ_0p = 0.3, σ_e = 30, σ_p = 30, σ = 0.005, Ω = 0.5, ℓz=0.8, γ = 0.77 (red solid curve) and γ = 0.88 (blue dashed curve). (a) RIIASW and (b) RIIAPTW.

Figure 11:

Variation of nonlinear rarefactive isothermal ion-acoustic waves for µ_0e = 0.5, µ_0p = 0.3, α = 0.11, γ = 0.77, σ_e = 30, σ_p = 30, Ω = 0.5, ℓz=0.8, σ = 0.005 (red solid curve) and σ = 0.001 (blue dashed curve). (a) RIIASW and (b) RIIAPTW.

Figure 12:

Variation of nonlinear rarefactive isothermal ion-acoustic waves for µ_0e = 0.5, µ_0p = 0.3, α = 0.11, γ = 0.77, σ_e = 30, σ_p = 30, σ = 0.005, ℓz=0.8, Ω = 0.5(red solid curve) and Ω = 0.3 (blue dashed curve). (a) RIIASW and (b) RIIAPTW.

To summarize, we have examined the linear and nonlinear propagation of IIAWs in a dense magnetoplasma comprising nondegenerate hot ions and ultrarelativistic degenerate inertialess electrons as well as positrons and stationary heavy negative ions. Using the small and finite-amplitude approximation method, we have obtained the nonlinear ZK equation. In the present investigation, the ZK equation supports either nonlinear compressive or rarefactive IIAWs. In our work, we focused only on the physical nature of RIIASWs and RIIAPTWs. Applying the bifurcation theory, we have analyzed the planar Hamiltonian system both analytically and numerically. In the proposed model, we have demonstrated that the chemical potentials of fermions, the ion cyclotron frequency and direction cosines affect the amplitude as well as the width of the RIIASWs and RIIAPTWs in magnetized ultrarelativistic degenerate plasmas. Finally, we believe that the present finding will help us to understand the essential characteristics of the nonlinear propagation of IIAWs in ultrarelativistic degenerate magnetized plasmas that may occur in many astrophysical compact objects, like white dwarfs.