The Reaction and Microscopic Electron Properties from Dynamic Evolutions of Condensed-Phase RDX Under Shock Loading

3.1 The Parameters Under Shock Loading

The ratio of the compressed volume to the primary volume, system pressure and the temperature of RDX which depends on the time under shock wave loading along a axis with the simulation time of 3.5 ps is presented in Figure 1. In these figures, one can see that the volumes reduce by 38.48 %, 41.25 % and 43 % at 8, 9 and 10 km ⋅ s⁻¹, respectively. Thermodynamic properties of RDX have a great relationship with shock velocities. The temperatures and pressures have experienced an overdrive state, basically reaching a balance from 0.5 ps to the end of our simulations. When the shock wave velocities change from 8 to 9 km ⋅ s⁻¹, the reaction temperatures are nearly stabilised at 1300 and 1700 K, respectively. However, the temperature reached to 3700 K and it kept a persistent increase at 10 km ⋅ s⁻¹. The pressures maintain a near-constant value of 45, 60 and 80 GPa at 8, 9 and 10 km ⋅ s⁻¹, respectively. The reported detonation pressure of RDX is 35.3 GPa [37]. Therefore, the shocked RDX reaches to detonation critical value under the shock wave velocities from 8 to 10 km ⋅ s⁻¹. But shock wave velocity of 8 km ⋅ s⁻¹ is a little lower than the steady detonation velocity of 8.754 km ⋅ s⁻¹ [37]. The strength of the shock wave is too weak to maintain the detonation chemical reaction to continue and gradually attenuate to a sound wave at 8 km ⋅ s⁻¹. So, the steady detonation cannot happen under this shock velocity. Although the shock wave velocity, temperature and pressure are all arrived at the condition of steady detonation of RDX, a few reactions and intermediates are presented. In addition, the calculated time scale may be too short to observe the full decomposition of RDX at 9 and 10 km ⋅ s⁻¹. According to the previous work, to obtain the full chemical behaviors, longer simulation times are required, but it needs much time and computing resources for the huge system in our study. Therefore, in the next discussions, we will mainly focus on investigating the reaction initiation of shocked α-RDX under shock loading with 8, 9 and 10 km ⋅ s⁻¹.

Figure 1:

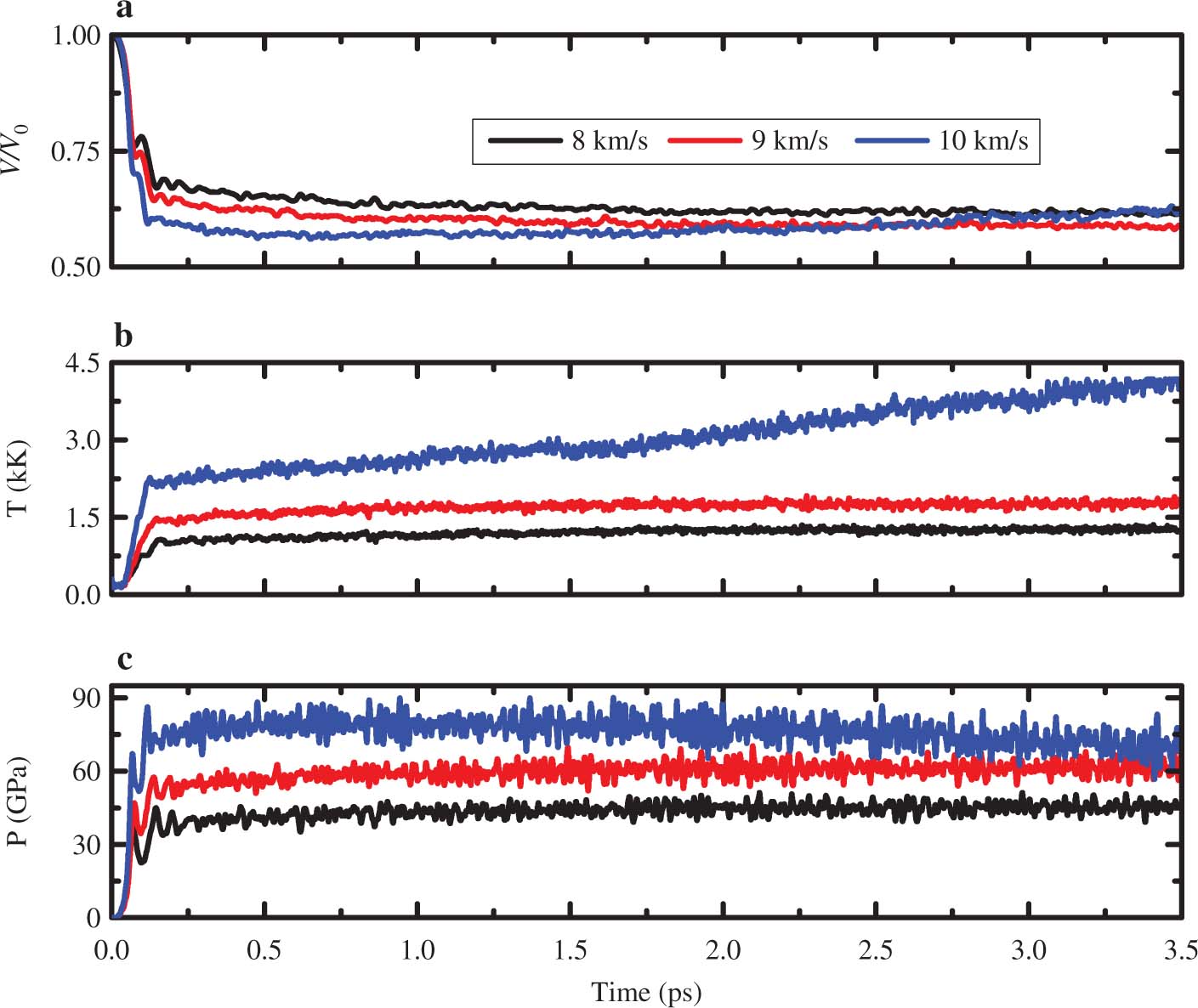
Time dependence of the ratio of the compressed volume to the primary volume (V/V₀), average temperature (T), and shock propagation direction pressure (P) calculated for the shock along the lattice vector a at different shock velocities of 8, 9 and 10 km ⋅ s⁻¹ for a time scale of up to 3.5 ps.

3.2 The Reaction Initiation of α-RDX Under Shock Wave Loading

The snapshots of the configurations for four instants under shock loading of 10 km ⋅ s⁻¹ are presented in Figure 2. From the simulation process, we could find that the system undergoes a persistent compressed process along with the molecular rotation. Before the primary decomposition, the system atoms are attracted or repelled with each other. Finally, the bonds between the conjoint atoms are compressed or stretched, which leading to the bonds rupture under shock loading. In our previous study [17], the C–N bond split of the opened ring has been demonstrated as the primary decomposition of shocked RDX at 10 km ⋅ s⁻¹. Our further study showed that the initially produced fragments are all due to the C–N split under different shock wave velocities of 8, 9 and 10 km ⋅ s⁻¹. The other proposed primary decomposition mechanisms are also found. However, from 8 to 10 km ⋅ s⁻¹, until at 115.55, 92.2 and 82.55 fs, respectively, the N–NO₂ bond dissociation happens. At 8 km ⋅ s⁻¹, there did not appear HONO elimination, but at 9 and 10 km ⋅ s⁻¹, the HONO was initially formed at 1855.3 and 334 fs, respectively.

Figure 2:

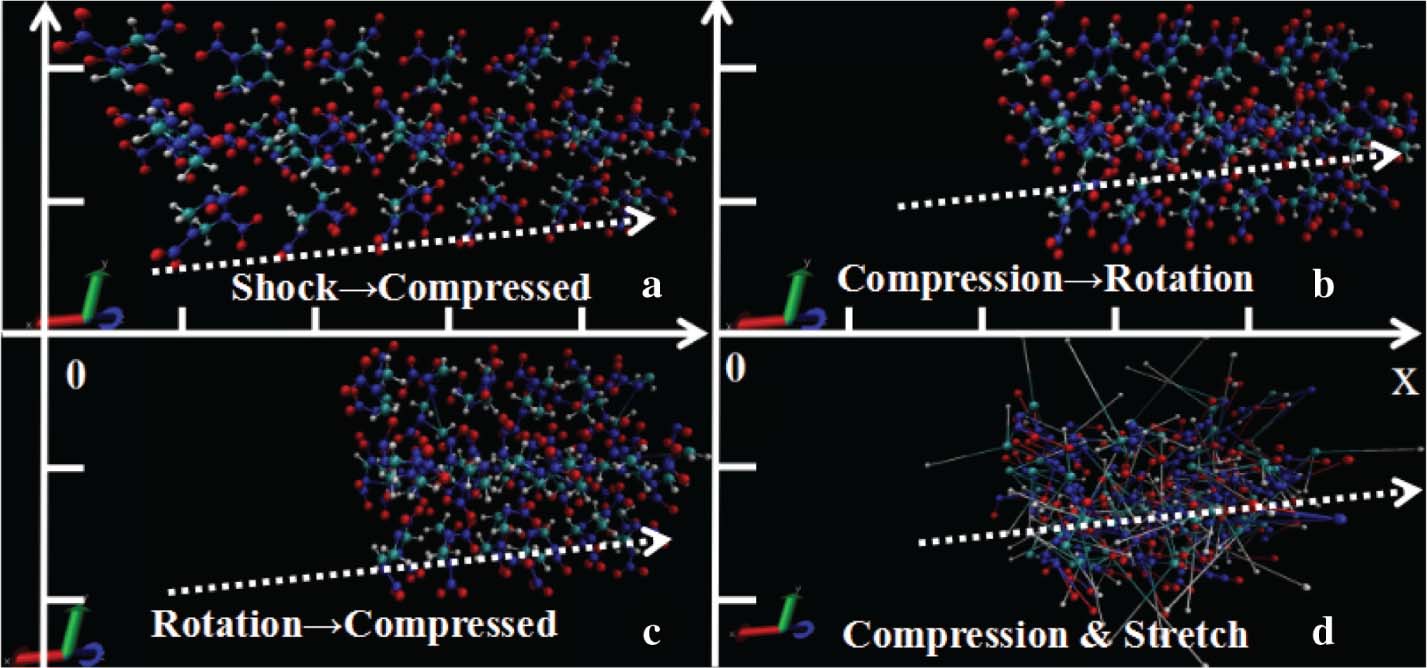
The snapshots of the change in the configurations for four instants under shock compression of 10 km ⋅ s⁻¹ along the lattice vectora. Grey, blue, red, and white spheres stand for C, N, O and H atoms, respectively. (a) Presents a persistent compressed process, (b) shows the rotation during the compression, (c) presents a compressed process while rotating and (d) shows the bonds rupture when compression reaches a certain level.

3.3 The Reaction Rates and Decomposition Products During the Shock Loading

The fitted density numbers of the products, C₃H₆N₆O₆ and their reaction rate depending on time under the shock loading of 8, 9 and 10 km ⋅ s⁻¹ are presented in Figure 3. We take derivatives of the density numbers with respect to time to observe the reaction rate. In Figure 3a, we can find that the system is compressed under the primary shock loading and this process lasts to 0.25 ps, the produced density number of the products shows an exponentially increase. In Figure 3b, with the persistent shock loading, the bonds of shocked RDX rupture and the decomposition begins. The opposite rule with the products, before 0.25 ps, the density number of RDX shows an exponentially decrease. There are few decompositions of shocked RDX at 8 and 9 km ⋅ s⁻¹. The shocked RDX shows a full decomposition state and the density numbers of RDX becomes zero from 0.3 ps at 10 km ⋅ s⁻¹. At the same time, the density number of the products shows nearly no change until 0.5 ps. But then the number of the products shows a linear increase to the end of our simulation at 10 km ⋅ s⁻¹, which showed that a large number of secondary reactions happens. From the reaction rate in Figure 3c,d, we can obviously find that both the decomposition rate and produced rate are more fast at the primary shock loading. With the shock velocity increasing, the reaction rate increases. Then the reaction rate tends to become zero at 8 and 9 km ⋅ s⁻¹, but the reaction rate at 10 km ⋅ s⁻¹ is higher than this value, which corresponds to the density numbers of the products increasing with time.

Figure 3:

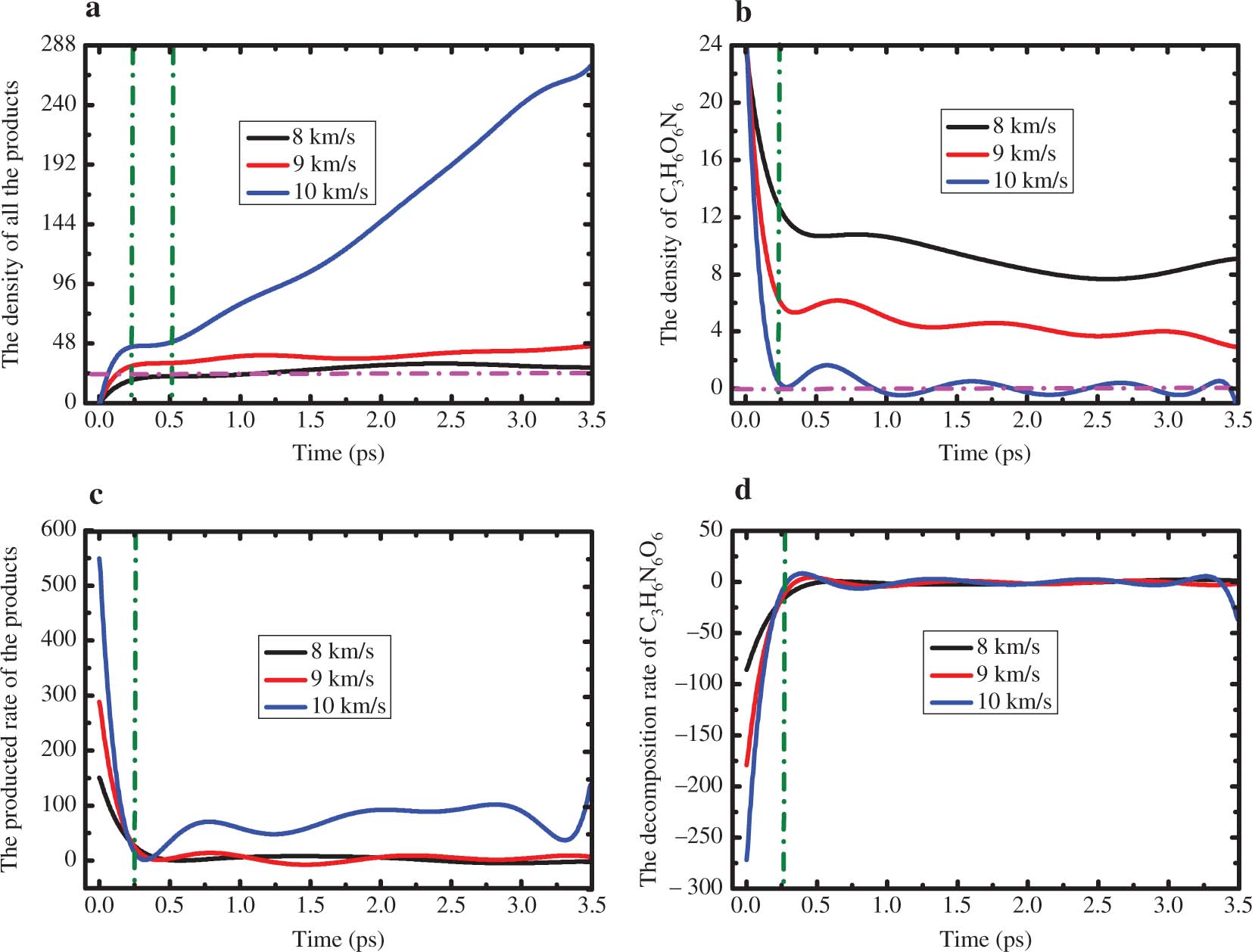
The fitted density numbers of the products (a) and C3H6N6O6 (b) along with the simulation time. The produced rate of products (c) and the decomposition rate of C3H6N6O6 (d) that varied with the simulation time under the shock loading of 8, 9 and 10 km ⋅ s⁻¹ along the lattice vector a.

This difference of the primary decomposition and reaction rate under the shock loading of 8, 9 and 10 km ⋅ s⁻¹ suggests that at higher shock velocities of 9 and 10 km ⋅ s⁻¹, the strong shock loading can lead to faster chemical reaction and the movements of the molecules become more severe than at 8 km ⋅ s⁻¹. Our results show that a few RDX molecules decompose and only NO₂ forms below the steady detonation shock velocity (8.754 km ⋅ s⁻¹). This result is consistent with the experimental result [38] by photoelectron spectroscopy analysis and the theoretic study with the nonequilibrium MD simulations [39]. However, newly produced molecules are NO, N₂O, H₂O at the shock velocity of 9 km ⋅ s⁻¹ and the many kinds of molecules including NO₂, NO, N₂O, H₂O, CO, CO₂, H₂, N₂ at 10 km ⋅ s⁻¹. The frontal analysis shows that at 8 km ⋅ s⁻¹, the temperatures and pressures reach the experimental critical detonation values, but the reaction of the NO₂ do not show noticeable change, which confirms no steady detonation formed under this shock velocity. The reaction rates of various products at 9 and 10 km ⋅ s⁻¹ increase quickly, indicating that RDX molecules are easier to decompose and the system arrives at a steady detonation stage. To further understand the decomposition mechanisms for the formation of the gas molecules, the origin of constituent atoms of the key gas molecules was investigated. The investigations showed that most of CO₂ and H₂O are formed from the intermolecular reaction pathways, while most of CO, NO, NO₂ and N₂ are formed from the intramolecular reaction pathways. This analysis shows that intramolecular reactions are the dominant pathways for shocked RDX decomposition. Our result showed that N₂ is formed by intramolecular reaction pathways. The produced N₂ is due to the N–NO₂ bonds rupture in a RDX molecule, which is different from the formation of gas products in the TATB molecule [8] and that most of the products are formed via the intermolecular reaction.

3.4 The Microscopic Electron Properties of α-RDX Under Shock Loading

As we all know energy band structure plays a key role in analysing the physical properties of materials. The energy difference that is the highest occupied molecular orbital–lowest unoccupied molecular orbital (HOMO–LUMO) energy gap indicates the insulating behavior of the solids. The HOMO–LUMO energy gap of RDX molecule was 5.269 eV [17] in our previous studies. The energy band structure of RDX in the ground state is presented in Figure 4. The result showed that RDX is a wide-gap insulator with the band gap energy of the system 5.12 eV, which is more consistent with the HOMO–LUMO energy gap by second-order perturbation theory of 5.25 eV [40], and the B3LYP [41] band gap of 5.54 eV for RDX. For more detail, we also studied the band structure of shocked RDX during the simulations at 8, 9 and 10 km ⋅ s⁻¹. We list the band gap energy as a function of the simulations time at 8, 9 and 10 km ⋅ s⁻¹ in Figure 5. The change of the band gap energy under different shock velocities shows the same orderliness. In addition, we can discover that with the simulations continuing, the band gap energy decreases with increasing pressure inside the wave front. From this figure, we can find that at 0.15 ps about 72 GPa and 2100 K, RDX shows obvious metallisation at 10 km ⋅ s⁻¹ that is higher than the experimentally measured steady detonation velocity, which is consistent with the metallisation with HMX under shock loading of 11 km ⋅ s⁻¹ at 0.15 ps about 130 GPa [20]. Until now, there is no available data for comparison of RDX band gap under shock loading on both experimental and theoretical results. The studies indicated that the metallisation pressure is 180 GPa [42] of pure RDX under static pressure conditions. Obviously, our work is studied based on a dynamic simulation, considering the temperature, the metallisation pressure of RDX under shock loading is lower than in the static pressure. At 9 km ⋅ s⁻¹, the temperature and pressure approach a condition of metallisation at 10 km ⋅ s⁻¹, with chemical reactions continuing, the band gap decreases to zero, but then it widens due to the fluctuations of electronic state energies during the simulation, so RDX shows semi-metallisation. However, at 8 km ⋅ s⁻¹ that a little lower than the steady detonation velocity, the pressure and temperature are far away from the condition of metallisation at 10 km ⋅ s⁻¹; it just shows the transformation from insulator to semiconductor.

Figure 4:

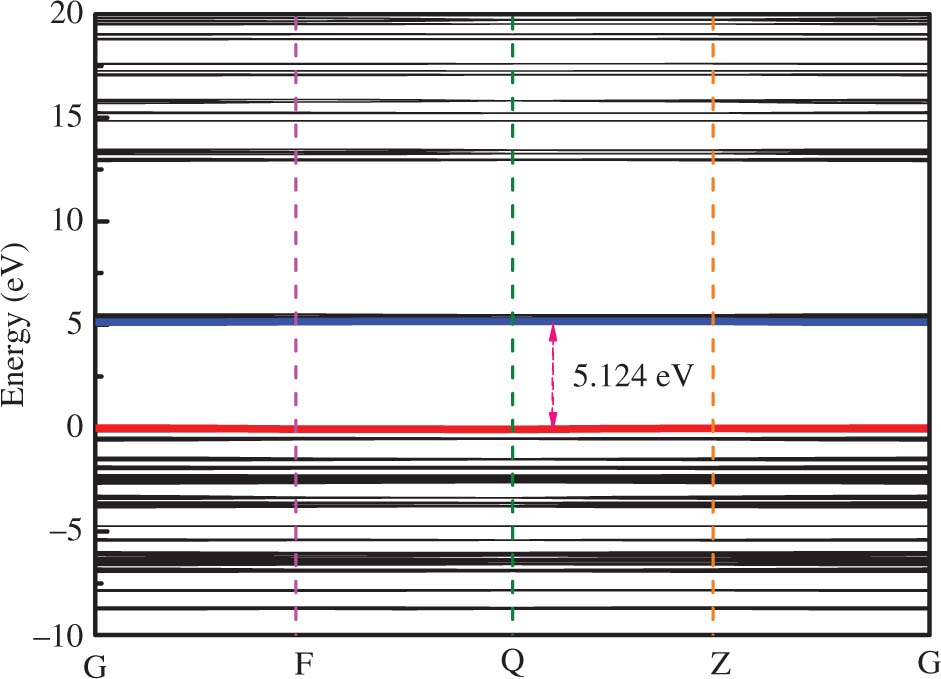
The calculated energy band structures of hexahydro-1,3,5-trinitro-1,3,5-triazine (RDX) at ground states.

Figure 5:

The band gap energy depends on the simulations time under the shock velocities of 8, 9 and 10 km ⋅ s⁻¹, respectively: (a) by Kuklj and Kunz using second-order perturbation theory [40], (b) by Perger using B3LYP [41], (c) present using density functional tight binding.