Abstract
Effects of Landau quantisation and exchange-correlation potential on Rayleigh–Taylor instability (RTI)/gravitational instability are investigated in inhomogeneous dense plasmas. Quantum hydrodynamic model is used for the electrons, while the ions are assumed to be cold and classical. RTI is modified with the inclusion of Landau quantisation related to plasma density, ambient magnetic field, exchange speed, and modified Fermi speed. Owing to the exchange-correlation effects, gravitational instability increases, whereas the Landau quantisation effects contribute in the opposite way for quantisation factor η < 1. Since the exchange-correlation potential is a function of density, by controlling the number density and magnetic field one can control RTI.
1 Introduction
Plasmas are enriched by heterogeneous phenomena, typically the challenge of inertial confinement fusion [1], growth of interface perturbations [2], tunnelling of aerodynamic wind [3], launching shock pulses into the foil of metal [4], material mixing, Doppler broadening of gamma rays [5], striking the interstellar clouds by blast waves [6], symmetry-breaking by supernova explosion [7], etc. These phenomena are rooted in the promising mechanism of Rayleigh–Taylor instability (RTI) or simply mixing instability. RTI is akin to falling water out of a glass, mixing the vinaigrette on shaking, flapping of the flags, and mushroom cloud from atomic explosion [7]. RTI explains the broad infrared emission of Fe-II, Ni-II, Ar-II, and Co-II, indicating the mixing from low-velocity to high-velocity cores. The production of hard X-rays is an indirect proof of mixing. Hence, understanding RTI helps in explaining the physical mechanism of fundamental research and technology, for example, nuclear weapons design [8].
There are many factors that may affect RTI, such as plasma density inhomogeneity [9], thickness scale of the perturbed interface, mass ablation [10], temperature-gradient-dependent magnetic field [11], inhomogeneous magnetic field [12], Weibel instability, resonant absorption, motion of superthermal electrons [13], stationary ponderomotive force [14], etc. All these are entirely studied in classical plasmas, therefore it is a need to introduce non-ideal effects such as Landau quantisation, exchange and correlation potential, etc. in quantum plasmas. Quantum plasma has emerged as a rapidly growing research area. Quantum plasma exists in dense astrophysical environments, particularly in the interior of Jupiter, white dwarfs, and neutron stars, as well as in metals and semiconductors. It is well known that quantum plasma has the properties of high particle number density and low temperature compared to classical plasmas, and therefore are associated with a de Broglie length longer than the inter-particle distance. Such plasmas are characterised by the Fermi pressure associated with degeneracy, where all quantum states are fully occupied below a certain level, tunnelling potential, exchange-correlation potential, and Landau quantisation [15], [16]. A recognised fact of moving either orbital-like gyro or spinning electrons is the magnetic field induction and the associated moment along the axis of gyration. Magnetic moment creates magnetism in the plasma. The external magnetic field alters the spinning. There are two magnetic effects due to the strong magnetic field: first is the Landau quantisation or Landau diamagnetism, which arises from the quantisation of the orbital-like gyro motion of charged particles; the second is the Pauli paramagnetism due to the spin of electrons. Landau quantisation effect and the tunnelling potential [17] are of a purely quantum nature. The external magnetic field enhances the total energy of the plasma system through Landau quantisation. The free electrons exhibit Landau diamagnetism at
Cao et al. [18] studied RTI using quantum magnetohydrodynamic equations and solved the second-order differential equation under fixed boundary conditions. They pointed out that the magnetic field has a stabilizing effect on RTI in a similar manner as in classical plasmas but is significantly affected by quantum effects. Ali et al. [19] investigated the RTI in an inhomogeneous, dense magnetoplasma and found that the density gradient modifies the growth rate of RTI. Modestov et al. [20] studied the influence of magnetic field on RTI in metal quantum plasmas. They observed that the paramagnetic effects in a quantum plasma make RTI weaker; however, for the case of ferromagnetic effects with perturbations of long and moderate wavelengths, certain stabilisation always takes place due to the nonlinear character of quantum plasma magnetisation. In 2012, Wang et al. [1] discussed the stabilisation of the RTI due to density gradients, magnetic fields, and quantum effects in ideal, incompressible quantum magnetoplasmas.
In this article, we present the RT wave instability in a non-uniform quantum magnetoplasma by assuming fluid-streaming due to the diamagnetic drift, gravitational drift, and additional diamagnetic-type drifts due to exchange-correlation potential under conditions
2 Mathematical Model
A dense quantum magnetoplasma consisting of ions and electrons is assumed. The quasi-neutrality condition for equilibrium is given as
To investigate the effects of Landau quantisation (Landau diamagnetism) due to the quantisation of the gyro-like orbital motion of the electrons in a strong magnetic field on the RTI in a quantum plasma with a density gradient, the following set of fluid equations is used in the quantum hydrodynamic (QHD) model:
Momentum equation
Continuity equation
where the exchange-correlations potential
Here,
The equation of continuity for electrons is
For the plasma ions, quantum effects can be neglected while the gravitational force is taken care of:
The continuity equation for ions is
Since all quantities vary sinusoidally,
According to the assumed geometry,
and
where
Eliminating
where
where
For the given geometry
and
So
On substituting vxe from (15) to
where
3 Dispersion Relation
To calculate the modified dispersion relation of RTI in a quantum plasma, we eliminate Ey 1,
where
Equation (20) is further solved for
4 Growth Rate
Let
and the growth rate is
Equation (22) is valid for
5 Results and Discussion
Equation (22) presents the analytical expression for the growth rate γ of RTI for dense plasmas. It is seen that the quantisation effects have a large impact on the growth rate of RTI. In this section, a graphical analysis of the growth rate of instability is presented for typical parameters in cgs units:
Figures 1–5 show a considerable impact over the normalised growth rate
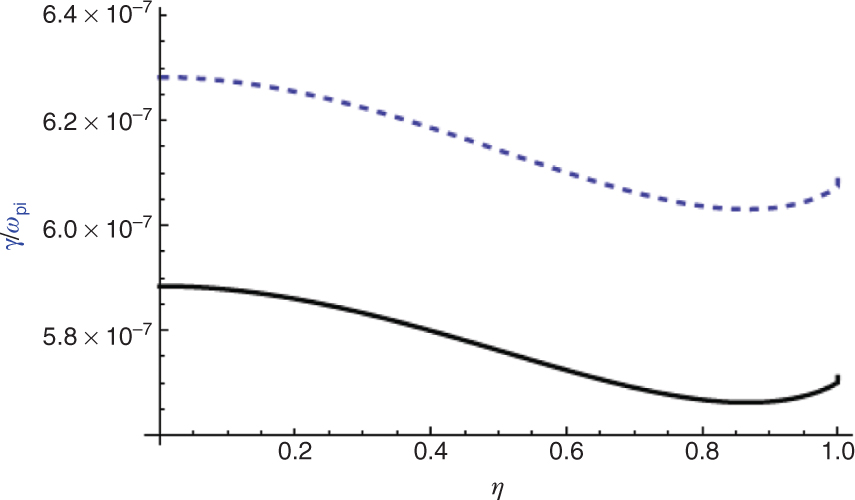
Normalised growth rate of RTI versus η. The dashed curve is for small
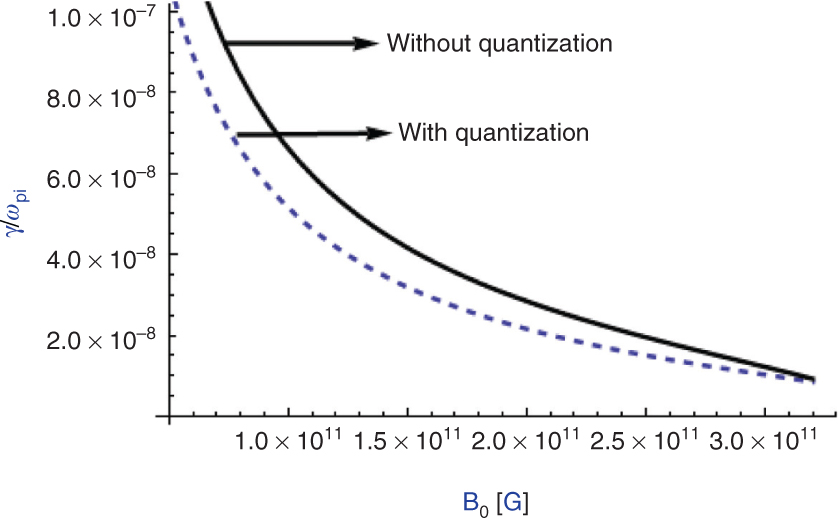
Normalised growth rate of RTI versus B0 (G). The solid curve is without quantisation and the dashed curve is with Landau quantisation for η < 1. Both curves meet at η = 1.
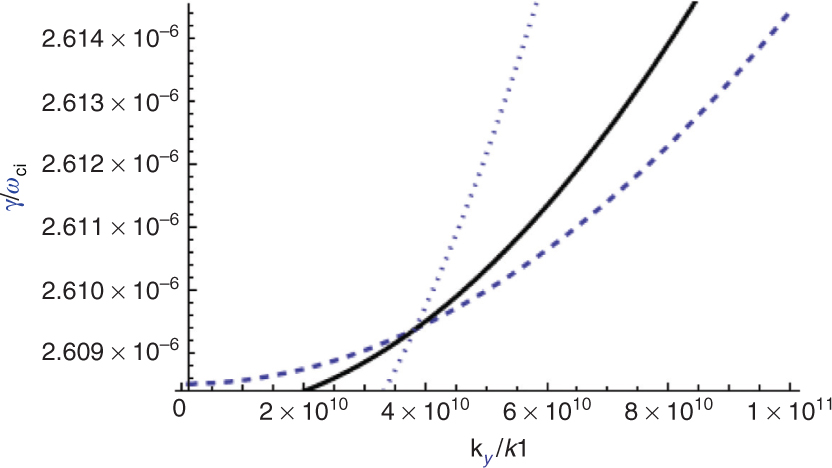
Normalised growth rate of RTI versus
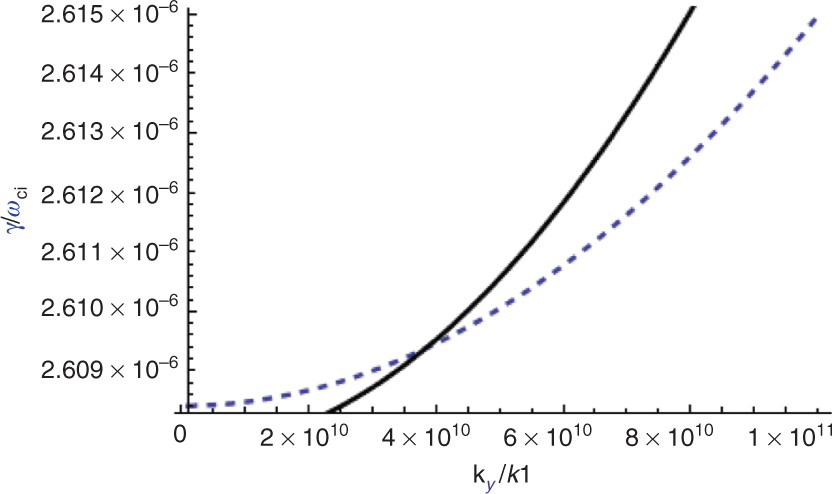
Normalised growth rate of RTI versus
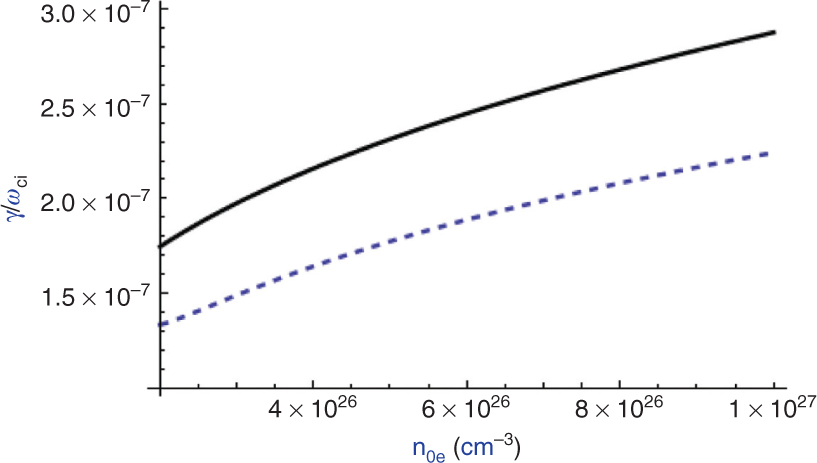
Normalised growth rate of RTI versus
Figure 3 shows
6 Summary
In summary, we studied RTI in quantum plasmas including quantum effects from Fermi pressure, Bohm potential, exchange-correlation potential, and Landau quantisation of the orbital motion of electrons. We found that the magnetic field B0 and hence the Landau quantisation play a role for the stabilisation of RTI for η < 1. The plasma density and the exchange-correlation potential, which directly depends on the density
References
[1] L. F. Wang, B. L. Yang, W. H. Ye, and X. T. He, Phys. Plasmas 19, 072704 (2012).10.1063/1.4737162Search in Google Scholar
[2] J. O. Kane, H. F. Robey, B. A. Remington, R. P. Drake, J. Knauer, et al., Phys. Rev. E 63, 055401 (2001).10.1103/PhysRevE.63.055401Search in Google Scholar PubMed
[3] D. Arnett, Astrophys. J. Suppl. Ser. 127, 213 (2000).10.1086/313364Search in Google Scholar
[4] D. H. Kalantar, B. A. Remington, E. A. Chandler, J. D. Colvin, D. M. Gold, et al., Astrophys. J. Suppl. Ser. 127, 357 (2000).10.1086/313324Search in Google Scholar
[5] J. Kane, D. Arnett, B. A. Remington, S. G. Glendinning, G. Bazan, et al., Astrophys. J. Suppl. Ser. 127, 365 (2000).10.1086/313349Search in Google Scholar
[6] F. Nakamura, C. F. Mckee, R. I. Klein, and R. T. Fisher, Astrophys. J. Suppl. Ser. 164, 477 (2006).10.1086/501530Search in Google Scholar
[7] A. Burrows, Nature 403, 727 (2000).10.1038/35001501Search in Google Scholar PubMed
[8] A. R. Piriza, J. J. López Celaa, M. C. Serna Morenoa, O. D. Cortázara, N. A. Tahirb, et al., Nucl. Instr. Methods Phys. Res. A 577, 250 (2007).10.1016/j.nima.2007.02.058Search in Google Scholar
[9] K. O. Mikaelian, Phys. Rev. Lett. 48, 1365 (1982).10.1103/PhysRevLett.48.1365Search in Google Scholar
[10] S. Bodner, Phys. Rev. Lett. 33, 761 (1974).10.1103/PhysRevLett.33.761Search in Google Scholar
[11] S. Chandrasekhar, Hydrodynamic and Hydromagnetic Stability, Oxford University, London 1961.Search in Google Scholar
[12] R. J. Mason and M. Tabak, Phys. Rev. Lett. 80, 524 (1998).10.1103/PhysRevLett.80.524Search in Google Scholar
[13] M. K. Srivastava, S. V. Lawande, M. Khan, D. Chandra, and B. Chakrborty, Phys. Fluids B 4, 4086 (1992).10.1063/1.860315Search in Google Scholar
[14] M. Jamil, A. Rasheed, M. Usman, W. Arshad, M. J. Saif, et al., Phys. Plasmas 26, 092110 (2019).10.1063/1.5096980Search in Google Scholar
[15] A. Rasheed, M. Jamil, Y.-D. Jung, A. Sahar, and M. Asif, Z. Naturforsch. A 72, 915 (2017).10.1515/zna-2017-0164Search in Google Scholar
[16] M. Jamil, Z. Mir, A. Rasheed, and A. Hussain, Z. Naturforsch. A 73, 1137 (2019).10.1515/zna-2018-0301Search in Google Scholar
[17] P. Sumera, A. Rasheed, M. Jamil, M. Siddique, and F. Areeb, Phys. Plasmas 24, 122107 (2017).10.1063/1.5002675Search in Google Scholar
[18] J. Cao, H. Ren, Z. Wu, and P. K. Chu, Phys. Plasmas 15, 012110 (2008).10.1063/1.2833588Search in Google Scholar
[19] S. Ali, Z. Ahmed, A. M. Mirzad, and I. Ahmad, Phys. Lett. A 373, 2940 (2009).10.1016/j.physleta.2009.06.021Search in Google Scholar
[20] M. Modestov, V. Bychkov, and M. Marklund, Phys. Plasmas 16, 032106 (2009).10.1063/1.3085796Search in Google Scholar
[21] A. Javed, A. Rasheed, M. Jamil, M. Siddique, and N. L. Tsintsadze, Phys. Plasmas 24, 112301 (2017).10.1063/1.4996601Search in Google Scholar
[22] Z. Mir, M. Jamil, A. Rasheed, and M. Asif, Z. Naturforsch. A 72, 891 (2017).10.1515/zna-2017-0093Search in Google Scholar
[23] M. Siddique, M. Jamil, A. Rasheed, F. Areeb, A. Javed, et al., Z. Naturforsch. A 7, 135 (2019).10.1515/zna-2017-0275Search in Google Scholar
©2020 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Frontmatter
- Atomic, Molecular & Chemical Physics
- Numerical Investigation of the Cooling Temperature of the InGaP/InGaAs/Ge Subcells Under the Concentrated Illumination
- Dynamical Systems & Nonlinear Phenomena
- Ion-Acoustic Cnoidal Waves with the Density Effect of Spin-up and Spin-down Degenerate Electrons in a Dense Astrophysical Plasma
- Hydrodynamics
- Landau Quantised Modification of Rayleigh–Taylor Instability in Dense Plasmas
- Interaction of a Singular Surface with a Characteristic Shock in a Relaxing Gas with Dust Particles
- Quantum Theory
- Path Integrals, Spontaneous Localisation, and the Classical Limit
- Proposal for a New Quantum Theory of Gravity III: Equations for Quantum Gravity, and the Origin of Spontaneous Localisation
- Quantum-Phase-Field: From de Broglie–Bohm Double-Solution Program to Doublon Networks
- Solid State Physics & Materials Science
- Photovoltaic Generator Based on Laser-Induced Reversible Aggregation of Magnetic Nanoparticles
- Thermodynamics & Statistical Physics
- Investigation of the Finite Size Properties of the Ising Model Under Various Boundary Conditions
Articles in the same Issue
- Frontmatter
- Atomic, Molecular & Chemical Physics
- Numerical Investigation of the Cooling Temperature of the InGaP/InGaAs/Ge Subcells Under the Concentrated Illumination
- Dynamical Systems & Nonlinear Phenomena
- Ion-Acoustic Cnoidal Waves with the Density Effect of Spin-up and Spin-down Degenerate Electrons in a Dense Astrophysical Plasma
- Hydrodynamics
- Landau Quantised Modification of Rayleigh–Taylor Instability in Dense Plasmas
- Interaction of a Singular Surface with a Characteristic Shock in a Relaxing Gas with Dust Particles
- Quantum Theory
- Path Integrals, Spontaneous Localisation, and the Classical Limit
- Proposal for a New Quantum Theory of Gravity III: Equations for Quantum Gravity, and the Origin of Spontaneous Localisation
- Quantum-Phase-Field: From de Broglie–Bohm Double-Solution Program to Doublon Networks
- Solid State Physics & Materials Science
- Photovoltaic Generator Based on Laser-Induced Reversible Aggregation of Magnetic Nanoparticles
- Thermodynamics & Statistical Physics
- Investigation of the Finite Size Properties of the Ising Model Under Various Boundary Conditions


