Structural, Electronic and Nonlinear Optical Properties of Novel Derivatives of 9,12-Diiodo-1,2-dicarba-closo-dodecaborane: Density Functional Theory Approach
-
Aijaz Rasool Chaudhry
, Shabbir Muhammad
Abstract
Using density functional theory (DFT) methods, we shed light on the structural, optical, electronic, and nonlinear optical (NLO) properties of three derivatives of 9,12-diiodo-1,2-dicarba-closo-dodecaborane(12) (C2H10B10I2). The DFT and time-dependent DFT methods are considered very precise and practical to optimize the ground and excited state geometries, respectively. A vibrant intramolecular charge transfer from highest occupied molecular orbitals (HOMOs) to the lowest unoccupied molecular orbitals (LUMOs) was observed in all compounds. The geometrical parameters of the experimental crystal structure, i.e. bond lengths/angles, have been successfully reproduced. The HOMO and LUMO energies, as well as their energy gaps (Eg), were also calculated and compared with each other for all derivatives. The effect of attached groups on electronic, optical, and NLO properties along with detailed structure-property relationship was discussed. For NLO response, the CAM-B3LYP functional along with relatively larger basis set 6-31+G** (for hydrogen, carbon, boron, and oxygen atoms) and LANL2DZ (for iodine atoms) have been used to optimize the compounds at ground states. The calculation of second-order NLO polarizabilities (βtot) shows that compounds 2 and 3 possess the βtot amplitudes of 3029 and 4069 a.u., respectively, with CAM-B3LYP method that are reasonably larger than similar prototype molecules. Owing to their unique V-shapes, the nonlinear anisotropy values are found to be 0.63, 0.34, and 0.44 for compounds 1–3, respectively, which show the significant two-dimensional character of these compounds. Thus, the NLO amplitudes as well as the nonlinear anisotropies indicate that the above-entitled compounds are good contenders for optical and NLO applications.
1 Introduction
Iodine (I) substituted at boron (B) atoms in carboranes has been intensively studied as precursors of a large number of B-carboranes [1], [2], [3]. Structural properties of some B-iodo-carboranes were also investigated [4], [5], [6]. Previously, boron-based 9,12-diiodo-1,2-dicarba-closo-dodecaborane(12) (C2H10B10I2) was reported [7] as an individual compound for the structural properties of this fascinating compound. Several iodinated ortho-carborane crystal structures were comprehensively investigated during the last few years, and the diversity of the intermolecular interactions was revealed, which these materials may adopt in the solid state [8]. Furthermore, these fascinating complexes have been reported as stable compounds to several chemical conditions and also illustrate a huge potential to incorporate with several substituents. The ortho-carboranes (1,2-dicarba-closo-dodecaboranes) had been described as a prospective building blocks in supramolecular chemistry [9], [10]. Although a large number of iodinated carboranes and decaboranes are available, still they have a lot of potentials to be explored, especially the nonlinear optical (NLO) response of these compounds. Previously, it has been shown that because of better phase matching and increased stability, two-dimensional chromophores having large off-diagonal β tensor components have advantage over one-dimensional chromophores [11], [12]. Nowadays, compounds with great off-diagonal β tensor components are being recommended as they can offer large macroscopic NLO responses. Hitherto, NLO properties of numerous two-dimensional compounds were studied by substituting donor and/or acceptor in V-shaped molecules [12], [13]. It was shown that the angle between the intramolecular charge transfer (ICT) axis is an important parameter to check the relative magnitude of off-diagonal and diagonal components. In the current study of dicarba-closo-dodecaborane derivatives, the CT comprises both sides of dicarba-closo-dodecaborane. Additionally, the work of Coe et al. showed that large off-diagonal β tensor components are intensely interconnected to oscillator strength, low-lying energy excited states with the electron transition dipole moment between two states that are perpendicular to the dipolar axis [13].
Earlier, ICT has been studied through bridging effect on first hyperpolarizability [14]. In some other studies, NLO response properties of various ICT compounds were explored [15], [16], [17]. There is great demand to improve new organic-inorganic hybrid compounds that can associate benefits of organic materials (high NLO efficiency) as well as inorganic materials (good stability, wide transparency range). Owing to good thermal stability of dicarba-closo-dodecaborane and its versatile nature, they are being used in various functional materials [18]. It is anticipated that dicarba-closo-dodecaborane derivatives might lead to better NLO properties because of their V-shaped structures. In the current study, we have designed organic-inorganic hybrid proficient NLO-phores. The present investigations aim to explore the structure-property relationship of V-shaped dicarba-closo-dodecaborane derivatives and their potential as NLO-phores.
The nonlinear response properties are characterized by second- and third-order polarizabilities. The NLO materials have important applications in many fields of modern hi-tech society including optical data processing and frequency doubling. Over the past few years, our group has reported many compounds with efficient NLO response [19], [20]. Similar to our several previous studies [21], we have calculated the static total second-order polarizabilities (βtot) of compounds 1–3 to check their possible NLO response. Furthermore, a comparison of βtot and βvec has been done and presented in Table 5 of Section 3.4 of the Results and Discussion.
It is also important to mention that the amplitude of βtot is always positive irrespective of the sign of individual tensorial components, which cannot be measured experimentally, whereas the amplitude of βvec may be positive or negative depending on the direction of dipole moment and charge transfer process for typical molecular system [15], [22]. The relation between βvec and βtot presents essential evidence about the direction of charge transfer in the molecules [15], [23] and specified by equation:
In the above equation, θ is the angle between the vector formed by the βvec components and the dipole moment vector. Usually, this ratio if near to one indicates a unidirectional charge transfer within the molecular systems where βtot and βvec carry similar amplitudes.
In the present study, we have selected 9,12-diiodo-1,2-dicarba-closo-dodecaborane(12) (C2H10B10I2) [7] as parent molecule (named as 1 in the text) and derived two new compounds ( 2 and 3, respectively) with the aim to tune the optoelectronic and NLO properties. In compound 2, 1-nitro-4-propynyl-benzene group was substituted at the X-positions, while in compound 3, 1-amino-4-propynyl-benzene has been attached at the X-positions of the parent compound ( 1); see Figure 1. The purpose of substituting 1-nitro-4-propynyl-benzene group (strong electron acceptor) and 1-amino-4-propynyl-benzene (strong electron donor) at the X-positions of the parent compound is to explore the effect of acceptor and donor ligands on the various properties of interest, respectively. Both the 1-nitro-4-propynyl-benzene group and 1-amino-4-propynyl-benzene groups are representative of the best electron donor and electron acceptor groups, respectively, which are often used as prototypes to check the electron donor-acceptor effects in push-pull molecules [24]. The aforementioned groups are used as general representative of acceptor and donor moieties of compounds to establish the electronic communication with 9,12-diiodo-1,2-dicarba-closo-dodecaborane(12). We have explored the structural, frontier molecular orbitals, optical spectra [absorption (λa) and emission (λe)], and NLO properties of the targeted compounds by density functional theory (DFT) [25] and time-dependent DFT (TD-DFT) [26], [27], [28], [29]. Moreover, the βtot and βvec values of the studied compounds 1–3 have been evaluated in detail to understand the direction of charge transfer in the molecules.
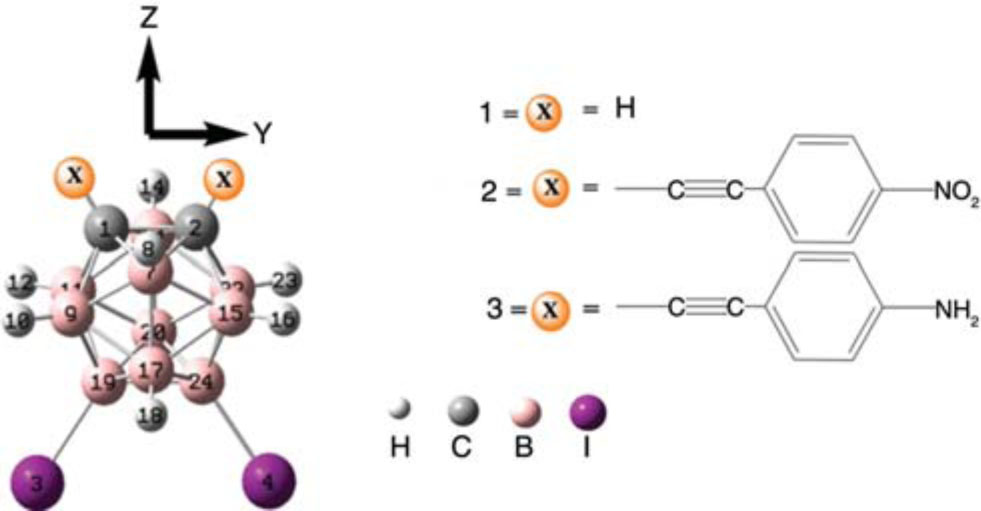
The optimized structures and schematic diagram of all derivatives investigated in the current study.
A contemporary survey of literature showed that there is no such computational study carried out heretofore on these studied compounds. This is the first time that we are going to have an in-depth study of 9,12-diiodo-1,2-dicarba-closo-dodecaborane(12) (C2H10B10I2) and two of its novel derivatives; see Figure 1.
2 Computational Details
In the present study, B3LYP method was adopted to optimize the ground state S0 geometries of molecules because the hybrid functional B3LYP of DFT has been widely used to reproduce the experimental electronic [30], [31] and geometric parameters [32], [33], [34], [35], [36], [37], [38]. The basis set Gen is a hybrid basis set including 6-31G** for hydrogen, carbon, boron, and oxygen atoms, while LANL2DZ is for iodine atoms. Preat et al. revealed that the B3LYP method is suitable for the ground state (S0) geometry optimizations [39], [40]. Moreover, Huong and co-workers confirmed that the B3LYP/6-31G** level is a decent approach to reproduce the experimental crystal data as well as rational for the electronic and charge transport properties [41]. The excited state (S1) geometries were optimized at TD-DFT [42] using the TD-B3LYP/6-31G** (LANL2DZ) level of theory. Then the same TD-DFT level was applied to evaluate the absorption and emission spectra, which was already verified to be a proficient method [29]. It is important to note down here that many critical studies indicated that B3LYP is not appropriate for the calculation of NLO polarizabilities as reported by Champagn et al. [43], [44]. Recently, Misra et al. [15] reported that the CAM-B3LYP and MP2 are suitable to calculate the NLO response, whereas the CAM-B3LYP is considered more appropriate for NLO response without compromising the computing cost and accuracy. Previously, the hybrid functional CAM-B3LYP has been reported as useful for evaluating the NLO response of several charge transfer base molecule [45], [46], [47]. To overcome such discrepancies, we have also optimized compounds 1–3 at CAM-B3LYP method along with relatively larger basis set 6-31+G** (LANL2DZ) for ground state. The static second-order polarizabilities at CAM-B3LYP/6-31+G** (LANL2DZ) have been evaluated for compounds 1–3 initially optimized at the B3LYP/6-31G** (LANL2DZ) level of theory and are tabulated in Tables 5 and S2 of the Supporting Information. Furthermore, we also compute the static second-order polarizabilities at CAM-B3LYP/6-31+G** (LANL2DZ) for compounds 1–3 optimized at the same level of theory and presented in Table 5.
It is found that there are noticeable differences among the amplitudes of βtot and βvec at different levels of theory. At two different levels of theory (B3LYP versus CAM-B3LYP), the approximate percentage differences among the amplitudes of βtot and βvec are found to be 32 %, 50 %, and 14 % for compounds 1, 2, and 3, respectively. A detailed analysis is given in Table S1 of the Supporting Information.
A well-known finite field approach combined with DFT method is used for the calculation of NLO response. In finite field method, a static electric field (F) is applied, and the energy (E) of the molecule is given by following equation:
where i, j, and k label the x, y, and z components, respectively. The total energy of the molecule is represented by E(0) without any field, while μ and α are the dipole moment and linear polarizability. Similarly, the β and γ are the second- and third-order nonlinear polarizabilities, respectively. It is obvious from (1) that differentiating E with respect to F attains the 27 components of β. According to Kleinman symmetry, βxyy = βyxy = βyyx, βyyz = βyzy = βzyy, …, likewise other permutations also take the same value. So the 27 components of second-order nonlinear polarizability (β) can be reduced to 10 components.
The values of βtot and βvec are calculated by the following equations:
where
All these quantum chemical calculations were performed using Gaussian09 package [48].
3 Results and Discussion
3.1 Molecular Geometries
The S0 and S1 significant geometrical parameters, i.e. bond lengths (Å) and bond angles (degrees, °), of the parent borane compound 1 and its derivatives 2 and 3 at the B3LYP/Gen and TD-B3LYP/Gen levels of theory are tabulated in Tables 1 and 2. It can be seen from Table 1 that the computed S0 bond lengths and bond angles were found in reasonable agreement with the experimental crystal structural geometric parameters. The bond lengths I3-B19, I4-B24, C2-B13, B20-B19, and B9-B19 were being overestimated, i.e. 0.014, 0.025, 0.014, 0.016, and 0.018 Å, respectively, for compound 1; 0.011, 0.021, 0.042, 0.034, 0.014, and 0.019 Å for compound 2; for compound 3, the increase in the bond lengths are 0.017, 0.027, 0.030, 0.013, and 0.026 Å, respectively, as compared with the experimental data. The increase in the bond lengths is because the experimental geometrical data are in the solid phase, whereas the computed parameters are in gas phase. The alteration in the bond angles I3-B19-B9, I3-B19-B9-I4-B24-B17, and I4-B24-B17 was observed as 2.98°, −2.51°, 1.17°, and 2.1° for parent compound 1; 3.3°, −2.83°, 1.5°, and 2.4° for compound 2, and 3.43°, −2.99°, 1.64°, and 2.55° for compound 3, respectively, in comparison to experimental data.
Selected optimized bond lengths (Angstrom, Å) and bond angles (degree, °) of ground state for borane derivatives at the B3LYP/Gena level of theory, respectively.
| Parameters | Exp.b | 1 | 2 | 3 |
|---|---|---|---|---|
| I3-B19 | 2.183 | 2.197 | 2.194 | 2.200 |
| I4-B24 | 2.173 | 2.198 | 2.194 | 2.200 |
| C1-B9 | 1.697 | 1.697 | 1.703 | 1.690 |
| C1-B7 | 1.723 | 1.718 | 1.738 | 1.734 |
| C2-B22 | 1.690 | 1.697 | 1.703 | 1.690 |
| C2-B13 | 1.704 | 1.718 | 1.738 | 1.734 |
| B7-B17 | 1.764 | 1.764 | 1.765 | 1.773 |
| B7-B9 | 1.786 | 1.777 | 1.783 | 1.789 |
| B11-B19 | 1.774 | 1.777 | 1.776 | 1.776 |
| B11-B20 | 1.790 | 1.782 | 1.778 | 1.776 |
| B11-B9 | 1.789 | 1.789 | 1.791 | 1.790 |
| B20-B13 | 1.773 | 1.764 | 1.765 | 1.773 |
| B20-B19 | 1.780 | 1.796 | 1.794 | 1.793 |
| B13-B22 | 1.773 | 1.777 | 1.765 | 1.789 |
| B15-B24 | 1.774 | 1.777 | 1.776 | 1.776 |
| B15-B22 | 1.790 | 1.789 | 1.791 | 1.790 |
| B9-B19 | 1.795 | 1.777 | 1.776 | 1.775 |
| B20-B24 | 1.792 | 1.796 | 1.794 | 1.793 |
| I3-B19-B24 | 124.10 | 124.21 | 124.23 | 124.10 |
| I3-B19-B11 | 119.70 | 119.69 | 119.47 | 119.25 |
| I3-B19-B20 | 119.20 | 122.18 | 122.50 | 122.63 |
| I3-B19-B17 | 121.80 | 122.18 | 122.50 | 122.65 |
| I3-B19-B9 | 122.20 | 119.69 | 119.37 | 119.21 |
| I4-B24-B19 | 123.30 | 124.21 | 124.24 | 124.10 |
| I4-B24-B17 | 121.00 | 122.17 | 122.50 | 122.64 |
| I4-B24-B15 | 119.15 | 119.68 | 119.40 | 119.25 |
| I4-B24-B22 | 119.10 | 119.69 | 119.40 | 119.21 |
| I4-B24-B20 | 120.10 | 122.20 | 122.50 | 122.65 |
| B7-C1-B9 | 62.83 | 62.70 | 62.43 | 62.98 |
aGen = 6-31G** for H, C, B, and O atoms, while Gen = LANL2DZ for I atoms. bExperimental (Exp.) data of compound 1 from [7].
Selected optimized bond lengths (Angstrom, Å) and bond angles (degree, °) of excited state for borane derivatives at the B3LYP/Gena level of theory, respectively.
| Parameters | 1 | 2 | 3 |
|---|---|---|---|
| I3-B19 | 2.293 | 2.280 | 2.218 |
| I4-B24 | 2.293 | 2.280 | 2.212 |
| C1-B9 | 1.687 | 1.640 | 1.645 |
| C1-B7 | 1.695 | 1.640 | 1.693 |
| C2-B22 | 1.687 | 1.640 | 1.623 |
| C2-B13 | 1.695 | 1.640 | 1.623 |
| B7-B17 | 1.715 | 1.792 | 1.764 |
| B7-B9 | 1.739 | 1.836 | 1.843 |
| B11-B19 | 1.799 | 1.770 | 1.762 |
| B11-B20 | 1.810 | 1.773 | 1.764 |
| B11-B9 | 1.853 | 1.820 | 1.797 |
| B20-B13 | 1.715 | 1.792 | 1.843 |
| B20-B19 | 1.770 | 1.794 | 1.809 |
| B13-B22 | 1.739 | 1.836 | 1.863 |
| B15-B24 | 1.800 | 1.770 | 1.778 |
| B15-B22 | 1.853 | 1.820 | 1.828 |
| B9-B19 | 1.732 | 1.770 | 1.762 |
| B20-B24 | 1.786 | 1.794 | 1.804 |
| I3-B19-B24 | 112.43 | 114.67 | 122.50 |
| I3-B19-B11 | 129.70 | 124.01 | 124.27 |
| I3-B19-B20 | 113.66 | 120.05 | 118.12 |
| I3-B19-B17 | 116.22 | 120.05 | 124.27 |
| I3-B19-B9 | 126.53 | 124.01 | 118.11 |
| I4-B24-B19 | 112.42 | 114.67 | 122.33 |
| I4-B24-B17 | 113.65 | 120.05 | 124.17 |
| I4-B24-B15 | 129.69 | 124.01 | 117.27 |
| I4-B24-B22 | 126.52 | 124.01 | 117.27 |
| I4-B24-B20 | 116.22 | 120.05 | 124.18 |
| B7-C1-B9 | 61.88 | 67.41 | 70.11 |
aGen = 6-31G** for H, C, B, and O atoms, while Gen = LANL2DZ for I atoms.
Here, the lengthening or shortening in the bond lengths, as well as variation in the bond angles, from S0 to S1 was also discussed. In compounds 1–3, the lengthening from the S0 to S1 was 0.096, 0.086, and 0.018 Å for the I3-B19 and I4-B24 bond lengths, respectively. For the B7-B17 bond length, the shortening was determined to be 0.049, 0.027, and 0.09 Å in 1–3 from S0 to S1, respectively. While for the B11-B9 bond length, the lengthening was noticed from S0 to S1, i.e. 0.073, 0.029, and 0.007 Å in 1–3, respectively. The bond angle I3-B19-B24 decreases to 11.10°, 9.56°, and 1.60°; the bond angle I3-B19-B11 increased by 10°, 4.54°, and 5.02°; the bond angle I3-B19-B20 decreases to 8.51° and 2.46° for 1 and 2, whereas it increased for 3 as 1.64°. The variation in the bond angles I3-B19-B17, I3-B19-B9, I4-B24-B19, I4-B24-B17, I4-B24-B15, I4-B24-B22, I4-B24-B20, and B7-C1-B9 from S0 to S1 was found as −5.96°, 4.73°, −11.79°, −8.52°, 10.01°, 6.52°, −5.98°, and −0.82° for 1 and for 2 as −2.45°, 4.69°, −9.57°, −2.46°, 4.6°, 4.6°, −2.45°, and 4.98°; however, for the derivative 3, the alteration in the aforementioned bond angles has been evaluated as 1.62°, −1.1°, −1.77°, 1.53°, −1.98°, −1.94°, 1.53°, and 7.13°, respectively. From these variations in the bond angle, a red shift behavior from S0 to S1 can be predicted for compounds 1–3.
3.2 Electronic Properties
The ground state and excited state energies of the frontier molecular orbitals and energy gaps of borane-based derivative compounds 1–3 have been tabulated in Table 3. The ground state and excited state highest occupied molecular orbital (HOMO) energies (EHOMO), lowest unoccupied molecular orbital (LUMO) energies (ELUMO), and HOMO-LUMO energy gaps (Eg) of compounds 1–3 were calculated at the B3LYP/6-31G** and TD-B3LYP/6-31G** levels of theory, respectively, which are tabulated in Table 3. The trend in the EHOMO is 3 > 1 > 2, while in the ELUMO, it is 1 > 3 > 2, for the ground and excited states. The tendency in the Eg was observed as 1 > 3 > 2 at ground state, while it is 1 > 2 > 3 at excited state. Here electron and hole injection energies were calculated to understand the charge injection behavior of the studied derivatives. The electron injection energy was calculated as [= −ELUMO − (−work function of metal)]. The work function of aluminum (Al) is −4.08 eV. The electron injection energy was found to be 3.24 eV [= −0.84 − (−4.08)], 0.75 eV [= −3.33 − (−4.08)], and 2.19 eV [= −1.89 − (−4.08)] from compounds 1–3 to Al electrode, respectively. It is expected that 2 might be a better electron transport contender having the smallest electron injection barrier to Al electrode. Moreover, the smaller and low-lying ELUMO of 2 than the other counterparts revealed that the prior compound might be thermodynamically more stable and charge transport cannot be quenched by losing the electrons. The hole injection energy of compounds 1–3 has been predicted, i.e. 2.55 eV [= −4.08 − (−6.63)], 2.71 eV [= −4.08 − (−6.79)], and 1.70 eV [= −4.08 − (−5.78)] from compounds 1–3 to the Al electrode, respectively. It is expected that 3 would be a better hole transport material. The charge distribution patterns of the HOMOs and LUMOs of boron-based derivatives 1–3 have been illustrated in Figure 2 for ground states, while for excited states, the HOMO and LUMO formations have been shown in Figure S2 of the supporting information.
The HOMO energies (EHOMO), LUMO energies (ELUMO), and HOMO-LUMO energy gaps (Eg) in eV for ground and first excited states computed at the B3LYP/Gena and TD-B3LYP/Gena levels of theory, respectively.
| Complexes | Ground states | First excited states | ||||
|---|---|---|---|---|---|---|
| EHOMO | ELUMO | Eg | EHOMO | ELUMO | Eg | |
| 1 | −6.63 | −0.84 | 5.78 | −5.73 | −3.61 | 2.12 |
| 2 | −6.79 | −3.33 | 3.47 | −6.10 | −4.37 | 1.73 |
| 3 | −5.78 | −1.89 | 3.89 | −5.27 | −3.65 | 1.62 |
aGen = 6-31G** for H, C, B, and O atoms, while Gen = LANL2DZ for I atoms.
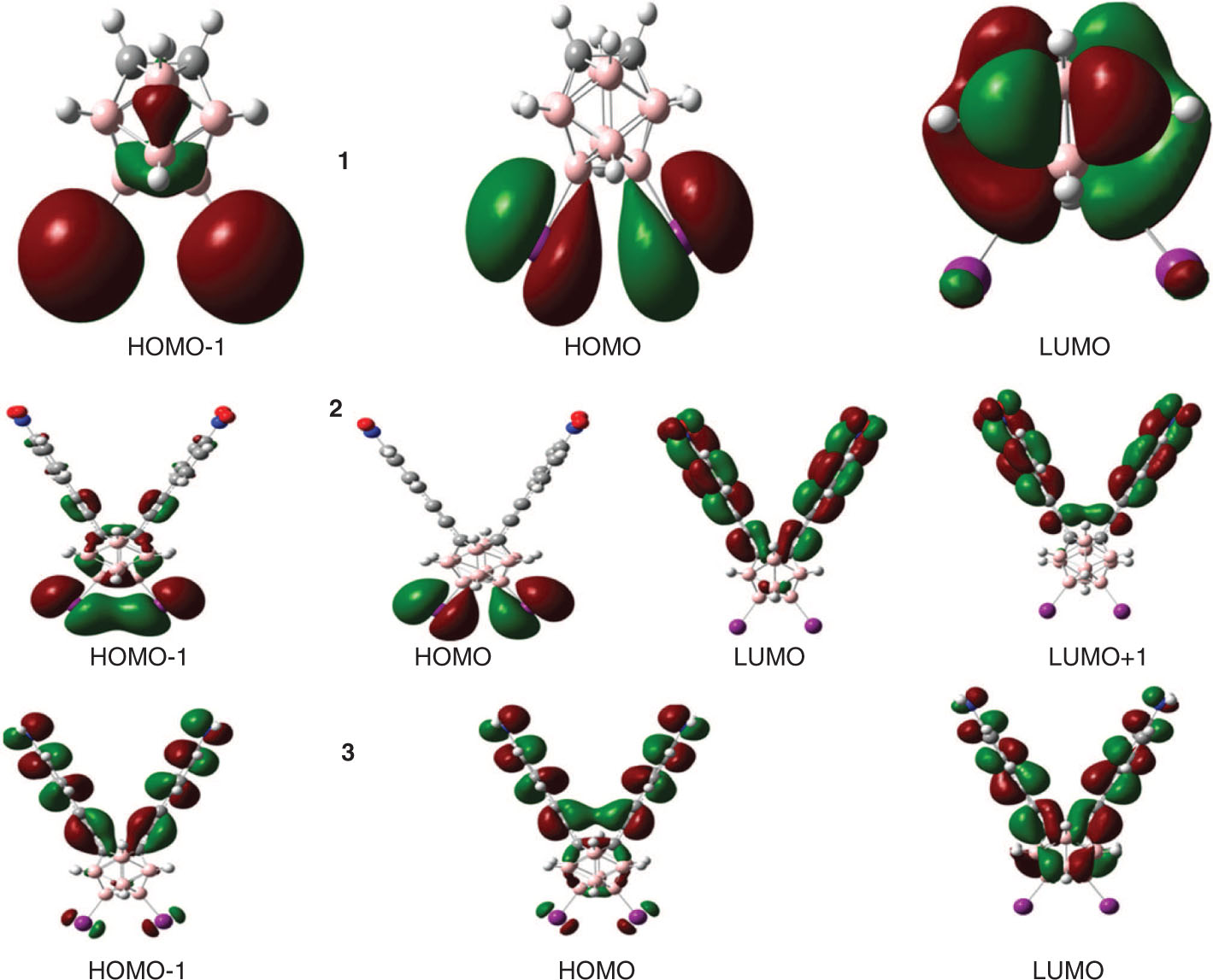
Distribution patterns of the HOMOs and LUMOs of compounds 1–3 at the ground states.
3.3 Optical Properties
The maximum absorption wavelengths (λa), emission wavelengths (λe), oscillator strengths (f), and major transitions involved at the TD-B3LYP/6-31G** (LANL2DZ) level of theory have been tabulated in Table 4 and Figure 3. It has been observed that introducing the 1-nitro-4-propynyl-benzene at the X-positions of the parent compound leads to a 92 nm red shift as in 2 in λa. Moreover, the introduction of 1-amino-4-propynyl-benzene at the X-positions of the parent compound leads to a 35 nm red shift ( 3) in λa. The maximum λa peaks of compounds 1–3 were observed at 241, 333, and 276 nm with the major transitions H-1 ⟶ L, H-3 ⟶ L+1, and H-1 ⟶ L, respectively. It was also found that the introduction of 1-nitro-4-propynyl-benzene at the X-positions of the parent compound leads to a 106 nm blue shift as in 2 in λe. Moreover, the introduction of 1-amino-4-propynyl-benzene at the X-positions of the parent compound leads to a 33 nm red shift ( 3) in λe. The maximum λe peaks of compounds 1–3 were observed at 532, 426, and 499 nm with the major transitions L ⟶ H-1, L ⟶ H-4, and L ⟶ H-5, respectively. The Stokes shift from the absorption to the emission wavelengths was observed as 291, 93, and 223 nm for compounds 1–3, respectively.
The absorption (λa) and emission wavelengths (λe) (nm), oscillator strengths (f), and major transitions of compounds 1–3 calculated at TD-B3LYP/Gena level of theory.
| Complexes | f | λa | Transition | f | λe | Transition |
|---|---|---|---|---|---|---|
| 1 | 0.0314 | 241 | H-1 ⟶ L | 0.0317 | 532 | L ⟶ H-1 |
| 2 | 0.0545 | 333 | H-3 ⟶ L+1 | 0.3169 | 426 | L ⟶ H-4 |
| 3 | 0.2649 | 276 | H-1 ⟶ L | 0.333 | 499 | L ⟶ H-5 |
Gen = 6-31G** for H, C, B, and O atoms, while Gen = LANL2DZ for I atoms.
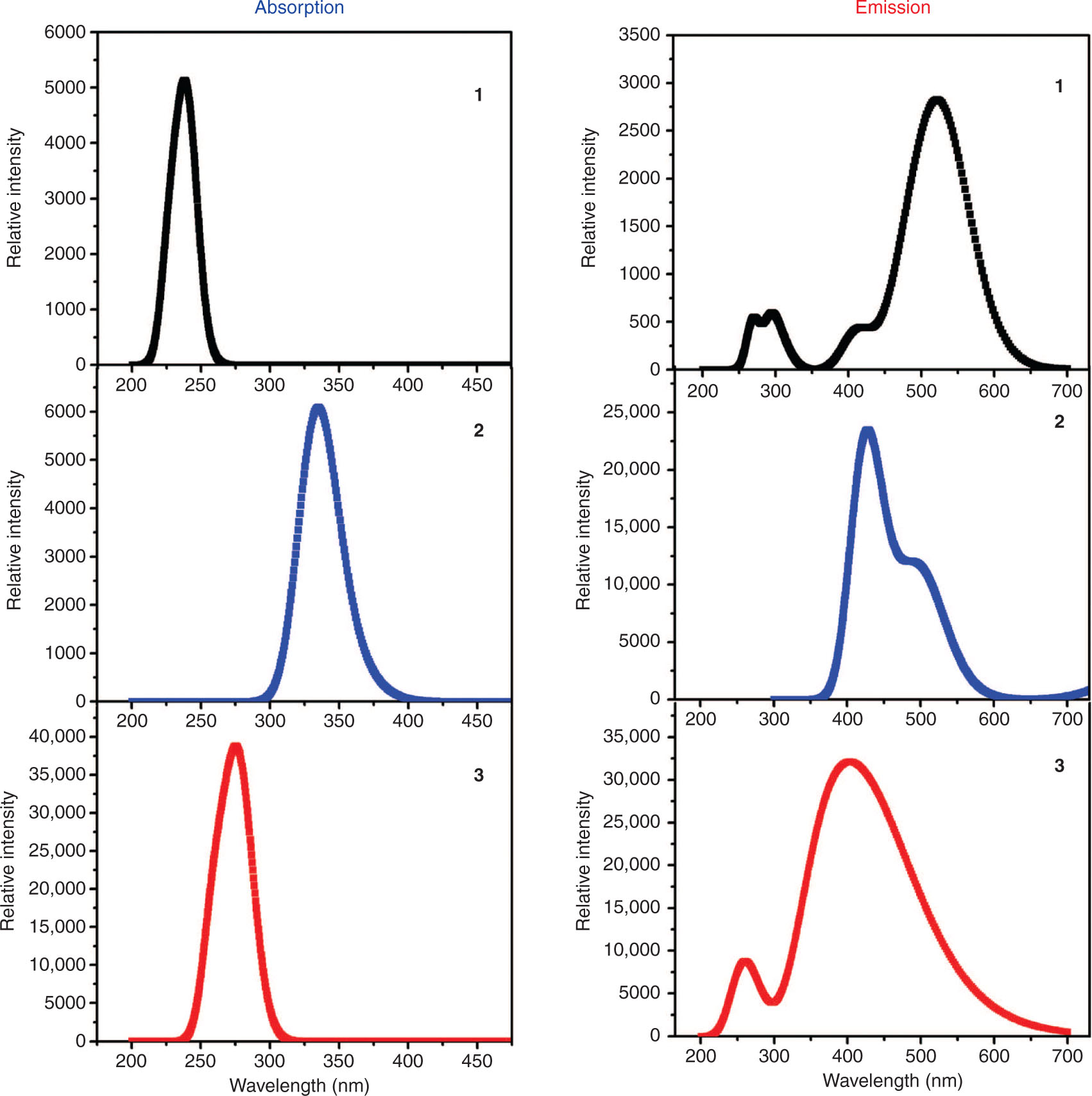
The absorption and emission spectra of compounds 1–3 calculated using the TD-B3LYP/6-31G** (LANL2DZ) level of theory.
3.4 NLO Properties
We optimized compounds 1–3 at the CAM-B3LYP/6-31+G** (LANL2DZ) and B3LYP/6-31G** (LANL2DZ) levels of theory for ground neutral states. The static second-order polarizabilities along with their individual components have been also computed at B3LYP/6-31G** (LANL2DZ) and CAM-B3LYP/6-31+G** (LANL2DZ) and given in Table 5 for comparison. In the present investigation, we have calculated the static total second-order polarizabilities (βtot) according to the equations (2–5) as given in the computational details (Section 2). From Table 5, it is seen that the second-order polarizability values are dominated by their diagonal (βzzz) components among all other components. Comparatively higher amplitudes of characteristic components of the second-order polarizability illustrate a significant delocalization/transfer of charges around these directions. For example, in the present case, the z-axis is the main axis of charge transfer (see Fig. 1), and it has the highest z-components of βtot values in almost all the systems as given in Table 5.
The calculated values of the total second-order polarizabilities (βtot and βvec, a.u.)a along with their individual components for compounds 1–3 at the B3LYP/Genb and CAM-B3LYP/Genb levels of theory, where geometries were also optimized using the same respective methods.
| 𝜷 | 1 | 2 | 3 | |||
|---|---|---|---|---|---|---|
| Optimized at B3LYP 6-31G** | Optimized at CAM-B3LYP 6-31+G** | Optimized at B3LYP 6-31G** | Optimized at CAM-B3LYP 6-31+G** | Optimized at B3LYP 6-31G** | Optimized at CAM-B3LYP 6-31+G** | |
| βxxx | 5 | 6 | 4 | 15 | 2 | −3 |
| βxxy | 6 | 0 | 1 | 1 | −4 | 4 |
| βxyy | 1 | 0 | −41 | −22 | 0 | 19 |
| βyyy | 7 | 0 | −101 | −28 | 94 | −204 |
| βxxz | 94 | −3 | −31 | −193 | 276 | 80 |
| βxyz | 1 | −2 | −24 | 23 | −72 | 17 |
| βyyz | 238 | 215 | 1587 | 818 | 2760 | 1256 |
| βxzz | 1 | −1 | −129 | −72 | −5 | 41 |
| βyzz | 8 | 0 | −20 | −7 | −19 | −19 |
| βzzz | 495 | 340 | 4832 | 2403 | 4305 | 2887 |
| βX | 7 | 5 | −166 | −79 | 3 | 57 |
| βY | 21 | 0 | −120 | −34 | −71 | −219 |
| βZ | 827 | 552 | 6388 | 3028 | 6789 | 4063 |
| βtot | 827 | 552 | 6391 | 3029 | 6789 | 4069 |
| βvec | 496 | 331 | 4808 | 1818 | 4074 | 2442 |
| ηc | 0.480 | 0.63 | 0.328 | 0.34 | 0.641 | 0.44 |
| βvec/βtot | 0.60 | 0.60 | 0.75 | 0.60 | 0.60 | 0.60 |
aConversion factors for βtot from a.u. to SI and esu units: 1 a.u. = 8.639418 × 10−33 esu. bGen. is a split basis set consisting of LANL2DZ for iodine atom. cη is the ratio between off-diagonal (βyyz) and diagonal (βzzz) components.
At the CAM-B3LYP/6-31+G** (LANL2DZ) level, the parent compound 1 has a βtot value of 552 a.u. that significantly increases in its derivatives in the order of 1 < 2 < 3. Compounds 2 and 3 have βtot values of 3029 and 4069 a.u., which are six and seven times larger than that of 1, respectively. Similar trend was observed for compounds 1–3 with some overestimated values of βtot when B3LYP/6-31G** (LANL2DZ) optimized geometries were used to calculate the β at the B3LYP/6-31G** (LANL2DZ) level of theory. The calculated βtot values were found to be 827, 6391, and 6789 a.u. for compounds 1–3, respectively.
To further elucidate the origin of NLO in compounds 1–3, their individual diagonal and off-diagonal components have been also shown in Table 5. The diagonal components for all the compounds are along the charge transfer z-axis. The ratio (η) between the diagonal (βzzz) and off-diagonal (βyyz) components is usually referred as nonlinear anisotropy, which is an important parameter for two-dimensional NLO chromophores. The two-dimensional NLO chromophores usually possess better phase matching and transparency, etc. The NLO anisotropies at CAM-B3LYP are 0.63, 0.34, and 0.44 for compounds 1–3, respectively, which show the significant two-dimensional character of these compounds. Thus, the NLO amplitudes and NLO anisotropies indicate that the above-entitled compounds might have significant potential to use them in NLO applications. Furthermore, a comparison of βtot and βvec is also presented in Table 5 because the ratio of βvec and βtot also specifies important information about the direction of charge transfer in the molecules. Usually, this ratio if near to one indicates a unidirectional charge transfer within the molecular systems where βtot and βvec carry similar amplitudes. It is also important to mention that the amplitude of βtot always possesses positive sign, whereas the amplitude of βvec may be positive or negative depending on the direction of dipole moment and charge transfer process for a typical molecular system.
The ratio of βvec and βtot has been calculated and is found to be 0.6 for compounds 1–3 computed at the CAM-B3LYP level (CAM-B3LYP optimized structures were used). These smaller values specify that the charge transfer process is not unidirectional because of the V-shape of the molecular systems, which lower the value of βvec as compared with the respective βtot amplitudes.
4 Conclusions
Hence, the current research study highlights numerous insights into the structure-property relationship of the above-entitled three novel borane-iodine compounds 1–3. The TD-DFT calculations show that 1-nitro-4-propynyl-benzene and 1-amino-4-propynyl-benzene at top terminal positions of the parent compound lead to a (92 and 35 nm) red shift and a (106 and 33 nm) blue shift for maximum absorption and emission wavelengths as in compounds 2 and 3, respectively. Likewise, frontier molecular orbitals study reveals the comprehensive intramolecular charge transfer from HOMO to LUMO. The smaller electron injection energy barrier (0.75 eV) of 2 as compared with the other compounds reveals that it would be a better n-channel contestant. Though the smaller hole injection energy barrier of compound 3 as compared with the other counterparts showed that the aforementioned derivative might be a better p-channel. The calculation of the second-order NLO polarizabilities (βtot) shows that compounds 2 and 3 possess the βtot amplitudes of 3029 and 4069 a.u., respectively, with the CAM-B3LYP method, which are reasonably larger than similar prototype molecules. The NLO anisotropies are 0.63, 0.34, and 0.44 for compounds 1–3, respectively, at the CAM-B3LYP level of theory, which revealed that the charge transfer process is not unidirectional because of the V-shape of the studied molecular systems. Thus, the NLO amplitudes and NLO anisotropies indicate that the above-entitled compounds might have significant potential to use them in NLO applications. Our quantum chemical exploration of the structural, electro-optical, and NLO properties demonstrates that these materials with trustworthy properties of interests might be prospective competitors for the electro-optical device as well as NLO applications.
Funding source: King Khalid University
Award Identifier / Grant number: R.G.P.1/18/38
Funding statement: The authors extend their appreciation to the Deanship of Scientific Research at King Khalid University (KKU) for funding this work through research groups program under grant number R.G.P.1/18/38. AR Chaudhry is grateful to the University of Bisha (UB) for providing the technical support and facilities to complete the research study.
References
L. I. Zakharkin, A. I. Kovredov, V. A. Ol’shevskaya, and Z. S. Shaugumbekova, J. Organomet. Chem. 226, 217 (1982).10.1016/S0022-328X(00)83405-1Search in Google Scholar
Z. Zheng, W. Jiang, A. A. Zinn, C. B. Knobler, and M. F. Hawthorne, Inorg. Chem. 34, 2095 (1995).10.1021/ic00112a023Search in Google Scholar
J. Li, C. F. Logan, and M. Jones, Inorg. Chem. 30, 4866 (1991).10.1021/ic00025a037Search in Google Scholar
W. Jiang, C. B. Knobler, C. E. Curtis, M. D. Mortimer, and M. F. Hawthorne, Inorg. Chem. 34, 3491 (1995).10.1021/ic00117a018Search in Google Scholar
T. D. McGrath, M. A. Fox, and A. J. Welch, Acta Crystallogr. Sect. C: Cryst. Struct. Commun. 56, 487 (2000).10.1107/S0108270100000743Search in Google Scholar PubMed
W. J. Marshall, R. J. Young, and V. V. Grushin, Organometallics 20, 523 (2001).10.1021/om0008575Search in Google Scholar
A. S. Batsanov, M. A. Fox, J. A. Howard, A. K. Hughes, A. L. Johnson, et al., Acta Crystallogr. Sect. C: Cryst. Struct. Commun. 59, O74 (2003).10.1107/S0108270102023582Search in Google Scholar PubMed
A. V. Puga, F. Teixidor, R. Sillanpää, R. Kivekäs, and C. Viñas, Chem. Eur. J. 15, 9764 (2009).10.1002/chem.200900926Search in Google Scholar PubMed
R. N. Grimes, Angew. Chem. Int. Ed. 32, 1289 (1993).10.1002/anie.199312891Search in Google Scholar
R. N. Grimes, Angew. Chem. 105, 1350 (1993).10.1002/ange.19931050907Search in Google Scholar
W.-J. Kuo, G.-H. Hsiue, and R.-J. Jeng, Macromolecules 34, 2373 (2001).10.1021/ma0017485Search in Google Scholar
M. Yang and B. Champagne, J. Phys. Chem. A 107, 3942 (2003).10.1021/jp0272567Search in Google Scholar
B. J. Coe, Acc. Chem. Res. 39, 383 (2006).10.1021/ar050225kSearch in Google Scholar PubMed
R. S. Roy and P. K. Nandi, RSC Adv. 5, 103729 (2015).10.1039/C5RA22615ESearch in Google Scholar
R. Misra, J. Phys. Chem. C 121, 5731 (2017).10.1021/acs.jpcc.6b13035Search in Google Scholar
R. Misra and S. P. Bhattacharyya, Intramolecular Charge Transfer: Theory and Applications, John Wiley & Sons, New York 2018.10.1002/9783527801916Search in Google Scholar
R. Misra and S. P. Bhattacharyya, Brief History of ICT Molecules, Wiley-VCH, Weinheim 2018.10.1002/9783527801916.ch2Search in Google Scholar
J. Z. Dávalos, J. González, A. Guerrero, D. Hnyk, J. Holub, et al., J. Phys. Chem. C 117, 1495 (2013).10.1021/jp3102354Search in Google Scholar
S. Muhammad, A. G. Al-Sehemi, Z. Su, H. Xu, A. Irfan, et al., J. Mol. Graph. Model. 72, 58 (2017).10.1016/j.jmgm.2016.12.009Search in Google Scholar PubMed
S. Muhammad, A. G. Al-Sehemi, A. Irfan, A. R. Chaudhry, H. Gharni, et al., J. Mol. Model. 22, 1 (2016).10.1007/s00894-015-2876-xSearch in Google Scholar PubMed
S. Muhammad, A. G. Al-Sehemi, A. Irfan, and A. R. Chaudhry, J. Mol. Graph. Model. 68, 95 (2016).10.1016/j.jmgm.2016.06.012Search in Google Scholar
R. Misra, R. Sharma, and S. Bhattacharyya, J. Comput. Methods Sci. Eng. 10, 149 (2010).10.3233/JCM-2010-0316Search in Google Scholar
D. F. Machado, T. O. Lopes, I. T. Lima, D. T. A. da Silva Filho, and H. C. de Oliveira, J. Phys. Chem. C 120, 17660 (2016).10.1021/acs.jpcc.6b01567Search in Google Scholar
S. Muhammad, H. Xu, Z. Su, K. Fukuda, R. Kishi, et al., Dalton Trans. 42, 15053 (2013).10.1039/c3dt51331aSearch in Google Scholar
A. Irfan, A. G. Al-Sehemi, S. Muhammad, A. R. Chaudhry, M. S. Al-Assiri, et al., C. R. Chim. 18, 1289 (2015).10.1016/j.crci.2015.05.020Search in Google Scholar
R. Bauernschmitt and R. Ahlrichs, Chem. Phys. Lett. 256, 454 (1996).10.1016/0009-2614(96)00440-XSearch in Google Scholar
C. Van Caillie and R. D. Amos, Chem. Phys. Lett. 317, 159 (2000).10.1016/S0009-2614(99)01346-9Search in Google Scholar
F. Furche and R. Ahlrichs, J. Chem. Phys. 117, 7433 (2002).10.1063/1.1508368Search in Google Scholar
G. Scalmani, M. J. Frisch, B. Mennucci, J. Tomasi, R. Cammi, et al., J. Chem. Phys. 124, 094107 (2006).10.1063/1.2173258Search in Google Scholar PubMed
J. Zhang, Y.-H. Kan, H.-B. Li, Y. Geng, Y. Wu, et al., J. Mol. Model. 19, 1597 (2013).10.1007/s00894-012-1719-2Search in Google Scholar PubMed
A. R. Chaudhry, R. Ahmed, A. Irfan, A. Shaari, A. R. M. Isa, et al., J. Mol. Model. 21, 1 (2015).10.1007/s00894-014-2561-5Search in Google Scholar PubMed
R. S. Sánchez-Carrera, V. Coropceanu, D. A. da Silva Filho, R. Friedlein, W. Osikowicz, et al., J. Phys. Chem. B 110, 18904 (2006).10.1021/jp057462pSearch in Google Scholar PubMed
B. M. Wong and J. G. Cordaro, J. Chem. Phys. 129 (2008).10.1063/1.3025924Search in Google Scholar PubMed
A. Irfan and A. G. Al-Sehemi, J. Saudi Chem. Soc. 19, 318 (2015).10.1016/j.jscs.2012.03.005Search in Google Scholar
R. Zhu, Y.-A. Duan, Y. Geng, C.-Y. Wei, X.-Y. Chen, et al., Comput. Theor. Chem. 1078, 16 (2016).10.1016/j.comptc.2015.12.017Search in Google Scholar
D. Cvejn, S. Achelle, O. Pytela, J.-P. Malval, A. Spangenberg, et al., Dyes Pigm. 124, 101 (2016).10.1016/j.dyepig.2015.09.012Search in Google Scholar
C. Zhang, W. Liang, H. Chen, Y. Chen, Z. Wei, et al., J. Mol. Struc. TheoChem 862, 98 (2008).10.1016/j.theochem.2008.04.035Search in Google Scholar
Y. Zhang, X. Cai, Y. Bian, X. Li, and J. Jiang, J. Phys. Chem. C 112, 5148 (2008).10.1021/jp710123rSearch in Google Scholar
J. Preat, D. Jacquemin, and E. A. Perpète, Environ. Sci. Technol. 44, 5666 (2010).10.1021/es100920jSearch in Google Scholar PubMed
J. Preat, C. Michaux, D. Jacquemin, and E. A. Perpe‘te, J. Phys. Chem. C 113, 16821 (2009).10.1021/jp904946aSearch in Google Scholar
V. T. T. Huong, H. T. Nguyen, T. B. Tai, and M. T. Nguyen, J. Phys. Chem. C 117, 10175 (2013).10.1021/jp401191aSearch in Google Scholar
D. Matthews, P. Infelta, and M. Grätzel, Sol. Energy Mater. Sol. Cells 44, 119 (1996).10.1016/0927-0248(96)00036-0Search in Google Scholar
B. Champagne, E. A. Perpete, D. Jacquemin, S. J. van Gisbergen, E.-J. Baerends, et al., J. Phys. Chem. A 104, 4755 (2000).10.1021/jp993839dSearch in Google Scholar
Z.-L. Cai, M. J. Crossley, J. R. Reimers, R. Kobayashi, and R. D. Amos, J. Phys. Chem. B 110, 15624 (2006).10.1021/jp063376tSearch in Google Scholar PubMed
P. A. Limacher, K. V. Mikkelsen, and H. P. Luthi, J. Chem. Phys. 130, 194114 (2009).10.1063/1.3139023Search in Google Scholar PubMed
A. Alparone, Chem. Phys. Lett. 563, 88 (2013).10.1016/j.cplett.2013.01.062Search in Google Scholar
Y. Bai, Z.-J. Zhou, J.-J. Wang, Y. Li, D. Wu, et al., J. Phys. Chem. A 117, 2835 (2013).10.1021/jp3120594Search in Google Scholar PubMed
M. J. Frisch, G. W. Trucks, H. B. Schlegel, G. E. Scuseria, M. A. Robb, et al. Gaussian 09, Revision B.01, Inc., Wallingford CT, 2009.Search in Google Scholar
Supplementary Material
The online version of this article offers supplementary material (https://doi.org/10.1515/zna-2018-0123).
©2018 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Frontmatter
- General
- Flower Buds Like MgO Nanoparticles: From Characterisation to Indigo Carmine Elimination
- Atomic, Molecular & Chemical Physics
- Selection and Enhancement of the Single Harmonic Emission Event in the Water Window Region
- Dynamical Systems & Nonlinear Phenomena
- A General Algorithm on the Natural Vibration Analysis of Composite Beams with Arbitrary Complex Interfaces
- Gravitation & Cosmology
- Towards a More Well-Founded Cosmology
- Solid State Physics & Materials Science
- Properties of Cmc21-X2As2O (X = Si, Ge, and Sn) by First-Principles Calculations
- Structural, Electronic and Nonlinear Optical Properties of Novel Derivatives of 9,12-Diiodo-1,2-dicarba-closo-dodecaborane: Density Functional Theory Approach
- Charge Carrier Mobility Behavior in the SubPc/C60 Planar Heterojunction
- Amplified Tunnelling from a Pair of Balanced Loss and Gain Cavities
- Thermodynamics & Statistical Physics
- The Free Energy for Rotating and Charged Black Holes and Banados, Teitelboim and Zanelli Black Holes
- Investigation on Neutron-Induced Fission Fragment Angular Distribution of 232Th and 238U
Articles in the same Issue
- Frontmatter
- General
- Flower Buds Like MgO Nanoparticles: From Characterisation to Indigo Carmine Elimination
- Atomic, Molecular & Chemical Physics
- Selection and Enhancement of the Single Harmonic Emission Event in the Water Window Region
- Dynamical Systems & Nonlinear Phenomena
- A General Algorithm on the Natural Vibration Analysis of Composite Beams with Arbitrary Complex Interfaces
- Gravitation & Cosmology
- Towards a More Well-Founded Cosmology
- Solid State Physics & Materials Science
- Properties of Cmc21-X2As2O (X = Si, Ge, and Sn) by First-Principles Calculations
- Structural, Electronic and Nonlinear Optical Properties of Novel Derivatives of 9,12-Diiodo-1,2-dicarba-closo-dodecaborane: Density Functional Theory Approach
- Charge Carrier Mobility Behavior in the SubPc/C60 Planar Heterojunction
- Amplified Tunnelling from a Pair of Balanced Loss and Gain Cavities
- Thermodynamics & Statistical Physics
- The Free Energy for Rotating and Charged Black Holes and Banados, Teitelboim and Zanelli Black Holes
- Investigation on Neutron-Induced Fission Fragment Angular Distribution of 232Th and 238U

