Estimation of long memory in volatility using wavelets

Lucie Kraicová; Jozef Baruník

doi:10.1515/snde-2016-0101

Article

Estimation of long memory in volatility using wavelets

Lucie Kraicová and Jozef Baruník

Published/Copyright: April 6, 2017

Published by

Become an author with De Gruyter Brill

Submit Manuscript Author Information

From the journal Studies in Nonlinear Dynamics & Econometrics Volume 21 Issue 3

Abstract

This work studies wavelet-based Whittle estimator of the fractionally integrated exponential generalized autoregressive conditional heteroscedasticity (FIEGARCH) model often used for modeling long memory in volatility of financial assets. The newly proposed estimator approximates the spectral density using wavelet transform, which makes it more robust to certain types of irregularities in data. Based on an extensive Monte Carlo study, both behavior of the proposed estimator and its relative performance with respect to traditional estimators are assessed. In addition, we study properties of the estimators in presence of jumps, which brings interesting discussion. We find that wavelet-based estimator may become an attractive robust and fast alternative to the traditional methods of estimation. In particular, a localized version of our estimator becomes attractive in small samples.

Keywords: FIEGARCH; long memory; Monte Carlo; volatility; wavelets; Whittle

Acknowledgments

We would like to express our gratitude to Ana Perez, who provided us with the code for MLE and FWE estimation of FIEGARCH processes, and we gratefully acknowledge financial support from the the Czech Science Foundation under project No. 13-32263S. The research leading to these results has received funding from the European Unions Seventh Framework Programme (FP7/2007-2013) under grant agreement No. FP7-SSH- 612955 (FinMaP).

A Appendix: Tables and Figures

Table 1:

Energy decomposition.

Coefficients	d	ω	α	β	θ	γ
(a) Coefficient sets
A	0.25	0	0.5	0.5	−0.3	0.5
B	0.45	0	0.5	0.5	−0.3	0.5
C	−0.25	0	0.5	0.5	−0.3	0.5
D	0.25	0	0.9	0.9	−0.3	0.5
E	0.45	0	0.9	0.9	−0.3	0.5
F	−0.25	0	0.9	0.9	−0.3	0.5
G	0.25	0	0.9	0.9	−0.9	0.9
H	0.45	0	0.9	0.9	−0.9	0.9

	A	B	C	D	E	F	G	H
(b) Integrals over frequencies respective to levels for the coefficient sets from Table 1
Level 1	1.1117	1.1220	1.0897	1.1505	1.1622	1.1207	1.1261	1.1399
Level 2	0.5473	0.5219	0.6274	0.4776	0.4691	0.5306	0.6187	0.6058
Level 3	0.3956	0.3693	0.4330	0.3246	0.3056	0.3959	1.1354	1.3453
Level 4	0.3029	0.3341	0.2425	0.5559	0.7712	0.3528	2.9558	4.8197
Level 5	0.2035	0.2828	0.1175	1.0905	2.1758	0.3003	6.0839	13.2127
Level 6	0.1279	0.2297	0.0550	1.4685	3.9342	0.1965	8.2136	23.4144
Level 7	0.0793	0.1883	0.0259	1.3523	4.7975	0.0961	7.6026	28.4723
Level 8	0.0495	0.1584	0.0123	1.0274	4.8302	0.0408	5.8268	28.7771
Level 9	0.0313	0.1368	0.0059	0.7327	4.5720	0.0169	4.1967	27.3822
Level 10	0.0201	0.1206	0.0029	0.5141	4.2610	0.0071	2.9728	25.6404
Level 11	0.0130	0.1080	0.0014	0.3597	3.9600	0.0030	2.0977	23.9192
Level 12	0.0086	0.0979	0.0007	0.2518	3.6811	0.0013	1.4793	22.2986
(c) Sample variances of DWT Wavelet Coefficients for the coefficient sets from Table 1
Level 1	4.4468	4.4880	4.3588	4.6020	4.6488	4.4828	4.5044	4.5596
Level 2	4.3784	4.1752	5.0192	3.8208	3.7528	4.2448	4.9496	4.8464
Level 3	6.3296	5.9088	6.9280	5.1936	4.8896	6.3344	18.1664	21.5248
Level 4	9.6928	10.6912	7.7600	17.7888	24.6784	11.2896	94.5856	154.2304
Level 5	13.0240	18.0992	7.5200	69.7920	139.2512	19.2192	389.3696	845.6128
Level 6	16.3712	29.4016	7.0400	187.9680	503.5776	25.1520	1051.3408	2997.0432
Level 7	20.3008	48.2048	6.6304	346.1888	1228.1600	24.6016	1946.2656	7288.9088
Level 8	25.3440	81.1008	6.2976	526.0288	2473.0624	20.8896	2983.3216	14733.8752
Level 9	32.0512	140.0832	6.0416	750.2848	4681.7280	17.3056	4297.4208	28039.3728
Level 10	41.1648	246.9888	5.9392	1052.8768	8726.5280	14.5408	6088.2944	52511.5392
Level 11	53.2480	442.3680	5.7344	1473.3312	16220.1600	12.2880	8592.1792	97973.0432
Level 12	70.4512	801.9968	5.7344	2062.7456	30155.5712	10.6496	12118.4256	182670.1312

Table 2:

Monte Carlo No jumps: d=0.25/0.45; MLE, FWE, MODWT(D4), 2: Corrected using Donoho and Johnstone threshold.

PAR	True	Method	No jumps; N=2048			No jumps; N=16,384			PAR	No jumps; N=2048
PAR	True	Method	Mean	Bias	RMSE	Mean	Bias	RMSE	PAR	Mean	Bias	RMSE
d^	0.250	WWE MODWT	0.165	−0.085	0.225	0.253	0.003	0.042	0.450	0.362	−0.088	0.170
		WWE MODWT 2	0.168	−0.082	0.227	–	–	–		–	–	–
		FWE	0.212	−0.038	0.147	0.251	0.001	0.036		0.415	−0.035	0.087
		FWE 2	0.213	−0.037	0.146	–	–	–		–	–	–
		MLE	0.220	−0.030	0.085	–	–	–		0.433	−0.017	0.043
		MLE 2	0.228	−0.022	0.086	–	–	–		–	–	–
ω^	−7.000	MLE	−7.076	−0.076	0.174	–	–	–		−7.458	−0.458	0.739
		MLE 2	−7.083	−0.083	0.182	–	–	–		–	–	–
		OTHER	−7.002	−0.002	0.197	−7.003	−0.003	0.074		−6.999	0.001	0.696
		OTHER 2	−7.015	−0.015	0.198	–	–	–		–	–	–
α^2	0.500	WWE MODWT	0.434	−0.066	0.349	0.328	−0.172	0.229		0.324	−0.176	0.395
		WWE MODWT 2	0.426	−0.074	0.358	–	–	–		–	–	–
		FWE	0.527	0.027	0.343	0.512	0.012	0.168		0.475	−0.025	0.348
		FWE 2	0.521	0.021	0.333	–	–	–		–	–	–
		MLE	0.503	0.003	0.121	–	–	–		0.487	−0.013	0.128
		MLE 2	0.464	−0.036	0.136	–	–	–		–	–	–
β^1	0.500	WWE MODWT	0.559	0.059	0.249	0.523	0.023	0.078		0.610	0.110	0.178
		WWE MODWT 2	0.561	0.061	0.253	–	–	–		–	–	–
		FWE	0.520	0.020	0.199	0.499	−0.001	0.065		0.554	0.054	0.135
		FWE 2	0.517	0.017	0.214	–	–	–		–	–	–
		MLE	0.529	0.029	0.101	–	–	–		0.527	0.027	0.063
		MLE 2	0.537	0.037	0.109	–	–	–		–	–	–
θ^	−0.300	WWE MODWT	−0.283	0.017	0.180	−0.337	−0.037	0.078		−0.314	−0.014	0.146
		WWE MODWT 2	−0.261	0.039	0.182	–	–	–		–	–	–
		FWE	−0.244	0.056	0.182	−0.279	0.021	0.077		−0.242	0.058	0.158
		FWE 2	−0.222	0.078	0.189	–	–	–		–	–	–
		MLE	−0.301	−0.001	0.026	–	–	–		−0.301	−0.001	0.024
		MLE 2	−0.282	0.018	0.031	–	–	–		–	–	–
γ^	0.500	WWE MODWT	0.481	−0.019	0.196	0.489	−0.011	0.085		0.504	0.004	0.218
		WWE MODWT 2	0.472	−0.028	0.193	–	–	–		–	–	–
		FWE	0.509	0.009	0.175	0.504	0.004	0.083		0.526	0.026	0.202
		FWE 2	0.497	−0.003	0.174	–	–	–		–	–	–
		MLE	0.499	−0.001	0.045	–	–	–		0.507	0.007	0.044
		MLE 2	0.491	−0.009	0.048	–	–	–		–	–	–

Table 3:

Monte Carlo jumps: d=0.25/0.45; Poisson lambda=0.028; N(0; 0.2); FWE, MODWT (D4), 2: Corrected using Donoho and Johnstone threshold.

PAR	True	Method	Jump [0.028, N(0, 0.2)]; N=2048			Jump [0.028, N(0, 0.2)]; N=16,384			PAR	Jump [0.028, N(0, 0.2)] N=2048
PAR	True	Method	Mean	Bias	RMSE	Mean	Bias	RMSE	PAR	Mean	Bias	RMSE
d^	0.250	WWE MODWT	0.145	−0.105	0.214	–	–	–	0.450	–	–	–
		WWE MODWT 2	0.154	−0.096	0.225	0.235	−0.015	0.042		0.347	−0.103	0.179
		FWE	0.195	−0.055	0.142	–	–	–		–	–	–
		FWE 2	0.206	−0.044	0.143	0.231	−0.019	0.038		0.403	−0.047	0.091
		MLE	0.018	−0.232	0.353	–	–	–		–	–	–
		MLE 2	0.099	−0.151	0.251	–	–	–		0.187	−0.263	0.314
ω^	−7.000	MLE	−5.662	1.338	1.450	–	–	–		–	–	–
		MLE 2	−6.282	0.718	0.801	–	–	–		−5.529	1.471	1.662
		OTHER	−6.887	0.113	0.221	–	–	–		–	–	–
		OTHER 2	−6.942	0.058	0.203	−6.941	0.059	0.096		−6.946	0.054	0.677
α^2	0.500	WWE MODWT	0.475	−0.025	0.437	–	–	–		–	–	–
		WWE MODWT 2	0.492	−0.008	0.402	0.557	0.057	0.243		0.390	−0.110	0.447
		FWE	0.561	0.061	0.454	–	–	–		–	–	–
		FWE 2	0.582	0.082	0.400	0.731	0.231	0.297		0.535	0.035	0.428
		MLE	0.667	0.167	0.385	–	–	–		–	–	–
		MLE 2	0.652	0.152	0.287	–	–	–		0.605	0.105	0.308
β^1	0.500	WWE MODWT	0.592	0.092	0.290	–	–	–		–	–	–
		WWE MODWT 2	0.578	0.078	0.264	0.535	0.035	0.087		0.636	0.136	0.203
		FWE	0.546	0.046	0.266	–	–	–		–	–	–
		FWE 2	0.529	0.029	0.231	0.519	0.019	0.068		0.579	0.079	0.164
		MLE	0.406	−0.094	0.452	–	–	–		–	–	–
		MLE 2	0.503	0.003	0.250	–	–	–		0.619	0.119	0.240
θ^	−0.300	WWE MODWT	−0.491	−0.191	0.272	–	–	–		–	–	–
		WWE MODWT 2	−0.385	−0.085	0.189	−0.398	−0.098	0.108		−0.384	−0.084	0.174
		FWE	−0.455	−0.155	0.246	–	–	–		–	–	–
		FWE 2	−0.348	−0.048	0.175	−0.356	−0.056	0.065		−0.324	−0.024	0.153
		MLE	−0.214	0.086	0.130	–	–	–		–	–	–
		MLE 2	−0.211	0.089	0.104	–	–	–		−0.176	0.124	0.137
γ^	0.500	WWE MODWT	0.203	−0.297	0.365	–	–	–		–	–	–
		WWE MODWT 2	0.322	−0.178	0.271	0.287	−0.213	0.231		0.276	−0.224	0.322
		FWE	0.257	−0.243	0.315	–	–	–		–	–	–
		FWE 2	0.365	−0.135	0.231	0.313	−0.187	0.202		0.317	−0.183	0.291
		MLE	0.287	−0.213	0.256	–	–	–		–	–	–
		MLE 2	0.340	−0.160	0.180	–	–	–		0.347	−0.153	0.179

Table 4:

Forecasting: N=2048; No jumps; MLE, FWE, MODWT(D4), DWT(D4), 2: Corrected using Donoho and Johnstone threshold.

Cat	Method	Main stats			MAD quantiles
Cat	Method	Mean err	MAD	RMSE	0.50	0.90	0.95	0.99
In	WWE MODWT	6.1308e−05	0.00039032	0.0052969	–	–	–	–
	WWE MODWT 2	2.2383e−05	0.00040778	0.0034541	–	–	–	–
	WWE DWT	8.3135e−05	0.00044932	0.011577	–	–	–	–
	WWE DWT 2	2.363e−05	0.00043981	0.0050438	–	–	–	–
	FWE	5.9078e−05	0.00037064	0.00087854	–	–	–	–
	FWE 2	1.4242e−05	0.00038604	0.0011961	–	–	–	–
	MLE	6.0381e−06	9.3694e−05	0.00019804	–	–	–	–
	MLE 2	−3.3242e−05	0.00011734	0.00028776	–	–	–	–
Out	WWE MODWT	105.3851	105.3856	3277.1207	0.00015361	0.0010525	0.0019431	0.0060853
	WWE MODWT 2	−7.6112e−05	0.00058276	0.0020436	0.00016482	0.0010512	0.0020531	0.0072711
	WWE DWT	0.00013817	0.00066928	0.0031579	0.00017219	0.0012156	0.0020541	0.0065611
	WWE DWT 2	0.00087082	0.0015663	0.027558	0.00017181	0.0012497	0.0022271	0.0072191
	FWE	2.9498e−05	0.00050763	0.0015745	0.00014566	0.0010839	0.0018926	0.005531
	FWE 2	0.00038499	0.0010395	0.014191	0.00015425	0.0011351	0.001989	0.0081017
	MLE	−1.5041e−06	0.00012211	0.00035147	4.0442e−05	0.00024483	0.00043587	0.001595
	MLE 2	−0.00010455	0.00024125	0.0015605	4.3599e−05	0.00030553	0.00063378	0.0038043
		Error quantiles A				Error quantiles B
		0.01	0.05	0.10		0.90	0.95	0.99
Out	WWE MODWT	−0.0033827	−0.0010722	−0.0004865		0.00063385	0.0010345	0.0048495
	WWE MODWT 2	−0.0045312	−0.0013419	−0.00062698		0.00053531	0.00089684	0.0051791
	WWE DWT	−0.0040691	−0.001223	−0.00059588		0.00065501	0.0012118	0.004838
	WWE DWT 2	−0.003994	−0.0013952	−0.00071166		0.00059679	0.0010616	0.0050457
	FWE	−0.0035752	−0.0010712	−0.00053169		0.00061822	0.001086	0.004636
	FWE 2	−0.0042148	−0.00129	−0.00063194		0.0005657	0.0010577	0.0048622
	MLE	−0.00079412	−0.00024382	−0.00013312		0.00010297	0.00026481	0.0013195
	MLE 2	−0.0019587	−0.00046351	−0.00021734		7.5622e−05	0.00018216	0.00077541

Not corrected: Mean of N-next true values to be forecasted: 0.0016845; Total valid=967, i.e. 96.7% of M fails-MLE=0%, fails-FWE=0.8%, fails-MODWT=2.1%, fails-DWT=1.5%, Corrected: Mean of N-next true values to be forecasted: 0.0016852; Total valid=959, i.e. 95.9% of M fails-MLE=0%, fails-FWE=1.3%, fails-MODWT=1.7%, fails-DWT=2.7%.

Table 5:

Forecasting: N=16,384, No Jumps; MLE, FWE, MODWT(D4), DWT(D4), 2: Corrected using Donoho and Johnstone threshold.

Cat	Method	Main stats			MAD quantiles
Cat	Method	Mean err	MAD	RMSE	0.50	0.90	0.95	0.99
In	WWE MODWT	7.522e−06	0.00015889	0.00032423	–	–	–	–
	WWE DWT	8.5378e−06	0.00017736	0.00038026	–	–	–	–
	FWE	6.3006e−06	0.00014367	0.00032474	–	–	–	–
	MLE	–	–	–	–	–	–	–
Out	WWE MODWT	9.3951e−06	0.00018394	0.00054618	7.1556e−05	0.00040438	0.0007369	0.0015565
	WWE DWT	2.1579e−05	0.0002107	0.00084705	7.1483e−05	0.00041876	0.00074376	0.0018066
	FWE	−3.3569e−06	0.00017794	0.00067805	5.6684e−05	0.00035132	0.0005922	0.001811
	MLE	–	–	–	–	–	–	–
		Error quantiles A				Error quantiles B
		0.01	0.05	0.10		0.90	0.95	0.99
Out	WWE MODWT	−0.0011566	−0.00040454	−0.00021569		0.00021003	0.0004025	0.0013515
	WWE DWT	−0.0011033	−0.00038209	−0.00018247		0.00023587	0.00049025	0.0016387
	FWE	−0.00087002	−0.00034408	−0.00018571		0.00018593	0.00035741	0.0010787
	MLE	–	–	–		–	–	–

Not corrected: Mean of N-next true values to be forecasted: 0.0015516; Total valid=1000, i.e. 100% of M fails-MLE=0%, fails-FWE=0%, fails-MODWT=0%, fails-DWT=0%.

Table 6:

Forecasting: N=2048; d=0.45; No jumps; MLE, FWE, MODWT(D4), DWT(D4), 2: Corrected using Donoho and Johnstone threshold.

Cat	Method	Main stats			MAD quantiles
Cat	Method	Mean err	MAD	RMSE	0.50	0.90	0.95	0.99
In	WWE MODWT	0.00026281	0.0010841	0.02023	–	–	–	–
	WWE DWT	0.00022639	0.0011206	0.013151	–	–	–	–
	FWE	0.00027127	0.0010458	0.005243	–	–	–	–
	MLE	5.7279e−05	0.00026995	0.0012167	–	–	–	–
Out	WWE MODWT	Inf	Inf	Inf	0.00016653	0.0024597	0.005308	0.040031
	WWE DWT	924.8354	924.8375	28648.7373	0.00017788	0.0024428	0.0049679	0.040403
	FWE	−0.00010684	0.0015807	0.0078118	0.00016022	0.0025471	0.0057388	0.031548
	MLE	0.0002289	0.0004843	0.0039972	4.2589e−05	0.00052307	0.0010187	0.0078509
		Error quantiles A				Error quantiles B
		0.01	0.05	0.10		0.90	0.95	0.99
Out	WWE MODWT	−0.013427	−0.0024269	−0.00087296		0.0010521	0.0026019	0.013128
	WWE DWT	−0.013075	−0.0025811	−0.0010018		0.00089545	0.0023095	0.0165
	FWE	−0.012356	−0.002209	−0.00081063		0.0010042	0.002777	0.014773
	MLE	−0.0016025	−0.00044789	−0.0002568		0.00017179	0.00056713	0.0051968

Not corrected: Mean of N-next true values to be forecasted: 0.0064152; Total valid=962, i.e. 96.2% of M fails-MLE=0%, fails-FWE=1%, fails-MODWT=1.9%, fails-DWT=2.1%.

Table 7:

Forecasting: N=2048; Jumps lambda=0.028, N(0, 0.2); MLE, FWE, MODWT(D4), DWT(D4), 2: Corrected using Donoho and Johnstone threshold.

Cat	Method	Main stats			MAD quantiles
Cat	Method	Mean err	MAD	RMSE	0.50	0.90	0.95	0.99
In	WWE MODWT	0.0024292	0.0027027	0.031109	–	–	–	–
	WWE MODWT 2	0.00049847	0.00088238	0.010266
	WWE DWT	0.0022873	0.0025833	0.029094	–	–	–	–
	WWE DWT 2	0.00051788	0.00092081	0.013946
	FWE	0.0024241	0.0026398	0.030474	–	–	–	–
	FWE 2	0.00046896	0.00080786	0.01562
	MLE	0.00099962	0.0013136	0.0022127	–	–	–	–
	MLE 2	0.00021708	0.0005767	0.0011708
Out	WWE MODWT	Inf	Inf	Inf	0.00027911	0.0019584	0.0043937	0.074726
	WWE MODWT 2	12837.4644	12837.4647	361761.8976	0.00020755	0.0012984	0.0021954	0.064956
	WWE DWT	0.010776	0.010967	0.14233	0.00032328	0.0020108	0.0048951	0.086811
	WWE DWT 2	Inf	Inf	Inf	0.00019516	0.0013594	0.002609	0.08235
	FWE	0.0098899	0.010026	0.15737	0.00025416	0.0019525	0.0047286	0.073048
	FWE 2	1.4046	1.4048	36.7106	0.00017622	0.0012063	0.0024169	0.057823
	MLE	0.0014788	0.0017573	0.0066777	0.00099906	0.001951	0.0027302	0.019721
	MLE 2	0.0022114	0.0025386	0.053463	0.00034636	0.00094187	0.0016393	0.0082677
		Error quantiles A				Error quantiles B
		0.01	0.05	0.10		0.90	0.95	0.99
Out	WWE MODWT	−0.0014262	−0.00061569	−0.00023517		0.0018119	0.0043937	0.074726
	WWE MODWT 2	−0.002004	−0.0007648	−0.00033609		0.0010397	0.0018978	0.064956
	WWE DWT	−0.0014902	−0.00065937	−0.00028371		0.0018904	0.0048951	0.086811
	WWE DWT 2	−0.002635	−0.00076962	−0.00031466		0.00099973	0.0020434	0.08235
	FWE	−0.00097176	−0.00039409	−0.00021056		0.0019269	0.0047286	0.073048
	FWE 2	−0.0019851	−0.00057545	−0.00025878		0.00087435	0.0020268	0.057823
	MLE	−0.0033888	−0.0004285	0.00016064		0.0018323	0.0023536	0.019688
	MLE 2	−0.0030739	−0.00075814	−0.00029836		0.00066214	0.00099507	0.0059062

Corrected: Mean of N-next true values to be forecasted: 0.001324; Total valid=801, i.e. 80.1% of M fails-MLE=0%, fails-FWE=7%, fails-MODWT=13.4%, fails-DWT=12.5% Not Corrected: Mean of N-next true values to be forecasted: 0.001324; Total valid=45.1, i.e. % of M fails-MLE=0%, fails-FWE=35.2%, fails-MODWT=43.4%, fails-DWT=41.6%.

Table 8:

Forecasting: N=16,384, Jumps lambda=0.028, N(0, 0.2); MLE, FWE, MODWT(D4), DWT(D4), 2: Corrected using Donoho and Johnstone threshold.

Cat	Method	Main stats			MAD quantiles
Cat	Method	Mean err	MAD	RMSE	0.50	0.90	0.95	0.99
In	WWE MODWT	0.00079621	0.0010536	0.019562	–	–	–	–
	WWE DWT	0.00074677	0.0010165	0.018346	–	–	–
	FWE	0.00052705	0.00074759	0.0094745	–	–	–	–
	MLE	–	–	–	–	–	–	–
Out	WWE MODWT	Inf	Inf	Inf	0.0002394	0.0015	0.0037696	0.088609
	WWE DWT	Inf	Inf	Inf	0.00022172	0.0016482	0.0039952	0.043464
	FWE	0.010034	0.010249	0.23919	0.00017951	0.0014685	0.0037604	0.04528
	MLE	–	–	–	–	–	–	–
		Error quantiles A				Error quantiles B
		0.01	0.05	0.10		0.90	0.95	0.99
Out	WWE MODWT	−0.0025009	−0.0006746	−0.00028513		0.0011776	0.0033089	0.088609
	WWE DWT	−0.0025573	−0.00057909	−0.00028814		0.0012299	0.0033547	0.043464
	FWE	−0.0018013	−0.00048645	−0.00022585		0.0011465	0.0030639	0.04528
	MLE	–	–	–		–	–	–

Corrected: Mean of N-next true values to be forecasted: 0.0016747; Total valid=948, i.e. 94.8% of M fails-MLE=−%, fails-FWE=0.4%, fails-MODWT=3.1%, fails-DWT=2.5%.

Figure 1:

Spectral density estimation (d=0.25/0.45/−0.25), T=2048 (2¹¹), level=10, zoom. (A) d=0.25. (B) d=0.45. (C) d=−0.25.

Figure 2:

Energy decomposition: (A) Integrals of FIEGARCH spectral density over frequency intervals, and (B) true variances of wavelet coefficients respective to individual levels of decomposition, assuming various levels of long memory (d=0.25, d=0.45, d=−0.25) and the coefficient sets from Table 1.

Figure 3:

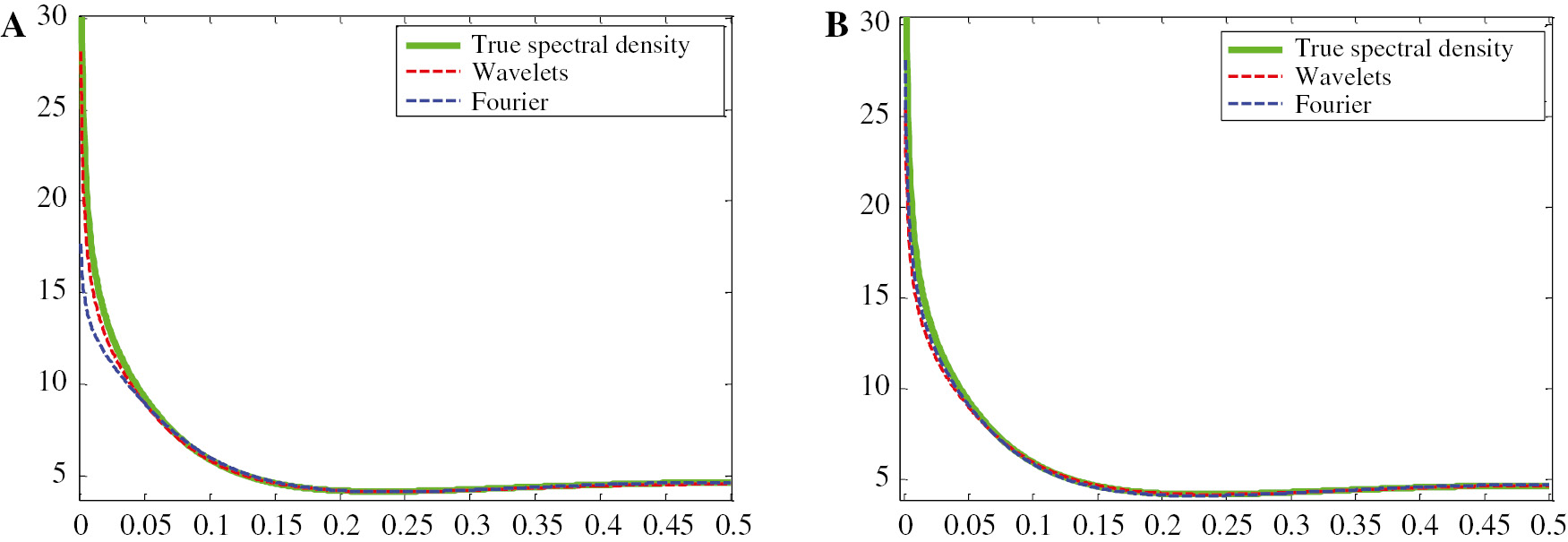
Spectral density estimation in small samples: Wavelets (Level 5) vs. Fourier. (A) T=512 (2⁹), level=5(D4). (B) T=2048 (2¹¹), level=5(D4).

Figure 4:

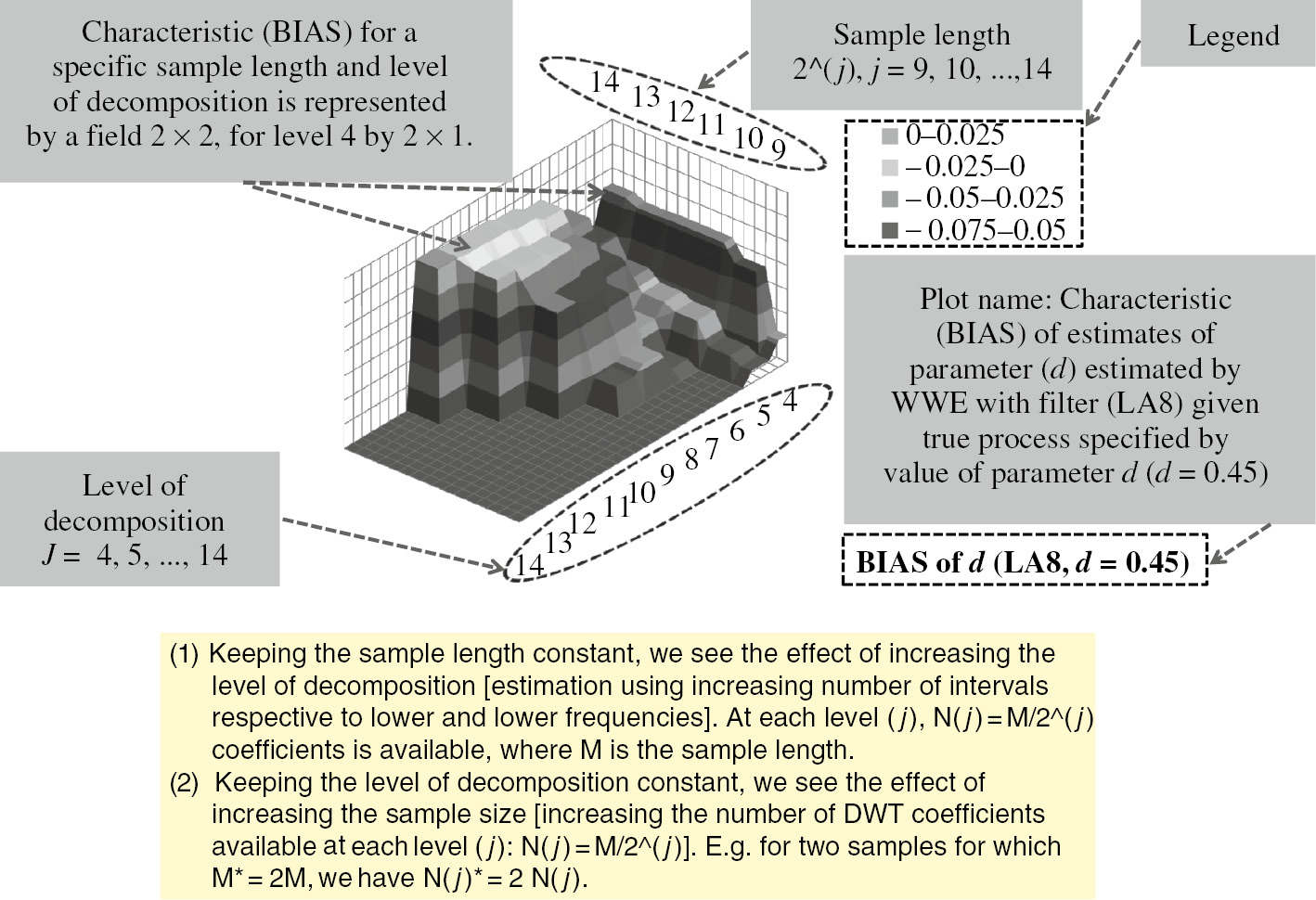
3D plots guide.

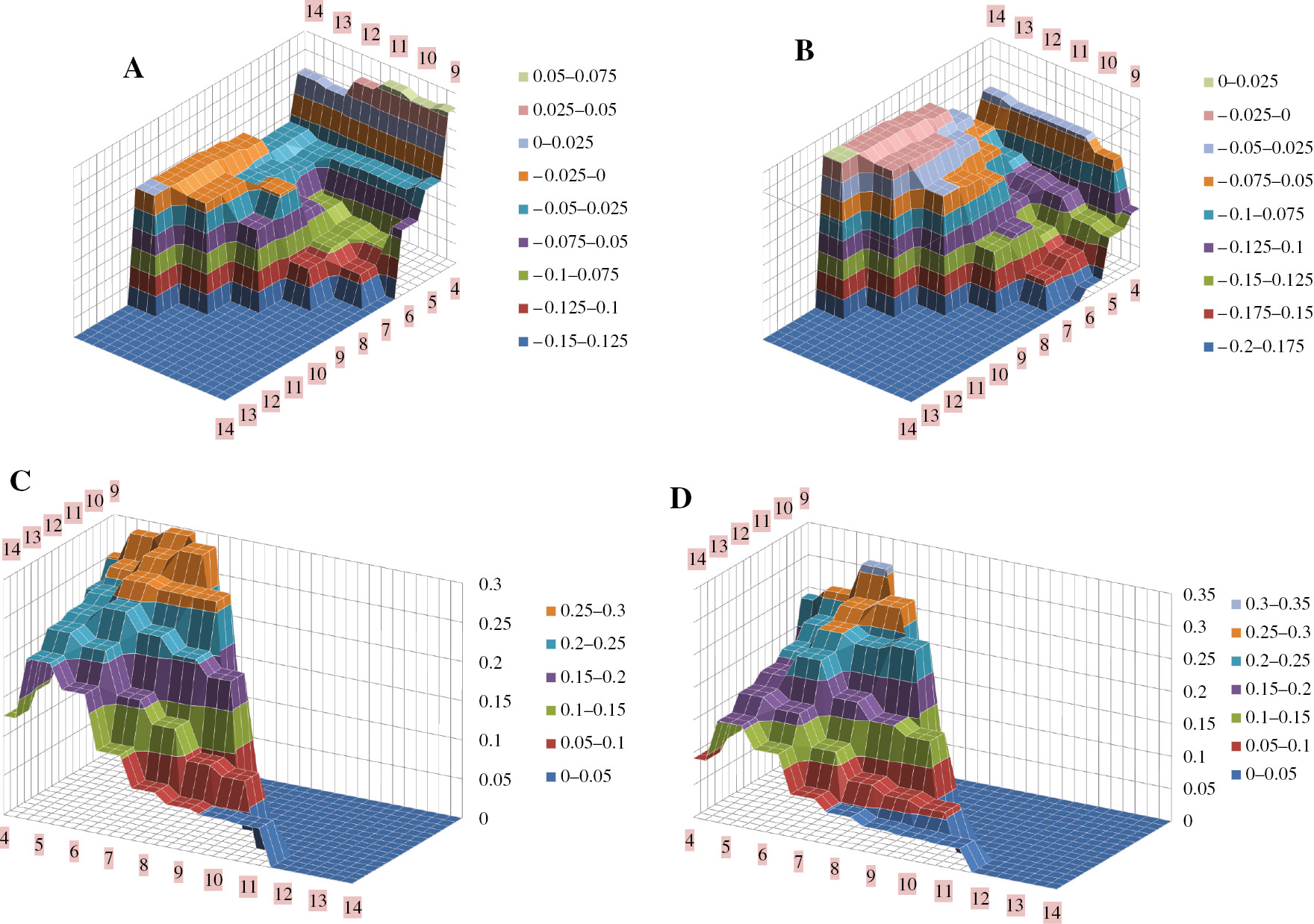
$Figure 5: 3D plots: Partial decomposition: d^:$\hat d:$ Bias and RMSE. (A) Bias of d^$\hat d$ (LA8, d=0.25). (B) Bias of d^$\hat d$ (LA8, d=0.45. (C) RMSE of d^$\hat d$ (LA8, d=0.25. (D) RMSE of d^$\hat d$ (LA8, d=0.45).$

Figure 5:

3D plots: Partial decomposition: d^: Bias and RMSE. (A) Bias of d^ (LA8, d=0.25). (B) Bias of d^ (LA8, d=0.45. (C) RMSE of d^ (LA8, d=0.25. (D) RMSE of d^ (LA8, d=0.45).

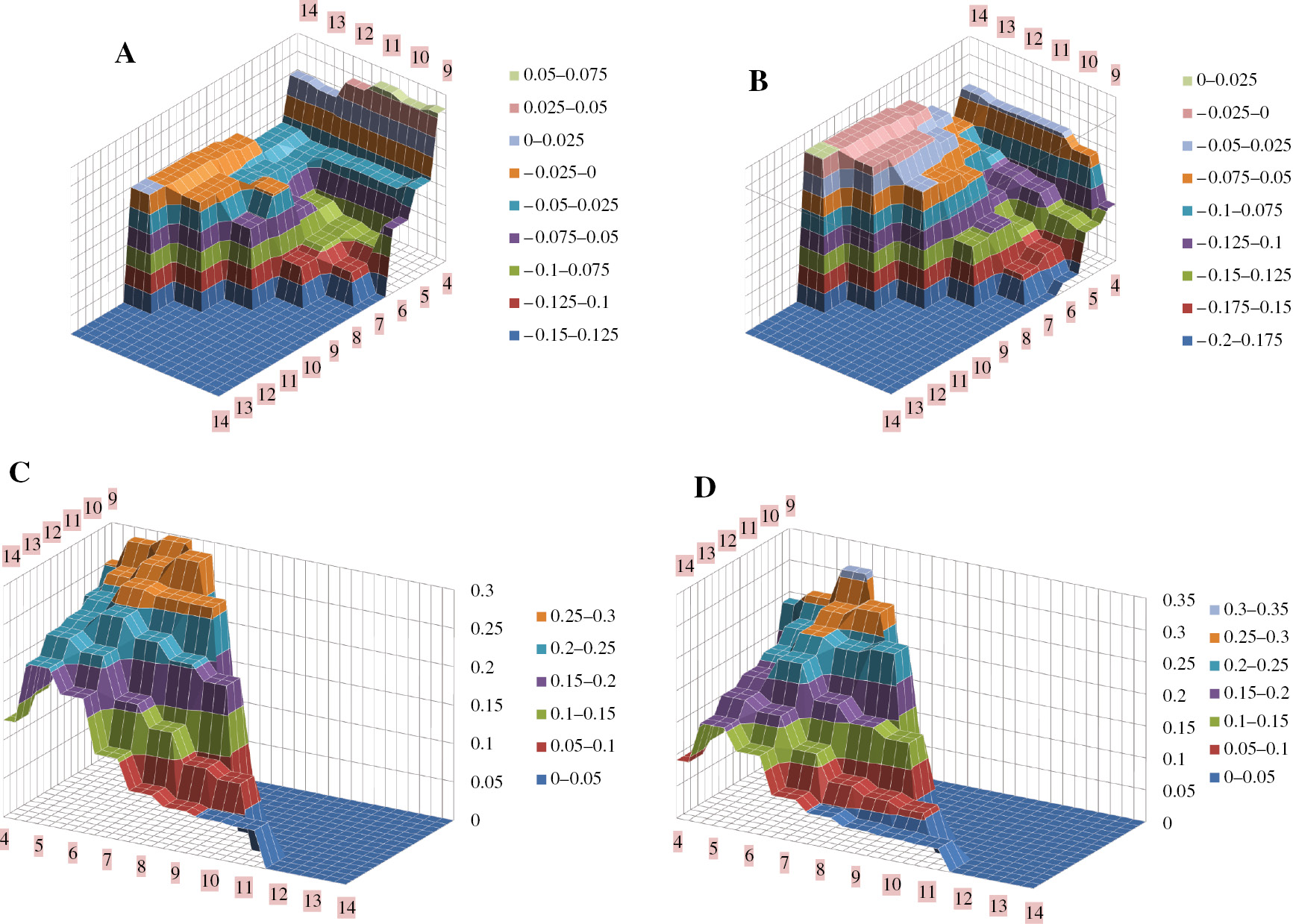
$Figure 6: 3D plots: Partial decomposition: α^:$\hat \alpha :$ Bias and RMSE. (A) Bias of α^$\hat \alpha $ (LA8, d=0.25. (B) Bias of α^$\hat \alpha $ (LA8, d=0.45). (C) RMSE of α^$\hat \alpha $ (LA8, d=0.25). (D) RMSE of α^$\hat \alpha $ (LA8, d=0.45).$

Figure 6:

3D plots: Partial decomposition: α^: Bias and RMSE. (A) Bias of α^ (LA8, d=0.25. (B) Bias of α^ (LA8, d=0.45). (C) RMSE of α^ (LA8, d=0.25). (D) RMSE of α^ (LA8, d=0.45).

References

Barunik, J., and L. Vacha. 2015. “Realized Wavelet-Based Estimation of Integrated Variance and Jumps in the Presence of Noise.” Quantitative Finance 15: 1347–1364.10.1080/14697688.2015.1032550Search in Google Scholar

Barunik, J., and L. Vacha. 2016. “Do Co-Jumps Impact Correlations in Currency Markets?” Papers 1602.05489, arXiv.org.10.2139/ssrn.2733736Search in Google Scholar

Barunik, J., T. Krehlik, and L. Vacha. 2016. “Modeling and Forecasting Exchange Rate Volatility in Time-Frequency Domain.” European Journal of Operational Reseach 251: 329–340.10.1016/j.ejor.2015.12.010Search in Google Scholar

Beran, J. 1994. Statistics for Long-Memory Processes. Monographs on statistics and applied probability, 61, Chapman & Hall.Search in Google Scholar

Bollerslev, T. 1986. “Generalized Autoregressive Conditional Heteroskedasticity.” Journal of Econometrics 31: 307–327.10.1016/0304-4076(86)90063-1Search in Google Scholar

Bollerslev, T. 2008. “Glossary to Arch (garch).” CREATES Research Papers 2008-49, School of Economics and Management, University of Aarhus, URL http://ideas.repec.org/p/aah/create/2008-49.html.10.2139/ssrn.1263250Search in Google Scholar

Bollerslev, T., and J. M. Wooldridge. 1992. “Quasi-Maximum Likelihood Estimation and Inference in Dynamic Models with Time-Varying Covariances.” Econometric Reviews 11: 143–172.10.1080/07474939208800229Search in Google Scholar

Bollerslev, T., and H. O. Mikkelsen. 1996. “Modeling and Pricing Long Memory in Stock Market Volatility.” Journal of Econometrics 73: 151–184.10.1016/0304-4076(95)01736-4Search in Google Scholar

Cheung, Y.-W., and F. X. Diebold. 1994. “On Maximum Likelihood Estimation of the Differencing Parameter of Fractionally-Integrated Noise with Unknown Mean.” Journal of Econometrics 62: 301–316.10.1016/0304-4076(94)90026-4Search in Google Scholar

Dahlhaus, R. 1989. “Efficient Parameter Estimation for Self-Similar Processes.” The Annals of Statistics 17: 1749–1766.10.1214/aos/1176347393Search in Google Scholar

Dahlhaus, R. 2006. “Correction: Efficient Parameter Estimation for Self-Similar Processes.” The Annals of Statistics 34: 1045–1047.10.1214/009053606000000182Search in Google Scholar

Donoho, D. L., and I. M. Johnstone. 1994. “Ideal Spatial Adaptation by Wavelet Shrinkage.” Biometrika 81: 425–455.10.1093/biomet/81.3.425Search in Google Scholar

Engle, R. F. 1982. “Autoregressive Conditional Heteroscedasticity with Estimates of the Variance of United Kingdom Inflation.” Econometrica 50: 987–1007.10.2307/1912773Search in Google Scholar

Fan, J., and Y. Wang. 2007. “Multi-Scale Jump and Volatility Analysis for High-Frequency Financial Data.” Journal of the American Statistical Association 102: 1349–1362.10.1198/016214507000001067Search in Google Scholar

Fan, Y., and R. Gençay. 2010. “Unit Root Tests with Wavelets.” Econometric Theory 26: 1305–1331.10.1017/S0266466609990594Search in Google Scholar

Faÿ, G., E. Moulines, F. Roueff, and M. S. Taqqu. 2009. “Estimators of Long-Memory: Fourier versus Wavelets.” Journal of Econometrics 151: 159–177.10.1016/j.jeconom.2009.03.005Search in Google Scholar

Fox, R., and M. S. Taqqu. 1986. “Large-Sample Properties of Parameter Estimates for Strongly Dependent Stationary Gaussian Time Series.” The Annals of Statistics 14: 517–532.10.1214/aos/1176349936Search in Google Scholar

Frederiksen, P. H., and M. O. Nielsen. 2005. “Finite Sample Comparison of Parametric, Semiparametric, and Wavelet Estimators of Fractional Integration.” Econometric Reviews 24: 405–443.10.1080/07474930500405790Search in Google Scholar

Gençay, R., and N. Gradojevic. 2011. “Errors-in-Variables Estimation with Wavelets.” Journal of Statistical Computation and Simulation 81: 1545–1564.10.1080/00949655.2010.495073Search in Google Scholar

Gencay, R., and D. Signori. 2015. “Multi-Scale Tests for Serial Correlation.” Journal of Econometrics 184: 62–80.10.1016/j.jeconom.2014.08.002Search in Google Scholar

Gonzaga, A., and M. Hauser. 2011. “A Wavelet Whittle Estimator of Generalized Long-Memory Stochastic Volatility.” Statistical Methods & Applications 20: 23–48.10.1007/s10260-010-0153-9Search in Google Scholar

Heni, B., and B. Mohamed. 2011. “A Wavelet-Based Approach for Modelling Exchange Rates.” Statistical Methods & Applications 20: 201–220.10.1007/s10260-010-0152-xSearch in Google Scholar

Jensen, M. J. 1999. “An Approximate Wavelet Mle of Short- and Long-Memory Parameters.” Studies in Nonlinear Dynamics Econometrics 3: 5.10.2202/1558-3708.1051Search in Google Scholar

Jensen, M. J. 2000. “An Alternative Maximum Likelihood Estimator of Long-Memory Processes using Compactly Supported Wavelets.” Journal of Economic Dynamics and Control 24: 361–387.10.1016/S0165-1889(99)00010-XSearch in Google Scholar

Johnstone, I. M., and B. W. Silverman. 1997. “Wavelet Threshold Estimators for Data with Correlated Noise.” Journal of the Royal Statistical Society: Series B (Statistical Methodology) 59: 319–351.10.1111/1467-9868.00071Search in Google Scholar

Mancini, C., and F. Calvori. 2012. “Jumps”, in Handbook of Volatility Models and Their Applications, edited by L. Bauwens, C. Hafner and S. Laurent, John Wiley & Sons, Inc., Hoboken, NJ, USA. doi: 10.1002/9781118272039.ch17.10.1002/9781118272039.ch17Search in Google Scholar

Moulines, E., F. Roueff, and M. S. Taqqu. 2008. “A Wavelet Whittle Estimator of the Memory Parameter of a Nonstationary Gaussian Time Series.” The Annals of Statistics 36: 1925–1956.10.1214/07-AOS527Search in Google Scholar

Nielsen, M. O., and P. H. Frederiksen. 2005. “Finite Sample Comparison of Parametric, Semiparametric, and Wavelet Estimators of Fractional Integration.” Econometric Reviews 24: 405–443.10.1080/07474930500405790Search in Google Scholar

Percival, D. P. 1995. “On Estimation of the Wavelet Variance.” Biometrika 82: 619–631.10.1093/biomet/82.3.619Search in Google Scholar

Percival, D. B., and A. T. Walden. 2000. Wavelet Methods for Time Series Analysis (Cambridge Series in Statistical and Probabilistic Mathematics). Cambridge University Press, URL http://www.worldcat.org/isbn/0521685087.Search in Google Scholar

Perez, A., and P. Zaffaroni. 2008. “Finite-Sample Properties of Maximum Likelihood and Whittle Estimators in Egarch and Fiegarch Models.” Quantitative and Qualitative Analysis in Social Sciences 2: 78–97.Search in Google Scholar

Tseng, M. C., and R. Gençay. 2014. “Estimation of Linear Model with One Time-Varying Parameter via Wavelets.”Search in Google Scholar

Whitcher, B. 2004. “Wavelet-Based Estimation for Seasonal Long-Memory Processes.” Technometrics 46: 225–238.10.1198/004017004000000275Search in Google Scholar

Whittle, P. 1962. “Gaussian Estimation in Stationary Time Series.” Bulletin of the International Statistical Institute 39: 105–129.Search in Google Scholar

Wornell, G. W., and A. Oppenheim. 1992. “Estimation of Fractal Signals from Noisy Measurements using Wavelets.” Signal Processing, IEEE Transactions on 40: 611–623.10.1109/78.120804Search in Google Scholar

Xue, Y., R. Gençay, and S. Fagan. 2014. “Jump Detection with Wavelets for High-Frequency Financial Time Series.” Quantitative Finance 14: 1427–1444.10.1080/14697688.2013.830320Search in Google Scholar

Zaffaroni, P. 2009. “Whittle Estimation of Egarch and Other Exponential Volatility Models.” Journal of Econometrics 151: 190–200.10.1016/j.jeconom.2009.03.008Search in Google Scholar

Supplemental Material:

The online version of this article (DOI: https://doi.org/10.1515/snde-2016-0101) offers supplementary material, available to authorized users.

Published Online: 2017-4-6

You are currently not able to access this content.

Supplementary material

Articles in the same Issue

https://doi.org/10.1515/snde-2016-0101

Keywords for this article

FIEGARCH; long memory; Monte Carlo; volatility; wavelets; Whittle

Estimation of long memory in volatility using wavelets

Article

Abstract

Acknowledgments

A Appendix: Tables and Figures

References

Supplemental Material:

Supplementary Material

Articles in the same Issue

Articles in the same Issue

Articles in the same Issue