Magneto-mechanical coupling of single domain particles in soft matter systems

2.1 Methodology

The strong size-dependent properties that are measured in nanorheological experiments on microstructured samples make this method a promising candidate for the development of a method capable of determining local rheological properties on a nanoscale. The use of magnetically blocked, nanoscopic particles as tracers under the influence of an oscillating magnetic field is a particularly promising approach. The response of the particles in terms of their magnetic susceptibility is recorded, and in analogy to classical macrorheology, the phase shift of the response signal delivers information on the complex susceptibility and thus on the frequency-dependent excitation of the particle rotation.

The magnetic nanoparticles (MP) that are used as probes in this approach ideally need to fulfill a number of requirements in order to facilitate a simple and meaningful data analysis. In order to result in a direct correlation of the magnetic susceptibility data and the hydrodynamic characteristics of the probes, it is important to make sure that they are well-dispersed in the sample material on a single-particle level in a nonagglomerated way, and that no significant adsorption of matrix components on the particle surface occurs. Further, it is beneficial if the size distribution is narrow, and the basic magnetic properties, such as the magnetic moment, of each individual particle are uniform. Finally, the magnetic anisotropy is required to be high enough to ensure that the particles are magnetically blocked and accordingly relax predominantly by Brownian rotation [29]. Within these limits, there are still a variety of tracer particles of different size, shape, and chemical composition possible, and meanwhile a range of different tracers are successfully employed for magnetic particle nanorheology (MNP) and related methods [18], [19], [30].

Among the particle systems suitable for application as tracers in MNP, magnetically blocked, single domain cobalt ferrite (CoFe₂O₄) nanoparticles, as shown in Figure 1 are particularly versatile. The inherent magnetocrystalline anisotropy of CoFe₂O₄ leads to strong pinning of the magnetization vector in the crystal lattice, thus providing a well-defined crystalline structure. This results in a high effective anisotropy constant and high volume-based saturation magnetization. Further, the particles can be stabilized in organic as well as aqueous media, and in order to tailor the hydrodynamic size of the probe particle, they can be decorated with a silica shell of variable thickness [18].

Figure 1:

TEM images of tracer particles of the same magnetic core size and varying SiO₂ shell thickness of a) 12 nm; b) 25 nm; c) 29 nm; d) 37 nm; and e) 42 nm. In f) the size distribution of the geometrical diameter d _g with corresponding log normal function is shown for the different probe particles (a) (blue); b) (orange); c) (red); d) (light green); e) (green)). Reproduced by permission of the PCCP Owner Societies from [18].

A suitable experimental setup is based on AC susceptometry. In a typical experiment, the sample is placed between a pair of excitation coils, while two pairs of detection coils are employed, one measuring the sample and the other measuring a blank. By amplification of the subtracted signals using a lock-in amplifier, the complex susceptibility is accessible. During the measurement a sinusoidal AC magnetic field with small amplitude is applied, which can be varied in frequency. The alternating field activates the magnetic nanoparticles in the sample to a frequency-dependent relaxation behavior. This rotational relaxation process of the particles occurs against the effective sample viscosity that might be influenced by the probe size and might further depend on frequency.

The simplest model to describe the frequency-dependent response function of the particle is given by the Debye model where the real part χ ′ and the imaginary part χ ″ of the susceptibility are expressed as functions of the excitation frequency ω and the relaxation time τ of the particle [31], [32],

Here, n denotes the number density of particles and m is the particle’s magnetic moment. For thermally blocked MP, the Brownian relaxation is dominant, and hence the corresponding relaxation time is accessible from a fit of the experimental data according to the Debye model. By application of the well-known Stokes-Einstein equation the obtained relaxation time τ _B is related to the viscosity η of the medium, the hydrodynamic radius of the particle r _h , and the rotational diffusion coefficient D _r .

This approach describes the behavior of monodisperse MP in Newtonian fluids. Once a real, polydisperse, particle system is analyzed, a broadening of the relaxation is observed, and the quality of the data description decreases significantly. In order to compensate for this, extended versions of the Debye model have been developed allowing a sufficiently good description of the measured data by introducing a size distribution term [17], [32], [33].

Here, χ ∗ is the complex susceptibility, f(r _h ) is the lognormal size distribution of the particle system and τ _B the Brownian relaxation time. While this approach works well for Newtonian fluids, as soon as more complex, non-Newtonian samples are analyzed, the extended Debye model fails to describe the data, therefore strongly limiting the applicability of this otherwise extremely versatile and attractive technique. Especially for the analysis of biological samples, this technique is promising as low sample amounts of 200 µL are characterized concerning their rheological data on the nanoscale in a non-destructive way employing small amounts of MP as tracers.

2.2 Application to complex fluids

The rheological properties of polymer-based fluids and soft, viscoelastic solids, e.g., gels or melts, typically show non-Newtonian behavior depending on the volume fraction and the average chain length of the polymer component. Concerning the nanorheological analysis of such systems, characteristic length scales of the polymer component become relevant in relation to the probe, such as mesh size in gels, the radius of gyration for polymer coils, or the tube diameter a and the correlation length ξ in polymer solutions. Rubinstein et al. developed a theory differentiating three categories with respect to the relation between probe size and characteristic length scales in the sample [34]. Here, particles with a hydrodynamic size smaller than the correlation length ξ are classified as small particles and their translational diffusion is determined by the solvent viscosity. The tracers are classified as large particles if their diameter is larger than the tube diameter a of the polymer chain. For this case, a (quasi)continuous behavior for long time scales is expected. In the intermediate size regime (ξ < MP < a), an effective viscosity is observed, which is related to the properties of the polymer strand on the probe scale [34]. The dependence of the observed viscosity on the probe size and characteristic length scales in the polymer solution leads to frequency-dependent rheological properties, as instead of a single relaxation process, as observed in Newtonian fluids, different relaxation processes, including relevant processes within the matrix itself, contribute to the signal. This offers the possibility to extract frequency-dependent rheological properties by modification of the data analysis approach.

Hence, the concept of MPN is established. Here, the German-DiMarzio-Bishop (GDB) model is employed and modified in order to correlate the measured frequency-dependent susceptibility to the complex modulus G ^* of the polymer solution. A frequency-dependent friction coefficient is introduced leading to the following equations for the loss modulus G″(ω) and the storage modulus G′(ω) [17].

with the constant K

and the abbreviations

With this in hand, a powerful method is provided that allows the determination of frequency-dependent rheological properties of soft matter systems on the length scale of the tracer particles employed.

2.2.1 MPN of Polymer Solutions

By employing magnetically blocked nanoparticles as nanoscopic, quasi-dipolar magnetic probes, the complex dynamic behavior of soft matter at the particle scale is investigated in fluid media of increasing complexity. This approach allows the extraction of the complex, frequency-dependent rheological information from AC-susceptibility measurements of tracer particles and polymer solutions. In Figure 2, exemplary AC-susceptibility curves of well-defined cobalt ferrite particles dispersed in aqueous solutions of ethylene glycol, triethylene glycol, and its polymeric analogues as analyzed by MPN are shown [17].

Figure 2:

ACS spectra for aqueous ethylene glycol (a); triethylene glycol (b); polyethylene glycol (M = 1000 g mol⁻¹) (c); and polyethylene glycol (M = 8000 g mol⁻¹) (d) solutions with CoFe₂O₄ nanoparticles as tracers. Reprinted by permission from Springer Nature: Springer, Colloid and Polymer Science, from reference [17], Copyright (2014).

Depending on the volume fraction of polymer, a shift of the maximum of the imaginary part of the susceptibility to lower frequencies is found, that is attributed to an increase of the viscosity of the dispersion medium in Eq. (4). For small chain length of the ethylene glycol derivatives (Figure 2a, b), no change of the shape of the relaxation peaks is observed and the spectra may be described by an extended Debye model, considering an increased viscosity. For larger chain length (Figure 2c, d), the shift is significantly more pronounced, but also the shape of the relaxation peak changes. In chapter 2.2, this effect is attributed to the presence of several simultaneously traced relaxation processes in the sample that are dependent on the relative size between probe and polymer length scale. Employing the analysis according to the GDB model, frequency depending moduli can be obtained.

In Figure 3a, this analysis is performed for PEG–water mixtures with high molar mass and compared to macrorheological analysis [35]. This allows extending the accessible frequency range of rheological data by several orders of magnitude [17], [18], [35]. The non-Newtonian behavior in polymer solutions leads to a complex frequency-dependent flow behavior for macrorheological experiments. The crossover point where G′ and G″ intersect is typically related to the longest relaxation time of the polymer chain, e.g., by reptation. It’s dependence on the polymer fraction gives access to the determination of the respective polymer fraction critical for entanglement formation (Figure 3b) [35]. A second relaxation time typically related to polymer segment mobility becomes visible at higher frequency values, as is discussed in more detail in section 2.2.3.

Figure 3:

a) Comparison of the frequency-dependent macroscopic (circles) and nanoscopic (squares) loss (G″, filled) and storage moduli (G′, unfilled) for an aqueous solution of PEG 35k (35 m%), b) relaxation times τ ₁ (filled) and τ ₂ (unfilled) versus polymer mass fraction μ _PEG for PEG8k (blue), PEG20k (green) and PEG35k (red).

2.2.2 Size effects

The rheological properties of non-Newtonian fluids strongly depend on the size and volume fraction of dissolved macromolecules, as discussed in section 2.2. For the nanorheological analysis, the system gets even more complex, as the probe is only sensitive to certain parts of the polymer depending on the probe’s size. In order to get a full picture of a sample system, it is therefore interesting to probe the sample on different time and length scales. For this, the combination of macro-, micro- and nanorheological methods is a promising tool. This is done in a comparative study of three different PEG–water mixtures with the same macroscopic zero-shear viscosity, but different chain length and volume fraction of the dissolved PEG macromolecules. Here, cobalt ferrite (d = 16.4 nm) as well as anisotropic Ni nanorods (l = 233 nm, d = 23.9 nm) are employed as tracers, thereby probing significantly different length scales. In addition to classical macrorheology and MPN, oscillating field optical transmission (OFOT) and DC-overlayed AC-susceptometry are used. The rotational dynamics of these probes with different sizes and shapes are correlated to the macrorheological analysis. Here, a strong dependence of the rheological properties of the samples depending on the length scales of the polymer compared to the size of the nanoparticle is observed. If the probe is smaller than the correlation length of the polymer, the apparent viscosity is found to be lower than the value determined by macrorheology and frequency-dependent with decreasing values for increasing frequency. If the probe on the other hand is large compared to tube diameter an average equivalent to the macroscopic measurement is obtained indicated by no frequency dependence and good agreement with the macroscopically determined zero-shear viscosity, see Figure 4 [12].

Figure 4:

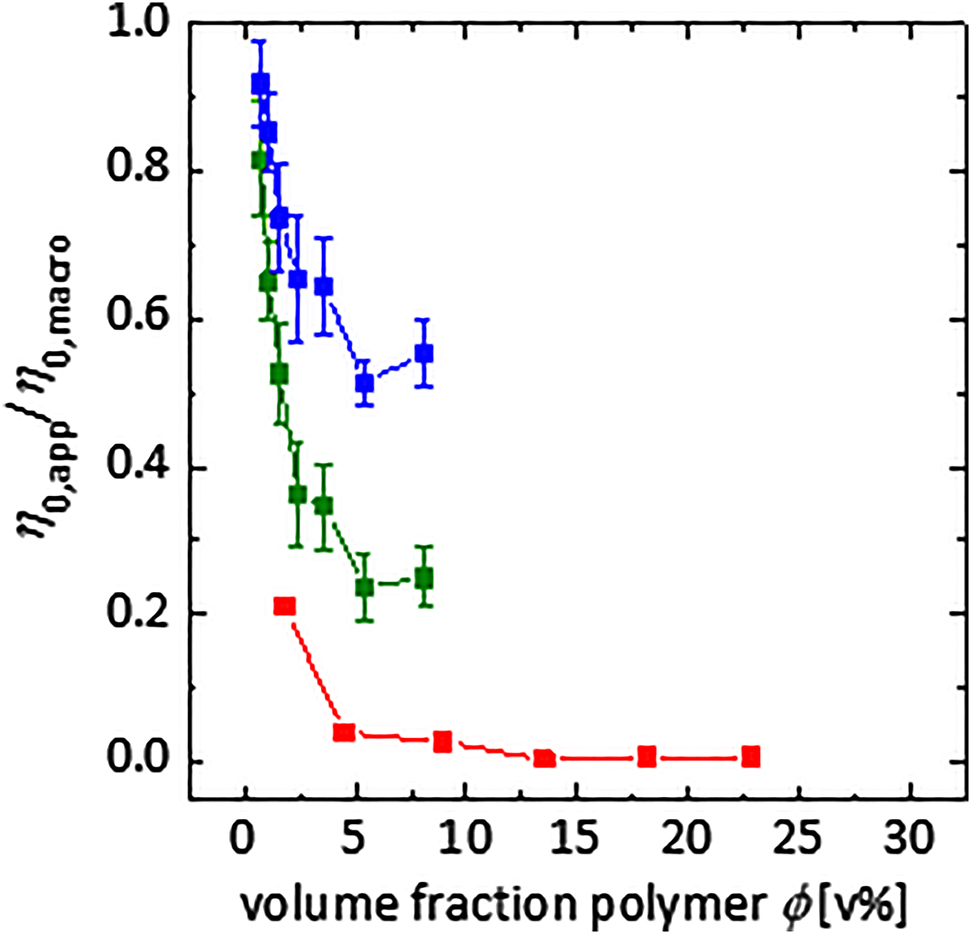
Apparent zero shear viscosity η o , app , ( ω ) of aqueous PEG300k solutions normalized by the macroscopic viscosity η 0 , macro ( ω ) in dependence on the polymer volume fraction ϕ for rod-like tracer particles with a length of 550 nm (blue) and 140 nm (green) and for spherical tracers with a diameter of 13.3 nm (red).

In Figure 5, macro- and nanorheologically obtained loss moduli are presented. If the chain length of the polymer in the complex fluid is low (Figure 5a), generally good agreement of macro- and nanorheological properties is found, indicating nearly Newtonian behavior. However, for polymers with a molar mass larger than the entanglement molar mass (Figure 5b), strong deviations between macro- and nanorheological results are found, which is attributed to the particle size being similar to the polymer correlation length in the solution.

Figure 5:

Frequency-dependent loss modulus G″ as obtained from macrorheology (solid symbols) and calculated according to the modified DGB model (open symbols) with 13 nm tracer particles; a) for PEG (M = 1.0 kg mol⁻¹) (adapted with permission from Springer Nature: Springer, Colloid and Polymer Science, from reference [17], Copyright (2014)); and b) for PEG (M = 35 kg mol⁻¹); c) scaling behavior of the loss modulus with frequency as expected from theoretical prediction, (b and c adapted by permission of the PCCP Owner Societies from [18]).

In order to obtain a complete picture of the polymer in solution, the sample can be probed with probes of different size. A systematic study in this context uses a size-tuneable silica shell around the probe particle to perform this experiment [18]. The systematic evaluation is shown in Figure 5c. If the particle is large compared to the size of the polymer chain, hence larger than the tube diameter a, a mean viscosity comparable to the macro-rheological result is obtained, as this curve and slope basically describe a Newtonian flow behavior. The corresponding relaxation time extractable from the nanorheological experiment therefore is given by the whole polymer chain. If the particle is significantly smaller than the correlation length of the polymer, on average the solvent in between the polymer segments is analyzed by the probe and again a scaling factor of 1.0 as for the Newtonian fluid is obtained. In the intermediate regime confinement of the probe particle by the polymer chain is expected leading to a subdiffusive behavior indicated by a scaling of 0.5 in Figure 5c. With a small number of independent experiments employing probes of different sizes this approach allows the determination of four different relaxation times, namely the relaxation of the whole polymer τ _rep , the relaxation time of an entangled polymer strand τ _e , the relaxation time of a polymer segment in the size range of the probe particle τ _d , and the relaxation time of the polymer connected to the correlation length τ ₂ [18]. The possibility to determine and distinguish multiple relaxation times inherent to soft matter systems is of importance for future investigations, as will be under more addressed in chapter 2.2.3.

2.2.3 Determination of relaxation times

The crossover point between the storage and loss modulus in a rheological experiment contains valuable information, as it indices a drastic change in flow behavior that is commonly related to a relaxation time of the material. A MPN experiment allows the determination of the frequency-dependent storage and loss modulus and therefore can also be used to extract the relevant relaxation times. As the material is probed on the nanoscale, with this approach also local relaxations are accessible. A sample system that is especially suitable for the analysis of relaxation times are dynamic physical gels, as these systems offer a variety of relaxation processes and an interesting flow behavior [36], [37]. One way to achieve this interesting architecture is to induce more specific dynamic interactions in the polymer matrix by introducing terpyridine-based end groups to star-shaped PEG molecules. These end groups show affinity to divalent transition metal cations in the form of 2:1 complexes, as shown in Figure 6c). Therefore, upon dissolving in water in the presence of metal ions, complexation of the latter is observed leading to the formation of dynamic supramolecular networks with intrinsic self-healing properties. The rheological properties of these dynamic networks can be probed on the nanoscale employing MPN, and afterwards related to macroscopically determined storage and loss moduli, see Figure 6. Here, the macroscopic results show the typical flow behavior of viscoelastic liquids as described by the Maxwell model with a relaxation time τ _l,macro found at the crossover point of storage and loss modulus. This relaxation time contains contributions from relaxation of whole star-shaped PEG molecules and the dissociation time of metal-ligand complexes leading to a chain extension, thereby actively slowing the molecular relaxation. For the nanorheological analysis, distinct differences are found in the shape of curves determined at different stoichiometric ratios r _M/P, which is defined as the molar ratio of the divalent metal ions to the total terpyridine functionalities. For this system bidentate complexes are expected, therefore a homogeneous network could be formed at a stoichiometric ratio of 2.0. For lower values broader meshes are expected [38].

Figure 6:

Comparison of macroscopic (full symbols) and nanoscopic (empty symbols) storage G′ (colored) and loss moduli G″ (black) in dependence on frequency for Zn²⁺ as counter ion to terpyridine functional tetrafunctional PEG stars with the stoichiometric ratios a) r _M/P = 0.65 and b) r _M/P = 1.09, reproduced by permission from The Royal Society of Chemistry from [38]. c) Molecular structure of the formed complex. M²⁺ denotes the employed metal cation (Mn²⁺, Zn²⁺, or Co²⁺) and R is the rest of the tetrafunctional ligand.

Depending on the stoichiometric ratio r _M/P, in the dynamic networks fundamentally different flow behavior is found by MPN. For low values of r _M/P the loss modulus is higher than the storage modulus indicating a pseudo-Newtonian-like flow behavior. This is also strengthened by the finding of only one relaxation time τ _l,nano. In the case of higher values of the r _M/P a rubbery plateau is found in the nanorheological investigation. Here, two relaxation times are accessible. In addition to τ _l,nano, which is associated to the breaking of the metal ligand bond, also a fast relaxation τ _f,nano is found and attributed to network-strand fluctuations. These data are used to on the one hand extract the mean mesh sizes of the dynamic network from the plateau storage modulus according to rubber elasticity theory and on the other hand to determine the respective relaxation times for all analyzed samples, depending on the stoichiometric ratio and the type of the metal ion, as shown in Figure 7 [38], [39].

Figure 7:

a) Mesh size ξ and b) relaxation times for different systems consisting of metal ion and tetrafunctional PEG (Mn²⁺ (green), Zn²⁺ (red), Co²⁺ (blue)) depending on the stoichiometric ratio, reproduced by permission from The Royal Society of Chemistry from [38].

2.2.4 Phase transitions

The determination of phase transitions of materials is of significant importance for daily life due to the properties of materials changing drastically upon the transition, thereby leading to potentially dangerous situations as material is out of the parameter range for application. The transition of the rheological properties of supramolecular networks as shown in chapter 2.2.3 from fluid-like to solid-like can be described as a sol-gel transition depending on the amount of metal ions in the sample. This shows the principle applicability of MPN to extract phase transition behavior.

In order to expand this concept, we will consider different phase transitions in this chapter. One example of a phase transition that should be detectable by MPN is the sol–gel transition, where the reaction mixture starts in a fluid phase and proceeds to a viscoelastic solid. Connected to this transition is a drastic change of the macroscopically measurable rheological properties that translates to the nanoscopically observed properties depending on the mesh size and the characteristic length scales in the gel [12], [18], [38].

A possible example for such systems are poly(acrylamide) (PAAm) hydrogels that are commonly used model systems. By analyzing samples with different crosslinking density as well as polymer volume fraction, the mechanical properties as well as the nanoscale structure of the gel samples are varied. For these well-defined model hydrogels rubber elasticity theory is successfully used to calculate the mean mesh size of the polymer networks from the plateau storage modulus obtained from macrorheological analysis [38], [39]. Analyzing the network formation kinetics, an approach frequently used for macroscopic gels and elastomers is the cure-curve. Here, a liquid reaction mixture is placed in a rheometer and the sample is analyzed at a constant frequency and strain in fixed time intervals. The obtained curve shows a transition from a liquid-like sample to a solid (visco-)elastic sample depending on the time. Using MPN, comparable to a macrorheologically determined cure–curve, the reaction kinetics can be determined by time-dependent measurements at a constant frequency yielding the dependence of the reaction rate on the initiator concentration.

Using the MPN approach as described in section 2.2, the frequency-dependent storage and loss modulus of PAAm hydrogels can be determined. In Figure 8 the modulus at the crossing point is shown depending on the macroscopically determined mean mesh size of the hydrogel. For mesh sizes smaller than the average particle size a strong increase of the modulus is found upon decreasing the mesh size, as the particle is trapped inside the meshes of the network. Upon reaching a mesh size that is equal to the particle diameter, a sharp drop of the modulus and a local minimum is found for the course of the cross modulus indicating that the size relation of probe to characteristic length scale in the sample is of great importance for the analysis and that the structure is in fact probed on a nanoscale.

Figure 8:

Modulus at the crossover point for PAAm hydrogels with different polymer volume fraction (light green: ϕ = 0.07, green: ϕ = 0.06, olive: ϕ = 0.05, dark green: ϕ = 0.04) in correlation with the experimental mesh size of the polymer network.

Gelation of samples can also be induced by a change in temperature. A prominent example for this is gelatin. The sol–gel phase transition is triggered by a change in the temperature of the medium leading to a change in the solvent condition of the dissolved macromolecules, as opposed to the gelation of polyacrylamide as described above, where the gelation is initiated by a chemical reaction forming the macromolecules in situ from respective monomers. For the analysis of the progressing gelation of gelatin the time-dependence is shown to be observable by a shift of the imaginary part of the magnetic susceptibility to lower frequencies [40], [41].

The most common phase transitions are temperature triggered, such as melting and glass transitions. Polymer solutions here are a rich and versatile sample system to study, as they show a number of thermal transitions that can oftentimes be tuned and shifted by the chain length and volume fraction of the dissolved polymer. Analyzing such systems with magnetic probes as tracers by zero-field-cooled-field-cooled (ZFC-FC) magnetization measurements clear features are observed that are related to the thermal transitions as found in differential scanning calorimetry (DSC) studies. In this way, it is shown that by doping materials with a tracer amount of MP it is possible to determine the temperature-dependent phase behavior of polymer solutions in a simple nondestructive way [42].

3.1 Conventional ferrogels

The most common way to build up a gel network is to introduce crosslinks into a system consisting of long polymeric chains. These chains may either be directly introduced to the system and crosslinked by a proper agent or be generated in situ by polymerization of monomers in presence of a crosslinker. The interaction of MP dispersed in these matrices are predominately determined by van der Waals interactions and typically strongly depend on the mesh size of the gel network relative to the particle size.

One important issue for the macroscopic material’s properties is the particle mobility in such structures on the particle scale. Oftentimes in elastic matrices especially for larger particles no information on the particle mobility is obtained by nanorheological investigations, as the relaxation processes are on time and length scales that are not accessible. Hence in a novel approach, Mössbauer spectroscopy has been used to gain information on the particle mobility of a sample system of spindle type hematite particles dispersed in crosslinked PAAm hydrogels with varying crosslinking degree and therefore also mesh size. Here, it is found that while all samples show no particle mobility in the dynamic magnetic field of a nanorheological investigation, a distinct trend of the line broadening in Mössbauer spectroscopy shows mobility for all particles on small time and length scales that is also depending on the mesh size of the polymer network [51].

For smaller particles, the mesh size change of the hydrogel matrix can have a significantly stronger effect on the particle mobility, as the particle size is in the range of the mesh size. As mentioned in section 2.1, MP exhibit two main mechanisms of relaxation after excitation by an external magnetic field, the Brown and the Néel mechanism. The Brownian relaxation is connected to a reorientation of the particle magnetic moment by rotation of the whole particle, while during the Néel mechanism the magnetic moment rotates inside the particle against the effective magnetocrystalline anisotropy. Hence, both mechanisms are fundamentally different, and also the heat dissipated by each respective mechanism is different and depends severely on the matrix and the properties of the magnetic particle. One way to separate these mechanisms and determine the individual contribution to the overall heating is presented by analysis of mesh size tunable PAAm hydrogels as a tissue model. Here, by varying the ratio of Aam to BIS at a constant polymer volume fraction the mesh size of prepared PAAm hydrogels is tuned systematically. Performing a macrorheological analysis, the obtained plateau storage modulus is correlated to the mean mesh size of the hydrogel network. By synthesizing the polymer network in the presence of magnetic iron oxide nanoparticles a homogeneous distribution of the MP in the resulting meshes is achieved. Analysis of magnetic heating experiments yields a distinct decrease of the heating efficiency with the mean mesh size, as presented in Figure 9. This drop in heating efficiency as represented by the specific loss power SLP is attributed to a gradual immobilization of the MP in meshes of the hydrogel and a blocking of the Brownian particle relaxation mechanism. Hereby, it is shown that the Brownian relaxation mechanism contributes to approximately 35 % of the overall the particle heating power of this particle system at the given field conditions [52].

Figure 9:

Normalized SLP values of MNP with a hydrodynamic diameter d _h of (18.9 ± 6.1) nm, as dispersed in water, in polymer solution, and gradually immobilized in hydrogels with decreasing mean mesh size. Adapted from reference [52] with permission from Elsevier.

One major focus of the research interest regarding ferrogels is based on anisotropic shape changes for possible applications as actuators. For this purpose, microgels are promising candidates due to their low switching times with respect to stimuli induced changes of the swelling degree. Magnetoresponsive microgels are obtained by immobilizing MP in the polymer network. Oftentimes poly(N-isopropylacrylamide) is employed, which is known for its thermoresponsive properties manifested in the volume phase transition temperature at a physiologically relevant temperature of 32 °C, therefore generating a multiresponsive system with temperature as well as magnetic field as stimuli. Loading of these microgel beads with MP leads to magnetoresponsive materials, where an anisotropic volume shrinkage is found upon application of a magnetic field [53]. The microgel bead is elongated parallel to the magnetic field and contracts perpendicular the field, which is in line with theoretical calculations for a comparable system [54].

3.2 Particle-crosslinked ferrogels

The architecture with the strongest interactions between MP and polymer chains is represented by particle-crosslinked ferrohydrogels. This type of stimuli responsive material gives rise to improved material properties due to a strong magneto-mechanical coupling and a novel response mechanism to an external magnetic field [55], [56], [57], [58], [59], [60]. A simple effect of the covalent attachment is that in contact with swelling media no particle loss is observed due to diffusion, and the materials may therefore be used over many cycles even in contact with biological tissue [61], [62], [63]. If the network is solely crosslinked by the magnetic nanoparticles, strongly particle content depending properties are obtained [14], [49]. As particle component in addition to classic spherical particles also anisotropic particles can be used as shown in Figure 10, where the structure and homogeneity is confirmed by cryo-TEM investigations. Here, the particle-crosslinked ferrohydrogel is based on spindle-type hematite particles as sole crosslinkers of a PAAm network [64].

Figure 10:

a) Cryo-TEM image of a particle-crosslinked ferrohydrogel, crosslinked with spindle-type hematite particles. b) Schematic representation of the network architecture of the particle-crosslinked ferrohydrogel. Adapted with permission from [64]. Copyright 2014 American Chemical Society.

Analyzing the properties of particle-crosslinked ferrohydrogels, a strong decrease of the swelling degree upon increasing the volume fraction of particulate crosslinkers is found. The data obtained for the swelling degree are further used to quantify the crosslinker functionality of the particles and the average molar mass of polymer segments between the particles, as shown in Figure 11. By comparison with macrorheological measurements and extraction of the same properties, we get to a more sophisticated image of the architecture of the solely particle-crosslinked ferrohydrogels, as shown in Figure 10b, where the network is built up by only a small fraction of elastically active particle-linking polymer chains and a large number of loops and dangling ends [64].

Figure 11:

Average network segment length M _c,FFR based on the Frenkel−Flory−Rehner model as a function of the particle volume fraction reprinted with permission from [64]. Copyright 2014 American Chemical Society.

When thermally blocked MP dispersed in a fluid medium are subjected to a homogeneous magnetic field, an orientation of the dispersed particles is observed. This anisotropic orientation can be immobilized by crosslinking the particles into the polymer backbone while applying a homogeneous magnetic field, leading to an angle-dependent magnetization behavior [65]. In this way, when employing spindle-type hematite particles as crosslinkers, a novel class of particle-crosslinked ferrohydrogels is prepared showing a permanent magnetic anisotropy as well as a geometric anisotropy since the magnetic properties of the spindle-type hematite particles are coupled to their geometric anisotropy. Due to the anisotropic magnetic properties, in magnetization measurements, a dependence of the magnetization curve on the angle between synthesis field and probe field is found, that is characterized in detail and presented in Figure 12. In these measurements two main components next to residual particle mobility can be found. In hard anisotropic ferrohydrogels, a strong dependence of the remanence magnetization on the respective angle is found and can be attributed to an immobilization of the particles in the elastic matrix with a preferred orientation of the magnetic moment, which is in agreement with a theoretical description by the Stoner–Wolfarth model. In soft anisotropic ferrohydrogels on the other hand a plastic deformation effect is found, leading to a significant deviation from the proposed Stoner–Wolfarth model and an attribution of the resulting magnetization behavior to an adaptive preferred orientation of the magnetization axis [66].

Figure 12:

a) Schematic illustration of the setup geometry and axes annotations. Magnetization curves of b) the isotropic hard gel in comparison with the particles measured as powder (grey); c) the anisotropic hard gel; d) the anisotropic soft gel; solid line: zy-plane, dashed line: xy-plane; θ _xy or θ _zy : 0° (green), 22.5° (blue), 45° (purple), 67.5° (red), 90° (orange); reproduced by permission of the PCCP Owner Societies from [66].

3.3 Nanostructuring by self-assembly

Structuring materials on a nanoscale opens the possibility for various applications ranging from surface modifications to filler networks in polymeric composite materials. Here, self-assembly has proven to be a very effective, yet elegant way to generate ordered structures on a nanoscale.

The self-assembly of 12-hydroxyoctadecanoic acid (12-HOA) in organic media leads to the formation of network structures that are formed from fibrillous strands of 12-HOA and therefore exhibit an intrinsically anisotropic shape of the meshes due to the highly anisotropic fibers building them. The dispersion of a commercial ferrofluid inside the pregel allows the preparation of organo-ferrogels. By application of a magnetic field during the synthesis, an anisotropic distribution of the MP can be conserved in the gelation process, leading to anisotropic ferrogels. In comparsion to the isotropic case, a significant difference of the birefringence is found with higher values of the saturation birefringence observed for the anisotropic samples [67].

Another interesting aspect is the self-organization of magnetic nanoparticles. Nanostructured magnetic materials are of interest for applications for data storage or actuation, if the anisotropy can be coupled to the mechanical properties of a suitable matrix, as described above. Spindle-type hematite nanoparticles, here, are a scientifically interesting model system as they show a magnetic as well as geometric anisotropy, a tunable aspect ratio, a comparably low polydispersity, and present an unusual magnetic orientation in external magnetic fields with their long axis perpendicular to the field vector [68], [69], [70]. The well described orientation mechanism for these particles in a homogeneous magnetic field leads to an orientation, where the long particle axis is distributed in a plane perpendicular to magnetic field vector. A novel orientation mechanism for this particle system could be established by application of a rotating magnetic field. Here, a truly uniaxial orientation could be achieved, as shown depicted on TEM images in Figure 13. The long particle axis is perpendicular to the applied field vector for all cases, but the rotating nature of the applied field therefore induces a uniaxial orientation of the particle. Analyzing the samples with small angle X-ray scattering (SAXS), the successful orientation of the particles is shown for larger ensembles by reproduction of the observed scattering patterns with simulations [71].

Figure 13:

SEM images of hematite nanospindles assembled in a) absence of magnetic field; b) static field of 38 mT in the indicated direction; c) and d) rotating magnetic field of 200 Hz and 20 mT, along with e) side view of a breaking edge of the sample assembled in a rotating field and f) detailed view. Scale bars represent 200 nm. Reproduced by permission of The Royal Society of Chemistry from [71].