Abstract
Chemical synthesis has its roots in the empirical approach of alchemy. Nonetheless, the birth of the scientific method, the technical and technological advances (exploiting revolutionary discoveries in physics) and the improved management and sharing of growing databases greatly contributed to the evolution of chemistry from an esoteric ground into a mature scientific discipline during these last 400 years. Furthermore, thanks to the evolution of computational resources, platforms and media in the last 40 years, theoretical chemistry has added to the puzzle the final missing tile in the process of “rationalizing” chemistry. The use of mathematical models of chemical properties, behaviors and reactivities is nowadays ubiquitous in literature. Theoretical chemistry has been successful in the difficult task of complementing and explaining synthetic results and providing rigorous insights when these are otherwise unattainable by experiment. The first part of this review walks the reader through a concise historical overview on the evolution of the “model” in chemistry. Salient milestones have been highlighted and briefly discussed. The second part focuses more on the general description of recent state-of-the-art computational techniques currently used worldwide by chemists to produce synergistic models between theory and experiment. Each section is complemented by key-examples taken from the literature that illustrate the application of the technique discussed therein.
1 Introduction
Since the days of Galileo Galilei, science has been approached using the scientific method. The routine of “curiosity sparking observation, formulation and testing of new hypotheses and birth of new theories” represents the first rudimentary iterative block-diagram algorithm to approach “scientifically” any natural phenomenon. Both the predictive and explanatory power of science, and so its evolution, reside in the use of models. Models are rescaled and simplified visions of reality that scientists create to afford an explanation and prediction of phenomena within certain levels of confidence. Leonhard Euler himself commented on the power of the model with his famous maxim: “Although to penetrate into the intimate mysteries of nature and thence to learn the true causes of phenomena is not allowed to us, nevertheless it can happen that a certain fictive hypothesis may suffice for explaining many phenomena”. Euler’s “fictive hypothesis” is an approximated, yet powerful tool to account for and, ultimately, influence or even control phenomena to the benefit of humanity. Nowadays, mathematical models are routinely employed to predict events in physics, engineering and natural sciences [1, 2].
What could be inferred about chemistry, then? Any dedicated scholar sooner or later stumbled upon the uncomfortable question: Can complex chemical reactions be predicted by rational models? Chemical sciences are intrinsically more bound to their empirical nature than other scientific disciplines, given the fact that the ultimate goal of chemistry is to make new molecules for market, technology, society or simply for scientific interest [3]. The construction of a priori models of complete reactions is currently regarded over-ambitious, given the extreme difficulty to characterize accurately Avogadro’s numbers of solvated molecules, predict their reactive events in such environment and simulate the course of n-parallel and competitive channels during a desired interval of time. While such search for rationality poses unparalleled challenges, it would also represent, if successful, the pinnacle of chemical manipulation and establish an evolved concept of understanding and doing chemistry. This evolution will lead to a new level of rational design of target compounds and transform chemistry into a discipline scientists can fully control, rather than merely observe and improve through trial-and-error strategy. The structure of the chapter has been organized in a way that the reader will receive a general, yet detailed, wide-angle history of chemistry, followed by a more specific treatment of theoretical disciplines. Each section will be integrated with interesting examples singled out from a massive multidisciplinary pool of excellent scientific works. The selection criteria were not only based on relevance, impact factor and citations of the works but also on the diversity of the field and author’s interests and familiarity with the works. The common trait d’union of these works is represented, however, by the synergistic interdisciplinary approach between theory, spectroscopy and experiment. The use of theoretical assets in solving chemical problems, whether a priori or a posteriori, serves as a proof of concept of rational chemistry. The author wishes to convey the idea that chemistry is a multifaceted scientific ground where experimental and theoretical approaches are far from being rivals; on the contrary, they imparted together an evolutionary rational momentum to the discipline.
This momentum allowed chemistry to blossom into a modern science during the last 400 years, from nothing more than a collection of esoteric notions. We could say that chemistry is a relatively young discipline since a scientific, systematic and non-serendipitous approach to this field has been introduced not earlier than the sixteenth century. Technological advances in synthetic methodologies, spectroscopy and data sharing allowed chemistry to reach unprecedented goals and successes. The development of computers carved an important role for theory into the full landscape of chemical disciplines. This chapter reviews the synergistic integration between practical and theoretical fields for the betterment of rational principle underlying chemistry. In line with the guiding philosophy of this project, there is not a preferred target audience for this chapter. The author simply hopes that it will be descriptive enough to interest theoreticians of any level and useful enough to show spectroscopists and experimentalists “what they can actually do” with theoretical methods, should they decide to use them as a viable first term of comparison in their researches.
2 The past: Birth of a discipline
In ancient Egypt the idea of a rational principle behind natural transformations was associated to the existence of Thoth, the god of wisdom, magic and writing. Back then, and for the rest of the ancient history, the use of simple chemical transformations was mostly relegated to common life activities, like metallurgy [4]. At the turn of the first millennium, the first sparkle of “scientific” approach made its entrance in history, with the work of the Persian mathematician and astronomer Ibn al-Haytham on light and optic [5]. Some decades later on, a new discipline grew strong in continental Europe, drenched in all the esoteric mysticism and symbolism that Medieval Age could spawn: alchemy [4]. The word from Greek-influenced Arabic language, al-kīmiyā, means the art of transmuting metals. Alchemic cult of the four natural elements (water, air, fire and earth) and the two philosophical elements (sulfur and mercury) rooted back to Hellenistic [4] and Arabic beliefs, like those of the Persian alchemist Jābir ibn Hayyān [6]. The alchemic period (Figure 1) lasted more or less until the Seventeen Century and was characterized by bizarre individuals like Paracelsus or N. Flamel, whose mysterious vaunted powers failed to achieve the envisioned goals, given the fact that neither the philosopher’s stone nor the elixir of eternal life has ever become solid realities. Alchemy incurred often in the wrath of the religious authorities, since it was regarded as a practice inspired by the Devil itself; ironically enough, it is exactly the art of combining substances that provided the Church with the most beautiful heritage for posterity, like the exceptional stained glasses we can still admire in Chartres cathedral.
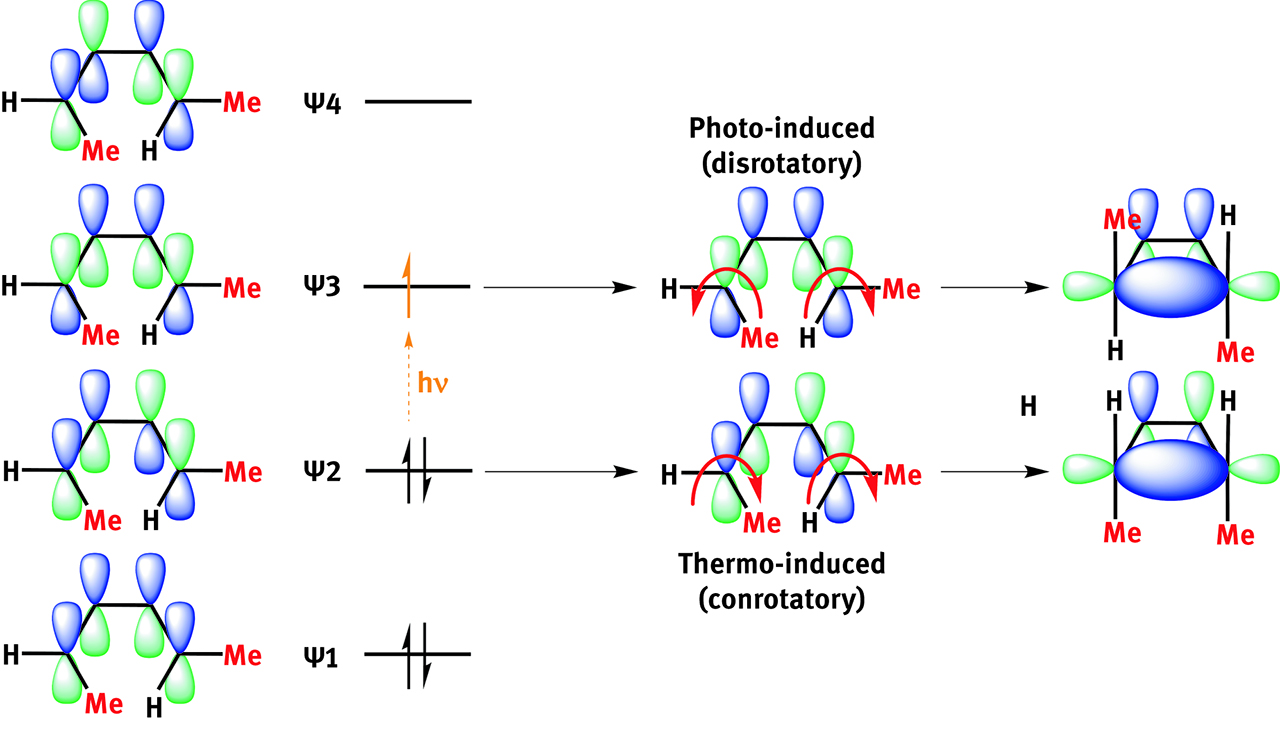
Electrocyclic reactions can be predicted through simple Huckel diagrams. (E,Z)-2,4-hexadiene can cyclize giving either cis- or trans-dimethylcyclobutene (on the right) depending on orbital control (and vice-versa for the ring-opening reaction).
Modern chemistry, as we intend it, was born in the late sixteenth century. The recognized fathers of modern chemistry are R. Boyle and A.L. Lavoisier [4]. They introduced a rational and scientific approach to chemistry that led them to an unprecedented understanding in the chemistry of gases, air and combustions and to the definitive destruction of the J.J. Becher’s phlogiston theory [4]. Lavoisier has been also credited for the first attempt in dissemination of chemistry by writing the first chemical book, Traité Elémentaire de Chimie (1789) [4]. As the years went by, J.L. Proust, J. Dalton and A. Avogadro postulated three famous laws that still carry their names and are taught to our freshmen within the first week of a general chemistry course: the law of constant composition, the law of partial pressures and Avogadro’s principle, respectively [4]. The interaction of electrical current with chemicals and solutions was pioneered by H. Davy, J.J. Berzelius and M. Faraday [4], who started the field of modern electrochemistry. The first statistical ordering of the properties of the elements by their atomic weight and valence was attempted independently by J.L. Meyer and D.I. Mendeleev through the construction of the first periodic tables. The power of such embryonic models was suddenly clear. A few elements and related properties could be predicted by Mendeleev in 1869–1871 (Table 1): for instance, Mendeleev’s eka-boron, eka-aluminium and eka-silicon were discovered in 1879, 1875 and 1886, respectively, and renamed scandium (1879), gallium (1875) and germanium (1886) [7]. It is finally with F. Wöhler and H. Kolbe that the word “chemical synthesis” starts to assume the meaning we ascribe to it today. Wöhler and Kolbe contributed to destroy vitalism demonstrating that organic molecules can be made from “anorganisch” compounds [8, 9]. The nineteenth century was a golden century for chemistry. F.A. Kekule’s studies on the structure of hydrocarbons and benzene opened the way for a systematic pursuit of organic chemistry. H.L. Le Chatelier, J.H. Van’T Hoff, W. Ostwald, J.W. Gibbs, S.A. Arrhenius and W. Nernst set the bases for the modern interpretation of thermodynamics, kinetics and electrochemical processes. L. Boltzmann recognized the strong connection between probability and thermodynamics and founded statistical thermodynamics.
Mendeleev’s early periodic table shows the power of prediction of a simple model.
| Chemical properties | Mendeleev’s prediction in 1871: Eka-silicon | Element properties: Germanium |
|---|---|---|
| Atomic weight | 72 | 72.61(2) |
| Density/g∙cm−3 | 5.5 | 5.323 |
| Molar volume/cm3∙mol−1 | 13.1 | 13.64 |
| MP/˚C | high | 945 |
| Specific heat/J∙g−1∙K−1 | 0.305 | 0.309 |
| Valence | 4 | 4 |
| Color | Dark grey | Greyish-white |
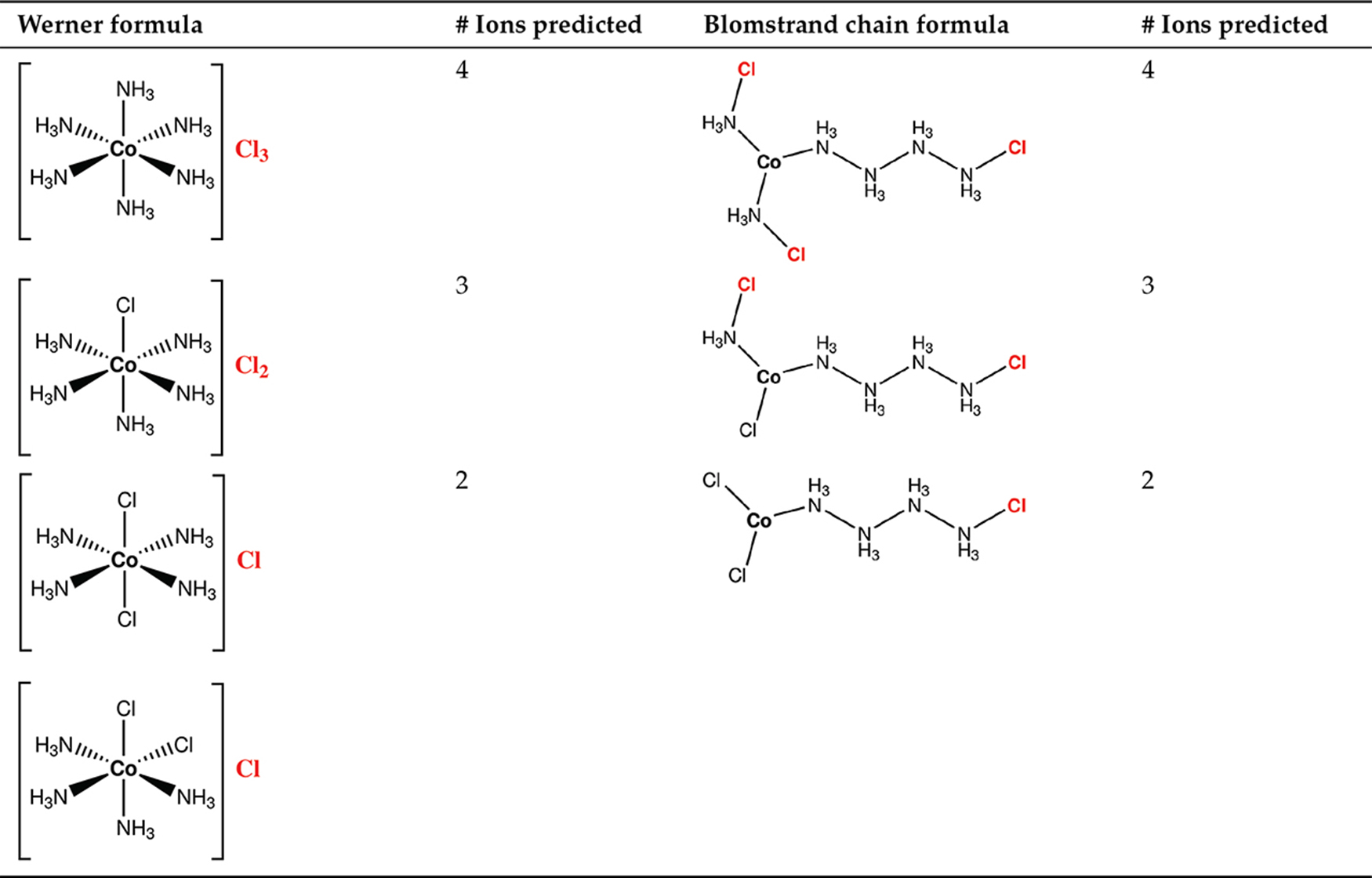
H.E.L. Fischer initiated the interest in biological chemistry with his studies on sugars, their reactivity and structural properties (i. e. stereochemistry); he also proposed the “lock and key” model to explain enzyme-substrate interactions. J.C. Maxwell formulated the classical theory of electromagnetism that holds together electricity, magnetism and light [5] and inspired the successive two greatest theories, relativity and quantum mechanics. At the end of nineteenth century and beginning of twentieth century new discoveries shed light on the structure of the atom. The fundamental particles that compose atoms were discovered by J.J. Thomson (electron in 1897), E. Rutherford (nucleus in 1911 and proton in 1919) [4], J. Chadwick (neutron, in 1932). In 1913, H.G.J. Moseley proved by x-ray spectra that Z, the number of protons in an element, defines its position in the periodic table [4]. Another meaningful example of simple models laid out to rationalize more complex phenomena is provided by Blomstrand-Jørgensen-Werner diatribe which arose in the late nineteenth century hoping to explain the peculiarity of the bond in metal-containing compounds. Some of these compounds, like Prussian blue, KFe[Fe(CN)6], and aureolin, K3[Co(NO2)6]0.6H2O, have been known since ancient times and used as pigments for their intense colors. The developing analytic techniques provided molecular formulas for these compounds; hence the need for a clear explanation about the nature of the bonding in these compounds, since they formally exceeded their valence or the concept of allowed valence developed until that point. Two models responded the call: Werner’s and Blomstrand-Jørgensen’s. A. Werner can be considered the father of modern coordination chemistry. His model consisted of metal centers able to expand their valence to bind extra “ligands”. In the case of the compounds that cobalt(III) trichloride forms with ammonia he hypothesized that the cobalt was in an octahedral environment surrounded by ammonia molecules (Table 2). According to different stoichiometries, the chloride ions could have been tightly bound (those primarily connected to the cobalt) or loosely bound (highlighted in red in Table 2). C.W. Blomstrand and later S.M. Jørgensen tried to explain the bonding mode of such cobalt compounds using a conventional model, the chain theory, more akin to the developing tetravalent carbon chemistry. They supposed that the loosely bound chlorides were those connected to NH3 moieties. Interestingly both models afforded the same answer in the rationalization of the ionic nature of some chloride ligands present in these complexes, as seen in Table 2. No evidence could put the final word to Werner-Jørgensen’s long-lasting rivalry until Blomstrand-Jørgensen’s model was finally disproved in 1907 when Werner synthesized two isomeric forms of [Co(NH3)4Cl2]+, one called (later on) cis, showing a violet color and one called trans, showing an intense green color. The chain theory was unable to explain this simple differentiation within the same molecular formula.
The first hypotheses on the structure of cobalt coordination compounds: Werner versus Blomstrand.
The twentieth century will be remembered as the century that saw the birth of quantum mechanics and relativity, two theories that challenged classical mechanics. N. Bohr [10], A. Sommerfeld, M. Planck and L. De Broglie fathered this early quantum theory. It rose to explain theoretically the position of line spectra in the Balmer series of hydrogen [4]. The first fundamental notion embedded in this new theory was that the energy state of any system is discreetly expressed in integer multiples of a constant, h (Planck’s constant). This managed to satisfactorily explain hitherto unexplained phenomena like black body radiation, the photoelectric effect and the Compton effect [11]. The second assumption was that particles have both matter and wave-like properties, having associated wave-lengths inversely proportional to their masses (λ ∝ m−1, de Broglie) [4]. The new quantum theory acquired the foundation of the early theory and expanded it with the new notion of wave-mechanics. E. Schrodinger formulated the famous eigenvalue equation that still bears his name and is at the foundation of modern quantum theory. Among several contributions, M. Born proposed the interpretation of the square of the wavefunction as the probability amplitude to find an electron in the r space and P. Erhenfest proposed his theorem on the behavior of expectations values for momentum and position operators. These theoretical insights brought about the famous three atomic quantum numbers (s, l, ml). A fourth quantum number, ms, was proposed by W. Pauli in 1924, after his famous formulation on the exclusion principle of two electron in the same quantum state [4]. The existence of the electronic spin was discovered by the Stern-Gerlach experiment in 1921 [4]. In 1927 W. Heisenberg formulated his uncertainty principle (λp∙λx ≥ ħ/2) on the impossibility to determine with absolute precision both momentum and position of a particle. These principles proposed by quantum mechanics struck a hard blow at the heart of the classical theories, whose principal aspect was the determinism of all the properties in a system. This was difficult to accept for many physicists. A. Einstein, for instance, regarded quantum mechanics as an “incomplete” theory in his famous Einstein-Podolsky-Rosen principle [12]. Supporting proofs of the consistency of the new theory, however, came with the discovery of particle tunneling through potential energy barriers and particle diffraction, typical aspects of wave-like behavior. The first phenomenon is known as radioactivity and deals with unstable nuclei expelling α-particles and internal β-electrons (both discovered by E. Rutherford in 1899, albeit the latter were erroneously believed to be rays). Radioactivity was discovered by the pioneering studies of H. Becquerel, W. Crookes, W. Rontgen, P. and M. Curie. The second phenomenon is electron diffraction, proved independently by G.P. Thomson and C.J. Davisson with L.H. Germer, which is the base of modern transmission electron microscopy (TEM) [13] and scanning electron microscopy (SEM) [14]. In the same years, P. Dirac, the founder of quantum electrodynamics, formulated his relativistic version of the Schrödinger equation [11, 15]. One of the final supporting proof on the non-locality nature of quantum entanglement, in violation of Bell inequality and EPR principle, came from experiments performed by R. Hanson’s group in 2015 [16].
All these discoveries sealed a definitive connection between physics and chemistry: the common ground allowed the development of a new theoretical body of investigation that will be treated at length in the next section. The Physics-chemistry partnership also lead to the development of new spectroscopic techniques that, in turn, provided structural insights as well as new chemical synthetic strategies, analysis and planning; nowadays, chemists can use powerful spectroscopic tools to characterize their products or test ongoing reactions in situ in a fast and efficient manner. Together with the improvement of laboratory technology and equipment, detection techniques like ionization mass spectrometry [17] and purification/separation techniques like high-performance liquid chromatography [18] or gas-chromatography [19] contributed to non-trivial betterments in the field of synthesis. In the Sixties, the process of rationalization of chemistry took a further step ahead with E. Corey’s retrosynthesis, a new way to look at and plan organic total syntheses [20]. Another fundamental improvement in the scientific community, often disregarded, came from the creation of the scientific literature, a platform for data-mining, dissemination and exchange of scientific peer-reviewed results. H. Oldenburg is the father of peer-reviewing mechanism and founding editor of the oldest and still active scientific journal The Philosophical Transactions of The Royal Society (1665) [21]. Thanks to the improvement of social media and the invention of cyberspace (i. e. Internet), scientific literature is a globally-accessible tool, essential for any starting and developing research project. Despite all this development, modern synthetic research still relies heavily upon serendipitous discoveries and empirical “trial-and-error” methodology to obtain target compounds. These combined approaches have brought chemistry to sensational discoveries throughout the years, but also contributed to generate chemical waste like volatile organic compounds (VOCs) [22, 23]. In the Nineties, Green Chemistry concept was proposed mainly in reply to the US Pollution Prevention Act and was codified into twelve rules by P. Anastas and J. Warnet [24]. Green chemistry provides a list of strategies to mitigate the environmental impact of large preparations and manufactures. In two centuries, von Liebig’s bulky glassware has been more and more replaced by fine glassworks, microreactors, pumps and robotics; new ways of doing chemistry have been developed, like flow chemistry [25] and combinatorial chemistry [26].
The ninth statement of Green Chemistry suggests that catalytic, rather than stoichiometric, protocols should be implemented [24], igniting the spark of an unprecedented “catalyst” rush; ever since, more and more efficient catalysts have been designed experimentally and trial-and-errored to assess their activity or lack of it. Nature exerts the same trial-and-error strategy in designing biologically active molecules to achieve efficiency, improved selectivity and durability. This endless process is called evolution and, unlike our methodologies so far, it is always economic and clean. The fourth statement suggests that chemicals should be designed to improve their desired function, while minimizing toxicity [24]. This is precisely where theoretical disciplines supported by computational methods make their grand entrance.
3 The present: Rise of a rational discipline
Early models based on the newly discovered atomic theories have been effectively used to solve experimental issues during the last century. Few very famous examples include:
Lewis Structures proposed by G.N. Lewis [27] to rationalize the nature of the chemical bond.
Valence Shell Electron Pair Repulsion (VSEPR) theory by R.J. Gillespie and R. Nyholm [28] to rationalize the nature of chemical bond and the shape of molecules.
Crystal Field Theory (CFT) proposed by H. Bethe and J.H. Van Vleck [32] to rationalize the bond in complexes between metal ions and simple ligands. The interactions were treated as simple fields of electrostatic repulsions between the ligands and the d orbitals of the metal pointing in the same direction (Figure 2). Crystal field theory and Racah parameters [33] gave birth to Tanabe-Sugano diagrams [34, 35, 36], powerful tools to explain and predict spectroscopic and magnetic properties of coordination complexes.
Molecular Orbital Theory (MO), also called Hund-Mulliken theory, originally proposed by F. Hund, R. Mulliken, J.C. Slater and J. Lennard-Jones [37] in the late Twenties to rationalize the nature of the chemical bond (localized and delocalized), in light of the new quantomechanical findings. It successfully predicted in 1929 the paramagnetism of molecular O2 in its ground state [37]. Mulliken predicted the existence of two excited states, above the ground state, 3Σg−[38]. 1Δg is commonly referred as singlet oxygen and it is 94.7 kJ/mol higher in energy than 3Σg−, while 1Σg+ is 157.8 kJ/mol higher than 3Σg-[39]. Molecular orbitals are expanded as linear combination of atomic orbitals (LCAO) to generate bonding, non-bonding and anti-bonding orbitals (Figure 3).
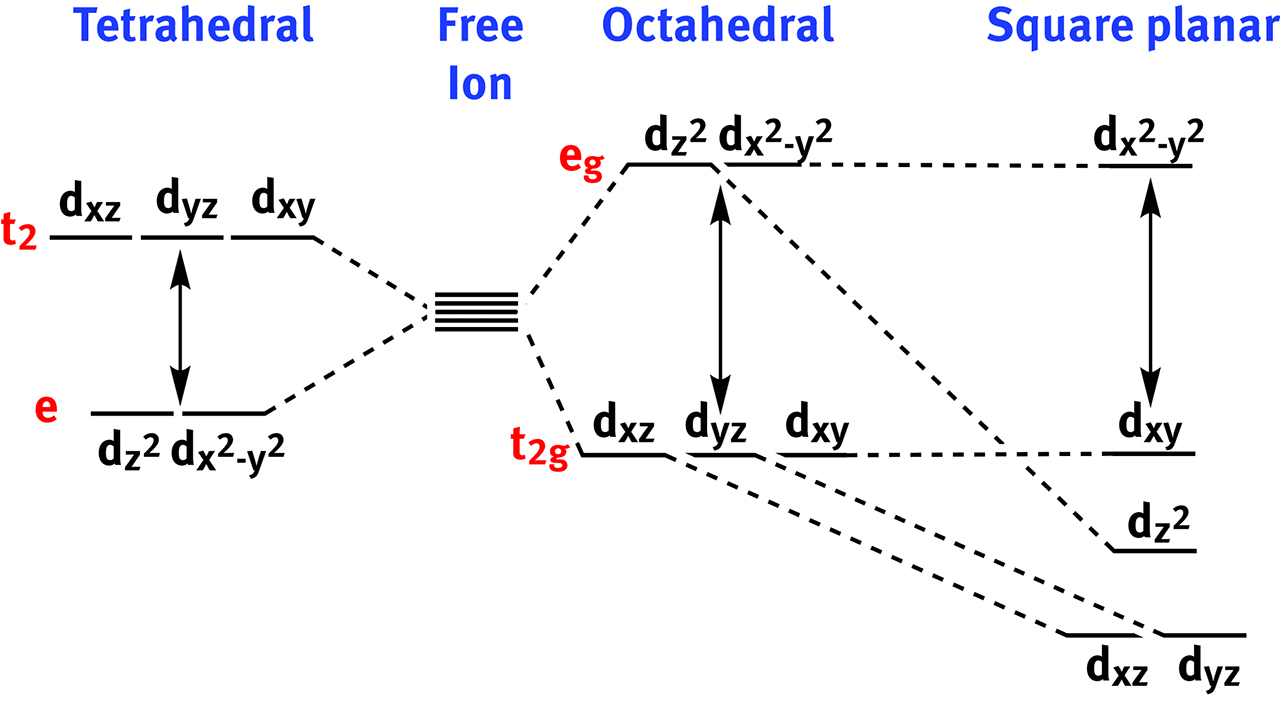
The destabilization of the orbitals of the metal, hence the crystal field splitting energy, depends upon the geometric arrangements of the ligands around it. The main classes of crystal fields are represented in this figure.

Molecular orbital sketch of O2. The simplest prediction extrapolated from it is that the triplet state is the most stable since it fully complies with Hund maximum multiplicity rule.
Though some of these models are still invoked by experimentalists to justify phenomena, chemistry has evolved and so did the challenges, goals and problems connected to it. Luckily, advanced quantum mechanics coupled to increased computational power (Figure 2), made possible by the development of hardware (e. g., J. Bardeen’s transistors in 1940–1950) and software (e. g., Gaussian 70 in the Seventies), triggered the construction of more powerful and descriptive in silico models in this last two decades. The next section covers the state-of-the-art in modern theoretical computation.
3.1 Electronic structure
Hartree–Fock (HF) theory uses a single Slater determinant in its wavefunction definition to comply with the anti-symmetric nature of electron spin. Initial trial molecular spinorbitals are expressed as linear combinations of atomic orbitals and optimized through the Fock operator (Roothaan-Hall equations) and an iterative process known as self-consistent field [43]. The limit of HF resides in its inexistent treatment of electron correlation. Atomic orbitals can be constructed using Slater functions (STO),
The early alternative to HF-based methods for large systems was represented by semi-empirical methods: they feature minimal quantum-mechanical treatment of the atomic valences through small basis sets, combined with zero differential overlap (ZDO) approximation [15] and parameterization with terms derived from experimental reference data [15]. Today neglect of diatomic differential overlap (NDDO) methods like PM7 [46] are excellent and inexpensive way to obtain semi-quantitative information on a system, particularly useful when conformational analysis is required. The second alternative is represented by density functional theory (DFT) methods. DFT theory has its roots in the work of W. Kohn, P. Hohenberg and L.J. Sham [47, 48]. Kohn–Hohenberg theorems bind the ground state electron-density of a molecular system,
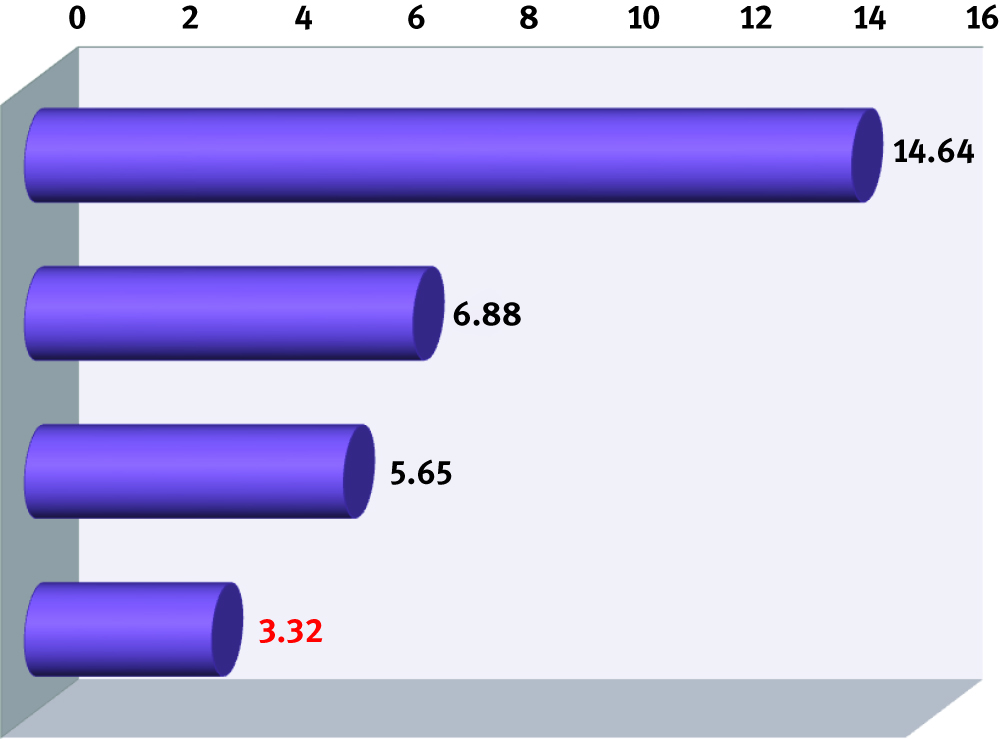
Average of mean unsigned errors (in kcal/mol) for all DFT functionals tested in Truhlar’s database CE345 and grouped according to their year of publication. This database includes 15 subgroups of different chemical properties.
Summary of DFT methods, definitions, dependencies and place on the Jacob’s ladder. PT2 stands for perturbational theory truncated at the 2nd term.
| Functionals combination | Type (# rung in Jacob’s ladder) | Dependencies |
|---|---|---|
| SVWN, PZ81, CP, PW92 | LDA (#1) | ρ(r) |
| BLYP, BP86, PBE, B97D | GGA (#2) | ρ(r), |∇ρ(r)| |
| t-HCTH, TPSS, VS98, VSXC, M06L | Meta-GGA (#3) | ρ(r), |∇ρ(r)|,∇2ρ(r) (τ) |
| B3LYP, B3PW91, B3P86, PBE0, mPW1PW91, BMK | Hybrid GGA (#4) | ρ(r), |∇ρ(r)|, %HF exchange |
| B1B95, BB1K, MPW1B95, MPW1KCIS, PBE1KCIS, TPSS1KCIS, TPSSh, M06, M06-2X, M11, MN12-SX | Hybrid Meta-GGA (#4) | ρ(r), |∇ρ(r)|, ∇2ρ(r) (τ), %HF exchange |
| MC3BB, MC3MPW, B2PLYP, B2KPLYP, B2TPLYP, mPW2PLYP, XYG3 | Double hybrid (#5?) | ρ(r), |∇ρ(r)|, %HF exchange, PT2 corrections to the correlation functional |
Heavy metals of the third row, especially Au [70], display electrons moving at nearly-relativistic speeds due to a high Z number. The moving mass of these fermions undergoes relativistic increment given by the equation
Effective core potential, ECP, like LAN [72], SDD [73, 74] and CEP [75]. Basis functions are replaced by potential functions at the core and the extent of the replacement defines large-core (frozen core and valence), medium-core or small-core (frozen core + valence treated by basis set) pseudopotentials. Accurate results are more likely to be obtained using small-core ECPs [76]. The basis sets complementing medium and small-core ECPs are designed to fit the pseudopotential used, generally through appropriate primitive contractions [77].
Relativistic Hamiltonians coupled with full-electron basis sets. Relativity can be brought into the Schrodinger equation through the Dirac equation. Douglas–Kroll–Hess (DKH) transformation is commonly used for its accuracy, efficiency and effectiveness [78]. Appropriate basis sets are built by contracting primitives [77].
The goal of electronic structure calculations is to generate potential energy hypersurfaces, alias “mapped” polydimensional surfaces that correlate the potential energy in function of the nuclear coordinates of the atoms. Wells or minima on these surfaces represent stable structures. Calculated metric parameters for these minima provide useful information to synthetic chemists because they can be compared with metric parameters derived from phase scattering of x-ray or neutron single-crystal diffraction experiments [79]. Vice versa, this is also an approach used by theoreticians to validate bona fide the goodness of their calculations. This approach is, however, a risky procedure and must be done carefully for two reasons: the maxima in scattering amplitudes may not coincide with nuclear positions in light atoms and structures in solid state are affected by crystal packing and dielectric fields, not present in the isolated calculated counterparts [80].
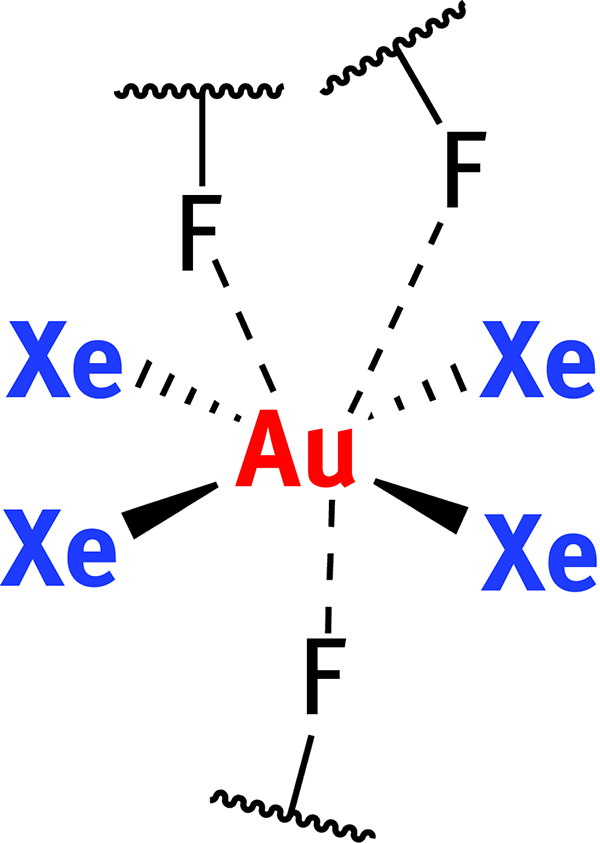
Seidel-Seppelt unique compound. Au•••F contacts with the counterions are shown.
Electronic structures predicted the existence of “impossible” compounds like AuXe+ and XeAuXe+ in 1995 [81]. The calculations were carried out by P. Pyykkö et al. using methods like MP2, MP4 and CCSD(T): the bond distance Au-Xe calculated at MP2 level was found to be 2.691 Å for AuXe+ and 2.66 Å for XeAuXe+. The stability of these compounds was attributed to the high electronegativity of gold, due to relativistic effects; the bond dissociation energy for AuXe+ decreases from 0.910 to 0.376 eV when relativistic effects are omitted at CCSD(T) level [81]. The existence of AuXe and XeAuXe+ was confirmed experimentally in 1998 by Schröder, Pyykkö et al. [82]. Finally, Seidel and Seppelt isolated the first stable gold compound with xenon, [AuXe4][Sb2F11]2 (Figure 5), in 2000[83]. The compound confirmed the stability postulated for this class of compounds being stable up to 40˚C. Metric parameters for Au-Xe bond distance, 2.728(1)-2.750(1) Å, extracted from X-ray diffraction agrees well with distances calculated at MP2 level, 2.787 Å [83]. Electronic structures and enthalpy of formation predicted also the existence of another “impossible” compound in the solid state, Na2He. The predicting algorithm in the USPEX code [84] suggested the existence of a cubic-phase structure of Na2He, stable at pressures above 160 GPa. The structure was effectively isolated as a cubic-phase, stable from 113GPa up to 1000 GPa, and characterized in matrix by A.R. Oganov et al. [85]. The electronic structure of the solid was studied by density of states, ELF and Bader’s analysis [85].
Electronic structures can be directly linked to magnetic spectroscopies based on the Zeeman effect [86]. In nuclear magnetic resonance (NMR)[87] and electronic paramagnetic resonance (EPR)[88], low frequencies waves (radiofrequencies for NMR and microwaves for EPR) are pulsed to make net nuclear (NMR) or electronic (EPR) spin magnetization process about an axis in a magnetic splitting field B0[89]. This precession is sensitive upon the chemical environment of each nuclear or electronic spin. NMR spectra (shift and spin-spin coupling) can be efficiently simulated in gas or in solvent phase by calculating 1D-NMR shielding tensor and susceptibilities using Gauge-Independent Atomic Orbital (GIAO) [90, 91, 92] or Continuous Set Of Gauge Transformations (CSGT)[92, 93, 94] methods. Accurate results versus experiment can be achieved by using high level of theory, usually DFT or MP2[92, 95, 96], in conjunction with large, polarized and diffused basis sets. Similarly, hyperfine coupling constants for EPR spectra can be calculated using EPR-II and EPR-III basis sets [97]. GIAO calculations using a pure GGA functional, BP86 (implemented in G03[98]), in conjunction with SBK basis [99] for metals and 6–311++G(d,p) for carbons and hydrogens have been employed by H.V.R. Dias and T.R. Cundari et al. to provide a comparison to experimental 1H and 13C{1H} NMR spectra in exceedingly rare adducts of ethane with coinage metals [100, 101], Table 4. A further model [102] was generated using a hybrid GGA, B3PW91, in conjunction with SDD pseudopotential and K.A. Peterson’s correlation consistent basis sets [77]. Theoretical values shown in Table 4 for both models along the homoleptic series [M(η2-C2H4)3][SbF6] (for M = Cu, Ag, Au) show amazing structural and spectroscopic reproduction of the studied species. Similar computational studies were carried out to explain the NMR and bonding patterns of a peculiar complexation between trans,trans,trans-1,5,9-cyclododecatriene, CuSbF6 and carbon monoxide [102, 103].
Theoretical computation can be used to validate experimental results, as in the case of reactive coinage wheels. Reference temperature for NMR data is 298 K.
| Compound | Data | 1H NMR, δ | 13C{1H} NMR, δ | M-C, C=C bond distances (Å) |
|---|---|---|---|---|
| [Cu(η2-C2H4)3][SbF6] | Exp. | 5.44 (CD2Cl2) | 109.6 (CD2Cl2) | 2.193(6),1.359(8) average |
| Comp. | 5.2 (gas) | 100.0 (gas) | 2.172, 1.374 (D3h) | |
| [Ag(η2-C2H4)3][SbF6] | Exp. | 5.83 (CD2Cl2) | 116.9 (CD2Cl2) | 2.410(9), 1.323(14) average |
| Comp. | 5.6 (gas) | 110.9 (gas) | 2.408, 1.367 (D3h) | |
| [Au(η2-C2H4)3][SbF6] | Exp. | 4.94 (CD2Cl2) | 92.7 (CD2Cl2) | 2.268(5), 1.364(7) average |
| Comp. | 5.0 (gas) | 92.6 (gas) | 2.308, 1.388 (D3h) |
Electronic structures can clarify the dynamic behavior of molecules whose potential energy surfaces change upon the absorption of photons of visible or ultra-violet light. Organic chromophores fall under this category, since light can cause transitions from bonding to antibonding orbitals [104]. Heavy metal complexes show also spin-allowed, Laporte-allowed transitions, ligand-to-metal (LMCT) and metal-to-ligand (MLCT) charge transfers [32]. The transition momentum from ψ1 to ψ2 eigenstate, M2,1 = <ψ2|μ|ψ1>, can be calculated for vertical excitations (complying with Born-Oppenheimer approximation) to provide transition energies, multiplicities, symmetry and oscillator strengths, thus simulate UV-Vis and circular dichroism spectra. UV-Vis spectroscopy [89] is used by experimental chemists to identify and quantify an active substance through absorbance and Beer-Lambert law; the description of this approach and its limits are well known [105]. Time dependent density functional theory (TDDFT) coupled with medium-to-large basis sets generally provides reasonably accurate results (i. e., within 0.4 eV from experimental transitions) at a very affordable cost, but it has limitations like the absence of double excitations [106]. Most used DFT functionals are B3LYP and PBE0, although the popularity of functional including long-range corrections to the Coulomb term (e. g., cam-B3LYP, LC-ωPBE and ωB97XD) is rising. More refined and resource-consuming alternatives to TDDFT feature CASSCF and CASPT2, techniques based on the complete active orbital space (including PT2 corrections in the latter) [107]. Modeling excited states encompasses the study of the reorganization energy of the molecule and the solvation layer after the absorption of light; bathochromic shifts can be obtained this way to simulate experimental fluorescence spectra. Study of intersystem crossing phenomena (i. e., conical intersections between different spin potential surfaces) can be valuable to study phosphorescence [108]. Intersystem crossings are more common for heavy metal complexes with strong spin-orbit coupling. Diffuse functions and long-range corrected functionals might be mandatory when studying excited states of higher energy (i. e. other than the first one). Photo-induced single transfer redox reactions via outer sphere mechanism involve bimolecular events between oxidants (electron acceptor) and reducing species (electron donor); Marcus theory was designed to calculate the barrier of activation in terms of free energy difference for such processes, ΔG‡ = (ΔG+λ)2/4λ (λ is the reorganization energy of all the atoms involved in the reaction)[109, 110]. The thermodynamic function that expresses quantitatively the propensity for the transfer of electron(s) is the standard reduction potential; it can be measured experimentally by cyclic voltammetry and calculated using a variety of methods involving implicit, explicit or mixed solvation schemes [111]. Mean unsigned errors of computed values versus experimental ones are reported in the range of 64 mV (~ 6 kJ·mol−1) and as low as 50 mV for selected classes of compounds [111]. Electrochemical methodologies are fundamental in processes like artificial photosynthesis and water splitting [112, 113].
3.2 Solvation schemes
The solvent influences kinetic and thermodynamic aspects of a chemical reaction, thus the accurate evaluation of solvation effects should be brought into the calculations. Several different solvation schemes are available: implicit, explicit or mixed implicit-explicit. Implicit methods allow for quanto-mechanical treatment of the solute and for bulk treatment of solvents as continuous envelopes around solutes, characterized by macroscopic properties like dielectric constants and microscopic properties like solvent radii. Usually computationally very affordable for spectator solvents and reasonably accurate, implicit solvation models are listed below:
Explicit methods allow for quantum mechanical treatment of the solute and treat solvents as discrete entities around the solute. They are strongly suggested when interactions between solvent and solute need to be characterized, as in the case of strong hydrogen bonds or coordination to heavy metals, but demanding in terms of resources. The nuclear motion of the solute can be simulated using molecular dynamics or multi-scale models [111]. Mixed methods are probably the best chemical option, although they should be chosen and set-up wisely to provide accurate results at affordable costs.
3.3 Ensemble properties
Physical observables represent macroscopic bulk properties of a chemical sample. Simulating those properties at microscopic level requires the average of all the possible states of a chosen ensemble. The taxonomy of statistical thermodynamics encompasses some notable ensembles for N-particle systems: microcanonical or NVE (constant N, volume and energy), canonical or NVT (constant N, volume and temperature), grand canonical or μVT (constant chemical potential, volume and temperature), isoenthalpic-isobaric or NPH (constant number of particles, pressure and enthalpy), isothermal-isobaric or NPT (constant N, pressure and temperature of the system). Calculating all the possible states within an ensemble is impossible, thus few clever simplifications are normally introduced, in order to combine accuracy with computational feasibility. Dynamics methods listed below are excellent examples of methods working on ensemble properties of many-particle systems. Molecular Dynamics, Langevin Dynamics and Quantum Dynamics are particularly suitable for heterogeneous systems, since they are composed of different phases, thus tend to be more affected than homogeneous systems by the multi-scale complexity of the system: the kinetics of diffusion-controlled reaction, for instance, is controlled by particle transport phenomena like diffusion, convection, migration, adsorption and desorption. Chemical reaction happening at the surface of metals, alloys or minerals are many and diverse. The knowledge of the principles ruling transformations in heterogeneous catalysis will allow one to “tailor” a catalyst to carry out the target transformation sought [124]. Figure 6 relates schematically the dimensionality of chemico-physical phenomena to the length/time scale of computational methods [125]
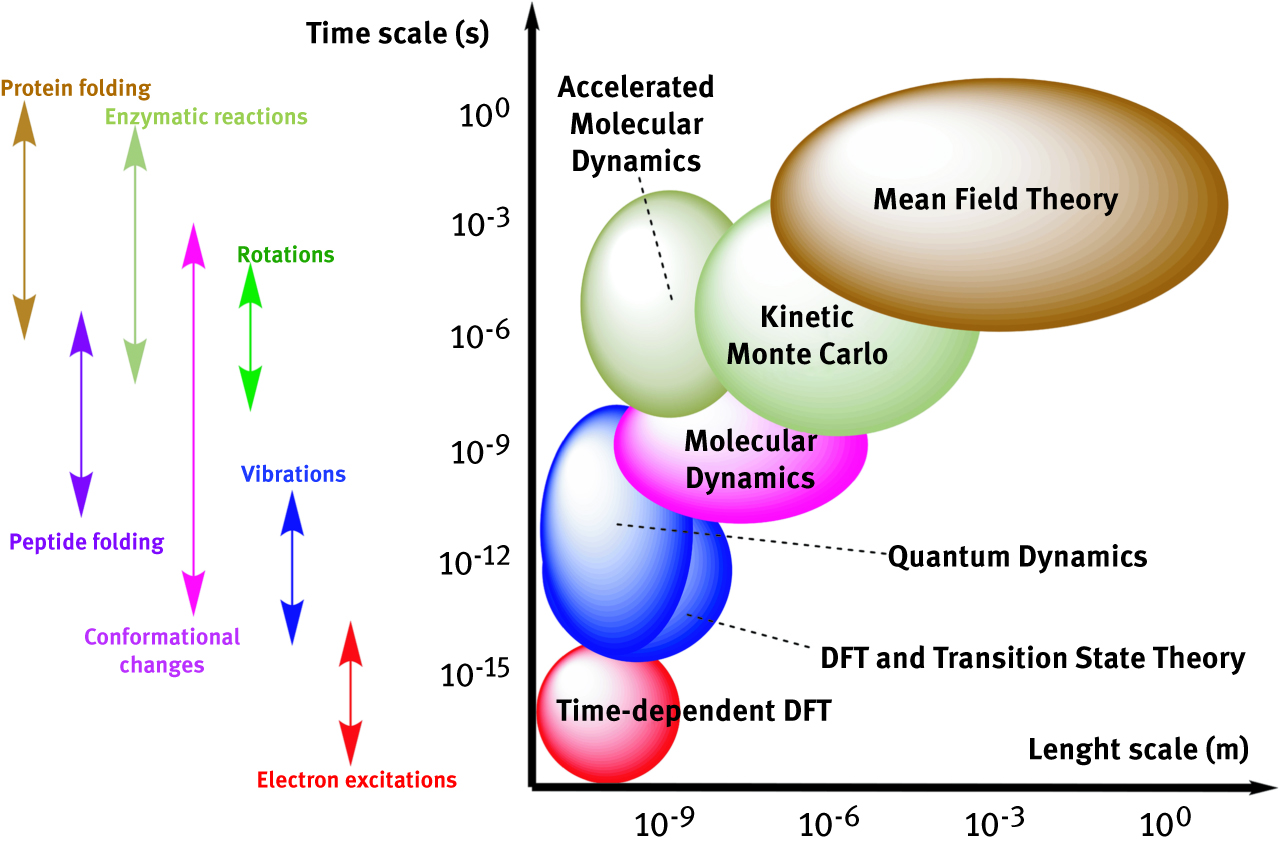
Multi-scale computational methods most frequently used associated to time-scales of chemico-physical phenomena.
3.3.1 Statistical thermodynamics
The calculation of the Hessian matrix (second derivative of energy with respect to atomic coordinates) leads to the recovery of force constants, that can be used to the simulate infrared (IR) spectra [89] and intensities; Raman spectra [89] can be obtained this way when Raman intensities are calculated for differentiation of dipole terms with respect to an external electric field (E). Clearly, obtaining first derivatives is less time-consuming than calculating superior orders in the expansion. MP2 and some DFT methods (e. g., GGA like BP86, B97D) in combination with medium-to-large basis sets usually simulate vibrational spectra with a maximum average error of 10–50 cm−1 versus spectroscopic experiment, while techniques like CCSD(T) can deliver much better results [49]. Simulations can also include the solvation effect through the methods seen before. These simulations might help synthetic chemists to explain the structure of unknown compounds through selection rules and fingerprint matching and assign calculated atomic motions to experimental fundamental or overtone bands of known compounds. In addition, vibrational analysis of harmonic modes and statistical thermodynamics afford a straightforward and convenient link from single-molecule electronic structure and potential energy to molar thermodynamic properties (zero-point energy (ZPE), thermal energy (E), enthalpy (H), entropy (S) and Gibbs free energy (G)) through partition functions [15]. Since most methods to calculate electronic structures feature analytic second derivatives, this is also a computationally advantageous approach [45]. Partition functions are generated in the framework of the ideal gas approximation as functions of the temperature (T) and volume (V) for the translational partition function. q(V,T) = qele(T)·qtra(V,T)·qrot(T)·qvib(T). In solvent phase rotations are substituted with liberation contributions and translations with liberational contributions [111]. Quantum harmonic oscillator [89] is an approximation that holds in most of the cases. When an accurate thermochemistry is expected, however, anharmonic corrections to zero-point energy (ZPE) and roto-vibrational coupling [89] are strongly recommended, since the Morse potential curve deviates sensibly from the harmonic curve at higher internuclear distances, near bond-breaking region [89]. Also, floppy molecules that have low-barrier torsions (hindered rotors) and vanishing-barrier vibrations (free rotors) show a dynamic behavior that falls far from HO approximation. Thus, without correction, large errors would be brought into the entropic partition function (consequently, into Gibbs free energies). Few different correction schemes for low frequency vibrations are available in the literature such as the Pitzer-Gwinn [126], Truhlar [127], McClurg [128] and quasi-harmonic approximations [129, 130, 131].
3.3.2 Mean field theory
Mean field theory is an important branch of condensed matter physics. “Mean field” definition applies to all those theories where the study of a multi-body network of interactions is reduced to an average interaction acting upon the individual under study [44]. In all but the simplest situations (like the Ising model [132]), the mean field simplification is very convenient. Without it, for instance, the calculation of the configuration integral ZN, thus the estimation of the potential energy term U(r) between particles, would become cumbersome in the study of dense fluids [44]. Mean field theory has been originally applied to fluid model (Van der Waals equation)[44], phase transitions, phase transition and ferromagnetism [133], alloys and superconductivity [134, 135]. Similar theoretical treatments were developed for game [136] and queueing theories [137].
3.3.3 Molecular dynamics
Molecular dynamics is a very popular and largely used technique among researchers in many fields. A many-particle system is left evolved in time through phase-space trajectories that respond to classical laws of motion (Newton):
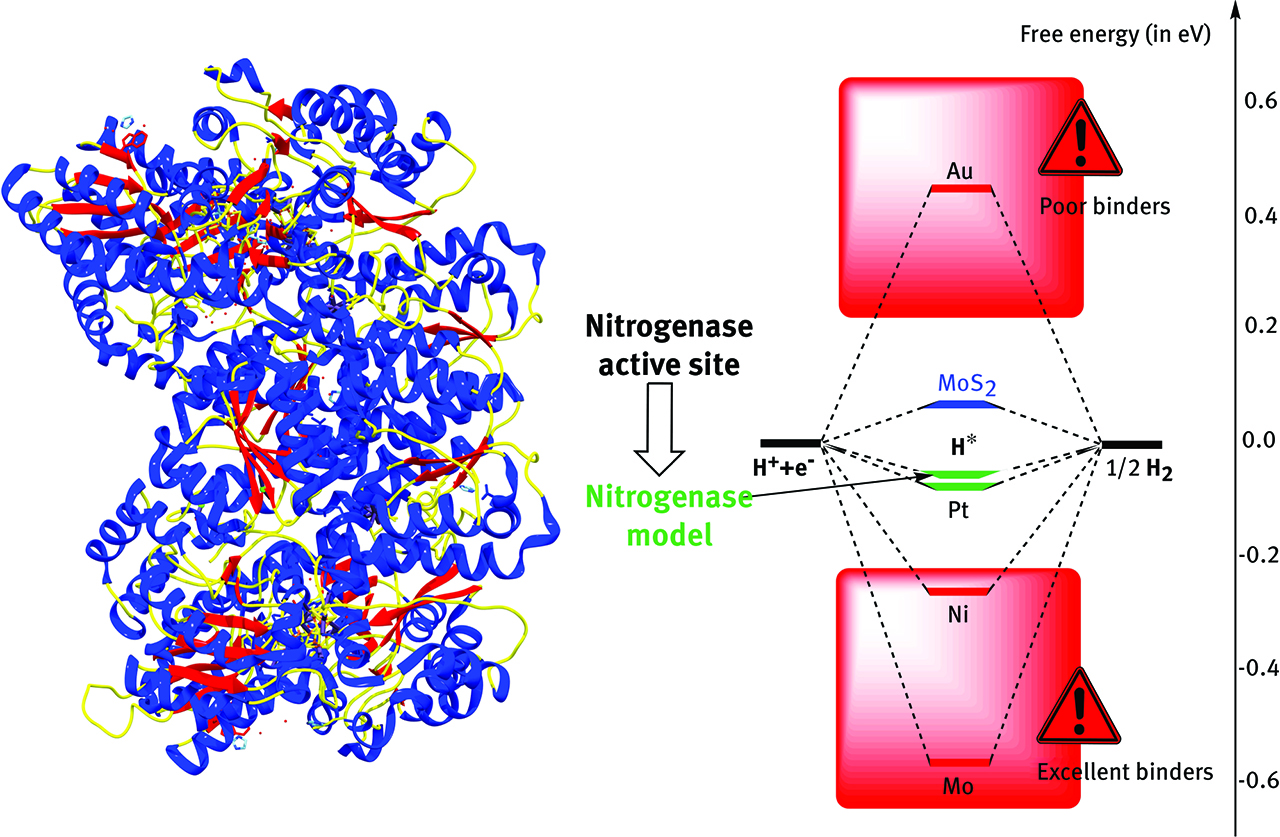
Learning from Nature. Mimicking the active site of enzymes like nitrogenase FeMo cofactor (left) leads to rational design of surfaces evolving H2, like nanosized MoS2.
Molecular dynamics, coupled with other techniques like umbrella sampling, conformational flooding, metadynamics, and adaptive force bias, plays a pivotal role in drug discovery as well [148]. Drug discovery deals with the energetics, affinity and selectivity of binding/unbinding events between naturally occurring biological receptors and synthetic inhibitors [148]. These events, however, span microseconds to milliseconds, while ab initio molecular dynamics can effectively sample a few femtoseconds at best [149]. G. de Fabritiis et al. published a paper [150] on the quantitative reconstruction of the binding process between β-trypsin and benzamidine using a Markov state model (MSM) [151]. High-throughput classical molecular dynamics parallelized on clusters of graphical processor units (GPUs) [152] allowed 495 simulations of this binding event of 100 ns each. 187 simulations gave productive bindings with root-mean-square deviation of atomic positions within 2Å compared to the crystal structure [153], Figure 8 left. The estimation of the standard free energy of binding is within 1 kcal/mol from the experimental value [150]. Similar routines are employed to screen and/or improve allosteric drugs (drugs that does not bind the orthosteric pocket of the receptor) and numerous methods to predict allosteric sites and their druggability are described and reviewed in literature [154].
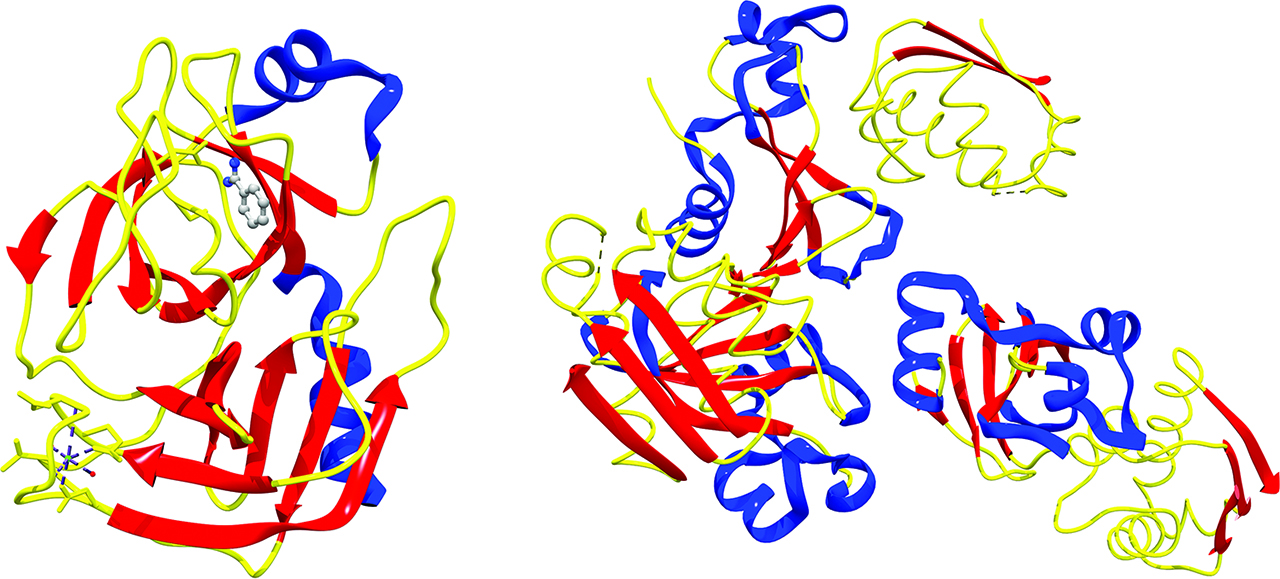
Left, X-ray crystal structure of the Ca2+-enzyme-inhibitor complex between benzamidine and serine protease β-trypsin (PDB ID: 3PTB). Right, X-ray crystal structure of the complex barnase-barstar (PDB ID: 1BRS).
3.3.4 Brownian and Langevin dynamics
Brownian dynamics (BD) is another method used to sample the binding/unbinding pathway of associative events [155, 156, 157]. The motion of molecules of interest is assumed to be Brownian [158, 159, 160], while the solvent is treated stochastically. BD is less time consuming than MD, though its accuracy in reproducing observables strongly depends upon the use of supportive models [161]. An interesting study using BD on the formation of complex barnase-barstar (a ribonuclease and its inhibitor) has been published by A. Spaar et al. in 2006[162]. The complex barnase-barstar is a well-known case for quantitative studies of protein–protein interactions (wild-type and mutant alike). The computational study focused on the characterization of the electrostatic binding region from diffusional regime to enzyme-inhibitor encounter region. The encounter region was modeled after the X-ray crystal structure [163], Figure 8 right. Two regions of preferential binding were authenticated and it was demonstrated that enzymatic mutations alter significantly the populations around these two minima [162]. A particular case of BD is represented by Langevin dynamics. LD complements molecular dynamics calculations with a stochastic treatment of solvent lighter particles perturbing solute heavier particles by the means of averaged frictional forces and collisions [139]. The equation of motion can be written in this case as:
3.3.5 Monte Carlo methods
These methods own their exotic name to the city of Monte Carlo in Monaco, renowned place where stochastic bets play a huge role in the casinos. MC simulations rely on the simulation of a system based on random or quasi-random numbers and can be divided into three main types: direct Monte Carlo, Monte Carlo integration and Metropolis Monte Carlo [139]. Direct MC uses random numbers to simulate events. MC integration calculates integrals on random numbers. Metropolis MC is based on building statistically- dependent configurations through Markov chains. The probability of each new configuration is built upon the probability of the previous configuration. Markov chains are normally ergodic: the conditions of irreducibility (every configuration can be accessed from any other configuration within a finite number of steps) and non-periodicity the same configuration does not repeat except after a fixed number of steps) are satisfied [139]. The functions p(X,t) that correlate the probability of occurrence of a certain configuration (X) at time t are called master equations [139]. MC simulations are usually carried out in NVT ensembles, but Metropolis MC can be used in NPT [165] or μVT [166] ensembles as well. MC methods are mostly used to calculate static properties of a system under study. Monte Carlo methods including quantomechanical treatments are called variational Monte Carlo, diffusion Monte Carlo, path-integral Monte Carlo [139]. Another interesting example is represented by Schaupen and Lewis’s work on molecular imprinted polymers (MIPs). MIPs are artificial polymeric receptors (“plastic antibodies”) synthesized using monomeric units assembled via cross-linkers and template effect [167]. They have antimicrobial, antiviral and anticancer applications [167]. Schaupen and Lewis employed the software ZEBEDDE (zeolites by evolutionary de novo design) to simulate an evolutionary growth of a MIP around selected templating molecules [168]. Nicotine and theophylline were chosen as templating agents. Random combinations of monomers/cross-linkers were allowed to grow around the templates only if their interactions with them were favorable (Figure 6). The results of these growths were optimized using molecular dynamics. Canonical Monte Carlo simulations were performed with the Sorption software included in Materials Studio and used to characterize various grown imprints and their bindings specificity [168]. The calculations showed that the imprints built this way show a remarkable preference to bind theophylline over similar substrates.
3.4 Transition state theory
H. Eyring, M.G. Evans and M. Polanyi proposed this theory in 1933 [169]. Transition structures are mathematical constructs of dynamical instability, dividing surfaces between short-time intrastate (within basin) from long-time interstate dynamics (basin to basin). They possess 3N-7 vibrational degrees of freedom, where the missing degree represents the reaction coordinate. Thus, transition states (TS) are not real structures and many scientists refers to TS-derived thermodynamics as talking of transition state-derived thermodynamics as quasi-thermodynamics [170]. Fundamental requirement of TST is that reactants (or products) and connected transition structures are thermally equilibrated [170]. Several minimization algorithms are available to locate transition structures: steepest descent, Newton-Raphson, rational function optimization, direct inversion of iterative space (GDIIS and GEDIIS) and synchronous transit-guided quasi-Newton (STQN) [171]. The immediate purpose of Eyring-Polanyi equation is to calculate (or estimate at the very least) rate constants for chemical reactive events. Conventional Transition State Theory (CTST) usually provides an upper-bound estimate of experimental reaction rate constants [170, 172]. Within this approach, the transition surface is placed at the saddle point and 100 % crossing-over efficiency is assumed between reactants and products. The variational optimization of the dividing surface in order to minimize re-crossing leads to the Variational Transition State Theory (VTST) [170, 173, 174, 175, 176]. VTST and its variants usually produce much better agreement with experimental kinetics than CTST [172]. The program POLYRATE [177] implements several variational approaches (e. g., Canonical VTST, Improved Canonical VTST, Microcanonical VTST), as well as several quantum tunneling corrections for light atoms. As a consequence of the dual particle-wave nature of matter, light particles like electrons or protons can “tunnel” through potential energy barriers [178, 179]. De-Broglie equation predicts a wavelength of ~27 Å associated to an electron and a ~0.6 Å wavelength associated to a proton moving with kinetic energy of 20 kJ/mol. Experimental signs of tunneling effect usually entail strong H/D isotopic effect, non-linear behaviors of the Arrhenius equation and temperature independence of the reaction rate. Examples of electron tunneling can be found in semiconductivity, superconductivity, scanning microscopy and biological phenomena related to charge transfer [180]. The first experimental proof of tunneling in a chemical reaction came from F. Williams’s work [181]. There are many experimental evidences claiming tunneling effects of light atoms like protons in elimination reactions [182]. Heavier atoms like carbon or nitrogen or systems with small reduced masses can experience tunneling effect as well, in reactions like conformational changes [183], isomerizations [184] and ring expansions [185]. The computation of tunneling effects is generally accomplished with accurate multidimensional derivations of WKB method [186], like the small-curvature (SCT), the large-curvature (LCT), the optimized multidimensional and the least-action tunneling approximations [170, 187]. The inclusion of a multiplicative factor, αT, called transmission coefficient, takes care of the corrections to the Eyring equation that relate to effects like tunneling, for instance. The inclusion of the transmission factor into the calculation of rate constants (therefore reaction equations) improves the goodness of calculated reaction rates versus experimental [170, 172, 188]. The following equations show the analogy between transition state theory and experimental kinetic laws in calculating rate constants (for standard state of 1 mol/L): (a) Eyring-Polanyi equation, (b) E-P equation with separated enthalpic and entropic terms and (c) Arrhenius law.
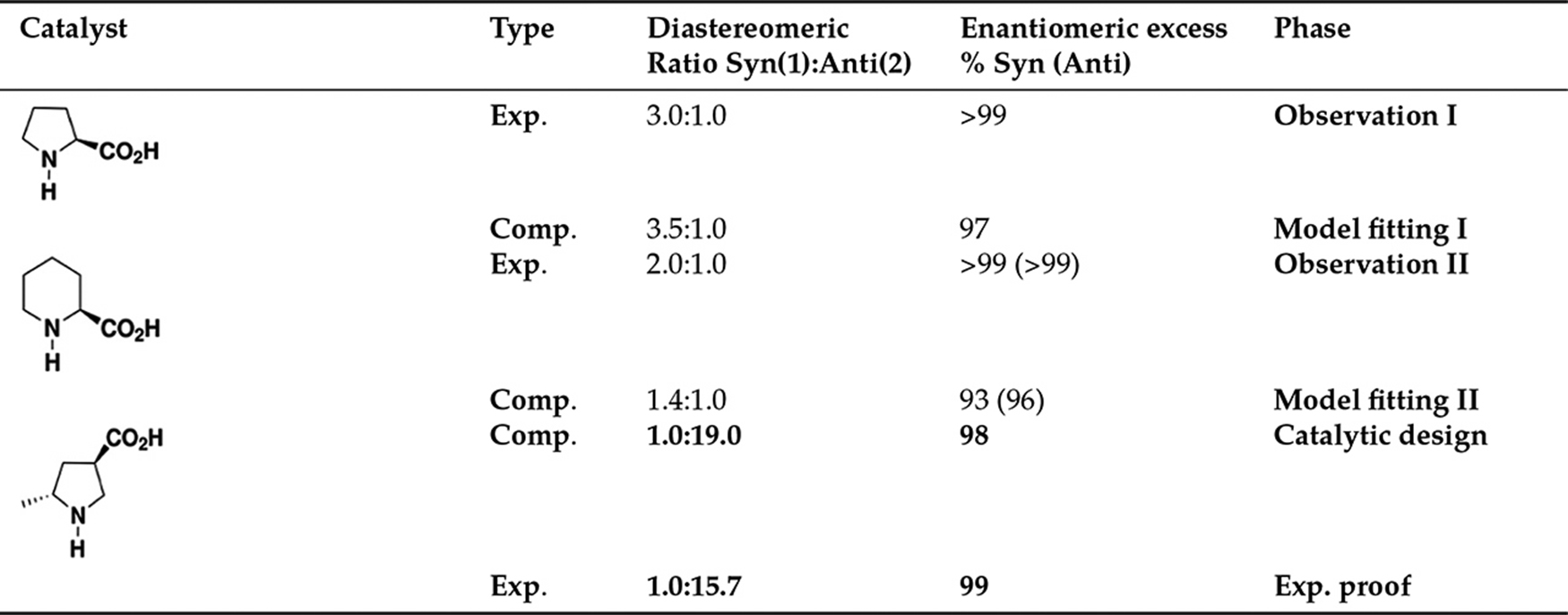
Transition state theory provides valuable kinetic discrimination of reaction-controlled events, alias events that need to cross an energy barrier. The first predictive use of transition state theory in organic chemistry involved the electro-cyclic ring opening of 3-formylcyclobutene; computational insights predicted for the latter system an unusual reactivity compared to its congener 3-methylcyclobutene [189]. The Hajos-Parrish reaction was the first organocatalysis to be studied from first principles [190, 191, 192]; yet again transition state theory proved to be an invaluable tool in uncovering the energetic of the stereoselection between the more stable s-trans geometry (3.5 kcal/mol) and the less stable s-cis [193]. The first example of computational design was applied to selective Mannich-type reactions. The reaction between propionaldehyde and N-PMP-protected α-iminoethyl glyoxylate is catalyzed by (S)-proline and affords Mannich products of syn configuration (syn:anti 3:1, 99 % enantiomeric excess, entry #1 in Table 5). K.N. Houk, C. Barbas et al. produced a computational model of the reaction at HF/6–31G* level in 2006. Transition state theory provided an excellent estimation of the observed diastereoselectivity, 3.5:1, and enantiomeric excess, ~95%[193]. They produced a second computational model where (S)-pipecolic acid replaced (S)-proline as active catalyst of the reaction (Figure 9 and entry #2 in Table 5) and noticed that a loss of diastereoselectivity in Syn(1) product was taking place in favor of Anti(2) product. Targeted catalytic design, based on the insight built during this strategic approach, lead to the first computational design of an organocatalyst in 2006. The catalyst, an artificial aminoacid (entry #3 in Table 5), was designed at HF/6-31G* level of theory to afford selective anti-Mannich reactions, a completely opposite reactive pathway in this type of systems. The predicted outcome of the reaction, 5:95 syn:anti and 98 % ee, were perfectly matched by the successive experimental findings, 6:94 syn:anti and 99 % ee.
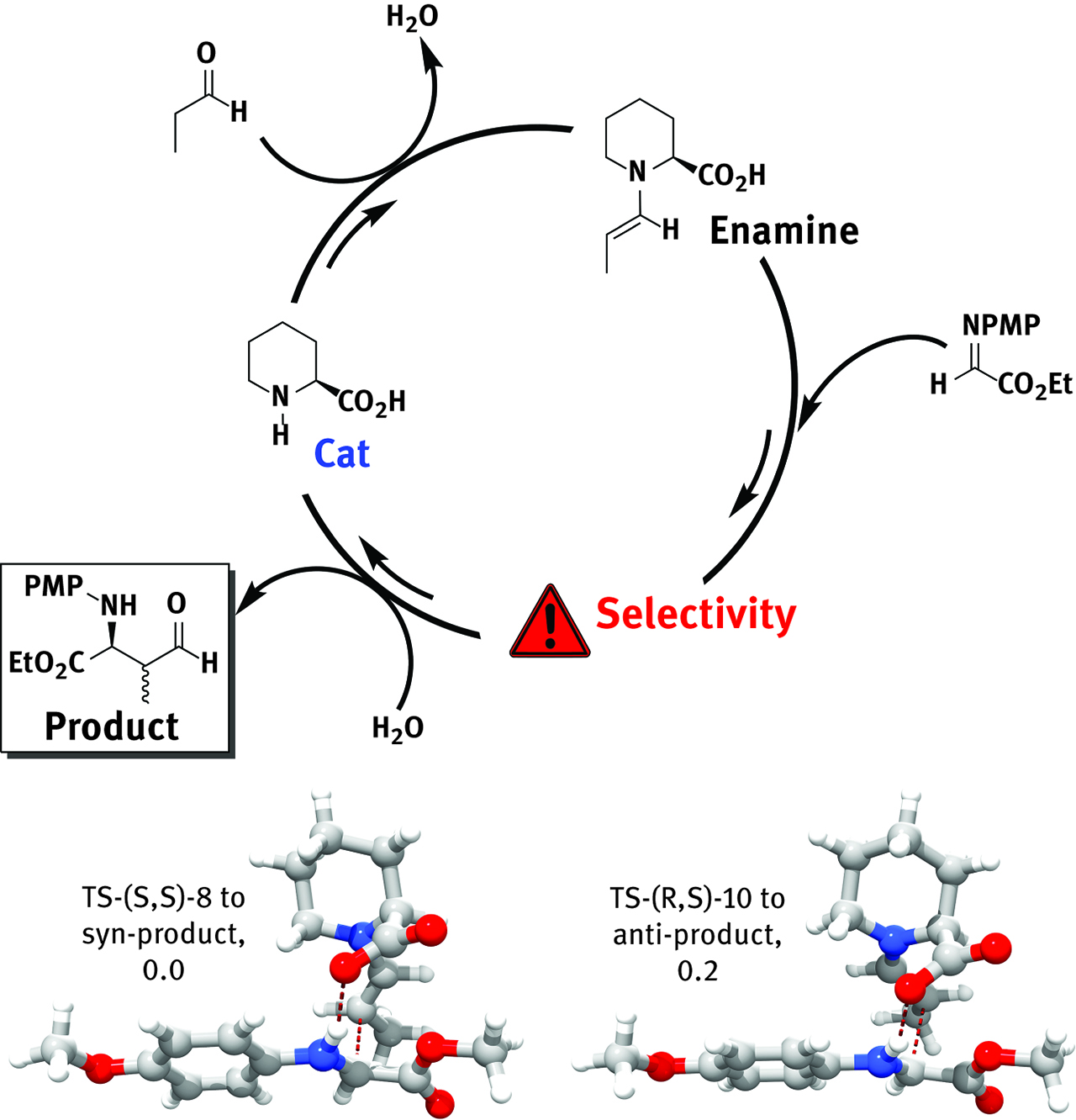
Schematic representation of Barbas-Houk’s Mannich-type reaction discussed in this section (top). Transition state theory lead to crucial observations (bottom) concerning structures and energetics that sparked computational design of a new catalyst with desired properties.
The strategy to catalytic design. Entry #1 shows the data for the Mannich-type reaction catalyzed by (S)-proline, entry #2 shows those for the reaction catalyzed by (S)-pipecolic acid. Computation designs experiment in entry #3.
While many other excellent examples of synergistic theory-synthesis approaches in chemistry can be found in literature [194, 195, 196, 197, 198, 199, 200, 201, 202, 203, 204, 205, 206, 207, 208], we report here a very interesting paper published by A. Kleij, C. Bo et al. on the use of triazabicyclodecene (TBD) as a organocatalyst of chemoselective ring-opening of cyclic carbonates to afford N-aryl carbamates in cheap and mild conditions [209]. Carbamates are products of CO2-incorporation. Greenhouse gases (GHG) like CO2 derived from anthropogenic activities are held responsible for the global warming scenario [210, 211, 212, 213, 214]. Sequestrating these gases from the atmosphere and incorporating them in building blocks for fine chemistry is highly sought after [215, 216, 217]. DFT-based (B97-D3/6-311G**/SMD) methods as implemented in G09[98] helped to uncover a favorable proton-relay mechanism as the main source of the fast catalytic effect of TBD at room temperature (Figure 10); two hydrogen bonds imprint a 8-membered ring transition state and lower considerably the barrier of activation at the rate-determining step. Two competitive pathways, namely the direct nucleophilic attack of the amine onto the cyclic carbonate and water-assisted pathway, are either kinetically unfeasible or not as effective as TBD (Figure 10). The crucial contribution of this proton-relay switch has been counter-checked by experiment: replacing TBD by methylated TBD (MTBD) leads to much poorer catalytic effect [209].
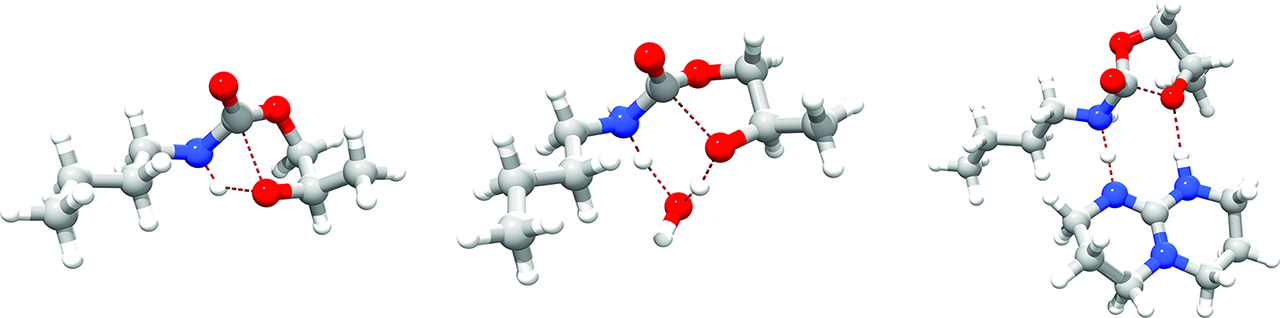
Transition structures for ring-opening of a cyclic carbonate enhanced by n-butylamine: left, non-catalyzed (ΔG‡ = 33.3 kcal/mol), center, H2O-catalyzed (ΔG‡ = 24.2 kcal/mol) and right, TBD-catalyzed (ΔG‡ = 18.2 kcal/mol).
A priori design of enzymatic pockets relies on transition state theory as well. Theozymes are theoretical catalysts tailored by optimizing the transition state of the reactants in a non-catalyzed reaction [218]. Though natural enzymes are molecular machines of unmatched efficiency in binding and transforming several substrates with high selectivity, synthetic enzymes can be designed to catalyze reactions unknown to natural enzymes. This is the case of the retro-aldol dissociation reaction of 4-hydroxy-4-(6-methoxy-2-naphthyl)-2-butanone [219], the Kemp rearrangement reaction of a benzisoxazole [220] and the Diels-Alder condensation between 4-carboxylbenzyl trans-1,3-butadiene-1-carbamate and N,N-dimethylacrylamide [221]. The group employed a sequential methodology involving data-mining, predictive design (Rosetta hashing algorithm [222]), transition state optimizations, selection of best leads and finally expression and directed evolution to generate synthetic enzymes. The strategic approach and the exceptional results of such computationally-assisted design are reported for the first two reactions in Figure 11 and Table 6, respectively. An experimental technique that could be conceptually linked to transition state theory is femtosecond spectroscopy. This technique allows pulsing wave-packets on a molecule by the means of an ultrafast laser. A vibrational normal mode of interest is excited and the structure rearranges trough an activated complex to the formation of the desired product. This spectroscopy allows the accurate mapping of the entire surface and its dynamics from the reactants to the products, thus providing important experimental details on the characteristics of the “near transition” region [11].
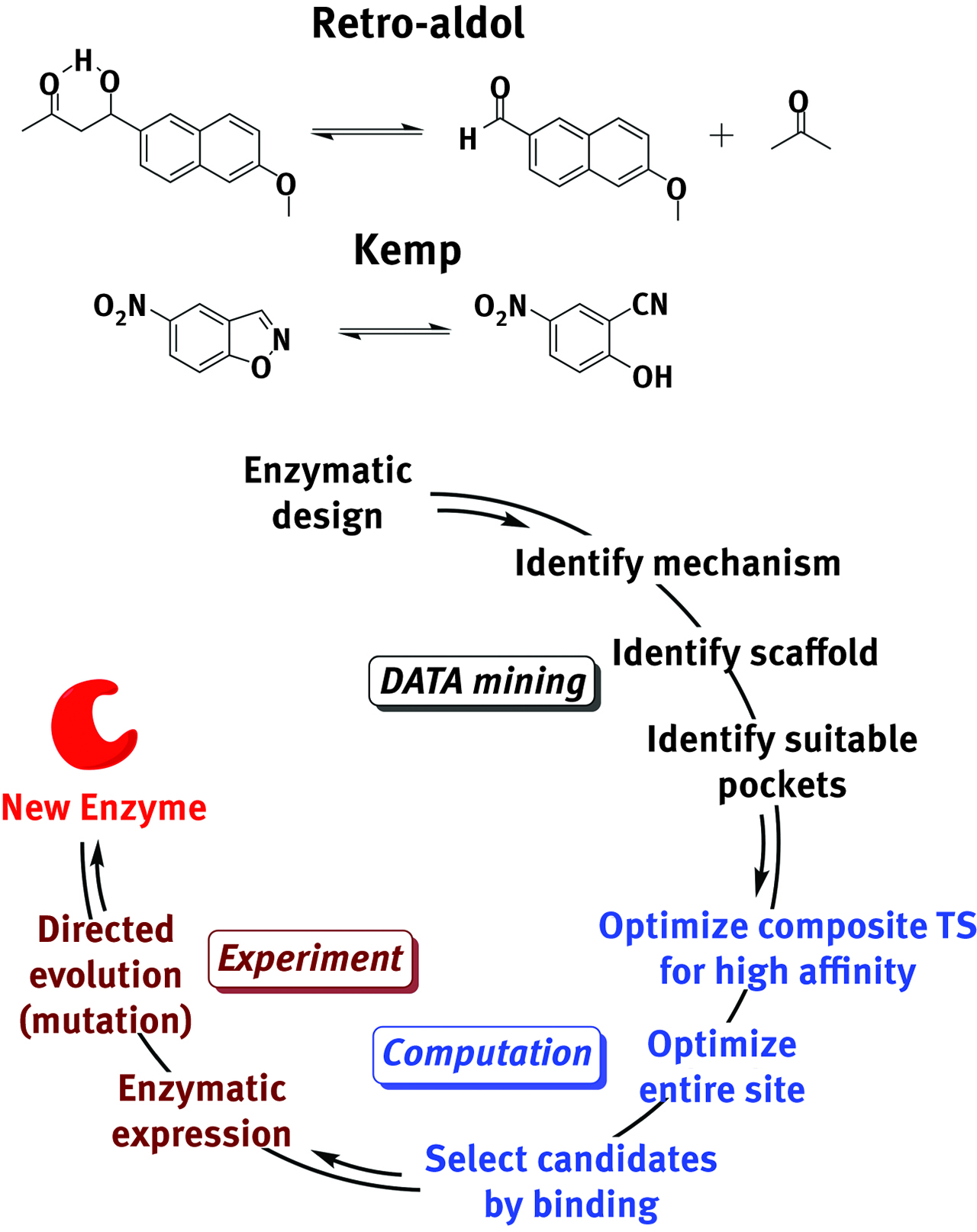
Nature does it better, but scientists are closing the gap. The route to “artificial” enzymes is an interplay ground for statistical techniques, theoretical computation and targeted synthesis.
Experimental activity and kinetic parameters of mutated artificial enzymes designed by computational methods.
| Design | Reaction | kuncat | kcat | KM (mM) | kcat/KM (M−1s−1) | kcat/kuncat |
|---|---|---|---|---|---|---|
| RA60 | Retro-aldol | 3.9·10–7 min−1 | (9.3 ± 0.9)·10–3 min−1 | 510 ± 33 | (0.30 ± 0.06)·10–3 | 2.4·104 |
| RA61 | Retro-aldol | 3.9·10–7 min−1 | (9.0 ± 1.0)·10–3 min−1 | 210 ± 50 | (0.74 ± 0.11)·10–3 | 2.3·104 |
| R7 2/5B | Kemp | 1.16·10–6 s−1 | (1.20 ± 0.08) s−1 | 0.86 ± 0.08 | 1.388 ± 44 | 1.03·106 |
| R7 10/11 G | Kemp | 1.16·10–6 s−1 | (1.37 ± 0.14) s−1 | 0.54 ± 0.12 | 2.590 ± 302 | 1.18·106 |
3.5 Kinetic models
Complex multi-step chemical reactions are the direct result of parallel, competitive and consecutive events establishing an intricate network of simultaneous equilibria in the medium: within this network, species appear and disappear following (sometimes) complex phenomenological laws [223]. Experimental kinetic laws use rate constants derived from macroscopic quantities like activation energies (e. g., Arrhenius [223] law) to average microscopic quantities deriving from particle transport and collisions (continuum → microscopic, Figure 12).
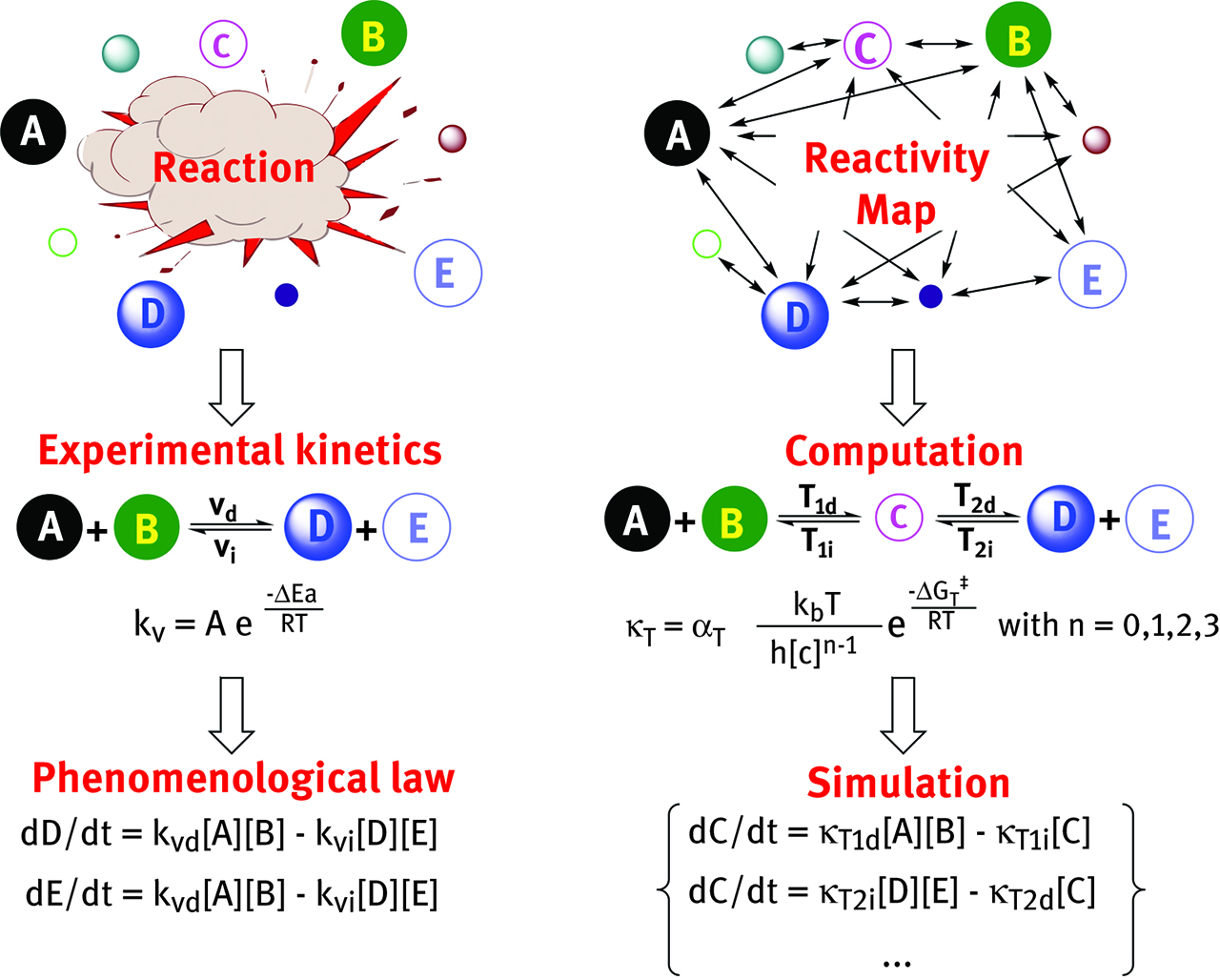
The different approach of experimental kinetics versus kinetic model.
A kinetic model uses integrated system concentrations over time of microscopic quantities (i. e. transition state thermodynamics) on elemental events to simulate the macroscopic reaction (microscopic → continuum, Figure 12): it is used to complement and corroborate mechanistic proofs derived from potential and free energy surfaces. In principles, a kinetic model should allow the accurate recovery of information on selectivity, turnover number and kinetics ↔ reactivity ↔ structure relation in conditions where Curtin-Hammett principle [224], Winstein-Holness equation [224] and steady-state approximation [223] are not always so easily applicable.
Kinetic models abide the principle of microscopic reversibility and represent a strong direct link between pure theory and experiment since they can be compared straightforwardly with plots obtained by experimental kinetics [225]. The higher the number of kinetic equations included in the simulation, the better the agreement of the model versus experiment. Kinetic models are particularly useful to model catalytic reactions, where the rate limiting step(s) may change throughout the reaction following the change in concentrations of the reactants/intermediates [223]. Analytical integration is prohibitive on large systems; therefore one should resort to robust numerical algorithms like Euler, 4th-order Runge-Kutta, Runge-Kutta-Fehlberg, Runge-Kutta-Cash-Karp, Runge-Kutta-Dormand-Prince, Bader-Stoer and Adams’ methods [223]. “Stiff” equations can be efficiently treated with Bader-Deuflhard algorithm [226]. An elegant example of kinetic models has been reported by F. Maseras et al. It concerns the computational study at B97-D3/6-311G(d)/SMD level of theory of a known 1,3-dipolar cycloaddition between propargylamine and azidoethylamine [227], Figure 13. The computed thermodynamic parameters reproduced successfully the experimental findings (ΔG‡ = 27.1 versus 27.3 kcal/mol, for the rate limiting step of the reaction) and the kinetic model helped to re-interpret the experimental mechanism of the reaction in light of the catalytic effect of host-guest encapsulation provided by cucurbit[6]uril (CB6) [227]. Another excellent example has been reported by Maseras et al. The work encompasses the use of non-adiabatic DFT calculations (ωB97X-D) supported by kinetic model in explaining the outcome of photo-activated aromatic perfluoroalkylations [228].
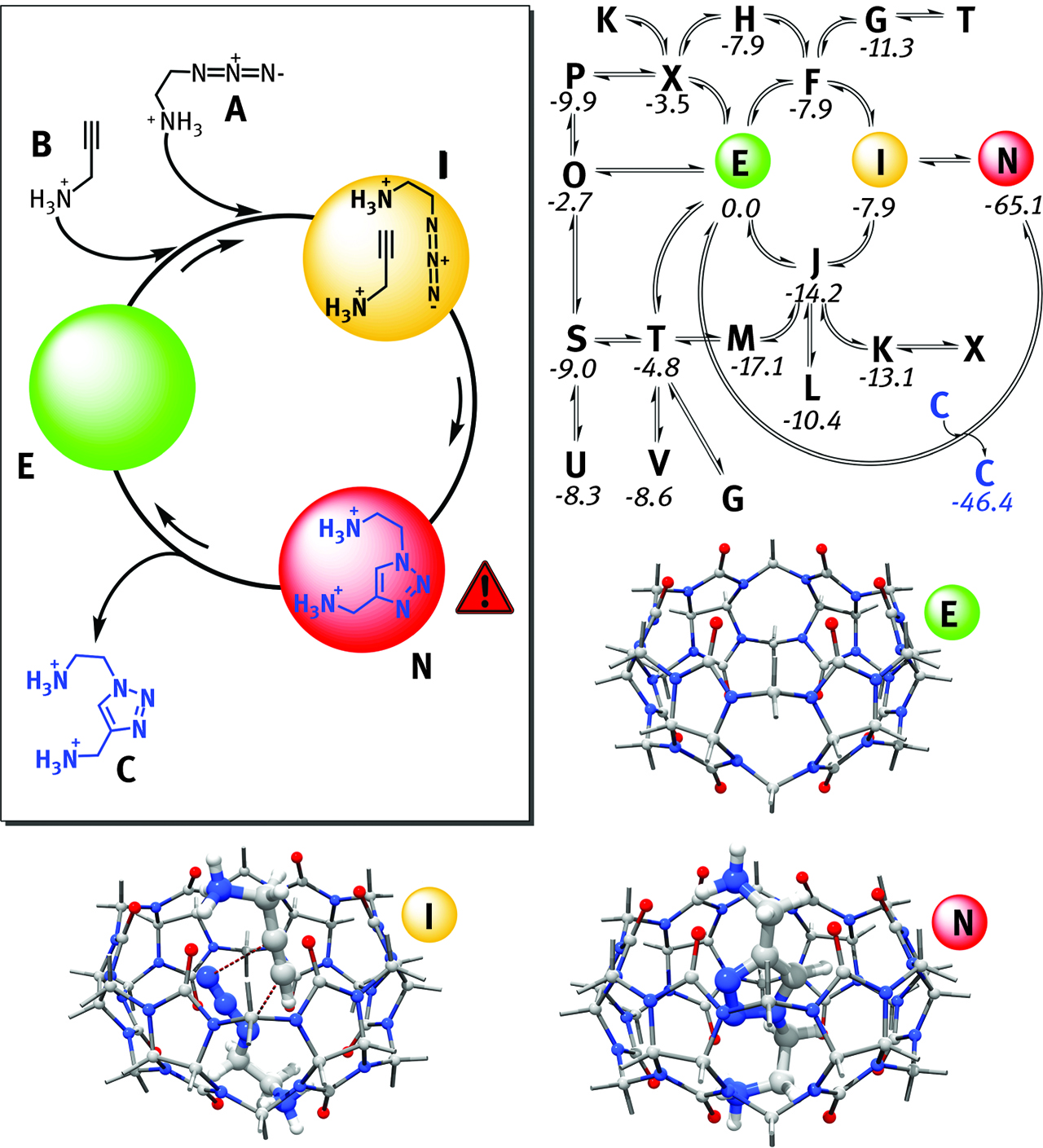
Schematic representation of the dipolar cycloaddition discussed in this section, top-left. Maseras’s pruned network of calculated competing events proves the “combinatorial” approach behind kinetic model, top right. Molecular structures of the most important intermediates in the reaction (bottom).
3.6 Multi-scale models
The idea of a consistent force-field was born in 1968 [229]. The total potential energy of a molecule can be calculated as a function of simple classical laws involving Hooke’s spring law for bonds, periodic laws for dihedral torsions, Lennard-Johns equation for Van der Walls interactions and Coulomb law for charge interactions [230]. The potential energy can be further related to energy minimization, intrastate and interstate dynamics and random moves (Monte Carlo)[230]. Multi-scale models were originally proposed in 1976. They allow the optimization and calculation of properties of very large systems (encompassing hundreds of thousands of atoms); thus they have been very useful in the calculations of large peptides, proteins and enzymes like lysozyme [231]. The general idea behind this method is that the chemical system under study can be divided into different layers, calculated separately using different methods. Larger areas that do not take direct part in the reaction (e. g., protein side chains) are calculated using inexpensive classical treatments like molecular mechanics (MM), while active site of reaction can be treated with higher-level quanto-mechanical theory (QM). For such reason these methods are called QM/MM methods. The energy of a total system, ESys, can be defined as:
ESys = EQMQM + EMMMM + EQMinterQM/MM + EMMinterQM/MM
The steric and polarization effects of the classically-treated low-level layer are contained in the term EMMMM, while EQMQM contains the quantum mechanics energy of the high-level layer. EQMinterQM/MM is called electronic embedding, while EMMinterQM/MM is called mechanical embedding. Different methods have different ways to calculate the latter two parameters. Two of these QM/MM methods are available and implemented in computational software: IMOMM [232] and ONIOM [233] methods.
There are excellent reviews [234, 235] and highlights [236] and commentaries [194] on QM/MM calculations in asymmetric catalysis via organometallic species; these works include reactions like hydrogenation, hydroboration, epoxidation and hydroformilation. F. Schoenebeck et al. used ONIOM(B3LYP/6-31+G(d)/LANL2DZ:HF/LANL2MB) level of theory to design a new small-bite phosphine ligand able to enhance the reductive elimination of PhCF3 from Pd(II) complexes. Contrarily to accepted knowledge, the group demonstrated computationally that the reactivity was not correlated with the bite-angle of the phosphine, rather with the repulsive electrostatic interactions between the phosphine and the leaving group (namely CF3) [237]. Calculations provided a good estimate of the activation enthalpy for elimination of PhCF3 in [(Xantphos)Pd(CF3)(Ph)], 25.1 kcal/mol versus the experimental value of 25.9 ± 2.6 kcal/mol [238]. Schoenebeck’s new complex [(dfmpe)Pd(CF3)(Ph)] (Figure 14), afforded an activation enthalpy range of ΔH‡ = 20.7–23.5 kcal/mol, depending on various theories [237]. Driven by the successful computational design, the group synthesized [(dfmpe)Pd(CF3)(Ph)] and demonstrated that the elimination of PhCF3 is complete after 3 hours at 80 °C after 100 min. Kinetic experiments by NMR measured the activation enthalpy as ΔH‡ = 27.9 ± 1.6 kcal/mol [237]. Another challenge for QM/MM methods is represented by designing chemotherapeutic agents with in vivo high affinity and selectivity towards target DNA helix. A synergistic approach between molecular dynamics simulations, QM/MM calculation, force fields and experimental resources (i. e., high-resolution structures of nucleosome-drug adduct) has been applied to further the knowledge on binding location, binding modes and selectivity of metallo-drugs versus DNA and proteins during these last years [239].
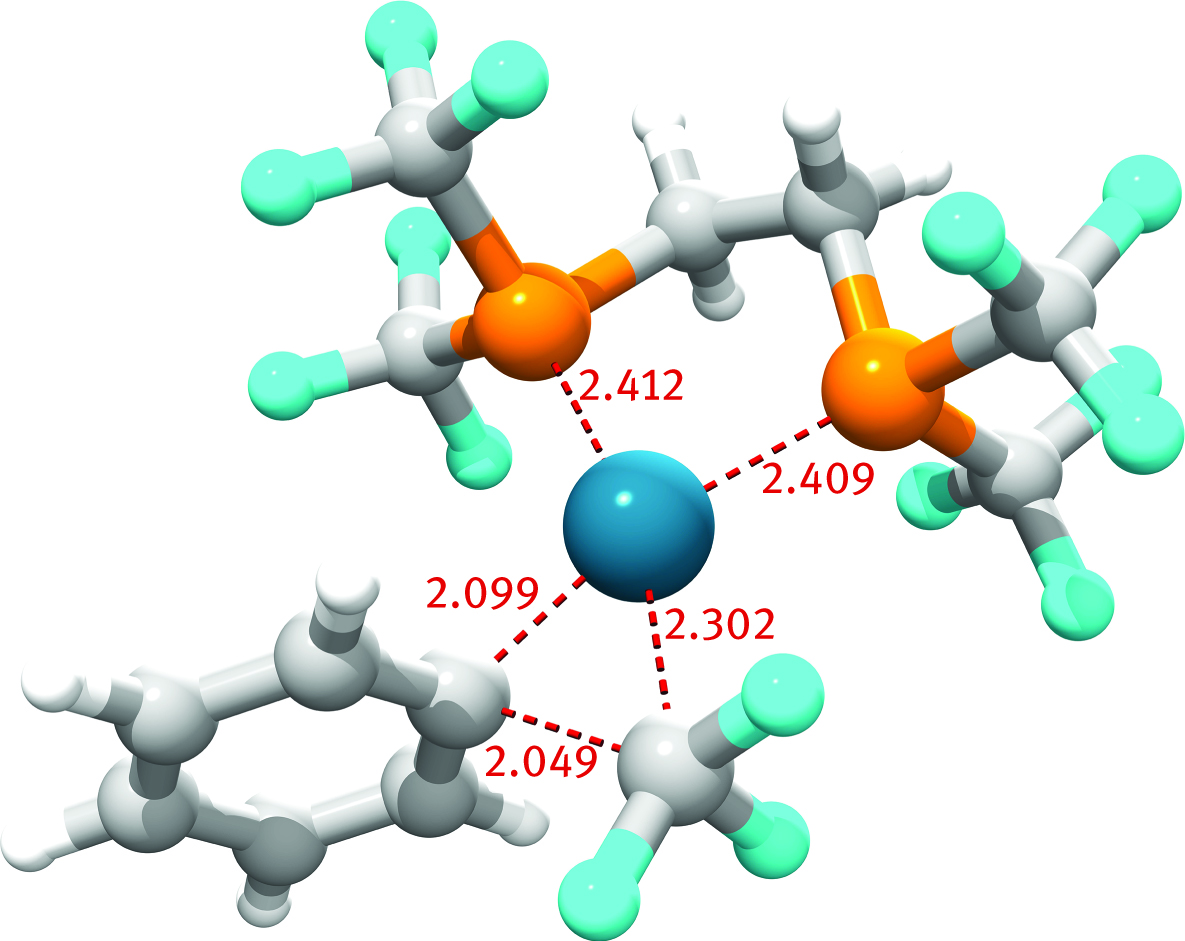
Bite-angle is not the issue, says theory. Schoenebeck’s designed palladium complex reductive-eliminates PhCF3, despite its small bit-angle phosphine. The figure shows the transition structure for such elimination (bond distances in Å).
3.7 Wavefunction analysis
Optimized wavefunctions at the stationary points,
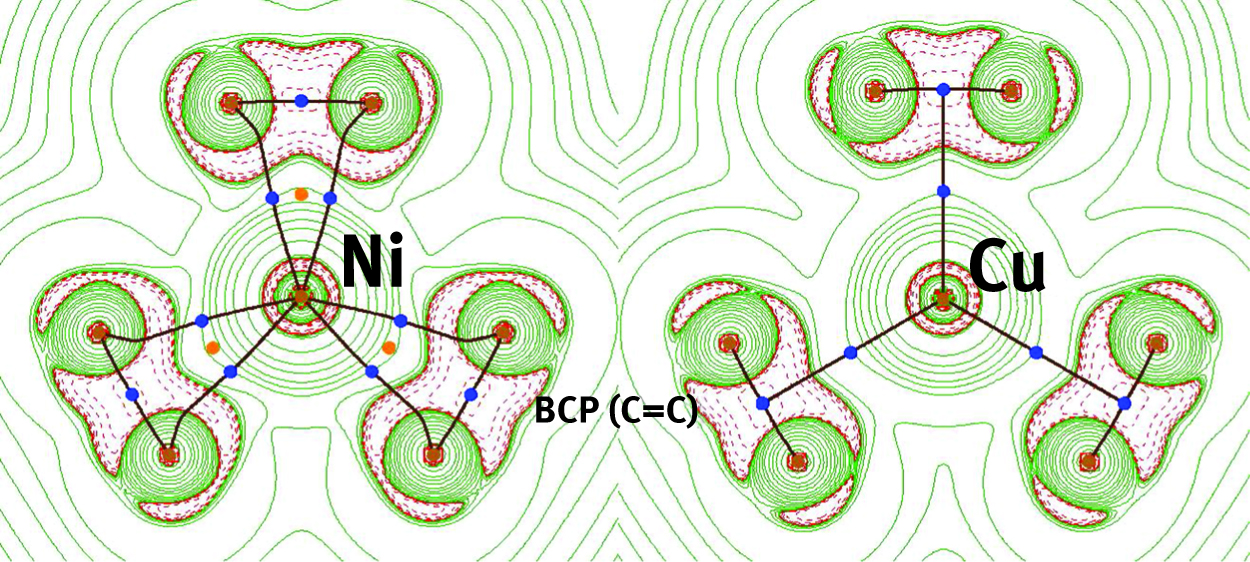
Molecular graphs of Ni(η2-C2H4)3, left, and Cu(η2-C2H4)3+, right, overlaid with their respective Laplacian maps, ∇2ρ(r). The structures have been calculated using B3PW91 in conjunction with the non-relativistic full-electron DGDZVP basis set. Blue dots represent bond critical points, or BCP (3,-1), orange dots represent ring critical points, or RCP (3,+1), and brown dots represent nuclear attractors (3,-3). Within green zones kinetic energy density dominates and the electron density is depleted {∇2ρ(r) > 0}. Within red zones potential energy dominates and the electron density is concentrated {∇2ρ(r) < 0}.
Among others, topological analysis functions are very useful and routinely used by chemists: electron localization function (ELF) [250, 251], localized orbital locator (LOL) [252, 253], reduced density gradient (RDG) [254] and source function [255]. ELF was used by M. Kaupp et al. to explain the bond in another uncommon compound, HgF4 [256]. The bond pattern, consistent with the representation of a low-spin d8 complex, defines mercury as real transition metal, rather than a post-transition element. Mercury in high oxidation state was theoretically predicted by Kaupp et al. to be stable as HgF4 since 1993[257, 258, 259], with weakly-coordinating ligands like SbF6- [260] and as HgH4 by P. Pyykkö et al. [261] and finally isolated and characterized spectroscopically in matrix in 2007 [256].
3.8 Chemoinformatics and machine-learning
Under the name of chemoinformatics falls a large and diverse number of different disciplines spanning from computational chemistry, mathematics, and statistics, data-mining to informatics. The accepted goal of chemoinformatics is to fabricate Hit-to-Lead-to-Candidate [262] predictions on unknown molecular systems using validated and statistically significant data obtained from libraries of known properties and chemical behaviors. Computational chemistry is primarily used in pharmaceutical industries to complement, integrate or prioritize targeted drug synthesis via virtual libraries and virtual screening [263]. Virtual libraries are collections of virtual molecules that can be studied to generate new molecule or to hypothesize chemical properties. Such libraries should be composed of large and fitting populations. These libraries can be increased using “trained” Markov chains like in fragment optimized growth (FOG) algorithm [264]. Virtual screening is the analysis of database of chemical compounds to identify viable candidates. Virtual screening uses in silico techniques like molecular docking [263]. Combinatorial and high-speed syntheses are used as lead or complementary synthetic methods to chemoinformatics, since they are designed to generate or screen large libraries of compounds [263]. High-throughput computational modeling uses languages like the Chemical Markup Language (CML) and the Simplified Molecular-Input Line-Entry System (SMILES). Physico-chemical properties are normally represented by descriptors: a descriptor is a compact transcription of a certain property within a sample or library of species into mathematical language. The goal of a descriptor is to convey the essence of the quantitative structure-activity relationship (QSAR) [265]. The complexity of the property described by the descriptor increases with the dimensionality of the descriptor itself: 1D-descriptors deal with simple macroscopic bulk properties like molecular weight, while 3D-descriptors capture the essence of the donor-acceptor interaction and binding affinity (polar surface area for instance). 1D-descriptors are used as first-approach filters, while 2D-descriptors (also called fingerprints) seem to work well in reproducing many chemical properties [266]. GRID is an interesting program for drug discovery applications and ADME predictions related to pharmacokinetics [43]. QSAR approach is used extensively in pharmaceutical chemistry [267, 268], but its use in catalytic applications involving small molecules results to be still sparse. An excellent example of QSAR, or in this case QSSR (quantitative structure-selectivity relationship), is represented by M.C. Kozlowski et al.’s work [269, 270]. The group aimed to correlate the structure of in situ-generated zinc catalysts (ZnBr2 + β-aminoacids) with the enantioselectivity of the asymmetric reduction of benzaldehyde to related alcohol. The group generated a grid-based QSAR approach whose descriptors provided a correct replica of the enantioselective footprint of catalysts under study. Since every transition structure have been generated using computationally low-demanding PM3 theory, this model provides important insight at very affordable costs [269].
Machine learning is a branch of computer science that deals with “supervised” or “unsupervised” learning of a machine. The goal of this discipline is the development of artificial intelligences, networks that mimic the human mind’s capability to learn, store and relay data using electrochemical signals [271]. Network analysis, for instance, has been applied in organic synthesis since the Sixties, when E. Corey created software called Logic and Heuristics Applied to Synthetic Analysis (LHASA). The software was meant to suggest the sequences of postulated steps in a de novo synthesis, based on a database of retrosynthetic rules [272]. In 2005, B. A. Grzybowski et al. developed in 2005 a revolutionary concept of a network connecting molecules (“nodes”) by chemical reactions (“arrows”)[273]. The network contains about 6 million organic compounds interrelated by 30,000 retrosynthetic rules. The group focused on the evolution of this network, the relations between connections in the network and reactivity and optimization/pruning of the network itself. The software developed after this network was called Chematica. It can successfully generate and optimize synthetic pathways [274, 275] and detect synthetic pathways leading to dangerous chemicals [276]. Other interesting examples on chemoinformatics and machine learning (i. e., artificial neural networks) can be found in literature [277].
4 The future: Conclusions and author’s perspectives
A brief evolution of the rational way of doing chemistry has been presented throughout this chapter. General principles and descriptions of rational improvements to chemistry have been introduced and described to provide the reader with a general background on this topic. Paradigmatic examples on the synergistic use of theory, spectroscopy and synthesis have been provided to show how the rational approach is more than advantageous in understanding, developing and planning new chemistry. It is certain that the evolution of transistors, semi-conductors and miniaturized circuits will provide a boost in the hardware performances (thus an incentive to study large and more complex systems raising the bar of the overall accuracy) in the next few decades, provided that Moore’s law will still be followed faithfully [278]. Furthermore, once the binary code will no longer hold sway, quantum-bits-based architectures might boost computational power and speed to new, far higher plateaus. At the present days, there are reports of commercialization of quantum architectures (e. g., D-Wave 2X) by Canadian company D-Wave System Inc. [279], but still, room is left for scientific debate and criticism [280, 281, 282, 283, 284]. Software improvements (i. e., implementation of improved routines, compilers, libraries, parallelization and so on) in commercialized computational programs (an extensive list of the major computational software used in chemistry, physics and material science can be found online [285, 286], as well as a list of the programs and suites to prepare input files and visualize output files [287]) will also play a protagonist role in speeding up the chemistry on screen. Technological improvements may also help experimentalists to keep a better and more functional record of their lab experiments; for instance, electronic laboratory notebooks (ELNs) [288] will become excellent platforms to track and share successful and failed synthetic attempts. These data, particularly the failures, when available on electronic supports for unrestricted mining and sharing, will be of tremendous importance in the validation, refinement and improvement of theoretical models on real systems.
Thus, all these betterments will surely contribute to keep the rational momentum of chemistry evolving in the near future. Truth is, the impact of a higher degree of rationality might profoundly influence the way chemistry is taught, discussed and disseminated as well. One of the greatest limitations in scientific fields is that specialized professionals speak different languages [289]. This loss in translation can sometimes be the cause of scientific misunderstandings, disagreements and loss or disregard of crucial snippets of information in shared projects and assignments. Thus, scientific team-work and collaborations [289] will benefit in efficiency from a new breed of chemist, groomed from early academic stages to blend theory, spectroscopy and synthesis (understanding powers and limits embedded in different approaches!) to pursue research duties and interests. Such a figure may deliver more powerful performances than his/her predecessors in academic and industrial environments alike.
Secondly, rational chemistry might lead to a positive relief of the environmental footprint that is a great concern in the modern era. Chemistry can be a double-edged sword: while in the past it has shown that it can improve the quality of life and fuel technology, it has also contaminated nature and its living creatures. The current drive in research funding is to push for the former without creating the latter as a deleterious effect. Though regulated by national agencies, chemical pollution is a transnational problem that leads inexorably to problems like endocrine disruption due to chronic exposure [290]. Paradoxically, since a clean man-made chemical reaction is a reaction that never took place, the concepts of atom-economy and solvent preservation need to be implemented to their fullest. Validated computational techniques could represent a greener and more sustainable way to design catalysts (or electrodes, membranes, polymers and so on) and tune catalytic effects than indiscriminate trial-and-error synthesis. Finally, there is the issue of the economic sustainability. Pharmaceutical companies are already incorporating some of the computational tools [267] presented in this chapter to design new bioactive molecules and pre-screen their biological activity. High-quality computation techniques are indeed less impacting on R&D budgets compared to trial-and-error synthesis. Furthermore, rational design of reagents could shield enterprises from legal internal liabilities deriving from the use and storage of harmful reagents and the stock and disposal of dangerous waste.
References
1 Fowler AC. Mathematical models in the applied sciences. Cambridge, UK: Cambridge University Press; 2004.Search in Google Scholar
2 Melnick R, editor. Mathematical and computational modeling: with applications in natural and social sciences, engineering, and the arts. New York, USA: John Wiley & Sons Inc; 2015.10.1002/9781118853887Search in Google Scholar
3 Ball P. Chemistry: why synthesize? Nature. 2015;528:327–329.10.1038/528327aSearch in Google Scholar PubMed
4 Mortimer CE. Chemistry: a conceptual approach. Belmont, CA, USA: Wadsworth Publishing Co. Inc; 1983.Search in Google Scholar
5 Francl M. The enlightenment of chemistry. Nat Chem. 2015;7(10):761–762.10.1038/nchem.2354Search in Google Scholar PubMed
6 Norris JA. The mineral exhalation theory of metallogenesis in pre-modern mineral science. Ambix. 2006;53(1):43–65.10.1179/174582306X93183Search in Google Scholar
7 Greenwood NN, Earnshaw A. Chemical periodicity and the periodic table, in chemistry of the elements. Oxford: Butterworth-Heinemann; 1997. p. 20–31.10.1016/B978-0-7506-3365-9.50008-0Search in Google Scholar
8 Kauffman GB. The quiet revolution. Hermann kolbe and the science of organic chemistry. Von A. J. Rocke. Angew Chem. 1994;106(21):2317–2318.10.1002/ange.19941062134Search in Google Scholar
9 Von Meyer E. Zur erinnerung an hermann kolbe. J Prakt Chem. 1884;30(1):417–467.10.1002/prac.18850300143Search in Google Scholar
10 Schwarz WHE. 100th anniversary of Bohr’s model of the atom. Angew Chem Int Ed. 2013;52(47):12228–12238.10.1002/anie.201306024Search in Google Scholar PubMed
11 Atkins P, De Paula J. Atkins’ physical chemistry, 8th ed. Oxford, UK: Oxford University Press, 2006.Search in Google Scholar
12 Einstein A, Podolsky B, Rosen N. Can quantum-mechanical description of physical reality be considered complete? Phys Rev. 1935;47(10):777–780.10.1103/PhysRev.47.777Search in Google Scholar
13 Williams DB, Carter CB. Transmission electron microscopy: a textbook for materials science. 2nd ed. New York, NY, USA: Springer-Verlag New York Inc.; 2009.10.1007/978-0-387-76501-3Search in Google Scholar
14 Goldstein, J., et al. Scanning electron microscopy and x-ray microanalysis. New York, NY, USA: Springer-Verlag New York Inc; 2013.Search in Google Scholar
15 Jansen F. Introduction to computational chemistry. 2nd ed. Hoboken, USA: John Wiley and Sons Ltd; 2007.Search in Google Scholar
16 Hensen, B., et al. Loophole-free bell inequality violation using electron spins separated by 1.3 kilometres. Nature. 2015;526(7575):682–686.10.1038/nature15759Search in Google Scholar PubMed
17 De Hoffmann E, Stroobant V. Mass spectrometry: principles and applications. 3rd ed. Hoboken, USA: John Wiley and Sons Ltd; 2007.Search in Google Scholar
18 Moldoveanu SC, David V. Mass spectrometry: principles and applications. USA: Elsevier Science Publishing Co Inc; 2016.Search in Google Scholar
19 Poole C. Gas chromatography. Amsterdam, Netherlands: Elsevier Science Publishing Co Inc; 2012.Search in Google Scholar
20 Corey EJ. Robert robinson lecture. retrosynthetic thinking-essentials and examples. Chem Soc Rev. 1988;17(0):111–133.10.1039/CS9881700111Search in Google Scholar
21 Oldenburg H. Epistle dedicatory. Philosophical Trans. 1665;1:1–22.Search in Google Scholar
22 Huang, B., et al. Chlorinated volatile organic compounds (Cl-VOCs) in environment - sources, potential human health impacts, and current remediation technologies. Environ Int. 2014;71:118–138.10.1016/j.envint.2014.06.013Search in Google Scholar PubMed
23 Ni, J.Q., et al. Volatile organic compounds at swine facilities: A critical review. Chemosphere. 2012;89(7):769–788.10.1016/j.chemosphere.2012.04.061Search in Google Scholar PubMed
24 Anastas PT, Warner JC. Green chemistry theory and practice. New York, USA: Oxford University Press; 1998.Search in Google Scholar
25 Mascia, S., et al. End-to-end continuous manufacturing of pharmaceuticals: integrated synthesis, purification, and final dosage formation. Angew Chem Int Ed. 2013;52(47):12359–12363.10.1002/anie.201305429Search in Google Scholar PubMed
26 Xiang, X.D., et al. A combinatorial approach to materials discovery. Science. 1995;268(5218):1738.10.1126/science.268.5218.1738Search in Google Scholar PubMed
27 Lewis GN. The atom and the molecule. J Am Chem Soc. 1916;38(4):762–785.10.1021/ja02261a002Search in Google Scholar
28 Gillespie RJ. Fifty years of the VSEPR model. Coord Chem Rev. 2008;252(12–14):1315–1327.10.1016/j.ccr.2007.07.007Search in Google Scholar
29 Hückel E. Zur quantentheorie der doppelbindung. Z Phys. 1930;60(7):423–456.10.1007/BF01341254Search in Google Scholar
30 Hückel E. Quantentheoretische beiträge zum benzolproblem. Z Phys. 1931;70(3):204–286.10.1007/BF01339530Search in Google Scholar
31 Woodward RB, Hoffmann R. Stereochemistry of electrocyclic reactions. J Am Chem Soc. 1965;87(2):395–397.10.1021/ja01080a054Search in Google Scholar
32 Figgis BN, Hitchman MA. Ligand field theory and its applications. New York, USA: John Wiley and Sons Ltd; 2000.Search in Google Scholar
33 Racah G. Theory of complex spectra. II. Phys Rev. 1942;62(9-10):438–462.10.1103/PhysRev.62.438Search in Google Scholar
34 Tanabe Y, Sugano S. On the absorption spectra of complex ions. I. J Phys Soc Jpn. 1954;9(5):753–766.10.1143/JPSJ.9.753Search in Google Scholar
35 Tanabe Y, Sugano S. On the absorption spectra of complex ions II. J Phys Soc Jpn. 1954;9(5):766–779.10.1143/JPSJ.9.766Search in Google Scholar
36 Tanabe Y, Sugano S. On the absorption spectra of complex ions, iii the calculation of the crystalline field strength. J Phys Soc Jpn. 1956;11(8):864–877.10.1143/JPSJ.11.864Search in Google Scholar
37 Lennard-Jones JE. The electronic structure of some diatomic molecules. T Faraday Soc. 1929;25(0):668–686.10.1039/tf9292500668Search in Google Scholar
38 Mulliken RS. The assignment of quantum numbers for electrons in molecules. I. Phys Rev. 1928;32(2):186–222.10.1103/PhysRev.32.186Search in Google Scholar
39 Schweitzer C, Schmidt R. Physical mechanisms of generation and deactivation of singlet oxygen. Chem Rev. 2003;103(5):1685–1758.10.1021/cr010371dSearch in Google Scholar PubMed
40 Pauling L. Nature of the chemical bond: an introduction to modern structural chemistry. 3rd ed. Ithaca, USA: Cornell University Press; 1960.Search in Google Scholar
41 Pauling L. The nature of the chemical bond. II. The one-electron bond and the three-electron bond. J Am Chem Soc. 1931;53(9):3225–3237.10.1021/ja01360a004Search in Google Scholar
42 Griffith JS, Orgel LE. Ligand-field theory. Quat Rev Chem Soc. 1957;11(4):381–393.10.1039/qr9571100381Search in Google Scholar
43 Cruciani G, editor. Molecular interaction fields: applications in drug discovery and adme prediction. Weinheim, Germany: Wiley-VCH Verlag GmbH; 2006.10.1002/3527607676Search in Google Scholar
44 Andres J, Bertran J. Theoretical and computational chemistry: foundations, methods and techniques. Castellón de la Plana, Spain: Universidad Jaume I. Servicio de Comunicación y Publicaciones; 2007.Search in Google Scholar
45 Foresman JB, Frisch A. Exploring chemistry with electronic structure methods: a guide to using gaussian. USA: Gaussian, Incorporated; 1993.Search in Google Scholar
46 Stewart JJP. Optimization of parameters for semiempirical methods VI: more modifications to the NDDO approximations and re-optimization of parameters. J Mol Model. 2013;19(1):1–32.10.1007/s00894-012-1667-xSearch in Google Scholar PubMed
47 Hohenberg P, Kohn W. Inhomogeneous electron gas. Phys Rev. 1964;136(3B):B864-B871.10.1103/PhysRev.136.B864Search in Google Scholar
48 Kohn W, Sham LJ. Self-consistent equations including exchange and correlation effects. Phys Rev. 1965;140x(3B):A1133-A1138.10.1103/PhysRev.140.A1133Search in Google Scholar
49 Koch W, Holthausen MC. A chemist’s guide to density functional theory. 2nd ed. Weinheim, Germany: Wiley-VCH Verlag GmbH; 2001.10.1002/3527600043Search in Google Scholar
50 Perdew, J.P., et al. Prescription for the design and selection of density functional approximations: more constraint satisfaction with fewer fits. J Chem Phys. 2005;123(6):062201.10.1063/1.1904565Search in Google Scholar
51 Dirac PAM. Note on exchange phenomena in the Thomas atom. Math Proc Cambridge. 1930;26(3):376–385.10.1017/S0305004100016108Search in Google Scholar
52 Lieb EH, Simon B. The Thomas-Fermi theory of atoms, molecules and solids. Adv Math. 1977;23(1):22–116.10.1016/0001-8708(77)90108-6Search in Google Scholar
53 Zhao Y, Truhlar DG. The M06 suite of density functionals for main group thermochemistry, thermochemical kinetics, noncovalent interactions, excited states, and transition elements: two new functionals and systematic testing of four M06-class functionals and 12 other functionals. Theor Chem Acc. 2008;120(1):215–241.10.1007/s00214-007-0310-xSearch in Google Scholar
54 Zhao Y, Truhlar DG. Density functionals with broad applicability in chemistry. Acc Chem Res. 2008;41(2):157–167.10.1021/ar700111aSearch in Google Scholar PubMed
55 Cohen AJ, Mori-Sánchez P, Yang W. Challenges for density functional theory. Chem Rev. 2012;112(1):289–320.10.1021/cr200107zSearch in Google Scholar PubMed
56 Zhao Y, Lynch BJ, Truhlar DG. Doubly hybrid meta dft: new multi-coefficient correlation and density functional methods for thermochemistry and thermochemical kinetics. J Phys Chem. 2004;108(21):4786–4791.10.1021/jp049253vSearch in Google Scholar
57 Karton, A., et al. Highly accurate first-principles benchmark data sets for the parametrization and validation of density functional and other approximate methods. derivation of a robust, generally applicable, double-hybrid functional for thermochemistry and thermochemical kinetics. J Phys Chem. 2008;112(50):12868–12886.10.1021/jp801805pSearch in Google Scholar PubMed
58 Schwabe T, Grimme S. Theoretical thermodynamics for large molecules: walking the thin line between accuracy and computational cost. Acc Chem Res. 2008;41(4):569–579.10.1021/ar700208hSearch in Google Scholar PubMed
59 Schwabe T, Grimme S. Towards chemical accuracy for the thermodynamics of large molecules: new hybrid density functionals including non-local correlation effects. Phys Chem Chem Phys. 2006;8(38):4398–4401.10.1039/b608478hSearch in Google Scholar PubMed
60 Schwabe T, Grimme S. Double-hybrid density functionals with long-range dispersion corrections: higher accuracy and extended applicability. Phys Chem Chem Phys. 2007;9(26):3397–3406.10.1039/b704725hSearch in Google Scholar PubMed
61 Grimme S. Semiempirical hybrid density functional with perturbative second-order correlation. J Chem Phys. 2006;124(3):034108.10.1063/1.2148954Search in Google Scholar PubMed
62 Zhang Y, Xu X, Goddard WA. Doubly hybrid density functional for accurate descriptions of nonbond interactions, thermochemistry, and thermochemical kinetics. Proc Nati Acad Sci USA. 2009;106(13):4963–4968.10.1073/pnas.0901093106Search in Google Scholar PubMed PubMed Central
63 Austin, A., et al. A density functional with spherical atom dispersion terms. J Chem Theory Comput. 2012;8(12):4989–5007.10.1021/ct300778eSearch in Google Scholar PubMed
64 Grimme S. Semiempirical GGA-type density functional constructed with a long-range dispersion correction. J Comput Chem. 2006;27(15):1787–1799.10.1002/jcc.20495Search in Google Scholar PubMed
65 Grimme, S., et al. A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu. J Chem Phys. 2010;132(15):154104.10.1063/1.3382344Search in Google Scholar PubMed
66 Grimme S, Ehrlich S, Goerigk L. Effect of the damping function in dispersion corrected density functional theory. J Comput Chem. 2011;32(7):1456–1465.10.1002/jcc.21759Search in Google Scholar PubMed
67 Chai J-D, Head-Gordon M. Long-range corrected hybrid density functionals with damped atom-atom dispersion corrections. Phys Chem Chem Phys. 2008;10(44):6615–6620.10.1039/b810189bSearch in Google Scholar PubMed
68 Peverati R., Truhlar D. G. Quest for a universal density functional: the accuracy of density functionals across a broad spectrum of databases in chemistry and physics. Philos T Roy Soc A. 2014;372:20120476–20120527.10.1098/rsta.2012.0476Search in Google Scholar
69 Sousa SF, Fernandes PA, Ramos MJ. General Performance of Density Functionals. J Phys Chem. 2007;111(42):10439–10452.10.1021/jp0734474Search in Google Scholar
70 Gorin DJ, Toste FD. Relativistic effects in homogeneous gold catalysis. Nature. 2007;446(7134):395–403.10.1038/nature05592Search in Google Scholar PubMed
71 Pyykko P, Desclaux JP. Relativity and the periodic system of elements. Acc Chem Res. 1979;12(8):276–281.10.1021/ar50140a002Search in Google Scholar
72 Hay PJ, Wadt WR. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J Chem Phys. 1985;82(1):270–283.10.1063/1.448799Search in Google Scholar
73 Fuentealba, P., et al. A proper account of core-polarization with pseudopotentials: single valence-electron alkali compounds. Chem Phys Lett. 1982;89(5):418–422.10.1016/0009-2614(82)80012-2Search in Google Scholar
74 Fuentealba, P., et al. On the reliability of semi-empirical pseudopotentials: simulation of Hartree-Fock and Dirac-Fock results. J Phys Pt B Atom M P. 1983;16(11):L323.10.1088/0022-3700/16/11/001Search in Google Scholar
75 Stevens WJ, Basch H, Krauss M. Compact effective potentials and efficient shared‐exponent basis sets for the first‐ and second‐row atoms. J Chem Phys. 1984;81(12):6026–6033.10.1063/1.447604Search in Google Scholar
76 Stoll H. Large-core vs. small-core pseudopotentials: A case study for Au2. Chem Phys Lett. 2006;429(1–3):289–293.10.1016/j.cplett.2006.07.083Search in Google Scholar
77 Peterson KA, Puzzarini C. Systematically convergent basis sets for transition metals. II. Pseudopotential-based correlation consistent basis sets for the group 11 (Cu, Ag, Au) and 12 (Zn, Cd, Hg) elements. Theor Chem Acc. 2005;114(4):283–296.10.1007/s00214-005-0681-9Search in Google Scholar
78 Nakajima T, Hirao K. The Douglas–Kroll–Hess approach. Chem Rev. 2012;112(1):385–402.10.1021/cr200040sSearch in Google Scholar PubMed
79 Guinier A. X-ray diffraction: in crystals, imperfect crystals, and amorphous bodies. New York, USA: Dover Publications Inc; 1994.Search in Google Scholar
80 Cramer CJ. Essential of computational chemistry: theories and models, 2nd ed. The Atrium, Southern Gate, Chichester, West Sussex PO19 8SQ. England: John Wiley & Sons Ltd, 2004.Search in Google Scholar
81 Pyykko P. Predicted chemical bonds between rare gases and Au+. J Am Chem Soc. 1995;117(7):2067–2070.10.1021/ja00112a021Search in Google Scholar
82 Schröder, D., et al. Cationic gold(I) complexes of xenon and of ligands containing the donor atoms oxygen, nitrogen, phosphorus, and sulfur. Inorg Chem. 1998;37(4):624–632.10.1021/ic970986mSearch in Google Scholar
83 Seidel S, Seppelt K. Xenon as a complex ligand: the tetra xenono gold(II) cation in AuXe42+(Sb2F11-)2. Science. 2000;290(5489):117.10.1126/science.290.5489.117Search in Google Scholar PubMed
84 Oganov AR, Glass CW. Crystal structure prediction using ab initio evolutionary techniques: principles and applications. J Chem Phys. 2006;124(24):244704.10.1063/1.2210932Search in Google Scholar PubMed
85 Dong, X., et al. A stable compound of helium and sodium at high pressure. Nat Chem. 2017;9:440–445.10.1038/nchem.2716Search in Google Scholar PubMed
86 Zeeman P. VII. Doublets and triplets in the spectrum produced by external magnetic forces. Philos Mag Ser 5. 1897;44(266):55–60.10.1080/14786449708621028Search in Google Scholar
87 Ernst RR, Bodenhausen G, Wokaun A. Principles of nuclear magnetic resonance in one and two dimensions. Oxford, UK: Oxford University Press; 1990.Search in Google Scholar
88 Eaton, G.R., et al. Quantitative EPR. Vienna, Austria: Springer Verlag GMBH; 2010.10.1007/978-3-211-92948-3Search in Google Scholar
89 Levine IN. Molecular spectroscopy. New York, USA: John Wiley and Sons Ltd; 1975.Search in Google Scholar
90 Ditchfield R. Self-consistent perturbation theory of diamagnetism. Mol Phys. 1974;27(4):789–807.10.1080/00268977400100711Search in Google Scholar
91 Wolinski K, Hinton JF, Pulay P. Efficient implementation of the gauge-independent atomic orbital method for NMR chemical shift calculations. J Am Chem Soc. 1990;112(23):8251–8260.10.1021/ja00179a005Search in Google Scholar
92 Cheeseman, J.R., et al. A comparison of models for calculating nuclear magnetic resonance shielding tensors. J Chem Phys. 1996;104(14):5497–5509.10.1063/1.471789Search in Google Scholar
93 Keith TA, Bader RFW. Calculation of magnetic response properties using atoms in molecules. Chem Phys Lett. 1992;194(1):1–8.10.1016/0009-2614(92)85733-QSearch in Google Scholar
94 Keith TA, Bader RFW. Calculation of magnetic response properties using a continuous set of gauge transformations. Chem Phys Lett. 1993;210(1):223–231.10.1016/0009-2614(93)89127-4Search in Google Scholar
95 Gauss J. Calculation of NMR chemical shifts at second-order many-body perturbation theory using gauge-including atomic orbitals. Chem Phys Lett. 1992;191(6):614–620.10.1016/0009-2614(92)85598-5Search in Google Scholar
96 Gauss J. Effects of electron correlation in the calculation of nuclear magnetic resonance chemical shifts. J Chem Phys. 1993;99(5):3629–3643.10.1063/1.466161Search in Google Scholar
97 Barone V, in Recent advances in density functional methods, Chong DP, editor 1996, World Scientific Publ. Co.: Singapore.Search in Google Scholar
98 Gaussian integer G03. Available from: http://gaussian.com/. Accessed 5 June 2017.Search in Google Scholar
99 Stevens, W.J., et al. Relativistic compact effective potentials and efficient, shared-exponent basis sets for the third-, fourth-, and fifth-row atoms. Can J Chem. 1992;70(2):612–630.10.1139/v92-085Search in Google Scholar
100 Dias, H.V.R., et al. Synthesis and characterization of the gold(I) tris(ethylene) complex [Au(C2H4)3][SbF6]. Angew Chem Int Ed. 2008;47(3):556–559.10.1002/anie.200703515Search in Google Scholar PubMed
101 Fianchini, M., et al. Use of [SbF6]− to isolate cationic copper and silver adducts with more than one ethylene on the metal center. Organometallics. 2013;32(10):3034–3041.10.1021/om4002439Search in Google Scholar
102 Fianchini M Scorpionate Supported And Unsupported Carbonyl And Ethylene Complexes Of Group 11 Metals - Ph.D. thesis. 2010; Available at: https://uta-ir.tdl.org/uta-ir/handle/10106/2059.Search in Google Scholar
103 Fianchini, M., et al. A non-classical copper carbonyl on a tri-alkene hydrocarbon support. Dalton Trans. 2009;12:2085–2087.10.1039/b902678aSearch in Google Scholar
104 Moliere A, Vigneron E, eds. New developments in chromophore research. New York, USA: Nova Science Publishers Inc; 2013.Search in Google Scholar
105 Mayerhöfer TG, Mutschke H, Popp J. Employing theories far beyond their limits—the case of the (boguer-) beer–lambert law. Chem Phys Chem. 2016;17(13):1948–1955.10.1002/cphc.201600114Search in Google Scholar
106 Elliott P, Furche F, Burke K. Excited states from time-dependent density functional theory. In: Lipkowitz K.B., Cundari T.R., editor(s). Reviews in computational chemistry Vol. 26. Hoboken, NJ, USA: John Wiley & Sons, Inc., 2008:91–165.Search in Google Scholar
107 Yarkony DR. Modern electronic structure theory: part 1. Singapore, Singapore: World Scientific Publishing Co Pte Ltd; 1995.10.1142/1957-part2Search in Google Scholar
108 Franz K.A., et al. Luminescent materials, in Ullmann’s encyclopedia of industrial chemistry. Weinheim, Germany: Wiley-VCH Verlag GmbH & Co. KGaA, 2000.Search in Google Scholar
109 Marcus RA. On the theory of oxidation‐reduction reactions involving electron transfer. I. J Chem Phys. 1956;24(5):966–978.10.1063/1.1742723Search in Google Scholar
110 Marcus RA. Electron transfer reactions in chemistry: theory and experiment (nobel lecture). Angew Chem Int Ed. 1993;32(8):1111–1121.10.1002/anie.199311113Search in Google Scholar
111 Marenich, A.V., et al. Computational electrochemistry: prediction of liquid-phase reduction potentials. Phys Chem Chem Phys. 2014;16(29):15068–15106.10.1039/C4CP01572JSearch in Google Scholar PubMed
112 Berardi, S., et al. Molecular artificial photosynthesis. Chem Soc Rev. 2014;43(22):7501–7519.10.1039/C3CS60405ESearch in Google Scholar PubMed
113 Zeng, Q., et al. Role of ligands in catalytic water oxidation by mononuclear ruthenium complexes. Coord Chem Rev. 2015;304–305:88–101.10.1016/j.ccr.2015.03.003Search in Google Scholar
114 Miertuš S, Scrocco E, Tomasi J. Electrostatic interaction of a solute with a continuum. A direct utilizaion of AB initio molecular potentials for the prevision of solvent effects. Chem Phys. 1981;55(1):117–129.10.1016/0301-0104(81)85090-2Search in Google Scholar
115 Cossi, M., et al. Energies, structures, and electronic properties of molecules in solution with the C-PCM solvation model. J Comp Chem. 2003;24(6):669–681.10.1002/jcc.10189Search in Google Scholar PubMed
116 Cances E, Mennucci B, Tomasi J. A new integral equation formalism for the polarizable continuum model: theoretical background and applications to isotropic and anisotropic dielectrics. J Chem Phys. 1997;107(8):3032–3041.10.1063/1.474659Search in Google Scholar
117 Marenich AV, Cramer CJ, Truhlar DG. Universal solvation model based on solute electron density and on a continuum model of the solvent defined by the bulk dielectric constant and atomic surface tensions. J Phys Chem B. 2009;113(18):6378–6396.10.1021/jp810292nSearch in Google Scholar PubMed
118 Marenich, A.V., et al. Self-consistent reaction field model for aqueous and nonaqueous solutions based on accurate polarized partial charges. J Chem Theory Comput. 2007;3(6):2011–2033.10.1021/ct7001418Search in Google Scholar PubMed
119 Marenich AV, Cramer CJ, Truhlar DG. Universal solvation model based on the generalized born approximation with asymmetric descreening. J Chem Theory Comput. 2009;5(9):2447–2464.10.1021/ct900312zSearch in Google Scholar PubMed
120 Marenich AV, Cramer CJ, Truhlar DG. Generalized born solvation model SM12. J Chem Theory Comput. 2013;9(1):609–620.10.1021/ct300900eSearch in Google Scholar PubMed
121 Klamt A, Schuurmann G. COSMO: a new approach to dielectric screening in solvents with explicit expressions for the screening energy and its gradient. J Chem Soc Perk T. 1993;2(5):799–805.10.1039/P29930000799Search in Google Scholar
122 Klamt, A., et al. Refinement and Parametrization of COSMO-RS. J Phys Chem. 1998;102(26):5074–5085.10.1021/jp980017sSearch in Google Scholar
123 Tomasi J, Mennucci B, Cammi R. Quantum mechanical continuum solvation models. Chem Rev. 2005;105(8):2999–3094.10.1021/cr9904009Search in Google Scholar PubMed
124 Norskov, J.K., et al. Towards the computational design of solid catalysts. Nat Chem. 2009;1(1):37–46.10.1038/nchem.121Search in Google Scholar PubMed
125 Stan M. Discovery and design of nuclear fuels. Mater Today. 2009;12(11):20–28.10.1016/S1369-7021(09)70295-0Search in Google Scholar
126 Pitzer KS, Gwinn WD. Energy levels and thermodynamic functions for molecules with internal rotation I. rigid frame with attached tops. J Chem Phys. 1942;10(7):428–440.10.1063/1.1723744Search in Google Scholar
127 Truhlar DG. A simple approximation for the vibrational partition function of a hindered internal rotation. J Comput Chem. 1991;12(2):266–270.10.1002/jcc.540120217Search in Google Scholar
128 McClurg RB. “The hindered rotor density-of-states interpolation function”. J Chem Phys. 1997;106(16):6675–6680.10.1063/1.473664Search in Google Scholar
129 Ribeiro, R.F., et al. Use of solution-phase vibrational frequencies in continuum models for the free energy of solvation. J Phys Chem B. 2011;115(49):14556–14562.10.1021/jp205508zSearch in Google Scholar PubMed
130 Mammen, M., et al. Estimating the entropic cost of self-assembly of multiparticle hydrogen-bonded aggregates based on the cyanuric acid·melamine lattice. J Org Chem. 1998;63(12):3821–3830.10.1021/jo970944fSearch in Google Scholar
131 Grimme S. Supramolecular binding thermodynamics by dispersion-corrected density functional theory. Chem-Eur J. 2012;18(32):9955–9964.10.1002/chem.201200497Search in Google Scholar PubMed
132 Brush SG. History of the Lenz-Ising model. Rev Mod Phys. 1967;39(4):883–893.10.1103/RevModPhys.39.883Search in Google Scholar
133 Kadanoff LP. More is the same; phase transitions and mean field theories. J Stat Phys. 2009;137(5):777.10.1007/s10955-009-9814-1Search in Google Scholar
134 Bardeen J, Cooper LN, Schrieffer JR. Microscopic theory of superconductivity. Phys Rev. 1957;106(1):162–164.10.1103/PhysRev.106.162Search in Google Scholar
135 Bardeen J, Cooper LN, Schrieffer JR. Theory of superconductivity. Phys Rev. 1957;108(5):1175–1204.10.1103/PhysRev.108.1175Search in Google Scholar
136 Lasry J-M, Lions P-L. Mean field games. Jpn J Math. 2007;2(1):229–260.10.1007/s11537-007-0657-8Search in Google Scholar
137 Baccelli, F., et al. A mean-field limit for a class of queueing networks. J Stat Phys. 1992;66(3):803–825.10.1007/BF01055703Search in Google Scholar
138 Martin RM. Basic theory and practical methods. Cambridge, UK: Cambridge University Press; 2008.Search in Google Scholar
139 Thijssen JM. Computational physics. Cambridge, UK: Cambridge University Press; 1999.Search in Google Scholar
140 Marx D, Hutter J. Ab initio molecular dynamics: basic theory and advanced methods. Cambridge, UK: Cambridge University Press; 2010.10.1017/CBO9780511609633Search in Google Scholar
141 Capdevila-Cortada M, Lopez N. Entropic contributions enhance polarity compensation for CeO2(100) surfaces. Nat Mater. 2017;16(3):328–334.10.1038/nmat4804Search in Google Scholar PubMed
142 DACAPO. Available at: https://wiki.fysik.dtu.dk/dacapo.Search in Google Scholar
143 Hinnemann, B., et al. Biomimetic hydrogen evolution: MoS2 nanoparticles as catalyst for hydrogen evolution. J Am Chem Soc. 2005;127(15):5308–5309.10.1021/ja0504690Search in Google Scholar PubMed
144 Dresselhaus MS, Thomas IL. Alternative energy technologies. Nature. 2001;414(6861):332–337.10.1038/35104599Search in Google Scholar PubMed
145 Rauchfuss TB. Research on soluble metal sulfides: from polysulfido complexes to functional models for the hydrogenases. Inorg Chem. 2004;43(1):14–26.10.1021/ic0343760Search in Google Scholar PubMed
146 Mejia-Rodriguez, R., et al. The hydrophilic phosphatriazaadamantane ligand in the development of H2 production electrocatalysts: iron hydrogenase model complexes. J Am Chem Soc. 2004;126(38):12004–12014.10.1021/ja039394vSearch in Google Scholar PubMed
147 Razavet, M., et al. All-iron hydrogenase: synthesis, structure and properties of {2Fe3S}-assemblies related to the di-iron sub-site of the H-cluster. Dalton Trans. 2003;4:586–595.10.1039/b209690kSearch in Google Scholar
148 Ferruz N, De Fabritiis G. Binding kinetics in drug discovery. Mol Inform. 2016;35(6-7):216–226.10.1002/minf.201501018Search in Google Scholar PubMed
149 Harvey MJ, De Fabritiis G. High-throughput molecular dynamics: the powerful new tool for drug discovery. Drug Discov Today. 2012;17(19–20):1059–1062.10.1016/j.drudis.2012.03.017Search in Google Scholar PubMed
150 Buch I, Giorgino T, De Fabritiis G. Complete reconstruction of an enzyme-inhibitor binding process by molecular dynamics simulations. Proc Nati Acad Sci USA. 2011;108(25):10184–10189.10.1073/pnas.1103547108Search in Google Scholar PubMed PubMed Central
151 Pande VS, Beauchamp K, Bowman GR. Everything you wanted to know about Markov state models but were afraid to ask. Methods. 2010;52(1):99–105.10.1016/j.ymeth.2010.06.002Search in Google Scholar PubMed PubMed Central
152 Buch, I., et al. High-throughput all-atom molecular dynamics simulations using distributed computing. J Chem Inf Model. 2010;50(3):397–403.10.1021/ci900455rSearch in Google Scholar PubMed
153 Marquart, M., et al. The geometry of the reactive site and of the peptide groups in trypsin, trypsinogen and its complexes with inhibitors. Acta Crystallogr B. 1983;39(4):480–490.10.1107/S010876818300275XSearch in Google Scholar
154 Wagner, J.R., et al. Emerging computational methods for the rational discovery of allosteric drugs. Chem Rev. 2016;116(11):6370–6390.10.1021/acs.chemrev.5b00631Search in Google Scholar PubMed PubMed Central
155 Votapka LW, Amaro RE. Multiscale estimation of binding kinetics using brownian dynamics, molecular dynamics and milestoning. PLoS Comput Biol. 2015;11(10):e1004381.10.1371/journal.pcbi.1004381Search in Google Scholar PubMed PubMed Central
156 Ermak DL, McCammon JA. Brownian dynamics with hydrodynamic interactions. J Chem Phys. 1978;69(4):1352–1360.10.1063/1.436761Search in Google Scholar
157 Gabdoulline RR, Wade RC. Protein-protein association: investigation of factors influencing association rates by brownian dynamics simulations1. J Mol Biol. 2001;306(5):1139–1155.10.1006/jmbi.2000.4404Search in Google Scholar PubMed
158 Cohen RD. Self similarity in brownian motion and other ergodic phenomena. J Chem Ed. 1986;63(11):933.10.1021/ed063p933Search in Google Scholar
159 Pearle P, Collett B. What Brown saw and you can too. Am J Phys. 2010;78(12):1278–1289.10.1119/1.3475685Search in Google Scholar
160 Von Smoluchowski M. Zur kinetischen Theorie der Brownschen Molekularbewegung und der Suspensionen. Ann Phys-Leipzig. 1906;326(14):756–780.10.1002/andp.19063261405Search in Google Scholar
161 Greives N, Zhou H-X. BDflex: A method for efficient treatment of molecular flexibility in calculating protein-ligand binding rate constants from Brownian dynamics simulations. J Chem Phys. 2012;137(13):135105.10.1063/1.4756913Search in Google Scholar PubMed PubMed Central
162 Spaar, A., et al. Diffusional encounter of barnase and barstar. Biophys J. 2006;90(6):1913–1924.10.1529/biophysj.105.075507Search in Google Scholar PubMed PubMed Central
163 Buckle AM, Schreiber G, Fersht AR. Biochemistry-US. 1994;33:8878–8889.10.1021/bi00196a004Search in Google Scholar PubMed
164 Schlick T. Molecular modeling and simulation: an interdisciplinary guide. 2nd ed. New York, NY, USA: Springer-Verlag New York Inc.; 2010.10.1007/978-1-4419-6351-2Search in Google Scholar
165 Wood WW. Monte carlo calculations for hard disks in the isothermal‐isobaric ensemble. J Chem Phys. 1968;48(1):415–434.10.1063/1.1667938Search in Google Scholar
166 Norman GE, Filinov VS. Investigations of phase transitions by a Monte Carlo method. High Temp USSR. 1969;7:216–222.Search in Google Scholar
167 Cowen T, Karim K, Piletsky S. Computational approaches in the design of synthetic receptors – A review. Anal Chim Acta. 2016;936:62–74.10.1016/j.aca.2016.07.027Search in Google Scholar PubMed
168 Schauperl M, Lewis DW. Probing the structural and binding mechanism heterogeneity of molecularly imprinted polymers. J Phys Chem B. 2015;119(2):563–571.10.1021/jp506157xSearch in Google Scholar PubMed
169 Eyring H. The activated complex in chemical reactions. J Chem Phys. 1935;3(2):107–115.10.1063/1.1749604Search in Google Scholar
170 Truhlar DG. Transition state theory for enzyme kinetics. Arch Biochem Biophys. 2015;582:10–17.10.1016/j.abb.2015.05.004Search in Google Scholar PubMed PubMed Central
171 Hratchian HP, Schlegel HB. Chapter 10 - Finding minima, transition states, and following reaction pathways on ab initio potential energy surfaces A2 - Dykstra, Clifford E. In: Frenking G, Kim KS, Scuseria GE, editors. AIP conference proceedings. Amsterdam: Elsevier; 2005. p. 195–249.10.1016/B978-044451719-7/50053-6Search in Google Scholar
172 Truhlar DG, Garrett BC, Klippenstein SJ. Current status of transition-state theory. J Phys Chem. 1996;100(31):12771–12800.10.1021/jp953748qSearch in Google Scholar
173 Wigner E. Calculation of the rate of elementary association reactions. J Chem Phys. 1937;5(9):720–725.10.1063/1.1750107Search in Google Scholar
174 Horiuti J. On the statistical mechanical treatment of the absolute rate of chemical reaction. B Chem Soc Jpn. 1938;13(1):210–216.10.1246/bcsj.13.210Search in Google Scholar
175 Keck JC. Variational theory of reaction rates. In: Prigogine I., editor(s). Advances in chemical physics Vol. 13. Hoboken, NJ, USA: John Wiley & Sons, Inc, 1967:85–121.Search in Google Scholar
176 Truhlar DG, Garrett BC. Variational transition state theory. Annu Rev Phys Chem. 1984;35(1):159–189.10.1146/annurev.pc.35.100184.001111Search in Google Scholar
177 Pu J, Gao J, Truhlar DG. Multidimensional tunneling, recrossing, and the transmission coefficient for enzymatic reactions. Chem Rev. 2006;106(8):3140–3169.10.1021/cr050308eSearch in Google Scholar PubMed PubMed Central
178 Bell RP. The tunnel effect in chemistry. Boston, MA, USA: Springer; 1980.10.1007/978-1-4899-2891-7Search in Google Scholar
179 Compton RG. Comprehensive chemical kinetics: electron tunnelling in chemistry - chemical reactions over large distances v. 30. Oxford, UK: Elsevier Science & Technology; 1990.Search in Google Scholar
180 Gray HB, Halpern J. Distant charge transport. Proc Nati Acad Sci USA. 2005;102(10):3533–3533.10.1073/pnas.0501035102Search in Google Scholar PubMed PubMed Central
181 Le Roy RJ, Murai H, Williams F. Tunneling model for hydrogen abstraction reactions in low-temperature solids. Application to reactions in alcohol glasses and acetonitrile crystals. J Am Chem Soc. 1980;102(7):2325–2334.10.1021/ja00527a033Search in Google Scholar
182 Miller DJ, Subramanian R, Saunders WH. Mechanisms of elimination reactions. 33. Carbon isotope effects in E2 reactions of (2-phenylethyl-2-14C)trimethylammonium ion. The role of tunneling. J Am Chem Soc. 1981;103(12):3519–3522.10.1021/ja00402a043Search in Google Scholar
183 Bettens, F.L., et al. The microwave spectrum, structure, and ring-puckering of the cyclic dipeptide diketopiperazine. J Am Chem Soc. 2000;122(24):5856–5860.10.1021/ja000042nSearch in Google Scholar
184 Carpenter BK. Heavy-atom tunneling as the dominant pathway in a solution-phase reaction? Bond shift in antiaromatic annulenes. J Am Chem Soc. 1983;105(6):1700–1701.10.1021/ja00344a073Search in Google Scholar
185 Zuev, P.S., et al. Carbon tunneling from a single quantum state. Science. 2003;299(5608):867.10.1126/science.1079294Search in Google Scholar PubMed
186 Marcus RA, Coltrin ME. A new tunneling path for reactions such as H+H2→H2+H. J Chem Phys. 1977;67(6):2609–2613.10.1063/1.435172Search in Google Scholar
187 Fernandez-Ramos A. Variational transition state theory with multidimensional tunneling. In: Lipkowitz K.B., Cundari T.R., editor(s). Reviews in computational chemistry Vol. 23. Hoboken, NJ, USA: John Wiley & Sons, Inc., 2007:125–232.10.1002/9780470116449.ch3Search in Google Scholar
188 Truhlar DG. Tunneling in enzymatic and nonenzymatic hydrogen transfer reactions. J Phys Org Chem. 2010;23(7):660–676.10.1002/poc.1676Search in Google Scholar
189 Rudolf K, Spellmeyer DC, Houk KN. Prediction and experimental verification of the stereoselective electrocyclization of 3-formylcyclobutene. J Org Chem. 1987;52(16):3708–3710.10.1021/jo00392a047Search in Google Scholar
190 Bahmanyar S, Houk KN. Transition states of amine-catalyzed Aldol reactions involving enamine intermediates: theoretical studies of mechanism, reactivity, and stereoselectivity. J Am Chem Soc. 2001;123(45):11273–11283.10.1021/ja011403hSearch in Google Scholar PubMed
191 Rankin KN, Gauld JW, Boyd RJ. Density functional study of the proline-catalyzed direct Aldol reaction. J Phys Chem. 2002;106(20):5155–5159.10.1021/jp020079pSearch in Google Scholar
192 Clemente FR, Houk KN. Computational evidence for the enamine mechanism of intramolecular Aldol reactions catalyzed by Proline. Angew Chem Int Ed. 2004;43(43):5766–5768.10.1002/anie.200460916Search in Google Scholar PubMed
193 Bahmanyar S, Houk KN. The origin of stereoselectivity in Proline-catalyzed intramolecular Aldol reactions. J Am Chem Soc. 2001;123(51):12911–12912.10.1021/ja011714sSearch in Google Scholar PubMed
194 Houk KN, Cheong PH-Y. Computational prediction of small-molecule catalysts. Nature. 2008;455(7211):309–313.10.1038/nature07368Search in Google Scholar PubMed PubMed Central
195 Mollar, C., et al. Competitive and selective Csp3-Br versus Csp2-Br bond activation in palladium-catalysed suzuki cross-coupling: an experimental and theoretical study of the role of phosphine ligands. Chem–Eur J. 2010;16(45):13390–13397.10.1002/chem.201001113Search in Google Scholar PubMed
196 Bedford, R.B., et al. Exploiting Boron–Zinc transmetallation for the arylation of benzyl halides: what are the reactive species? Angew Chem Int Ed. 2012;51(22):5435–5438.10.1002/anie.201202219Search in Google Scholar PubMed
197 Harmata, M., et al. Combined computational and experimental studies of the mechanism and scope of the retro-Nazarov reaction. J Am Chem Soc. 2004;126(35):10954–10957.10.1021/ja048942hSearch in Google Scholar PubMed
198 Butts, C.P., et al. Structure-based rationale for selectivity in the asymmetric allylic alkylation of cycloalkenyl esters employing the trost ‘standard ligand’ (TSL): isolation, analysis and alkylation of the monomeric form of the cationic η3-cyclohexenyl complex [(η3-c-C6H9)Pd(TSL)]+. J Am Chem Soc. 2009;131(29):9945–9957.10.1021/ja8099757Search in Google Scholar PubMed
199 Nielsen MC, Lyngvi E, Schoenebeck F. Chemoselectivity in the reductive elimination from high oxidation state palladium complexes – scrambling mechanism uncovered. J Am Chem Soc. 2013;135(5):1978–1985.10.1021/ja312047bSearch in Google Scholar PubMed
200 Proutiere F, Aufiero M, Schoenebeck F. Reactivity and stability of dinuclear Pd(I) complexes: studies on the active catalytic species, insights into precatalyst activation and deactivation, and application in highly selective cross-coupling reactions. J Am Chem Soc. 2012;134(1):606–612.10.1021/ja209424zSearch in Google Scholar PubMed
201 Sköld, C., et al. Transmetallation versus β-hydride elimination: the role of 1,4-benzoquinone in chelation-controlled arylation reactions with arylboronic acids. Chem–Eur J. 2012;18(15):4714–4722.10.1002/chem.201102678Search in Google Scholar PubMed PubMed Central
202 Schreiner, P.R., et al. Methylhydroxycarbene: tunneling control of a chemical reaction. Science. 2011;332(6035):1300.10.1126/science.1203761Search in Google Scholar PubMed
203 Wondimagegn, T., et al. Computational design of C2-symmetric metallocene-based catalysts for the synthesis of high molecular weight polymers from ethylene/propylene copolymerization. Organometallics. 2008;27(24):6434–6439.10.1021/om800731ySearch in Google Scholar
204 Tantillo DJ. Using theory and experiment to discover catalysts for electrocyclizations. Angew Chem Int Ed. 2009;48(1):31–32.10.1002/anie.200804908Search in Google Scholar PubMed
205 Lin Z. Interplay between theory and experiment: computational organometallic and transition metal chemistry. Acc Chem Res. 2010;43(5):602–611.10.1021/ar9002027Search in Google Scholar PubMed
206 Donoghue, P.J., et al. Prediction of enantioselectivity in rhodium catalyzed hydrogenations. J Am Chem Soc. 2009;131(2):410–411.10.1021/ja806246hSearch in Google Scholar PubMed
207 Conley, B.L., et al. Design and study of homogeneous catalysts for the selective, low temperature oxidation of hydrocarbons. J Mol Cat A-Chem. 2006;251(1–2):8–23.10.1016/j.molcata.2006.02.035Search in Google Scholar
208 Alapati SV, Karl Johnson J, Sholl DS. Using first principles calculations to identify new destabilized metal hydride reactions for reversible hydrogen storage. Phys Chem Chem Phys. 2007;9(12):1438–1452.10.1039/b617927dSearch in Google Scholar PubMed
209 Guo, W., et al. A metal-free synthesis of N-Aryl carbamates under ambient conditions. Angew Chem Int Ed. 2015;54(40):11686–11690.10.1002/anie.201504956Search in Google Scholar PubMed
210 Fiore AM, Naik V, Leibensperger EM. Air quality and climate connections. J Air Waste Manage. 2015;65(6):645–685.10.1080/10962247.2015.1040526Search in Google Scholar PubMed
211 Antonakakis N, Chatziantoniou I, Filis G. Energy consumption, CO2 emissions, and economic growth: an ethical dilemma. Renew Sust Energ Rev. 2017;68:808–824.10.1016/j.rser.2016.09.105Search in Google Scholar
212 Rogelj, J., et al. Paris agreement climate proposals need a boost to keep warming well below 2 °c. Nature. 2016;534(7609):631–639.10.1038/nature18307Search in Google Scholar
213 Smith, P., et al. Biophysical and economic limits to negative CO2 emissions. Nat Clim Change. 2016;6(1):42–50.10.1038/nclimate2870Search in Google Scholar
214 Gattuso J.P., et al. Contrasting futures for ocean and society from different anthropogenic CO2 emissions scenarios. Science. 2015;349(6243):AAC4722–AAC4722-10.10.1126/science.aac4722Search in Google Scholar
215 Aresta M, Dibenedetto A, Angelini A. Catalysis for the valorization of exhaust carbon: from CO2 to chemicals, materials, and fuels. technological use of CO2. Chem Rev. 2014;114(3):1709–1742.10.1021/cr4002758Search in Google Scholar PubMed
216 Liu, Q., et al. Using carbon dioxide as a building block in organic synthesis. Nat Commun. 2015;6:5933.10.1038/ncomms6933Search in Google Scholar PubMed
217 Yu B, He L-N. Upgrading carbon dioxide by incorporation into heterocycles. Chem Sus Chem. 2015;8(1):52–62.10.1002/cssc.201402837Search in Google Scholar
218 Tantillo DJ, Jiangang C, Houk KN. Theozymes and compuzymes: theoretical models for biological catalysis. Curr Opin Chem Biol. 1998;2(6):743–750.10.1016/S1367-5931(98)80112-9Search in Google Scholar PubMed
219 Jiang, L., et al. De novo computational design of retro-aldol enzymes. Science. 2008;319(5868):1387.10.1126/science.1152692Search in Google Scholar PubMed PubMed Central
220 Rothlisberger, D., et al. Kemp elimination catalysts by computational enzyme design. Nature. 2008;453(7192):190–195.10.1038/nature06879Search in Google Scholar PubMed
221 Siegel, J.B., et al. Computational design of an enzyme catalyst for a stereoselective bimolecular Diels-Alder reaction. Science. 2010;329(5989):309.10.1126/science.1190239Search in Google Scholar PubMed PubMed Central
222 Zanghellini, A., et al. New algorithms and an in silico benchmark for computational enzyme design. Protein Sci. 2006;15(12):2785–2794.10.1110/ps.062353106Search in Google Scholar PubMed PubMed Central
223 Metiu H. Physical Chemistry: kinetics. CT, USA: Taylor & Francis Inc; 2006.10.1201/9780429258916Search in Google Scholar
224 Seeman JI. The Curtin-Hammett principle and the Winstein-Holness equation: new definition and recent extensions to classical concepts. J Chem Ed. 1986;63(1):42.10.1021/ed063p42Search in Google Scholar
225 Rush LE, Pringle PG, Harvey JN. Computational kinetics of cobalt-catalyzed alkene hydroformylation. Angew Chem Int Ed. 2014;53(33):8672–8676.10.1002/anie.201402115Search in Google Scholar PubMed
226 Bader G, Deuflhard P. A semi-implicit mid-point rule for stiff systems of ordinary differential equations. Numer Math. 1983;41(3):373–398.10.1007/BF01418331Search in Google Scholar
227 Goehry C, Besora M, Maseras F. Computational study on the mechanism of the acceleration of 1,3-dipolar cycloaddition inside cucurbit[6]uril. ACS Catal. 2015;5(4):2445–2451.10.1021/cs501703tSearch in Google Scholar
228 Fernández-Alvarez, V.M., et al. Computational study with DFT and kinetic models on the mechanism of photoinitiated aromatic perfluoroalkylations. Org Lett. 2015;17(11):2676–2679.10.1021/acs.orglett.5b01069Search in Google Scholar PubMed
229 Lifson S, Warshel A. Consistent force field for calculations of conformations, vibrational spectra, and enthalpies of cycloalkane and n‐alkane molecules. J Chem Phys. 1968;49(11):5116–5129.10.1063/1.1670007Search in Google Scholar
230 Levitt M. Birth and future of multiscale modeling for macromolecular systems (nobel lecture). Angew Chem Int Ed. 2014;53(38):10006–10018.10.1002/anie.201403691Search in Google Scholar PubMed
231 Warshel A, Levitt M. Theoretical studies of enzymic reactions: dielectric, electrostatic and steric stabilization of the carbonium ion in the reaction of lysozyme. J Mol Biol. 1976;103(2):227–249.10.1016/0022-2836(76)90311-9Search in Google Scholar PubMed
232 Maseras F, Morokuma K. IMOMM: A new integrated ab initio + molecular mechanics geometry optimization scheme of equilibrium structures and transition states. J Comput Chem. 1995;16(9):1170–1179.10.1002/jcc.540160911Search in Google Scholar
233 Vreven, T., et al. Combining quantum mechanics methods with molecular mechanics methods in ONIOM. J Chem Theory Comput. 2006;2(3):815–826.10.1021/ct050289gSearch in Google Scholar PubMed
234 Balcells D, Maseras F. Computational approaches to asymmetric synthesis. New J Chem. 2007;31(3):333–343.10.1039/b615528fSearch in Google Scholar
235 Bo C, Maseras F. QM/MM methods in inorganic chemistry. Dalton Trans. 2008;22:2911–2919.10.1039/b718076dSearch in Google Scholar PubMed
236 Brown JM, Deeth RJ. Is enantioselectivity predictable in asymmetric catalysis? Angew Chem Int Ed. 2009;48(25):4476–4479.10.1002/anie.200900697Search in Google Scholar PubMed
237 Nielsen MC, Bonney KJ, Schoenebeck F. Computational Ligand design for the reductive elimination of ArCF3 from a small bite angle PdII complex: remarkable effect of a perfluoroalkyl phosphine. Angew Chem Int Ed. 2014;53(23):5903–5906.10.1002/anie.201400837Search in Google Scholar PubMed
238 Anstaett P, Schoenebeck F. Reductive elimination of ArCF3 from bidentate PdII complexes: a computational study. Chem-Eur J. 2011;17(44):12340–12346.10.1002/chem.201101373Search in Google Scholar PubMed
239 Palermo, G., et al. Fighting cancer with transition metal complexes: from naked DNA to protein and chromatin targeting strategies. Chem Med Chem. 2016;11(12):1199–1210.10.1002/cmdc.201500478Search in Google Scholar PubMed PubMed Central
240 Parr RG, Yang W. Density functional approach to the frontier-electron theory of chemical reactivity. J Am Chem Soc. 1984;106(14):4049–4050.10.1021/ja00326a036Search in Google Scholar
241 Dapprich S, Frenking G. Investigation of donor-acceptor interactions: a charge decomposition analysis using fragment molecular orbitals. J Phys Chem. 1995;99(23):9352–9362.10.1021/j100023a009Search in Google Scholar
242 Weinhold F, Landis CR, Glendening ED. What is NBO analysis and how is it useful? Int Rev Phys Chem. 2016;35(3):399–440.10.1080/0144235X.2016.1192262Search in Google Scholar
243 Glendening ED, Landis CR, Weinhold F. NBO 6.0: natural bond orbital analysis program. J Comput Chem. 2013;34(16):1429–1437.10.1002/jcc.23266Search in Google Scholar PubMed
244 Zubarev DY, Boldyrev AI. Developing paradigms of chemical bonding: adaptive natural density partitioning. Phys Chem Chem Phys. 2008;10(34):5207–5217.10.1039/b804083dSearch in Google Scholar PubMed
245 Bader RFW. A quantum theory of molecular structure and its applications. Chem Rev. 1991;91(5):893–928.10.1021/cr00005a013Search in Google Scholar
246 Lu T, Chen F. Multiwfn: a multifunctional wavefunction analyzer. J Comput Chem. 2012;33(5):580–592.10.1002/jcc.22885Search in Google Scholar PubMed
247 Lu T MULTIWFN: a multifunctional wavefunction analyzer. Available at: http://sobereva.com/multiwfn/. Accessed 5 June 201710.1002/jcc.22885Search in Google Scholar
248 Software, B.f.I. Aim2000. Available at: http://www.aim2000.de/impressum.htm. Accessed 5 June 2017Search in Google Scholar
249 Keith TA AIMAll. Available at: http://aim.tkgristmill.com/ Accessed 5 June 2017.Search in Google Scholar
250 Becke AD, Edgecombe KE. A simple measure of electron localization in atomic and molecular systems. J Chem Phys. 1990;92(9):5397–5403.10.1063/1.458517Search in Google Scholar
251 Savin, A., et al. Electron localization in solid-state structures of the elements: the diamond structure. Angew Chem Int Ed. 1992;31(2):187–188.10.1002/anie.199201871Search in Google Scholar
252 Schmider HL, Becke AD. Chemical content of the kinetic energy density. J Mol Struc-Theochem. 2000;527(1–3):51–61.10.1016/S0166-1280(00)00477-2Search in Google Scholar
253 Jacobsen H. Localized-orbital locator (LOL) profiles of chemical bonding. Can J Chem. 2008;86(7):695–702.10.1139/v08-052Search in Google Scholar
254 Johnson, E.R., et al. Revealing noncovalent interactions. J Am Chem Soc. 2010;132(18):6498–6506.10.1021/ja100936wSearch in Google Scholar PubMed
255 Bader RFW, Gatti C. A green’s function for the density. Chem Phys Lett. 1998;287(3–4):233–238.10.1016/S0009-2614(97)01457-7Search in Google Scholar
256 Wang, X., et al. Mercury is a transition metal: the first experimental evidence for HgF4. Angew Chem Int Ed. 2007;46(44):8371–8375.10.1002/anie.200703710Search in Google Scholar
257 Kaupp M, Von Schnering HG. Gaseous mercury(IV) fluoride, HgF4: an ab initio study. Angew Chem Int Ed. 1993;32(6):861–863.10.1002/anie.199308611Search in Google Scholar
258 Kaupp, M., et al. Oxidation state +IV in group 12 chemistry. Ab initio study of Zinc(IV), Cadmium(IV), and mercury(IV) fluorides. Inorg Chem. 1994;33(10):2122–2131.10.1021/ic00088a012Search in Google Scholar
259 Liu W, Franke R, Dolg M. Relativistic ab initio and density functional theory calculations on the mercury fluorides: is HgF4 thermodynamically stable? Chem Phys Lett. 1999;302(3–4):231–239.10.1016/S0009-2614(99)00147-5Search in Google Scholar
260 Riedel S, Straka M, Kaupp M. Can weakly coordinating anions stabilize mercury in its oxidation state +IV? Chem–Eur J. 2005;11(9):2743–2755.10.1002/chem.200401130Search in Google Scholar PubMed
261 Pyykko P, Straka M, Patzschke M. HgH4 and HgH6: further candidates for high-valent mercury compounds. Chem Commun. 2002;16:1728–1729.10.1039/B203585ESearch in Google Scholar
262 Manly, C.J., et al. Strategies and tactics for optimizing the hit-to-lead process and beyond—A computational chemistry perspective. Drug Discov Today. 2008;13(3–4):99–109.10.1016/j.drudis.2007.10.019Search in Google Scholar PubMed
263 Manly CJ. Computational chemistry, data mining, high-throughput synthesis and screening - informatics and integration in drug discovery. J Autom Meth Manag. 2001;23(6):191–192.Search in Google Scholar
264 Kutchukian PS, Lou D, Shakhnovich EI. FOG: fragment optimized growth algorithm for the de novo generation of molecules occupying druglike chemical space. J Chem Inf Model. 2009;49(7):1630–1642.10.1021/ci9000458Search in Google Scholar PubMed
265 Cherkasov, A., et al. QSAR modeling: where have you been? Where are you going to? J Med Chem. 2014;57(12):4977–5010.10.1021/jm4004285Search in Google Scholar PubMed PubMed Central
266 Bajorath J. Selected concepts and Investigations in compound classification, molecular descriptor analysis, and virtual screening. J Chem Inf Comp Sci. 2001;41(2):233–245.10.1021/ci0001482Search in Google Scholar PubMed
267 Goodford PJ. A computational procedure for determining energetically favorable binding sites on biologically important macromolecules. J Med Chem. 1985;28(7):849–857.10.1021/jm00145a002Search in Google Scholar PubMed
268 Cramer RD, Patterson DE, Bunce JD. Comparative molecular field analysis (CoMFA). 1. Effect of shape on binding of steroids to carrier proteins. J Am Chem Soc. 1988;110(18):5959–5967.10.1021/ja00226a005Search in Google Scholar PubMed
269 Kozlowski, M.C., et al. Quantum mechanical models correlating structure with selectivity: predicting the enantioselectivity of β-amino alcohol catalysts in aldehyde alkylation. J Am Chem Soc. 2003;125(22):6614–6615.10.1021/ja0293195Search in Google Scholar PubMed
270 Ianni, J.C., et al. A priori theoretical prediction of selectivity in asymmetric catalysis: design of chiral catalysts by using quantum molecular interaction fields. Angew Chem Int Ed. 2006;45(33):5502–5505.10.1002/anie.200600329Search in Google Scholar PubMed
271 Gentili PL. Small steps towards the development of chemical artificial intelligent systems. Rsc Adv. 2013;3(48):25523–25549.10.1039/c3ra44657cSearch in Google Scholar
272 Corey EJ, Howe WJ, Pensak DA. Computer-assisted synthetic analysis. Methods for machine generation of synthetic intermediates involving multistep look-ahead. J Am Chem Soc. 1974;96(25):7724–7737.10.1021/ja00832a019Search in Google Scholar
273 Fialkowski, M., et al. Architecture and evolution of organic chemistry. Angew Chem Int Ed. 2005;44(44):7263–7269.10.1002/anie.200502272Search in Google Scholar PubMed
274 Gothard, C.M., et al. Rewiring chemistry: algorithmic discovery and experimental validation of one-pot reactions in the network of organic chemistry. Angew Chem Int Ed. 2012;51(32):7922–7927.10.1002/anie.201202155Search in Google Scholar PubMed
275 Kowalik, M., et al. Parallel optimization of synthetic pathways within the network of organic chemistry. Angew Chem Int Ed. 2012;51(32):7928–7932.10.1002/anie.201202209Search in Google Scholar PubMed
276 Fuller, P.E., et al. Chemical network algorithms for the risk assessment and management of chemical threats. Angew Chem Int Ed. 2012;51(32):7933–7937.10.1002/anie.201202210Search in Google Scholar PubMed
277 Mitchell JBO. Machine learning methods in chemoinformatics. Wires Comput Mol Sci. 2014;4(5):468–481.10.1002/wcms.1183Search in Google Scholar PubMed PubMed Central
278 Moore GE. Cramming more components onto integrated circuits, reprinted from electronics, volume 38, number 8, April 19, 1965, pp0.114 ff. IEEE Solid-State Circuits Soc Newsletter. 2006;11(5):33–35.10.1109/N-SSC.2006.4785860Search in Google Scholar
279 D-Wave System Inc. Available at: https://www.dwavesys.com/.Search in Google Scholar
280 Boixo, S., et al. Experimental signature of programmable quantum annealing. Nat Commun. 2013;4:2067.10.1038/ncomms3067Search in Google Scholar PubMed
281 Albash, T., et al. Consistency tests of classical and quantum models for a quantum annealer. Phys Rev. 2015;91(4):042314.10.1103/PhysRevA.91.042314Search in Google Scholar
282 Lanting, T., et al. Entanglement in a quantum annealing processor. Phys Rev X. 2014;4(2):021041.10.1103/PhysRevX.4.021041Search in Google Scholar
283 Cho A. Quantum or not, controversial computer yields no speedup. Science. 2014;344(6190):1330.10.1126/science.344.6190.1330Search in Google Scholar PubMed
284 Steiger, D.S., et al. Performance of quantum annealing hardware. in Proc. SPIE 9648, Electro-Optical and Infrared Systems: Technology and Applications XII; and Quantum Information Science and Technology. 2015.10.1117/12.2202661Search in Google Scholar
285 Wikipedia, t.f.e. List of quantum chemistry and solid-state physics software. Available at: https://en.wikipedia.org/wiki/List_of_quantum_chemistry_and_solid-state_physics_software. Accessed 5 June 2017.Search in Google Scholar
286 Wikipedia, t.f.e. Category: computationalchemistry software. Available from: https://en.wikipedia.org/wiki/Category:Computational_chemistry_software. Accessed 5 June 2017Search in Google Scholar
287 Wikipedia, t.f.e. List of molecular graphic systems. Available at: https://en.wikipedia.org/wiki/List_of_molecular_graphics_systems. Accessed 5 June 2017.Search in Google Scholar
288 Butler D. Electronic notebooks: A new leaf. Nature. 2005;436(7047):20–21.10.1038/436020aSearch in Google Scholar PubMed
289 Choi BCK, Pak AWP. Multidisciplinarity, interdisciplinarity, and transdisciplinarity in health research, services, education and policy: 2. Promotors, barriers, and strategies of enhancement. Clin Invest Med. 2007;30(6):E224-E232.10.25011/cim.v30i6.2950Search in Google Scholar PubMed
290 Zhang, Y., et al. Biological impact of environmental polycyclic aromatic hydrocarbons (ePAHs) as endocrine disruptors. Environ Pollut. 2016;213:809–824.10.1016/j.envpol.2016.03.050Search in Google Scholar PubMed
© 2017 Walter de Gruyter GmbH, Berlin/Boston

