Abstract
The study of bimetallic nanoalloy clusters is of immense importance due to their diverse applications in the field of science and engineering. A deep theoretical insight is required to explain the physico-chemical properties of such compounds. Among such nanoalloy clusters, the compound formed between Ag and Au has received a lot of attention because of their marked electronic, catalytic, optical and magnetic properties. Density Functional Theory (DFT) is one of the most successful approaches of quantum mechanics to study the electronic properties of materials. Conceptual DFT-based descriptors have turned to be indispensable tools for analysing and correlating the experimental properties of compounds. In this report, we have investigated the ground state configurations and physico-chemical properties of Ag2AuNλ (N = 1–7, λ=±1, 0) nanoalloy clusters invoking DFT methodology. Our computed data exhibits interesting odd-even oscillation behaviour. A close agreement between experimental and our computed bond length supports our theoretical analysis.
1 Introduction
In the recent decades, nanotechnology and its applications have deeply integrated into human’s daily life due to its large-scale applications. Since last few years, nanotechnology has emerged as a new research dimension in the domain of science and engineering [1]. The classification of nanoparticles has been done in terms of size range, which has at least one dimension in the range of 1 to 100 nm. That particular size range exists between the levels of atomic/molecular and bulk materials [1, 2, 3, 4, 5]. Nanoparticles possess unique physico-chemical properties due to existence of a large number of quantum mechanical and electronic effects [2, 3, 4]. However, there are still some instances of nonlinear alteration which shows certain physical properties may vary depending on their size, shape and composition [6]. There are a large number of available scientific reports which illustrate the effects on size and geometry to change the electronic, magnetic, optical, mechanical, chemical and other physical properties of nanoparticles [1, 3, 4]. A deep insight into the study of nanoparticles with well-defined size and geometry may open some better alternatives [7]. The nanoparticles due to its numerous applications in the field of nanotechnology, nano-electronics, material science, bio-medicine, catalysis etc. are of great interest [1, 3, 7, 8, 9, 10].
Now a days, study of noble metal clusters such as Cu, Ag, and Au has gained a significant due to their marked optical, electronic, catalytic and magnetic properties [11, 12, 13, 14, 16, 17, 18, 19]. Especially, gold nanoclusters are very much popular and potential candidates for fabrication, bio-physics, and medical applications due to its unique catalytic, optical and electronic properties [20, 21, 22, 23, 24, 25, 26, 27, 28, 29, 30, 31, 32, 33, 34, 35]. Study of bimetallic nanoalloy clusters has emerged as an important topic from both theoretical and experimental point of view, since they exhibit new type of characteristics which are distinct from the pure and bulk metallic systems [11]. In recent days, different compositions of nanoalloys are being utilized for advancement of methodologies and characterization techniques [13, 19, 21]. The study based on core shell structure of nano-compounds is very popular because its properties can be altered through proper control of other structural and chemical parameters. Group 11 metal (Cu, Ag and Au) clusters possess filled d orbitals and one unpaired electron in s shell [22]. This peculiar electronic arrangement is responsible to reproduce the exactly similar shell effects, which are experimentally observed in the alkali metal clusters [23, 24, 25, 26, 27, 28, 29, 30].
Many experimental and theoretical studies have been reported on Ag-Au nanoalloy clusters. Negishi et al. [36] have studied geometrical structure and electronic states of AunAgm− (2 ≤ n + m ≤ 4) clusters using photoelectron spectroscopy technique. Heiles et al. [37] have investigated the composition of 8-atom Au-Ag clusters using GA-DFT approach. Transition from 2D to 3D between Au6Ag2 and Au5Ag3 clusters are reported. Weis et al. [38] have reported ion mobility measurement and DFT calculations of AgmAun+, m+n˂6 clusters. In that report, they have pointed out that trimeric ions are in generally triangular shape whereas most of the tetrameric clusters are in rhombus shape, with the exception of Ag3Au+. Lee et al. [39] have studied structure and electronic properties of Ag, Au and Ag-Au clusters invoking DFT calculations. They have mentioned that in even number clusters are more stable as compared to odd number for neutral state, however in anionic state reverse trend is observed. Geometries, ionization energies and vertical detachment energies for neutral, cationic and anionic bimetallic AgmAun 3 ≤ m + n ≤ 5 clusters are also reported by Bonacic- Koutecky et al. [40]. Recently, Tafoughalt et al. [41] have reported ground state configurations, binding energy, HOMO–LUMO gap, magnetic moment, ionization energy, electron affinity and chemical hardness of AgnAum clusters, up to eight atoms. The result indicate that addition of Au atoms in the cluster exhibits in high binding energy and ionization potential. Shayeghi et al. [42] have computed electronic and optical properties of AgnAu4-n+ (n = 1–3) clusters in terms of DFT method and made a comparative analysis with experimental data. Zhao et al. [43] have reported computational study on structures, stabilities, growth-pattern behaviours and electronic properties of bimetallic M2Aun (M = Ag, Cu; n = 1–10) clusters. Their result indicates that Ag2Au4 and Cu2Au2 clusters are the most stable structures. A study of Geometry and electronic properties of AumAgn (2 ≤ m + n≤ 8) clusters has been reported by Zhao et al. [44]. Investigation of electronic and photoluminescence properties of AgnAu25-n2+ nanoclusters in terms of time-dependent density functional calculations has been done by Miranda et al. [45]. The result suggests that silver doping improves the fluorescence behaviour. In another study Tafoughalt et al. [46] have also discussed binding energies, second-order difference in energies, dissociation energies and HOMO–LUMO gap of AgAun-1 (n = 3–13) clusters. Recently, Shayeghi et al. [47] have reported vibrational spectra of AunAgm+.Ark (n+m=4,5; k = 1–4) clusters invoking FIR-MPD spectroscopy in terms of Messenger-Atom technique and Density Functional Theory (DFT) methodology. The computational data are in similar line with the FIR-MPD experiments. Chi et al. [48] has proved that gold improves the stability of AgAu cluster. The binding energy of the bimetallic clusters also increases with the increasing number of gold atoms.
DFT is one of the most popular approaches for the quantum mechanical computation of molecular system [49]. Due to its computational friendly behaviour, DFT is widely accepted method to study the many-body systems. In the domain of material science research, particularly in super conductivity of metal-based alloys, structural, electronic, magnetic and optical properties of nano-alloy clusters, quantum fluid dynamics, molecular dynamics, nuclear physics, DFT has gained a huge importance [50]. The study of DFT covers three major domains viz. theoretical, conceptual and computational [51, 52, 53, 54]. Conceptual DFT is established as an important approach to study the chemical reactivity of materials [55, 56, 57]. The Conceptual DFT is highlighted following Parr’s dictum “Accurate calculation is not synonymous with useful interpretation. To calculate a molecule is not to understand it” [58]. We have rigorously applied conceptual density functional-based local and global descriptors to study physico-chemical properties of nano-engineering materials and drug designing process [59, 60, 61, 62, 63, 64, 65, 66, 67, 68, 69].
In the present venture, we have investigated bi-metallic nanoalloy clusters of Ag2AuNλ (N = 1–7, λ=±1,0) invoking DFT-based global descriptors. An attempt has been made to correlate the properties of the compounds with their computational counterparts.
2 Computational details
A computational investigation on the bi-metallic nanoalloy clusters of Ag2AuNλ (N = 1–7, λ= ±1,0) is performed invoking electronic structure theory. Geometry optimizations have been done using Gaussian 03 [70] within DFT framework. The Local Spin Density Approximation [71] (LSDA) of exchange correlation has been adopted with basis set LanL2dz [72, 73, 74, 75]. LSDA functional is popular in computational study of the materials [65, 76, 77, 78, 79, 80]. High accuracy of LanL2dz basis set for metallic clusters is already reported [6, 43, 80, 81, 82, 83]. In spite of less complexity of LDA functional, it is highly effective in study of solid state physics [71], where accurate phase transitions in solids [72] and liquid metals [73, 74] are predicted, and for lattice crystals, in which 1 % precision are successfully achieved [75].
Restriction on molecular spin is not imposed during geometry optimization. Z-axis is considered as spin polarization axis and Symmetrized Fragment Orbitals (SFOs) are combined with auxiliary Core Functions (CFs) to ensure orthogonalization on the (frozen) Core Orbitals (Cos) [84, 85].
Invoking Koopman’s approximation [55], Ionization Energy (I) and Electron Affinity (A) of all the nanoalloys have been computed in terms of following
Thereafter, using I and A, the conceptual DFT-based descriptors viz. electronegativity (χ), global hardness (η), molecular softness (S) and electrophilicity index (ω) have been computed as:
where µ represents the chemical potential of the system.
3 Results and discussion
3.1 Equilibrium geometries
For bi-metallic Ag2AuNλ (N = 1–7, λ= ±1, 0) clusters, the optimized ground state configurations of neutral, cationic and anionic state are shown in Figure 1–Figure 3 respectively. For Ag2Au cluster (N = 1 and λ = ±1,0), we have computed triangular geometrical structure with symmetry group C2v. This is in line with the previous results reported by Bonacic- Koutecky et al. [40] and Tafoughalt et al. [41]. In Ag2Au+ cluster, the Ag-Au bond length is 2.60 Å and in neutral Ag2Au cluster, Ag-Au bond length is 2.64 Å which are in agreement with the previous values reported by Weis et al. [38]. For N = 2, Ag2Au2 cluster has rhombus structure, observed as the most stable geometry for tetramers. In this geometry, gold atoms are located at the corners of the clusters, while silver atoms connected to each other with short diagonal. The ground state configuration of Ag2Au3 cluster is found as trapezoidal structure with symmetry group C2v. Here, three gold atoms form a triangular structure in the middle of the cluster, while silver atoms occupy the corners. For N = 4, the most stable structure is planar for neutral and anionic whereas cationic cluster has 2D structure. For neutral and anionic forms of Ag2Au4 cluster, the structures are extension of Ag2Au2 cluster with C2v symmetry in which two gold atoms are connected on both the corners of rhombus structure and two silver atoms are connected in the middle of the cluster. It supports to form maximum number of bonds with gold atoms. The cluster Ag2Au5 has silver atom at the centre to form maximum number of Ag-Au bonds. The Ag2Au5 has symmetry group Cs. The same structure was reported by Zhao et al. [44]. The most stable structure of Ag2Au6 is obtained due to extension of Ag2Au5. Here the silver atoms, located at the centre, are surrounded by gold atoms. And consequently maximum number of Ag-Au bonds are formed. The cluster Ag2Au6 is under C1 symmetry group. For N = 7, all nine atoms are planar with symmetry group D2h. In this structure, four gold atoms are connected as a rectangular format and one gold atom, located in the middle, is connected with these atoms. Two gold and two silver atoms are connected to form edge capping from all the sides.
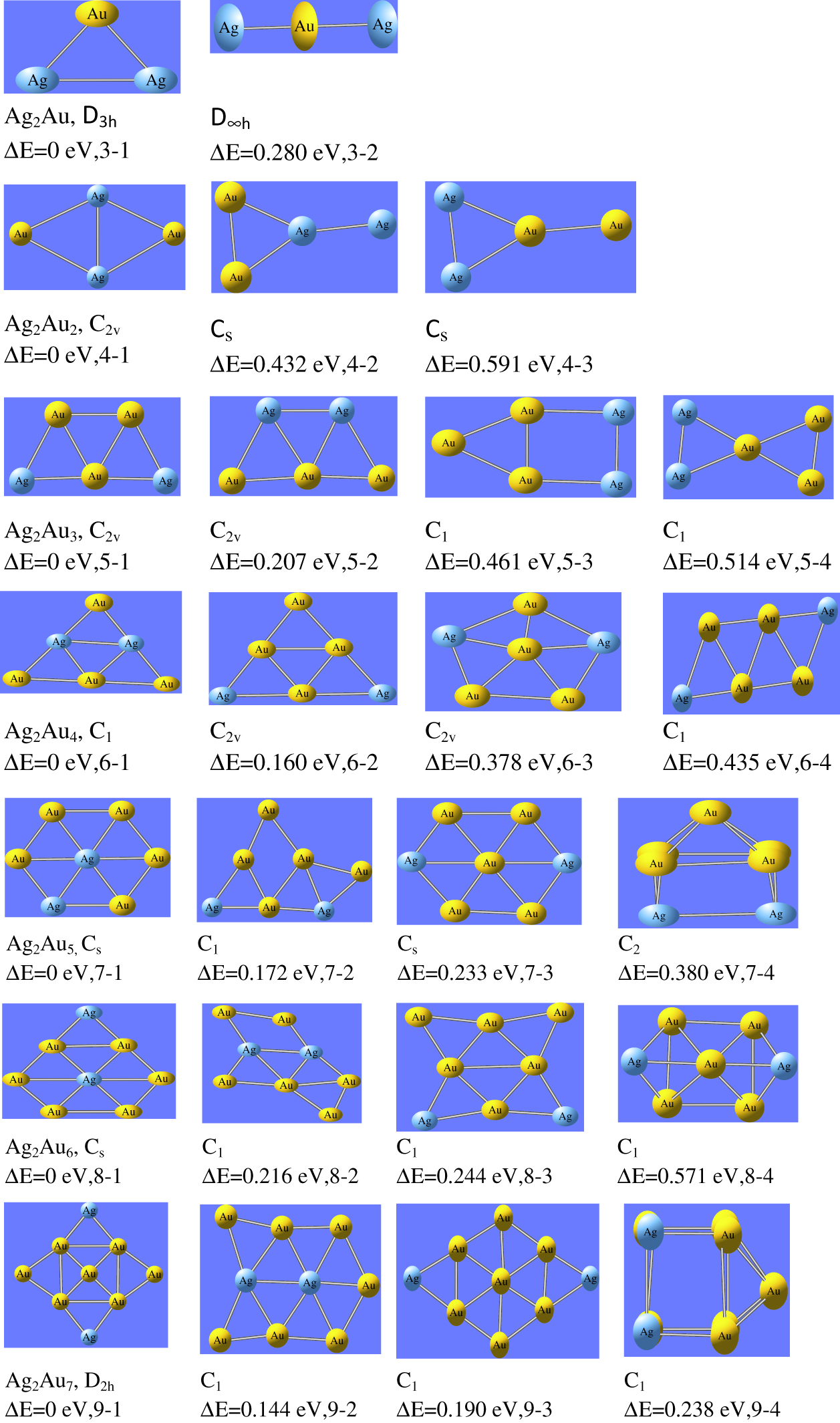
The ground state configurations of Ag2AuNλ (N = 1–7, λ=0) nanoalloy clusters.
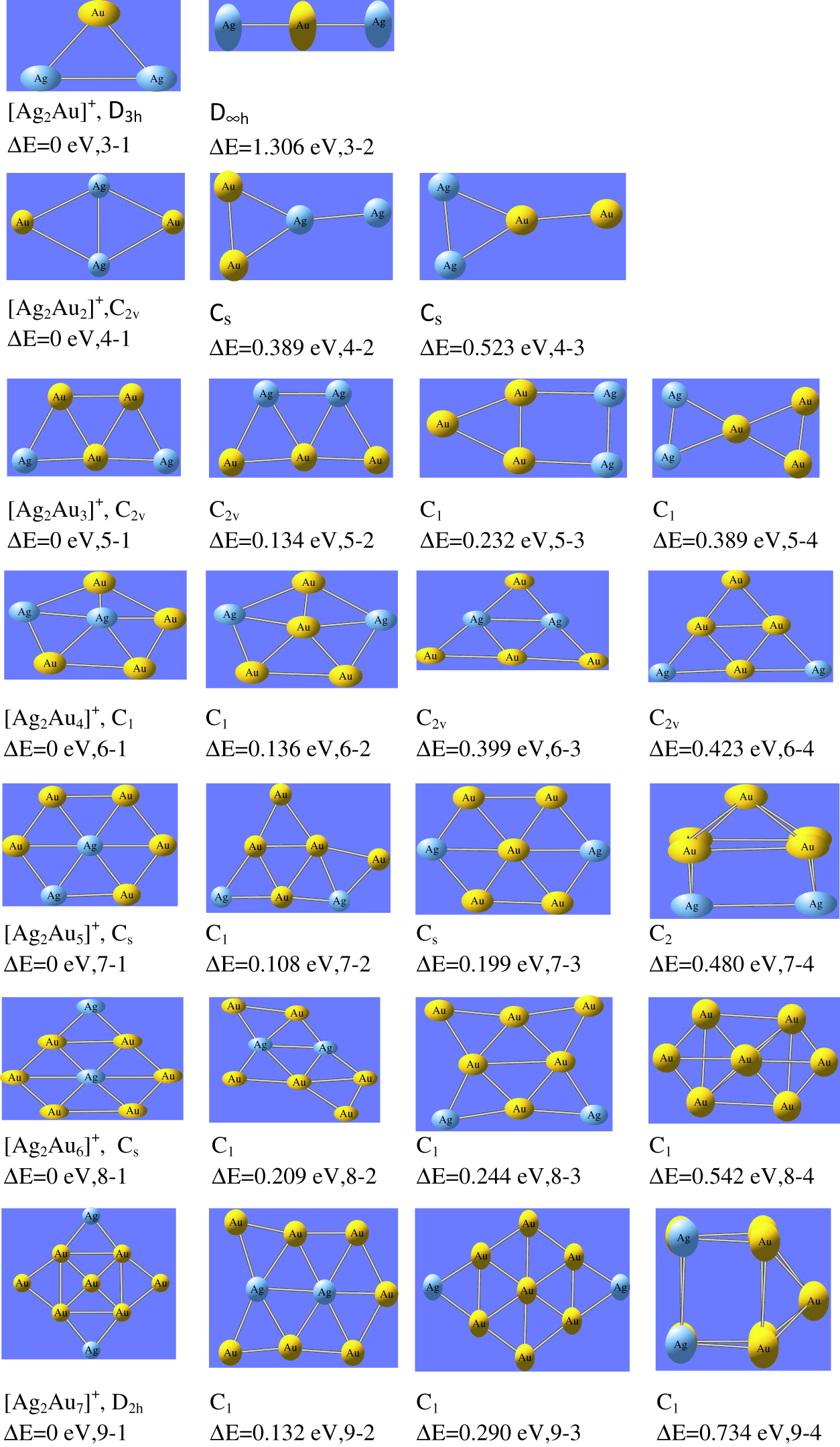
The ground state configurations of Ag2AuNλ (N = 1–7, λ=+1) nanoalloy clusters.
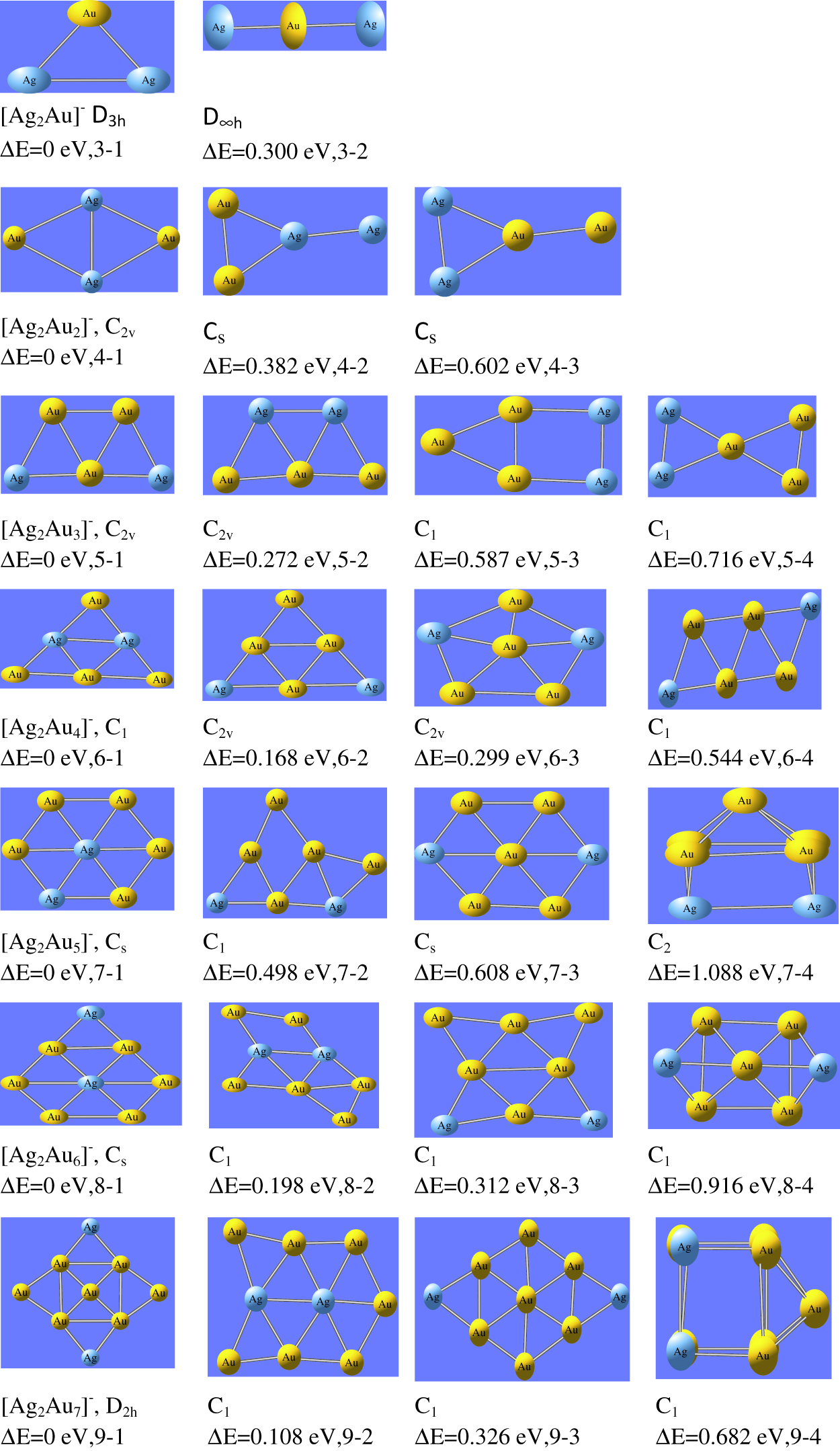
The ground state configurations of Ag2AuNλ (N = 1–7, λ=−1) nanoalloy clusters.
3.2 Electronic properties and DFT-based descriptors
Computational investigation of bimetallic Ag2AuNλ (N = 1–7, λ= ±1, 0) nanoalloy clusters has been performed invoking DFT method. The orbital energies in form of HOMO (Highest Occupied Molecular Orbital)-LUMO (Lowest Unoccupied Molecular Orbital) gap along with computed DFT-based descriptors viz. hardness, softness, electronegativity, electrophilicity index and dipole moment have been studied and analysed.
3.2.1 Bimetallic Ag2AuN (N = 1–7) nanoalloy clusters
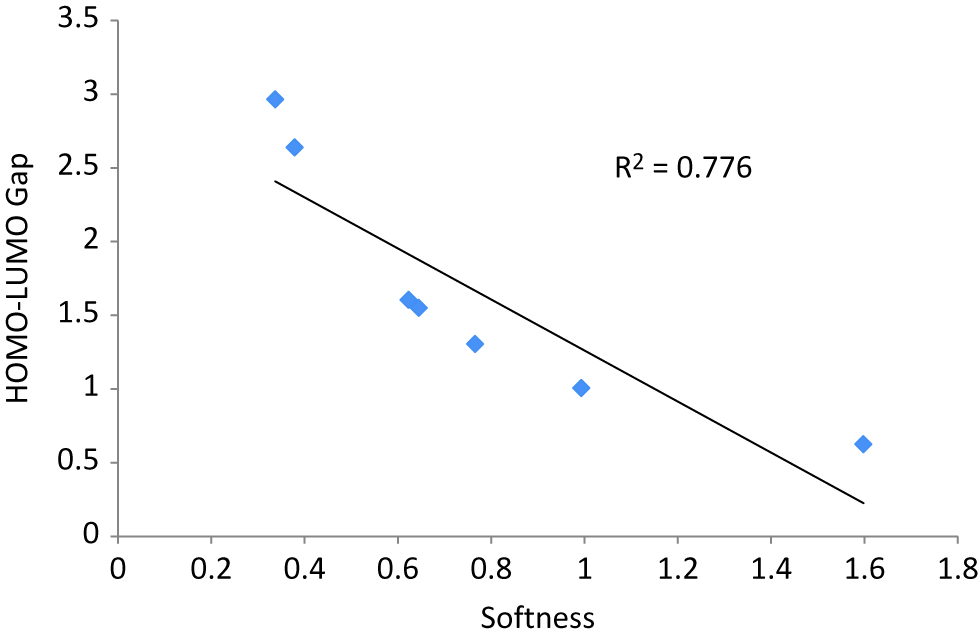
The HOMO–LUMO energy gap along with computed global descriptors namely, hardness, softness, electronegativity, electrophilicity index and dipole moment of neutral Ag2AuN (N = 1–7) nanoalloy clusters are reported in Table 1. Our data supports the relationship between HOMO–LUMO energy gap and stability of the compounds. Result from Table 1 reveals that HOMO–LUMO energy gap of clusters run hand in hand with their computed hardness values. Magnitude of hardness values increases with increase of frontier orbital energy gap increases. The cluster having the highest HOMO–LUMO energy gap will be least prone towards any external perturbation. From Table 1, it is concluded that the Ag2Au4 with symmetry group C1 has maximum HOMO–LUMO energy gap (1.823 eV), whereas Ag2Au cluster with symmetry group C2v possess the lowest energy gap (0.570 eV). In absence of any quantitative data for optical properties of these clusters, we have tacitly assumed that a direct relationship between optical properties of Ag-Au clusters with their computed HOMO–LUMO energy gap. The assumption is based on the fact that optical properties of clusters are interrelated with flow of electrons within the systems, which in turn depends on the energy gap between valence and conduction band. Xiao et al. [86] have already established a relationship between HOMO–LUMO gap and energy difference of valence-conduction band. In view of that, we may conclude that optical properties of the bimetallic clusters exhibit a direct relationship hardness values and similarly, molecular softness exhibits an inverse relationship with the optical properties [87, 88]. The correlation diagram between HOMO–LUMO energy gap and computed softness is reported in Figure 4. High value of regression coefficient (R2 = 0.956) also establishes the relationship between HOMO–LUMO and computed softness. Electrophilicity index measures the energy lowering of a ligand due to maximal electron flow between donor and acceptor and it depends on conjoint action of ionization potential and electron affinity [89]. There is an inverse relationship HOMO–LUMP energy gap and electrophilicity index.
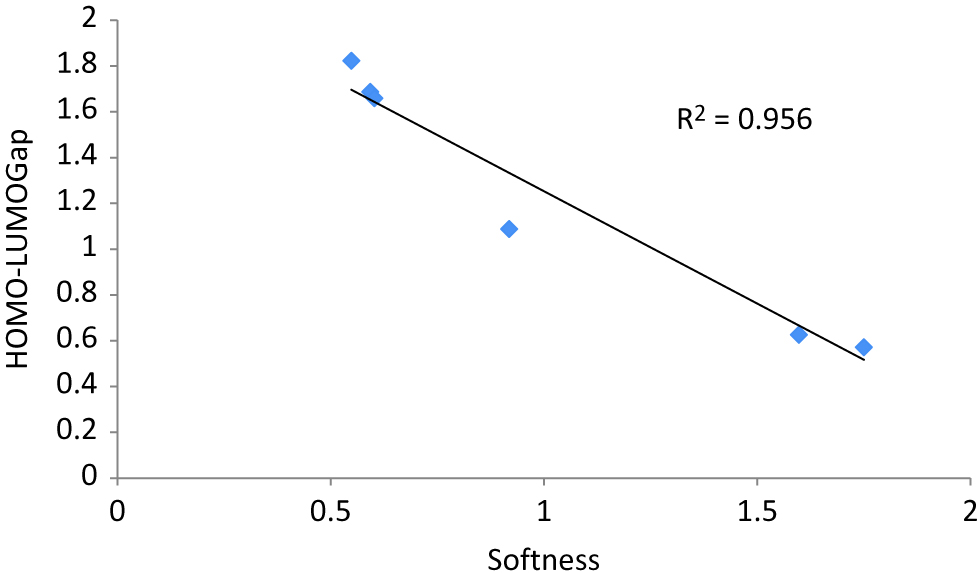
A linear correlation plot between Softness vs. HOMO–LUMO gap of Ag2AuN (N = 1–7) nanoalloy clusters.
Computed density functional theory-based descriptors of Ag2AuN (N = 1–7) nanoalloy clusters.
| Species | HOMO–LUMO Gap (eV) | Electronegativity (eV) | Hardness (eV) | Softness (eV) | Electrophilicity Index (eV) | Dipole Moment (Debye) |
|---|---|---|---|---|---|---|
| Ag2Au | 0.570 | 4.584 | 0.285 | 1.740 | 36.788 | 2.168 |
| Ag2Au2 | 1.687 | 5.278 | 0.843 | 0.592 | 16.517 | 5.450 |
| Ag2Au3 | 1.659 | 4.856 | 0.829 | 0.602 | 14.212 | 2.164 |
| Ag2Au4 | 1.823 | 5.673 | 0.911 | 0.548 | 17.655 | 1.010 |
| Ag2Au5 | 0.626 | 5.074 | 0.312 | 1.597 | 41.148 | 0.000 |
| Ag2Au6 | 1.088 | 5.578 | 0.544 | 0.918 | 28.587 | 2.824 |
| Ag2Au7 | 0.572 | 5.755 | 0.287 | 1.751 | 57.961 | 0.000 |
Dissociation energy and second difference in energy have a high impact on the relative stability of nanoalloy clusters [90, 91, 92]. These energies are highly sensitive and they exhibit an odd-even oscillation behaviour as a function of cluster size [90, 91, 92]. The HOMO–LUMO energy gap of any compound also shows an odd-even oscillation behaviour. HOMO–LUMO energy gap as a function of cluster size is depicted in Figure 5. Figure 5 displays an odd-even oscillation behaviour in terms of HOMO–LUMO energy gap. The clusters with an even number of total atoms possess larger HOMO–LUMO energy gap as compared to the neighbour clusters having odd number of total atoms. The closed-shell electronic configuration supports the stability of clusters with even number of total atoms. So, our computation runs hand in hand with reported even-odd oscillation behaviour of bimetallic nanoalloy clusters.
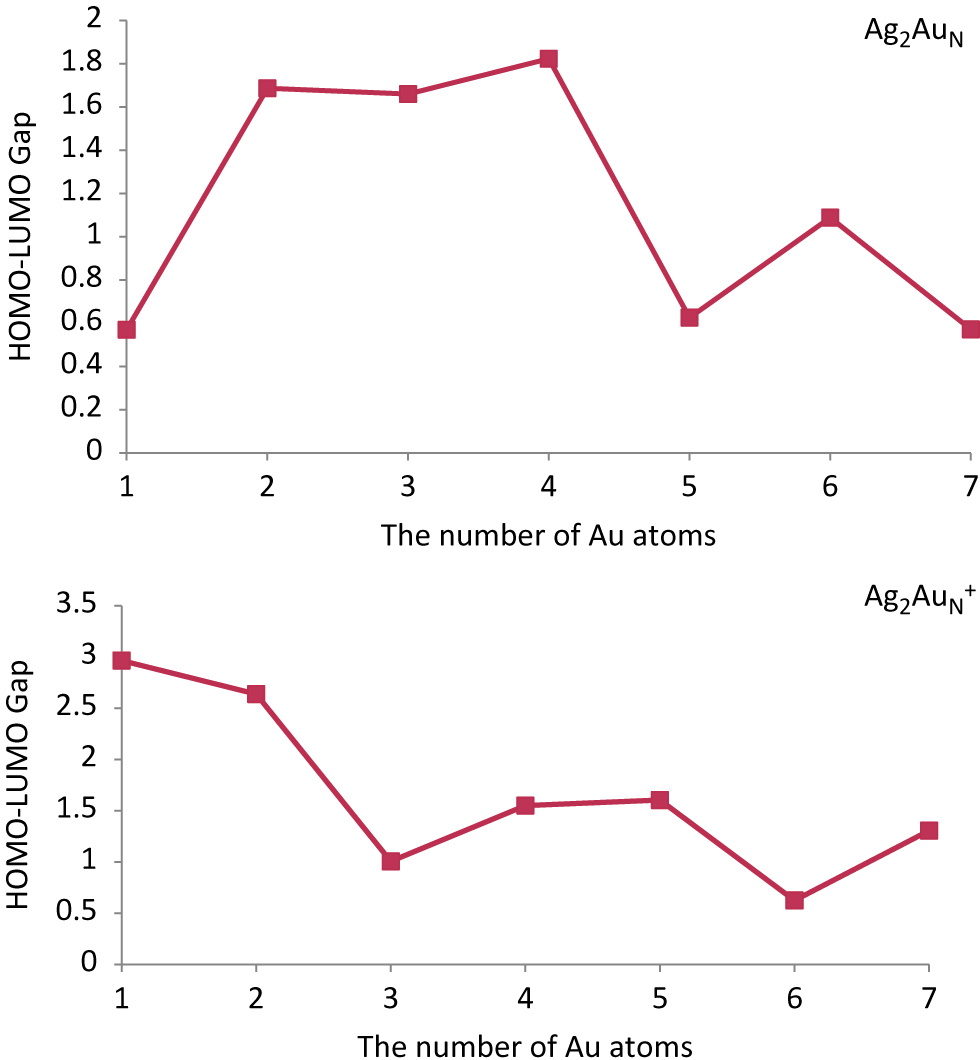
Size dependence of the HOMO–LUMO gaps for the lowest energy structures of Ag2AuN/Ag2AuN+ (N = 1–7) clusters.
In order to apply our computed data in the real field, bond length of some of the species have been computed. A comparative analysis has been reported between experimental bond length [93, 94, 95] and our data in Table 2. A close agreement in magnitude between experimental bond length and our computation is observed from Table 2.
3.2.2 Bimetallic Ag2AuN+(N = 1–7) nanoalloy clusters
In this section, we have discussed about the HOMO–LUMO energy gap and computed DFT-based descriptors of cationic bimetallic nanoalloy clusters. Results are reported in Table 3. It is observed from Table 3 that Ag2Au+ cluster, with symmetry group C2v, has the maximum HOMO–LUMO energy gap whereas Ag2Au6+ cluster, with symmetry group C1, possesses the least energy gap. The HOMO–LUMO energy gap of Ag2AuN+ cluster maintains a linear relationship with its hardness. However, softness and electrophilicity index exhibit an inverse relationship with the HOMO–LUMO energy gap. The linear correlation between HOMO–LUMO energy gap and computed softness of cationic Ag2AuN+ cluster is plotted in Figure 6. A high regression coefficient is obtained from Figure 6.
A linear correlation plot between Softness vs. HOMO–LUMO gap of Ag2AuN+ (N = 1–7) nanoalloy clusters.
Computed density functional theory–based descriptors of Ag2AuN+ (N = 1–7) nanoalloy clusters.
| Species | HOMO–LUMO Gap (eV) | Electronegativity (eV) | Hardness (eV) | Softness (eV) | Electrophilicity Index (eV) | Dipole Moment (Debye) |
|---|---|---|---|---|---|---|
| Ag2Au+ | 2.965 | 10.897 | 1.483 | 0.337 | 40.041 | 3.424 |
| Ag2Au2+ | 2.639 | 9.891 | 1.319 | 0.378 | 37.065 | 4.961 |
| Ag2Au3+ | 1.006 | 10.245 | 0.503 | 0.993 | 104.245 | 3.011 |
| Ag2Au4+ | 1.551 | 9.646 | 0.775 | 0.645 | 59.991 | 1.364 |
| Ag2Au5+ | 1.605 | 9.890 | 0.803 | 0.623 | 60.937 | 0.000 |
| Ag2Au6+ | 0.625 | 9.618 | 0.313 | 1.597 | 147.835 | 3.879 |
| Ag2Au7+ | 1.306 | 9.605 | 0.653 | 0.765 | 70.637 | 0.000 |
The HOMO–LUMO energy gap of Ag2AuN+ (N = 1–7) clusters is reported in Figure 5. Odd-even oscillation behaviour of cationic clusters is in terms of HOMO–LUMO energy gap also reported in Figure 5.
3.2.3 Bimetallic Ag2AuN−(N = 1–7) nanoalloy clusters
Anionic clusters of Ag2AuN− is investigated in terms of DFT-based descriptors and results are reported in Table 4. Table 4 reveals that the cluster Ag2Au3−, with symmetry group C2v, have the highest HOMO–LUMO energy gap whereas the cluster Ag2Au−, with symmetry group C2v, possesses the lowest energy gap. The inverse relationship between HOMO–LUMO energy gap and global softness of anionic clusters is plotted in Figure 7. R2 = 0.883 is obtained as regression coefficient.
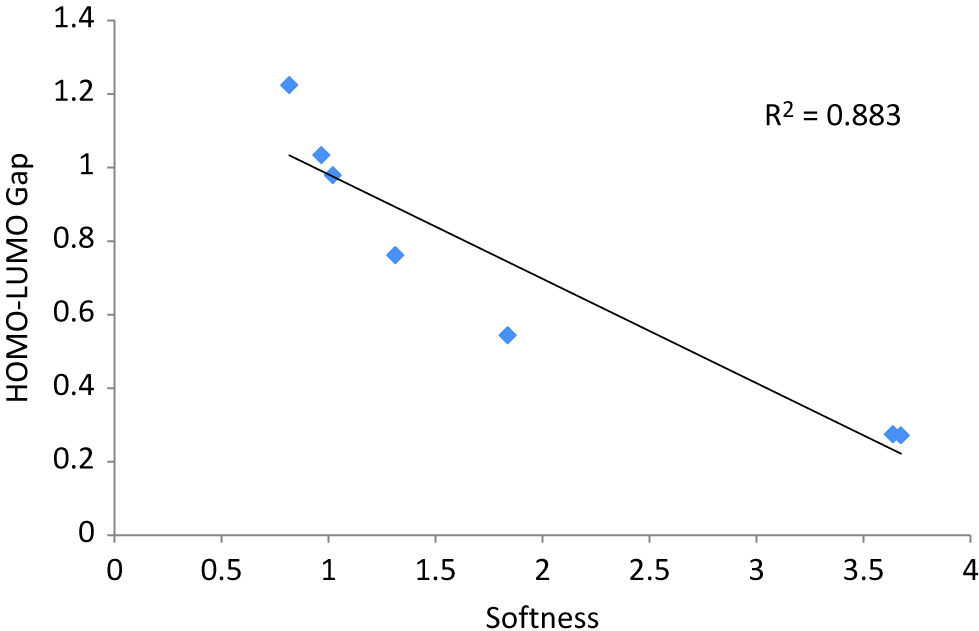
A linear correlation plot between Softness vs. HOMO–LUMO gap of Ag2AuN- (N = 1–7) nanoalloy clusters.
Computed density functional theory–based descriptors of Ag2AuN− (N = 1–7) nanoalloy clusters.
| Species | HOMO–LUMO Gap (eV) | Electronegativity (eV) | Hardness (eV) | Softness (eV) | Electrophilicity Index (eV) | Dipole Moment (Debye) |
|---|---|---|---|---|---|---|
| Ag2Au− | 0.272 | 0.082 | 0.136 | 3.675 | 0.025 | 0.558 |
| Ag2Au2− | 0.762 | 0.054 | 0.381 | 1.312 | 0.004 | 0.000 |
| Ag2Au3− | 1.224 | 0.803 | 0.612 | 0.817 | 0.526 | 0.971 |
| Ag2Au4− | 1.034 | 0.816 | 0.517 | 0.967 | 0.644 | 1.346 |
| Ag2Au5− | 0.544 | 1.306 | 0.272 | 1.837 | 3.134 | 0.000 |
| Ag2Au6− | 0.979 | 1.605 | 0.489 | 1.021 | 2.631 | 2.018 |
| Ag2Au7− | 0.275 | 0.077 | 0.137 | 3.638 | 0.021 | 0.000 |
Our computed data reveals that the magnitude of HOMO–LUMO energy gap of cationic clusters are higher than anionic counterparts with exception of Ag2Au3+ and Ag2Au6+ clusters.
4 Conclusion
Due to diverse applications in the real field, the study of bimetallic nanoalloy clusters has gained a significant importance. In this report, we have investigated the structure and physico-chemical properties of Ag2AuNλ (N = 1–7, λ= ±1,0) clusters in terms of DFT study. DFT-based global descriptors namely, HOMO–LUMO energy gap, hardness, softness, electronegativity, electrophilicity index and dipole moment of cationic, anionic and neutral Ag2AuN clusters are computed and reported. The result reveals a direct relationship between HOMO–LUMO energy gap with global hardness and inverse relationship with softness. Considering optical property of clusters as a function of energy gap, we have tried to explain optical properties/HOMO–LUMO energy gap in terms of computed descriptors. Our predicted trend is also in similar line with experimental facts. Odd-even oscillation behaviour of neutral and charged clusters are also established invoking our computed data. The neutral clusters with even number of total atoms possess larger energy gap as compared to their neighbour clusters with odd number of total atoms. It is concluded that Ag2Au+ cluster is the most stable cluster among all molecular system. Our computed bond length for the species of Ag2, Au2 and Ag-Au are in well agreement with the experimental values. It strengthens our computational analysis.
References
1. Khosousi AZ, Dhirani AA. Charge transport in nanoparticle assemblies. Chem Rev 2008;108:4072.10.1021/cr0680134Search in Google Scholar PubMed
2. Daniel MC, Astruc D. Gold nanoparticles: assembly, supramolecular chemistry, quantum-size-related properties, and applications toward biology, catalysis and nanotechnology. Chem Rev 2004;104:293.10.1021/cr030698+Search in Google Scholar PubMed
3. Ghosh SK, Pal T. Photophysical aspects of molecular probes near nanostructured gold surfaces. Chem Rev 2007;107:4797.10.1039/b817373gSearch in Google Scholar PubMed
4. Chaudhuri RG, Paria S. Core/shell nanoparticles: classes, properties, synthesis mechanisms, characterization, and applications. Chem Rev 2012;112:2373.10.1021/cr100449nSearch in Google Scholar PubMed
5. Alivisatos AP. Semiconductor clusters, nanocrystals and quantum dots. Science. 1996;271:933.10.1126/science.271.5251.933Search in Google Scholar
6. Wang HQ, Kuang XY, Li HF. Density functional study of structural and electronic properties of bimetallic copper-gold clusters: comparison with pure and doped gold clusters. Phys Chem Chem Phys 2010;12:5156.10.1039/b923003cSearch in Google Scholar PubMed
7. Roucoux A, Schulz J, Patin H. Reduced transition metal colloids: a novel family of reusable catalysts? Chem Rev 2002;102:3757.10.1021/cr010350jSearch in Google Scholar PubMed
8. Rao CN, Cheetham AK. Science and technology of nanomaterials: current status and future prospects. J Mater Chem 2001;11:2887.10.1039/b105058nSearch in Google Scholar
9. Munoz-Flores BM, Kharisov BI, Jimenez-Perez VM, Martinez PE, Lopez ST. Recent advances in the synthesis and main applications of metallic nanoalloys. Ind Eng Chem Res 2011;50:7705.10.1021/ie200177dSearch in Google Scholar
10. Murray RW. Nanoelectrochemistry: metal nanoparticles, nanoelectrodes and nanopores. Chem Rev 2008;108:2688.10.1021/cr068077eSearch in Google Scholar PubMed
11. Yin F, Wang ZW, Palmer RE. Formation of bimetallic nanoalloys by Au coating of size selected Cu clusters. J Nanopart Res 2012;14:1124.10.1007/s11051-012-1124-xSearch in Google Scholar
12. Teng X, Wang Q, Liu P, Han W, Frenkel AI, Wen MN, et al. Formation of Pd/Au nanostructures from Pd nanowires via galvanic replacement reaction. J Am Chem Soc 2008;130:1093.10.1021/ja077303eSearch in Google Scholar PubMed
13. Ferrando R, Jellinek J, Johnston RL. Nanoalloys: from theory to applications of alloy clusters and nanoparticles. Chem Rev 2008;108:845.10.1021/cr040090gSearch in Google Scholar PubMed
14. Henglein A. Physicochemical properties of small metal particles in solution: “microelectrode” reactions, chemisorption, composite metal particles, and the atom-to-metal transition. J Phys Chem 1993;97:5457.10.1021/j100123a004Search in Google Scholar
15. Davis SC, Klabunde KJ. Unsupported small metal particles: preparation, reactivity and characterization. Chem Rev 1982;82:153.10.1021/cr00048a002Search in Google Scholar
16. Lewis LN. Chemical catalysis by colloids and clusters. Chem Rev 1993;93:2693.10.1021/cr00024a006Search in Google Scholar
17. Schmid G. Large clusters and colloids. Metals in the embryonic state. Chem Rev 1992;92:1709.10.1021/cr00016a002Search in Google Scholar
18. Schon G, Simon U. A fascinating new field in colloid science: small ligand-stabilized metal clusters and possible applications in microelectronics. Colloid Polym Sci 1995;273:101.10.1007/BF00654007Search in Google Scholar
19. Oderji HY, Ding H. Determination of melting mechanism of Pd24Pt14 nanoalloy by multiple histogram method via molecular dynamics simulations. Chem Phys 2011;388:23.10.1016/j.chemphys.2011.07.011Search in Google Scholar
20. Huang X, Sayed IE, Qian W, Sayed MA. Cancer cell imaging and photothermal therapy in the near-infrared region by using gold nanorods. J Am Chem Soc 2006;128:2115.10.1021/ja057254aSearch in Google Scholar PubMed
21. Hainfeld J, Slatkin D, Smilowitz HM. The use of gold nanoparticles to enhance radiotherapy in mice. Phys Med Biol 2004;49:309.10.1088/0031-9155/49/18/N03Search in Google Scholar
22. Wu D, Zhang XD, Liu PX, Zhang LA, Fan FY, Guo ML. Gold nanostructure: fabrication, surface modification, targeting imaging, and enhanced radiotherapy. Curr Nanosci 2011;7:110.10.2174/157341311794480246Search in Google Scholar
23. Zhang X, Guo M, Wu D, Liu P, Sun Y, Zhnag L, et al. First-principles investigation of Ag-doped gold nanoclusters. Int J Mol Sci 2011;12:2972.10.3390/ijms12052972Search in Google Scholar PubMed PubMed Central
24. Chen J, Wang D, Xi J, Au L, Siekkinen A, Warsen A, et al. Immuno gold nanocages with tailored optical properties for targeted photothermal destruction of cancer cells. Nano Lett 2007;7:1318.10.1021/nl070345gSearch in Google Scholar PubMed PubMed Central
25. Robinson JM, Takizawa T, Vandre DD. Applications of gold cluster compounds in immunocytochemistry and correlative microscopy: comparison with colloidal gold. J Microsc 2000;199:163.10.1046/j.1365-2818.2000.00734.xSearch in Google Scholar PubMed
26. Whetten RL, Khoury JT, Alvarez MM, Murthy S, Vezmar I, Wang ZL, et al. Nanocrystal gold molecules. Adv Mater 1996;5:428.10.1007/978-94-015-8682-5_28Search in Google Scholar
27. Andres RP, Bein T, Dorogi M, Feng S, Henderson JI, Kubiak CP, et al. “Coulomb Staircase” at room temperature in a self-assembled molecular nanostructure. Science 1996;272:1323.10.1126/science.272.5266.1323Search in Google Scholar PubMed
28. Mirkin CA, Letsinger RL, Mucic RC, Storho昀f JJ. A DNA-based method for rationally assembling nanoparticles into macroscopic materials. Nature 1996;382:607.10.1038/382607a0Search in Google Scholar PubMed
29. Alivisatos AP, Johnsson KP, Peng XG, Wilson TE, Loweth CJ, Bruchez MP, et al. Organization of ‘nanocrystal molecules’ using DNA. Nature 1996;382:609.10.1038/382609a0Search in Google Scholar PubMed
30. Andres RP, Bielefeld JD, Henderson JI, Janes DB, Kolagunta VR, Kubiak CP, et al. Self-assembly of a two-dimensional superlattice of molecularly linked metal clusters. Science 1996;273:1690.10.1126/science.273.5282.1690Search in Google Scholar
31. Garzon IL, Michaelian K, Beltran MR, Amarillas AP, Ordejon P, Artacho E, et al. Lowest energy structures of gold nanoclusters. Phys Rev Lett 1998;81:1600.10.1103/PhysRevLett.81.1600Search in Google Scholar
32. Garzon IL, Rovira C, Michaelian K, Beltran MR, Ordejon P, Junquera J, et al. Do thiols merely passivate gold nanoclusters? Phys Rev Lett 2000;85:5250.10.1103/PhysRevLett.85.5250Search in Google Scholar PubMed
33. Michaelian K, Rendon N, Garzon IL. Structure and energetics of Ni, Ag, and Au nanoclusters. Phys Rev B 1999;60:2000.10.1103/PhysRevB.60.2000Search in Google Scholar
34. Schaa昀f TG, Whetten RL. Giant gold-glutathione cluster compounds: intense optical activity in metal-based transitions. J Phys Chem B 2000;104:2630.10.1021/jp993691ySearch in Google Scholar
35. Priyanka, Dharamvir K. The structural and electronic properties of tubular gold clusters with a spinal support. Phys Chem Chem Phys 2013;15:12340.10.1039/c3cp51259bSearch in Google Scholar PubMed
36. Negishi Y, Nakamura Y, Nakajima A, Kaya K. Photoelectron spectroscopy of gold-silver binary cluster anions (AunAgm-; 2≤n+m≤4). J Chem Phys 2001;115:3657.10.1063/1.1388036Search in Google Scholar
37. Heiles S, Logsdail AJ, Schfer R, Johnston RL. Dopant-induced 2D-3D transition in small Au-containing clusters: DFT-global optimization of 8-atom Au-Ag nanoalloys. Nanoscale 2012;4:1109.10.1039/C1NR11053ESearch in Google Scholar
38. Weis P, Welz O, Vollmer E, Kappes MM. Structures of mixed gold-silver cluster cations (AgmAun+, m+n<6): ion mobility measurements and density-functional calculations. J Chem Phys 2004;120:677.10.1063/1.1630568Search in Google Scholar PubMed
39. Lee HM, Ge M, Sahu BR, Tarakeshwar P, Kim KS. Geometrical and electronic structures of gold, silver and gold-silver binary clusters: origins of ductility of gold and gold-silver alloy formation. J Phys Chem B 2003;107:9994.10.1021/jp034826+Search in Google Scholar
40. Kouteckẏ VB, Burda J, Mitrić R, Ge M. Density functional study of structural and electronic proeprties of bimetallic silver-gold clusters: comparison with pure gold and silver clusters. J Chem Phys 2002;117:3120.10.1063/1.1492800Search in Google Scholar
41. Tafoughalt MA, Samah M. Density functional investigation of structural and electronic properties of small bimetallic silver-gold clusters. Phys B 2012;407:2014.10.1016/j.physb.2012.01.131Search in Google Scholar
42. Shayeghi A, Heard CJ, Johnston RL, Schäfer R. Optical and electronic properties of mixed Ag-Au tetramer cations. J Chem Phys 2014;140:054312.10.1063/1.4863443Search in Google Scholar PubMed
43. Zhao YR, Kuang XY, Zheng BB, Li YF, Wang SJ. Equilibrium geometries, stabilities, and electronic properties of the bimetallic M2 doped Aun (M=Ag, Cu; n=1-10) clusters: comparison with pure gold clusters. J Phys Chem A 2011;115:569.10.1021/jp108695zSearch in Google Scholar PubMed
44. Zhao GF, Zeng Z. Geometrical and electronic structures of AumAgn (2≤m+n≤8). J Chem Phys 2006;125:014303.10.1063/1.2210470Search in Google Scholar PubMed
45. Miranda FM, Menziani MC, Pedone A. Influence of silver doping on the photoluminescence of protected AgnAu25-n nanoclusters: A time-dependent density functional theory investigation. J Phys Chem C 2015;119:10766.10.1021/acs.jpcc.5b02655Search in Google Scholar
46. Tafoughalt MA, Samah M. Structural properties and relative stability of silver-doped gold clusters AgAun-1 (n=3-13): density functional calculations. Comput Theor Chem 2014;1033:23.10.1016/j.comptc.2014.01.023Search in Google Scholar
47. Shayeghi A, Schfer R, Rayner DM, Johnston RL, Fielicke A. Charge-induced dipole vs. relativistically enhanced covalent interactions in Ar-tagged Au-Ag tetramers and pentamers. J Chem Phys 2015;143:024310.10.1063/1.4923255Search in Google Scholar PubMed
48. Chi Y, Zhao L, Lu X, An C, Guo W, Wu CM. Effect of alloying on the stabilities and catalytic properties of Ag-Au bimetallic subnanoclusters: A theoretical investigation. J Mater Sci 2016;51:5046.10.1007/s10853-016-9808-8Search in Google Scholar
49. Cramer CJ, Truhlar DG. Density functional theory for transition metals and transition metal chemistry. Phys Chem Chem Phys 2009;11:10757.10.1039/b907148bSearch in Google Scholar PubMed
50. Hafner J, Wolverton C, Ceder G. Toward computational materials design: the impact of density functional theory on materials research. MRS Bull 2006;31:659.10.1557/mrs2006.174Search in Google Scholar
51. Parr RG, Yang W. Density-functional theory of the electronic structure of molecules. Annu Rev Phy Chem 1995;46:701.10.1146/annurev.pc.46.100195.003413Search in Google Scholar
52. Kohn W, Becke AD, Parr RG. Density functional theory of electronic structure. J Phys Chem 1996;100:12974.10.1021/jp960669lSearch in Google Scholar
53. Liu S, Parr RG. J Chem Phys 1997;106:5578.10.1063/1.473580Search in Google Scholar
54. Ziegler T. Chem Rev 1991;91:651.10.1021/cr00005a001Search in Google Scholar
55. Parr RG, Yang W. Density functional theory of atoms and molecules. Oxford: Oxford University Press, 1989.Search in Google Scholar
56. Chermette H. Chemical reactivity indexes in density functional theory. J Comput Chem 1999;20:129.10.1002/(SICI)1096-987X(19990115)20:1<129::AID-JCC13>3.0.CO;2-ASearch in Google Scholar
57. Geerlings P, Pro昀t FD, Langenaeker W. Conceptual density functional theory. Chem Rev 2003;103:1793. Washington, DC.10.1021/cr990029pSearch in Google Scholar PubMed
58. Geerlings P, Pro昀t FD. Chemical reactivity as described by quantum chemical methods. Int J Mol Sci 2002;3:276.10.3390/i3040276Search in Google Scholar
59. Ranjan P, Dhail S, Venigalla S, Kumar A, Ledwani L, Chakraborty T. A theoretical analysis of bi-metallic (Cu-Ag)n=1-7 nano alloy clusters invoking DFT based descriptors. Mater Sci Pol 2015;33:719.10.1515/msp-2015-0121Search in Google Scholar
60. Ranjan P, Venigalla S, Kumar A, Chakraborty T. Theoretical study of bi-metallic AgmAun; (m+n=2-8) nano alloy clusters in terms of DFT based descriptors. New Front Chem 2014;23:111.Search in Google Scholar
61. Venigalla S, Dhail S, Ranjan P, Jain S, Chakraborty T. Computational study about cytotoxicity of metal oxide nanoparticles invoing nano-QSAR technique. New Front Chem 2014;23:123.Search in Google Scholar
62. Ranjan P, Kumar A, Chakraborty T. Computational study of AuSin (n=1-9) nanoalloy clusters invoking DFT based descriptors. AIP Conf Proc 2016;1724:020072.10.1063/1.4945192Search in Google Scholar
63. Ranjan P, Kumar A, Chakraborty T. Theoretical analysis: electronic and optical proeprties of gold-silicon nanoalloy clusters. Mat Today Proc 2016;3:1563.10.1016/j.matpr.2016.04.043Search in Google Scholar
64. Ranjan P, Kumar A, Chakraborty T, Mishra GC. Computational study of nanomaterials invoking DFT based descriptors. Environmental sustainability: concepts, principles, evidences and innovations. New Delhi: Excellent Publishing House, 2014:239–242.Search in Google Scholar
65. Ranjan P, Venigalla S, Kumar A, Chakraborty T, Chakraborty T, Ledwani L. A theoretical analysis of bi-metallic Ag-Aun;(n=1-7) nano alloy clusters invoking DFT based descriptors. Recent methodology in chemical sciences: experimental and theoretical approaches. USA: Apple Academic Press and CRC Press, 2015:337–346.Search in Google Scholar
66. Ranjan P, Kumar A, Chakraborty T. Computational investigation of Ge doped Au nanoalloy clusters: A DFT study. IOP Conf Series Mater Sci Eng 2016;149:012172.10.1088/1757-899X/149/1/012172Search in Google Scholar
67. Dhail S, Ranjan P, Chakraborty T, Ramasami P, Bhowon MG, Laulloo SJ, et al. Correlation of the experimental and theoretical study of some novel 2-phenazinamine derivatives in terms of DFT-based descriptors. Crystallizing ideas- the role of chemistry. Switzerland: Springer, 2016:97–112.10.1007/978-3-319-31759-5_7Search in Google Scholar
68. Ranjan P, Kumar A, Chakraborty T, Chakraborty T, Ranjan P, Pandey A. Theoretical analysis: electronic and optical properties of small Cu-Ag nano alloy clusters. Computational chemistry methodology in structural biology and material sciences. USA: Apple Academic Press and CRC Press, In Press. ISBN- 9781315207544.Search in Google Scholar
69. Ranjan P, Chakraborty T, Kumar A, Haghi AK, Pogilani L, Castro EA, et al. A theoretical study of bimetallic CuAun (N=1-7) nanoalloy clusters invoking conceptual DFT based descriptors. Applied chemistry and chemical engineering Vol. 4. USA: Apple Academic Press and CRC Press, In Press. ISBN- 9781315207636.Search in Google Scholar
70. Frisch MJ, Trucks GW, Schlegel HB, Scuseria GE, Robb MA, Cheeseman JR, et al. Gaussian 03, Revision C.02. Wallingford CT: Gaussian, Inc., 2004.Search in Google Scholar
71. Jones RO, Gunnarsson O. The density functional formalism, its applications and prospects. Rev Mod Phys 1989;61:689.10.1103/RevModPhys.61.689Search in Google Scholar
72. Zupan A, Blaha P, Schwarz K, Perdew JP. Pressure-induced phase transitions in solid Si, Sio2, and Fe: performance of local-spin-density and generalized-gradient-approximation density functionals. Phys Rev B 1998;58:11266.10.1103/PhysRevB.58.11266Search in Google Scholar
73. Theilhaber J. Quantum-molecular-dynamics simulations of liquid metals and highly degenerate plasmas. Phys Fluids B 1992;4:2044.10.1063/1.860013Search in Google Scholar
74. Stadler R, Gillan MJ. First-principles molecular dynamics studies of liquid tellurium. J Phys Condens Matter 2000;12:6053.10.1088/0953-8984/12/28/304Search in Google Scholar
75. Argaman N, Makov G. Density functional theory-a introduction. Am J Phys Condens Matter 2000;68:69.10.1119/1.19375Search in Google Scholar
76. Chen FY, Johnston RL. Structure and spectral characteristics of the nanoalloy Ag3Au10. Appl Phys Lett 2007;90:153123.10.1063/1.2722702Search in Google Scholar
77. Chen FY, Johnston RL. Charge transfer driven surface segregation of gold atoms in 13-atom Au-Ag nanoalloys and its relevance to their structural, optical and electronic properties. Acta Mater 2008;56:2374.10.1016/j.actamat.2008.01.048Search in Google Scholar
78. Jug K, Zimmermann B, Calaminici P, Köster AM. Structure and stability of small copper clusters. J Chem Phys 2002;116:4497.10.1063/1.1436465Search in Google Scholar
79. Hay PJ, Wadt WR. Ab initio effective core potentials for molecular calculations. Potentials for the transition metal atoms Sc to Hg. J Chem Phys 1985;82:299.10.1063/1.448975Search in Google Scholar
80. Assadollahzadeh B, Schwerdtfeger P. A systematic search for minimum structures of small gold clusters Aun (n=2-20) and their electronic properties. J Chem Phys 2009;131:064306.10.1063/1.3204488Search in Google Scholar
81. Chiodo S, Russo N, Sicilia E. LANL2DZ basis sets recontracted in the framework of density functional theory. J Chem Phys 2006;125:104107.10.1063/1.2345197Search in Google Scholar PubMed
82. Jiang ZY, Lee KH, Li ST, Chu SY. Structures and charge distributions of cationic and neutral Cun-1Ag clusters (n=2-8). Phys Rev B 2006;73:235423.10.1103/PhysRevB.73.235423Search in Google Scholar
83. Mielich B, Savin A, Stoll H, Preuss H. Results obtained with the correlation energy density functionals of Becke and Lee, Yang and Parr. Chem Phys Lett 1989;157:200.10.1016/0009-2614(89)87234-3Search in Google Scholar
84. Petrie S. Pitfalls for the frozen-core approximation: Gaussian-2 calculations on the sodium cation affinities of diatomic fluorides. J Phys Chem A 1998;102:6138.10.1021/jp9802432Search in Google Scholar
85. Purwanto W, Zhang S, Krakauer H. Frozen-orbital and downfolding calculations with auxiliary-field quantum Monte Carlo. J Chem Theory Comput 2013;9:4825.10.1021/ct4006486Search in Google Scholar PubMed
86. Xiao H, Kheli JT, Goddard WA. Accurate band gaps for semiconductors from density functional theory. J Phys Chem Lett 2011;2:212.10.1021/jz101565jSearch in Google Scholar
87. Parr RG. Absolute electronegativity and hardness correlated with molecular orbital theory. Proc Natl Acad Sci 1986;83:8440.10.1073/pnas.83.22.8440Search in Google Scholar PubMed PubMed Central
88. Kaya Y, Yilmaz VT, Buyukgungor O. Synthesis, spectroscopic, structural and quantum chemical studies of a new imine oxime and its palladium (II) complex: hydrolysis mechanism. Molecules 2016;21:52.10.3390/molecules21010052Search in Google Scholar PubMed PubMed Central
89. Parr RG, Szentpaly LV, Liu S. Electrophilicity index. J Am Chem Soc 1999;121:1929.10.1021/ja983494xSearch in Google Scholar
90. Ding LP, Kuang XY, Shao P, Zhao YR, Li YF. A comparative study on geometries, stabilities and electronic properties between bimetallic AgnX (X=Au, Cu; n=1-8) and pure silver clusters. Chin Phys B 2012;21:043601.10.1088/1674-1056/21/4/043601Search in Google Scholar
91. Hakkinen H, Landman U. Gold clusters (AuN, 2<~N<~10). Phys Rev B 2000;62:2287.10.1103/PhysRevB.62.R2287Search in Google Scholar
92. Li XB, Wang HY, Yang XD, Zhu ZH, Tang YJ. Size dependence of the structures and energetic and electronic properties of gold clusters. J Chem Phys 2007;126:084505.10.1063/1.2434779Search in Google Scholar PubMed
93. Beutel V, Kramer HG, Bhale GL, Kuhn M, Weyers K, Demtroder W. High-resolution isotope selective laser spectroscopy of Ag2 molecules. J Chem Phys 1993;98:2699.10.1063/1.464151Search in Google Scholar
94. Huber KP, Herzberg G. Constraints of diatomic molecules. New York: Van Nostrand Reinhold Company, 1979.10.1007/978-1-4757-0961-2_2Search in Google Scholar
95. Fabbi JC, Langenberg JD, Costello QD, Morse MD, Karlsson L. Dispersed fluorescence spectroscopy of AlNi, NiAu and PtCu. J Chem Phys 2001;115:7543.10.1063/1.1407273Search in Google Scholar
Acknowledgement
This article is also available in: Ramasami, Computational Sciences. De Gruyter (2017), isbn 978-3-11-046536-5.
© 2017 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Ecology
- Vortices at Microwave Frequencies
- Mechanism of nucleophilic substitution reactions of 4-(4ˊ-nitro)phenylnitrobenzofurazan ether with aniline in acetonitrile.
- Environmental geology and hydrology
- Growing your green chemistry mindset
- Computational Investigation of Cationic, Anionic and Neutral Ag2AuN (N = 1–7) Nanoalloy Clusters
Articles in the same Issue
- Ecology
- Vortices at Microwave Frequencies
- Mechanism of nucleophilic substitution reactions of 4-(4ˊ-nitro)phenylnitrobenzofurazan ether with aniline in acetonitrile.
- Environmental geology and hydrology
- Growing your green chemistry mindset
- Computational Investigation of Cationic, Anionic and Neutral Ag2AuN (N = 1–7) Nanoalloy Clusters

