Thermodynamic and kinetic insights into B₁₀H₁₄ and B₁₀H₁₄ ²⁻

Introduction

Decaborane (B₁₀H₁₄) is a colorless crystalline boron hydride whose synthesis in the early 20th century marked a milestone in boron chemistry. ¹ It is widely used as a precursor for various borohydrides, including the decaborate dianion, [B₁₀H₁₀]²⁻, ^{2 , 3} the dodecaborate dianion [B₁₂H₁₂]²⁻, ^{4 , 5} and the tetradecahydrodecaborate dianion [B₁₀H₁₄]²⁻. ^{6 , 7 , 8 , 9} Its corresponding dianion [B₁₀H₁₄]²⁻ was first prepared in 1958 via the reaction of sodium with B₁₀H₁₄ in ammonia. ¹⁰ Subsequent attempts to obtain its alkali salts (e.g., Na₂B₁₀H₁₄ and K₂B₁₀H₁₄) ^{11 , 12} encountered low yields and byproduct formation, particularly when using sodium amalgam or KBH₄. ⁶ In 2023, Chen and co-workers ⁹ reported a mercury-free, high-yield (83 %) synthesis of M₂B₁₀H₁₄ (M = Na and K) using alkali metal amidoboranes (MNH₂BH₃) in tetrahydrofuran at room temperature. This approach avoids reactive sodium metal and provides a safer, more practical route. ^{6 , 10 , 11 , 12} This improved accessibility and purity of these compounds has renewed interest in their fundamental properties and potential applications.

The structures of B₁₀H₁₄ and [B₁₀H₁₄]²⁻ were elucidated by Harker ¹³ and Lipscomb, ^{7 , 14} through X-ray diffraction and later supported by ab initio SCF-MO calculations. ¹⁵ According to Wade-Mingos rules, these compounds are classified as nido- and arachno-borohydrides, respectively. ^{16 , 17 , 18} Both adopt C _2v symmetry and share an incomplete octadecahedral boron skeleton, differing mainly in hydrogen arrangements (Fig. 1). nido-B₁₀H₁₄ contains ten BH units and four B–H–B bridges, whereas arachno-[B₁₀H₁₄]²⁻ has eight BH units, two BH₂ groups, and two bridging hydrogens. In principle, adding two electrons to nido-B₁₀H₁₄ induces minor structural changes, ¹⁹ breaking two B–H–B bridges to form two BH₂ units while retaining C _2v symmetry (Fig. 1).

Fig. 1:

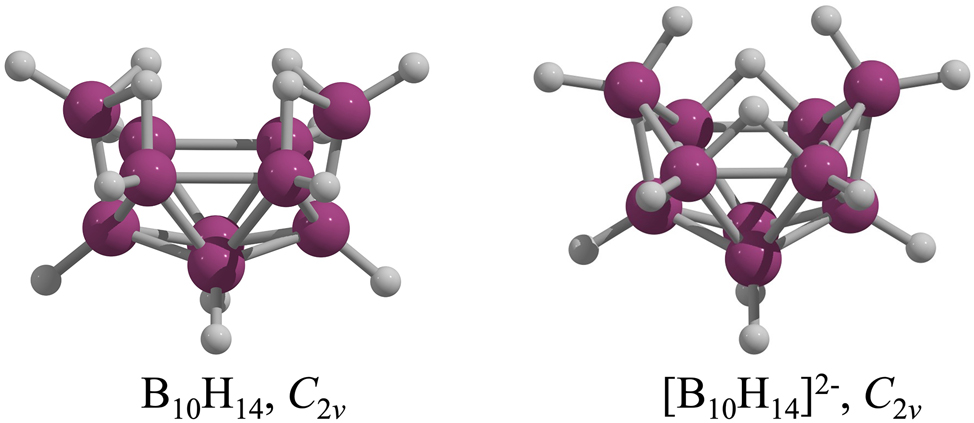
Structures of neutral (left) and dianionic (right) B₁₀H₁₄.

Our recent studies indicate that some boranes deviate from their predicted structures upon electron removal. ^{20 , 21} For instance, [B₁₂H₁₂]²⁻, an icosahedron in its anionic form, adopts a structure with ten B–H bonds and one B–H₂ bond after two-electron removal. ²⁰ Similarly, [B₅H₅]²⁻ has a trigonal bipyramidal form with D _3h symmetry, whereas its neutral counterpart, B₅H₅, forms an asymmetric 3D structure rather than a planar or cage-like arrangement. ²¹ These findings raise the question of whether the arachno structure represents the global minimum for B₁₀H₁₄ ²⁻. Our systematic exploration shows that it does not; the global minimum corresponds to a complex formed by a closo-[B₁₀H₁₀]²⁻ fragment interacting with two hydrogen molecules. The arachno structure lies approximately 21 kcal mol⁻¹ higher in energy but persists as a kinetically stable local minimum. This behavior contrasts with [B₁₂H₁₂]²⁻, where the deltahedral cage is the global minimum, and underscores the stability of B₁₀H₁₄ ²⁻, motivating the present study.

Computational details

The potential energy surface (PES) of B₁₀H₁₄ ²⁻ was explored using a genetic algorithm implemented in GLOMOS, ²² as described elsewhere. ²³ Initial screening was performed at the PBE0/def2-SVP level, ^{24 , 25} considering both singlet and triplet spin states. Identified structures were reoptimized and fully characterized at the TPSS/aug-cc-pVTZ ^{26 , 27} level, including Grimme’s D3 dispersion correction. ²⁸ A quadratically convergent SCF procedure (XQC) was used to improve the convergence process. Single-point energies were calculated on TPSS geometries using CCSD(T) ²⁹ method with the aug-cc-pVTZ basis set. Relative Gibbs free energies were calculated at the CCSD(T)/def2-TZVP//TPSS-D3/def2-TZVP level, including entropic and thermal corrections derived from the TPSS-D3/aug-cc-pVTZ level at 298.15 K in the gas phase. Solvent effects of tetrahydrofuran were assessed using the SMD model ^{30 , 31} at the TPSS-D3/aug-cc-pVTZ level. Conversion mechanisms between arachno-[B₁₀H₁₄]²⁻ and the complex [B₁₀H₁₀]²⁻⋯2H₂ were evaluated using the intrinsic reaction coordinate (IRC) ³² method. All calculations were performed with Gaussian 16. ³³

Bonding was analyzed at the TPSS-D3/aug-cc-pVTZ level using the natural bond orbital (NBO) method in NBO 6.0, ³⁴ and the adaptive natural density partitioning (AdNDP) ³⁵ approach implemented in Multiwfn. ³⁶ AdNDP describes bonding through n-center-two-electron (nc-2e) bonds, recovering both classical Lewis concepts (e.g., lone pairs, 2c-2e bonds) and delocalized bonds. Non-covalent interactions (NCI) of the global minimum were analyzed by generating the reduced density gradient (RDG) isosurfaces (s = 0.5 au) with NCIPLOT. ^{37 , 38} The isosurfaces were colored according to sign(λ ₂)ρ in the range −0.5 au < sign(λ ₂)ρ < +0.5 au, highlighting strong interactions in blue, weak interactions in green, and repulsions in red.

The dynamic behavior of B₁₀H₁₄ ²⁻ was investigated via Born-Oppenheimer Molecular Dynamics (BO-MD) ³⁹ simulations at 1200 K for 30 ps with 1 fs time step, using a Nosé–Hoover chain thermostat for temperature control. ^{40 , 41 , 42} This temperature provides sufficient kinetic energy to overcome barriers, enabling efficient interconversions of structures within the simulation time. BO-MD computations were conducted with deMon-2k ⁴³ at the PBE0/DZVP level. ⁴⁴

Results and discussion

The global minimum (1) is a singlet state with C _s symmetry, corresponding to a closo-[B₁₀H₁₀]²⁻ bicapped-square antiprism with two H₂ molecules oriented toward adjacent triangular faces of the boron skeleton (Fig. 2). The next lowest-energy structure, 2, lies 21.5 kcal mol⁻¹ higher and corresponds to the arachno-[B₁₀H₁₄]²⁻ dianion with C _2v symmetry reported by Chen and coworkers (Fig. 1). ⁹ Structures 3, 4, and 5 involve a dissociated hydrogen molecule from the borohydride cluster. Specifically, 3 is a closo-[B₉H₉]²⁻ cluster with an attached BH₃ fragment, while 4 and 5 adopt nido-[B₁₀H₁₂]²⁻ framework, with relative Gibbs free energy ranges from 32 and 39 kcal mol⁻¹ above 1. Structure 6 (C _s symmetry) resembles 2, containing ten BH units, two BH₂ units, and two B–H–B bridges, but with different bridge arrangements, resulting in a ΔG _2-6 of 17.9 kcal mol⁻¹. In 2, the bridges are opposite each other and distant from the BH₂ units, whereas in 6, one bridge connects a BH₂ unit to an adjacent boron atom (B–H–BH₂). Structure 7 is an irregular half-open cage with a relative energy of 52.8 kcal mol⁻¹ above 1, and 8, a butterfly-like half-open cage linked by an HB–BH fragment, is 55.7 kcal mol⁻¹ higher. Finally, 9 is a C _2v half-open cage that binds a hydrogen molecule, with a relative energy of 58.5 kcal mol⁻¹.

Fig. 2:

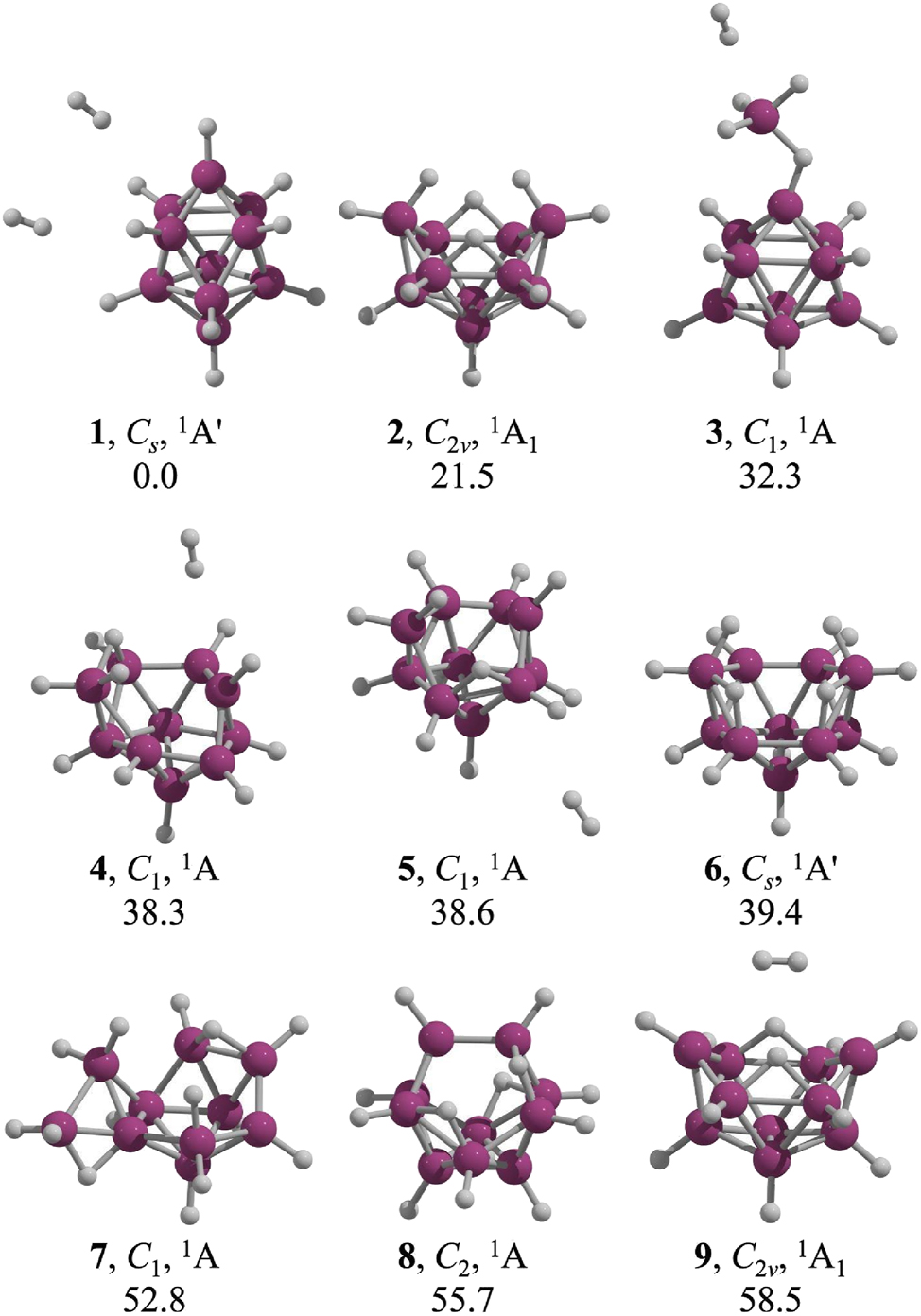
Low-lying local minima of B₁₀H₁₄ ²⁻. Relative Gibbs free energies (kcal mol⁻¹) were computed at the CCSD(T)/aug-cc-pVTZ//TPSS-D3/aug-cc-pVTZ level at 298.15 K. All structures were confirmed as local minima by frequency analysis.

Comparison of the geometric parameters of 2, 1, and nido-B₁₀H₁₄ shows B–H distances of 1.18–1.20 Å (Fig. 3). The B–H–B bridges in nido-B₁₀H₁₄ and 2 have comparable bond lengths (around 1.34 Å). In nido-B₁₀H₁₄, the four boron atoms (B1 to B4) forming the closed cap have B–B bond lengths of 1.79 Å, which shorten by 0.04 Å in 2. A similar trend is found at the open side (B5 to B10). In nido-B₁₀H₁₄, the B5–B10 distance is 1.98 Å, 0.09 Å longer than in 2. In contrast, bonds B5–B6, B6–B7, B8–B9, and B9–B10 are 0.11 Å longer in 2 than in nido-B₁₀H₁₄. In structure 1, B–B lengths are slightly shorter than in nido-B₁₀H₁₄ and 2 forms. The closo-[B₁₀H₁₀]²⁻ fragment in 1 consists of two four-membered rings at the equatorial position and two boron atoms at the apical position. Bond lengths between equatorial boron atoms (1.84 Å) or between the four-membered rings (1.82 Å) are longer than those between apical and equatorial boron atoms (1.71 Å), indicating compaction of the boron framework. Notably, interaction with the hydrogen molecules does not alter the [B₁₀H₁₀]²⁻ framework in 1.

Fig. 3:

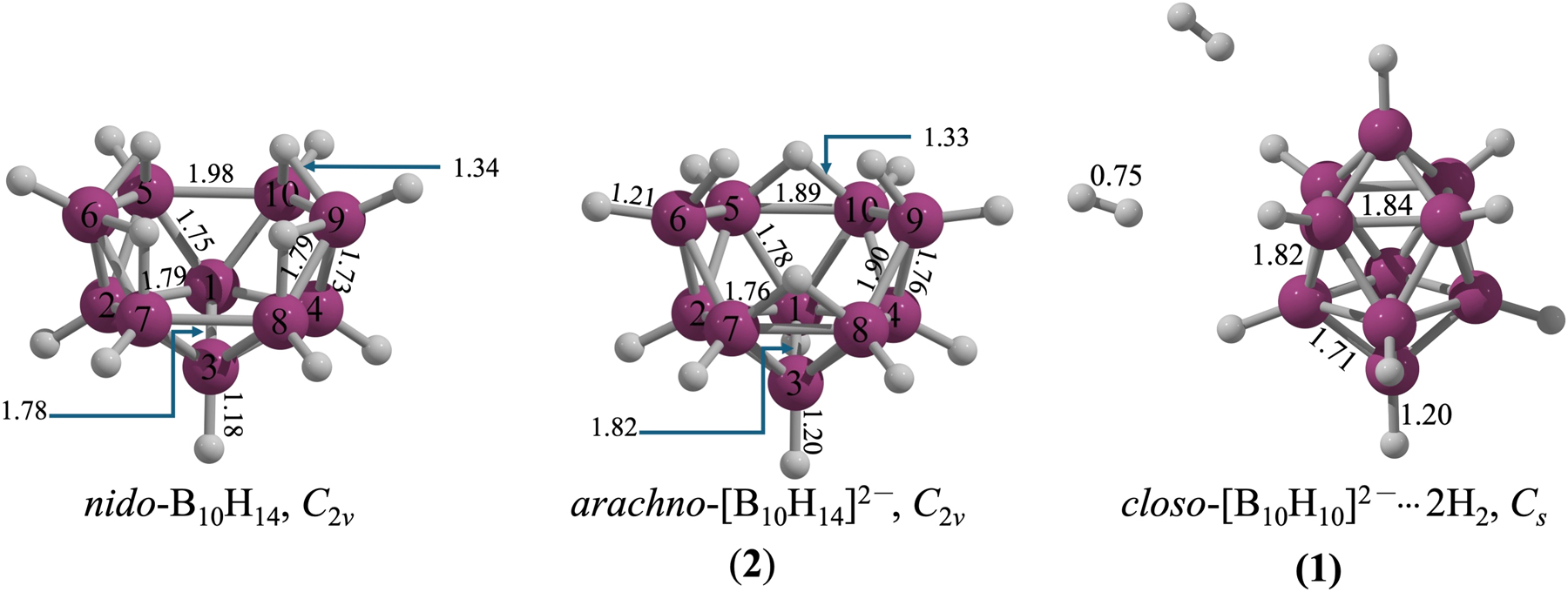
Structural comparison among B₁₀H₁₄, 2, and 1 structures.

To evaluate the thermal stability of complex 1, we computed its Gibbs free energies and its dissociated products, relative to the intact complex, from 0 to 400 K (Fig. 4a) in the gas phase using the Eyringpy software, ^{45 , 46} at the TPSS-D3/aug-cc-pVTZ level. At 0 K, 1 is more stable than both [B₁₀H₁₀]²⁻⋯H₂ + H₂ and [B₁₀H₁₀]²⁻ + 2H₂ by 0.8 and 2.0 kcal mol⁻¹, respectively. Above 110 K, 1 dissociates into [B₁₀H₁₀]²⁻ and 2H₂. At room temperature, dissociation into [B₁₀H₁₀]²⁻⋯H₂ + H₂ is exergonic (ΔG = 4.2 kcal mol⁻¹), and [B₁₀H₁₀]²⁻⋯H₂ further dissociates into [B₁₀H₁₀]²⁻ + H₂ with ΔG = 2.5 kcal mol⁻¹. So, these results indicate that 1 is stable only at low temperatures.

Fig. 4:

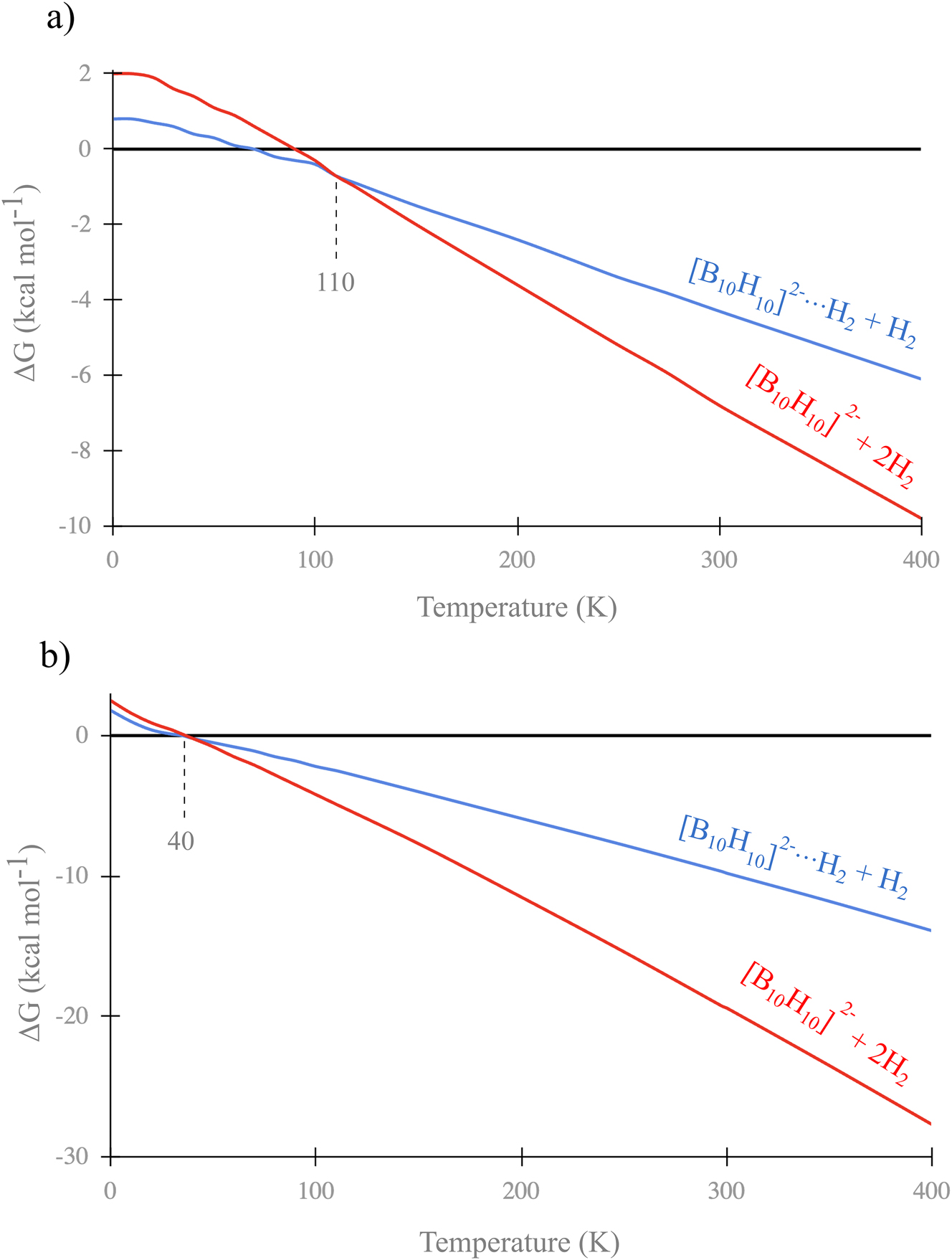
Stability of 1 at different temperatures a) in the gas phase and b) in solution.

In both phases, structure 1 is the global minimum at the DFT level (see Figure S1). Structure 2 lies 20.5 kcal mol⁻¹ above 1 in the gas phase and 24.7 kcal mol⁻¹ in solution, showing that solvent effects slightly influence the relative Gibbs energies. However, the dissociation differs between phases. In solution, 1 begins to dissociate into [B₁₀H₁₀]²⁻⋯H₂ + H₂ and [B₁₀H₁₀]²⁻ + 2H₂ at 40 K (Fig. 4b), approximately 70 K lower than in the gas phase (T < 110 K). Therefore, 1 is viable in solution only at very low temperatures, dissociating as the temperature increases.

To analyze the bonding, an AdNDP study was performed for nido-B₁₀H₁₄, 2 and 1 (Fig. 5). nido-B₁₀H₁₄ contains ten 2c-2e σ-bonds, whereas 2 and 1 have twelve, two of which in 1 correspond to H₂ molecules. nido-B₁₀H₁₄ also shows six delocalized 3c-2e bonds (four in a B₂H ring and two in a B₃ ring) and six 5c-2e bonds that stabilize the boron skeleton; these are absent in 2 and 1. In contrast, 2 retains only two 3c-2e bonds in a B₂H ring, while the closo-[B₁₀H₁₀]²⁻ framework in 1 lacks 3c-2e bonding altogether. The stability of 2 arises from nine 4c-2e bonds distributed over B₄ units, while the boron moiety in 1 is stabilized by 11 4c-2e bonds delocalized throughout the boron cage. So, the number of electron pairs in the [B₁₀H₁₀]²⁻ fragment of 1 stabilizes the closo structure in accordance with Wade’s rules for n = 10. ¹⁶ Moreover, the NCI analysis of 1 reveals non-covalent interactions not only between the B₁₀H₁₀ framework and the H₂ molecules, but also between the two H₂ molecules (Figure S2). These non-covalent interactions contribute to the stabilization of 1 at low temperatures.

Fig. 5:

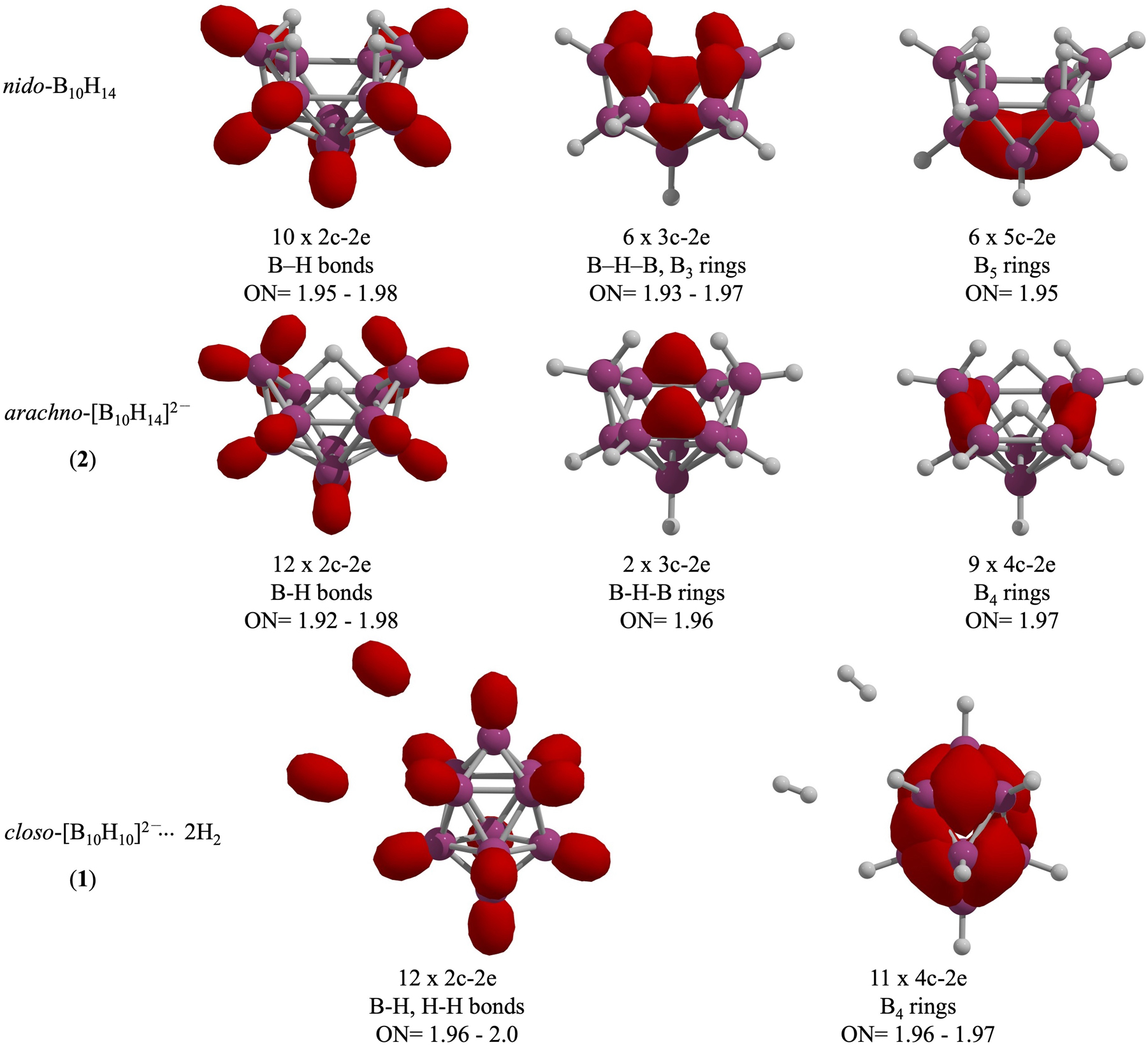
AdNDP analysis for B₁₀H₁₄, 2, and 1. Occupation numbers (ONs) are given in |e|.

The thermodynamic analysis indicates that the bonding in 1 enhances delocalization, contributing to its lower energy. However, the isolation of 2 by Chen et al. shows that it is kinetically viable. Transformation of 2 into 1 requires detachment of two H₂ molecules and closure of the boron skeleton to form a closo-B₁₀H₁₀ moiety.

Two pathways for this conversion were explored. The first, involving H₂ removal from BH₂ units (Fig. 6a), has a high activation barrier (ΔG ^⧧ = 65.7 kcal mol⁻¹) leading to 9, and the formation of 9 is highly endergonic (ΔG = 58.5 kcal mol⁻¹), rendering this pathway unfeasible. The second pathway involves stepwise hydrogen elimination (Fig. 6b). Initially, 2 converts to 6 via TS _2-6 with a moderate barrier (ΔG ^⧧ = 19.9 kcal mol⁻¹), during which hydrogen atoms rearrange into B–H–B bridges and migrate toward BH₂ groups to form B–H–BH₂ units. Next, two hydrogen atoms are released as H₂ through TS _6-4 (ΔG ^⧧ = 22.8 kcal mol⁻¹). Finally, another H₂ molecule is eliminated, promoting closure of the boron skeleton in 4 to yield 1 via TS _4-1 (ΔG ^⧧ = 31.3 kcal mol⁻¹). The overall formation of [B₁₀H₁₀]²⁻ and two H₂ molecules is exergonic (ΔG _rxn = −6.7 kcal mol⁻¹), indicating spontaneous dissociation of 1. Although the first hydrogen detachment via TS _6-4 is feasible, the second is hindered by its high barrier, preventing 2 from converting into 1 or dissociated into [B₁₀H₁₀]²⁻ and molecular hydrogen.

Fig. 6:

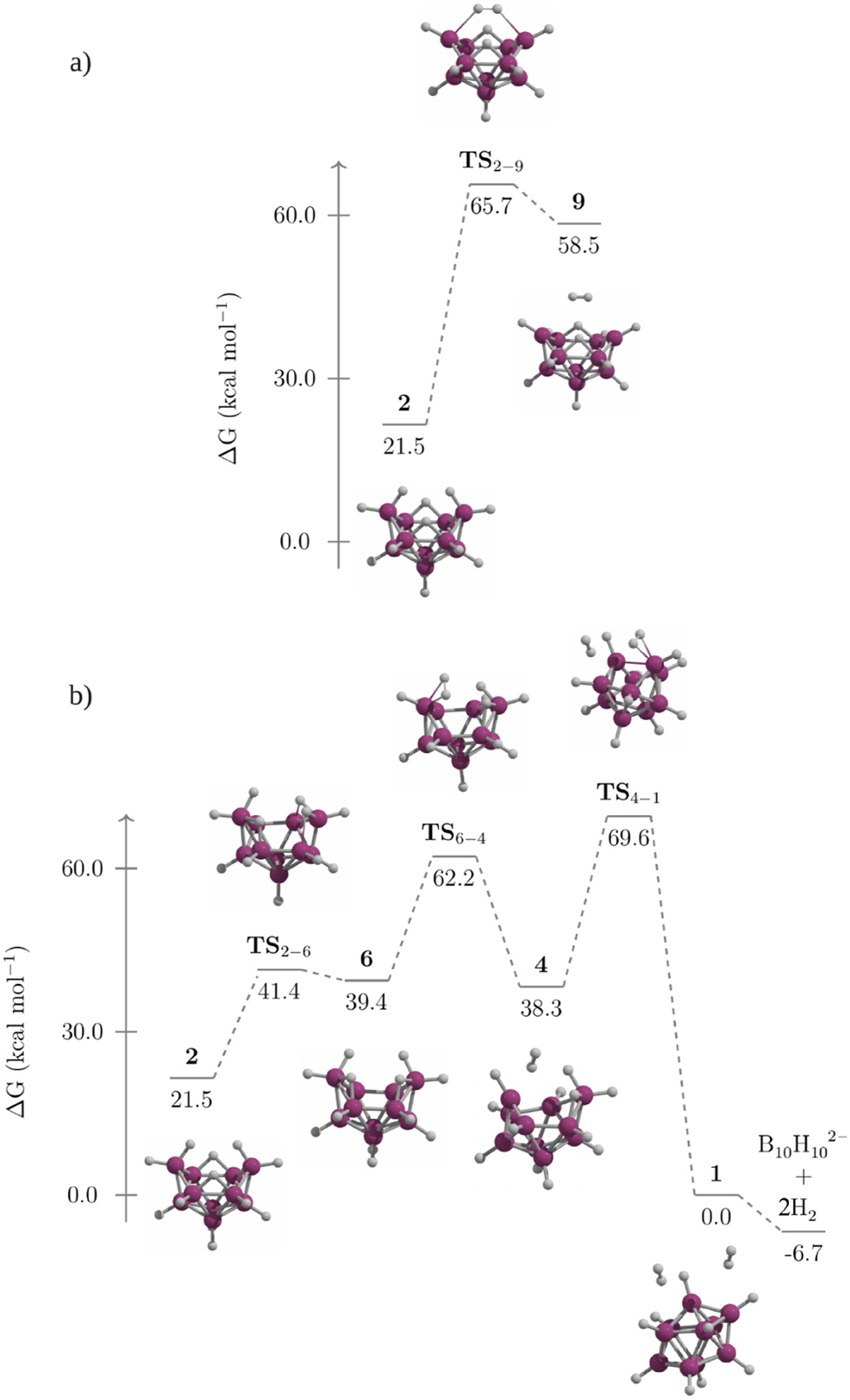
Gibbs energy profile for the conversion of 2 to 1.

Born-Oppenheimer molecular dynamics simulations at 1200 K for 30 ps confirm the kinetic stability of 2, which undergoes only minor distortions while maintaining its arachno structure (see Movie S1 in the ESI). Solvent effects on the barriers are minimal at room temperature, with relative energy variations of only 0.7–3.7 kcal mol⁻¹ (Figure S3).

Finally, to evaluate the effect of counterions, we performed structural optimizations of dianionic isomers 1 and 2 in the presence of Na⁺ at the TPSS-D3/aug-cc-pVTZ level (Figure S4). The Na₂B₁₀H₁₀⋯2H₂ structure is 25.5 kcal mol⁻¹ more stable than the Na₂B₁₀H₁₄ structure, indicating that the addition of counter-ions increases the relative energy difference between 1 and 2 by 4.0 kcal mol⁻¹ (see Figure S1). Importantly, the Na₂B₁₀H₁₀⋯2H₂ structure remains energetically more stable than the Na₂B₁₀H₁₄ form. Structurally, the B–B and B–H bond distances in both dianionic forms interacting with sodium counter-ions change only slightly, by 0.01–0.04 Å.

Conclusions

This study shows that arachno-[B₁₀H₁₄]²⁻, although kinetically stable, is not the global minimum. The [B₁₀H₁₀]²⁻⋯2H₂ complex is more stable by approximately 21.5 kcal mol⁻¹. Conversion pathways indicate that the arachno form is stabilized by a high activation barrier (ΔG ^⧧ = 31.3 kcal mol⁻¹), preventing its transformation to the [B₁₀H₁₀]²⁻⋯2H₂ complex under standard conditions. Molecular dynamics simulations confirm the kinetic stability of the arachno form, with minimal distortions over time. Our calculations show that the global minimum remains stable at low temperatures (T < 110 K) but dissociates into [B₁₀H₁₀]²⁻⋯H₂ + H₂ and closo-[B₁₀H₁₀]²⁻ + 2H₂ at high temperatures, suggesting that closo-[B₁₀H₁₀]²⁻ can adsorb two hydrogen molecules under cold conditions. Solvent effects are minor, although they reduce the dissociation temperature of the global minimum to T < 40 K relative to the gas phase. The effects of counterions induce negligible structural and energetic changes. So, the addition of two electrons to neutral B₁₀H₁₄ significantly alters the structure of the global minimum. These results provide insight into borohydride chemistry, particularly regarding the design and stabilization of borane structures.