The Jahn-Teller effect in mixed aqueous solution: the solvation of Cu2+ in 18.6% aqueous ammonia obtained from ab initio quantum mechanical charge field molecular dynamics
Abstract
The solvation structure and dynamics of Cu2+ in 18.6 % aqueous ammonia have been investigated using an ab initio quantum mechanical charge field molecular dynamics (QMCF MD) simulation approach at the Hartree–Fock (HF) level of theory applying the LANL2DZ ECP and Dunning DZP basis sets for Cu2+, ammonia and water, respectively. During a simulation time of 20 ps, only NH3 molecules are observed within the first solvation shell of Cu2+, resulting in the formation of an octahedral [Cu(NH3)6]2+ complex. While no exchange of these ligands with the second solvation shell are observed along the simulation, the monitoring of the associated N-Ntrans distances highlight the dynamics of the associated Jahn-Teller distortions, showing on average 2 elongated axial (2.19 Å) and 4 equatorial Cu–N bonds (2.39 Å). The observed structural properties are found in excellent agreement with experimental studies. In addition, an NBO analysis was carried out, confirming the strong electrostatic character of the Cu2+–NH3 interaction.
Introduction
Detailed studies focused on the solvation of transition metal ions, in particular Cu2+, are essential to obtain a detailed understanding of the broad range of physico-chemical properties being also highly relevant for environmental and biochemistry as well as material sciences [1], [2], [3], [4], [5]. Experimental investigations of ion solvation are generally performed via diffraction and spectroscopic investigations. In addition to these experimental studies, theoretical approaches executed at a quantum chemical level of theory proved as a highly successful alternative route to achieve an accurate description of solvated systems at the molecular scale [6], [7], [8], [9], [10]. Both, experimental and theoretical studies have been widely employed to explore the properties of solvated ionic species, and in particular to study structure (e.g. ion-solvent distance, coordination number) and dynamics (e.g. ligand exchange, conformational changes) of the solvation complex. However, in case of Cu2+ in solution [11], [12], [13] a degree of uncertainty with respect to the precise number of solvent molecules remains, which can be linked to the d9 electron configuration of Cu2+, which make the system susceptible to Jahn-Teller distortion resulting in a deformation of the underlying structural motifs [14], [15].
The properties of purely hydrated as well as ammonia-coordinated Cu2+ in aqueous solution have been characterized using various experimental and theoretical approaches. The hydration of Cu2+ has been investigated by neutron diffraction [13], X-ray absorption near-edge spectroscopy (XANES) [16], neutron and X-ray scattering [17], and was also studied using computational methods like hybrid quantum mechanical/molecular mechanical molecular dynamics (QM/MM MD) simulations [11] as well as the quantum mechanical charge field molecular dynamics (QMCF MD) approach [15]. These studies report 5- as well as 6-fold coordination complexes to be formed. The predominantly 5-fold coordination observed in the majority of experimental studies concluded that the Jahn-Taller destabilization is remarkably present in this system. Extended X-ray Absorption Fine Structure (EXAFS) measurements [18] of Cu2+ containing complexes in the solid-state often show an octahedral configuration subject to dominant tetragonal Jahn-Teller distortions [19]. Similarly, computational studies at quantum mechanical level of theory [11], [15] report a stable octahedral coordination complex for aqueous Cu2+.
The structure of Cu2+ complexes in pure liquid and aqueous ammonia have also been target of experimental and computational investigations. EXAFS studies of Cu2+ in aqueous ammonia solution showed that the solvation of Cu2+ changed from axially-elongated octahedral to distorted square-planar upon increase of the pH value of the solution [1]. Nilsson et al. [7] investigated the coordination structure of Cu2+ in liquid and aqueous ammonia solution and reported that the solvation structure corresponds to a Jahn-Teller distorted octahedron with distinct equatorial and axial coordination sites. A QM/MM MD simulation study of Cu2+ in pure liquid ammonia also showed that the structural motif corresponding to a distorted octahedron predominates in the simulation, however, the structure undergoes rapid re-arrangement of axial and equatorial ligands on the picosecond scale due to the dynamical properties of the Jahn-Teller effect in solution [12].
Although several experimental methods have been applied to study the solvation of Cu2+ in solution, its tendency to lead to Jahn-Teller distortions makes the study of structural and dynamical properties of Cu2+ in solution highly challenging. On the other hand, theoretical methods provide the possibility to access ultrafast dynamical phenomena occurring on much shorter time frames than can be accessed with the majority of experimental techniques. To the best of knowledge no QM-based simulation study focusing on the solvation of Cu2+ in aqueous ammonia has been carried out as of yet.
A particularly successful class of methods to study ion solvation are QM/MM MD simulation techniques, since in these approaches the immediate ion-ligand interactions are treated via electronic structure theory [15], [20], [21], [22], [23], [24], [25]. However, if the QM-region is restricted to only accommodate the solvent and its entire first solvation shell, ion-ligand non-Coulombic potentials representing the interaction between the ion located in the center of the QM zone and solvent molecules in the MM region have to be provided. In many cases, the construction of these QM/MM non-Coulombic coupling potentials is difficult and time-consuming while at the same time the achievable accuracy is often limited [26]. A strategy to overcome this obstacle is to extend the size of the QM-region to include both the first and the second solvation shell as realized in the QMCF-MD approach [27], [28]. As a result of the increased distance between the solute and MM molecules, the application of the ion-solvent QM/MM coupling potential is not required, while at the same time the two-shell QM treatment leads to an improved description of the system [27], [28]. The QMCF MD technique has proven to be an accomplished method for studying ion solvation [29], [30], [31], [32], [33], [34], [35], [36], [37], [38], [39], [40] and has been successfully applied to investigate the structural and dynamical properties of various systems in aqueous ammonia solution [41], [42].
The natural bond orbital (NBO) approach is a method to evaluate electronic orbitals and their respective population based on the analysis of the quantum mechanical wave function, by translating the description resulting from occupied molecular orbitals into a representation corresponding to the concepts of chemical bonding [43]. An NBO analysis provides detailed information about bond formation as well as electronic donor-acceptor properties of the involved molecular species [44], [45], [46], [47]. The numerical value correlated to the number of electron pairs localized in a bond between two atoms, the Wiberg bond index (WBI), is one of the main results obtained from an NBO analysis [48]. The dominating contribution to the ion-ligand interaction in solvated systems involves the delocalization of the ionic charge, which is influenced by the number of coordinating ligands and the respective coordination geometry [49], [50].
In the present work, a combination of the QMCF-MD simulation approach and an NBO analysis was applied to study the structural and dynamical properties of Cu2+ in 18.6% aqueous ammonia solution, with special focus on the characterisation of the underlying Jahn-Teller effect. The solvation structure has been analyzed via radial and angular distribution functions (RDFs, ADFs) as well as coordination number distributions (CNDs). The dynamical properties have been evaluated using the velocity autocorrelation function (VACFs) projected onto the fundamental modes of the octahedral coordination complex, while the calculation of mean ligand residence times (MRTs) was carried out via the “direct method” for NH3 and H2O ligands in the second solvation shell. In addition, the time-evolution of first shell N–N trans-pairs provides an intuitive measure to highlight the dynamical character of the Jahn-Teller effect in solution. Finally, the results of an NBO evaluation are reported, providing detailed insight of the underlying ion-ligand interaction and the respective donor-acceptor stabilization energies.
Computational methodology
In this work the QMCF MD simulation approach [27], [29] is employed to achieve a computational description of the system. In this method the extended QM region is further divided into two sub-regions, being the inner core region containing the Cu2+ ion and the ammonia molecules of the first solvation shell, while the outer solvation layer includes the entire second solvation shell of the solute. Furthermore, the atomic partial charges of all MM molecules within the Coulombic cutoff are included as an external potential into the Hamiltonian of the QM system. This approach referred to as electrostatic embedding modulates the electron density close to the QM/MM interface and was shown to improve the coupling between the QM and MM zone. The partial charges of all atoms inside the QM region were obtained using Mulliken population analysis in every simulation step [28], [51]. To ensure a smooth transition of molecules between the QM and MM zone, a smoothing region with thickness of 0.2 Å is applied at the QM/MM interface. Here, the forces are computed twice, the first time at the QM level and a second time as if the molecule was already part of the MM zone, enabling an interpolation of the force contributions according to a continuous smoothing function. Further details on the calculations of the interactions in QMCF-MD approach have been published previously [51], [52], [53].
Simulation protocol
The QMCF-MD simulation was performed in a cubic simulation cell with a side length of 31.75 Å consisting of one Cu2+ ion, 815 ammonia and 184 water molecules. This setup corresponds to 18.6% aqueous ammonia at the experimental density of 0.927 g cm−3 [54]. The simulation was carried out in a canonical (NVT) ensemble under periodic boundary conditions and the minimum image convention was applied to all interactions. A second order Adams–Bashforth predictor-corrector algorithm was used to integrate the equation of motions with a time step of 0.5 fs. The temperature was set to 298.15 K corresponding to the experimental temperature employed to study 18.6% aqueous ammonia solutions [54]. To maintain constant temperature conditions along the simulation the Berendsen algorithm with a bath relaxation time of 0.1 ps was employed [55]. The Barker-Watts reaction field approach was used to account for the cutoff of long-range electrostatic interactions in the simulation [56].
The radius of the QM region was set to 6.5 Å, and a smoothing region with a thickness of 0.2 Å was applied to ensure continuous transitions of molecules between the QM and MM zones [57]. The calculation method of this simulation was Hartree-Fock, the respective basis sets applied to Cu2+ and all solvent molecules (H2O, NH3) were LANL2DZ-ECP and Dunning DZP, respectively. The flexible BJH-CF2 water model [58] was employed to describe all water interactions, enabling the description of explicit hydrogen motion. A flexible ammonia potential model [59] was used to describe the respective intra- and inter-molecular potential contributions. The interaction between NH3 and H2O in the MM region is described using a previously published pair potential [60]. The starting configuration for the QMCF MD simulation was obtained via classical MD employing published pair potentials for the Cu2+–O and Cu2+–N interactions [61]. First, the system was equilibrated for several hundred picoseconds using classical MD until a stationary temperature control was achieved after including heating and cooling conditions. After confirming stationary total energy and temperature, the system was re-equilibrated using QMCF MD for 4 ps to reach rapid equilibration. Next, data sampling was carried out for 20 ps. All quantum mechanical calculations in the QMCF MD simulation were executed using TURBOMOLE 5.9 [62], [63]. The VMD package was employed to visualize the trajectory data [64].
The NBO analysis was performed using Gaussian 09 [65], applying the respective molecular coordinates extracted from the QMCF MD simulation trajectory. The specific frame with the most stable geometry was employed as starting configuration for the NBO analysis, which was subsequently energy minimized at the HF level of theory using the LANL2DZ ECP basis set for Cu(II) and Dunning DZP for the solvent molecules. Finally, the NBO analysis was carried out, and the associated Wiberg bond index and stabilization energies were calculated.
Analysis
The structural properties of the Cu2+-solvation are analyzed via radial and angular distribution functions (RDFs, ADFs), as well as the respective coordination number distributions (CNDs). In addition, to investigate the exchange dynamics of water and ammonia ligands in the second solvation shell, the MRTs are calculated by counting the number of successful ligand exchange via the “direct method” [38]:
tsim represents the simulation time, Nav is the average coordination number of ligands in the respective shell, and
The frequencies of the octahedral vibrational modes are calculated via Fourier transform of the respective velocity autocorrelation functions (VACFs) C(t) as defined in Eq. 2.
with N and Nt representing the number of particles and time origins tI, respectively, and vJ corresponds to a particular velocity components of particle J. By projecting the velocities onto the fundamental modes of the octahedral coordination complex, a decomposition of the vibrational characteristics according to the fundamental modes being A1g, Eg, T1u and T2g is achieved [66].
A second-order perturbation theory analysis of the Fock matrix is performed to calculate the donor-acceptor interactions in the NBO basis [67]. The interactions are based on the loss of occupancy from the localized NBOs in the idealized Lewis structure into empty non-Lewis orbitals. For each donor NBO (i) and acceptor NBO (j), the stabilization energy associated with the delocalization i→j is estimated as [67].
with qi being the donor orbital occupancy, εi and εj are the associated orbital eigenenergies, and F(i, j) is the respective off-diagonal NBO Fock matrix element.
Results and discussion
Structural properties
The radial distribution functions (RDFs) of the Cu2+-ligand interaction (i.e. Cu–N,O) and the respective individual Cu–O and Cu–N contributions along with the respective running integration are depicted in Fig. 1. To improve the clarity, the Cu-ligand RDF is shown at an offset of +0.5. The details of the structural data are summarized in Table 1.
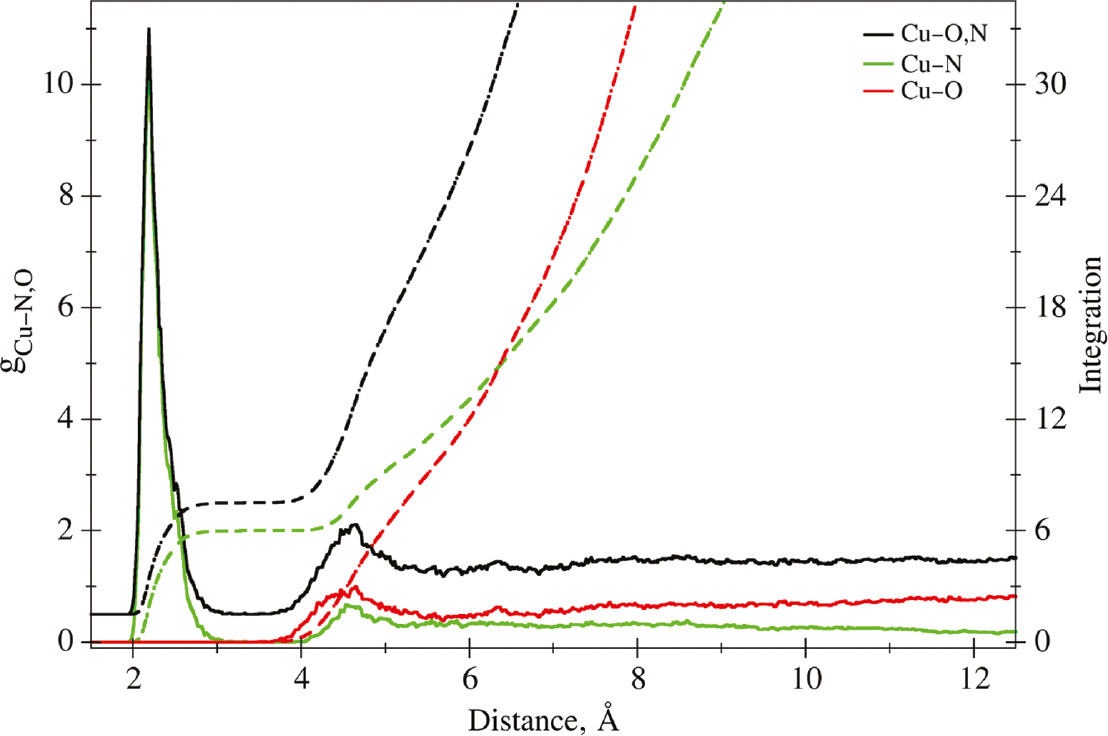
Radial distribution functions (RDFs) of Cu2+ in 18.6% aqueous ammonia. Solid lines show the RDFs, and the dashed lines indicate the associated integration numbers.
Characteristic values of the ion-ligand radial distribution functions for Cu2+ in 18.6% aqueous ammonia solution obtained from the QMCF-MD simulation.
| Pairs | CN1 | CN2 | ||||
|---|---|---|---|---|---|---|
| Cu2+–N | 2.19 | 3.17 | 4.53 | 5.70 | 6 | 4.7 |
| Cu2+–O | – | – | 4.59 | 5.48 | – | 8.8 |
The maximum and minimum distances of the respective solvation shells rM and rm are given in Å, CN1 and CN2 are the respective average coordination numbers.
The Cu–N,O RDF shows a narrow first shell peak in the range of 1.97–3.17 Å (peak maximum at 2.19 Å) composed of six ligands followed by broad second shell peak ranging from 3.17 to 5.45 Å (peak maximum at 4.55 Å) being on average populated by 13.5 ligand molecules. Decomposition of the total RDF into the contributions arising from the Cu–N and Cu–O interaction shows that the first shell is exclusively occupied by ammonia molecules. In contrast, the second shell is on average populated by 8.8 H2O molecules, whereas the average number of NH3 ligands is only about 4.7. The Cu-O and Cu-N pair distribution also show, that the ammonia content tends to decrease upon increasing Cu-ligand distance, while at the same time the pair density of H2O molecules is increasing.
Close inspection of the first shell peak demonstrates a pronounced tailing towards larger distances, which has been attributed to the influence of the Jahn-Teller (JT) distortion of the solvation complex [68], [69]. In order to obtain detailed insight into the impact of the JT effect and the associated ligand dynamics, the pair distances observed for the three trans-NN pairs present in the first solvation shell have been plotted against the simulation time (see Fig. 2a–d). It can be seen that the three NN-distances undergo structural changes between stationary distances being at approximately 4.3 and 5.0 Å at the picosecond time scale. Whenever the distance between ligands associated to an elongated NN-pair is shortened, this process is compensated by elongating the distance of another NN-pair. Thus, on average two NN-pairs are found at distances close to 4.3 Å, whereas the third pair adopts an elongated distance. The observed ligand separations of 4.3–5.0 Å correspond to stable ion-N distances amounting to approx. 2.15 and 2.50 Å, respectively. However, it can be seen that in many instances the instantaneous N–N distances are at an intermediate state in the range of 4.5–4.7 Å (corresponding to Cu–N distances of 2.25–2.35 Å) arising from the conformational changes of the solvation complex occurring on the picosecond scale. This may explain why the accurate determination of the axial and equatorial distance is particularly challenging. Decomposition of the first shell peak of the Cu–N distribution (see Fig. 2e) demonstrates that each of the three N-N pairs indeed show highly similar contributions to the overall Cu–N RDF.
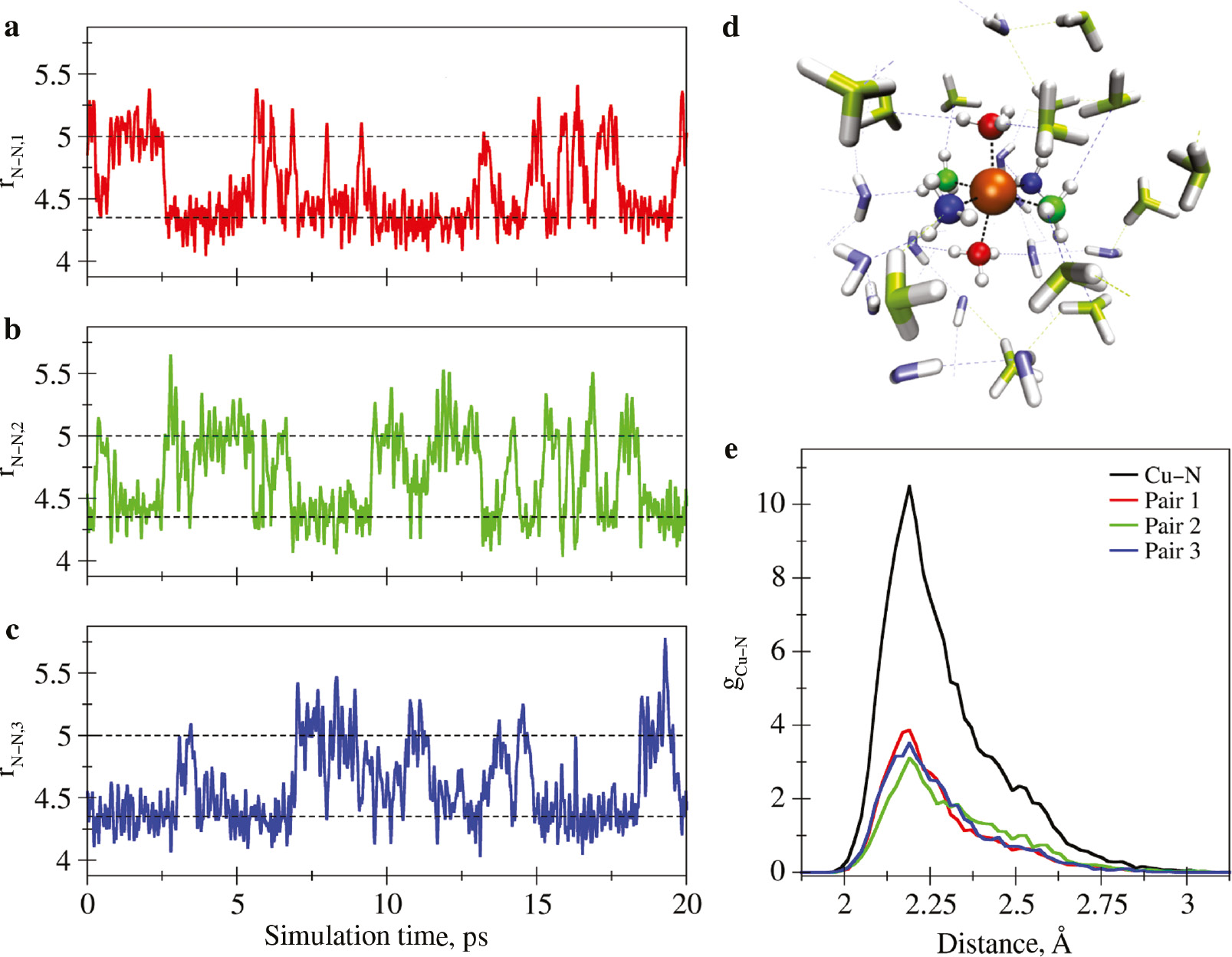
(a–c) Time evolution of the instantaneous N–N distance of the three trans-pairs in the first solvation shell. The dashed lines mark the two stable N–N distances of 4.3 and 5.0 Å arising due to the Jahn-Teller distortion, corresponding to average Cu–N distances of 2.15 and 2.5 Å, respectively. (d) Snapshot depicting the N-atoms of the three trans-pairs in red, blue and green. Second shell NH3 and H2O molecules are highlighted in light green and light blue, respectively. (e) Decomposition of the first shell RDF peak into the contributions arising from the respective trans-pairs.
A comparison between the structural data obtained from this simulation study and data reported in the literature is presented in Table 2. The structural properties are consistent with the experimental study based on EXAFS [7] reporting the solvation of Cu2+ in aqueous ammonia as an octahedral structure with the presence of four equatorial and two elongated axial ligands. The remaining deviation in the ion-nitrogen distances can be attributed to the challenging nature of the dynamic Jahn-Teller effect on the one hand and the possibly influence of perchlorate as counter ions at the comparably high concentrations employed in the experimental studies [7]. The distance of the Cu2+–NH3 interaction in aqueous ammonia is shorter than that observed in the aqueous case [6], [15], which was shown to be longer than in pure liquid ammonia solutions [7], [12]. These findings highlight the impact of the presence of water on the interaction between Cu2+ and NH3 ligands in aqueous ammonia, which is in line with the hard/soft Lewis acids and bases (HSAB) classification [70] of water being a hard ligand compared to NH3, which is typically attributed as being soft [71], [72].
Structural properties of Cu2+ in various solutions obtained via different experimental and computational approaches.
| Method | dCu-Ligand | CN | System | Reference |
|---|---|---|---|---|
| QMCF | 2.19 | 6 | 18.6% Aqueous ammonia (815 ammonia+184 water molecules) | This work |
| EXAFS | 2.051 (equatorial) 2.289 (axial) | 6 | [Cu(NH3)6]2+ in aqueous ammonia conc. 0.3 mol dm−3 | [7] |
| EXAFS | 2.065 (equatorial) 2.288 (axial) | 6 | [Cu(NH3)6]2+ in liquid ammonia | [7] |
| EXAFS | 2.04 | 5 | Cu2+ in liquid ammonia | [9] |
| EXAFS | 2.25 | 6 | Cu(H2O)6(NO3)2 | [74] |
| UV-VIS, FTIR | – | 4 | Cu2+ in (NH4)2SO4 | [75] |
| EXAFS, XANES | 2.028 | 4 | Cu2+ in ammoniacal solutions | [1] |
| XANES | 2.24 | 5-6 | Cu2+ in water | [16] |
| Neutron and X-ray scattering | – | 5 | Cu(ClO4)2 in water | [17] |
| QM/MM (HF) | 2.05 | 5.98 | Cu2++215 ammonia molecules | [12] |
| QM/MM (B3LYP) | 2.02 | 5.30 | Cu2++215 ammonia molecules | [12] |
| Monte Carlo Simulation | 2.26 | 6 | CuCl2 in 18.6% aqueous ammonia | [76] |
| QMCF | 2.06 | 6 | Cu2++999 water molecules | [15] |
The first shell Cu-ligand distance rCu-Ligand is reported in Å, CN is the associated coordination number of the first solvation shell.
In contrast to the zero RDF intensity separating the first and second shell peak in the Cu–N RDF, which is associated to the absence of first shell ligand exchange, the broad second shell peaks in the Cu–N and Cu–O RDFs imply that a higher solvent mobility linked to the exchange of ligands with the surrounding bulk phase is observed. Since the coordination numbers obtained from the integration of the radial distribution functions correspond to the ensemble average over the whole simulation trajectory, the respective variation has been investigated using coordination number distribution (CND) plots shown in Fig. 3. As expected, the coordination number in the first solvation shell is found to be exclusively six.
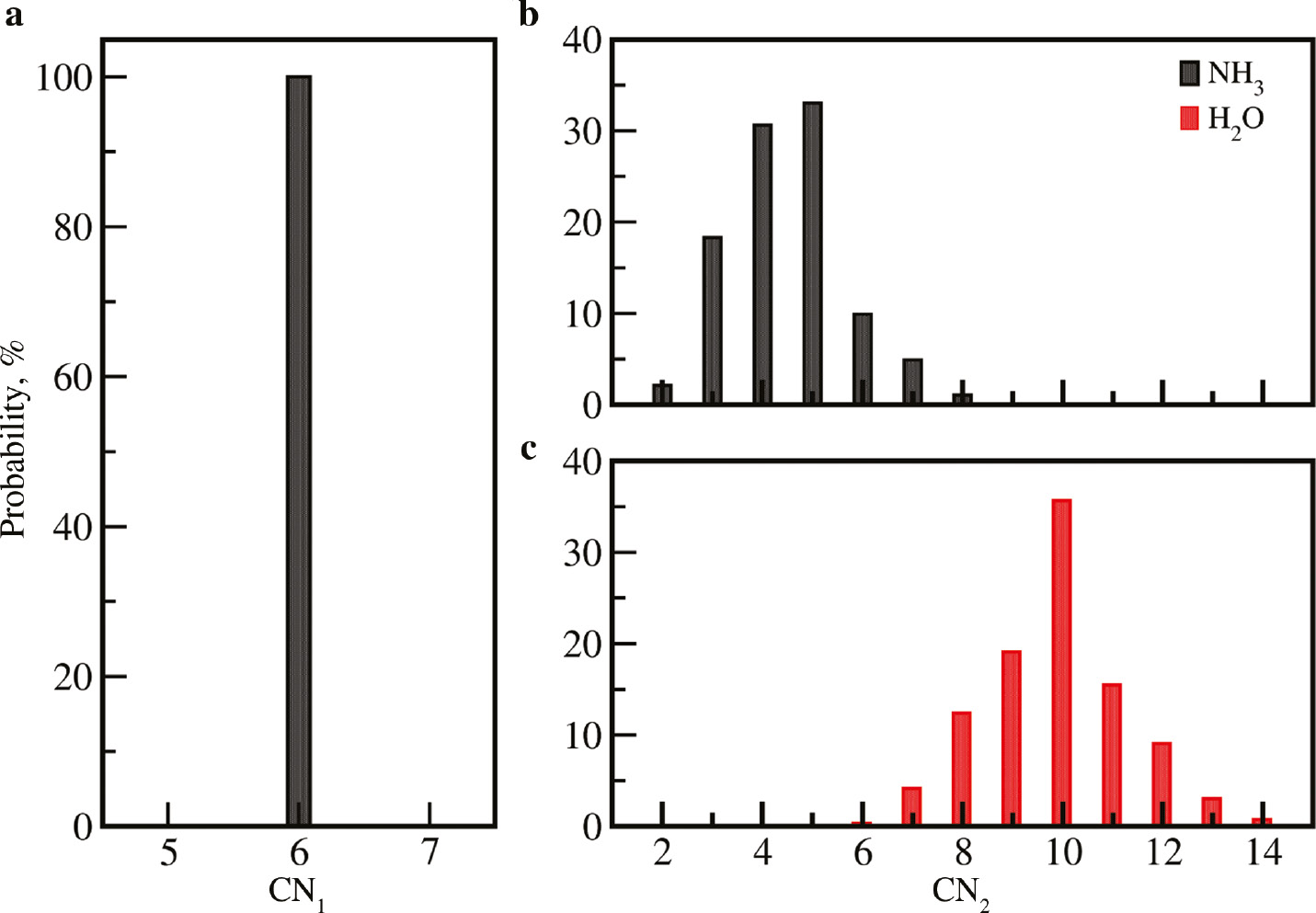
Coordination number distributions (CNDs) of the (a) first and (b, c) second solvation shell of Cu2+ in 18.6% aqueous ammonia obtained from the QMCF MD simulation.
In the second solvation shell, a broad distribution of coordination numbers of NH3 ligands ranging from 2 to 8 with the highest probability of 33.0% being observed for coordination number 5. This broad distribution results due to the large distances between the ion and ligands that cause a high ligand mobility and rapid ligand exchange between the second shell and the bulk phase. The associated fluctuating time series of second shell coordination numbers shown in Fig. 4 point towards the occurrence of a large number of ligand exchange events. Despite the rapid fluctuation of the individual time series of water and ammonia, the respective sum displays a notably smaller variation over the simulation trajectory.
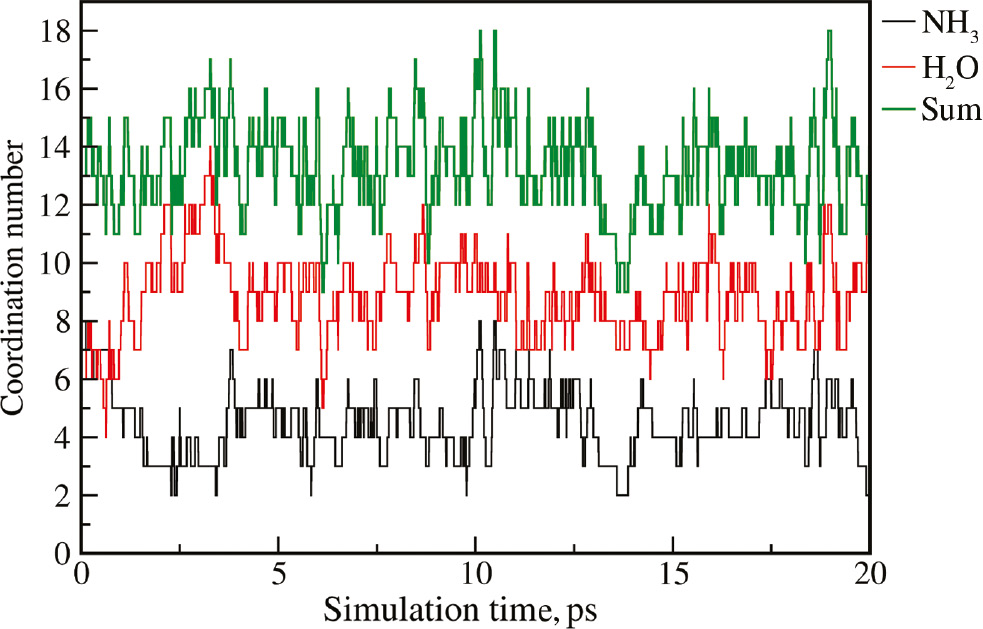
Time series of the coordination number of NH3 and H2O ligands in the second solvation shell along with the respective sum.
In order to obtain further details on the structural properties in the first solvation shell, the ligand-ion-ligand angular distribution function (ADF) was evaluated. Because only ammonia ligands are present within the first solvation shell, only the N–Cu2+–N angle had to be calculated (Fig. 5). Two peaks ranging from 69.5°–114.5° and 155.5°–179.5° with maxima at 90.5° and 174.5° are visible, which correspond to the octahedral geometry of the solvation complex. Thus, despite the dynamical character of the Jahn-Teller effect leading to strong variations of the instantaneous Cu2+–N distances, the average angle distribution analysed over the whole simulation trajectory corresponds to that of an ideal octahedral solvation complex.
![Fig. 5: Angular distribution function (ADF) of the N–Cu2+–N angle in the first solvation shell with the visualization of the [Cu(NH3)6]2+ solvation complex.](/document/doi/10.1515/pac-2018-1115/asset/graphic/j_pac-2018-1115_fig_005.jpg)
Angular distribution function (ADF) of the N–Cu2+–N angle in the first solvation shell with the visualization of the [Cu(NH3)6]2+ solvation complex.
Ligand dynamics
The ligand dynamics in the solvation shells is evaluated employing the time evolution of all ligand visiting the first and second solvation layers of Cu2+ (see Fig. 6). This dynamical analysis confirms that only N-atoms are present in the first shell and no ligand exchange between first and second solvation shell is observed. In contrast, ligands in the second shell show a high degree of mobility and frequently undergo exchange reactions with the bulk phase. The mean residence time (MRT) of second shell ligands was determined via direct monitoring of ligand exchange events [38]. The resulting MRT values were determined as 2.2 ps and 2.6 ps for ammonia and water ligands, respectively. Thus, although ammonia forms a highly stable first solvation shell, the second shell MRT value is shorter than that of water, which can be attributed to the weak hydrogen bond properties of the NH3 molecules compared to H2O.
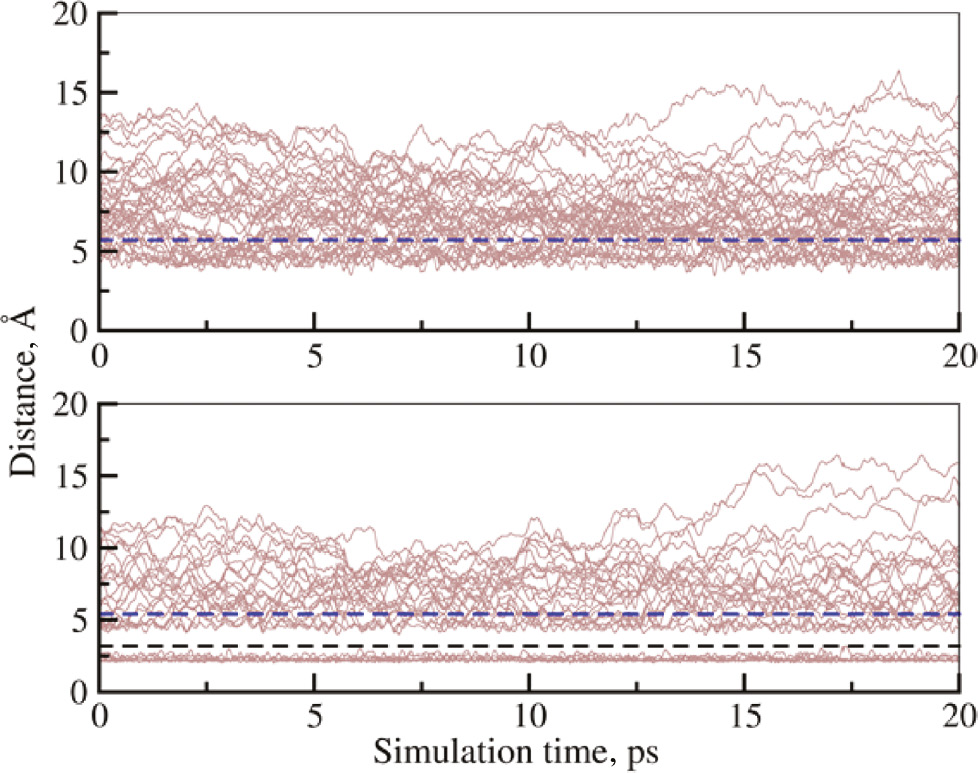
Time evolution of (a) the Cu2+–O and (b) the Cu2+–N distance of all ligand molecules registered in the first or second solvation layer. The black dashed line represent the boundary between first and second solvation shell, the blue dashed lines indicate the boundary between the second shell and the bulk phase.
The vibrational power spectra of the octahedral A1g, Eg, T1u and T2g-modes of the [Cu(NH3)6]2+ complex obtained via Fourier transform of the projected velocity auto-correlation functions are depicted in Fig. 7. The A1g-mode corresponding to the symmetric stretch vibration enables a direct analysis of the associated ion-ligand force constants. Two peaks at 200 and 385 cm−1 are visible in the spectrum of the A1g-mode, with corresponding average force constants of 27 N m−1 and 100 N m−1, representing the different bond strength of the equatorial and axial ion-ligand interactions present in the Jahn-Teller distorted complex. This finding agrees well with the force constants for Cu2+ in aqueous solution [15] reported as 63 and 121 N m−1.
![Fig. 7: The vibrational power spectra of the octahedral A1g, Eg, T1u and T2g-modes of the [Cu(NH3)6]2+ complex obtained via Fourier transform of the projected velocity auto-correlation functions (VACFs).](/document/doi/10.1515/pac-2018-1115/asset/graphic/j_pac-2018-1115_fig_007.jpg)
The vibrational power spectra of the octahedral A1g, Eg, T1u and T2g-modes of the [Cu(NH3)6]2+ complex obtained via Fourier transform of the projected velocity auto-correlation functions (VACFs).
Natural bond orbital (NBO)
The application of the NBO analysis was employed as an additional characterization to evaluate the properties of the ion-ligand interaction and the associated stabilization energy. Recently, this analysis has been successfully employed to characterize the ion-ammonia interaction in studies of K+ and Rb+ in pure liquid ammonia [36], [41] as well as Cu+ in aqueous ammonia solution [73].
In this work, the NBO analysis is applied to the solvated complex [Cu(NH3)6]2+. The Cu2+–NH3 binding is dominated by orbital interactions between the unoccupied valence non-bonding (LP*) of Cu2+ and (i) the lone-pair orbitals (LP) of the N-atoms as well as (ii) the bonding N–H orbitals (BD) of ammonia. The associated Wiberg bond indices (WBIs) and the stabilization energy of specific donor-acceptor NBOs are listed in Table 3. The values for the WBIs in the range from 0.15 to 0.23 imply that although the ion-ligand interaction is dominated by electrostatic contributions, a residual covalent contribution appears to be present in the Cu2+–NH3 binding.
Wiberg bond index and associated contribution to the stabilisation energy obtained from a natural bond orbital (NBO) analysis of an energy minimised [Cu(NH3)6]2+ complex.
| [Cu(NH3)6]2+ | Wiberg bond index | Donor NBO | Acceptor NBO | Stabilisation energy (kJ mol−1) |
|---|---|---|---|---|
| Cu–NH3 (1) | 0.2271 | BD (N–H) | LP* Cu | 54.1828 |
| LP (N) | LP* Cu | 176.3138 | ||
| Cu–NH3 (2) | 0.2289 | BD (N–H) | LP* Cu | 66.98584 |
| LP (N) | LP* Cu | 193.3426 | ||
| Cu–NH3 (3) | 0.2314 | BD (N–H) | LP* Cu | 64.18256 |
| LP (N) | LP* Cu | 181.1672 | ||
| Cu–NH3 (4) | 0.2302 | BD (N–H) | LP* Cu | 61.58848 |
| LP (N) | LP* Cu | 183.0082 | ||
| Cu–NH3 (5) | 0.1696 | BD (N–H) | LP* Cu | 30.334 |
| LP (N) | LP* Cu | 128.3651 | ||
| Cu–NH3 (6) | 0.1512 | BD (N–H) | LP* Cu | 25.5224 |
| LP (N) | LP* Cu | 102.8846 |
The nature of the Jahn-Teller distorted solvation complex is visible in the Wiberg bond indices as well. While the four equatorial ammonia ligands show consistent bond indices of 0.23, the associated values for the axial NH3 pair only amount to 0.15 and 0.17, respectively. The same trend is visible in the respective stabilization energy estimated for individual orbital interactions. While values in the range from 230 to 260 kJ mol−1 are observed for the four equatorial ligands, significantly lower stabilization energies of 128 and 159 kJ mol−1 are obtained for the NH3 molecules in axial position. As expected, the main contribution to the donor-acceptor interaction stems from the LP of the N-atoms acting as donor NBO, however, the contributions from the N–H bonding orbitals still are significant. This analysis demonstrates that the analysis of natural bond orbitals can also be employed to study complex chemical interactions in a Jahn-Teller distorted coordination complex.
Conclusion
This QMCF MD simulation study of Cu2+ in 18.6% ammonia solution demonstrates that theoretical approaches provide a reliable alternative route to study challenging solvation complexes in mixed aqueous solutions and that the simulation results can be further supported by the results of a natural bond orbital analysis. The structural and dynamical properties obtained from the simulation as well as the energetic properties resulting from the NBO calculation clearly highlight a pronounced impact of the Jahn-Teller effect. A stable, octahedral first-shell solvation complex composed of six ammonia ligands, [Cu(NH3)6]2+, was observed along the 20 ps simulation trajectory, whereas the second solvation shell shows a higher population by water molecules. The analysis of the impact of Jahn-Teller distortion on opposite first shell NH3 pairs showed that on average two ligands are located at elongated coordination sites, whereas the remaining four ligands are observed at shorter distances. However, these distortions of the underlying octahedral coordination are found to be highly dynamical and interchange within the picosecond scale. Despite the frequent conformational changes, no exchange of first shell ligands along the simulation was observed. In contrast, both ammonia and water ligands in the second shell are highly mobile, resulting in frequent ligand exchange reactions between the second shell and the bulk phase. The second shell mean residence time of water is slightly longer than that of ammonia, which can be attributed to the weaker hydrogen bonding for the latter molecules.
The vibrational frequency of the Cu2+–NH3 interactions is also influenced by the Jahn-Teller effect, resulting in a lower ion-ligand stretching frequency and a weaker average ion-ligand bond force constant consistent with the results reported for aqueous Cu2+.
The Wiberg bond indices obtained from the NBO analysis in the range of 0.15–0.23 show that the Cu–N interactions in the [Cu(NH3)6]2+ complex are predominantly coulombic with a residual covalent character. As expected, the main contribution to the Cu2+–NH3 binding results from orbital interactions between the unoccupied LP* of Cu2+ and the lone-pair orbital of the nitrogen atoms, however, the interaction between LP* and the N–H bonding orbitals were found to provide a minor contributions as well.
Article note
A collection of invited papers based on presentations at the 15th Eurasia Conference on Chemical Sciences (EuAsC2S-15) held at Sapienza University of Rome, Italy, 5–8 September 2018.
Acknowledgements
The authors dedicate this publication to the memory of Dr. rer. nat. Ria Armunanto. W.D. Saputri acknowledges a Ph.D. scholarship (PMDSU) issued by the Ministry of Research, Technology and Higher Education of the Republic of Indonesia (1511/E4.4/2015). The authors are grateful to Niko Prasetyo for his technical help at the initial stage of the simulation. Research reported in this publication was jointly supported by the ASEAN-European Academic University Network (ASEA-UNINET), the Austrian Federal Ministry of Science, Research and Economy, and the Austrian Agency for International Cooperation in Education and Research (OeAD-GmbH).
References
[1] J. Hu, Q. Chen, H. Hu, Z. Jiang, D. Wang, S. Wang, Y. Li. J. Phys. Chem. A117, 12280 (2013).10.1021/jp404768eSearch in Google Scholar
[2] J. B. Hilton, S. W. Mercer, N. K. H. Lim, N. G. Faux, G. Buncic, J. S. Beckman, B. R. Roberts, P. S. Donnelly, A. R. White, P. J. Crouch. Sci. Rep.7, 1 (2017).10.1038/s41598-016-0028-xSearch in Google Scholar
[3] X. Li, H. Qiu, P. Gao, Y. Yang, Z. Yang, N. Huang. NPG Asia Mater.10, 482 (2018).10.1038/s41427-018-0052-3Search in Google Scholar
[4] M. Tao, L. Xue, Z. Sun, S. Wang, X. Wang, J. Shi. Sci. Rep.5, 1 (2015).10.1038/srep13764Search in Google Scholar
[5] M. V. Kirillova, P. T. De Paiva, W. A. Carvalho, D. Mandelli, A. M. Kirillov. Pure Appl. Chem.89, 61 (2017).10.1515/pac-2016-1012Search in Google Scholar
[6] G. Chillemi, E. Pace, M. D’Abramo, M. Benfatto. J. Phys. Chem. A120, 3958 (2016).10.1021/acs.jpca.6b03569Search in Google Scholar
[7] K. B. Nilsson, L. Eriksson, V. G. Kessler, I. Persson. J. Mol. Liq.131–132, 113 (2007).10.1016/j.molliq.2006.08.060Search in Google Scholar
[8] J. V. Burda. Theochem683, 183 (2004).10.1016/j.theochem.2004.06.013Search in Google Scholar
[9] M. Valli, S. Matsuo, H. Wakita, T. Yamaguchi, M. Nomura. Inorg. Chem.35, 5642 (1996).10.1021/ic960475kSearch in Google Scholar
[10] H. D. Pranowo. Chem. Phys.291, 153 (2003).10.1016/S0301-0104(03)00205-2Search in Google Scholar
[11] C. F. Schwenk, B. M. Rode. J. Am. Chem. Soc.126, 12786 (2004).10.1021/ja046784oSearch in Google Scholar PubMed
[12] C. F. Schwenk, B. M. Rode. ChemPhysChem5, 342 (2004).10.1002/cphc.200300972Search in Google Scholar PubMed
[13] A. Pasquarello, I. Petri, P. S. Salmon, O. Parisel, R. Car, E. Toth, D. H. Powell, H. E. Fischer, L. Helm, A. Merbach, Science291, 856 (2001).10.1126/science.291.5505.856Search in Google Scholar PubMed
[14] A. C. T. Van Duin, V. S. Bryantsev, M. S. Diallo, W. A. Goddard, O. Rahaman, D. J. Doren, D. Raymand, K. Hermansson. J. Phys. Chem. A114, 9507 (2010).10.1021/jp102272zSearch in Google Scholar PubMed PubMed Central
[15] S. T. Moin, T. S. Hofer, A. K. H. Weiss, B. M. Rode. J. Chem. Phys.139, 014503 (2013).10.1063/1.4811114Search in Google Scholar PubMed
[16] G. Chillemi, E. Pace, M. D’Abramo, M. Benfatto. J. Phys. Chem. A120, 3958 (2016).10.1021/acs.jpca.6b03569Search in Google Scholar PubMed
[17] D. T. Bowron, M. Amboage, R. Boada, A. Freeman. RSC Adv.3, 17803 (2013).10.1039/c3ra42400fSearch in Google Scholar
[18] K. B. Nilsson, I. Persson. Dalton Trans.9, 1312 (2004).10.1039/B400888JSearch in Google Scholar PubMed
[19] I. Persson, P. Persson, M. Sandström, A.-S. Ullström. J. Chem. Soc. Dalton Trans. 1256 (2002).10.1039/b200698gSearch in Google Scholar
[20] M. Hitzenberger, T. S. Hofer. J. Comput. Chem.36, 1929 (2015).10.1002/jcc.24032Search in Google Scholar PubMed
[21] M. Hitzenberger, D. Schuster, T. S. Hofer. Front. Chem.5, 1 (2017).10.3389/fchem.2017.00076Search in Google Scholar
[22] Z. Futera, K. Sodeyama, J. V. Burda, Y. Einaga, Y. Tateyama. Phys. Chem. Chem. Phys.16, 19530 (2014).10.1039/C4CP02307BSearch in Google Scholar
[23] V. Vchirawongkwin, C. Kritayakornupong, A. Tongraar, B. M. Rode. Dalt. Trans.41, 11889 (2012).10.1039/c2dt31117hSearch in Google Scholar
[24] C. B. Messner, G. K. Bonn, T. S. Hofer. Mol. Biosyst.11, 232 (2015).10.1039/C4MB00424HSearch in Google Scholar
[25] T. S. Hofer, P. H. Hünenberger. J. Chem. Phys.148, 222814 (2018).10.1063/1.5000799Search in Google Scholar
[26] S. S. Azam, T. S. Hofer, B. R. Randolf, B. M. Rode. J. Phys. Chem.113, 1827 (2009).10.1021/jp8093462Search in Google Scholar
[27] T. S. Hofer, A. B. Pribil, B. R. Randolf, B. M. Rode. Adv. Quantum Chem.59, 213 (2010).10.1016/S0065-3276(10)59007-5Search in Google Scholar
[28] B. M. Rode, T. S. Hofer, B. R. Randolf, C. F. Schwenk, D. Xenides, V. Vchirawongkwin. Theor. Chem. Acc.115, 77 (2005).10.1007/s00214-005-0049-1Search in Google Scholar
[29] W. D. Saputri, K. Wijaya, R. Armunanto. Indones. J. Chem.17, 531 (2017).10.22146/ijc.26809Search in Google Scholar
[30] M. Saleh, T. S. Hofer. Dalton Trans.46, 9630 (2017).10.1039/C7DT01548HSearch in Google Scholar PubMed
[31] N. Prasetyo, L. R. Canaval, K. Wijaya, R. Armunanto. Chem. Phys. Lett.619, 158 (2015).10.1016/j.cplett.2014.11.066Search in Google Scholar
[32] M. Saleh, T. S. Hofer. Chem. Phys. Lett.661, 274 (2016).10.1016/j.cplett.2016.09.002Search in Google Scholar
[33] N. Prasetyo, W. Utami, R. Armunanto, T. S. Hofer. J. Mol. Liq.242, 286 (2017).10.1016/j.molliq.2017.07.005Search in Google Scholar
[34] A. K. H. Weiss, T. S. Hofer, B. R. Randolf, B. M. Rode. Phys. Chem. Chem. Phys. 14, 7012 (2012).10.1039/c2cp23497aSearch in Google Scholar
[35] A. Bhattacharjee, T. S. Hofer, A. B. Pribil, B. R. Randolf, L. H. V Lim, A. F. Lichtenberger, B. M. Rode. J. Phys. Chem. B113, 13007 (2009).10.1021/jp905848xSearch in Google Scholar
[36] Y. Hidayat. J. Mol. Model. 24, 122 (2018).10.1007/s00894-018-3668-xSearch in Google Scholar
[37] L. Herald, V. Lim, A. Bhattacharjee, B. R. Randolf, B. M. Rode. Phys. Chem. Chem. Phys. 12, 12423 (2010).10.1039/c0cp00459fSearch in Google Scholar
[38] T. S. Hofer, H. T. Tran, C. F. Schwenk, B. M. Rode. J. Comput. Chem.25, 211 (2004).10.1002/jcc.10374Search in Google Scholar
[39] T. S. Hofer, B. M. Rode, A. B. Pribil, B. R. Randolf. Adv. Inorg.62, 143 (2010).10.1016/S0898-8838(10)62004-1Search in Google Scholar
[40] A. K. H. Weiss, T. S. Hofer, M. A. Kurt. RSC Adv.3, 1606 (2013).10.1039/C2RA21873ASearch in Google Scholar
[41] Y. Hidayat, H. D. Pranowo, R. Armunanto. Chem. Phys. Lett.699, 234 (2018).10.1016/j.cplett.2018.03.067Search in Google Scholar
[42] N. Prasetyo, R. Armunanto. Chem. Phys. Lett.652, 243 (2016).10.1016/j.cplett.2016.04.010Search in Google Scholar
[43] F. Weinhold, C. R. Landis, E. D. Glendening. Int. Rev. Phys. Chem.35, 399 (2016).10.1080/0144235X.2016.1192262Search in Google Scholar
[44] Y. T. Zhou, B. Zhang, S. J. Zheng, J. Wang, X. Y. San, X. L. Ma. Sci. Rep.4, 1 (2014).10.1038/srep03604Search in Google Scholar
[45] L.-Y. Ai, H.-Y. Zhao, H.-M. Ma, J. Wang, Y. Liu. Sci. Rep.8, 4167 (2018).10.1038/s41598-018-22381-ySearch in Google Scholar PubMed PubMed Central
[46] F. Weinhold, J. Comput. Chem.33, 2363 (2012).10.1002/jcc.23060Search in Google Scholar PubMed
[47] W. Zou, D. Nori-Shargh, J. E. Boggs, J. Phys. Chem. A117, 207 (2013).10.1021/jp3104535Search in Google Scholar PubMed
[48] R. A. Evarestov, V. A. Veryazov. Theor. Chim. Acta81, 95 (1991).10.1007/BF01113380Search in Google Scholar
[49] F. Diendere, I. Guiguemde, A. Bary. Res. J. Chem. Sci.4, 20 (2014).Search in Google Scholar
[50] K. Morokuma, K. Hashimoto. J. Am. Chem. Soc.117, 4151 (1995).10.1021/ja00119a032Search in Google Scholar
[51] T. S. Hofer. Pure Appl. Chem.86, 105 (2014).10.1515/pac-2014-5019Search in Google Scholar
[52] B. M. Rode, T. S. Hofer, B. R. Randolf, C. F. Schwenk, D. Xenides, V. Vchirawongkwin. Theor. Chem. Acc.115, 77 (2006).10.1007/s00214-005-0049-1Search in Google Scholar
[53] T. S. Hofer, A. O. Tirler. J. Chem. Theory Comput.11, 5873 (2015).10.1021/acs.jctc.5b00548Search in Google Scholar PubMed
[54] K. Emerson, R. C. Russo, R. E. Lund, R. V. Thurston. J. Fish. Res. Board Canada32, 2379 (1975).10.1139/f75-274Search in Google Scholar
[55] H. J. C. Berendsen, J. P. M. Postma, W. F. Van Gunsteren, A. Dinola, J. R. Haak, J. Chem. Phys.81, 3684 (1984).10.1063/1.448118Search in Google Scholar
[56] D. J. Adams, E. M. Adams, G. J. Hills. Mol. Phys.38, 387 (1979).10.1080/00268977900101751Search in Google Scholar
[57] B. M. Rode, C. F. Schwenk, T. S. Hofer, B. R. Randolf. Coord. Chem. Rev.249, 2993 (2005).10.1016/j.ccr.2005.03.032Search in Google Scholar
[58] P. Bopp, G. Jancsó, K. Heinzinger. Chem. Phys. Lett.98, 129 (1983).10.1016/0009-2614(83)87112-7Search in Google Scholar
[59] K. H. S. V. Hannongbua, T. Ishida, E. Spohr. Z. Naturforsch.582, 572 (1988).10.1515/zna-1988-0608Search in Google Scholar
[60] C. F. Schwenk, B. M. Rode. Phys. Chem. Chem. Phys.5, 3418 (2003).10.1039/b304898eSearch in Google Scholar
[61] H. D. Pranowo, B. M. Rode. J. Phys. Chem.103, 4298 (1999).10.1021/jp990264bSearch in Google Scholar
[62] R. Ahlrichs, M. Bar, H. Marco, H. Horn, C. Ktjlmel. Chem. Phys. Lett.162, 165 (1989).10.1016/0009-2614(89)85118-8Search in Google Scholar
[63] S. Brode, H. Horn, M. Ehrig, D. Moldrup, J. E. Rice. J. Comput. Chem.14, 1142 (1993).10.1002/jcc.540141004Search in Google Scholar
[64] W. Humphrey, A. Dalke, K. Schulten. J. Mol. Graph.7855, 33 (1996).10.1016/0263-7855(96)00018-5Search in Google Scholar
[65] T. H. Dunning. J. Chem. Phys.53, 2823 (1970).10.1063/1.1674408Search in Google Scholar
[66] T. S. Hofer, B. R. Randolf, B. M. Rode. Chem. Phys. Lett.422, 492 (2006).10.1016/j.cplett.2006.03.012Search in Google Scholar
[67] J. P. Foster, F. Weinhold. J. Am. Chem. Soc.102, 7211 (1980).10.1021/ja00544a007Search in Google Scholar
[68] C. F. Schwenk, B. M. Rode. ChemPhysChem4, 931 (2003).10.1002/cphc.200300659Search in Google Scholar PubMed
[69] S. T. Moin, T. S. Hofer, A. K. H. Weiss, B. M. Rode. J. Chem. Phys.139, 014503-1 (2013).10.1063/1.4811114Search in Google Scholar
[70] E. C. Koch. Propellants Explos. Pyrotech.30, 5 (2005).10.1002/prep.200400080Search in Google Scholar
[71] G. Pearson. J. Am. Chem. Soc.85, 3533 (1963).10.1021/ja00905a001Search in Google Scholar
[72] R. G. Pearson. J. Chem. Educ.45, 581 (1968).10.1021/ed045p581Search in Google Scholar
[73] W. D. Saputri, Y. Hidayat, K. Wijaya, H. D. Pranowo, T. S. Hofer. J. Mol. Liq.275, 859 (2019).10.1016/j.molliq.2018.11.022Search in Google Scholar
[74] T. S. Hofer, B. R. Randolf, B. M. Rode, I. Persson. Dalton Trans. 1512 (2009).10.1039/b819248kSearch in Google Scholar PubMed
[75] J. Hu, Q. Chen, H. Hu, X. Chen, Q. Ma, Z. Yin. Hydrometallurgy127–128, 54 (2012).10.1016/j.hydromet.2012.06.013Search in Google Scholar
[76] H. D. Pranowo. Chem. Phys.291, 153 (2003).10.1016/S0301-0104(03)00205-2Search in Google Scholar
©2019 Saputri et al., published by De Gruyter, Berlin/Boston
This work is licensed under the Creative Commons Attribution 4.0 Public License.
Articles in the same Issue
- Frontmatter
- In this issue
- Preface
- 15th Eurasia Conference on Chemical Sciences (EuAsC2S-15) – 5th–8th September 2018, Rome, Italy
- Conference papers
- The Jahn-Teller effect in mixed aqueous solution: the solvation of Cu2+ in 18.6% aqueous ammonia obtained from ab initio quantum mechanical charge field molecular dynamics
- Facile synthesis of hydrogel-nickel nanoparticle composites and their applications in adsorption and catalysis
- The effect of pore morphology on the catalytic performance of β-glucosidase immobilized into mesoporous silica
- Competitive pseudo-ELISA based on molecularly imprinted nanoparticles for microcystin-LR detection in water
- Titanium based complexes with melanin precursors as a tool for directing melanogenic pathways
- Stability of PMMA-grafted/Ti hybrid biomaterial interface in corrosive media
- High performance liquid chromatographic profiling of antioxidant and antidiabetic flavonoids purified from Azadirachta indica (neem) leaf ethanolic extract
- Effects mediated by M2 muscarinic orthosteric agonist on cell growth in human neuroblastoma cell lines
- Heterogeneous palladium SALOPHEN onto porous polymeric microspheres as catalysts for heck reaction
- Transfer of chemical elements from milk to dairy products
- Is hydrogen electronegativity higher than Pauling’s value? New clues from the 13C and 29Si NMR chemical shifts of [CHF3] and [SiHF3] molecules
- How alkali-activated Ti surfaces affect the growth of tethered PMMA chains: a close-up study on the PMMA thickness and surface morphology
- Dual inhibitors of urease and carbonic anhydrase-II from Iris species
- Electrochemical synthesis and amidation of benzoin: benzamides from benzaldehydes
Articles in the same Issue
- Frontmatter
- In this issue
- Preface
- 15th Eurasia Conference on Chemical Sciences (EuAsC2S-15) – 5th–8th September 2018, Rome, Italy
- Conference papers
- The Jahn-Teller effect in mixed aqueous solution: the solvation of Cu2+ in 18.6% aqueous ammonia obtained from ab initio quantum mechanical charge field molecular dynamics
- Facile synthesis of hydrogel-nickel nanoparticle composites and their applications in adsorption and catalysis
- The effect of pore morphology on the catalytic performance of β-glucosidase immobilized into mesoporous silica
- Competitive pseudo-ELISA based on molecularly imprinted nanoparticles for microcystin-LR detection in water
- Titanium based complexes with melanin precursors as a tool for directing melanogenic pathways
- Stability of PMMA-grafted/Ti hybrid biomaterial interface in corrosive media
- High performance liquid chromatographic profiling of antioxidant and antidiabetic flavonoids purified from Azadirachta indica (neem) leaf ethanolic extract
- Effects mediated by M2 muscarinic orthosteric agonist on cell growth in human neuroblastoma cell lines
- Heterogeneous palladium SALOPHEN onto porous polymeric microspheres as catalysts for heck reaction
- Transfer of chemical elements from milk to dairy products
- Is hydrogen electronegativity higher than Pauling’s value? New clues from the 13C and 29Si NMR chemical shifts of [CHF3] and [SiHF3] molecules
- How alkali-activated Ti surfaces affect the growth of tethered PMMA chains: a close-up study on the PMMA thickness and surface morphology
- Dual inhibitors of urease and carbonic anhydrase-II from Iris species
- Electrochemical synthesis and amidation of benzoin: benzamides from benzaldehydes

