Abstract
Lewis Carroll has been credited for developing a “Method of Trees” for solving multi-literal sorites problems, which anticipates several aspects of contemporary “tableau” or tree systems of logical proof. In particular, Carroll’s method pioneers the use of branching paths as a means of displaying or illustrating inclusive disjunction. However, rather than focusing on the respects in which Carroll’s tree diagrams resemble contemporary tree systems, I propose to focus instead on significant aspects in which they differ. In particular, I will show how the sorts of multi-literal sorites problems that Carroll’s method of trees is designed to solve are particularly ill-suited for resolution by more contemporary tree methods. I will also show how Carroll likely used something like this method, not only to solve but also to craft some of the trickier logical puzzles for which he is also famous.
1. Lewis Carroll (or Charles Dodgson[1]) was not only famous for his whimsical children’s literature but also well known for the construction of logical puzzles, many of which he would circulate to friends – and friendly rivals (frenemies, perhaps?) – by means of letters, short published notes, or pamphlets.[2] Many of these would take the form of multi-literal sorites problems, where the challenge is to determine the strongest conclusion from a sequence of premises such as the following:
A simpleton, who is not always shouting, is sure to be a crab;
None but spiders are good humoured;
No unsuccessful frog is despised, so long as it is healthy;
All oysters are good humoured;
All spiders are healthy, except the green ones;
Unsuccessful crabs, if good humoured, are popular;
Green crabs are always singing;
The only simpletons, that are popular, are frogs;
Rash young oysters are always unsuccessful;
None but simpletons are good humoured and yet despised;
No old crabs are healthy;
A rash spider is always despised.[3]
One doesn’t encounter many of these types of exercises in contemporary texts in formal logic. Such texts will often ask students to derive a specific conclusion from a given set of premises, or otherwise determine (say, by means of a truth table) whether given conclusions follow from given premises. Either way, all of the elements of an argument (premises and conclusion) are usually supplied in advance. However, it is quite reasonable to think that one major application of logic is to trace out the deductive consequences of a given set of commitments and thus to identify the strongest conclusions that follow from them.[4] In other words, despite their whimsical subject matter, the type of exercise that Carroll is asking us to perform in problems like these are of more than mere recreational value.
2. Problems such as these are sorites, but with a twist. They are multi-literal in that their subjects and predicates may themselves contain more than a single category term, several more in some cases. As a result, the various premises can loop in and out of one another in a devilish tangle, and demonstrations or justifications of any proposed solution quickly threaten to become incomprehensibly convoluted. By all accounts, Carroll was a master at solving and crafting such puzzles. So though Carroll does not today enjoy the reputation as a logician as many of his contemporaries, it would be rash to dismiss him altogether. For these puzzles display a certain cunning. How on Earth did Carroll manage to craft or conceive them in the first place? They are clearly not the product of a rank amateur. In this article, we will describe a “method of trees,” which Carroll claims to have discovered for demonstrating the solution for such sorites problems. As I will show, this method anticipates and bears interesting similarities to contemporary tree (or Tableau) methods for evaluating the validity of arguments. At the same time, I shall comment upon some significant differences as well. Finally, I will show how this same method can also be deployed to generate novel sorites problems. It seems altogether likely that Carroll used some form of this method to craft the tricky puzzles that so bedevilled his contemporaries (and still exercise us). Taken as a whole, I shall make a case that despite his evident distaste for the sort of formal logic that would come to dominate the field, Carroll nevertheless deserves credit and admiration for originating significant diagramming techniques for displaying logical relationships.
3. A clue to Carroll’s thought process can be found in a July 16, 1894 diary entry. There he announced:
Today has proved to be an epoch in my logical work. It occurred to me to try a complex Sorites by the method I have been using for ascertaining what cells, if any, survive for possible occupation when certain nullities are given. I took one of 40 premises, with ‘pairs within pairs,’ & many bars, & worked it like a geneaology, each term proving all its descendants. It came out beautifully, & much shorter than the method I have used hitherto – I think of calling it the ‘Genealogical Method.’[5]
Carroll eventually settled on calling his new method the “Method of Trees” instead, and under that title circulated draft presentations of it among a few of his confidants, most notably Cook Wilson, for eventual inclusion in the second part of his Symbolic Logic. Unfortunately, Carroll died in 1898, before that work could be seen through to publication. Much of the material for it then languished in various and obscure archival files. More than 70 years passed before William Bartley III attempted to reconstruct Carroll’s Symbolic Logic, which was finally published in 1977. Bartley incorporated Carroll’s description of the method of trees in Part II of this reconstruction. In the interval, other tree systems of demonstrating consequence relations had been developed and popularized.[6]
4. Like (most forms of) logical tableau, Carroll’s method of trees takes the form of demonstrating an inconsistency between premises and a hypothetical claim representing the negation of a proposed conclusion. The method has one hypothesize the existence of an object and then show how the various premises of the sorites work together to rule that object out of existence. Carroll describes the process as follows:
In the Method of Trees this process is reversed. Its essential feature is that it involves a Reduction ad Absurdum. That is, we begin by assuming, argumenti gratia, that the aggregate of the Retinends (which we wish to prove to be a Nullity) is an Entity: from this assumption we deduce a certain result: this result we show to be absurd: and hence we infer that our original assumption was false, i.e., that the aggregate of the Retinends is a Nullity. [7]
Commentators have thus hailed Carroll’s Method of Trees as anticipating tree or “Tableau” methods of logical proof first developed by Beth and Hintikka in the 1950s and popularized by Jeffries and Smullyan a decade later.[8] There is some justice in this claim. Like contemporary Tableau systems, Carroll’s method uses branching structures as an especially efficient means of navigating a space of possibility or permissibility afforded by a given set of constraints. Closed branches represent “dead ends” – possibilities not allowed by those constraints. Fully closed trees represent inconsistencies among a set of constraints or hypotheses, as they do in the tree systems most commonly presented in current texts.[9] In particular, as I will explain later, Carroll appears to be among the first to use branching structures to diagram explicitly inclusive disjunction. However, despite these considerable commonalities between Carroll’s trees and contemporary tree systems, we should take care not to blow claims that herald Carroll as anticipating contemporary tree systems out of proportion. Rather than focusing on the respects in which Carroll’s tree diagrams resemble contemporary tree systems, I propose to focus instead on significant aspects in which they differ. Indeed, as I will show, assimilating Carroll’s Method of Trees to contemporary Tableau systems for detecting logical entailments actually threatens to minimize or occlude some of the more distinctive, and innovative, features of Carroll’s method.
5. To illustrate Carroll’s method of trees, let’s apply it to a problem of Carroll’s own devising. Problem #40 of Carroll’s Symbolic Logic consists of the following premises:
All the young and hopeful like toffy;
All old gorilla-keepers are good-tempered;
All gay cyclists ought to take snuff;
Young people never despair;
Good-tempered people need not take snuff;
Young people, who like toffee, are inexperienced;
All good-tempered captains ride bicycles;
People of experience, who suffer from low spirits, do not keep gorillas.
When we replace the natural language with the “dictionary” Carroll proposes (Univ. “persons”; a = captains; b = cyclists; c = experienced; d = gay; e = good-tempered; h = hopeful; k = keeping gorillas; l = liking toffy; m = needing to take snuff; n = old.), we obtain the following:
All the non-n h are l;
All n k are e;
All d b are m;
Non-n are h;
e are not m;
Non-n who l are not c;
All e a are b;
c, who are non-d, do not k.
6. Carroll’s first step is to reduce these premises to a workable logical notation. The crucial thing is that they can all be recast as expressing the non-existence or incompatibility between various sets of attributes and non-attributes. For instance, the first premise, “(1) All the young and hopeful like toffy;” – a universal affirmative – rules out the existence of anything which is simultaneously young, hopeful, and not a toffy-liker. Employing Carroll’s translation scheme (where young is to be understood as not-old), this premise rules out anything being not-n, h, and not-l. Carroll terms such a string of excluded literals[10] a “nullity,” which he symbolizes by appending their string with a subscript zero. Thus, alongside his convention of using an apostrophe to signify the possession of an attribute’s complement (or the non-possession of an attribute), this nullity is to be expressed as n’hl’0.[11] Since all the premises of such a sorites are, in effect, universal statements (whether affirmative or negative), they can all similarly be recast as nullities. To wit:
n’ h l’0
n k e’0
d b m’0
n’ h’0
e m0
n’ l c0
e a b’0
c d’ k0
It is entirely possible that Carroll came to this idea from Peirce’s student, Christine Ladd-Franklin, with whose work he was evidently familiar.[12] As I shall explain presently, one particularly nice feature of expressing these premises as nullities is that the order in which the terms of a nullity are listed does not matter logically. For instance, the nullity in premise (1), that nothing is n’, h, and l’ (or n’ h l’0) is logically equivalent to the nullity that nothing is h, l’, and n’ (or h l’ n’0).
7. The root of a Carroll tree embodies a proposed conclusion, which, should the proof be completed, is subsequently rejected as absurd. It takes the form of a list of features possessed by a hypothetical “entity” (an “aggregate of the Retinends”). However, these sorites exercises do not include any explicit statement of a conclusion with which to evaluate a proposed entailment. Instead, the features of the entity “which we wish to prove to be a Nullity” have to be generated from the premises. The particular literals forming the root of a Carroll Tree are determined by looking at the nullities represented by the premises and discerning the end-terms of the sorites (“retinends”) from its middle terms (“eliminands”). This task can be accomplished by constructing what Carroll calls a “register.”
8. The register begins with a list of all of the attributes spoken of in the sorites. Alongside each attribute, one then notes the various premises in which those attributes appear, divided according to whether that attribute is mentioned affirmatively (without an apostrophe) or negatively (with an apostrophe). Here, then, is the register for the previous set of premises:
| Attribute | a | b | c | d | e | h | k | l | m | n |
|---|---|---|---|---|---|---|---|---|---|---|
| Affirmative | 7 | 3 | 6, 8 | 3 | 5, 7 | 1 | 2, 8 | 6 | 5 | 2 |
| Negative | 7 | 8 | 2 | 4 | 1 | 3 | 1, 4, 6 |
The first row of this table lists all the attributes in the sorites. Underneath each attribute, the cells in the second row contain all of premises (expressed as nullities) which include that attribute affirmatively, while the third row lists all of the premises which include that attribute negatively (or which features its complement). After the register has been constructed, what should stand out is the presence of three empty cells: the negative cells in columns for the attributes a, c, and k. Since they are empty, there will be no possibility of using these attributes as middle terms as we develop our tree. Instead, we place their complements – a, c, and k – on the trunk and use their presence there as material to spur further development.[13]
a (retinend)
c (retinend)
k (retinend)
9. One of the most striking differences between Carroll’s trees and Tableau tree proofs concerns the representational content or significance of the various items on the trees – their “leaves” or “fruits.” While the items appearing on Tableau tree proofs represent complete statements or propositions, which (when compound) might stand in need of further decomposition, those on Carroll’s trees represent the attributes (or their complements) possessed by a single hypothesized entity. The representational significance of a Carroll tree is thus more akin to a Peircean line of identity than a chain of explicit argumentation. The trunk of a Carroll tree represents a hypothetical object possessing the traits listed: in this case a, c, and k. We then “grow” the tree by spinning out consequences of applying particular nullities in the sorites to a growing list of attributes possessed by this hypothetical entity. Notice that premise (8) excludes anything that is simultaneously c, d’, and k. Since the trunk lists both c and k, we may conclude that the object it hypothetically represents must not be d’ (or not a non-d); given our premise, it would have to be d. So we place that attribute below the others. Following Carroll, I shall also note the premise involved to the side. Not only is this convenient, it gives the tree a more familiar “look” or appearance of a proof.
a (retinend)
c (retinend)
k (retinend)
d (8)
10. Although contemporary systems of tree proof place premises directly on the tree diagram, Carroll leaves these constraints off to the side. As a result, Carroll’s trees grow from “without” rather from “within.” Moreover, unlike contemporary Tableau, the specific product (or “fruit”) of developing a given premise may take different forms, depending upon what attributes lie along the path being developed. From the nullity ahcb’0, for instance, one could infer several different attributes. If a, h, and c were on a path, the premise bids us to write down m; if a, c, and b’ were on a path, the premise would require us to write down h’ instead, and so on.
11. A Carroll tree thus grows through the systematic comparison of the literals along a tree path to the multi-literal incompatibilities expressed by the statements in the sorites. As we continue working this particular example, however, we see that none of the remaining premises will allow us to rule out a single literal and conclude therefore that its complement must be placed on the trunk. The best we can do is rule out certain combinations of literals. For instance, since d is listed on the trunk as an attribute of our hypothetical object, and since premise (3) tells us that nothing may be d, b, and m’ (bdm’ is a nullity), we may conclude that our object cannot be b and m’ together. It must either be not-b (b’) or m. This, of course, is where branching enters the picture. We split our path in two, and place the complement of one literal at the head of one branch, and the complement of the other literal at the head of the other.
12. Here’s what Carroll has to say about such situations. Considering a similar case in which one needs to represent that the conjunction of two attributes, b and c, has been ruled out, Carroll writes:
The Reader will easily see that the three possible pairs bc’, b’c, b’c’, can be grouped under these two headings. Under b’ we can place b’c and b’c’; and under c’ we can place bc’ and b’c’.
This is, of course, a case of overlapping, or what is called “Cross Division,” since b’c’ appears under both headings. Now there is no reason to be so lavish of accommodation for this pampered class b’c’: it ought to be quite content with one appearance. So we may fairly say it shall not appear under the heading b’: that heading shall contain the class b’c only. This result we can secure by tacking on to b’ the Letter c; so that the two headings will be b’c and c’. Or we may, if we prefer it, say it shall not appear under the heading c’; that heading shall contain the Class bc’ only. And this result we can secure by tacking on c’ the Letter b; so that the two headings will be b’ and c’b. It is worthwhile to note that, in each case, we tack on, to one of the single Letters, the Contradictory of the other: this fact should be remembered as a rule.
[Thus, if we found a Premiss proving that the Thing could not have the Pair of Attributes b’c, we might say it must have b or c’. And we might afterwards tack on, at pleasure, either c to b, making the heading bc and c’, or b’ to c’, making them b and c’b’.]
We have now a Rule of Procedure, to be observed whenever we are obliged to divide our Tree into two branches, and, instead of saying the Thing must have this one attribute, we may say it must have one or other of these two attributes.[14]
Those who have taught contemporary tree methods will recognize in this rather cumbrous passage their own endeavours to convey to students that the branches of logic trees represent inclusive disjunctions, and that some possibilities might be covered, at least temporarily, by multiple paths at once. Here is at least one great similarity between Carroll trees and Tableau tree proofs. Paths in a logic tree are not like forks in a road; instead, like particles in a two-slit experiment, possibilities may be thought of as traveling down multiple by-ways at once, until further developments intervene. Carroll is clearly a pioneer in this way of conceiving tree diagrams, though I will qualify this claim in a bit.
13. We then continue down either branch, as if they were their own independent paths, using the literals at their head in conjunction with those previously listed earlier up the path to the root as fodder for spinning out further consequences from the premises expressed as nullities. An alert reader will note that this reasoning from incompatibility or nullity is, once again, of the same basic form as that championed by Charles Peirce’s student, Christine Ladd-Franklin. Moreover, knowledgeable readers might further notice that the inferences in Carroll’s trees are essentially equivalent to applications of the rule of deuteration in Peirce’s (alpha) system of existential graphs. From a grouping of incompatible items (which in Peirce’s notation would thereby be enclosed inside one of his fences or cuts) alongside the affirmation of some subset of those items, one may infer the incompatibility or negation of the remainder, also represented by enclosure within a single fence.[15] The inference engine driving Carroll’s trees is essentially the same, including that which drives the branching rule.
14. As in Tableau-style proofs, the goal is to force the branch in question into a contradiction, either by showing that our hypothesized object must possess some attribute and its complement, or equivalently, by showing that it must have some combination of literals explicitly ruled out by some premise. Once a branch has been shown to be contradictory, it is closed off, and no further work needs to be done. If all the branches of a tree can be closed off, then that demonstrates that the hypothetical object in question is collectively ruled out by the premises.[16] The specific set of literals constituting its root is thus a nullity in its own right.
15. Here, then, is a completed Carroll tree for Problem #40, with closed branches marked off (as Carroll does) with a circle (Figure 1):
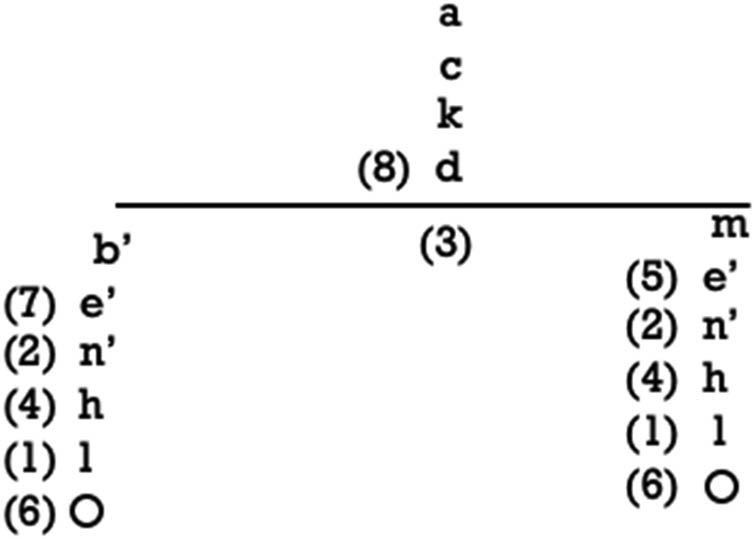
Carroll tree for Problem #40.
We conclude therefore that the root string of literals, a c k, is a nullity (ack0). When we translate that back into natural language, we obtain “No experienced captain keeps gorillas,” or one of its several equivalents, such as “All captains who keep gorillas must be inexperienced.”[17]
16. It’s time to turn to the qualification mentioned a couple of paragraphs earlier. Note that Carroll tells us that once we have created a disjunctive branch, “we might afterwards tack on, at pleasure,” the contradictory of the head of one branch to the head of the other. For instance, we might add m’ to the left branch, since m is at the head of the right branch. In effect, adding this literal to the left turns an inclusive disjunction into an exclusive one and adds potential fodder for the application of the inference engine. However, the benefit might be much less than anticipated, and we must take care to add a rule to the effect that one cannot use the premise that created a branch to close it as well (otherwise, any branch will immediately and illegitimately close once its counterpart has). Indeed, as one can verify, adding the extra literal in the example above turns out not to matter at all, since it isn’t of the valence necessary to gain traction with any of the remaining premises. While adding the extra literal to a branch can result in some simplifications of a tree on occasion, adding b to the second branch in the example above does nothing to advance the demonstration. Perhaps this is what Carroll meant when he said that one can add the extra literal “at pleasure.”
17. Thus, we have Carroll’s Method of Trees. As one can see, while certain aspects of the method resemble and anticipate contemporary Tableau methods of logical demonstration, Carroll’s method differs significantly in other respects. Nowhere is this more evident than in the construction of the register. Recall that the purpose of the register is to identify a sorites’ end-terms or “retinends,” through which one can then identify the specific traits of a hypothetical object that is then ruled out as impossible by the closure of the tree. Admittedly, Carroll’s method applies to a rather narrow type of exercise. However, lest one smugly think that contemporary tree methods are, by their greater generality, automatically superior to Carroll’s method, it pays to ask: what would happen if you were to take one of Carroll’s sorites exercises, dispense with the registry, and then try to develop all of the premises of the sorites together on a single tree using contemporary Tableau techniques, with an aim perhaps of determining where such premises lead, and whether they point to some specific conclusion? As I will show, the result is disastrous, and spectacularly so. By way of illustration, let’s consider Carroll’s problem #32. The premises of this exercise are as follows:[18]
All active old Jews are healthy;
All indolent magistrates are unpopular;
All rich snuff-takers are unhealthy;
All sarcastic magistrates are Jews;
All young snuff-takers are pale;
All rich, old men, who are unhealthy, are sarcastic;
All magistrates, who are not poets, are studious;
All rosy magistrates are talented men;
All talented and popular students are rich;
All pale snuff-takers are unpopular;
All unpopular magistrates abstain from snuff;
All talented poets, who are active, are rich.
For this problem, Carroll proposes the following dictionary of symbolization: Univ. “persons”; a = active; b = healthy; c = Jews; d = magistrates; e = men; h = old; k = poets; l = popular; m = rich; n = rosy; r = sarcastic, s = snuff-takers; t = studious, v = talented. Consequently, we have the following symbolized premises, and their corresponding nullities:
| (1) All ahc are b. | (1) ahcb’0 |
| (2) All a’d are l’. | (2) a’dl0 |
| (3) All ms are b’. | (3) msb0 |
| (4) All rd are c. | (4) rdc’0 |
| (5) All h’s are n’. | (5) h’sn0 |
| (6) All mheb’ are r. | (6) mheb’r’0 |
| (7) All dk’ are t. | (7) dk’t’0 |
| (8) All nd are ve. | (8) nd[ve]’0 |
| (9) All vlt are m. | (9) vltm’0 |
| (10) All n’s are l’. | (10) n’sl0 |
| (11) All l’d are s’. | (11) l’ds0 |
| (12) All vka are m. | (12) vkam’0 |
18. Before we compare Carroll’s method with contemporary Tableau, I should pause to point out a wrinkle in this problem that is worthy of comment, but which Carroll himself does not explicitly discuss. That concerns premise (8). Note that in this premise, unlike the others, the predicate of a universal affirmative also contains multiple literals. When we convert that into a nullity, those literals form what is in effect a single compound category in its own right. It rules out anything possessing the attributes of n, d, and not both v and e together. As such, it is not equivalent to the nullity that would simply be symbolized by ndv’e’0, but rather to a nullity expressing the idea that nothing could be n, d, and either not v or not e. In some other parts of his logical work, though not in his discussion of his method of trees, Carroll inserts a § between literals as an explicit sign of (nonexclusive) disjunction between them (much as we use the wedge), in which case the nullity in (8) could be expressed as ndv’§e’0. [19] Instead, I’ve chosen to indicate this by dispensing with an explicit symbol for disjunction and placing v and e together within brackets and then appending an apostrophe to the bracketed whole to indicate the negation of their conjunction. The inspiration for my own departure from Carroll’s notation comes from Peirce’s notation of the graphs.[20]
19. Either way, the extension of Carroll’s method to encompass such multilateral predicates also requires elaboration of the rules for developing or growing Carroll trees. Fortunately, though they go well-beyond Carroll’s explicit articulation of the method, these elaborations are relatively intuitive. When a bracketed string of literals appears in a nullity affirmatively, all of literals within that string must appear on a path before one can apply the method’s inference rule to add the complement of another item within the nullity onto a tree. Correlatively, when a bracketed string of literals appears in a nullity negatively (with an apostrophe, as it does in our example), then all it takes to apply the rule for developing Carroll trees is the complement of at least one of the literals within the nullity. Furthermore, if the inference rule calls us to place a bracketed category on a tree affirmatively, we may simply list all of its elements on the appropriate path independently, while a bracketed list placed negatively, then one forms branches for each element of the bracketed list, and places the complement of each element on its own respective branch. This latter is a significant elaboration, for which there is little evidence that Carroll anticipates. Carroll appears to treat wrinkles like this in an ad hoc manner.
20. We also need to consider how to treat bracketed items in the construction of the register. In the example above, since [ve]’ is essentially the disjunction of v’ and e’, we consider premise (8) to be included among the premises that list v and e negatively. Thus, the register for Problem #32 will then be as follows:
| Attribute | Affirmative | Negative |
|---|---|---|
| a | 1, 12 | 2 |
| b | 3 | 1, 6 |
| c | 1 | 4 |
| d | 2, 4, 7, 8, 11 | |
| e | 6 | 8 |
| h | 1, 6 | 5 |
| k | 12 | 7 |
| l | 2, 9, 10 | 11 |
| m | 3, 6 | 9, 12 |
| n | 5, 8 | 10 |
| r | 4 | 6 |
| s | 3, 5, 10, 11 | |
| t | 9 | 7 |
| v | 9, 12 | 8 |
21. When completed, the tree for this puzzle will look something like this (Figure 2). It’s a nice tree exercise with one branch embedded inside another. Carroll’s contemporary Cook Wilson, with whom Carroll shared his method of trees, called it a “capital problem indeed” (Cook Wilson 1896). In addition to the embedded branching, notice that lines 19 and 24 illustrate the point that one and the same premise can produce different fruits, depending on the specific attributes lying along a path. Branch closures occur when an attribute and its complement both appear on a path. The complete closure of all the branches of the tree thus indicates the nullity of the two starting attributes. That is, the premises rule out the possibility of something being both d and s; ds0 is thus our conclusion: “No magistrates take snuff” (or its obverse, “No snuff-takers are magistrates”).[21]

Carroll Tree for Problem #32.
21. Let’s return now to the question of comparing Carroll’s method of trees with contemporary Tableau. Even when one suppresses quantification concerns (by assuming that all of these statements apply by default to one and the same individual), the development of a Tableau-style tree with these premises quickly gets out of hand. Considered as conditionals, each of these premises requires a path to split, with one branch leading to the negation of the antecedent and the other to the consequent. Moreover, since all these antecedents are conjunctions, then the development of them in turn will require a separate branch for each and every element of the antecedent negated. Since these branchings compound – one must develop a formula on each and every open branch below it – one is very quickly overwhelmed by a combinatorial explosion. Without factoring branches that close, the number of branches generated will be 38435 (3 to the power of the number of three-term statements [there are 8 such, including the 8th premise] multiplied by 4 to the power of the number of four-term statements [there are three such] multiplied by 5 to the power of the number of five-term statements [1, the 6th]). That means that there are potentially 2,099,520 separate branches to consider! Granted, some of these premises will interact with one another to produce branch closures. However, the problem is that this exercise is set up in such an unmerciful manner that it stymies quick pruning. By identifying suitable end-terms, the register does this pruning work for us. The situation is no better when one considers these premises as Carroll does: as nullities of attributes (or negated conjunctions); when developed within tableau-style trees, they too generate the same proliferation of branches. Considering that Carroll reportedly verified his method with a sorites of “40 premises, with ‘pairs within pairs,’ & many bars” (that is, with multi-literal predicates and consequents, and several terms negated), it is little wonder then that Bartley reports that when confronted with such problems, contemporary logicians, even those of “high distinction,” tend to “scamper off like white rabbits.”[22]
22. As pointed out earlier, modern techniques are generally well adapted to exercises in which an entire argument is given, not so many problems like these, in which some element goes missing. Here, it is worth pointing out that Carroll’s method can be readily adapted into one in which the task instead is to identify, not just a conclusion, but rather a missing or implicit premise that would render a sorites with conclusion valid. The basic idea is to construct an extended antilogism. This one can be done simply by forming a nullity from the negated conclusion and treating it as a premise in its own right. One then identifies the retinends (as the literals that will tie the reasoning together), and the desired missing premise will be the nullity formed by those retinends which close the Carroll tree. In other words, the idea here is to extend Ladd-Franklin’s antilogism, not just to the number of literals involved but rather to the number of statements which comprise it.
23.Turning once again to the diary passage with which I began this article, observe that Carroll says of his method that it is one which “I have been using for ascertaining what cells, if any, survive for possible occupation when certain nullities are given.” While no cells happen to survive in the example above, there may be other setups that do not close, indicating that the initial proposed object is indeed compatible with the premises of the sorites. Just as with contemporary trees, non-closure indicates consistency. Carroll’s statement above suggests that he had found a way to put that further result to use as well. And indeed he could – by using the various attributes on open paths to generate further premises that could produce eventual branch closure. This diary passage suggests that for at least a little time prior to 1894, Carroll had been using his method of trees, or something very much like it, not primarily as a means of verifying that a certain conclusion followed, but rather as a device for crafting or constructing these multilateral sorites exercises for which he is so well known.
24. With that in mind, let’s turn to a different task: that of using a Carroll tree to devise a new Carroll-type sorites exercise. The procedure will be to start from a given set of retinends, and from there, systematically add premises to grow a tree fruit-by-fruit and branch-by-branch, all while keeping in mind that the original fruits must remain retinends (their complement may never appear in one of the premises) and that for any subsequent literal (“fruit”) placed on the tree, it and its complement must appear in at least one of the premises. This will guarantee its place as a middle term (an “eliminand”). Finally, one will need to see to it that all the branches of the tree close. That can be accomplished simply by adding a premise that creates a nullity of some items already appearing on any given open path. To create the complexity of some of Carroll’s more devilish exercises, one can force a tree to branch by ensuring that there are no premises which include all but one of the literals leading up to a given branching point. Moreover, to introduce a further complexity, one can reuse attribute signs that factor into one path along other paths.
25. Admittedly, the procedure takes some practice, but can be used satisfactorily to generate new sorites puzzles. Here is one such tree so generated (Figure 3):
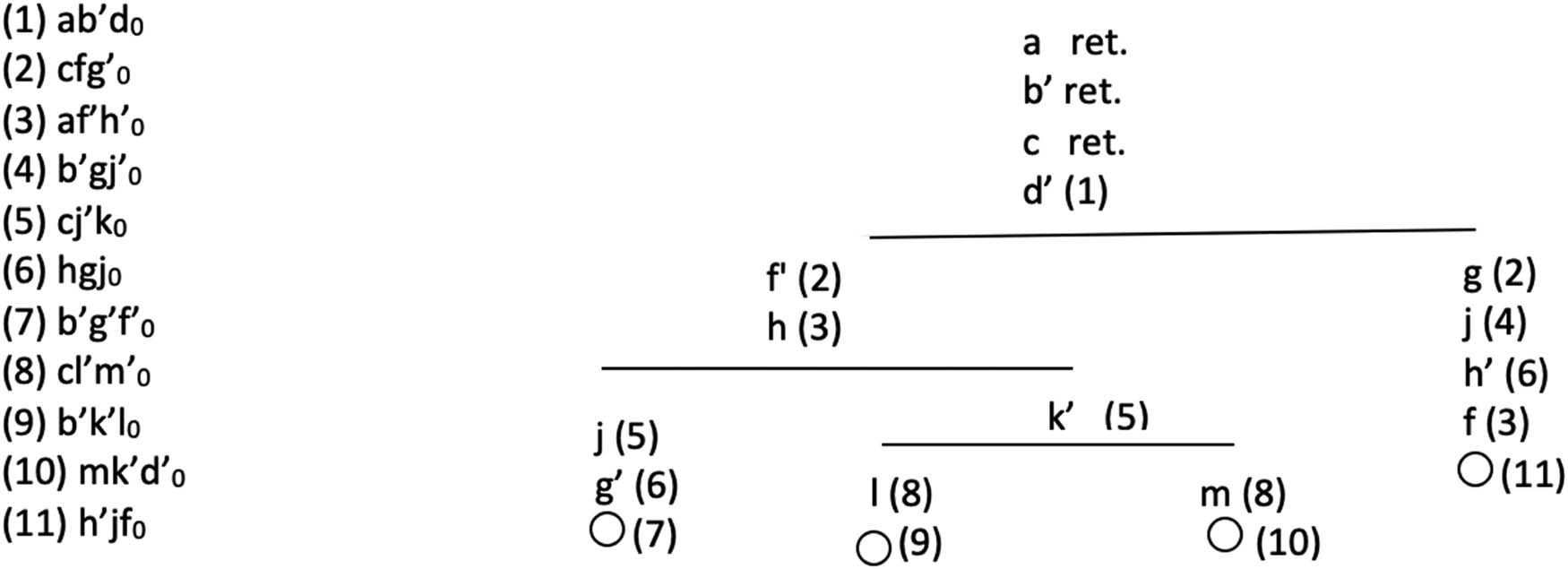
New Carroll Tree.
One can verify that from the given retinends, only one premise, the first one, can be applied without branching, and that even when the literal produced by that application is added to the trunk, branching will be required to grow the tree further. Moreover, this tree is slightly more complex than problem #32, in that it contains two embedded branches. It also reuses category terms along multiple branches, for the purpose of tangling or interweaving the categories into one another in the way that Carroll’s best problems do. Nevertheless, I’ve kept the problem simple in at least one respect: all of the nullities expressed by the premises contain just three items (3 being the minimum required to generate branching).
26. Carroll hints that he first used his method of trees (then the “genealogical method”) to verify a proposed solution to a sorites exercise. We can similarly use the method to verify the solution to this sorites by developing the tree with a different order of branching. Instead of developing premise (2) as the first branch, when we opt instead for premise (3), we obtain the following (Figure 4):

New Carroll Tree (Alternative Solution).
This tree does indeed confirm that the sorites is valid and the conclusion ab’c is a nullity (abc0). Interestingly, some of the complexity is reduced as we no longer have a doubly embedded branch. We still, however, have a pleasant reuse of premises (namely, the 2nd and the 4th) across multiple branches, in which the application of the premise yields different fruits.
27. I’ll take this illustration to provide some proof of the concept that Carroll’s method of trees can be used to construct novel and challenging sorites exercises. While It’s unclear that Carroll used the same method in any systematic way to develop his own problems, his writings suggests that he used something like it in at least an ad hoc manner, and that it was this that eventually led to his description of the method for inclusion in Volume II of Symbolic Logic. The only thing left to do to make this a more recognizably Carroll-type exercise is to render the premises in natural language using the whimsical sorts of categories he did. Since they are unproblematic, the categories and dictionary he uses for problem #38 will serve us well. And so we obtain something like this:
Dictionary:
Univ. “creatures”; a = good-humoured; b = rash; c = crabs; d = despised; f = simpleton; g = green; h = oysters; j = successful; k = popular; l = healthy, m = old.
ab’d0 – Any creature who is rash but not despised is ill-humoured.
cfg’0 – No non-green crab is a simpleton.
af’h’0 – One who is good-humoured but not a simpleton is an oyster.
b’gj’0 – Popular creatures that aren’t rash are always successful.
cj’k0 – Unsuccessful crabs aren’t popular.
hgj – No green oyster is successful.
b’g’f’ – Only simpletons are neither green nor rash.
cl’m’ – Unhealthy crabs are old.
b’k’l – Nothing is healthy unless it is either rash or popular.
mk’d’ – Old creatures that aren’t popular are despised.
h’jf – All successful simpletons are oysters.
Voila! A new Carroll sorites-type exercise generated from his own method of trees.[23]
Acknowledgements
Versions of this paper were presented at the 2nd Pan-American Conference on the History of Logic (UCLA, 2023), the MidSouth Philosophy Conference (Memphis, 2023), and a workshop on Lewis Carroll s Logic organized at the UNILOG conference (Crete, 2023). Special thanks to Henry Olree and Katie Hoffman for comments on a draft and to Amirouche Moktefi for continued advice and encouragement on all things Carroll.
-
Author contribution: The author confirms the sole responsibility for the conception of the study, presentation of results, and preparation of manuscript.
-
Conflict of interest: Author states no conflict of interest.
References
Abeles, Francine. “Lewis Carroll’s Method of Trees: Its Origins in Studies in Logic.” Modern Logic 1 (1990), 25–35.Search in Google Scholar
Anellis, Irving. “From Semantic Tableaux to Smullyan Trees: A History of the Development of the Falsifiability Tree Method.” Modern Logic (1990), 36–69.Search in Google Scholar
Beisecker, Dave. “Regions of Force: Peirce, Frege, Carroll, and Bilateral Proof Trees.” Logique et Analyse 251 (2020), 317–40.Search in Google Scholar
Beisecker, Dave and Amirouch Moktefi. “John Cook Wilson’s Hanging Plants: A Contribution to the History of Early Logic Trees.” In Diagrammatic Representation and Inference, edited by V. Giardino et al., 338–46. Switzerland: Springer LNCS 13462, 2022.10.1007/978-3-031-15146-0_29Search in Google Scholar
Carroll, Lewis. Symbolic Logic, Part I and Part II, edited by William Warren Bartley, III. New York: Clarkson N Potter, 1977.Search in Google Scholar
Cook Wilson, John. Letter to Charles L. Dodgson, 3 November 1896. Cook Wilson Papers, The Wilson – Dodgson Box, Bodleian Library, University of Oxford.Search in Google Scholar
Fitts, Jesse and Dave Beisecker. “Two-Sided Trees for Sentential Logic, Predicate Logic, and Sentential Modal Logic.” Teaching Philosophy 42 (2019), 41–56.10.5840/teachphil2019116101Search in Google Scholar
Ladd, Christine. “On the Algebra of Logic.” In Studies in Logic, edited by C. S. Peirce, 17–71. Baltimore: Johns Hopkins, 1883.10.1037/12811-004Search in Google Scholar
Moktefi, Amirouche. “Are Other People’s Books Difficult to Read? The Logic Books in Lewis Carroll’s Private Library.” Acta Baltica Historiae Et Philosophiae Scientiarum 5 (2017), 28–49.10.11590/abhps.2017.1.02Search in Google Scholar
Moktefi, Amirouche. “Why Make Things Simple When You Can Make Them Complicated? An Appreciation of Carroll’s Symbolic Logic.” Logica Univsarsalis 15 (2021), 359–79.10.1007/s11787-021-00286-1Search in Google Scholar
© 2024 the author(s), published by De Gruyter
This work is licensed under the Creative Commons Attribution 4.0 International License.
Articles in the same Issue
- Special issue: Happiness in Contemporary Continental Philosophy, edited by Ype de Boer (Radboud University, the Netherlands)
- Editorial for Topical Issue “Happiness in Contemporary Continental Philosophy”
- Badiou and Agamben Beyond the Happiness Industry and its Critics
- Happiness and the Biopolitics of Knowledge: From the Contemplative Lifestyle to the Economy of Well-Being and Back Again
- Reanimating Public Happiness: Reading Cavarero and Butler beyond Arendt
- Thinking from the Home: Emanuele Coccia on Domesticity and Happiness
- A Strategy for Happiness, in the Wake of Spinoza
- Das Unabgeschlossene (das Glück). Walter Benjamin’s “Idea of Happiness”
- The Role and Value of Happiness in the Work of Paul Ricoeur
- On the “How” and the “Why”: Nietzsche on Happiness and the Meaningful Life
- Albert Camus and Rachel Bespaloff: Happiness in a Challenging World
- Symptomatic Comedy. On Alenka Zupančič’s The Odd One In and Happiness
- Happiness and Joy in Aristotle and Bergson as Life of Thoughtful and Creative Action
- Special issue: Dialogical Approaches to the Sphere ‘in-between’ Self and Other: The Methodological Meaning of Listening, edited by Claudia Welz and Bjarke Mørkøre Stigel Hansen (Aarhus University, Denmark)
- Sonic Epistemologies: Confrontations with the Invisible
- The Poetics of Listening
- From the Visual to the Auditory in Heidegger’s Being and Time and Augustine’s Confessions
- The Auditory Dimension of the Technologically Mediated Self
- Calling and Responding: An Ethical-Existential Framework for Conceptualising Interactions “in-between” Self and Other
- More Than One Encounter: Exploring the Second-Person Perspective and the In-Between
- Special issue: Lukács and the Critical Legacy of Classical German Philosophy, edited by Rüdiger Dannemann (International Georg-Lukács-Society) and Gregor Schäfer (University of Basel)
- Introduction to the Special Issue “Lukács and the Critical Legacy of Classical German Philosophy”
- German Idealism, Marxism, and Lukács’ Concept of Dialectical Ontology
- The Marxist Method as the Foundation of Social Criticism – Lukács’ Perspective
- Modality and Actuality: Lukács’s Criticism of Hegel in History and Class Consciousness
- “Objective Possibility” in Lukács’s History and Class Consciousness
- The Hegelian Master–Slave Dialectic in History and Class Consciousness
- “It Would be Helpful to Know Which Textbook Teaches the ‘Dialectic’ he Advocates.” Inserting Lukács into the Neurath–Horkheimer Debate
- Everyday Hegemony: Reification, the Supermarket, and the Nuclear Family
- Critique of Reification of Art and Creativity in the Digital Age: A Lukácsian Approach to AI and NFT Art
- Special issue: Theory Materialized–Art-object Theorized, edited by Ido Govrin (University of Tessaly, Greece)
- Material–Art–Dust. Reflections on Dust Research between Art and Theory
- Nancy in Jerusalem: Soundscapes of a City
- Zaniness, Idleness and the Fall of Late Neoliberalism’s Art
- Enriching Flaws of Scent عطر עטרה A Guava Scent Collection
- Special issue: Towards a Dialogue between Object-Oriented Ontology and Science, edited by Adrian Razvan Sandru (Champalimaud Foundation, Portugal), Federica Gonzalez Luna Ortiz (University of Tuebingen, Germany), and Zachary F. Mainen (Champalimaud Foundation, Portugal)
- Retroactivity in Science: Latour, Žižek, Kuhn
- The Analog Ends of Science: Investigating the Analogy of the Laws of Nature Through Object-Oriented Ontology and Ontogenetic Naturalism
- The Basic Dualism in the World: Object-Oriented Ontology and Systems Theory
- Knowing Holbein’s Objects: An Object-Oriented-Ontology Analysis of The Ambassadors
- Relational or Object-Oriented? A Dialogue between Two Contemporary Ontologies
- The Possibility of Object-Oriented Film Philosophy
- Rethinking Organismic Unity: Object-Oriented Ontology and the Human Microbiome
- Beyond the Dichotomy of Literal and Metaphorical Language in the Context of Contemporary Physics
- Revisiting the Notion of Vicarious Cause: Allure, Metaphor, and Realism in Object-Oriented Ontology
- Hypnosis, Aesthetics, and Sociality: On How Images Can Create Experiences
- Special issue: Human Being and Time, edited by Addison Ellis (American University in Cairo, Egypt)
- The Temporal Difference and Timelessness in Kant and Heidegger
- Hegel’s Theory of Time
- Transcendental Apperception from a Phenomenological Perspective: Kant and Husserl on Ego’s Emptiness
- Heidegger’s Critical Confrontation with the Concept of Truth as Validity
- Thinking the Pure and Empty Form of Dead Time. Individuation and Creation of Thinking in Gilles Deleuze’s Philosophy of Time
- Ambient Temporalities: Rethinking Object-Oriented Time through Kant, Husserl, and Heidegger
- Special issue: Existence and Nonexistence in the History of Logic, edited by Graziana Ciola (Radboud University Nijmegen, Netherlands), Milo Crimi (University of Montevallo, USA), and Calvin Normore (University of California in Los Angeles, USA) - Part I
- Non-Existence: The Nuclear Option
- Individuals, Existence, and Existential Commitment in Visual Reasoning
- Cultivating Trees: Lewis Carroll’s Method of Solving (and Creating) Multi-literal Branching Sorites Problems
- Abelard’s Ontology of Forms: Some New Evidence from the Nominales and the Albricani
- Boethius of Dacia and Terence Parsons: Verbs and Verb Tense Then and Now
- Regular Articles
- “We Understand Him Even Better Than He Understood Himself”: Kant and Plato on Sensibility, God, and the Good
- Self-abnegation, Decentering of Objective Relations, and Intuition of Nature: Toomas Altnurme’s and Cao Jun’s Art
- Nietzsche, Nishitani, and Laruelle on Faith and Immanence
- Meillassoux and Heidegger – How to Deal with Things-in-Themselves?
- Arvydas Šliogeris’ Perspective on Place: Shaping the Cosmopolis for a Sustainable Presence
- Raging Ennui: On Boredom, History, and the Collapse of Liberal Time
Articles in the same Issue
- Special issue: Happiness in Contemporary Continental Philosophy, edited by Ype de Boer (Radboud University, the Netherlands)
- Editorial for Topical Issue “Happiness in Contemporary Continental Philosophy”
- Badiou and Agamben Beyond the Happiness Industry and its Critics
- Happiness and the Biopolitics of Knowledge: From the Contemplative Lifestyle to the Economy of Well-Being and Back Again
- Reanimating Public Happiness: Reading Cavarero and Butler beyond Arendt
- Thinking from the Home: Emanuele Coccia on Domesticity and Happiness
- A Strategy for Happiness, in the Wake of Spinoza
- Das Unabgeschlossene (das Glück). Walter Benjamin’s “Idea of Happiness”
- The Role and Value of Happiness in the Work of Paul Ricoeur
- On the “How” and the “Why”: Nietzsche on Happiness and the Meaningful Life
- Albert Camus and Rachel Bespaloff: Happiness in a Challenging World
- Symptomatic Comedy. On Alenka Zupančič’s The Odd One In and Happiness
- Happiness and Joy in Aristotle and Bergson as Life of Thoughtful and Creative Action
- Special issue: Dialogical Approaches to the Sphere ‘in-between’ Self and Other: The Methodological Meaning of Listening, edited by Claudia Welz and Bjarke Mørkøre Stigel Hansen (Aarhus University, Denmark)
- Sonic Epistemologies: Confrontations with the Invisible
- The Poetics of Listening
- From the Visual to the Auditory in Heidegger’s Being and Time and Augustine’s Confessions
- The Auditory Dimension of the Technologically Mediated Self
- Calling and Responding: An Ethical-Existential Framework for Conceptualising Interactions “in-between” Self and Other
- More Than One Encounter: Exploring the Second-Person Perspective and the In-Between
- Special issue: Lukács and the Critical Legacy of Classical German Philosophy, edited by Rüdiger Dannemann (International Georg-Lukács-Society) and Gregor Schäfer (University of Basel)
- Introduction to the Special Issue “Lukács and the Critical Legacy of Classical German Philosophy”
- German Idealism, Marxism, and Lukács’ Concept of Dialectical Ontology
- The Marxist Method as the Foundation of Social Criticism – Lukács’ Perspective
- Modality and Actuality: Lukács’s Criticism of Hegel in History and Class Consciousness
- “Objective Possibility” in Lukács’s History and Class Consciousness
- The Hegelian Master–Slave Dialectic in History and Class Consciousness
- “It Would be Helpful to Know Which Textbook Teaches the ‘Dialectic’ he Advocates.” Inserting Lukács into the Neurath–Horkheimer Debate
- Everyday Hegemony: Reification, the Supermarket, and the Nuclear Family
- Critique of Reification of Art and Creativity in the Digital Age: A Lukácsian Approach to AI and NFT Art
- Special issue: Theory Materialized–Art-object Theorized, edited by Ido Govrin (University of Tessaly, Greece)
- Material–Art–Dust. Reflections on Dust Research between Art and Theory
- Nancy in Jerusalem: Soundscapes of a City
- Zaniness, Idleness and the Fall of Late Neoliberalism’s Art
- Enriching Flaws of Scent عطر עטרה A Guava Scent Collection
- Special issue: Towards a Dialogue between Object-Oriented Ontology and Science, edited by Adrian Razvan Sandru (Champalimaud Foundation, Portugal), Federica Gonzalez Luna Ortiz (University of Tuebingen, Germany), and Zachary F. Mainen (Champalimaud Foundation, Portugal)
- Retroactivity in Science: Latour, Žižek, Kuhn
- The Analog Ends of Science: Investigating the Analogy of the Laws of Nature Through Object-Oriented Ontology and Ontogenetic Naturalism
- The Basic Dualism in the World: Object-Oriented Ontology and Systems Theory
- Knowing Holbein’s Objects: An Object-Oriented-Ontology Analysis of The Ambassadors
- Relational or Object-Oriented? A Dialogue between Two Contemporary Ontologies
- The Possibility of Object-Oriented Film Philosophy
- Rethinking Organismic Unity: Object-Oriented Ontology and the Human Microbiome
- Beyond the Dichotomy of Literal and Metaphorical Language in the Context of Contemporary Physics
- Revisiting the Notion of Vicarious Cause: Allure, Metaphor, and Realism in Object-Oriented Ontology
- Hypnosis, Aesthetics, and Sociality: On How Images Can Create Experiences
- Special issue: Human Being and Time, edited by Addison Ellis (American University in Cairo, Egypt)
- The Temporal Difference and Timelessness in Kant and Heidegger
- Hegel’s Theory of Time
- Transcendental Apperception from a Phenomenological Perspective: Kant and Husserl on Ego’s Emptiness
- Heidegger’s Critical Confrontation with the Concept of Truth as Validity
- Thinking the Pure and Empty Form of Dead Time. Individuation and Creation of Thinking in Gilles Deleuze’s Philosophy of Time
- Ambient Temporalities: Rethinking Object-Oriented Time through Kant, Husserl, and Heidegger
- Special issue: Existence and Nonexistence in the History of Logic, edited by Graziana Ciola (Radboud University Nijmegen, Netherlands), Milo Crimi (University of Montevallo, USA), and Calvin Normore (University of California in Los Angeles, USA) - Part I
- Non-Existence: The Nuclear Option
- Individuals, Existence, and Existential Commitment in Visual Reasoning
- Cultivating Trees: Lewis Carroll’s Method of Solving (and Creating) Multi-literal Branching Sorites Problems
- Abelard’s Ontology of Forms: Some New Evidence from the Nominales and the Albricani
- Boethius of Dacia and Terence Parsons: Verbs and Verb Tense Then and Now
- Regular Articles
- “We Understand Him Even Better Than He Understood Himself”: Kant and Plato on Sensibility, God, and the Good
- Self-abnegation, Decentering of Objective Relations, and Intuition of Nature: Toomas Altnurme’s and Cao Jun’s Art
- Nietzsche, Nishitani, and Laruelle on Faith and Immanence
- Meillassoux and Heidegger – How to Deal with Things-in-Themselves?
- Arvydas Šliogeris’ Perspective on Place: Shaping the Cosmopolis for a Sustainable Presence
- Raging Ennui: On Boredom, History, and the Collapse of Liberal Time

