Out-of-plane uniaxial loading of paperboard: experimental procedure and evaluation

1 Introduction

In the packaging industry, paperboard is one of the prime materials to ensure structural stability of packages containing food and beverages. Paperboard is built up by cellulose fibers, typically as a mixture of softwood and hardwood with representative fiber lengths of 3.6 mm and 1.2 mm, respectively (Retulainen et al. 1998). The material is orthotropic with three characteristic directions: MD, CD and ZD. During the manufacturing process, fibers are continuously sprayed in the direction of a web-nostril which results in a preferred fiber orientation, i.e. the machine direction, MD. The cross direction, CD, is perpendicular to MD and they span the in-plane sheet dimension while the ZD direction is the out-of-plane stacking direction of fibers. Paperboard is a thin structure with a typical thickness in the range of 0.2–0.5 mm. The elastic modulus along MD is approximately two times larger compared to the CD direction and approximately 100 times the magnitude of the ZD direction. Since the mechanical behavior along the in-plane and out-of-plane direction differs to such a large extent, paperboard is challenging to model.

There exists a number of continuum scale constitutive models for paperboard, several are outlined in the recent review by Simon (Simon 2020). Calibrating and validating such models requires reliable experimental data. Since paperboard is thin, such that the plane stress assumption often holds, in-plane models have been developed in, (Borgqvist et al. 2014; Li et al. 2016; Mäkelä and Östlund 2003), where the out-of-plane behavior is not considered. However, although paperboard is thin, the out-of-plane mechanical characteristics are important for many industrial applications. For instance during creasing, when paperboard is locally deformed to reduce its bending resistance along predefined patterns, and during folding when the package is formed. Since creasing and folding involve both out-of-plane delamination and shearing, cf. (Borgqvist et al. 2015, 2016; Robertsson et al. 2023), in-plane models are insufficient. Another important application that requires full three-dimensional models is embossing where the material is deformed through out-of-plane deformation. In recent years, a number of three-dimensional continuum paperboard models have been developed, cf. (Borgqvist et al. 2015; Li et al. 2018; Robertsson et al. 2021), and there is a need for reliable experiments to calibrate such models.

To calibrate the out-of-plane response, three experiments are often considered: out-of-plane tension, compression and shearing. Stenberg et al. (2001) used a modified Arcan device (Arcan et al. 1978) to perform out-of-plane measurements on paperboard. The specimens where glued to metal blocks using high-viscocity adhesives and attached to the device with fast-curing epoxy adhesives. The effective paperboard thickness after the gluing process was estimated such that the out-of-plane compression response align with and without the use of glue. Furthermore, in (Nygårds 2008) conventional uniaxial devices were used to perform cyclic out-of-plane experiments in tension, compression and shearing. The effective paperboard thickness was not measured in (Nygårds 2008) since the displacement history was deemed sufficient for out-of-plane shearing and tension. In (Li et al. 2018), out-of-plane experiments where performed without considering the paperboard thickness reduction due to the gluing procedure. While cyclic loading has been performed separately for out-of-plane tension, compression and shear, combined mode testing has only been done for compression and shearing, (Li et al. 2018; Stenberg et al. 2001). Surprisingly, continuous loading from compression to tension has not been reported in the literature even though this load path is present during, for instance, creasing and folding. An experimental device and protocol tailored for continuous loading from compression to tension has been developed in the current work.

A number of constitutive models, cf. (Borgqvist et al. 2015; Borgqvist et al. 2016; Nygårds et al. 2009), use a switch function to separate the elastic out-of-plane response between compression and tension since measurements indicates that the initial modulus differ in tension and compression. The switch function that is used to capture the initial soft tail during compression was eliminated in Robertsson et al. (2021) since the initial difference in compression and tension was assumed to be an experimental artifact. The use of a switch function will be revisited in the current work using the developed experimental procedure and setup. The load path from compression to tension requires that the paperboard specimen is glued to the experimental device, hence, the effective specimen thickness needs to be estimated. In contrast to (Stenberg et al. 2001), the effective paperboard sample thickness in our procedure is based on direct measurements.

The article is structured as follows. In Section 2, the experimental procedure and device is presented while in Section 3 the paperboard material is introduced. In Section 4, the impact of gluing the samples to the experimental device is investigated while Sections 5 and 6 present the experimental findings for continuous loading in compression and tension.

2 Experimental procedure

In Figure 1, the developed experimental device is shown together with a schematic illustration where the individual parts are labeled¹⁻⁹. The setup is used with a hydraulic MTS uniaxial tensile test machine and consists of portable upper⁶ and lower⁹ blocks that connect to the device. A spherical joint is mounted on the upper block to mitigate the effect of minute misalignments. To accommodate for cyclic out-of-plane compression and tension loading without axial play, the device contains a movable socket³ at its upper portion. During compression, the spherical joint is fixed manually by tightening the socket using screws². When the upper and lower blocks are glued to the paperboard sample, out-of-plane tensile loading can be performed in a controlled fashion.

Figure 1:

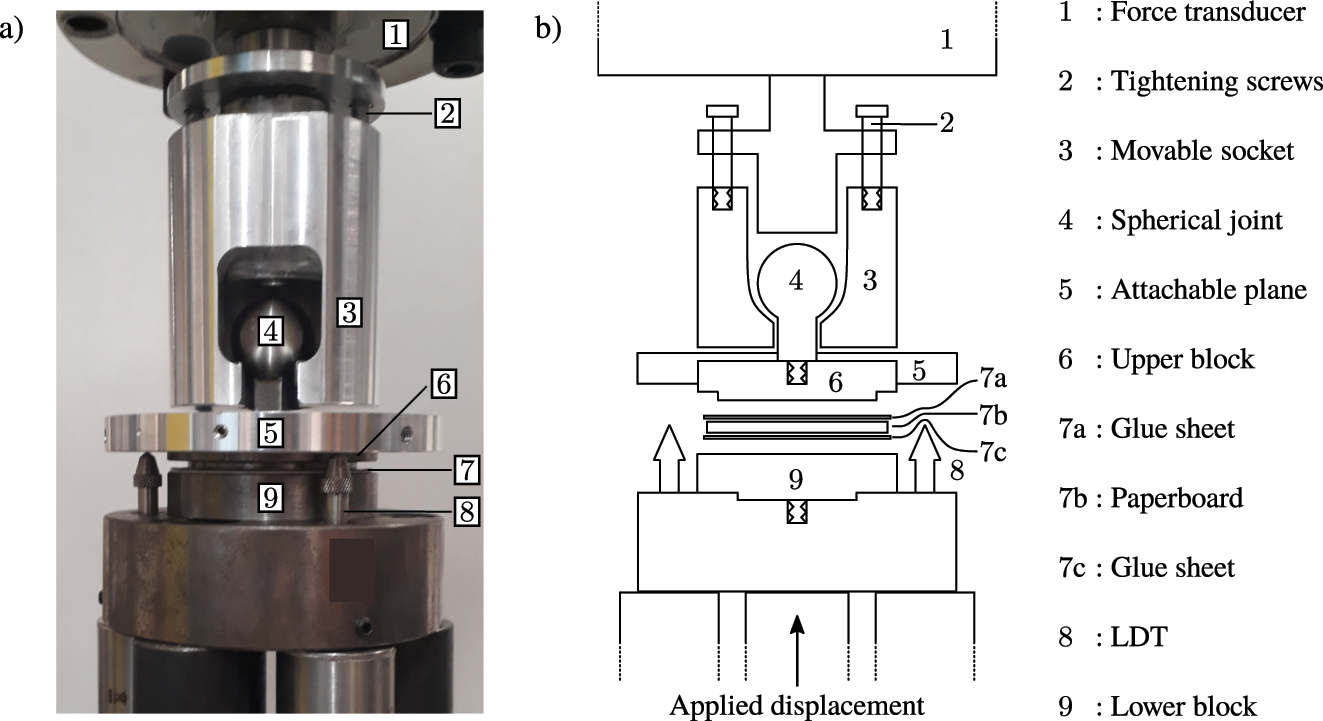
Experimental device in (a) laboratory setting and (b) schematic illustration highlighting individual components.

The displacement between the lower and upper block is measured using three TLDT10MM linear displacement transducers (LDT)⁸. The applied load is measured using a TC4 force transducer¹ with a maximum load range of 25 kN. Both the force transducer and the three displacement sensors are manufactured by AEP Transducers, Italy. The measured force together with the displacements from the LDTs constitutes the results for the macroscopic response.

The experimental procedure for cyclic out-of-plane loading is as follows. First, the upper and lower blocks, a circular paper specimen and two circular sheets of porous glue adhesives (Colormount Dry Mount Adhesive, D&K Expression) are glued together outside the experimental device. The area of the upper block, A = 1256 mm², is used to normalize the force to obtain the nominal stress. Prior to gluing, a micrometer is used to measure the combined thickness, t comb block , of the upper and lower block. In addition, the thickness of the glue sheets and paperboard sample are measured individually. After the thickness measurements, the sandwich structure is placed in an oven for 2 h at temperature T = 100 °C. The heat treatment is followed by a conditioning phase where the sandwich structure is placed in the laboratory environment for 48 h. After conditioning, the effective thickness of the combined sandwich, t eff sand , i.e. paperboard, blocks and glue, is measured. The effective paperboard thickness, t eff paper , used to extract the strain from normalizing the displacement, is calculated as

where t eff glue is the effective glue thickness. The effective glue thickness is estimated using a sample containing only the two glue sheets and blocks, i.e. excluding paperboard. The same protocol is adopted as before where the sandwich is placed in an oven followed by conditioning. The combined thickness of the blocks and glue, denoted as t eff ⋆ sand , are measured after the oven treatment. The effective glue thickness is obtained from

During cyclic loading between compression and tension, the procedure for fixating the spherical joint is as follows. The initial compressive step is performed until a predefined maximum compressive force is reached. At this load level, the movable socket³ is tightened around the spherical joint⁴ using the tightening screws². The tightening step takes 60 s and during this process the sample is kept under constant force which generates unavoidable creep.

The compliance of the experimental setup with glue, excluding paperboard, is smaller than the response for paperboard and glue, however not negligible. To compensate for this compliance, the displacement obtained from tests with glue and paperboard are adjusted by subtracting the displacement measured from experiments with the setup where only glue is present.

3 Material selection

A commercial paperboard is characterized using the developed experimental procedure. The paperboard is a single ply and the fibers are a mixture of softwood and hardwood. The nominal thickness is 398 μm while the grammage of the board is 315 gm⁻². One side of the board is claycoated, thus relatively smooth, while the opposite side is uncoated. The surface roughness of the uncoated side is characterized by optical surface measurements in Figure 2a where coherence scanning interferometry (CSI) technology was used at 4 regions with the NewView™ 9000 instrument, Zygo Corporation, USA. The pixel size of the measurements are 1.5 μm. The surface roughness measurements of the 4 regions in Figure 2a are extracted and visualized in Figure 2b where the measurements are fitted to a normal distribution.

Figure 2:

Four characteristic images (a) of the topology roughness from optical CSI measurements with (b) the corresponding extracted surface roughness profile.

4 Impact of glue during compression

Before considering the proposed experimental procedure for the compression and tension loading tests, the effect of gluing the samples is evaluated. For this endeavor, samples were compressed with and without glue. The stress-displacement response for the glued and unglued tests are shown in Figure 3. The most pronounced difference is seen in the initial phase of the loading where the unglued paperboard samples have a compliant, highly non-linear, response compared to the glued specimens. In addition, the experimental scatter is larger for the series without glue.

Figure 3:

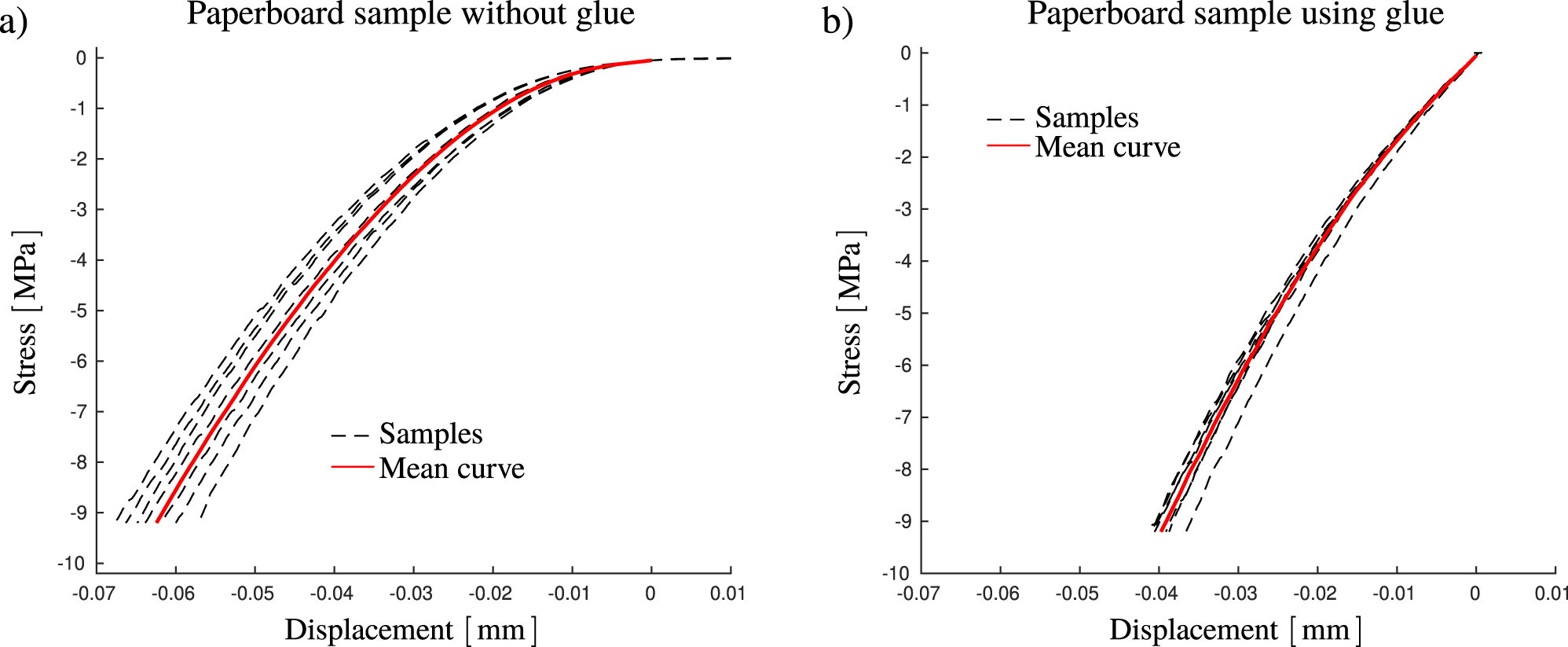
The displacement history for the compressive behavior using (a) only paperboard and (b) glued paperboard samples.

The initial compliant phase has previously been observed in the literature, cf. (Borgqvist et al. 2015) and (Robertsson et al. 2021). Two questions are associated with this compliant response. The first one is the arbitrariness of defining the initiation of paperboard deformation due to the initial compliant response. The second question is related to the continuity requirement between compression and tension. Clearly, since the initial response in Figure 3 differs between the glued and unglued samples, at least one of them will produce a discontinuity with respect to the initial tensile response. This discontinuity will be considered later in this paper.

To evaluate the initial compliant phase, a pressure sensitive film (Fujifilm prescale, super low LLW and ultrasuperlow LLLW) is used to determine the contact distribution during compression. The pressure sensitive films are manufactured by Fujifilm corporation, Japan. Results are shown in Figure 4 where the tests have been performed at two compressive stress levels, σ = −0.4 MPa and σ = −1 MPa. The compressed area is heterogeneous in both cases, hence, the surface roughness is assumed to have a large impact on the initial compliant response. In Figure 4, the fluctuations in intensity of the red patches are clearly correlated to the flocks of fibers observed as yellow patches in Figure 2. Similar observations for the heterogeneous surface was made in (Johansson et al. 2023) where X-ray tomography was performed during in-situ out-of-plane compression. In this study, the contact area was observed to be continuously increasing during loading with a rapid increase in the initial compliant phase.

Figure 4:

Pressure distribution when compressing a paper sample to (a) σ = −0.4 MPa and (b) σ = −1 MPa.

A conceptual illustration of the compression test for the unglued sample as well as for the glued sample is shown in Figure 5 together with the measured effective paperboard thickness. As the glue occupies the vacancies created by the surface roughness, the compressive force is expected to be evenly distributed along the initial paperboard layer, hence the measured response is not influenced by an evolving contact area as in the case of the unglued sample.

Figure 5:

Schematic of the compression test with (a) unglued and (b) glued sample. The figures are not to scale.

To further investigate our claim that surface roughness contributes to the compliant initial response, a numerical model of the experimental setup is created. The simulation is performed in Abaqus (Dassault Systems 2013) using a linear elastic material model with the elastic module E = 55 MPa and vanishing Poisson’s ratio, cf. Stenberg and Fellers (2002). The initial paperboard thickness t₀ = 400 μm is assumed and the sample is modeled as a square with a uniformly discretized mesh using roughly 300,000 fully integrated 3D linear continuum brick elements. The upper and lower blocks, cf. Figure 1, are modeled as rigid planar bodies. Contact between the blocks and the paperboard are modeled using a tangential penalty formation with a friction coefficient of 0.3. The surface roughness is defined by perturbating the out-of-plane coordinates of the initial nodal layer according to the normal distribution obtained from CSI measurements in Figure 2b.

The numerical results in Figure 6 shows that the soft, initial, response of an unglued sample is well captured by the model when introducing surface roughness in the simulation. This further strengthens the hypothesis that the soft response is due to geometrical effects rather than material behavior. To conclude, the surface roughness is not an intrinsic material feature and should be excluded from the constitutive description of the material. Hence, to measure the compressive material response of paperboard, the glued samples are deemed superior and should be used.

Figure 6:

Finite element simulation showing the impact of introducing surface roughnesses. For demonstration purposes, the curves are translated to align at σ = −2.5 MPa.

5 Continuous loading in compression and tension

Creasing, unloading, and subsequent folding implies that the material response alters from compression to tension which eventually leads to local delamination. To estimate the out-of-plane compressive stress levels during creasing and folding, the model developed in (Robertsson et al. 2023) is used to simulate line creasing. The out-of-plane Kirchhoff stress is shown in Figure 7 and as delamination usually initiates in the gap between the two creasing tools, a stress level of σ = −10 MPa is deemed appropriate for investigation.

Figure 7:

Simulation of the creasing procedure using the model in (Robertsson et al. 2023) showing the out-of-plane compressive projection of the Kirchhoff stress.

In Figure 8, the experimental results for continuous deformation from compression to tension using the described experimental procedure is shown. Since creep occurs during the 60 s when tightening the fixture, the mean response is extracted by calculating the average creep. As discussed in previous section, there is no compliant initial part in the compressive response in Figure 8a. The non-linear unloading behavior is well-known from the literature, cf. (Nygårds 2008). During tension, cf. Figure 8b, the peak load is followed by a cohesive region characterized by exponential softening which is attributed to fracture and delamination, see also (Biel et al. 2022).

Figure 8:

Compression and tension cycle using the proposed experimental procedure with paperboard and glue. The compressive and tensile parts of the response is shown in (a) and (b), respectively.

The strain in Figure 8 is obtained by dividing the displacement by the effective thickness t eff paper , calculated for each sample using equation (1). The expected value of the effective paperboard thickness using 26 samples is 381 μm with a standard deviation of 5 μm. The methodology for measuring t eff paper is deemed acceptable since the scatter is of the same order of magnitude as the initial thickness where the expected value is 398 μm with a standard deviation of 3.5 μm.

To further evaluate the transition from compression to tension, measurements are performed at a lower compressive stress level, σ = −2 MPa, where the inelastic strains are less pronounced. Four samples are used to extract the mean curve and the response is compared with the results obtained for the higher compressive stress level in Figure 8. The mean response for both stress levels are shown in Figure 9 with three regions being highlighted. In Figure 9b, the transition between out-of-plane compression and tension is smooth and therefore the response of the glued samples are concluded to be continuous with respect to compression and tension. The different compressive and tensile response for the unglued and glued samples in Figure 3 has been recognized in previous models by introducing a switch function that abruptly change the elastic properties for compression and tension, see (Borgqvist et al. 2015) and (Nygårds et al. 2009). However, based on our findings, a switch function is deemed as questionable from a modeling perspective. In addition, the tensile region shown in Figure 9c reveals that almost the same response is obtained when comparing the two load cycles except for a small shift in the stress-strain response that depends on the compressive load level.

Figure 9:

The mean curve for compression and tension at two different compressive levels. Three sections of the curves are highlighted, (a) the compressive part, (b) the transition between compression and tension, (c) the delamination during tension.

6 Cyclic experiments

Next, combined cyclic out-of-plane compression and tension measurements are performed. The aim is to glean further insight into the material response of paperboard since, to the authors knowledge, such experiments have not yet been published. One representative measurement is presented for each experimental series and compared to the mean curve, henceforward denoted as the reference, obtained from the single-cyclic experiment in Figure 8.

First, cyclic compression measurements are performed, see Figure 10. This type of cyclic loading is often used in the literature to track the evolution of inelastic strain. As expected, the cyclic loading curve follows the monotonic response of the reference experiment during compressive loading. The hysteresis present during loading and unloading in Figure 10 is similar to previous observations for paperboard, cf. (Borgqvist et al. 2015) and (Li et al. 2018). One reason for the hysteresis is the viscous effects that are clearly present as observed from the creep period during the fixation of the joint. From a modeling perspective, kinematic hardening can be used in combination with viscosity to capture this phenomena. This approach was adopted in (Girlanda et al. 2016; Tjahjanto et al. 2015) where a similar hysteresis for pressboard was measured and modeled.

Figure 10:

Representative curve for cyclic loading in compression and the mean curve obtained in Figure 8.

In Figure 11, cyclic loading in compression and tension is shown. After one cycle with large deformations, repeated cyclic loading is performed between a fixed, relatively low, compression and tensile state such that delamination is avoided. Since the response from the cyclic test closely resembles the reference experiment, this type of cyclic loading is deemed to have a low impact on the material tensile response. It is therefore concluded that during cyclic loading at low stress levels, damage is not evolving.

Figure 11:

Representative response for repeated cycling in compression and tension between two stress levels below the strength level in tension. The compressive and tensile parts of the response is shown in (a) and (b), respectively. The cyclic loading is compared to the mean curve shown in Figure 8.

Cyclic measurements with increasing compressive load in each loading cycle and constant tension below the delamination threshold strength is presented in Figure 12. Again, a similar phenomena is observed where the cohesive behavior during tensile loading follows the monotonic load path obtained from the reference experiment, i.e. the compressive cyclic loading does, as expected, not result in any significant damage evolution. In addition, the hysteresis from cyclic loading resembles the one obtained in Figure 10.

Figure 12:

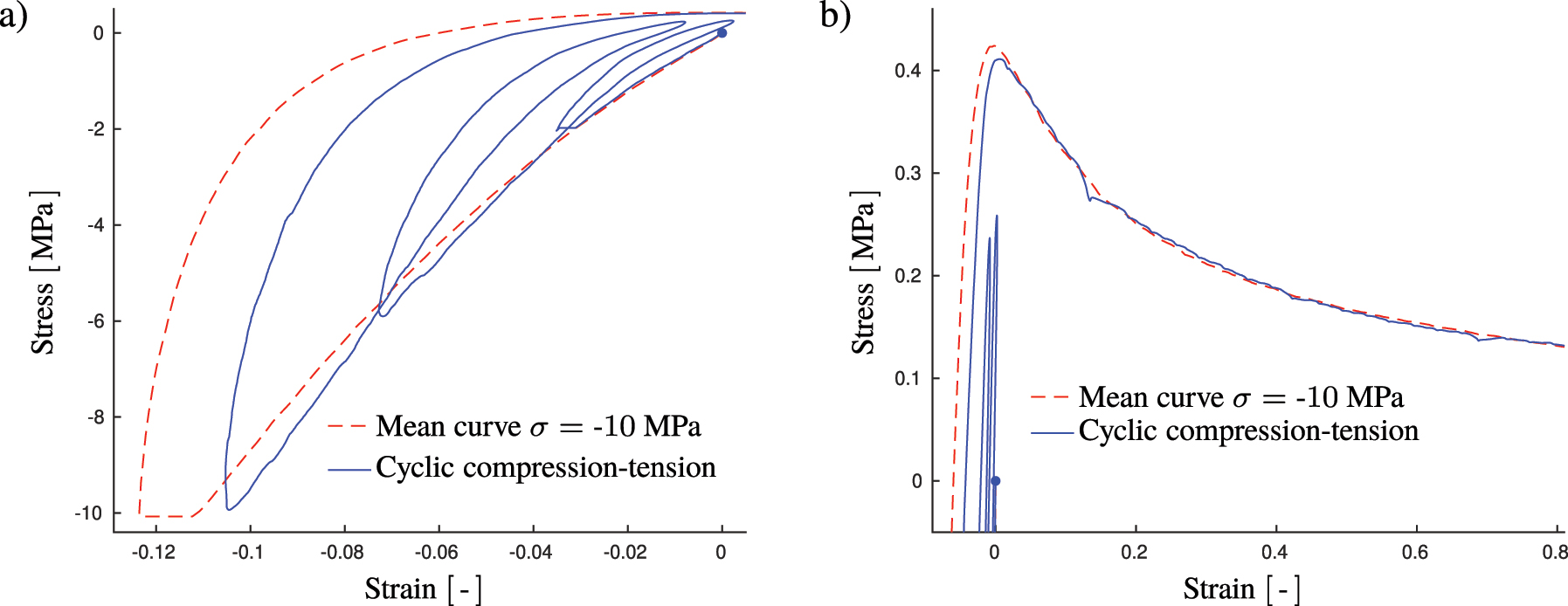
Representative response for repeated cycling in compression and tension below the tensile strength level with increasingly larger compressive levels. The compressive and tensile parts of the response is shown in (a) and (b), respectively. The cyclic loading is compared to the mean curve shown in Figure 8.

Finally, cyclic loading experiments with increasing strains during both compression and tension is presented in Figure 13 where the tensile load levels are beyond the expected damage evolution threshold. As seen in Figure 13b, during loading and reloading, the tensile load path follows the monotonic cohesive path of the reference experiment which indicates that no further damage is accumulating during cyclic loading. Furthermore, as seen in Figure 13, a hysteresis is observed that develops in a continuous manner when unloading in the cohesive tensile region and reloading from the compressive state. Surprisingly, a conceptually similar non-linear hysteresis is observed in the cohesive region for concrete, (Reinhardt et al. 1986), a material that is evidently different in nature from paperboard.

Figure 13:

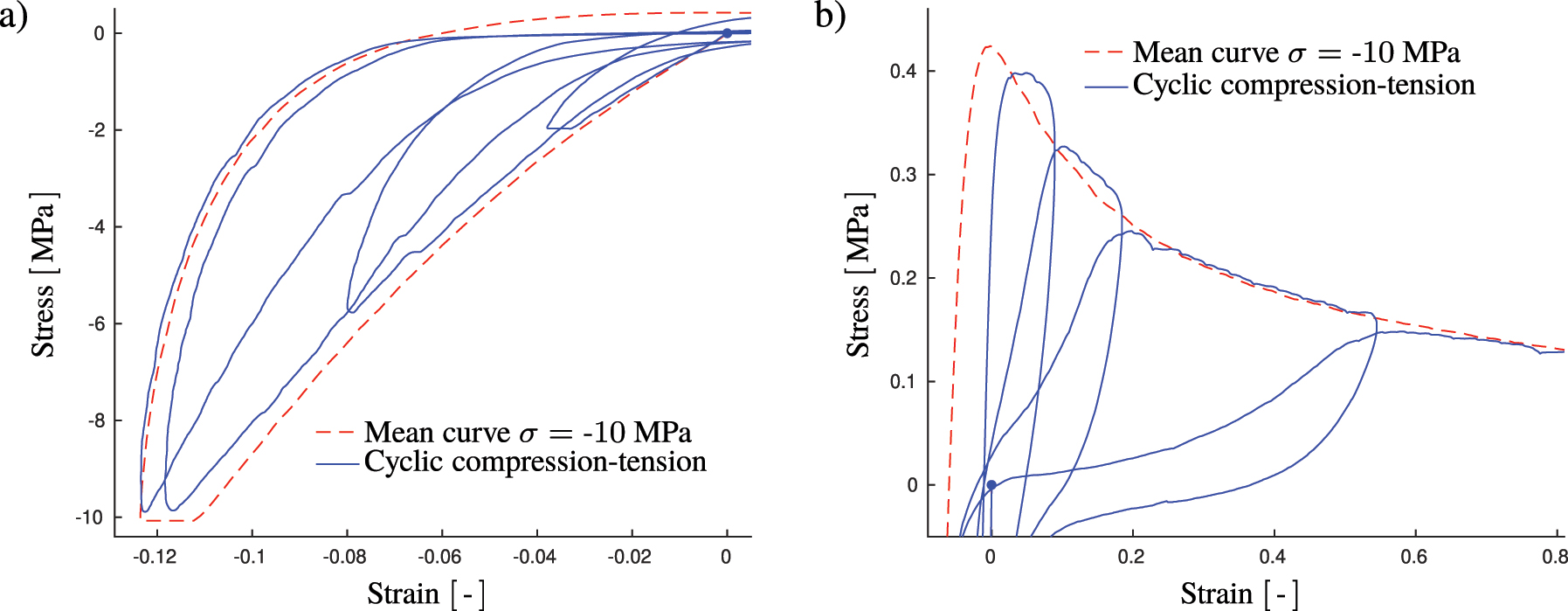
Representative response for repeated cycling loading during compression and tension in the region after the strength level is reached in tension. The compressive and tensile parts of the response is shown in (a) and (b), respectively. The cyclic loading is compared to the mean curve shown in Figure 8.

The small deviation from the monotonic load path when performing cyclic loading could be connected to differences in the underlying mechanisms during compression and tension. For out-of-plane tension, delamination occurs when bonding and interlocking between fibers starts to break while during compressive loading the mechanical response is the result of individual fibers being compressed and the frictional behavior between fibers. The results in Figure 13 suggests that the bonds between fibers are not recovered, i.e. there is no healing effect, when the sample is compressed since the strength in tension would be higher when unloading from the cohesive region and reloading from the compressive state.

7 Conclusions

An experimental setup and procedure has been developed to measure the mechanical response of paperboard during out-of-plane compression and tension cyclic loading. The impact of gluing the paperboard samples to the experimental device has been evaluated by comparing measurements with and without the gluing process.

A soft initial response is obtained when compressing samples without glue, a feature that is not present when the samples are glued. From simulations and experiments, the surface roughness of paperboard without glue is found to be the main source for the compliant initial response. As the surface roughness is a geometric property and not a material response, gluing the samples to the experimental device is deemed as a superior strategy for measuring the material response since the glue reduces the impact of the surface roughness.

The stress transition from compression to tension is smooth as observed from the loading and unloading experiments. Hence a switch function, used in many previous models to separate the initial elastic response between compression and tension, is regarded as unnecessary for constitutive modeling.

A number of novel cyclic experiments has been performed, alternating between compression and tension. The results suggest that compressive loading does not repair fiber bonds after they have been broken through delamination during tension. In addition, no tensile damage is accumulated when cyclic loading is performed between compression and a fixed tensile level.