Home Parameter simulation of multidimensional urban landscape design based on nonlinear theory
Article Open Access

Parameter simulation of multidimensional urban landscape design based on nonlinear theory

  • Congru Liu , Mingsen Lin , Hozan Latif Rauf EMAIL logo and Sardar S. Shareef
Published/Copyright: January 23, 2022
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nonlinear Engineering
From the journal Nonlinear Engineering Volume 10 Issue 1

Abstract

To solve the problem of large difference degree in multi-dimensional urban landscape design, a multidimensional urban landscape design method based on nonlinear theory is proposed. Research on multidimensional nonlinear landscape design methods in improving the rationality of architectural landscape design and improving the living environment is important for optimizing the structure of multidimensional nonlinear landscape design and improving the effect of urban landscape design. Firstly, according to the input and output data of the system, the multidimensional nonlinear landscape image is sampled, the virtual scene space visual planning method is used to simulate the parameters of the multidimensional nonlinear landscape design, and the block detection method is used to reconstruct the region of the multidimensional nonlinear landscape image. Combined with RGB feature decomposition method, the parameter vectorized feature extraction of multidimensional nonlinear landscape design was carried out, and the parameterized model of multidimensional nonlinear landscape view was extracted. Based on the parameterized model method, the multidimensional nonlinear landscape design is realized, and the quantitative analysis ability of multidimensional nonlinear landscape design is improved. The simulation results show that the mean of regression standard deviation is 0.567, the standard value is 0.753, and the F-test value is 0.655. Therefore, the visual feature expression ability of multidimensional nonlinear landscape design using the proposed method is better and the effect of landscape design is improved.

Keywords: Landscape design; parameter simulation; nonlinear theory

1 Introduction

Since the 20th century, with the continuous advancement of ecological landscape construction and the improvement of living environment, people's quality standards for landscape construction have been continuously improved, so it is necessary to carry out multidimensional nonlinear landscape design, and nonlinear science has gradually penetrated into many other disciplines. The study of nonlinear science has an important impact on human society, ecological environment, scientific progress, economy, and the development of information technology [1, 2]. In recent years, the emergence of nonlinear science has brought about profound changes in the view of nature and science. And the nonlinear thinking is imperceptibly affecting people's life behavior and thinking mode. Combined with the functional orientation of the landscape to optimize the structure of multidimensional nonlinear landscape design, improve the effect of urban landscape design, research on multidimensional nonlinear landscape design methods in improving the rationality of architectural landscape design and improving the living environment has important significance, the nonlinear landscape design structure is shown in Figure 1 [3]. According to the development orientation of landscape construction and the guiding factors of government policies, landscape construction planning and design are carried out to improve the spatial expression ability of landscape design. The multidimensional nonlinear landscape design is carried out by using computer vision image analysis method, and the parameterized analysis model of multidimensional nonlinear landscape design is constructed. The optimization design of multidimensional nonlinear landscape design is carried out by using structured image analysis and parameter simulation method. A multidimensional nonlinear landscape design method based on parameterized model was proposed to improve the quantitative analysis ability of multidimensional nonlinear landscape design [4].

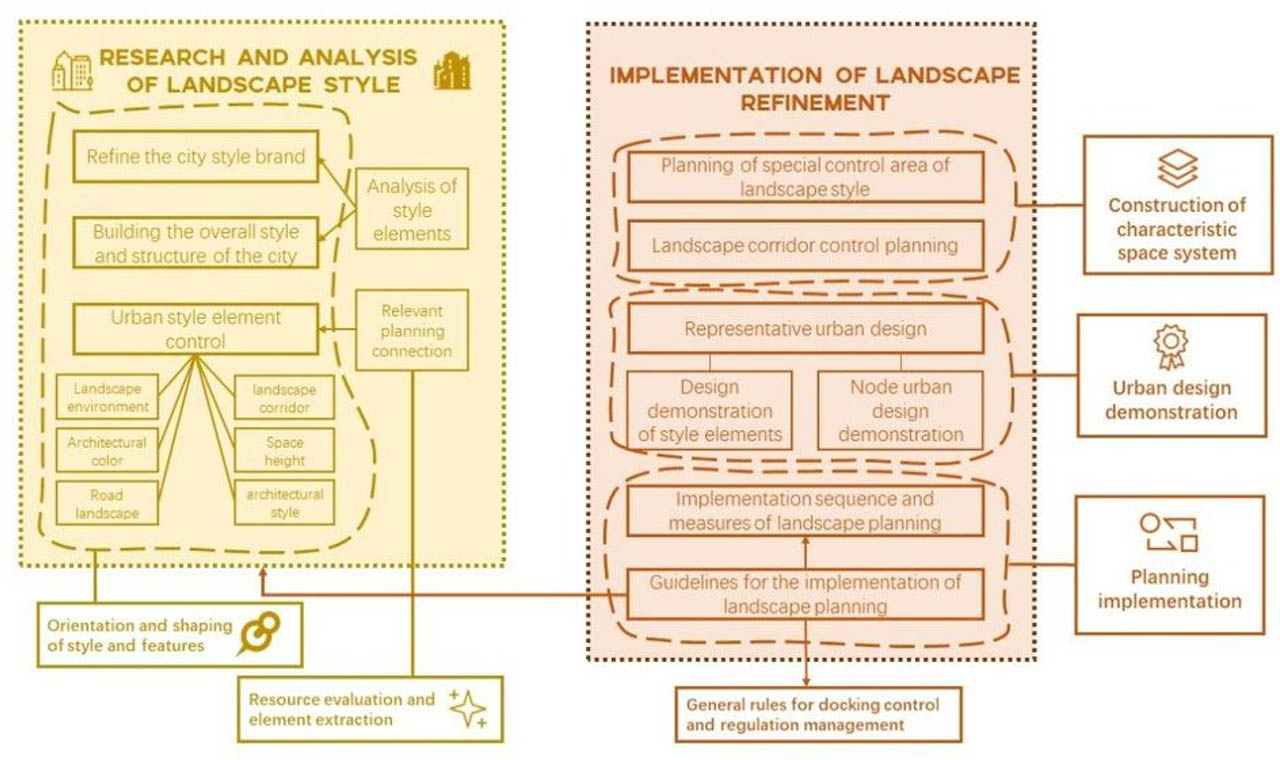
Figure 1 Nonlinear landscape design structures
Figure 1

Nonlinear landscape design structures

As “another revolution” in the history of science in the 20th century, nonlinear science has affected almost all fields of natural science and humanities and social science and is changing people's traditional view of the real world. Xiao et al. believes that the study of nonlinear science not only has great scientific significance, but also has immeasurable influence on human society, ecological environment, medical diagnosis, economic development, information, and decision-making [5]. Without considering the nonlinear factors, it is impossible to reflect the objective law truly and accurately without establishing the nonlinear model. The reason is that the world as a whole, from cosmology to macro to micro, is inherently nonlinear. Nonlinearity is the root cause of complexity and diversity in nature. The development of nonlinear science has also brought about profound changes in philosophy and methodology. The contribution to its exploration is not only that it has created a new subject field, but also that it has brought about great changes in the view of nature, the view of science, methodology, and even the way of thinking. Nonlinear interaction has more intrinsic and essential meanings than linear interaction. The linear interaction is only a highly simplified and approximate treatment of the nonlinear interaction. Kumar et al. studied the viscosity of Newton's Boussinesq fluid with Rayleigh Benard deficient defect fluid with period boundary temperature modulation using A weakly nonlinear theoretical framework. The critical Rayleigh number is calculated using the energy method accompanied by the variational algorithm for the asymptotic stability criterion. It is found that the subcritical instability occurs under two conditions: When the modulation is in the resistance phase, only the modulation is applied at the lower boundary. Witness supercritical stability during in-phase modulation. In all three cases of relative phases of the two boundary temperatures, the effect of the infinite disturbance is found to be weak. The findings of this study can be of major concern in several applications where appropriate temperature modulation is applied [6]. Kamei et al. clarified that the thermal effect not only contributes to the dissipative effect, but also produces nonlinear effects. The nonlinear term coefficient includes the ratio of the proportion of ideal gas within a bubble. We then conclude that the wave propagation process is determined by thermodynamic processes within the bubble [7]. Miao et al. summarized several characteristics of architecture: Architecture should be close to nature and use natural vocabulary; Architecture should reflect the nature of the universe; Architecture reflects the hierarchy, multivalence and complexity of the system; Diversity of architecture is realized through collage and juxtaposition [8]. Yao et al., one of the institutions for theoretical practice and teaching of nonlinear architectural design, has become a pioneer and an important camp in the research and teaching of nonlinear architectural design after years of construction [9]. Demir et al. systematically introduced the new technology-assisted design method relied on: CAD computer aided design, CAE computer aided analysis, CAM computer aided manufacturing, multi-disciplinary comprehensive application, multi-work coordination, jointly assist architects to complete nonlinear architecture from design conception, technical analysis, event production and other whole process of construction work; In addition, tracking records have been made from design conception to scheme deepening to the actual construction process of all realized engineering examples, and the application of design methods has been summarized [10]. Paquin Lefebvre et al. pointed out that the details of the symbols are common forms of traditional expression, and the symbols with high traditional meanings should be simplified into the composition elements of the space combination, combined with modern design ideas, and organically combined with other elements to reflect the environmental theme and atmosphere to be expressed, as well as the unique cultural background. Only by incorporating the detail modeling symbols into the style of the overall environment can such detail processing have vitality [11]. Chen et al. pointed out that for the relationship between details and the building as a whole, function provides the origin and meaning of details, while the connecting part between different functions, structures and forms provides us with the producing part of details. The operation in form makes details take root and become reality [12]. In the aforementioned section, an introduction was given about the paperwork. Section 2 contains the research methodology used in the paper. Section 3 discusses the result analysis. And at last, Section 4 has concludes the paperwork.

The proposed nonlinear theory for multidimensional urban landscape design has been proposed. It helped in improving the living environment, optimizing the structure of landscape design and improving the effect of urban landscape design. Multidimensional nonlinear landscape design is accomplished using the parameterized model technique, and the quantitative analysis ability of multidimensional nonlinear landscape design is increased. Hence, this could be a better way of landscape design.

2 Research methods

2.1 Construction of nonlinear thinking mode in landscape design

The world is inherently nonlinear, and linearity is a special case. Therefore, in such a nonlinear world, one must use nonlinear thinking to deal with it. First of all, because the landscape is a complex nonlinear system, including cultural, artistic, ecological, human experience, and other issues at different levels, it needs to be analyzed and considered from different levels, different perspectives, and different approaches, but cannot be satisfied with a simple interpretation of one cause and one effect. Of course, due to the limited nature of human knowledge and the endless nonlinear interactions in complex systems, it is difficult for human beings to achieve perfect ideal results. Therefore, some simplification is necessary. Secondly, chaos theory points out that the evolution of nonlinear systems cannot be predicted for a long time, so we need to adhere to a limited view of prediction. Chaos or potential chaos is the nature of nonlinear systems. The smallest uncertainty in a system is amplified by feedback coupling, causing a sudden change at a point of divergence that makes even a simple system potentially horribly complex, making the entire system's prospects completely unpredictable. For example, changes in human behavior, plant growth, and other elements of the landscape system can affect the development of the future system. In addition, nonlinear thinking also puts forward a higher request to the practitioner. The rapid development of computer and information technology has affected the way of life of people in almost all fields. Similarly, in the field of landscape, the development and evolution of the landscape environment can be simulated by a computer, and the landscape form can be generated, making the construction of nonlinear landscape system possible. The nonlinear thinking view can be constructed through holistic thinking, relational thinking, and process thinking.

(1) Holistic thinking

The first is to take a holistic view of the landscape system. Adhere to the nonlinear holistic view; people believe that an environmental system, its own properties and functions, as well as the law of movement, from the perspective of the whole, can be reflected. Only by relying on the system as a whole, can each component within the system reflect its own characteristics that it does not have originally. Therefore, it is not to add up each element, but to coordinate the various relationships between them to form a landscape system. Landscape system is an important part of the urban system, and it is also an independent natural system. We should not only pay attention to its integrity, but also pay attention to the characteristics of each part. Landscape system because of the various elements, and most of them are nonlinear, these elements affect each other and increase the complexity of landscape. Therefore, only by adopting a holistic way of thinking to carry out planning, can the site be effectively utilized.

(2) Procedural thinking

In landscape design, if nonlinear thinking is adopted, it is necessary to break the space limit and expand the space of thinking. At the same time, the time dimension is introduced, and the dynamic structural analysis method is adopted to design the relationship between various elements. That is to say, the landscape space is regarded as a dynamic system, which forms the space and fills the content with time structure. The space system constructed in this way has both the organizational structure of the landscape system and the function of a system and maintains a harmonious relationship with the surrounding environment. The landscape design under the view of nonlinear thinking should get rid of the system of settings or background and regard the landscape as “landscape field” rather than “objects”. In the view of relational theory, the landscape system can exist, be defined, described, and understood only in relationship with the environment and background.

(3) Associative thinking

What the Greeks meant by “nature” was that which grew and changed. To the Greek philosophers, the world was essentially something that came out of chaos and developed. The landscape design based on nonlinear thinking should not be limited to spatial thinking and static structural analysis but should pay attention to the addition of time dimension, event sequences, dynamic relationship network, and evolutionary mechanisms [13]. In other words, the landscape system should be regarded as a dynamic system, and the space-time structure should be established [14]. This space-time structure contains the function, organization and relationships between the system and the environment of the landscape system and shows a self-organizing synergistic principle in the process of such interaction [15]. Designers can not regard the landscape system as an isolated object but should form a unified and coordinated relationship with the surrounding environment, so that it can be integrated into the environment and become a member of the environmental organization [16]. Therefore, designers should pay attention to the relevance of thinking, carry out a detailed analysis of the surrounding environmental elements of the landscape, and find the relevance points among them. Get rid of the thinking mode of setting and background, regard the landscape as the place of the landscape, determine the correlation in the whole place, make it become a background environment, and be better highlighted [17].

2.2 Multidimensional nonlinear landscape image analysis

(1) Multidimensional nonlinear landscape image sampling

To realize multidimensional nonlinear landscape design, model parameterization, analysis, and feature extraction are needed. Based on multidimensional nonlinear landscape image block matching, detection and recognition, we build a multidimensional nonlinear dynamic characteristics of the landscape image distribution model, combining with the fuzzy association feature point detection, the method of multidimensional nonlinear optimization of landscape data extraction, combined with the fuzzy feature extraction method, and collect multidimensional nonlinear optimization of landscape image of character recognition, Multi-dimensional nonlinear landscape image processing and information fusion are carried out by using the reconstruction method of pixel feature points [18]. The geometric invariant moment generation model for constructing multidimensional nonlinear landscape images is as follows:

(1) Dif(C1,C2)=minυi∈C1,υj∈C2(υi,υj)∈Ew[(υi,υj)+FE]

Type, FE=1nI1nD , represents the feature sampling points of the multidimensional nonlinear landscape image and uses the virtual scene spatial visual planning method to simulate the parameters of the multidimensional nonlinear landscape design and constructs the spatial regional distribution model of the multidimensional nonlinear landscape image [19]. The regional fusion of multidimensional nonlinear landscape in the gradient direction and the template matching method are combined to obtain the edge information of multidimensional nonlinear landscape image as follows:

(2) Gx(x,y,t)=∂u(x,y,t)∂x

(3) Gy(x,y,t)=∂u(x,y,t)∂y

In the formula, the edge information of landscape image is decomposed into two components along the gradient direction, Xi,j is used to represent the edge pixel distribution set of landscape rationality distribution at the position of central pixel (i, j), distributed reconstruction method of visual features is used to make multidimensional nonlinear landscape parameterized design decision, the length of landscape area distribution L = xmax −xmin, H = zmax −zmin. The template block area matching method was adopted to traversal all sub-blocks. Combined with high-resolution information fusion technology, the multidimensional nonlinear landscape parameter simulation was carried out, and the scale space was obtained as follows:

(4) Mi,j=med(Xi−1,j−1⋯Xi,j⋯Xi+1,j+1)

There are:

(5) Fi,j={1,|Xi,j−Mi,j|≥T0,|Xi,j−Mi,j|<T

Combined with the frame matching method, the block detection and feature matching of multidimensional nonlinear landscape are carried out, and the pixel set between frames is Ic, and adjacent frames are represented as NFc = {n : c − k ≤ n ≤ c + k}. A multi-dimensional nonlinear landscape parameter template matching model is established, and the plane pheromone of nonlinear landscape design is defined as G (x, y, t), where:

(6) u(x,y,t)=G(x,y,t)

In multiscale space, multi-dimensional nonlinear landscape image sampling is carried out, and nonlinear landscape design is carried out according to the results of image sampling [20].

(2) Parameter simulation of multidimensional nonlinear landscape design

The spatial visual planning method of the virtual scene was used to simulate the parameters of multidimensional nonlinear landscape design. Combined with the distribution characteristics of each pixel, the similarity analysis of the multidimensional nonlinear landscape image was carried out, and the spatial regional feature matching model of landscape design was obtained as follows:

(7) F=p˜(x,y)=p(x,y)(υ(x)υ(y))1/2

The matrix X was used to express the neighboring phase points, and the entropy weight feature distribution set was established to realize the parametric design of a multidimensional nonlinear landscape. The pixel covariance function of the multidimensional nonlinear landscape under the multiscale feature decomposition mode was obtained as follows:

(8) p(x,y)=k(x,y)υ(x)υ(x)=∑yk(x,y)

The affine invariant region segmentation of the multidimensional nonlinear landscape image was carried out with pixel point i as the center. According to the number of observations in the training set, the training function was obtained to satisfy 0 ≤ w (i, j) ≤ 1 and ∑j∈Ωw(i,j)=1 . After initializing the prior shape, the parameter distribution matrix of the multidimensional nonlinear landscape design was obtained as follows:

(9) D=[Ix2IxIyIxIyIY2]

According to the parameter simulation results of multidimensional nonlinear landscape design, regional reconstruction is carried out, and combined with RGB feature decomposition method, feature extraction of parameter vectorization of multidimensional nonlinear landscape design is carried out [21, 22].

2.3 Multidimensional nonlinear landscape design optimization

Parametric design is actually a parametric design. In the process of parametric design, the parameter is an important factor that affects the whole design, and the change of the parameter will change the result of the whole design. For example, when making a landscape design, the site is taken as a function, and many factors that affect the site design (sunshine, crowd, terrain, climate, wind direction, surrounding environment, traffic, etc.) are taken as variables of this function [23]. In this way, the relationship between landscape and the many factors that influence its generation is no longer linear, but nonlinear. Parametric design does not take shape as the purpose, but through a set of form generation logic, to achieve a certain design intention. Combined with RGB feature decomposition method, parameterized segmentation of the multidimensional nonlinear landscape model was carried out [24]. The fuzzy matching feature number of the multidimensional nonlinear landscape image is extracted. Within the area inside and outside the target edge of the landscape image, the estimated value of the parameter of the significant feature points is:

(10) NLM[g(i)]=∑j∈Ωw(i,j)g(j)

Based on the idea of metric learning, the three-dimensional feature reconstruction parameters of multidimensional nonlinear landscape images are uniformly distributed, that is, the pixel sequence meets n∈N(0,σn2) . The parameterized model is used for structural analysis, and the second moment of multidimensional nonlinear landscape design is obtained as follows:

(11) μpq=∑m=1M∑n=1N(x−x˙)p(y−y˙)qf(x,y)

First-order moments m01 and m02 are used to represent the edge fuzzy feature quantity of multidimensional nonlinear landscape images, and block fusion technology is adopted to obtain that the edge template area of landscape design meets normal distribution in nc × nr subblocks. The extraction results of fine-grained feature points of landscape images are as follows:

(12) I1=n20n02−n112n004

(13) Emij=∑k=0255emkij

(14) emkij={−pklogpk,pk≠00,pk=0

Type: pk is the vectorization dimension of spatial data of landscape image; m = 1, 2, … N. The parameterized model of multidimensional nonlinear landscape view is extracted, and the multidimensional nonlinear landscape design is realized based on the parameterized model method. The vector quantization feature set of multidimensional nonlinear landscape image is obtained as follows:

(15) pi,j(A)={wi,jwi,i≠j,ei,j∈A0,i≠j,ei,j∉A1−j:ei,j∈Awi, i=j

Parameterized segmentation of the multidimensional nonlinear landscape model was carried out by block template matching method, and the distribution results of the parameterized model of multidimensional nonlinear landscape design were obtained as follows:

(16) x(k)=[x1(k),x2(k),⋯,xm(k)],i=1,2,⋯,m

Where: K is the sampling node of multidimensional nonlinear landscape data; Xi (k) is the data stream. The implementation process of the whole model is shown in Figure 2 [25, 26].

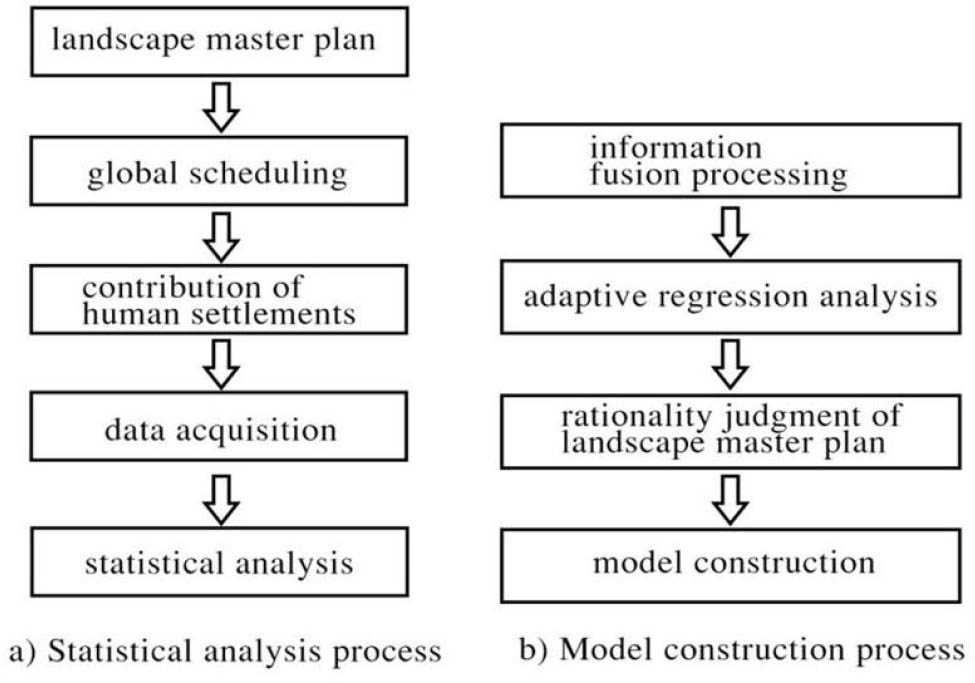
Figure 2 Implementation process of landscape design
Figure 2

Implementation process of landscape design

2.4 Nonlinear morphology generation

The generation of landscape form reflects the generation process from macro to micro (internal) and from micro to macro (external) in the application of nonlinear thinking mode in landscape design. Each part of the micro factors in accordance with their own growth rules and influence each other superimposed to promote the formation of the internal landscape of macroscopic form; the external is through the sunlight, gravity, wind and other natural external force factors directly acting on the macroscopic form of the intervention [27, 28]. Due to the parameterized design idea and working mode, the shapes generated through Digital Projects, Rhinoceros, Grasshoppers, and other software can be said to be “controllable random shapes”. The formation of this controllable random form is the result under the influence of various complex factors. The core logic of the design method, which proposes that complex factors lead to the formation of nonlinear forms, is expressed through the generation process of the nonlinear form, as shown in Figure 3 [29]. It is a four step procedure for the generation of landscape design. Input parameters were given at the initial stage. Then after reaction process, randomly generated morphological diversity is generated. Finally, the optimized selection is done.

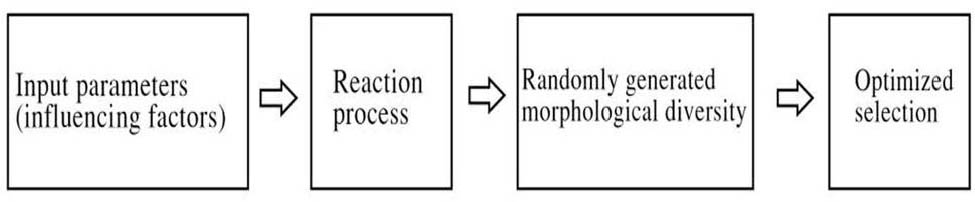
Figure 3 Non-linear morphology generation process
Figure 3

Non-linear morphology generation process

3 Result analyses

MATLAB simulation design was adopted in the experiment. The sample pixel size of landscape images ranged from 100 to 600, the pixel distribution of landscape images was 300×300, the metric learning module was 100, and the number of iterations was 1200. The results of descriptive statistical analysis of correlation parameters were shown in Table 1.

Table 1

Descriptive statistical analysis results

Number of samples Landscape correlation Similarity coefficient Contribution level The fuzzy factor
100 0.723 0.456 0.775 0.532
200 0.434 0.556 0.564 0.545
300 0.531 0.434 0.454 0.554
400 0.534 0.634 0.554 0.545
500 0.422 0.434 0.324 0.544
600 0.345 0.454 0.455 0.434

According to the descriptive statistical analysis results in Table 1, the multidimensional nonlinear landscape image sampling was carried out, and the virtual scene space visual planning method was used to simulate the parameters of the multidimensional nonlinear landscape design, to realize the landscape optimization design. The design effect results were shown in Figure 4. It can be seen from the analysis of Figure 4 that the method presented in this paper has a better effect in multidimensional nonlinear landscape design. Various variable parameters which are important for multidimensional urban landscape design development were discussed and compared in Table 2. The mean, standard values and f test values were obtained. Parameters such as regression analysis values and test values were tested, and the results were shown in Table 2. The mean, standard, f test values have been evaluated for different parameters. It can be seen from Table 2 that the method adopted in this paper has better visual feature expression ability and higher structural fitting accuracy of parameter distribution in multidimensional nonlinear landscape design.

Figure 4 Landscape design results
Figure 4

Landscape design results

Table 2

Regression analysis values and test values

The variable name The mean Standard values F test value
Landscape planning structure 0.456 1.432 0.456
Habitat satisfaction level 0.754 1.544 0.656
Environmental risk factor 0.467 1.676 0.265
Level of ecological improvement 0.435 1.545 0.645
Landscape construction scale 0.567 0.545 0.367
Decision evaluation value 0.365 0.567 0.655
Overall planning allocation efficiency 0.545 0.545 0.345
Regression standard deviation 0.567 0.753 0.655

4 Conclusions

This paper proposes a multidimensional urban landscape design method based on nonlinear theory, extracts the parameterized model of multidimensional nonlinear landscape view, and uses the parameterized model method to realize the multidimensional nonlinear landscape design. The multidimensional nonlinear landscape design is carried out by using the computer vision image analysis method, and the parameterized analysis model of multidimensional nonlinear landscape design is constructed. Combined with the fuzzy feature extraction method, the multidimensional nonlinear landscape image optimization collection and feature recognition are carried out. The multidimensional nonlinear landscape image sampling was carried out, and the virtual scene space visual planning method was used to simulate the parameters of the multidimensional nonlinear landscape design, to realize the landscape optimization design. The method adopted in this paper has better visual feature expression ability and higher structural fitting accuracy of parameter distribution in multidimensional nonlinear landscape design. The results show that this method can express the visual features of multidimensional nonlinear landscape design better, and the effect of landscape design is better.

  1. Funding information: The authors state no funding involved.

  2. Author contributions: All authors have accepted responsibility for the entire content of this manuscript and approved its submission.

  3. Conflict of interest: The authors state no conflict of interest.

References

[1] Zhou J. VR-based urban landscape artistic design. J Landsc Res. 2020;12(1):114–116.Search in Google Scholar

[2] Jagota V, Sethi AP, Kumar K. Finite Element Method: an Overview. Walailak J Sci Technol. 2013;10(1):1–8.Search in Google Scholar

[3] Solikhov DK, Dvinin SA, Khobilov DU. Using numerical modeling of nonlinear theory, the equations for Mandelstam–brillouin stimulated scattering in plasma. Russ Phys J. 2020;62(12):2204–11.10.1007/s11182-020-01967-ySearch in Google Scholar

[4] Young G, Vosloo P. Isivivane Freedom Park: a critical analysis of the relationship between commemoration, meaning, and landscape design in post-apartheid South Africa. Acta Structilia. 2020;27(1):85–118.10.18820/24150487/as27i1.4Search in Google Scholar

[5] Xiao Y, Bhola J. Design and optimization of prefabricated building system based on BIM technology. International Journal of System Assurance Engineering and Management; 2021 https://doi.org/10.1007/s13198-021-01288-4.10.1007/s13198-021-01288-4Search in Google Scholar

[6] Kumar A, Raju V, Das S. Onset of Rayleigh-benard convection with periodic boundary temperatures using weakly nonlinear theory. Microgravity Sci Technol. 2020;32(6):1237–43.10.1007/s12217-020-09844-6Search in Google Scholar

[7] Kamei T, Kanagawa T, Ayukai T. Weakly nonlinear theory on a thermal effect inside a bubble on plane pressure waves in bubbly water. J Acoust Soc Am. 2020;148(4):2495–2495.10.1121/1.5146918Search in Google Scholar

[8] Miao F, Lu N, Zhang P, Zhang Z, Shao G. Multidimension-controllable synthesis of ant nest-structural electrode materials with unique 3D hierarchical porous features toward electrochemical applications. Adv Funct Mater. 2019;29(29):1808994.10.1002/adfm.201808994Search in Google Scholar

[9] Yao Q, Shabaz M, Lohani TK, Wasim Bhatt M, Panesar GS, Singh RK. 3D modelling and visualization for Vision-based Vibration Signal Processing and Measurement. J Intell Syst. 2021;30(1):541–53.10.1515/jisys-2020-0123Search in Google Scholar

[10] Demir OT, Bjornson E. The Bussgang decomposition of nonlinear systems: basic theory and MIMO extensions [lecture notes]. IEEE Signal Process Mag. 2021;38(1):131–6.10.1109/MSP.2020.3025538Search in Google Scholar

[11] Paquin-Lefebvre F, Nagata W, Ward MJ. Weakly nonlinear theory for oscillatory dynamics in a one-dimensional pde-ode model of membrane dynamics coupled by a bulk diffusion field. SIAM J Appl Math. 2020;80(3):1520–45.10.1137/19M1304908Search in Google Scholar

[12] Chen L, Jagota V, Kumar A. Research on optimization of scientific research performance management based on BP neural network. Int J Syst Assur Eng Manag. 2021 https://doi.org/10.1007/s13198-021-01263-z.10.1007/s13198-021-01263-zSearch in Google Scholar

[13] Dou C, Zheng L, Wang W, Shabaz M. Evaluation of Urban Environmental and Economic Coordination Based on Discrete Mathematical Model. Math Probl Eng. 2021;2021:1–11.10.1155/2021/1566538Search in Google Scholar

[14] Li L, Lin W, Wang X, Yang G, Bahrami K, Kot AC. No-Reference Image Blur Assessment Based on Discrete Orthogonal Moments. IEEE Trans Cybern. 2016 Jan;46(1):39–50.10.1109/TCYB.2015.2392129Search in Google Scholar PubMed

[15] Wang B, Yao X, Jiang Y, Sun C, Shabaz M. Design of a Real-Time Monitoring System for Smoke and Dust in Thermal Power Plants Based on Improved Genetic Algorithm. J Healthc Eng. 2021 Jul;2021:7212567.10.1155/2021/7212567Search in Google Scholar PubMed PubMed Central

[16] Lincoln R, Galloway S, Stephen B, Burt G. Comparing Policy Gradient and Value Function Based Reinforcement Learning Methods in Simulated Electrical Power Trade. IEEE Trans Power Syst. 2012;27(1):373–80.10.1109/TPWRS.2011.2166091Search in Google Scholar

[17] Mathews VJ, Xie Z. A stochastic gradient adaptive filter with gradient adaptive step size. IEEE Trans Signal Process. 1993;41(6):2075–87.10.1109/ICASSP.1990.115645Search in Google Scholar

[18] Nguyen PH, Arsalan M, Koo JH, Naqvi RA, Truong NQ, Park KR. LightDenseYOLO: A Fast and Accurate Marker Tracker for Autonomous UAV Landing by Visible Light Camera Sensor on Drone. Sensors (Basel). 2018 May;18(6):1703.10.3390/s18061703Search in Google Scholar PubMed PubMed Central

[19] Lincoln R, Galloway S, Stephen B, Burt G. Comparing Policy Gradient and Value Function Based Reinforcement Learning Methods in Simulated Electrical Power Trade. IEEE Trans Power Syst. 2012;27(1):373–80.10.1109/TPWRS.2011.2166091Search in Google Scholar

[20] Li L, Wu D, Wu J, Li H, Lin W, Kot AC. Image Sharpness Assessment by Sparse Representation. IEEE Trans Multimed. 2016;18(6):1085–97.10.1109/TMM.2016.2545398Search in Google Scholar

[21] Li L, Zhu H, Yang G, Qian J. Referenceless Measure of Blocking Artifacts by Tchebichef Kernel Analysis. IEEE Signal Process Lett. 2014;21(1):122–5.10.1109/LSP.2013.2294333Search in Google Scholar

[22] Mu B, Liu C, Tian G, Xu Y, Zhang Y, Mayer AL, et al. Conceptual Planning of Urban–Rural Green Space from a Multidimensional Perspective: A Case Study of Zhengzhou, China. Sustainability. 2020;12(7):2863.10.3390/su12072863Search in Google Scholar

[23] Mathews VJ, Xie Z. A stochastic gradient adaptive filter with gradient adaptive step size. IEEE Trans Signal Process. 1993;41(6):2075–87.10.1109/ICASSP.1990.115645Search in Google Scholar

[24] Li Z, Nie F, Chang X, Yang Y. Beyond Trace Ratio: Weighted Harmonic Mean of Trace Ratios for Multiclass Discriminant Analysis. IEEE Trans Knowl Data Eng. 2017;29(10):2100–10.10.1109/TKDE.2017.2728531Search in Google Scholar

[25] Rembeza M, Sas-Bojarska A. International architectural – urban – landscape design workshops to strengthen students’ education, capabilities and mobility. World Trans Eng Tech Educ. 2020;18(2):190–6.Search in Google Scholar

[26] Jagota V., Sharma R.K. Impact of austenitizing temperature on the strength behavior and scratch resistance of AISI H13 Steel. J Inst Eng (India): D. 2020;101:93–104 https://doi.org/10.1007/s40033-020-00205-6.10.1007/s40033-020-00205-6Search in Google Scholar

[27] Li L, Xia W, Lin W, Fang Y, Wang S. No-Reference and Robust Image Sharpness Evaluation Based on Multiscale Spatial and Spectral Features. IEEE Trans Multimed. 2017;19(5):1030–40.10.1109/TMM.2016.2640762Search in Google Scholar

[28] Xue C, Zheng X, Zhang B, Yuan Z. Evolution of a multidimensional architectural landscape under urban regeneration: A case study of Jinan, China. Ecol Indic. 2015;55:12–22.10.1016/j.ecolind.2015.02.036Search in Google Scholar

[29] Yatabe T, Ayukai T, Kanagawa T. Weakly nonlinear theory and numerics of pressure wave propagation in a flowing water containing many translational bubbles acting as a drag force. J Acoust Soc Am. 2020;148(4):2572–2572.10.1121/1.5147138Search in Google Scholar
Received: 2021-09-15
Accepted: 2021-12-12
Published Online: 2022-01-23

© 2021 Congru Liu et al., published by De Gruyter

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Nonlinear absolute sea-level patterns in the long-term-trend tide gauges of the East Coast of North America
  2. Insight into the significance of Joule dissipation, thermal jump and partial slip: Dynamics of unsteady ethelene glycol conveying graphene nanoparticles through porous medium
  3. Numerical results for influence the flow of MHD nanofluids on heat and mass transfer past a stretched surface
  4. A novel approach on micropolar fluid flow in a porous channel with high mass transfer via wavelet frames
  5. On the exact and numerical solutions to a new (2 + 1)-dimensional Korteweg-de Vries equation with conformable derivative
  6. On free vibration of laminated skew sandwich plates: A finite element analysis
  7. Numerical simulations of stochastic conformable space–time fractional Korteweg-de Vries and Benjamin–Bona–Mahony equations
  8. Dynamical aspects of smoking model with cravings to smoke
  9. Analysis of the ROA of an anaerobic digestion process via data-driven Koopman operator
  10. Lie symmetry analysis, optimal system, and new exact solutions of a (3 + 1) dimensional nonlinear evolution equation
  11. Extraction of optical solitons in birefringent fibers for Biswas-Arshed equation via extended trial equation method
  12. Numerical study of radiative non-Darcy nanofluid flow over a stretching sheet with a convective Nield conditions and energy activation
  13. A fractional study of generalized Oldroyd-B fluid with ramped conditions via local & non-local kernels
  14. Analytical and numerical treatment to the (2+1)-dimensional Date-Jimbo-Kashiwara-Miwa equation
  15. Gyrotactic microorganism and bio-convection during flow of Prandtl-Eyring nanomaterial
  16. Insight into the significance of ramped wall temperature and ramped surface concentration: The case of Casson fluid flow on an inclined Riga plate with heat absorption and chemical reaction
  17. Dynamical behavior of fractionalized simply supported beam: An application of fractional operators to Bernoulli-Euler theory
  18. Mechanical performance of aerated concrete and its bonding performance with glass fiber grille
  19. Impact of temperature dependent viscosity and thermal conductivity on MHD blood flow through a stretching surface with ohmic effect and chemical reaction
  20. Computational and traveling wave analysis of Tzitzéica and Dodd-Bullough-Mikhailov equations: An exact and analytical study
  21. Combination of Laplace transform and residual power series techniques to solve autonomous n-dimensional fractional nonlinear systems
  22. Investigating the effects of sudden column removal in steel structures
  23. Investigation of thermo-elastic characteristics in functionally graded rotating disk using finite element method
  24. New Aspects of Bloch Model Associated with Fractal Fractional Derivatives
  25. Magnetized couple stress fluid flow past a vertical cylinder under thermal radiation and viscous dissipation effects
  26. New Soliton Solutions for the Higher-Dimensional Non-Local Ito Equation
  27. Role of shallow water waves generated by modified Camassa-Holm equation: A comparative analysis for traveling wave solutions
  28. Study on vibration monitoring and anti-vibration of overhead transmission line
  29. Vibration signal diagnosis and analysis of rotating machine by utilizing cloud computing
  30. Hybrid of differential quadrature and sub-gradients methods for solving the system of Eikonal equations
  31. Developing a model to determine the number of vehicles lane changing on freeways by Brownian motion method
  32. Finite element method for stress and strain analysis of FGM hollow cylinder under effect of temperature profiles and inhomogeneity parameter
  33. Novel solitons solutions of two different nonlinear PDEs appear in engineering and physics
  34. Optimum research on the temperature of the ship stern-shaft mechanical seal end faces based on finite element coupled analysis
  35. Numerical and experimental analysis of the cavitation and study of flow characteristics in ball valve
  36. Role of distinct buffers for maintaining urban-fringes and controlling urbanization: A case study through ANOVA and SPSS
  37. Significance of magnetic field and chemical reaction on the natural convective flow of hybrid nanofluid by a sphere with viscous dissipation: A statistical approach
  38. Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications
  39. Research on vibration monitoring and fault diagnosis of rotating machinery based on internet of things technology
  40. An improved image processing algorithm for automatic defect inspection in TFT-LCD TCON
  41. Research on speed sensor fusion of urban rail transit train speed ranging based on deep learning
  42. A Generalized ML-Hyers-Ulam Stability of Quadratic Fractional Integral Equation
  43. Study on vibration and noise influence for optimization of garden mower
  44. Relay vibration protection simulation experimental platform based on signal reconstruction of MATLAB software
  45. Research on online calibration of lidar and camera for intelligent connected vehicles based on depth-edge matching
  46. Study on fault identification of mechanical dynamic nonlinear transmission system
  47. Research on logistics management layout optimization and real-time application based on nonlinear programming
  48. Complex circuit simulation and nonlinear characteristics analysis of GaN power switching device
  49. Seismic nonlinear vibration control algorithm for high-rise buildings
  50. Parameter simulation of multidimensional urban landscape design based on nonlinear theory
  51. Research on frequency parameter detection of frequency shifted track circuit based on nonlinear algorithm
https://doi.org/10.1515/nleng-2021-0049
Keywords for this article
Landscape design; parameter simulation; nonlinear theory
Creative Commons
BY 4.0

Articles in the same Issue

  1. Nonlinear absolute sea-level patterns in the long-term-trend tide gauges of the East Coast of North America
  2. Insight into the significance of Joule dissipation, thermal jump and partial slip: Dynamics of unsteady ethelene glycol conveying graphene nanoparticles through porous medium
  3. Numerical results for influence the flow of MHD nanofluids on heat and mass transfer past a stretched surface
  4. A novel approach on micropolar fluid flow in a porous channel with high mass transfer via wavelet frames
  5. On the exact and numerical solutions to a new (2 + 1)-dimensional Korteweg-de Vries equation with conformable derivative
  6. On free vibration of laminated skew sandwich plates: A finite element analysis
  7. Numerical simulations of stochastic conformable space–time fractional Korteweg-de Vries and Benjamin–Bona–Mahony equations
  8. Dynamical aspects of smoking model with cravings to smoke
  9. Analysis of the ROA of an anaerobic digestion process via data-driven Koopman operator
  10. Lie symmetry analysis, optimal system, and new exact solutions of a (3 + 1) dimensional nonlinear evolution equation
  11. Extraction of optical solitons in birefringent fibers for Biswas-Arshed equation via extended trial equation method
  12. Numerical study of radiative non-Darcy nanofluid flow over a stretching sheet with a convective Nield conditions and energy activation
  13. A fractional study of generalized Oldroyd-B fluid with ramped conditions via local & non-local kernels
  14. Analytical and numerical treatment to the (2+1)-dimensional Date-Jimbo-Kashiwara-Miwa equation
  15. Gyrotactic microorganism and bio-convection during flow of Prandtl-Eyring nanomaterial
  16. Insight into the significance of ramped wall temperature and ramped surface concentration: The case of Casson fluid flow on an inclined Riga plate with heat absorption and chemical reaction
  17. Dynamical behavior of fractionalized simply supported beam: An application of fractional operators to Bernoulli-Euler theory
  18. Mechanical performance of aerated concrete and its bonding performance with glass fiber grille
  19. Impact of temperature dependent viscosity and thermal conductivity on MHD blood flow through a stretching surface with ohmic effect and chemical reaction
  20. Computational and traveling wave analysis of Tzitzéica and Dodd-Bullough-Mikhailov equations: An exact and analytical study
  21. Combination of Laplace transform and residual power series techniques to solve autonomous n-dimensional fractional nonlinear systems
  22. Investigating the effects of sudden column removal in steel structures
  23. Investigation of thermo-elastic characteristics in functionally graded rotating disk using finite element method
  24. New Aspects of Bloch Model Associated with Fractal Fractional Derivatives
  25. Magnetized couple stress fluid flow past a vertical cylinder under thermal radiation and viscous dissipation effects
  26. New Soliton Solutions for the Higher-Dimensional Non-Local Ito Equation
  27. Role of shallow water waves generated by modified Camassa-Holm equation: A comparative analysis for traveling wave solutions
  28. Study on vibration monitoring and anti-vibration of overhead transmission line
  29. Vibration signal diagnosis and analysis of rotating machine by utilizing cloud computing
  30. Hybrid of differential quadrature and sub-gradients methods for solving the system of Eikonal equations
  31. Developing a model to determine the number of vehicles lane changing on freeways by Brownian motion method
  32. Finite element method for stress and strain analysis of FGM hollow cylinder under effect of temperature profiles and inhomogeneity parameter
  33. Novel solitons solutions of two different nonlinear PDEs appear in engineering and physics
  34. Optimum research on the temperature of the ship stern-shaft mechanical seal end faces based on finite element coupled analysis
  35. Numerical and experimental analysis of the cavitation and study of flow characteristics in ball valve
  36. Role of distinct buffers for maintaining urban-fringes and controlling urbanization: A case study through ANOVA and SPSS
  37. Significance of magnetic field and chemical reaction on the natural convective flow of hybrid nanofluid by a sphere with viscous dissipation: A statistical approach
  38. Special Issue: Recent trends and emergence of technology in nonlinear engineering and its applications
  39. Research on vibration monitoring and fault diagnosis of rotating machinery based on internet of things technology
  40. An improved image processing algorithm for automatic defect inspection in TFT-LCD TCON
  41. Research on speed sensor fusion of urban rail transit train speed ranging based on deep learning
  42. A Generalized ML-Hyers-Ulam Stability of Quadratic Fractional Integral Equation
  43. Study on vibration and noise influence for optimization of garden mower
  44. Relay vibration protection simulation experimental platform based on signal reconstruction of MATLAB software
  45. Research on online calibration of lidar and camera for intelligent connected vehicles based on depth-edge matching
  46. Study on fault identification of mechanical dynamic nonlinear transmission system
  47. Research on logistics management layout optimization and real-time application based on nonlinear programming
  48. Complex circuit simulation and nonlinear characteristics analysis of GaN power switching device
  49. Seismic nonlinear vibration control algorithm for high-rise buildings
  50. Parameter simulation of multidimensional urban landscape design based on nonlinear theory
  51. Research on frequency parameter detection of frequency shifted track circuit based on nonlinear algorithm
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 5.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/nleng-2021-0049/html
Scroll to top button