Free-electron coupling to surface polaritons mediated by small scatterers

2.1 Electron field near a planar surface

Working in frequency space ω, the electric field directly created by the electron as it moves in free space can be written as [77]

where k ‖ = ( ω / v ) x ̂ + k y y ̂ is the in-plane wave vector, κ = ( ω / v γ ) 2 + k y 2 describes an evanescent decay away from z = b, and γ = 1 / 1 − v 2 / c 2 . This equation shows that the electron field is composed of components satisfying the condition k _‖ ≤ ω/v, corroborating that modes above the electron line in Figure 1(b) cannot be directly excited by the electron.

The presence of the planar surface at z = −z ₀ produces a reflected field that can be conveniently expressed in terms of Fresnel’s reflection coefficients r k ‖ p and r k ‖ s for p and s polarization, respectively. To do so, we note that the integrand in Eq. (1) is orthogonal to the wave vector k ‖ + i sign { z − b } κ z ̂ (i.e., the field is transverse), so it can be projected on p- and s-polarization components represented by the unit vectors e ̂ k ‖ p ± = ( 1 / k k ‖ ) ( ± k z k ‖ − k ‖ 2 z ̂ ) (with k = ω/c and k z = k 2 − k ‖ 2 + i 0 + ; here, we take square roots yielding positive real parts, while the infinitesimally small imaginary part is inherited from the adoption of the retarded response formalism to guarantee that Im{k _z } > 0) and e ̂ k ‖ s ± = ( 1 / k ‖ ) ( − k y x ̂ + k x y ̂ ) , respectively, which we eventually evaluate at k _x = ω/v and k _z = iκ. In these expressions, upper (lower) signs correspond to waves propagating upward (downward). The direct electron field is then expressed in the form

for z < b (i.e., it consists of downward waves emanating from the e-beam). By applying the reflection coefficients to each wave vector and polarization component, the reflected field in the z > − z ₀ region above the surface is found to be

The total field generated by the electron in the presence of the surface then becomes E e ( r , ω ) = E e dir ( r , ω ) + E e ref ( r , ω ) . Here, we assume b > 0 (i.e., the electron moves above the scatterer). An extension to b < 0 (electron moving in the region separating the surface from the scatterer) is straightforward but should not add qualitatively different results.

2.2 Self-consistent particle-near-surface response

The field generated by the electron polarizes the dipolar particle placed at the origin, which displays a dipole moment

in the frequency domain. Here, E ( 0 , ω ) = E e ( 0 , ω ) + E dip ref ( 0 , ω ) is the total field acting on the particle, which consists of the electron field and the reflection of the dipole field by the surface E dip ref ( 0 , ω ) .

We follow a similar procedure as with the electron field to express E dip ref ( 0 , ω ) in terms of p- and s-polarization components, starting from the direct dipole field [77] E dip dir ( r , ω ) = [ k 2 p ( ω ) + p ( ω ) ⋅ ∇ ∇ ] e i k r / r and projecting it on in-plane wave-vector and polarization components to yield [40]

where s = sign{z}. The surface-reflected field is then obtained by introducing the reflection coefficients as

Finally, setting r = 0 (the dipole position) and carrying out the azimuthal integral in k _‖, we find

in terms of a Green tensor G ( ω ) = G ‖ ( ω ) R ̂ ⊗ R ̂ + G ⊥ ( ω ) z ̂ ⊗ z ̂ with in- and out-of-plane components given by

Combining this result with Eq. (3), we can write the self-consistently induced dipole as

where

is an effective polarizability that takes into account the effect of the surface, so only the electron field is now required to evaluate the induced dipole [cf. Eqs. (3) and (6a)]. Incidentally, the fraction in Eq. (6b) must be understood as the inverse of the 3 × 3 tensor in the denominator.

2.3 The limit of strongly confined surface polaritons

We are interested in generating SPs of small wavelength λ _p compared with the light wavelength λ ₀ = 2πc/ω. In this limit, we can neglect the contribution of s-polarization components to the surface response (i.e., r k ‖ s → 0 ) and approximate k _z ≈ ik _‖ in the dipolar self-interaction (because k _‖ ≫ ω/c), so the Green tensor reduces to

For simplicity, we take the e-beam to intersect the surface normal at the particle position. Again, we neglect s-polarization components in the surface-reflected electron field, but retain the relativistic γ factors, so that our results remain valid at high electron velocities, even though the response of the particle–surface system is treated electrostatically. Then, evaluating Eq. (2b) at the particle position (r = 0), we find

For the direct electron field, we can analytically integrate Eq. (1), which yields [41]

where K _m are modified Bessel functions.

The λ _p ≪ λ ₀ condition is generally satisfied if the surface consists of a thin film, which, neglecting nonlocal and retardation effects, can be described through a frequency-dependent 2D surface conductivity σ(ω) and treated as a zero-thickness layer. When the film is deposited on a substrate of real permittivity ϵ, the Fresnel reflection coefficient for p polarization from the vacuum side reduces to [78]

where R p = 1 / ϵ ̄ with ϵ ̄ = ( ϵ + 1 ) / 2 , while k p = i ω ϵ ̄ / 2 π σ ( ω ) is the complex polariton wave vector identified as a pole in r k ‖ p [30], [79], whose existence requires fulfilling the condition Im{σ} > 0. The SP wavelength is then defined as λ _p = 2π/Re{k _p}.

We consider long-lived polaritons characterized by low inelastic losses (i.e., Re{σ}≪|σ|) such as, for example, SPPs in high-quality doped graphene [30], [80], [81], whose surface conductivity can be approximated as

in the Drude model, where ω _D = E _F/πℏ is a frequency weight proportional to the doping Fermi energy E _F and we introduce a phenomenological inelastic damping rate γ. This type of response is also found in thin noble metal films, where ω D = ℏ ω bulk 2 d / 4 π e 2 depends on the bulk plasma energy ℏω _bulk (e.g., 9.17 eV in silver [82]) and the film thickness d [5]. Assuming the surface conductivity in Eq. (10), the SPP dispersion relation obtained from the k _‖ = k _p pole in Eq. (9) is universally given by k ‖ = ( ϵ ̄ ℏ / 2 π e 2 ω D ) ω ( ω + i γ ) and exhibits a characteristic ω ∝ k ‖ scaling, as shown in Figure 1(b).

Using the reflection coefficient in Eq. (9), the k _‖ integral in Eq. (7) can be performed analytically, leading to

with θ = 2k _p z ₀ and Ei denoting the exponential integral function (see Eqs. 3.353–5 of Ref. [83]). The ω dependence of the Green tensor is then encapsulated in k _p. In the low-loss limit (γ ≪ ω), we can approximate

with k _p = 2π/λ _p taken as a real number. Inserting this expression into Eq. (7), we find

We use this result in what follows.

In the low-loss limit, noticing that the polariton pole dominates the surface response, we can also obtain an analytical expression for the surface-reflected electron field by calculating the residue due to the k _‖ = k _p pole of r k ‖ p in Eq. (8a). To this end, we multiply and divide the R p term in the integrand by k _‖ − k _p, close the integration contour in the complex k _y plane, and ignore the contributions of branching points and any other poles in the integrand. The field contributed by the first term in the right-hand side of Eq. (9) takes the same form as the direct field in Eq. (8b), but with b replaced by b + 2z ₀ and the sign of the x component flipped. In this polariton-pole approximation (PPA), inserting the result in Eq. (6a) together with the direct field from Eq. (8b), the electron field in the absence of the particle reduces to

where μ = k _p v/ω and ν = μ 2 − v 2 / c 2 . The first, second, and third terms inside each of the curly brackets in Eq. (13) origine from the direct electron field [Eq. (8b)], the surface-reflected field contributed by the unity term in r k ‖ p , and the result of the remaining part of r k ‖ p , respectively.

2.4 Polariton excitation probability

Under the conditions of Figure 1(a) and (b), assuming that the electron line ω = k _‖ v lies below the mode dispersion curve, direct SP excitation by the electron is kinematically forbidden, so SPs are exclusively excited via the induced particle dipole [Eq. (6a)]. We now calculate the number of the so-emitted surface quanta. To this end, we first consider a dipole p(t) placed in free space. By integrating the radial Poynting vector over both time and the surface of a large sphere centered at the dipole, we find a total emitted energy ( 2 / 3 π c 3 ) ∫ 0 ∞ ω 4 d ω | p ( ω ) | 2 . We then divide each frequency component by ℏω to obtain the total number of emitted quanta ∫ 0 ∞ d ω Γ 0 ( ω ) , where Γ₀(ω) = (2ω ³/3πℏc ³)|p(ω)|² gives the spectral decomposition of the emission probability. This result differs by a factor of 1/2π from the decay rate of a transition dipole in free space [84].

For clarity, we note that the time-domain induced dipole is obtained from Eq. (6a) by performing the Fourier transform p(t) = (2π)⁻¹ ∫dω e^−iωt p(ω). Now, following the same analysis as in Ref. [84], we find that the presence of a material structure changes the spectral probability to Γ(ω) = Γ₀(ω) + (1/πℏ) Im{p*(ω) ⋅E ^ind}, where E ^ind is the self-induced electric field at the dipole position. In particular, near a planar surface, this field is given by E dip surf ( 0 , ω ) in Eq. (5), and consequently, Γ ( ω ) = Γ 0 ( ω ) + ( 1 / π ℏ ) I m | p ‖ ( ω ) | 2 G ‖ ( ω ) + | p z ( ω ) | 2 G ⊥ ( ω ) . Adopting again the electrostatic limit [Eq. (7)], this leads to

for the spectrally resolved probability of emitting SPs, where I m { G ‖ ( ω ) } is proportional to R p , indicating that Γ_SP(ω) is only contributed by SP emission within the geometry and approximations under consideration. Incidentally, this result coincides with the integral of the absorption density within the 2D film (see Section 5.3 in Methods).

We aim to maximize the probability of exciting surface modes, which is enhanced when α ^eff(ω) increases [see Eq. (6a)], and therefore, optimum emission should occur if the scatterer is lossless (i.e., composed of nonabsorbing materials, such that Im{−1/α _s (ω)} = 2k ³/3 for each of the polarization directions s = ‖, ⊥) and resonant (i.e., Re { 1 / α s ( ω ) − G s ( ω ) } = 0 , a condition that can be generally fulfilled at specific resonance frequencies [40]). Combining these two conditions, we have

for the effective polarizability of a perfect scatterer.

To illustrate the magnitude of Γ_SP(ω) in Eq. (14) and its dependence on geometrical parameters, we find it convenient to normalize it to the EELS probability produced by a free-standing particle (without the surface) [85] Γ EELS ( ω ) = ( 4 e 2 ω 2 / π ℏ v 4 γ 2 ) ( 1 / γ 2 ) K 0 2 ω b / v γ Im { α ‖ } + K 1 2 ω b / v γ Im { α ⊥ } , which we evaluate for a perfect scatterer by setting α(ω) = 3i/2k ³:

The resulting ratio Γ_SP(ω)/Γ_EELS(ω) is presented in Figure 1(c) as a function of frequency and particle–surface separation z ₀ for a fixed impact parameter b, assuming a lossless resonant particle [Eq. (15)] and a 2D Drude material described by the conductivity of Eq. (10).

Despite the indirect mechanism for SP generation, the probability plotted in Figure 1(c) takes sizeable values about one order of magnitude lower than the maximum possible EELS probability for a dipolar scatterer. This figure also reveals the presence of a maximum in the emission probability Γ_SP(ω) for an optimum value of z ₀. The latter depends on SP frequency and lies in the z ₀ < λ _p range [Figure 1(c), yellow line]. As a function of SP frequency, this maximum remains nearly constant over the explored frequency range [Figure 1(d)] for the particular choice of the chosen parameters. We note that Figure 1(b) and (d) is calculated analytically using Eqs. (6a), (12), (14), and (15) combined with the PPA expression for the electron field in Eq. (13), but almost identical results are obtained when the latter is computed without approximations from the sum of Eqs. (8a) and (8b) (Supplementary Materials, Figure S1).

Upon inspection of the analytical expressions in Eqs. (12) and (13), we find that I m { G ( ω ) } and the PPA electron field E _e(0, ω) depend on ω and z ₀ only through the ratios ω/ω _D and z ₀/λ _p, and consequently, the PPA approach yields universal results for a lossless resonant scatterer and a thin film described through a low-loss Drude conductivity [Eq. (10)]. The SP emission probability is also dependent on damping and impact parameter through γ/ω _D and b/λ _p. To corroborate this result, we show that the emission probabilities obtained for graphene and a thin silver film (also described in the Drude model as explained in Section 5.1; see Methods) yield nearly identical results as a function of ω/ω _D and z ₀/λ _p (Supplementary Materials, Figure S2).

2.5 Excitation of graphene plasmons assisted by a hBN disk

So far, we have considered lossless, resonant scatterers to mediate the excitation of SPPs in Drude-like films. We now show that similar results are obtained when these ideal conditions are relaxed and we consider resonant hBN particles to excite mid-infrared plasmons in graphene. These particles have low losses, although still much higher than those associated with radiative emission in free space (see Supplementary Materials, Figure S4). However, losses arising from SP emission when the particles are placed close to the surface become dominant at short separations, so the small intrinsic damping due to material losses in the particle does not play a major effect.

We then consider a feasible configuration in which a hBN disk (thickness d and diameter D ≫ d) acts as a relatively lossless scatterer that couples to SPs in a graphene film. To make the system more realistic, we assume the graphene film to be supported on a dielectric substrate (permittivity ϵ) and coated by a dielectric film of thickness z ₀ (same material). The hBN disk is taken to be directly deposited on the surface of the coating layer, with vacuum above it [Figure 2(a)]. Again, we assume that all the involved distances are small compared with the light wavelength, so the system can be described in the electrostatic limit. In addition, the thickness of the hBN disk is assumed to be small compared with the polariton wavelength, and consequently, it can be represented by a surface conductivity (see Section 5.1 in Methods).

Figure 2:

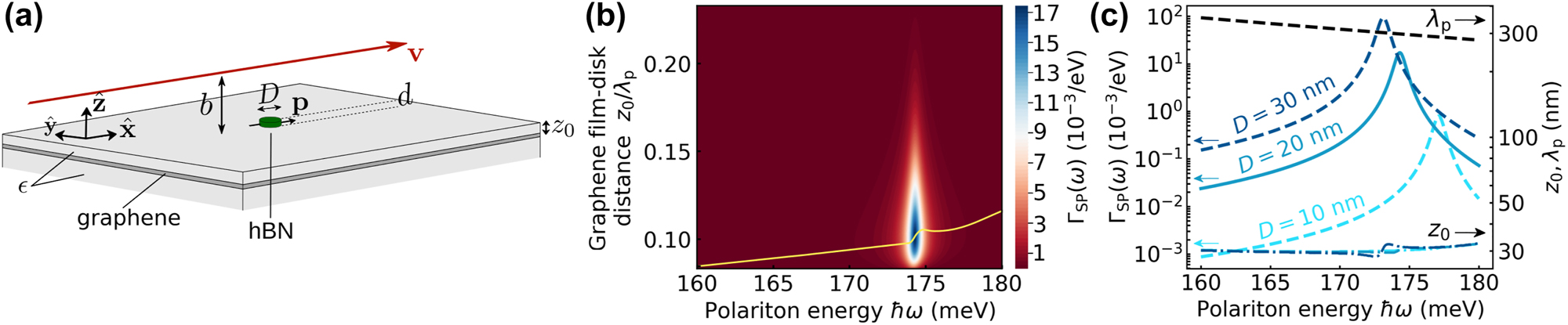
Free-electron excitation of graphene plasmons mediated by a hBN disk scatterer. (a) Geometry under consideration, comprising a graphene film and an hBN disk of diameter D and thickness d. The disk is directly deposited on the top dielectric layer of thickness z ₀. The electron passes at a distance b above the disk. The dielectric substrate and coating layer have a permittivity ϵ. (b) Spectrally resolved probability of graphene-plasmon emission Γ_SP(ω) under the conditions of (a) as a function of plasmon energy ℏω and coating-layer thickness z ₀ for D = 20 nm, d = 1 nm, ϵ = 2, b = 10 nm, and v = 0.04 c. We set the graphene Fermi energy to E _F = 1 eV. (c) Maximum Γ_SP(ω) (left vertical scale, solid curve) and optimum coating thickness z ₀ along with the SP wavelength λ _p (right scale) as a function of emission frequency under the conditions of (b). In (c), we also show results for the maximum Γ_SP(ω) with D = 10 nm and 30 nm (see labels).

The effective disk polarizability cannot be calculated by following the approach used above for a self-standing scatterer because the Green tensor diverges as the disk-surface separation is reduced. Instead, we use an analytical expression for the polarizability of a disk deposited on a homogeneous substrate obtained from an electrostatic modal expansion [86], and then introduce the effect of the graphene layer through an ad hoc Green tensor, as shown in Methods (Section 5.2). In addition, the surface reflection coefficient needs to be modified to account for the new layered structure. A Fabry–Perot-type of analysis readily leads to

where r ₀ = (ϵ − 1)/(ϵ + 1) and r k ‖ p ′ = k ‖ / ( k ‖ − k p ′ ) with k p ′ = i ω ϵ / 2 π σ ( ω ) are the reflection coefficients of the homogeneous ϵ surface and the ϵ-embedded graphene layer [78], respectively.

Finally, the SP emission probability differs for the geometry in Figure 2(a) relative to Figure 1(a). A calculation based on the absorption density within the graphene film yields the result (see Section 5.3 in Methods)

similar to Eq. (14) but with p _z = 0 (i.e., the induced disk dipole is parallel to the surface) and a modified Green tensor

which reduces to Eq. (7) when setting ϵ = 1.

We now use Eq. (18) combined with Eq. (19) to calculate the surface-polariton emission probability in the configuration of Figure 2(a). Here, the induced dipole p x ( ω ) = α ‖ eff ( ω ) E e , x ( 0 , ω ) is obtained by using the modified polarizability in Eqs. (25) (see Section 5.2 in Methods) together with the electron field given by the sum of Eqs. (8a) and (8b). In particular, Eq. (8a) is evaluated by inserting the multilayer reflection coefficient given in Eq. (17) with z ₀ = 0 because the electron moves at a distance b from the outer surface on which the direct electron field is reflected.

In Figure 2(b), we plot the resulting probability Γ_SP(ω) as a function of disk–2D-layer spacer z ₀ and frequency around the upper hBN Reststrahlen band for a disk thickness d = 1 nm (corresponding to 3 monolayers) and diameter D = 20 nm ≫ d. This choice for the disk diameter is motivated to enable a dipolar resonance within that band and boost the polarizability. In agreement with Figure 1, coupling to graphene plasmons is also maximized for an optimum frequency-dependent value of z ₀/λ _p. However, we now observe a strong dependence of Γ_SP(ω) on mode frequency, with a sharp increase at a specific spectral position that is controlled by the intrinsic diameter-dependent resonance of the disk [see Figure 2(b) for D = 20 nm and Figure 2(c) for D = 10, 10, and 30 nm; see also Supplementary Materials, Figure S3(a) for the disk resonance frequency]. This feature demonstrates that the coupling scheme here considered allows us to select the excitation frequency of narrowband plasmons in a region where they would otherwise be inaccessible via direct electron excitation. Interestingly, the optimum z ₀/λ _p ratio takes smaller values than in Figure 1, presumably as a result of the weak scattering strength of the hBN disk compared to a perfect scatterer (see Supplementary Materials, Figure S4). This hypothesis is consistent with the observation that the maximum Γ_SP(ω) and the optimum z ₀ are both increasing with disk diameter [see the probability curves for D = 10, 20, and 30 nm in Figure 2(c)].

3.1 Electron interaction with a linear array of scatterers

To analyze polaritonic Smith–Purcell emission, we assume again low inelastic losses, so that SPs can propagate far from the interaction region, where the direct and surface-reflected electron fields are negligible at frequencies below the crossing of the electron line and the mode dispersion [see Figure 1(b)]. In those far surface regions, the polariton field is dominated by the contribution of the k _‖ = k _p pole in r k ‖ p [Eq. (9)] to E dip ref ( r , ω ) [Eq. (4b)]. In the electrostatic limit, this contribution to the field reduces to E dip ref ( r , ω ) = − ∇ ϕ dip ref ( r , ω ) , written in terms of the associated scalar potential

with

for an individual dipole placed at the origin.

We now consider an infinite linear array of period a formed by dipolar scatterers at positions R j = j a x ̂ , indexed by an integer number j. Because of periodicity, the external electron potential at a generic scatterer j ≠ 0 differs from the potential at scatterer j = 0 by just a phase factor e^i(ω/v)aj [see Eq. (1)], and this dependence is directly imprinted on the self-consistent dipole fields. Therefore, the potential produced by all dipoles in the array can be written as ϕ array ref ( r , ω ) = ∑ j = − ∞ ∞ e i ( ω / v ) a j ϕ dip ref ( r − R j , ω ) in terms of the potential of one dipole at j = 0 [Eq. (21)]. We can perform the j sum by using the identity ∑ j = − ∞ ∞ e i ( ω / v − k x ) a j = ( 2 π / a ) ∑ n = − ∞ ∞ δ ( k x − k n x ) , where k _nx = ω/v + 2πn/a with n running over diffraction orders. The δ-functions in this expression allow us to readily carry out the k _x integral and find the result

with k n ‖ = k n x x ̂ + k y y ̂ .

At large transverse distances |y| from the array, we expect the potential to be dominated by SP components emanating from the k _‖ = k _p pole in Eq. (9). Using the same PPA procedure that allowed us to perform the k _y integral in Eq. (8a) and obtain Eq. (13), we transform Eq. (22) into

with k y → k n y = k p 2 − k n x 2 . The far in-plane field is then found to be made of different diffracted SP plane waves labeled by n. The associated wave vectors k _n‖ form angles θ _n with the x axis (i.e., the e-beam) determined by cos θ _n = k _nx /k _p. This condition can directly be recast into Eq. (20) by neglecting the imaginary part of the SP wave vector and writing k _p = 2π/λ _p.

Periodicity also allows us to write the induced dipoles as p(ω) e^i(ω/v)aj , where the dependence on the position of each particle j reduces to a phase factor. In the absence of interaction among particles, p(ω) would be given by Eqs. (6a) and (6b). However, particle–particle interaction may become relevant for strong scatterers and small separations, so we include it in our calculations by defining the effective polarizability of each particle in the array as in Eq. (6b) but with the Green tensor supplemented by the contribution of the direct and surface-reflected fields produced by the rest of the dipoles. This is calculated in Methods (see Section 5.4), and in what follows, we use Eq. (6b) combined with Eq. (29) to obtain α ^eff(ω) for particles in the array.

To obtain the number of SPs produced by the passage of the electron, we consider the power density transported by a mode characterized by an electrostatic electric field E 0 ( x ̂ + i z ̂ ) e k ‖ ( i x − z − z 0 ) − i ω t + c . c . in the vacuum region outside (z > − z ₀) a polariton-supporting planar surface placed at the z = −z ₀ plane. The power per unit of length along the transverse direction y is given by [39] I p = | ω E 0 2 / 2 π R p k p 2 | , where we assume a reflection coefficient r k ‖ p ≈ R p k p / ( k ‖ − k p ) dominated by a pole at k _‖ = k _p and neglect inelastic losses (i.e., Im{k _p}≪|k _p|, so k _p is treated as a real number). We now substitute E ₀ by the in-plane field amplitude associated with the nth diffracted beam in Eq. (23) [i.e., 2 π | R p k p 2 ( i p x cos θ n + p z ) | / a sin θ n , where we have used the relation k _ny = k _p sin θ _n ], then divide by ℏω to transform energy into number of SP quanta, and finally multiply by the length a sin θ _n (the period projected on the SP wavefront direction). By following this procedure, we obtain the expression

for the number of emitted SPs normalized to the number of scatterers in the array. For a given set of geometrical parameters and frequency, Smith–Purcell emission is only allowed for orders n satisfying the condition −k _p ≤ 2πn/a + ω/v ≤ k _p. In addition, Eq. (24) suggests that the Smith–Purcell emission at a given order n is boosted when polaritons are emitted along the direction of the array (i.e., sin θ _n = 0), as we corroborate below.

We consider an array of perfect scatterers like the one sketched in Figure 3(a) and evaluate Γ_SP,n (ω) using Eq. (24) with p(ω) calculated from Eqs. (6a), (13) and (15). The latter involves s = xx and zz components evaluated from Eq. (29) (notice that the direct lattice sum does not contribute to the imaginary part of the Green tensor). An illustrative result is presented in Figure 3(b) for all allowed emission orders n, normalized to the perfect-scatterer EELS probability [Eq. (16)]. Like in the configuration studied in Figure 1 for an individual scatterer, we find again a maximum emission at an optimum array–surface separation z ₀, which is roughly independent of the order n. In Figure 3(c), we show the dependence of Γ_SP,n for the strongest allowed mode n = −4 as a function of lattice period a and surface–array distance z ₀. We observe singularities in the probability at specific values of a corresponding to the onset of new emission orders n < −1 (see Supplementary Materials, Figure S5). Nevertheless, the optimum value of z ₀ that maximizes the emission is roughly independent of a. Incidentally, n = −4 emission is kinematically forbidden in the white regions in Figure 3(c) and (d). For each emission order n, plasmonic Smith–Purcell emission can thus be finely tuned by playing with the electron velocity, the period, and the array–surface separation.

Interestingly, similar singularities of Γ_SP,−4 as a function of period a and electron velocity v are present in Figure 3(d), corresponding to light-blue contours in the color plot. In particular, contours with a positive slope emerge from the condition θ _n = π (i.e., anti-parallel emission relative to the electron velocity vector) for different orders n = −4, − 5, … (from left to right). The origin of these features is analogous to lattice resonances in particle arrays [87], emerging when the wavelength matches the lattice period, or equivalently, at the onset of every diffraction order. Ultimately, this is the result of the accumulation of in-phase fields emanating from the different particle dipoles in the array [88]. In our system, the array period is small compared with the light wavelength, so free light propagation cannot produce in-phase contributions. However, fields propagating as surface modes can be in phase when the polariton wavelength λ _p is close to the period a. This translates into a divergent-like behavior of the lattice sum in Eq. (28) (see Supplementary Materials, Figure S5 for a plot of this sum), that in turn permeates the induced dipoles and the resulting emission probability in Eq. (24). Likewise, features in Figure 3(d) emerging as negative-slope contours also originate in lattice resonances for forward-propagating polaritons at θ _n = 0 with n = 1, 2, … from left to right.

3.2 Smith–Purcell emission with an array of hBN nanodisks

In Figure 4, we consider a linear array of hBN nanodisks with similar substrate and size parameters as in Figure 2. For simplicity, we assume ϵ = 1 (this condition is nearly met by amorphous silica at the mid-infrared frequencies under consideration), so we can apply the above formalism and calculate the probability from Eq. (24) with p x ( ω ) = α x x eff ( ω ) E e , x ( 0 , ω ) and p _z (ω) = 0. Here, we use Eq. (8) for E _e,x (0, ω) with the reflection coefficient r k ‖ p taken from Eq. (17); we set α x x eff ( ω ) = [ α x x ( ω ) − G x x ( ω ) ] − 1 with α _xx (ω) defined by Eq. (25a); and G x x ( ω ) is computed by numerical integration of Eq. (28) (see Section 5.4 in Methods). We note that ϵ ̄ = R p = 1 because of the choice of ϵ = 1.

Figure 4:

Smith–Purcell emission of surface-plasmon polaritons in grapheme. We consider a geometry similar to Figure 2(a) but with an array of hBN disks instead of just an individual particle and setting ϵ = 1 for simplicity [see inset in (b)]. (a) Emission probability per particle Γ_SP,n (ω) for different orders n and fixed energy ℏω = 174 meV (SP wavelength λ _p = 299 nm) as a function of z ₀. We set the period to a = 2 λ _p = 598 nm, while the rest of the disk and substrate parameters are the same as in Figure 2. Emission angles θ _n for the propagating orders n are indicated in the inset on a top view of the linear array (green circles). (b) Emission probability per particle for orders shown in (a) as a function of period a for z ₀ = 40 nm and v = 0.04 c. The dashed-black line marks the value a = 598 nm used in panel (a). Each order n exhibits a vertical asymptote at a specific value of a, below which is not allowed. (c) Emission probability per particle for n = −4 as a function of a and v/c for z ₀ = 40 nm, with all other parameters the same as in (b). The white region corresponds to conditions for which n = −4 Smith–Purcell emission is kinematically forbidden. The conditions cos θ ₋₄ = −1 and cos θ ₋₄ = 0 are indicated by dashed-blue and dashed-orange curves, respectively.

Figure 4(a) shows the Smith–Purcell emission probability for all allowed orders. Similar to Figure 3, the Smith–Purcell emission probability is maximized at an optimum value of z ₀ that is rather independent of n. This effect can be understood for the disks under consideration because there is no out-of-plane polarization (i.e., p _z = 0), and therefore, the dependences of Eq. (24) on either n or z ₀ can be factorized. Interestingly, the emission is strongest for n = −4 because the chosen lattice period a is close to the onset of this order [see Figure 4(b)], so the emission angle θ ₋₄ = 162° is close to grazing [see inset of Figure 4(a)] and the probability scales as 1/sin θ ₋₄ [see Eq. (24)]. In Figure 4(c), we show the onset of the n = −4 order by a dashed-blue curve corresponding to the condition θ ₋₄ = 180°, which makes Γ_SP,−4 divergent. Conversely, cos θ ₋₄ = 90° and Γ_SP,−4 vanishes along the dashed-orange line [see also Eq. (24)].

5.1 Optical response of the materials under consideration

The optical response of supported graphene is described through its surface conductivity in the Drude model [Eq. (10)], with ω _D = E _F/πℏ depending on the doping Fermi energy E _F. For silver, the permittivity can be well-approximated by a modified Drude model ϵ ( ω ) = ϵ b − ω bulk 2 / ω ( ω + i γ ) with parameters ϵ _b = 4, ℏω _bulk = 9.17 eV, and ℏγ = 21 meV extracted from optical measurements [82], [91]; in our calculations, we set ϵ _b = 1 for simplicity, as this parameter does not influence the results significantly for the plasmon frequencies under consideration. For thin hBN, polarization in the material is dominated by in-plane directions described by the corresponding permittivity component ϵ _hBN(ω), and consequently, we ignore the out-of-plane permittivity and approximate [92] ϵ hBN ( ω ) = ϵ ∞ − f ω 0 2 / ω ( ω + i γ ) − ω 0 2 with parameters ϵ _∞ = 4.90, f = 2.00, ℏω ₀ = 168.6 meV, and ℏγ = 0.87 meV in the upper Reststrahlen band.

An effective surface conductivity σ(ω) = iωd[1 − ϵ(ω)]/4π can be extracted from the material permittivity ϵ(ω) for a film of small thickness d compared with the polariton wavelength. We apply this approach to describe silver and hBN disks by setting ϵ(ω) to the respective permittivities of these materials (see above). For silver, this procedure leads to the Drude conductivity in Eq. (10) with ω D = ℏ ω bulk 2 d / 4 π e 2 .

5.2 Effective polarizability of a thin disk near an embedded 2D layer

In the electrostatic limit, the in-plane polarizability of a thin disk of diameter D supported on a homogeneous substrate of permittivity ϵ can be expressed as [86]

in terms of contributions arising from different polaritonic eigenmodes j, which enter through their associated dipolar matrix elements ζ _j and eigenvalues η _j . Here, ϵ ̄ = ( ϵ + 1 ) / 2 is the average permittivity of the media on both sides of the disk, while η ( ω ) = i σ ( ω ) / ϵ ̄ ω D captures the response of the disk material through its surface conductivity σ(ω). We dismiss the out-of-plane polarizability (i.e., α _⊥ = 0) under the assumption that the disk thickness d is small compared with D. The response is dominated by the lowest-order dipolar mode j = 1, for which one finds the parameters [86] ζ ₁(x) = ae ^bx + c and η ₁(x) = a′e ^{b ′ x} + c′, which depend on the thickness-to-diameter ratio x = d/D and is parametrized with material-independent constants a = −0.01267, b = −45.34, c = 0.8635, a′ = 0.03801, b′ = −8.569, and c′ = −0.1108. For hBN disks, we set the thickness to d = 1 nm (roughly 3 hexagonal atomic monolayers).

The polarizability in Eq. (25a) assumes a thick substrate of permittivity ϵ. However, under the configuration considered in Figures 2 and 4, a 2D material layer [surface conductivity σ(ω)] is placed at a distance z ₀ below the outer surface on which the disk is lying. This layer changes the polarizability to an effective value α ‖ eff ( ω ) given by an expression analogous to Eq. (6b), but with G ‖ ( ω ) reinterpreted as the field that is self-induced by the presence of the 2D layer on a unit parallel dipole placed at the position of the disk [i.e., the effect of the homogeneous substrate of permittivity ϵ is already included in Eq. (25a)]. Considering the p-polarization electrostatic reflection coefficient r k ‖ p ′ = k ‖ / ( k ‖ − k p ′ ) with k p ′ = i ω ϵ / 2 π σ ( ω ) for a 2D layer embedded in an infinite material of permittivity ϵ [78] [cf. this expression and Eq. (9) for a supported 2D layer], as well as r ₀ = (ϵ − 1)/(ϵ + 1) for the substrate alone, we find

with α _‖(ω) given by Eq. (25a) and

Compared to Eq. (7), this expression incorporates an overall factor 4ϵ/(ϵ + 1)² arising from the forward and backward field transmission across the outer planar surface, as well as a denominator accounting for multiple scattering in the cavity defined by the surface and the 2D material. We use Eq. (25b) for the effective polarizability of the disk in Figures 2 and 4.

5.3 2D polariton emission probability by an induced dipole

We can obtain the SP emission probability from the energy absorbed by the 2D material in the configuration of Figure 1(a) under the assumption that the response is dominated by SPs. The energy absorbed by a material of permittivity ϵ _m (ω) occupying a region V and exposed to an optical field E(r, ω) (in the frequency domain) is given by [77] ∫ 0 ∞ d ω ℏ ω Γ ( ω ) , where

For the 2D material, we consider an arbitrarily small thickness d, which yields a high permittivity ϵ _m (ω) = 1 + 4πiσ(ω)/ωd expressed in terms of the surface conductivity σ(ω). The normal electric field inside the material is therefore negligible because of the continuity of the normal displacement, while the parallel field created by the dipole at the surface plane is continuous and given by Eqs. (4a) and (4b) with z = −z ₀. In the electrostatic limit, this field reduces to

Inserting this result into Eq. (26), carrying out the R integral analytically, and reducing the z integral to a factor d, we find

which, upon consideration of Eq. (9) and the dispersion relation k p = i ω ϵ ̄ / 2 π σ ( ω ) for the supported film in Figure 1(a), finally transforms into Eq. (14) with I m { G ‖ ( ω ) } defined by Eq. (7). To obtain this result, we have used the expressions R e { σ ( ω ) } = ( ω ϵ ̄ / 2 π ) I m { − 1 / k p } and k ‖ | r k ‖ p − 1 | 2 = R p I m { r k ‖ p } / I m { − 1 / k p } (with R p = 1 / ϵ ̄ ) derived from the relations between k _p, σ(ω), and r k ‖ p .

For the SP emission probability in the configuration of Figure 2(a), the in-plane field acting on the 2D layer takes a similar form as Eq. (27), but now setting p _z = 0 for the disk, replacing r k ‖ p by the reflection coefficient r k ‖ p ′ of the fully ϵ-embedded 2D film (see Section 5.2), and inserting an additional factor t 0 / 1 + r 0 r k ‖ p ′ e − 2 k ‖ z 0 in the integrand to account for the transmission of the dipole field across the topmost surface [transmission coefficient t 0 = 2 ϵ / ( ϵ + 1 ) ] as well as multiple Fabry–Perot scattering within the surface–2D-film cavity. Then, by following the same steps as above but using the so-modified field, we trivially obtain Eq. (18) with the Green tensor defined in Eq. (19).

5.4 Dipole–dipole interaction in linear arrays

In a linear array, the dipole self-interaction needs to be supplemented by the contribution of the field induced by other dipoles. We thus redefine G ( ω ) = G dir ( ω ) + G ref ( ω ) as the sum of a direct term contributed by all other dipoles in the array plus a surface-reflected term produced by all dipoles. Starting from Eqs. (4a) and (4b) and adopting the electrostatic limit, the modified Green tensor is found to have vanishing off-diagonal components. The direct contribution can easily be evaluated by numerically summing the analytical expression for the free-space dipole–dipole interaction, yielding G x x dir ( ω ) = 2 S dir and G y y dir ( ω ) = G z z dir ( ω ) = − S dir with

For the surface-reflected components, we follow a procedure similar to the derivation of Eq. (22) and write

with k _nx = ω/v + 2πn/a and k n ‖ = k n x 2 + k y 2 . Now, we consider low-loss SPs and a surface reflection coefficient satisfying Eq. (11), which allows us to evaluate the k _y integral and write

for the surface-reflected component of the Green tensor in the array, where R p = 1 / ϵ ̄ and k _p are approximated as real numbers and the n sum is restricted by |k _nx | < k _p (see Supplementary Materials, Figure S5).