Surface plasmon polariton–enhanced upconversion luminescence for biosensing applications

2.1 Theoretical background

In this work, UCNPs were composed of NaYF₄:Yb³⁺, Er³⁺, which exhibit efficient energy transfer upconversion (ETU) [15], [41]. In ETU process, the Yb³⁺ ion acts as an activator, which absorbs 976 nm wavelength. The Er³⁺ ion is the sensitizer, which receives energy from the Yb³⁺ ion and emits upconverting photons. The absorption cross section of an UCNP is [41]

where |E(r ₀)| is the local field amplitude at the location of the UCNP, and |E ₀| is the incident field amplitude. In the emission process, we considered UCNPs as independent emitters with a quantum yield [42]

where η ⁰ is the intrinsic quantum yield of UCNPs, γ ⁰ _rad is the radiative decay rate of UCNPs in free space, and γ ^p _rad and γ ^p _abs are the radiative decay rate and the absorption rate in the presence of the plasmonic structure, respectively. The details are described in Section 1 in the Supplementary Information.

2.2 Computational modeling

Plasmon-enhanced UCL aims to boost either the absorption process or emission process [18]. An increase in the absorption process results in better enhancement in UCL, especially in weak excitation [15]. Therefore, the goal is, here, to optimize the SPP resonance matching with the 976 nm absorption wavelength of UCNPs. SPPs were excited using a gold grating, as illustrated in Figure 1(a). The phase matching condition of SPP coupling on grating is [32]

where n is the refractive index of the medium above the grating surface, ε _Au is the dielectric constant of gold, m is the integer of the diffraction order, θ is the incidence angle, λ is the 976 nm excitation wavelength, and p is the grating period. Since the sample was in dry condition, we assumed n = 1.

Figure 1:

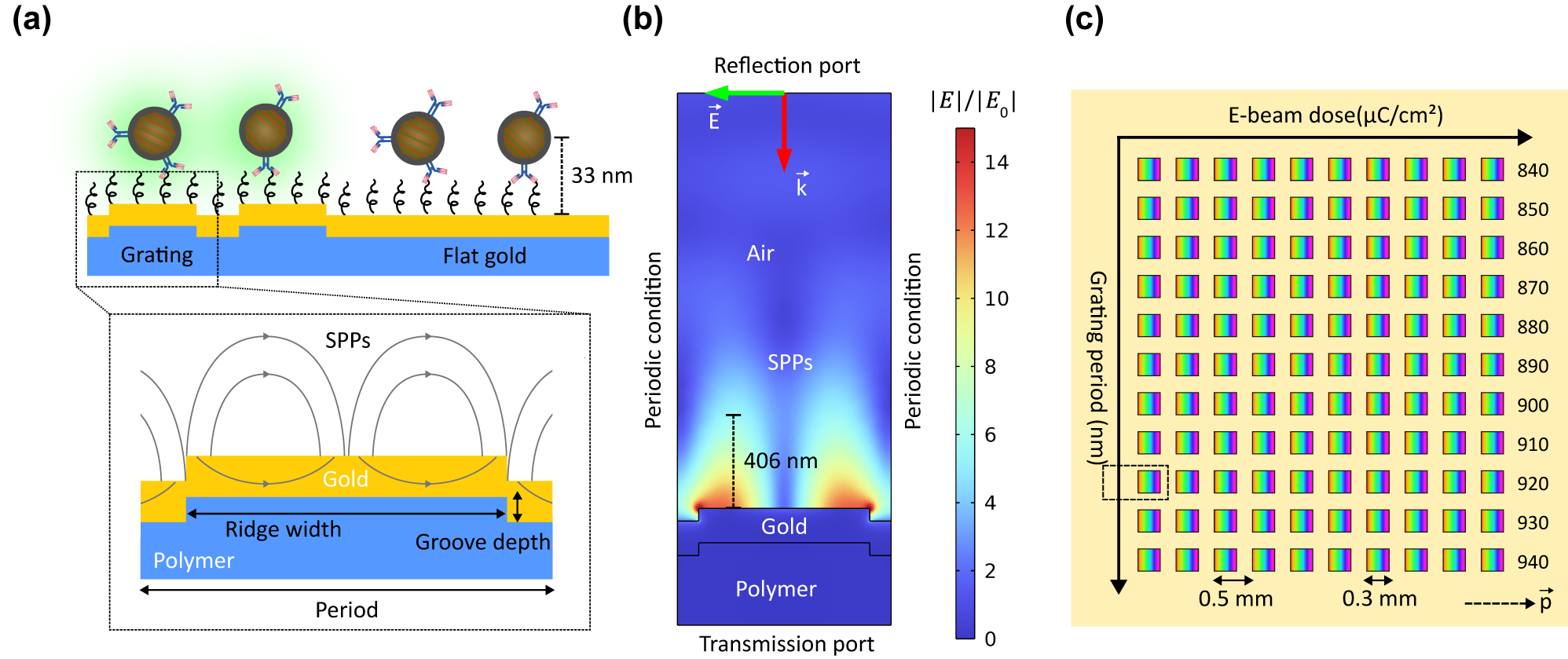
Grating-based SPP-enhanced UCL. (a) Illustration of SPP-enhanced UCL on gold grating in comparison with flat gold. (b) 2D FEM model of a grating unit cell for structural optimization with the normalized field distribution corresponding to the optimal grating. (c) The grating matrix containing 110 square-shaped gratings with an area of 0.3 × 0.3 mm² each and a space of 0.2 mm between them for studying UCL enhancement as a function of the grating period. The yellow area around the gratings is flat gold. The dashed arrow shows the grating vector. The dashed rectangle indicates the scanning area including the optimal grating for enhancement factor calculation.

2.3 Fabrication

The grating matrix was written by using E-beam lithography and subsequently transferred to a silicon master by reactive ions etching. The silicon master was then replicated to a polymeric material by using UV nanoimprinting. Finally, the replicates were coated with a 5 nm chromium layer as an adhesive layer and then a 150 nm gold layer. The details of the fabrication process are described in our previous work [43]. Scanning electron microscope (SEM) images of the silicon master and gold-coated replicates are shown in Figure S2.

2.4 UCNP immobilization

UCNPs were conjugated with antibodies and indirectly immobilized on the surface of the grating matrix using 3,3′-dithiobis (sulfosuccinimidyl propionate) (DTSSP) cross-linking, as illustrated in Figure 1(a). UCNPs (UPCON 540, product no. 43-07, 8.8 mg/ml UCNP, Kaivogen Oy) were conjugated with antibodies (C-reactive protein antibody, Anti-h CRP 6405 SPTN-5, Medix Biochemica) as a custom service by Kaivogen Oy. The core of UCNPs had a diameter of 36 nm and was composed of NaYF₄:Yb³⁺, Er³⁺. UCNPs had a 12 nm hydrophilic shell. C-reactive protein antibody (CRP Ab) was conjugated with the hydrophilic shell to form UCNP-CRP Ab. The emission spectrum of UCNP-CRP Ab is shown in Figure 2.

Figure 2:

Emission spectra of the used UCNP-CRP Abs with and without an emission filter (540 nm–580 nm) in the experimental setup under 976 nm excitation.

The surface of the grating matrix was functionalized with a water-soluble sulfonated form of Lomant’s reagent [44], DTSSP (Sigma-Aldrich, 322133), to add amine-reactive sites on the surface [45]. DTSSP linkers adsorbed onto the surface through the disulfide group [46], and its terminal succinimidyl groups [45] allow covalent attachments of amino-containing biomolecules [45], [47]. UCNP-CRP Abs were attached to the self-assembled DTSSP monolayer by covalent bonds formed between the CRP Ab and the active sulfosuccinimide easter groups of DTSSP. TSA buffer (50 mM Tris-HCl, 0.9 % NaCl, 0.05 % NaN₃, 0.01 % Tween20, 0.5 % BSA & 1 mM KF in dH₂O) was used as washing buffer after the immobilization of UNCP-CRP Ab. To stabilize the UNCP-CRP Ab during long incubations and washes, UCNP stabilizer (50× concentrate, product no. 46-19, Kaivogen Oy) was supplied in the buffer solutions. The detailed protocol is described in Section 5 in the Supplementary Information.

2.5 Experimental setup

The experimental setup is illustrated in Figure 3. The excitation source was a picosecond laser (LDH-D-F-980, PicoQuant) in continuous-wave operation mode with a central wavelength of 976 nm and a spectral bandwidth of 1 nm. For time-resolved measurements, the laser worked at pulsed mode with a spectral bandwidth of 15 nm. A single photon avalanche detector (SPAD) (SPD_VIS_M1, Aurea Technology) was synchronized to the laser by an event timer. A high-speed motorized XY linear stage (MLS203-1, Thorlabs) was used to perform UCL intensity raster scanning. The repeatability and the minimum incremental movement of the stage was 0.25 µm and 0.1 µm, respectively. The excitation beam from the laser was guided by a polarization maintaining single mode fiber (PM980-XP, Thorlabs). The beam was collimated (F810APC-850, Thorlabs) and then filtered by an excitation filter (ET780lp, Chroma Technology) in one side of the filter cube to prevent any side modes of the laser. The collimated beam was reflected by a dichroic mirror (DMSP805R, Thorlabs) and focused on the sample by a 10× objective (N10X-PF-10X, Nikon) to excite UCNPs on the surface of the grating matrix. The diameter of the collimated beam in front of the objective was estimated to be around 7.8 mm. The scattering light and upconversion emissions were collected by the same objective. They were filtered by an emission filter with a band-pass range from 540 nm to 580 nm (ET560/40×, Chroma Technology). The filtered light was coupled by a collimator (F810FC-543, Thorlabs) to a multimode fiber (FG050LGA, Thorlabs) and guided to SPAD.

Figure 3:

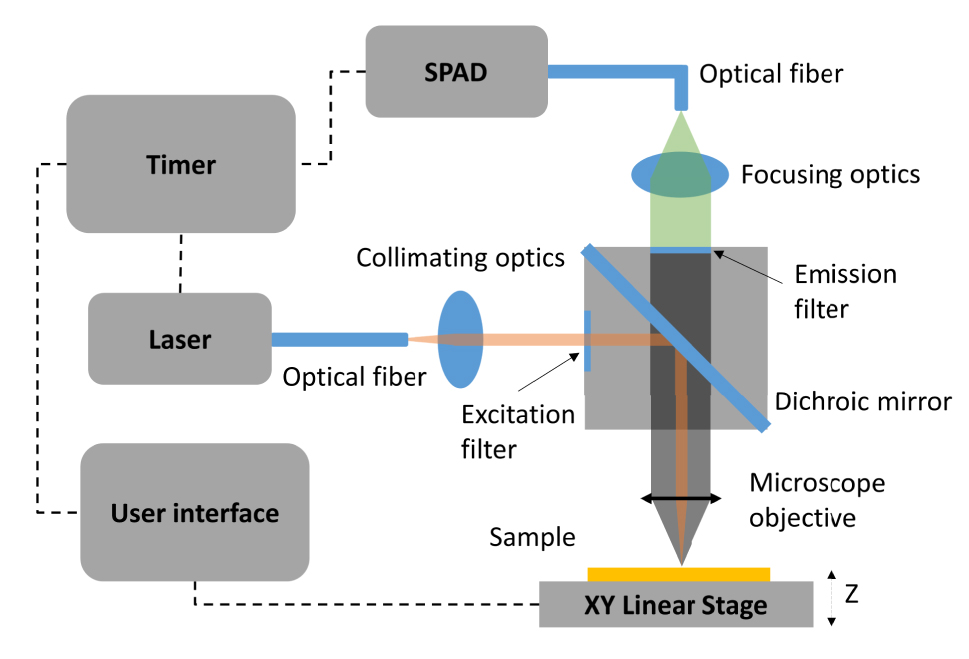
Schematic of the experiment setup for UCL intensity raster scanning using an XY linear stage. The laser operates in continuous-wave mode for scanning UCL measurements and in pulsed mode for time-resolved measurements.

3.1 Absorption enhancement

3.1.1 Surface plasmon polariton excitation

The grating matrix with functionalized UCNPs was characterized with the experimental setup. Figure 4(a) shows the obtained UCL intensity of the matrix under TM illumination. The scanning area was 6 × 6 mm² with an incremental XY linear stage movement of 50 µm. When rotating the grating, the intensity gradually decreased, reaching a minimum at TE configuration. The corresponding TE illumination result in Figure 4(b) was obtained by rotating the matrix with an angle of 90°. In Figure 4, the matrix was clearly visible under TM illumination, while it was invisible with TE polarization. This was expected since SPPs are only excited with TM polarization. The excitation of SPPs on the grating surface led to an increase in the local field at the location of UCNPs. Therefore, the absorption cross section of UCNPs was enhanced, resulting in higher UCL intensity in comparison with the flat gold surrounding the grating matrix or gratings under TE illumination.

Figure 4:

UCL measurement of the grating matrix with (a) TM polarization and (b) TE polarization. The scanning area is 6 × 6 mm² with an incremental XY linear stage movement of 50 µm. The insets illustrate functionalized UCNPs on the surface of the matrix.

3.1.2 Focused Gaussian beam analysis

The UCL intensity depended on the grating period, excitation wavelength, and incidence angle. With the excitation wavelength fixed, the intensity varied with the grating period and the incidence angle. We optimized the grating with a period of 920 nm for the normal-incidence Gaussian beam used in the experimental setup in Figure 3. Tilted Gaussian beams would result in decrease in the intensity. A normal-incidence Gaussian beam is illustrated in Figure 5(a). The maximum incidence angle was limited by the entrance pupil diameter and the effective focal length of the objective. In our setup, the maximum obtainable incidence angle was 16.5°. Gaussian beams with different diameters exhibit varying SPP coupling efficiencies for each period in the grating matrix. To investigate this, we compared UCL intensities computationally and experimentally of two sets of collimators (F810APC-850 and CFP5-980A, Thorlabs), namely, 7.8 mm beam and 1 mm beam.

Figure 5:

Focused Gaussian beam analysis. (a) Illustration of focused Gaussian beam on the grating surface. The maximum obtainable incidence angle is limited by the entrance pupil diameter and the effective focal length of the objective. Normalized power distribution as a function of incidence angle of (b) 7.8 mm beam and (b) 1 mm beam. (d) Computational SPP coupling efficiency as a function of incidence angle of gratings with a groove depth of 55 nm, a duty cycle of 0.8, and a varying period from 840 nm to 940 nm.

In COMSOL Multiphysics, the focused Gaussian beam was modeled by decomposing the beam into plane waves with an incidence angle varying from −16.5° to +16.5° and a sampling step of 0.1°. The normalized power distributions as a function of incidence angle, P(θ), for 7.8 mm and 1 mm beams are shown in Figure 5(b) and (c). The details are described in Section 6 in the Supplementary Information. We modeled the SPP coupling efficiency as a function of incidence angle η(θ), shown in Figure 5(d), for gratings with a groove depth of 55 nm, a duty cycle of 0.8, and a varying period from 840 nm to 940 nm, corresponding to the period of the grating matrix in Figure 1(c). For each period, the computational UCL intensity was

(4) I si ≈ ∑ θ = − 16.5 ◦ + 16.5 ◦ P θ × η θ .

The computational UCL intensity was then normalized with the maximum intensity and plotted in Figure 6(a) and (b). Computationally, we found that when narrowing the beam diameter, the intensity exhibited the highest value at the optimal period of 920 nm and dropped significantly at other periods. This was the result of compressing the excitation power closer to the normal incidence angle as shown in Figure 5(c).

Figure 6:

Effect of focused Gaussian beams on SPP-enhanced UCL. Comparison between simulation and experiment of normalized UCL intensity as a function of grating period when using (a) a 7.8 mm beam and (b) a 1 mm beam. Experimental UCL intensities with beam diameters of (c) 7.8 mm and (d) 1 mm in front of the objective in the experimental setup. The white squares indicate the gratings in the matrix.

Experimentally, we replaced the 7.8 mm beam with the 1 mm beam and measured the UCL intensity of the grating matrix at the same laser power and incremental movement. The measured UCL intensities of the grating matrix caused by the 7.8 mm beam and the 1 mm beam are shown in Figure 6(c) and (d), respectively. It is worth noting that the focal spot diameter was different between the 7.8 mm beam and the 1 mm beam (3.2 µm and 24.9 µm, respectively) at the excitation wavelength of 976 nm. The UCL intensity dropped as the result of the decrease in power density, i.e., 4.35 kW/cm² and 0.07 kW/cm², respectively. As predicted by the simulations, the 920-nm period gratings in the matrix in Figure 6(d) exhibit the highest UCL intensity with the 1 mm beam. To compare with simulation results, the measured UCL intensity was area-averaged for each individual grating in the matrix. For each period, the experimental UCL intensity was

(5) I ex = ∑ k = 1 10 I ̄ k 10 .

The experimental UCL intensity was then normalized with the maximum intensity and plotted in Figure 6(a) and (b). There was a good agreement between the simulation and experiment. We also found that fabrication tolerances led to variations in the measured UCL intensity within the 10 nominally similar gratings, as shown in Figure S3. Another factor contributing to these variations was the nonuniform distribution of UCNPs, which can be observed in Figure 4(b). In the following sections, we used the 1 mm beam to investigate the quenching effect and UCL enhancement.

3.2 Quenching effect in the emission process

In Section 3.1, we found that the increase in the local field, caused by the SPP coupling on the grating surface, led to UCL enhancement. However, the presence of the plasmonic surface can cause also a strong quenching effect in the emission process [19], [24]. Feng et al. and Greybush et al. showed that there was a strong quenching effect when the distance between UCNPs and plasmonic surfaces was below 8 nm [21], [24]. In this work, core–shell UCNPs with a shell thickness of 12 nm were used to minimize the quenching effect. Computationally and experimentally, we investigated the quenching effect on flat gold and grating. Supported by the SEM images of the grating matrix with UCNP immobilization in Figure S4, we made the assumption that, since UCNPs were distributed individually on the surface, only a single UCNP would be present within the focal spot.

In Figure 7(a), we computationally studied the quenching effect when a UCNP was on flat gold or on grating at six cases x ₁, x ₂, x ₃, x ₄, x ₅, and x ₆. Case x ₁ featured a UCNP positioned in the middle of the grating ridge, whereas case x ₆ corresponded to a UCNP placed in the middle of the grating groove. The spacing between two consecutive cases was defined as (0.5 × period)/5. The quantum yield ratio was calculated as a function of the dipole emission angle when the UCNP was either near the gold surface (η _p) or in the free space (η ₀). The quenching effect happened when this ratio was smaller than 1. The dipole emission angle was from −16.5° to +16.5°, corresponding to the collection angle of the used 10× objective with a numerical aperture of 0.3. As shown in Figure 7(b), flat gold caused a slight quenching effect. On grating, the quenching effect depended on the location of the UCNP. When the UCNP was on the ridge (x ₁, x ₂, and x ₃), there was no quenching effect. However, when the UCNP was near or inside the groove (x ₄, x ₅, and x ₆), the groove acted as a light-trapping cavity, causing a strong quenching effect. The curves in cases x ₁ and x ₆ exhibited a symmetry similar to that of flat gold. Cases x ₂, x ₃, x ₄, and x ₅ showed asymmetric curves, depending on the distance between the UCNP and the groove. By taking an average of six cases of the UCNP on grating (solid black line), the quenching effect was similar to flat gold (dashed black line). In Figure 7(c) and (d), we investigate the influence of the grating period on the quenching effect at the locations x ₁ and x ₆, respectively. The quenching variations among the periods were negligible.

Figure 7:

Computational investigation of the quenching effect with a UCNP near a gold surface. (a) Illustration of the location of the UCNP on flat gold or on grating with six cases (x ₁, x ₂, x ₃, x ₄, x ₅, and x ₆). (b) The quenching effect of the UCNP on flat gold and on grating as a function of the dipole emission angle. The quenching effect is evaluated by the quantum yield ratio of the UCNP near the gold surface (η _p) and in free space (η ₀). The dipole emission angle is determined by the collection angle of the used objective. The quenching effect with the UCNP at the locations (c) x ₁ – on the ridge and (d) x ₆ – inside the groove of gratings with a period from 840 nm to 940 nm.

Experimentally, we conducted time-resolved UCL measurements on flat gold and on one of the 920 nm gratings. To improve the signal-to-noise ratio, particularly for the time-resolved UCL measurement on the flat gold, a 100× objective was used. The measurement results are presented in Figure 8. The excitation pulse width was 100 µs. The data were smoothened with the Savitzky–Golay filter in MATLAB and normalized in the range from 0 to 1. To determine the decay rate, the experimental decay data were fitted with exponential curves, as shown in Figure 8. Both the flat gold and the grating exhibited rather similar radiative decay times, which were 138 µs and 125 µs, respectively. Therefore, the quenching effect was comparable between the grating and the flat gold, aligning with the expectations from the computational investigations. Furthermore, this was in agreement with the observation in Figure 4(b). When there was no absorption enhancement under TE illumination, the difference in UCL intensity between the gratings and flat gold was not observable.

Figure 8:

Time-resolved UCL measurements on flat gold and on one of the 920 nm gratings and their corresponding fitted exponential decay curves. The excitation pulse width is 100 µs.

3.3 Upconversion luminescence enhancement

The UCL enhancement was calculated by taking the ratio of the area-averaged UCL intensity between grating and flat gold. We scanned a 0.5 × 1.0 mm² area around a grating, as illustrated in the dashed rectangle in Figure 1(c), using various laser powers. The raster scan was done with an incremental XY linear stage movement of 50 µm. The UCL measurement is shown in the inset in Figure 9(b). We masked the grating and the flat gold with the red squares having an area of 0.2 × 0.2 mm². The masking area was smaller than the grating area (0.3 × 0.3 mm²) to avoid the edge effect. UCL intensities were area-averaged for the grating and the flat gold. The averaged UCL intensities was then subtracted from the SPAD background noise (around 50 photons) and plotted as a function of power density in Figure 9(a). The enhancement factor is shown in Figure 9(b). At low power density, it exceeded 40 and gradually decreased to below 10 as the power density increased. This was consistent with the theory of the UCL enhancement in absorption process [15]. In particular, the enhancement factor is proportional to |E/E ₀|⁴ at low power density and |E/E ₀|² at high power density for the two-photon upconversion process [15]. This enhancement factor is comparable to those reported in the literature. For instance, a 17-fold enhancement has been reported at a power density of 1 kW/cm² [36], compared to our 28-fold enhancement at the same power density. At a very high power density of 100 kW/cm², enhancement factors of 2.4-fold [35] and 4-fold [36] have been reported, while we achieved an 8-fold enhancement at the maximum power density of 10 kW/cm². However, it is worth noting that there was a slight quenching effect when UCNPs were on flat gold and grating, which might affect the enhancement factor. We also evaluated the UCL enhancement using a commercial UCL reader (Labrox Oy, Turku, Finland). The results are discussed in Section 10 in the Supplementary Information.

Figure 9:

Experimental UCL enhancement. (a) Area-averaged UCL intensities on grating and on flat gold as a function of excitation power density. The area-averaged UCL intensities are subtracted with the SPAD background noise (around 50 photons). (b) Enhancement factor as a function of excitation power density. The enhancement factor is the ratio between averaged UCL intensity on grating and on flat gold.