Home Broadband high-efficiency near-infrared graphene phase modulators enabled by metal–nanoribbon integrated hybrid plasmonic waveguides
Article Open Access

Broadband high-efficiency near-infrared graphene phase modulators enabled by metal–nanoribbon integrated hybrid plasmonic waveguides

  • Longfang Ye ORCID logo EMAIL logo , Kouxiang Yuan , Chunhui Zhu , Yao Zhang , Yong Zhang and Kunzhong Lai
Published/Copyright: December 21, 2021
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nanophotonics
From the journal Nanophotonics Volume 11 Issue 3

Abstract

The phase modulator is a key component in optical communications for its phase modulation functions. In this paper, we numerically demonstrate a variety of ultra-compact high-efficiency graphene phase modulators (GPMs) based on metal–nanoribbon integrated hybrid plasmonic waveguides in the near-infrared region. Benefiting from the good in-plane mode polarization matching and strong hybrid surface plasmon polariton and graphene interaction, the 20 μm-length GPM can achieve excellent phase modulation performance with a good phase and amplitude decoupling effect, a low insertion loss around 0.3 dB/μm, a high modulation efficiency with V π L π of 118.67 V μm at 1.55 μm, which is 1–3 orders improvement compared to the state-of-the-art graphene modulators. Furthermore, it has a wide modulation bandwidth of 67.96 GHz, a low energy consumption of 157.49 fJ/bit, and a wide operating wavelength ranging from 1.3 to 1.8 μm. By reducing the overlap width of the graphene–Al2O3–graphene capacitor, the modulation bandwidth and energy consumption of the modulator can be further improved to 370.36 GHz and 30.22 fJ/bit, respectively. These compact and energy-efficient GPMs may hold a key to various high-speed telecommunications, interconnects, and other graphene-based integrated photonics applications.

Keywords: graphene; integrated optics devices; modulators; waveguides

1 Introduction

As one of the crucial components for optical communications [1, 2], sensing [3], and integrated optical interconnections and circuits [4], optical modulators have gained considerable attention in recent years [5]. Taking the advantage of the amplitude or phase modulation schemes of high-efficiency optical modulators, the spectral efficiency and transmission rates for the communication systems can be greatly enhanced. One mainstream route to achieving efficient high-speed modulators is based on silicon photonics (SiPh) using the plasma dispersion effects, which has been commercially implemented in various communication links [6]. However, these all-silicon modulators still suffer from some drawbacks like limited modulation efficiency, optical bandwidth, large footprint, and inherent amplitude and phase modulation coupling [6]. To further enhance the modulation performance, many materials with strong electro-optic (electro-refractive, or electro-absorptive) effects such as germanium, ferroelectrics, III–V semiconductors, organic electro-optic materials, and 2D materials, have been investigated and integrated into the SiPh platform. Especially, the integration of new 2D materials may provide promising routes for high-performance modulators to meet the blistering surge in transmission capacity for optical interconnections and communications.

Graphene, an anatomically thick two-dimensional carbon nanomaterial, has attracted considerable interest because of its excellent electrical and optical properties, high carrier mobility, good thermal conductivity, large optical modulation, high-speed operation, and good SiPh compatibility [7], [8], [9]. This makes it an ideal electro-optic material for efficient amplitude and phase modulators. In recent years, a lot of graphene amplitude modulators have been investigated and developed. For example, Liu et al. first experimentally demonstrate graphene optical amplitude modulators with a modulation depth of ∼0.1–0.16 dB/μm [10, 11]. Since then, many different modulators based on single/double-layer graphene integrated with high refractive index waveguide core, metal ribbons, or photonic crystal structures have been proposed to improve the light confinement, enhance light-graphene interaction, and increase modulation depth while maintaining acceptable insertion loss [12], [13], [14], [15], [16], [17], [18]. On the other hand, graphene has also been introduced and integrated into various waveguide structures to achieve high-efficient phase modulators, which are crucial for encoding the phase information in complex formats [5, 13, 19], [20], [21], [22]. For example, in 2015, Sorianello et al. numerically demonstrated two phase modulators based on graphene–insulator–silicon capacitor and graphene–insulator–graphene capacitor with a modulation efficiency, namely the production of π-phase-shift voltage and length (V π L π ), of 1600 V μm and 1000 V μm at 1.55 μm, respectively [13]. Then, in 2017, they experimentally demonstrated a graphene-silicon phase modulator with V π L π of 2800 V μm [5]. In 2018, Shu et al. proposed a compact graphene modulator based on silicon waveguide using the electro refractive effect of graphene with V π L π of 1290 V μm [19]. Moreover, Mao et al. proposed a low voltage and ultrafast graphene integrated phase modulator on semiconductor and dielectric platforms with V π L π of 2150 V μm [20]. Despite the recent progress, the performance of most of the reported graphene phase modulators (GPMs) is still limited. Specifically, the modulation efficiency is restricted because of the large footprint and the weak light-graphene interaction caused by the mode polarization mismatch between them. It is remarkable that a longer phase modulator length allows a larger phase shift but inevitably induces higher insertion loss. There is a trade-off between optical loss, footprint, and V π L π for the current GPMs. Therefore, how to drastically increase the light-graphene interaction and develop broadband high-performance GPMs with much higher modulation efficiency, smaller modulation length, and lower energy consumption, as well as maintain excellent decoupling between phase and amplitude modulation in the near-infrared region remains a challenge.

In this paper, we demonstrate a new type of high-efficiency GPM based on a dual-semicircular-metal–nanoribbon integrated graphene–insulator–graphene capacitor hybrid plasmonic waveguide structure for near-infrared applications. In this design, the surface plasmon polariton mode confinement, polarization matching (in-plane electric field components of graphene), and light-graphene interactions are drastically enhanced, enabling excellent phase modulation performance. To investigate the proposed modulator, we study and discuss the electric field distributions, the effective index Re(neff), attenuation constant, phase change, the geometrical parameter effects, and the 3 dB modulation bandwidth characteristics at 1.55 μm. After dimensional optimization, the short 20 μm GPM shows a low optical loss around 0.3 dB/μm, a large 3 dB modulation bandwidth of 67.9 GHz, a low energy consumption of 157.49 fJ/bit, and a wide optical wavelength ranging from 1.3 to 1.8 μm. The GPM demonstrates a good phase and amplitude decoupling effect and a very high modulation efficiency with a small V π L π of 118.6 V μm by changing the graphene chemical potential from 0.55 to 0.75 eV at 1.55 μm, which can be implemented in various efficient Mach–Zehnder (MZ) modulator. Especially, by reducing the overlap width of the graphene–Al2O3–graphene capacitor, the modulation bandwidth and energy consumption of the modulator can be further improved to 370.36 GHz and 30.22 fJ/bit, respectively. Finally, we present a comparison of the performance of the recently reported phase modulators. This work provides a new path for the design of high-efficiency GPMs relied on hybrid plasmonic effects and may have great potentials in near-infrared interconnects and telecommunication applications.

2 Design and consideration

The 3D schematic configuration and 2D cross-sectional view of the proposed GPM are shown in Figure 1a and b, respectively. In this design, the modulator structure is made up of a dual-semicircular-silver-nanoribbon integrated graphene–insulator (Al2O3)–graphene capacitor placed above a SiO2 waveguide on a Topas buffer layer and a silicon substrate. The silicon substrate layer is with a thickness of 100 nm and a relative permittivity ( ϵ s i ) of 11.7. The Topas buffer layer is with a relative permittivity ( ϵ Topas ) of 2.35 [23]. To avoid graphene chemical doping by other materials, the Al2O3 layer with a relative permittivity ( ϵ Al 2 O 3 ) of 2.09 and a thickness of 5 nm is selected as the insulator layers placed above and below the graphene layers [24]. Two semicircular silver nanoribbons are identical with a radius of 100 nm and placed on the top Al2O3 layer with a gap g of 10 nm. The relative permittivity of silver is obtained from Lorentz–Drude model [25, 26]. The graphene layer can be considered as a 2D homogenous anisotropic material and can be modeled as a surface conductivity layer without thickness [17]. The surface conductivity ( σ g ) of the single graphene layer is calculated by the Kubo formula [27, 28]:

(1) σ g ( ω , μ c , Γ , T ) = j e 2 π ℏ 2 ( ω − j 2 Γ ) ∫ 0 ∞ ( ∂ f d ( ξ , μ c , T ) ∂ ξ − ∂ f d ( − ξ , μ c , T ) ∂ ξ ) ξ d ξ + j e 2 ( ω − j 2 Γ ) π ℏ 2 ∫ 0 ∞ f d ( ξ , μ c , T ) − f d ( − ξ , μ c , T ) ( ω − j 2 Γ ) 2 − 4 ξ / ℏ 2 d ξ ,

where ω is the angular frequency, μc is the Fermi level, T is the temperature, the scattering rate Γ = 2τ−1, the relaxation time τ = μμc/(evF2), μ is the mobility, vF is the Fermi velocity, e is the electron charge, ξ is the energy, ћ is the reduced Planck constant, kB is the Boltzmann constant, and the Fermi–Dirac distribution f d ( ξ , μ c , T ) = ( e ( ξ − μ c ) / k B T + 1 ) − 1 . In this study, we set τ = 0.5 ps and T = 300 K [29], [30], [31]. A gate voltage Vg is applied to the graphene-insulator-graphene capacitor to control the graphene conductivity via electrostatic doping to achieve phase modulation effect, as illustrated in Figure 1a.

Figure 1: Schematic configuration of the GPM. (a) 3-D schematic illustration, (b) cross-sectional view. The structure dimensions are set as s = 100 nm, p = 800 nm, l = 600 nm, t = 5 nm, r = 100 nm, and g = 10 nm.
Figure 1:

Schematic configuration of the GPM.

(a) 3-D schematic illustration, (b) cross-sectional view. The structure dimensions are set as s = 100 nm, p = 800 nm, l = 600 nm, t = 5 nm, r = 100 nm, and g = 10 nm.

Furthermore, the GPM can be fabricated through the typical large-scale graphene synthesis and transfer techniques, and the state-of-art nano processes, such as electron-beam evaporation and nanoimprint lithography [16]. The high quality of the graphene transferring is the key to achieving the high-efficiency phase modulation. The atomic-layer-deposited (ALD) technology can be used for the ultrathin Al2O3 layer deposition to avoid electric contact between graphene layers and ensure the high electron mobility of graphene [21, 24]. Then the top dual-semicircular-silver-nanoribbon can be etched using laser interference lithography or nanoimprint lithography. Rapid thermal processing is adopted to improve the contact quality between metal electrodes and graphene to reduce the contact resistance, thus improving the modulation bandwidth of the proposed phased modulator.

3 Results and discussion

3.1 Guiding mode analysis

According to (1), we first analyze the graphene conductivity as a function of graphene chemical potential μc at operating wavelength λ = 1.55 μm. As shown in Figure 2a, the Re(σg) is very sensitive to μc, where Re(σg) decreases drastically from 60.7 to 0.17 μS (over 350 times) as μc increases from 0 to 0.85 eV. Figure 2b shows that Im(σg) changes from positive to negative by adjusting μc from 0 to 0.85 eV, which implies the properties of graphene switching from “metallic” to “dielectric” states. The great tunability of graphene conductivity indicates the great modulation potential of graphene in the proposed GPMs. To investigate the guiding mode characteristics, we simulate the complex effective refractive index neff, attenuation constant α, and the field distributions of the proposed GPM on xoy plane using the mode analysis solver of COMSOL Multiphysics. The scattering boundary conditions are assigned to all the outer boundaries (enough far away from the center of the modulator) to mimic the free space. The real and imaginary parts of the effective refractive index Re(neff) and Im(neff) at 1.55 μm under different μc from 0 to 0.85 eV, as shown in Figure 2c. It is found that the modulator can achieve both strong electro-absorptive and electro-refractive effects owning to the huge change range in terms of Re(neff) and Im(neff). The Im(neff) of the modulator drops quickly from 0.047 to 0.009 as μc increases from 0.2 to 0.55 eV. The proposed modulator may operate as an amplitude or intensity modulator when switching μc from 0.2 to 0.55 eV. Especially, it is observed that the Re(neff) decreases linearly in a wide range from 1.97 to 1.94 with tiny Im(neff) reduces from 0.0089 to 0.0086 as the μc increases from 0.55 to 0.85 eV. The real effective refractive index change ΔRe(neff) is 0.03 while the Im(neff) change is as small as 0.0003, resulting in a large Δ Re ( n eff ) / Δ Im ( n eff ) of 100 (in the order of 102). That is to say, the light propagation of the modulator undergoes significant phase change with very low optical loss. To investigate the effect of the metal–nanoribbons, the Im(neff) of the proposed GPM without metal–nanoribbons are also calculated, as shown in Figure 3d. The ΔRe(neff) of the modulator without metal–nanoribbons is about 0.0014 between 0.55 and 0.85 eV, which is much one order smaller than that of modulator with metal–nanoribbons. Meanwhile, the Im(neff) remains around 0.049 and the ΔIm(neff) is of 0.0004, as well as a small Δ Re ( n eff ) / Δ Im ( n eff ) is of 3.5 between 0.55 and 0.85 eV. Clearly, the modulator with metal–nanoribbons shows much higher Δ Re ( n eff ) / Δ Im ( n eff ) and much smaller Im(neff), implying higher phase modulation efficiency and lower insertion loss, compared with the modulator without metal–nanoribbons. Therefore, when switching the μc from 0.55 to 0.85 eV, the proposed modulator with metal–nanoribbons may operate as efficient phase modulator with an excellent phase and amplitude decoupling effect. Here, we only focus on electro-refractive effect-based phase modulation performance in the following discussion.

Figure 2: Calculated graphene surface conductivity Re(σg) (a) and Im(σg) (b) as a function of the graphene chemical potential μc. Simulated Re(neff) and Im(neff) as a function of graphene chemical potential μc for the proposed GPM with metal–nanoribbons (c) and without metal–nanoribbons (d).
Figure 2:

Calculated graphene surface conductivity Re(σg) (a) and Im(σg) (b) as a function of the graphene chemical potential μc. Simulated Re(neff) and Im(neff) as a function of graphene chemical potential μc for the proposed GPM with metal–nanoribbons (c) and without metal–nanoribbons (d).

Figure 3: Simulated electric field distributions on the xy plane of the GPM with μc = 0.55 eV. (a) Electric field magnitude |E|. (b) Electric field component in x-direction (E x ). (c) Electric field component in the y-direction (E y ). (d) Electric field component in z-direction (E z ).
Figure 3:

Simulated electric field distributions on the xy plane of the GPM with μc = 0.55 eV.

(a) Electric field magnitude |E|. (b) Electric field component in x-direction (E x ). (c) Electric field component in the y-direction (E y ). (d) Electric field component in z-direction (E z ).

To better understand the mechanism, the guiding mode field distributions of the GPM at 1.55 μm is analyzed. Figure 3 shows the electric field magnitude |E| and components E x , E y , and E z distributions (unit: V/m) at 0.55 eV, respectively. Clearly, strong subwavelength confinement is achieved in all cases with intense hybrid SPP fields located around two semicircular silver nano-ribbons gap and closed to the graphene layers. Owing to the integration of dual silver nanoribbons, the hybrid SPP electric fields of GPM is dominantly polarized along the x-direction (E x ) and z-direction (E z ) but rare polarized in the y-direction (E y ), as shown in Figure 3b–d. It is remarkable that the major E x and E z components are parallel to the graphene plane, allowing the good in-plane mode polarization matching, strong light-graphene interaction, and excellent electro-optic modulation effects.

3.2 Phase change and loss characteristics

To investigate the modulation characteristics of the proposed GPM, we calculate the phase change (Δφ) and attenuation constant (α) as follows:

(2) Δ φ = 2 π λ Δ Re ( n eff ) L ,
(3) α = 40 π Im ( n eff ) λ ln 10 ,

where λ is the wavelength in free space, and L is the length of the modulator. From Figure 2c, the phase change Δφ and the attenuation constant α for a 20 μm length GPM without and with metal–nanoribbons as a function of μc at 1.55 μm can be obtained, as shown in Figure 4a and b, respectively. As shown in Figure 4a, when μc is increasing from 0.55 to 0.75 eV, the Δφ of the proposed modulator with metal–nanoribbons decreases almost linearly from 0 to 1.86π with α keeps around 0.31 dB/μm. The π phase shift only needs a small μc change of 0.1 eV from 0.55 to 0.65 eV. While, as shown in Figure 4b, the modulator without metal–nanoribbons shows a very small Δφ of 0.073π and a high α of ∼1.72 dB/μm, respectively. Clearly, the proposed modulator with the metal–nanoribbons demonstrates an efficient phase modulation with negligible phase and amplitude coupling effect.

Figure 4: Phase change Δφ and attenuation constant α for the 20 μm length GPM under different chemical potential μc ranging from 0.55 to 0.75 eV at 1.55 μm (a) with the metal–nanoribbons. (b) Without the metal–nanoribbons.
Figure 4:

Phase change Δφ and attenuation constant α for the 20 μm length GPM under different chemical potential μc ranging from 0.55 to 0.75 eV at 1.55 μm (a) with the metal–nanoribbons. (b) Without the metal–nanoribbons.

In an MZ modulator based on the GPM with metal–nanoribbons, as schematically shown in Figure 5a, the optical transmission is given by

(4) T ( λ ) = 1 4 [ e − α 1 L + e − α 2 L + 2 e − α 1 L + α 2 L 2 cos ( Δ φ ) ]

where the modulator arm’s length L = 20 μm, α 1 and α 2 represent the loss of the two arms respectively, and Δφ is the phase difference between two arms when different μc values are applied. The relationship between the gate voltage Vg and μc is given by V g = e n s t / 2 ϵ 0 ϵ Al 2 O 3 , where the charge density n s = 2 π ℏ v F 2 ∫ 0 ∞ ξ [ f d ( ξ , μ c , T ) − f d ( ξ , 2 μ c , T ) ] d ξ [27]. As shown in Figure 5b, the gate voltage Vg should increase from 4.25, 5.93, to 7.89 V to obtain the μc ranging from 0.55, 0.65–0.75 eV. By applying Vg1 and Vg2 as 4.25 and 5.93 V for the two modulator arms, the μc difference between them of 0.1 eV is obtained. Figure 5c and d show the phase difference Δφ and transmission T of the MZ modulator under different μc at the operating wavelength of 1.55 μm, where the μc one arm is ranging from 0.55 to 0.75 eV while for the other arm is fixed as 0.55 eV. In this case, the extinction ratio (ER) can reach over 80 dB due to the phase difference between two arms approaching π, as shown in Figure 5d. Therefore, the proposed modulator shows high modulation efficiency with V π L π  = 5.93 V × 20 μm = 118.67 V μm, which is a significant improvement with respect to previously reported GPMss.

Figure 5: MZ modulator based on GMPs. (a) Schematic of the MZ modulator. (b) The relationship between the gate voltage Vg and μc. (c) Phase difference Δφ as a function of μc at 1.55 μm. (d) Transmission T as a function of μc at 1.55 μm.
Figure 5:

MZ modulator based on GMPs.

(a) Schematic of the MZ modulator. (b) The relationship between the gate voltage Vg and μc. (c) Phase difference Δφ as a function of μc at 1.55 μm. (d) Transmission T as a function of μc at 1.55 μm.

3.3 Effect of operating wavelength and geometric parameters

The effect of optical operating wavelength on the performance of the proposed GPM with metal–nanoribbons is studied. As shown in Figure 6a and b, the modulator’s effective refractive index Re(neff) and attenuation constant α under μc = 0.55 and 0.75 eV keep a similar downward trend with wavelength increasing from 1.3 to 1.8 μm. Specially, the Re(neff) decreases from 2.04 to 1.92 (from 2.01 to 1.89), and the α decreases from 0.46 dB/μm to 0.28 dB/μm (from 0.36 dB/μm to 0.27 dB/μm) under μc = 0.55 eV (μc = 0.75 eV), respectively. As shown in Figure 6c, the Δφ decreases from 2.46π to 1.82π and the Δα decreases from 0.09 dB/μm to 0.01 dB/μm as the wavelength increases from 1.3 to 1.8 μm. Therefore, the proposed modulator exhibits excellent phase modulation and low insertion loss in an ultra-wide operating wavelength range of 1.3–1.8 μm.

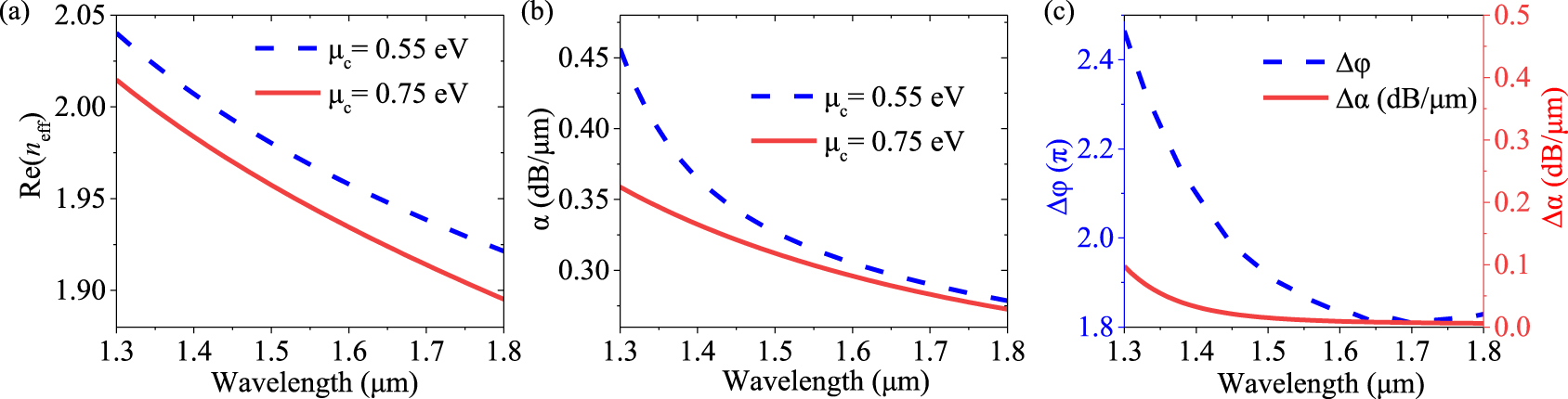
Figure 6: (a)–(c) Dependence of Re(neff), α, Δφ and Δα of the proposed GPM on the operating wavelength ranging from 1.3 to 1.8 μm.
Figure 6:

(a)–(c) Dependence of Re(neff), α, Δφ and Δα of the proposed GPM on the operating wavelength ranging from 1.3 to 1.8 μm.

The proposed phase modulator is based on hybrid plasmonic waveguides with dual semicircular silver nano-ribbons and graphene- Al 2 O 3 -graphene capacitor. Here, we further investigate the effects of the key geometrical parameters such as insulator spacer thickness (t), the semicircle radius (r), and the gap (g) on the modulator’s effective refractive index Re(neff), attenuation α, the 20 μm-length modulator phase change Δφ, and Δα under μc of 0.55 and 0.75 eV at the operating wavelength of 1.55 μm, as shown in Figure 7. As is shown in Figure 7a–c, the Re(neff) and α increase, Δφ (Δα) decreases from 1.9π to 0.45π (from 0.022 dB/μm to 0.005 dB/μm) as t increases from 2 to 10 nm. The interaction between the propagating light and graphene will be weaker as t increases, resulting in a decline in phase change and modulation efficiency. In Figure 7d–i, the Re(neff), α and Δφ keep a similar downward trend as r and g increase. The Δφ remains large phase change over 1.7π while the Δα remains negligible level from 0.015 dB/μm to 0.01 dB/μm between 0.55 and 0.75 eV in the whole r and g ranges, implying the proposed phase modulator has good phase modulation without obvious amplitude modulation. In this work, the parameters t, r and g for the modulator are selected as 5, 100, 10 nm for a moderate trade-off between the modulation efficiency, insertion loss, and fabrication complexity.

Figure 7: (a)–(c) Dependence of Re(neff), α, Δφ and Δα on thickness t ranging from 2 to 10 nm with r = 100 nm and g = 10 nm. (d)–(f) Thickness t ranging from 2 to 10 nm the radius r ranging from 50 to 145 nm with g = 10 nm and t = 5 nm. (g)–(i) Gap g ranging from 5 to 13 nm with r = 100 nm and t = 5 nm under different μc of 0.55 and 0.75 eV at 1.55 μm, respectively.
Figure 7:

(a)–(c) Dependence of Re(neff), α, Δφ and Δα on thickness t ranging from 2 to 10 nm with r = 100 nm and g = 10 nm. (d)–(f) Thickness t ranging from 2 to 10 nm the radius r ranging from 50 to 145 nm with g = 10 nm and t = 5 nm. (g)–(i) Gap g ranging from 5 to 13 nm with r = 100 nm and t = 5 nm under different μc of 0.55 and 0.75 eV at 1.55 μm, respectively.

3.4 Modulation bandwidth

Bandwidth is one of the key parameters for the optical phase modulator, which can be used to evaluate the modulation speed. To further study broadband properties, we calculate the bandwidth (f3dB) with an equivalent circuit model as shown in Figure 8a. The modulation process can be equivalent to the switching states between the charge and discharge of the graphene-insulator-graphene capacitor. The modulator’s total RC-limited bandwidth is given by

(5) f 3 d B = 1 2 π 2 R c + 2 R g C ,

where Rg is graphene resistance, Rc is contact resistance, and C is the capacity of the graphene-insulator-graphene capacitor. The Rg is usually defined through RSQ in the unit of resistance per square, which is related to carrier mobility of graphene and typically located between 100 and 500 Ω/sq [32, 33]. The high Rc is determined by the contact resistivity ρc, which was shown in the range of 100–1000 Ω μm experimentally [34], [35], [36]. And the capacity value is related to permittivity ϵ Al 2 O 3 , capacitor area S and distance t. Their values can be calculated by

(6) R g = R SQ w g L ,
(7) R c = ρ c L ,
(8) C = ϵ 0 ϵ Al 2 O 3 s t ,

where wg (3.2 μm) is the width of graphene, L (20 μm) is the length of the modulator, ϵ 0 is the permittivity, the overlap width of graphene layers is 0.6 μm, S (12 μm2) is the area of the capacity, and t (5 nm) is the distance between two graphene sheets. Therefore, C is 55.8 fF, and the bandwidth can be calculated from Eq. (5), as shown in Figure 8b. The 3 dB modulation bandwidth can be up to 67.96 GHz when ρc is 100 Ω μm. Notably, L does not impact the 3 dB modulation bandwidth but has a significant influence on phase change and insertion loss. Furthermore, in terms of energy consumption, the energy per bit is calculated by: Eb = CΔV2/4, where the difference value of voltage to achieve phase modulation ΔV = Vgπ − Vg0 = 1.68 V. In this case, the phase modulator shows a low energy consumption of about 157.49 fJ/bit and a small footprint of 12 μm2, which is promising for near-infrared modulation applications.

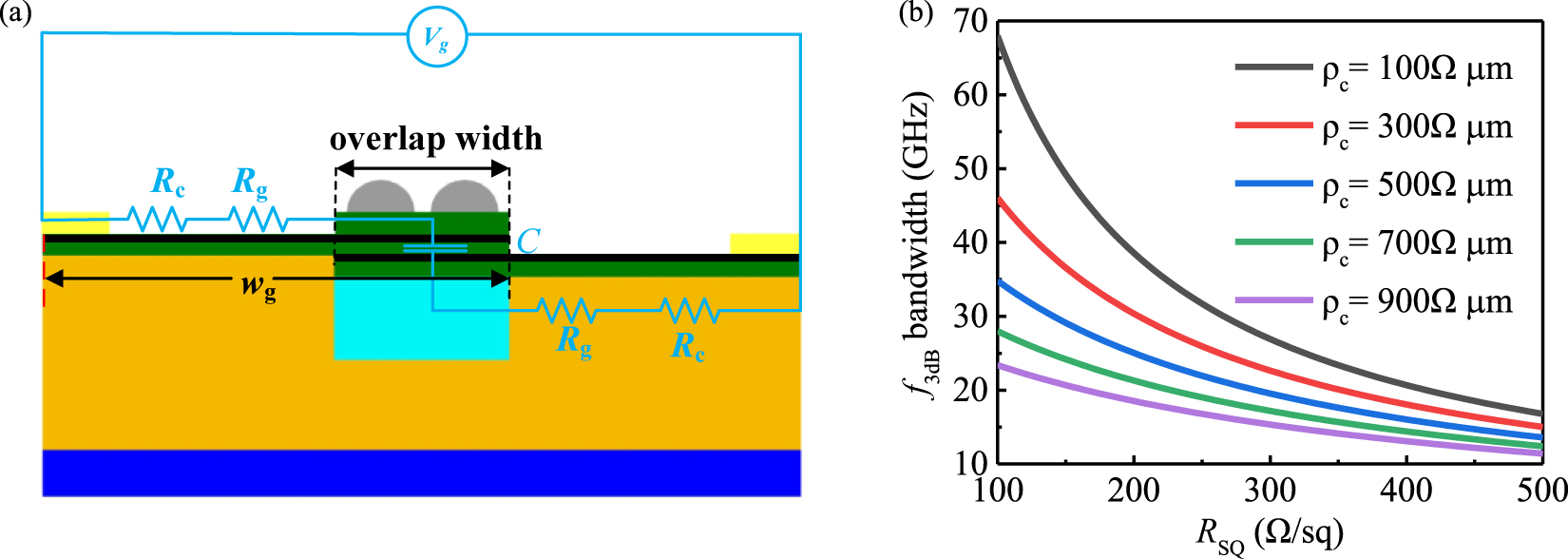
Figure 8: (a) The equivalent circuit of the proposed GPM. (b) f 3 d B ${f}_{3dB}$ bandwidth as a function of RSQ and ρc, where the geometry and dielectric combination are the same as those in Figure 1.
Figure 8:

(a) The equivalent circuit of the proposed GPM. (b) f 3 d B bandwidth as a function of RSQ and ρc, where the geometry and dielectric combination are the same as those in Figure 1.

The modulation bandwidth can be further improved by reducing the graphene overlap width of the graphene–Al2O3–graphene capacitor to reduce the capacity. The improved phase modulator with reduced overlap width is shown in Figure 9a. When the overlap width of graphene is reduced from 600 to 110 nm, the bandwidth will increase from 67.9 to 370.36 GHz under RSQ = 100 Ω/sq and ρc = 100 Ω μm. It is remarkable that the electric field of the modulator is mainly confined in the small metal-ribbon gap area above the graphene layers, ensuring the strong interaction between the field and graphene layers. Therefore, the reduction of overlap width will greatly reduce the C and increase the bandwidth without affecting the phase modulation performance. As shown Figure 9b, this improved phase modulator shows Δφ of 1.82π and α of 0.3 dB/μm with L = 20 μm as the μc switches from 0.55 to 0.75 eV, which is very close to the original design with Δφ of 1.86π and α of 0.3 dB/μm as shown in Figure 4. Clearly, this improved phase modulator may be applied to the integrated circuits for wider bandwidth or faster modulation speed.

Figure 9: Improved GPM with reduced overlap width of the graphene capacitor. (a) Equivalent circuit of the improved modulator. (b) Δφ and α as functions of μc of the improved modulator.
Figure 9:

Improved GPM with reduced overlap width of the graphene capacitor.

(a) Equivalent circuit of the improved modulator. (b) Δφ and α as functions of μc of the improved modulator.

3.5 Comparison of different phase modulators

To better demonstrate the advantage of the proposed design, we present the performance comparison of the proposed phase modulator with some recently reported works, as shown in Table 1. For example, Mohin et al. experimentally demonstrated a GPM with a large V π L π of 3 × 105 V μm, which results from the weak light and graphene interaction [21]. Sorianello et al. proposed an electro-refractive modulator based on single or double-layer graphene on top of silicon waveguides experimentally and numerically showing a V π L π of 2800 V μm and a bandwidth of 5 GHz [5], as well as a V π L π of 1600 V μm and a bandwidth of 30 GHz [13]. Shu et al. experimentally proposed a graphene-based silicon MZ modulator with V π L π of 1290 V μm [19]. To achieve small Vπ, Mao et al. proposed an integrated phase modulator based on graphene-Si photonic crystal waveguide with a small V π L π of 2150 V μm but need a huge modulation Lπ of 2870 μm [20].

Table 1:

A comparison of some recent reported GPMs.

References Length (μm) V π L π (V μm) 3 dB modulation bandwidth (GHz) Energy consumption (fJ/bit) Operating wavelength (μm)
Experimental results Mohin et al. [21] 200 3 × 105 – – 1.53–1.57
Sorianello et al. [5] 300 2800 5 – 1.55
Shu et al. [19] 40 1290 – – 1.55
Numerical results Sorianello et al. [13] 500 1600 30 0.38 1.55
Mao et al. [20] 2870 2150 67 – 1.55
Yuki et al. [22] 227 450 – – 4
This work: initial structure 20 118.67 67.96 157.49 1.3–1.8
Improved structure 20 120.50 370.36 30.22 1.3–1.8

Here, the proposed phase modulator shows excellent performance with the length (Lπ) of 20 μm, high modulation efficiency with the V π L π of 118.67 V μm, large 3 dB modulation bandwidth of 67.96 GHz, small energy consumption of 157.49 fJ/bit, and wide optical operating wavelength range of 1.3–1.8 μm. By reducing the overlap width of the graphene-Al2O3-graphene capacitor, the improved modulator demonstrates an ultra-wide modulation bandwidth of 370.36 GHz and extremely low energy consumption of 30.22 fJ/bit. Therefore, these proposed graphene modulators possess obvious advantages compared with the recent designs, which may have extensive potential applications in low energy consumption integrated silicon-based platforms.

4 Conclusions

In this work, we proposed a new variety of ultra-compact high-efficiency GPMs based on hybrid plasmonic waveguides for near-infrared applications. We numerically study the key characteristics of the proposed modulators including the guiding mode, phase change, transmission loss, modulation efficiency, bandwidth, and energy consumption, as well as the effect of operating wavelength and geometric parameters. It is found that owing to the mode polarization matching and strong light-graphene interaction, the proposed GPM possesses excellent performance with a high modulation efficiency with V π L π of 118.67 V μm and a low energy consumption of 157.49 fJ/bit, which is superior to the recently reported graphene-based modulators. By reducing the overlap width of the graphene–Al2O3–graphene capacitor, the modulation bandwidth and energy consumption of the modulator can be further improved to 370.36 GHz and 30.22 fJ/bit, respectively. These modulators also show a good phase and amplitude decoupling effect. This study may offer a new way to design efficient electro-absorptive or electro-refractive modulators, which may have potential applications in various high-speed telecommunications, interconnects, and other graphene-based integrated photonic devices.

Corresponding author: Longfang Ye, Institute of Electromagnetics and Acoustics, Xiamen University, Xiamen 361005, China; and Shenzhen Research Institute of Xiamen University, Shenzhen 518057, China, E-mail:

Funding source: State Key Laboratory of Millimeter Waves

Award Identifier / Grant number: k202101

Funding source: Fundamental Research Funds for the Central Universities

Award Identifier / Grant number: 20720210048

Funding source: Shenzhen Science and Technology Projects

Award Identifier / Grant number: JCYJ20180306172733197

Award Identifier / Grant number: JCYJ20210324121606017

  1. Author contribution: All the authors have accepted responsibility for the entire content of this submitted manuscript and approved submission.

  2. Research funding: This work was supported in part by the Shenzhen Science and Technology Projects (JCYJ20210324121606017, JCYJ20180306172733197), the State Key Laboratory of Millimeter Waves (k202101), and the Fundamental Research Funds for the Central Universities (20720210048).

  3. Conflict of interest statement: There are no conflicts to declare.

References

[1] A. M. Gobin, M. H. Lee, N. J. Halas, W. D. James, R. A. Drezek, and J. L. West, “Near-infrared resonant nanoshells for combined optical imaging and photothermal cancer therapy,” Nano Lett., vol. 7, no. 7, pp. 1929–1934, 2007. https://doi.org/10.1021/nl070610y.Search in Google Scholar PubMed

[2] M. Toyoshima, Y. Takayama, and T. Takahashi, “Ground to satellite laser communication experiments,” IEEE Aero. Electron. Syst. Mag., vol. 23, no. 8, pp. 10–18, 2018.10.1109/MAES.2008.4607894Search in Google Scholar

[3] C. Haffner, D. Chelladurai, and Y. Fedoryshyn, “Low-loss plasmon-assisted electro-optic modulator,” Nature, vol. 556, pp. 483–486, 2018. https://doi.org/10.1038/s41586-018-0031-4.Search in Google Scholar PubMed PubMed Central

[4] J. F. Liu, M. Beals, and A. Pomerene, “Waveguide-integrated, ultralow-energy GeSi electro-absorption modulators,” Nat. Photonics, vol. 2, pp. 433–437, 2008. https://doi.org/10.1038/nphoton.2008.99.Search in Google Scholar

[5] V. Sorianello, M. Midrio, G. Contestabile, et al.., “Graphene–silicon phase modulators with gigahertz bandwidth,” Nat. Photonics, vol. 12, pp. 40–44, 2018. https://doi.org/10.1038/s41566-017-0071-6.Search in Google Scholar

[6] A. Rahim and A. Hermans, “Talking silicon photonics modulators to a higher performance level: state-of-art and a review of new technologies,” Adv. Photonics, vol. 3, no. 2, 2021, Art no. 024003. https://doi.org/10.1117/1.ap.3.2.024003.Search in Google Scholar

[7] M. Romagnoli, V. Sorianello, M. Midrio, et al.., “Graphene-based integrated photonics for next-generation datacom and telecom,” Nat. Rev. Mater., vol. 3, pp. 392–414, 2018. https://doi.org/10.1038/s41578-018-0040-9.Search in Google Scholar

[8] X. T. Gan, R. J. Shiue, and Y. D. Gao, “High-contrast electrooptic modulation of a photonic crystal nanocavity by electrical gating of graphene,” Nano Lett., vol. 13, no. 2, pp. 691–696, 2013. https://doi.org/10.1021/nl304357u.Search in Google Scholar PubMed

[9] Q. L. Bao and K. P. Loh, “Graphene photonics, plasmonics, and broadband optoelectronic devices,” ACS Nano, vol. 6, no. 5, pp. 3677–3694, 2012. https://doi.org/10.1021/nn300989g.Search in Google Scholar PubMed

[10] M. Liu, X. B. Yin, and E. Ulin-Avila, “A graphene-based broadband optical modulator,” Nature, vol. 474, pp. 64–67, 2011. https://doi.org/10.1038/nature10067.Search in Google Scholar PubMed

[11] M. Liu, X. Yin, and X. Zhang, “Double-layer graphene optical modulator,” Nano Lett., vol. 12, no. 3, pp. 1482–1485, 2012. https://doi.org/10.1021/nl204202k.Search in Google Scholar PubMed

[12] Y. T. Hu, M. Pantouvaki, J. Van Campenhout, and S. Brems, “Broadband 10 Gb/s operation of graphene electro-absorption modulator on silicon,” Laser Photon. Rev., vol. 10, pp. 307–316, 2016. https://doi.org/10.1002/lpor.201500250.Search in Google Scholar

[13] V. Sorianello, M. Midrio, and M. Romagnoli, “Design optimization of single and double layer graphene phase modulators in SOI,” Opt. Express, vol. 23, pp. 6478–6490, 2015. https://doi.org/10.1364/oe.23.006478.Search in Google Scholar

[14] M. Y. Su, B. Yang, J. M. Liu, et al.., “Broadband graphene-on-silicon modulator with orthogonal hybrid plasmonic waveguides,” Nanophotonics, vol. 9, no. 6, pp. 1529–1538, 2020. https://doi.org/10.1515/nanoph-2020-0165.Search in Google Scholar

[15] X. Peng, R. Hao, Z. W. Ye, et al.., “Highly efficient graphene-on-gap modulator by employing the hybrid plasmonic effect,” Opt Lett., vol. 42, no. 9, pp. 1736–1739, 2017. https://doi.org/10.1364/ol.42.001736.Search in Google Scholar PubMed

[16] Z. Cheng, X. L. Zhu, M. Galili, et al.., “Double-layer graphene on photonic crystal waveguide electro-absorption modulator with 12 GHz bandwidth,” Nanophotonics, vol. 9, no. 8, pp. 2377–2385, 2020.10.1515/nanoph-2019-0381Search in Google Scholar

[17] L. F. Ye, K. H. Sui, Y. Zhang, and Q. H. Liu, “Broadband optical waveguide modulators based on strongly coupled hybrid graphene and metal nanoribbons for near-infrared applications,” Nanoscale, vol. 11, no. 7, pp. 3229–3239, 2019. https://doi.org/10.1039/c8nr09157a.Search in Google Scholar PubMed

[18] L. F. Ye, K. H. Sui, Y. H. Liu, M. Zhang, and Q. H. Liu, “Graphene-based hybrid plasmonic waveguide for highly efficient broadband mid-infrared propagation and modulation,” Opt. Express, vol. 26, no. 12, pp. 15935–15947, 2018. https://doi.org/10.1364/oe.26.015935.Search in Google Scholar PubMed

[19] H. W. Shu, Z. T. Su, L. Huang, et al.., “Significantly high modulation efficiency of compact graphene modulator based on silicon waveguide,” Sci. Rep., vol. 8, p. 991, 2018. https://doi.org/10.1038/s41598-018-19171-x.Search in Google Scholar PubMed PubMed Central

[20] D. Mao, C. Cheng, F. F. Wang, et al.., “Device architectures for low voltage and ultrafast graphene integrated phase modulators,” IEEE J. Sel. Top. Quantum Electron., vol. 27, no. 2, pp. 1–9, 2021. https://doi.org/10.1109/jstqe.2020.3026357.Search in Google Scholar PubMed PubMed Central

[21] M. Mohsin, D. Neumaier, D. Schall, et al.., “Experimental verification of electro-refractive phase modulation in graphene,” Sci. Rep., vol. 5, p. 10967, 2015. https://doi.org/10.1038/srep10967.Search in Google Scholar PubMed PubMed Central

[22] Y. Yiki, T. Shinichi, and T. Mitsuru, “Low-loss graphene-based optical phase modulator operating at mid-infrared wavelength,” J. Appl. Phys., vol. 57, no. 4, 2018, Art no. 04FH06.10.7567/JJAP.57.04FH06Search in Google Scholar

[23] F. A. Vallejo and L. M. Hayden, “Design of ultra-broadband terahertz polymer waveguide emitters for telecom wavelengths using coupled mode theory,” Opt. Express, vol. 21, no. 5, pp. 5842–5858, 2013. https://doi.org/10.1364/oe.21.005842.Search in Google Scholar PubMed

[24] R. M. Costescu, D. G. Cahill, F. H. Fabreguette, Z. A. Sechrist, and S. M. George, “Ultra-low thermal conductivity in W/Al2O3 nanolaminates,” Science, vol. 303, no. 5660, pp. 989–990, 2004. https://doi.org/10.1126/science.1093711.Search in Google Scholar PubMed

[25] A. D. Rakić, A. B. Djurišić, J. M. Elazar, and M. L. Majewski, “Optical properties of metallic films for vertical cavity optoelectronic devices,” Appl. Opt., vol. 37, no. 22, pp. 5271–5283, 1998.10.1364/AO.37.005271Search in Google Scholar PubMed

[26] M. A. Ordal, R. J. Bell, R. W. Alexander, L. L. Long, and M. R. Querry, “Optical properties of fourteen metals in the infrared and far infrared: Al, Co, Cu, Au, Fe, Pb, Mo, Ni, Pd, Pt, Ag, Ti, V, and W,” Appl. Opt., vol. 24, no. 24, pp. 4493–4499, 1985. https://doi.org/10.1364/ao.24.004493.Search in Google Scholar PubMed

[27] G. W. Hanson, “Dyadic Green’s functions and guided surface waves for a surface conductivity model of graphene,” J. Appl. Phys., vol. 103, no. 6, 2008, Art no. 064302. https://doi.org/10.1063/1.2891452.Search in Google Scholar

[28] G. W. Hanson, “Dyadic Green’s functions for an anisotropic, non-local model of biased graphene,” IEEE Trans. Antenn. Propag., vol. 56, no. 3, pp. 747–757, 2008. https://doi.org/10.1109/tap.2008.917005.Search in Google Scholar

[29] K. I. Bolotin, K. J. Sikes, Z. Jiang, et al.., “Ultrahigh electron mobility in suspended graphene,” Solid State Commun., vol. 146, nos 9–10, pp. 351–355, 2008. https://doi.org/10.1016/j.ssc.2008.02.024.Search in Google Scholar

[30] W. Gao, J. Shu, C. Qiu, and Q. Xu, “Excitation of plasmonic waves in graphene by guided-mode resonances,” ACS Nano, vol. 6, no. 9, pp. 7806–7813, 2012. https://doi.org/10.1021/nn301888e.Search in Google Scholar PubMed

[31] C. R. Dean, A. F. Young, I. Meric, et al.., “Boron nitride substrates for high-quality graphene electronics,” Nat. Nanotechnol., vol. 5, no. 10, p. 722, 2010. https://doi.org/10.1038/nnano.2010.172.Search in Google Scholar PubMed

[32] A. Pachoud, M. Jaiswal, P. K. Ang, K. P. Loh, and B. Ozyilman, “Graphene transport at high carrier densities using polymer electrolyte gate,” Europhys. Lett., vol. 92, no. 2, p. 27001, 2010. https://doi.org/10.1209/0295-5075/92/27001.Search in Google Scholar

[33] W. S. Leong, H. Gong, and J. T. L. Thong, “Low-contact-resistance graphene devices with nickel-etched-graphene contacts,” ACS Nano, vol. 8, no. 1, pp. 994–1001, 2014. https://doi.org/10.1021/nn405834b.Search in Google Scholar PubMed

[34] A. Venugopal, L. Colombo, and E. M. Vogel, “Contact resistance in few and multilayer Graphene devices,” Appl. Phys. Lett., vol. 96, no. 1, 2010, Art no. 013512. https://doi.org/10.1063/1.3290248.Search in Google Scholar

[35] K. Nagashio, T. Nishimura, K. Kita, and A. Toriumi, “Contact resistivity and current flow path at metal/Graphene contact,” Appl. Phys. Lett., vol. 97, no. 14, p. 143514, 2010. https://doi.org/10.1063/1.3491804.Search in Google Scholar

[36] F. A. Chaves, D. Jimenez, A. W. Cummings, and S. Roche, “Physical model of the contact resistivity of metal-Graphene junctions,” J. Appl. Phys., vol. 115, no. 16, p. 164513, 2014. https://doi.org/10.1063/1.4874181.Search in Google Scholar
Received: 2021-11-12
Accepted: 2021-12-10
Published Online: 2021-12-21

© 2021 Longfang Ye et al., published by De Gruyter, Berlin/Boston

This work is licensed under the Creative Commons Attribution 4.0 International License.

Articles in the same Issue

  1. Frontmatter
  2. Reviews
  3. A review of terahertz phase modulation from free space to guided wave integrated devices
  4. Intelligent on-demand design of phononic metamaterials
  5. Light activation of 3D-printed structures: from millimeter to sub-micrometer scale
  6. Research Articles
  7. Unveiling radial breathing mode in a particle-on-mirror plasmonic nanocavity
  8. Controlling asymmetric transmission phase in planar chiral metasurfaces
  9. Rayleigh anomaly-enabled mode hybridization in gold nanohole arrays by scalable colloidal lithography for highly-sensitive biosensing
  10. Enhanced terahertz detection of multigate graphene nanostructures
  11. The anisotropic broadband surface plasmon polariton and hot carrier properties of borophene monolayer
  12. Probing higher order optical modes in all-dielectric nanodisk, -square, and -triangle by aperture type scanning near-field optical microscopy
  13. Cascaded microsphere-coupled surface-enhanced Raman spectroscopy (CMS-SERS) for ultrasensitive trace-detection
  14. Morphology adjustable microlens array fabricated by single spatially modulated femtosecond pulse
  15. Design framework for polarization-insensitive multifunctional achromatic metalenses
  16. Electro-optically modulated lossy-mode resonance
  17. Double Rabi splitting in methylene blue dye-Ag nanocavity
  18. Broadband high-efficiency near-infrared graphene phase modulators enabled by metal–nanoribbon integrated hybrid plasmonic waveguides
https://doi.org/10.1515/nanoph-2021-0709
Keywords for this article
graphene; integrated optics devices; modulators; waveguides
Creative Commons
BY 4.0

Articles in the same Issue

  1. Frontmatter
  2. Reviews
  3. A review of terahertz phase modulation from free space to guided wave integrated devices
  4. Intelligent on-demand design of phononic metamaterials
  5. Light activation of 3D-printed structures: from millimeter to sub-micrometer scale
  6. Research Articles
  7. Unveiling radial breathing mode in a particle-on-mirror plasmonic nanocavity
  8. Controlling asymmetric transmission phase in planar chiral metasurfaces
  9. Rayleigh anomaly-enabled mode hybridization in gold nanohole arrays by scalable colloidal lithography for highly-sensitive biosensing
  10. Enhanced terahertz detection of multigate graphene nanostructures
  11. The anisotropic broadband surface plasmon polariton and hot carrier properties of borophene monolayer
  12. Probing higher order optical modes in all-dielectric nanodisk, -square, and -triangle by aperture type scanning near-field optical microscopy
  13. Cascaded microsphere-coupled surface-enhanced Raman spectroscopy (CMS-SERS) for ultrasensitive trace-detection
  14. Morphology adjustable microlens array fabricated by single spatially modulated femtosecond pulse
  15. Design framework for polarization-insensitive multifunctional achromatic metalenses
  16. Electro-optically modulated lossy-mode resonance
  17. Double Rabi splitting in methylene blue dye-Ag nanocavity
  18. Broadband high-efficiency near-infrared graphene phase modulators enabled by metal–nanoribbon integrated hybrid plasmonic waveguides
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 20.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/nanoph-2021-0709/html
Scroll to top button