Purcell-enhanced emission from individual SiV⁻ center in nanodiamonds coupled to a Si₃N₄-based, photonic crystal cavity

2.1 Photonic crystal cavity

Our platform consists of a free-standing, crossed-waveguide PCC in Si₃N₄ featuring low-loss transmission and high-mode confinement together with a minimized cross-talk between pump and probe waveguide (∼−20 dB). On-chip, off-resonant excitation and emission is spatially separated. While the pump waveguide is optimized for 532 nm, the probe waveguide is optimized for 740 nm, which matches the ZPL of the SiV⁻ center. Both waveguides are connected to grating couplers, which allow for out-of-plane excitation and readout. The on-chip excitation of the SiV⁻ centers is achieved by evanescent coupling to the pump waveguide. The probe waveguide hosts a 1D PCC with its modes superimposed to the pump volume. Each cavity mirror consist of N = 53 holes with a period of a = 265 nm. This periodic variation of permittivity forms a band gap in the visible range. A distance cav = 232 nm between these two mirrors is inserted, which results in spectrally separated states inside the photonic band gap optimized by finite difference time domain (FDTD) simulations. The nanophotonic circuit is post-processed with an SiV⁻ ensemble inside the crossing area of pump and probe beam (interaction zone), which is sketched in Figure 1A.

Figure 1:

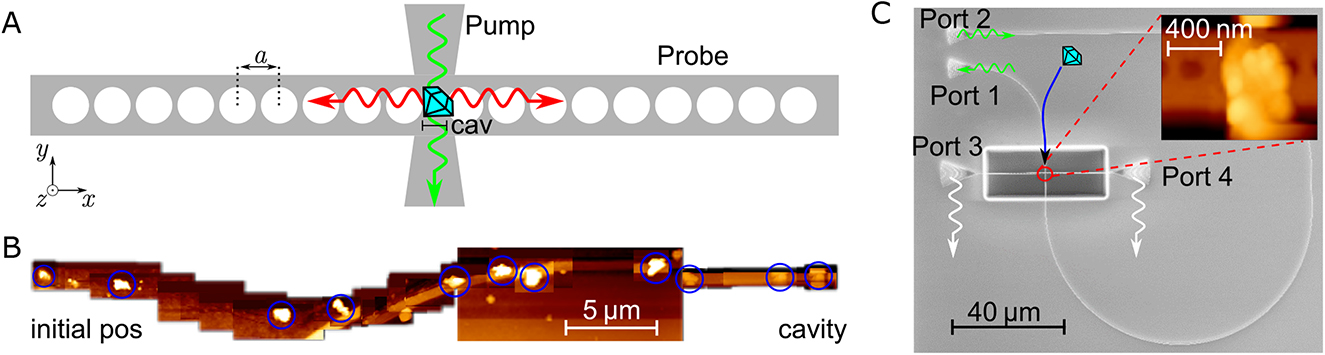
Nanopositioning of ND within cavity mode. A The periodic change a of the material on both sides of the probe waveguide lead to a photonic band gap, while the cavity is formed by the distance cav. The positioned ND can be evanescently excited through the pump waveguide. B AFM images during nanopositioning of SiV⁻ ensemble into PCC. The distance of the initial position was approximately 40 µm to the final position on top of the cavity. C SEM image of the PCC. The device has four grating couplers – two for coupling of green light (port 1 and 2) to off-resonantly excite the emitter in the interaction zone – and two grating couplers (port 3 and 4) for collecting the emission of the cavity system. The inset shows an AFM image of the ND ensemble placed in the interaction zone.

2.2 Post-processing

The post-processing step for placing the ND within the interaction zone of the PCC follows the procedure described in Reference [14], [17]. A dispersion of NDs in water with incorporated SiV⁻ color centers is coated on the surface of the PCC chip. Suitable SiV⁻ center are preselected using a custom-build confocal microscope. Superimposing the confocal scan with an AFM image enables the precise localization of the SiV⁻ center host crystal. After the preselected ND is found, the AFM cantilever tip is used to push the ND in the interaction zone of the PCC. Several steps of the positioning procedure are shown in Figure 1B. The ND is pushed along a total distance of over 40 µm.

The manipulation path is schematically drawn in the SEM image of the photonic device in Figure 1C. The positioned ND is off-resonantly excited through port 1 and its emission into the cavity-waveguide can be read out at port 3 and 4. The small inset shows an AFM image of the positioned ND in the interaction zone. A cross-talk measurement of the empty PCC probes the resonance modes. Therefore, a 532 nm laser with 0.6 mW is coupled into port 1 and the cavity signal is collected at port 3. The signal, arising from Si₃N₄ background fluorescence, is shown in Figure 3A (green). The occurring peaks correspond to the respective cavity modes, where the highest resonance at 721 nm shows a quality factor of Q = 2260 and the resonance near 737.4 nm has a Q-factor of Q = 1000.

2.3 Simulation of Local Density of States

The design of the freestanding PCC is numerically optimized via 3D FDTD simulations [22]. The PCC consists of two modulated Bragg mirrors with inserted cavity region in between. The periodicity of the holes (a = 265 nm) is determined to match the bandgap region of the PCC to the investigated wavelength of the SiV⁻ ZPL. To achieve high Q-factors optimization on the cavity length and hole diameter was performed [14], [23].

For a maximum enhancement of the emitted light, the source need to be placed in the antinode of the electric field distribution of the resonance mode [24]. Thus, the position of the SiV⁻ embedded in a ND is carried out via 3D FDTD simulations [22] in two steps. For the simulation a cube-shaped (200 nm) ND is placed on the cavity region.

The coupling strength between the optical dipole transition and the cavity field mode depends, in particular, on the dipole orientation and the position with respect to the cavity field. Both parameters can be accessed by nanomanipulation as demonstrated in reference [16] without altering the optical properties of the SiV⁻ center. While the dipole orientation shows a cosine dependence the dipole position requires a more sophisticated study. The first optimization step is the enhancement of the Local Density of States (LDOS) dependent on the emitter position (see Figure 2A). The LDOS is proportional to the overlap integral between the electric field distribution of the resonance mode and the emitter [25]. According to the axes in Figure 1A the dipole position, embedded in a ND placed on the cavity, is centered along y- and z-direction and varied along the longitudinal x-direction, since this component shows the strongest contribution to the convolution. The rotational orientation of the dipole is aligned to the PCC axis for highest coupling. The overlap integral of the dipole and the electric field follows a cosine dependence and is therefore one for the aligned case and zero for the orthogonal orientation. The normalized LDOS enhancement is calculated for each position of the dipole with respect to the field distribution of the mode. Therefore, the enhancement of the LDOS through the cavity is divided by the LDOS enhancement for a waveguide without cavity. The highest enhancement (see Figure 2A) for odd modes is achieved for a dipole shift of ∼ (0.4–0.45) a from the symmetry plane of the center of the cavity, matching an antinode of the electric field distribution. For a reduction in simulation time, the number of segments in each Bragg-mirror was reduced to N = 18, since the electric field distribution (position of minimum and maximum) of resonance modes changes in a minor way with varying number of segments.

Figure 2:

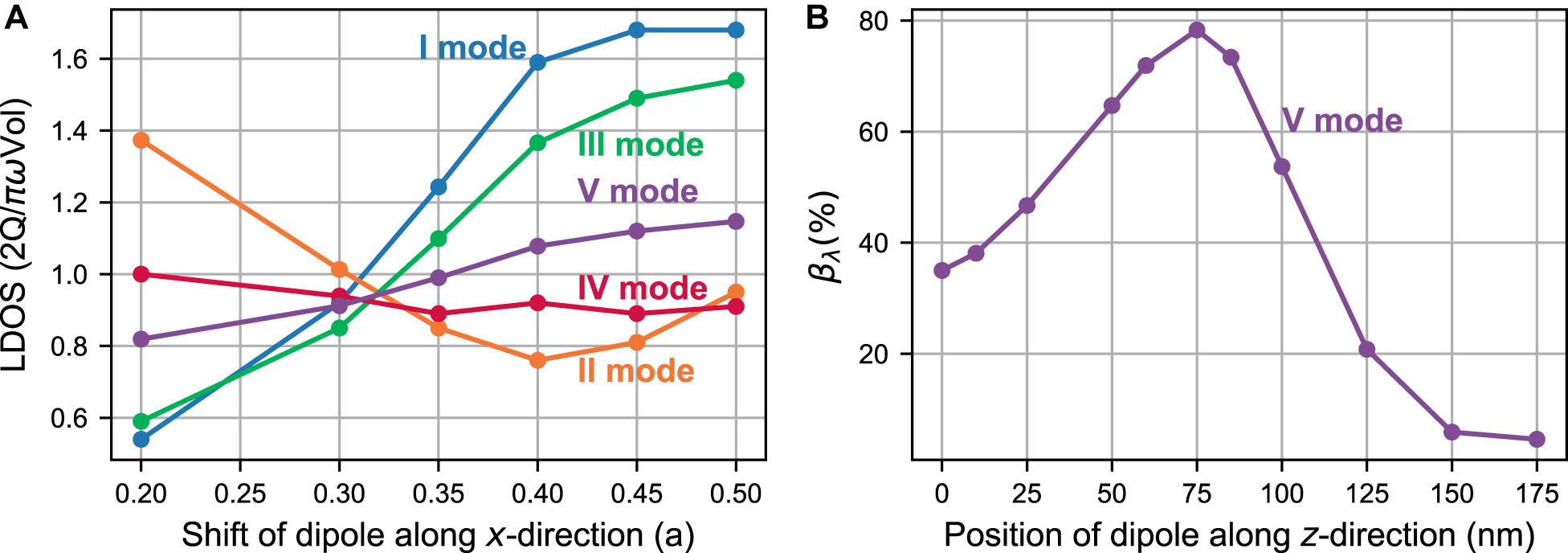
Simulation of ND position on cavity interaction zone. A Simulated LDOS enhancement for different resonance modes of the emitted light from the dipole embedded in a 200 nm cube-shaped ND, dependent on its longitudinal position weighted by the cavity periodicity a. The position of the ND is chosen according to its experimental position in Figure 1C, while the dipole position is varied along the x-direction. B Simulated on-resonance coupling efficiency βλ into researched V-order resonance mode, dependent on the position of the dipole along the z-axis (keeping y and x position fixed at its optimum). The highest coupling efficiency is achieved for a displacement of 60 nm above the cavity surface.

The second part of the 3D FDTD simulations targeted the position optimization of the ND embedded emitter along the z-axis. Therefore, we quantify the coupling of the emitter to the cavity with the β-factor [14], which gives the ratio of coupled spontaneous emission Γ_cav and the total amount of spontaneously emitted photons to free space and in the cavity Γ_free + Γ_cav:

The βλ-factor (spectrally resolved β-factor [14]), correlating with LDOS enhancement, of the emission into the researched V-order resonance mode was examined. To consider the experimental degradation of the PCC due to the presence of the ND in the simulation, the number of segments in each Bragg-mirror was reduced. For this purpose, the number of holes is gradually adjusted from N = 53 to 27 until the simulated Q-factor matches the experimentally examined Q-factor. The center of the ND was shifted according the to the position in the AFM image in Figure 1C. The x-position of the dipole inside the ND is set to its optimal according to Figure 2A, while the z-distance from the surface of the cavity is altered. The resulting coupling efficiencies for different z-positions are shown in Figure 2B. The maximum βλ value of 78% is reached for the source being located 75 nm above the surface of the cavity.

FDTD simulations are carried out to compute the Purcell enhancement [24] for the Vth-order resonance mode of the cross-bar PCCs with N = 27 and N = 53 holes, each with a 200 nm cube-shaped ND crystal on the cavity region as described above. The resulting Purcell-factors read F_P = 20 and F_P = 29, respectively for a spectrally and polarization matched resonance mode and an emitter located at the antinode of the electric field.

2.4 Purcell-enhanced photon emission

After the ND is positioned on top of the interaction zone, the sample is placed inside a flow-cryostat and cooled to approximately 150 K. The emitter-cavity system is excited via port 1 with 130 µW of green laser while the emission is collected through port 3 (shown in Figure 3A in orange). In blue, the free space emission of the SiV⁻ center is shown, where the ensemble is evanescently excited through port 1 and the emission is collected at the center position of the ND. Both collection procedures are shown in the small insets in Figure 3A.

Figure 3:

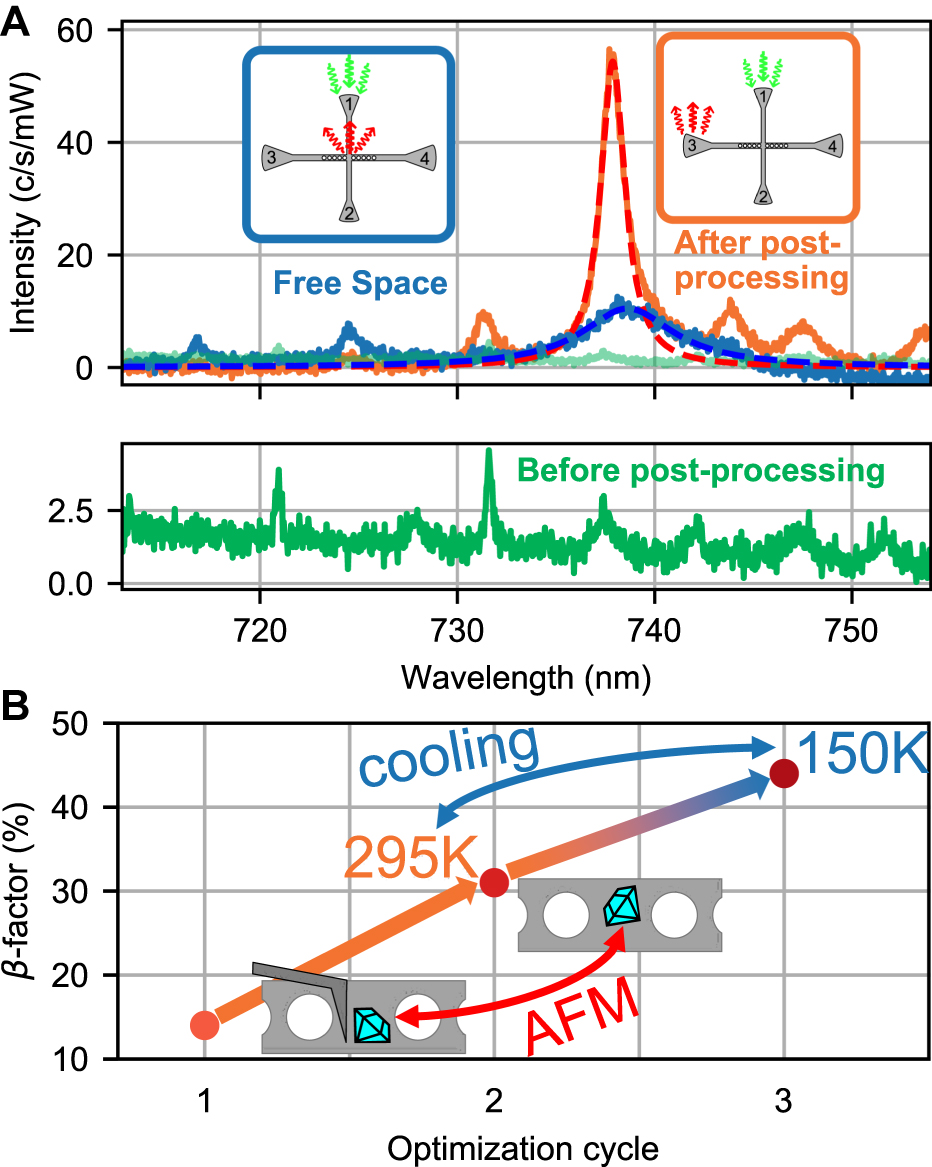
Optimized emitter-cavity coupling. A The cross-talk spectrum of the cavity (green) before the ND was placed, shows a resonance at 737.4 nm. In blue the free space emission of the SiV⁻ ensemble for ≈150 K. The free space emission was collected in the center, while excited over port 1, as it can be seen in the small inset. The spectrum of the coupled cavity emission in orange shows a clear magnification of the emission rate for the resonance at 737.9 nm (excited over port 1 and collected from port 3). A β-factor of 0.44 corresponding to a Purcell of 0.79 was calculated from the Lorentzian fits on the free space and the cavity-emitter emission spectra. B Coupling evolution for three optimization cycles utilizing different tuning mechanism like positioning of the ND inside the interaction zone (step 1 and 2) and temperature tuning (step 3). The highest ensemble coupling was achieved for Position 2 and 150 K.

The presence of the ND in the interaction zone changes the effective refractive index of the cavity. This leads to a red shift of the desired cavity resonance. Together with a change in temperature the shift is approximately 0.4 nm. The altered mode at ∼737.9 nm of the PCC is fed by the ZPL of the SiV⁻ ensemble. The other resonances are slightly enhanced due to phonon side band coupling and scattered background fluorescence. The Q-factor of the desired resonance decreased from Q_cav = 1000 for the empty cavity to Q_coupled = 480 for the coupled system caused by scattering losses and degradation of the PCC. For obtaining the emitted photon rates we compare the photoluminescence (PL) intensities I_cav, I_free, weighted by their relative efficiencies.

According to equation (1), we obtain a coupling of:

where I_free, I_cav are the detected intensities of the free-space and cavity emission, ηcav=0.14 is the coupler efficiency and ηfree=0.082 is the collection efficiency of the free space emission. The coupler efficiency ηcav is determined via a transmission measurement of a laser at the desired wavelength through the probe beam. Therefore, the laser is coupled into port 3 and the transmission is detected at port 4, while keeping all efficiencies of the optical components tracked. The power of the laser coupled into the waveguide is compared to the power obtained after the waveguide. The free space collection efficiency ηfree is limited due to a NA = 0.55 objective. Integrating over the radiative emission profile overlapping with the solid angle of the objective leads to a collection efficiency of 0.082. Please note, that the dipole alignment of the SiV⁻ center is such that high free-space emission corresponds to the best coupled SiV⁻ centers, while our geometry does not allow for artificially decreased ratio between free-space and waveguide emission. A decrease in confocal contrast would equally lead to a decrease in waveguide coupling. Conversely, a decrease in waveguide coupling not necessarily leads to a decrease in confocal coupling. The achieved β-factor corresponds to nearly every second photon being emitted into the cavity resonance and leads to an average Purcell-enhancement [26] of

for all emitters inside the SiV⁻ ensemble. The tuning mechanisms for modifying the ensemble coupling utilized so far, are position of the ND and temperature. In Figure 3B the β-factors after optimizing the position of the ND and after temperature tuning are shown. The position and orientation of the ND in the interaction zone can be controlled by AFM-based nanomanipulation [16], which yields to a better dipole alignment of the ND to the cavity axis. Position 1 and position 2 in Figure 3B correspond to a coupling averaged over the whole ensemble of 0.14 and 0.31, respectively. At position 2 we cooled the sample from 295 K to ∼150 K. This further increased the average ensemble β-factor to 0.44 (as shown in Figure 3A and given in equation (1)).

Additional reduction of the temperature to ∼4 K reveals the fine structure splitting of the SiV⁻ centers in the ensemble. Thus, instead of the average ensemble coupling the β-factors of individual transitions of single SiV⁻ centers can be determined, as depicted in Figure 4. Again, the free space emission (blue) needs to be compared to the joint emitter cavity signal (insets Figure 3A). Freezing and unfreezing processes, together with temperature tuning further shifted the central frequency of the resonance mode to approximately 740.3 nm (depicted in gray Figure 4 top). This implies a detuning from the average ensemble ZPL resonance at ∼738 nm leading to decreased average coupling. The detuning enables the coupling of individual, however more strained, SiV⁻ centers (Figure 4 top), apparent when zooming into the red square (Figure 4 bottom). A splitting of (244 ± 10) GHz between the doublet of (A,B) and (C,D) is observed, while the splitting between C and D is (37 ± 10) GHz. These four lines arise from one SiV⁻ center with an excited state splitting of 252 GHz and a ground state splitting of 46.3 GHz influenced by the strain inside the ND [4], where the ZPL position of the SiV⁻ can be shifted (axial strain) while keeping the state splitting constant (low transverse strain) [27]. The used NDs have proven to inhere low transverse strain [4]. For the SiV⁻ center transition A and D have the same dipole orientation as well as transition B and C [28]. Figure 4 confirms that transition B and C show a better coupling to the cavity mode than transition A and D originating from dipole alignment of the emitter to the cavity axis. Due to strain induced differences in the selection rules, transition B and C show different enhancement factors [29].

Figure 4:

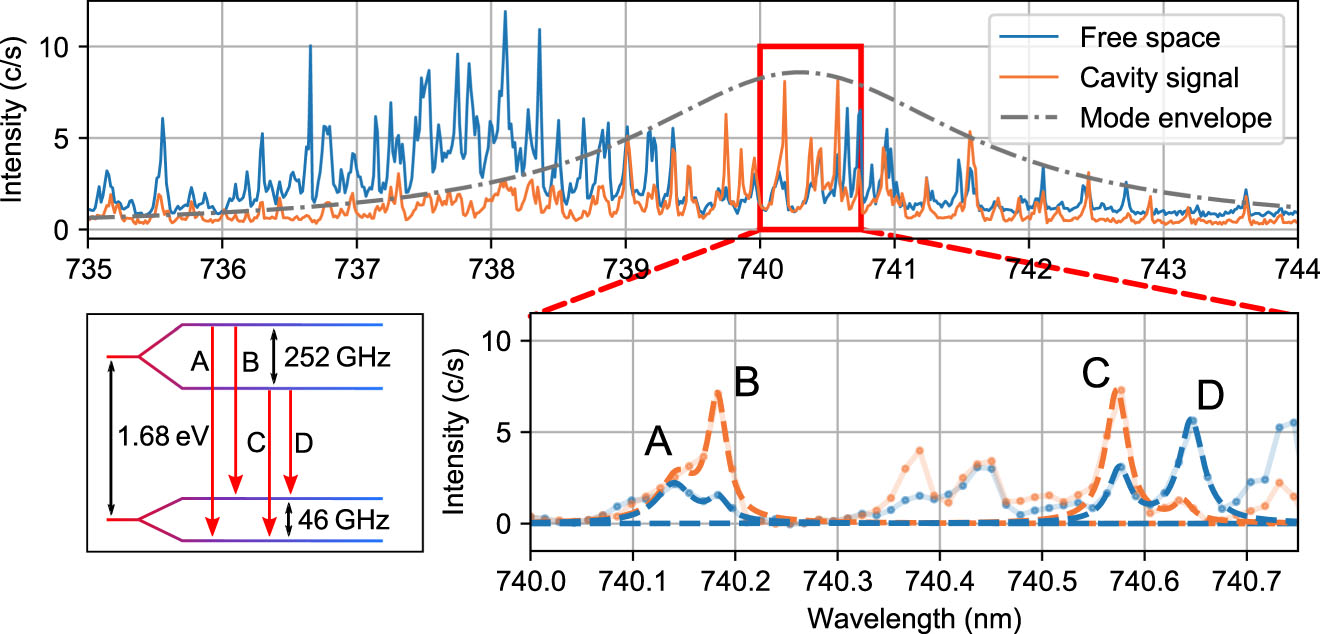
Spectrum of coupled emitter-cavity system at cryogenic temperatures. Cavity emission of coupled SiV⁻ ensemble in orange. Free space emission in blue and envelope resonance mode in gray. For some spectral lines, the emission into the cavity mode reaches higher counting rates than into free space. The lower plot shows a zoom of the area in the red rectangle and the four transitions A–D (level scheme sketched on the right) of the SiV⁻ center are referenced to the lines according to their spacing.

Similar dipole orientation of the transitions reach higher (B and C) and lower (A and D) coupling efficiencies to the cavity mode. From these values according to equation (1), we estimate the β-factor for all four transitions. The highest coupling was achieved for transition B, which is βB=0.81. This value translates to a Purcell enhancement of

4/5 of the total spontaneous emission are channeled into the photonic circuit. The measured β-factor of 0.81 corresponds to a lifetime reduction of 0.2τ0, where τ0 is the lifetime of the SiV⁻ without cavity. The reduced lifetime for the SiV⁻ on resonance with the cavity is about 340 ps, too short to be observed with our current experimental equipment.

4.1 Fabrication of nanodiamonds

SiV⁻ containing diamond nanoparticles were obtained by HPHT treatment of the metal catalysts-free growth system based on a homogeneous mixture of naphthalene (C₁₀H₈), fluorographite (CF_1.1), and tetrakis(trimethylsilyl)silane (C₁₂H₃₆Si₅) which was used as the Si doping component. (Introduction of fluorine-containing compounds into the growth system was intended to reduce the content of NV centers in NDs-SiV⁻) HPHT treatment of the initial homogeneous mixtures was carried out in a high-pressure apparatus of “Toroid” type. The experimental procedure consists of loading the high-pressure apparatus to 8.0 GPa, heating the samples up to 1450 °C and short (3 s) isothermal exposures at these temperatures.

4.2 Fabrication of the photonic chip

Free-standing PCC devices on chip were realized on Silicon nitride-on-insulator wafers consisting of 200 nm stoichiometric Si₃N₄ on top of a 2 µm thick SiO₂ layer on top of Si. Fabrication of the nanophotonic circuits involved several steps of electron-beam lithography (e-beam) followed by reactive ion etching. The nanophotonic circuits were defined on top of the Si₃N₄ layer using negative tone photoresist ma-N 2403 in the first lithography step and after were 75% dry-etched into the silicon nitride layer using an CHF₃/O₂ plasma. To realize freestanding PCC underneath SiO₂ should be removed, which was achieved by opening a window around the photonic crystal region in the second step of lithography by means of exposing positive photoresist PMMA in this area. In the following step, the remaining 25% of silicon nitride in the window area was etched, while the waveguide inside of the window was protected with a ma-N 2403 photoresist; the waveguides outside the windows were protected by unexposed PMMA photoresist. After that, both photoresists were removed by O₂ plasma. In the last fabrication step SiO₂ layer in the windows was removed by wet etching, namely by immersing the chip in hydrofluoric acid (HF).

4.3 Optical methods

The optical readout was established by a self build confocal microscope setup with an NA = 0.55 objective (×50 magnification). For scanning the sample, a galvo mirror system was used. With the help of a second laser path and a 4f-lens system, the laser can be set on a fixed position, while the readout is collected from a different position. The readout can be directed on a spectrometer and an avalanche photo diode.