Maximized vertical photoluminescence from optical material with losses employing resonant excitation and extraction of photonic crystal modes

1 Introduction

Low optical quality of a material with otherwise perfect physical and chemical properties can significantly reduce its practical application in the field of photonics. One such material is the nanocrystalline diamond, which shares high mechanical and chemical stability [1], or the ability to host single-photon sources [2], [3] with the monocrystalline diamond. However, its optical quality is significantly worse due to the optical losses and light scattering on grain boundaries [4], [5], [6]. Another material in which optical quality hinders its usage as an efficient light source, for example, as an alternative to the materials used nowadays for organic light-emitting diodes, are halide perovskites [7], [8]. In addition to the optical losses, the relatively high refractive index causes that only a small portion of light within an escape cone is radiated out from the thin layers of these materials [9]. The major part of the emitted light is coupled to guided modes supported by the layer and then gradually absorbed [10]. The extraction is slightly enhanced due to the scattering on inhomogeneities [11], [12]. Nevertheless, the emission has a Lambertian radiation pattern, which requires the usage of sophisticated optical elements in order to achieve reasonable collection efficiency [13].

Various photonic structures can be used for manipulating light emission from materials with absorption and scattering losses [14], [15], [16], [17], [18]. For instance, both the total internal reflection and the amount of absorbed light can be reduced by fabricating a suitable two-dimensional photonic crystal (PhC) on the top of a thin layer [19], [20], [21], [22], [23]. Luminescence of the embedded light-emitters couples to the leaky photonic modes of the PhCs which then radiate to air under defined directions via the Bragg diffraction phenomenon [24]. The extracted emission is thus strongly directional and the far-field radiation pattern can be tuned based on the required application by dimensions of the PhC [25].

This is particularly important for etendue limited applications [26] because then the extracted light can be easily collected by a simple optical system or sent directly onto a detector. Moreover, the amount of absorbed radiation is reduced due to relatively short optical path [27]. Recently, we have shown that by using 2D PhCs on a polycrystalline diamond, up to 14-fold extraction efficiency enhancement of the vertical light emission on a peak wavelength can be achieved [28]. The vertical extraction provides the highest emission intensity with respect to other extraction directions due to the degeneracy of the vertically out-coupled modes [29].

When optical excitation is used for generating emission, the PhC structure can be designed so that the excitation beam is coupled into the layer through an excitation leaky mode. This causes a significant increase of the excitation efficiency and by this also the enhancement of the photoluminescence (PL) intensity without the need to increase the excitation power. The concept which combines excitation and collection via leaky modes was first introduced in 2007 by Ganesh et al. [30], [31], and is called the resonant excitation and extraction, and it is successfully employed for the materials with negligible optical losses and surface deposited light-emitters. The authors argued, and their experiments proved that the main factor affecting the efficiency of this process, are the Q-factors of the excitation and extraction modes. Namely, the high Q-factor of the excitation mode enables the long-lasting localization of the pumping beam within the layer and, on the other hand, the low Q-factor of the extraction mode causes fast out-coupling of the emitted radiation to the desired direction.

In this contribution we demonstrate that the enhancement of the PL intensity into vertical direction from light-emitters distributed homogeneously inside a thin layer with low optical quality can be also significantly enhanced by accommodating the resonant excitation and extraction scheme, but in a specific regime. Namely, we propose and verify that employing one type of the leaky mode for both the excitation and the extraction in combination with maximized coupling of the emission to the extraction mode is pivotal when the emitters are distributed homogeneously inside the material. Further we show that the Q-factor analysis must also include absorption and scattering of light in the material with low optical quality. On the example of a nanocrystalline diamond layer with a PhC on its surface, we demonstrate up to 115-fold PL intensity enhancement at the wavelength of the extraction leaky mode using this approach. The nanocrystalline diamond was chosen because it comprises optical losses due to absorption and scattering [4], and in the same time it possesses spectrally broad visible PL [32]. The latter enabled us to elaborate this scheme for both the fundamental TE and TM modes on the similar sample. Finally, we demonstrate that our experimental results agree with the outputs of the simulations.

2 Sample design

The PhCs were designed with a goal to achieve resonant excitation with blue (or green) laser and, at the same time, efficient resonant extraction of the wavelengths within a red spectral region. The resonant excitation and resonant extraction scheme includes the following steps (Figure 1A): (1) in-coupling of blue excitation beam into the leaky mode of the photonic structure, (2) absorption of the in-coupled light by the material, (3) emission of red PL from the excited emitters and its subsequent coupling into the extraction leaky mode, and (4) out-coupling of the light via the extraction leaky mode into the vertical direction. Some other effects such as direct absorption of laser beam or direct emission from the material into space also contribute to the observed PL intensity in a vertical direction. However, their contribution is marginal, and we concentrate solely on the resonant excitation and extraction scheme.

Figure 1:

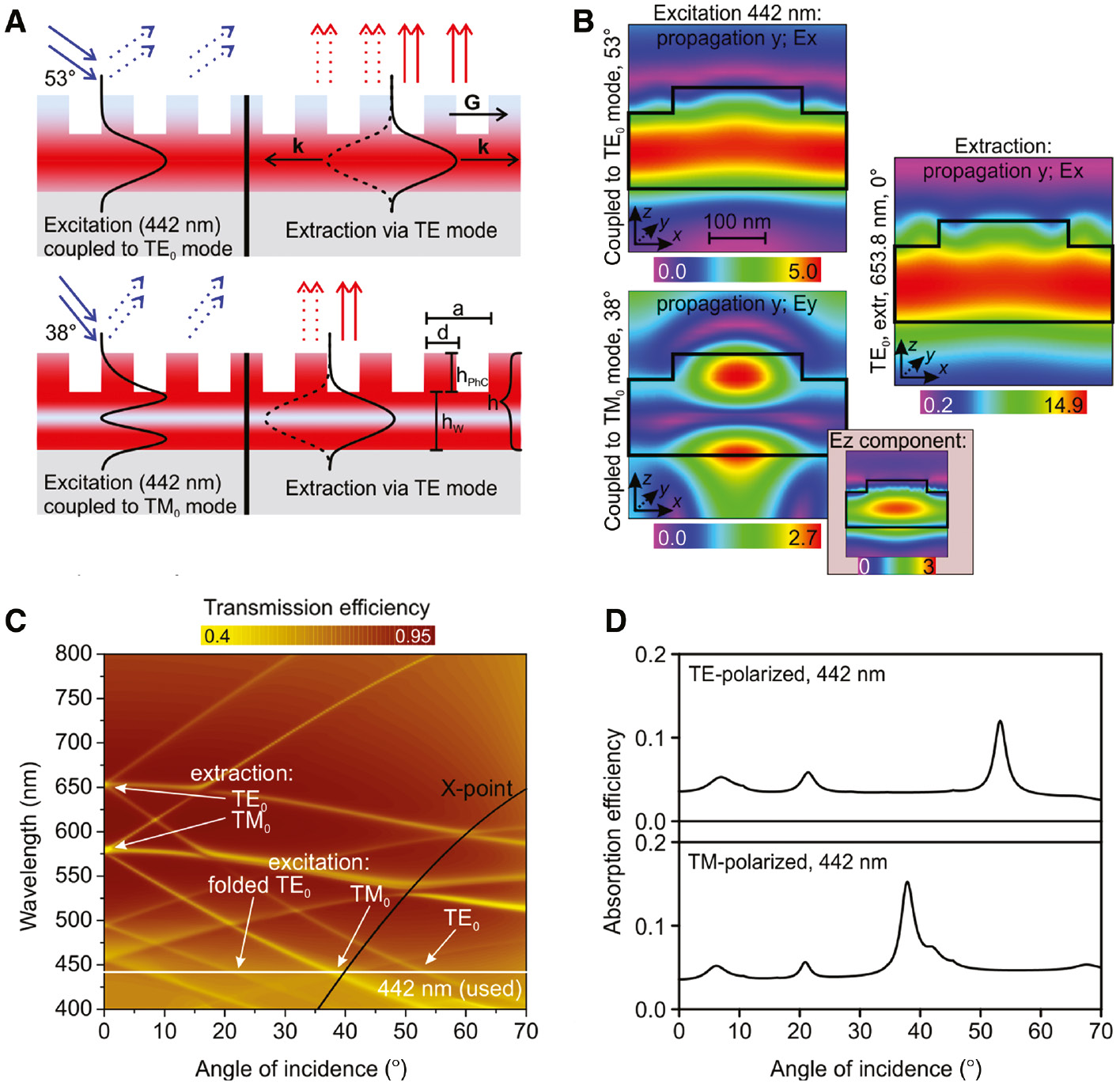
Principle of light extraction via leaky modes and the properties of leaky modes.

(A) Schematic sketch of the resonant excitation (left part of the image) and extraction (right part) of photoluminescence (PL) via Bragg diffraction of leaky modes. Excitation laser (blue solid arrows) is coupled into the leaky mode of the photonic crystal (PhC) (black solid curve). While propagating in the material, it is partially absorbed (red region) and partially diffracted out (blue dashed arrows). The excited emitters (located in red region) then emit light that partially couples to the extraction leaky mode (black solid and dashed curves) and is diffracted out from the material (red arrows). Spatial overlap of the excited region (defined by the excitation leaky mode) with the extraction leaky mode is crucial for maximizing PL enhancement using the resonant excitation/extraction scheme. (B) Simulated electric field intensity for the PhC-A sample (see Figure 2) for TE₀ and TM₀ excitation mode (left) and TE₀ extraction mode (right). Note that the TM₀ mode has two nonzero components of E-field with different distributions. The black line shows the boarders of PhC unit cell. The intensity of the field is normalized to the unit amplitude of the incident wave. See Figure S5 in Suppl. info for simulations of field components of all modes relevant for the discussion throughout the paper. (C) Simulated photonic band diagram of PhC-A sample for angles of incidence between 0° and 70°. The graph shows the transmission efficiency of unpolarized light for given wavelength and angle of incidence. (D) Simulated absorption efficiency of PhC-A as a function of the angle of incidence (between 0° and 70°). Increased absorption at 442 nm matches the position of leaky modes in (C). The effects of scattering and fabrication defects are not included.

The steps (1), (2), and (4) depend on the dimensions of the PhC and their efficiency can be described by the Q-factors of the excitation and extraction leaky modes. The total Q-factor of the mode is composed of three contributions, which quantify the losses caused by individual mechanisms:

where ω₀ is the central frequency of the leaky mode and Δω is the leaky mode full width at half maximum and Q_dif, Q_abs, and Q_scat characterizes the losses caused by Bragg diffraction, absorption, and scattering (both on material inhomogeneities and on defects caused by fabrication) of light, respectively. The out-coupling efficiency of a leaky mode from the PhC slab is maximized when the Q_dif is minimized, and simultaneously Q_abs and Q_scat are maximized. Subsequently, most of the light is diffracted into defined direction instead of being absorbed or randomly scattered. On the other hand, the excitation efficiency is maximized when Q_abs is minimized, and Q_dif and Q_scat are maximized. The low Q_abs implies high absorption and high Q_dif and Q_scat extend the optical path of the mode in the material. The absorption and scattering losses are given by characteristics of the material, which we do not try to tune (although it is possible by changing the deposition conditions). Nevertheless, all, Q_dif, Q_abs, and Q_scat, can be changed by the physical dimensions of the PhC. Note that it follows from the above-discussion, that the Q_dif and Q_abs requirements on the extraction and excitation leaky modes are exactly opposite.

The efficiency of step (3) depends on the single-mode local density of optical states (SM-LDOS) that quantifies the power that is coupled to the specific mode from the dipole source. Note that the total LDOS is higher than SM-LDOS because it includes also light that couples to other modes and the light that is directly radiated to space. The spatial profile of the SM-LDOS is proportional to the electric field distribution of the respective mode. The efficiency of step (3) is thus proportional to the spatial integral overlap between the electric field distribution of the extraction mode (black curve in the right part of Figure 1A) and the region of excited light-emitters (red-colored region in Figure 1A), in accordance with Fermi’s golden rule [33]. The distribution of excited light-emitters follows the intensity profile of the excitation leaky mode, when resonant excitation is used. Figure 1A outlines this situation for two cases of the excitation mode: fundamental TE (TE₀) and fundamental TM (TM₀). Clearly, the highest spatial overlap between the excited region and the electric field distribution of extraction mode is achieved when both excitation and extraction is done via the leaky modes with similar intensity distributions (Figure 1A top), i.e. modes of the same type (TE or TM) and order. When two different modes are used (e.g. TM₀ for excitation and TE₀ for extraction Figure 1A bottom) the spatial overlap is reduced. The simulated electric field distribution for the modes is shown in Figures 1B and S5 in the Suppl. info. We chose the TE₀ mode for extraction and excitation as it has the highest overlap of the electric field distribution with the layer, and thus provides the highest SM-LDOS, when the light-emitters are distributed homogeneously in the layer, as we confirmed also experimentally. On the other hand, TM₀ mode is advantageous when the emitters are located near the surface because its electric field distribution is localized near edges of the structure (Figure 1B).

Overall, for maximizing the efficiency of the whole excitation/extraction process, we require high Q_dif for excitation leaky mode, low Q_dif for extraction leaky mode, and the usage of the same type and order of the excitation and extraction leaky mode. However, it is not possible to fulfill all the three requirements in the same time as the Q-factors on one photonic mode branch cannot be tuned separately. As we will show, the excitation/extraction scheme realized via the similar mode is for the case of materials with low optical quality, and emitters inside the material more important than choosing different types of modes with ideal Q-factors.

The other factor that influences the efficiency of the step (3) is the thickness of the diamond layer. Optimal layer thickness, for which the SM-LDOS in PhC is maximized, exist for each mode [34]. Both LDOS and SM-LDOS can be estimated by performing 3D finite-difference time-domain (FDTD [35]) simulations. For the case of waveguide that supports only fundamental modes, the FDTD simulation directly shows the amount of light coupled to the respective photonic mode, which is proportional to the SM-LDOS of that mode [36]. We performed simulations for the dipole source placed in the middle, in the top and bottom quarter, and on the top and bottom edge of the planar diamond waveguide (Suppl. info section: 2. coupling efficiency to modes). The simulation confirms that the coupling efficiency depends on the electric field distribution of the modes. For instance, the highest portion of light is coupled to the TE₀ mode for the dipole source positioned in the middle of the waveguide, because the TE₀ mode has maximal electric field there. Moreover, we used a wide-frequency source, which allows to detect the optimal thickness-to-wavelength ratio for obtaining optimal coupling of emitted light to the guided mode (the ratio for which the SM-LDOS of the extraction mode is maximized).

The optimal thickness of diamond layers (n_D=2.32, see Figure S7 in Suppl. info) on SiO₂ substrate (nSiO2=1.45) for red light (around 650 nm) coupling to the TE₀ mode lies in the range of 78 and 124 nm as follows from the FDTD simulation (see Figures S2–S4 in Suppl. info). For light source located in the middle of the layer with optimal thickness, the TE₀ mode carries more than 77% of the total power, which would be emitted by the same source into homogeneous medium. The basic idea of excitation and extraction via the same type of leaky mode is valid also for structures, which support higher order modes at the extraction wavelength. Nevertheless, the PL can couple to all supported modes and the efficiency of coupling into the specific extraction leaky mode is reduced.

Upon acquiring the optimal thickness (h_w) for the main waveguiding layer, we computed dimensions (lattice constant a, column diameter d, and column height h_PhC, see the schematic image in Figure 1A) of square-lattice PhCs to be fabricated on the top of it. We designed and fabricated two PhC structures (Figure 2) to support vertical extraction of the PL in red spectral region via TE₀ leaky mode. The first structure (PhC-A) had waveguiding layer (h_w, see Figure 1A) within the range of the optimal thickness. The second structure (PhC-B) was designed to have low Q_dif on extraction wavelength, which denotes more effective out-coupling of the extraction leaky mode into the vertical direction. The total thickness (h=h_w+h_PhC) was 160 nm for both samples. The main idea was to show that the effect of efficient coupling to extraction mode (pronounced in PhC-A) leads to better overall enhancement than high efficiency in out-coupling of the extraction leaky mode alone (PhC-B; Figure S13 in Suppl. info shows the TE₀ mode profile of this sample). The square symmetry was chosen because it has less complicated photonic band structure than the hexagonal one and the effect of resonant excitation/extraction can be thus more easily demonstrated.

Figure 2:

Scanning electron microscopy micrographs of the diamond-based 2D PhCs.

(A) PhC-A: lattice constant a=345 nm, column diameter d=205 nm, thickness of diamond layer before etching h=160 nm, and thickness of diamond layer after etching h_w=120 nm. (B) PhC-B: lattice constant a=390 nm, column diameter d=215 nm, thickness of diamond layer before etching h=160 nm, and thickness of diamond layer after etching h_w=55 nm. The insets show the morphology of respective samples under 45° angle.

3 Results

3.1 PL enhancement

The sample was excited with the TE (s) or TM (p) polarized cw laser beam (442 nm) incident along the Γ-X [37] direction of high symmetry. The excitation angle of incidence was varied from 7.5° to 67.5° and the PL signal was collected with an optical fiber being perpendicular with respect to the sample surface in order to collect only the normally extracted leaky modes within a small collection cone. An example of such a PL spectrum for the nonresonant excitation of the PhC-A is shown in Figure 3A. The extraction leaky modes are manifested as sharp resonances at particular wavelengths. Their spectral positions are in agreement with the computed ones (Figure 1C).

Figure 3:

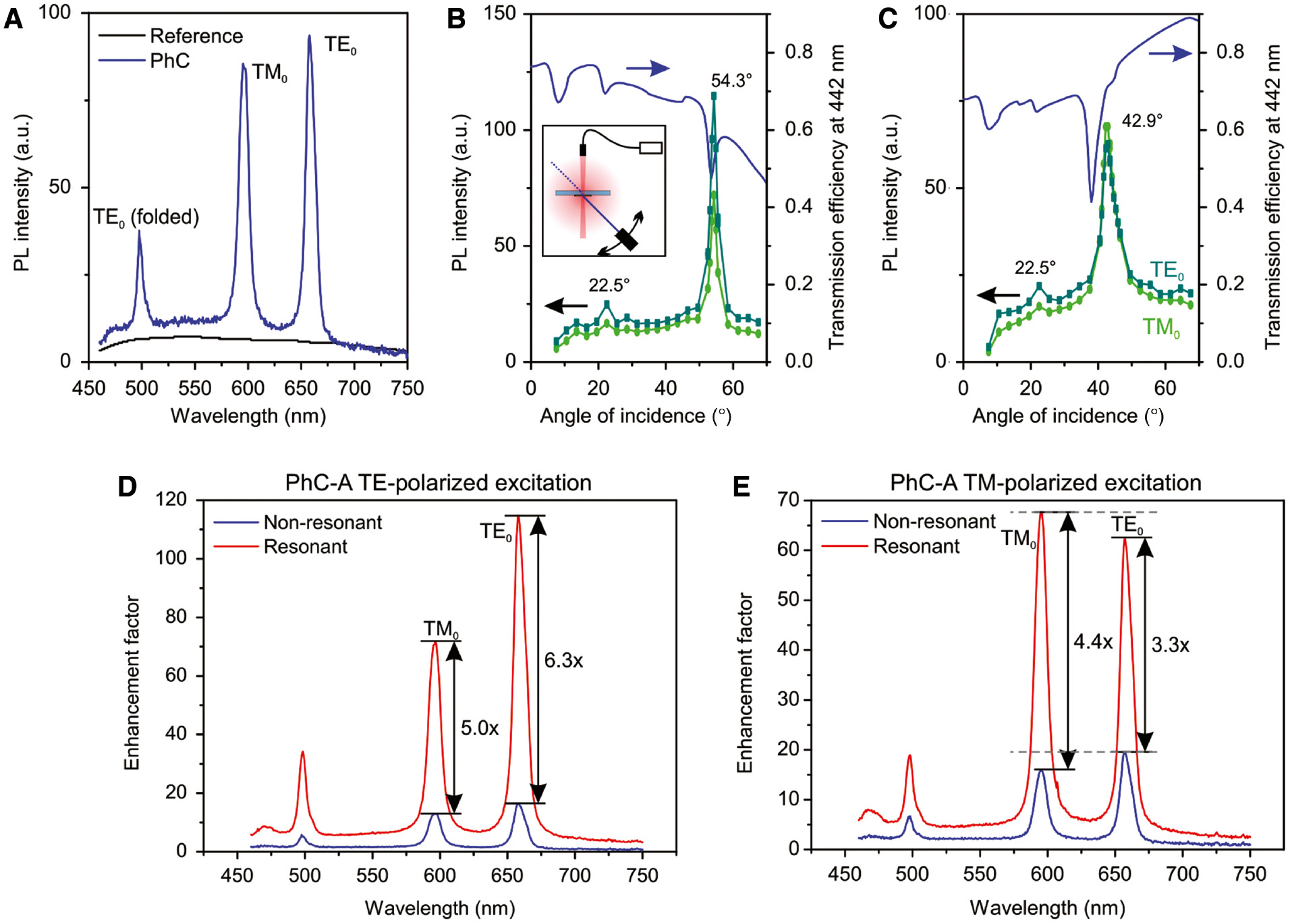
PL spectra and enhancement factor under non-resonant and resonant excitation.

(A) The comparison of PL intensity measured on plain diamond layer (black) and on PhC-A (blue, nonresonant excitation). (B, C) The normalized PL intensity measured on PhC-A sample at the wavelength of the TE₀ (658 nm) and TM₀ (596 nm) extraction leaky mode as a function of the angle of incidence of the excitation beam (the connecting lines are guides to the eye), and rigorous coupled-wave analysis (RCWA) simulated transmission efficiency of the excitation beam (442 nm-blue line): (B) TE-polarized excitation beam; inset shows the measurement setup (see Suppl. info for details), (C) TM-polarized excitation beam. (D, E) The enhancement factor of PhC-A sample when excited with (D) TE-polarized and (E) TM-polarized excitation beam.

Figure 3B plots the measured PL intensity at the wavelength of the TE₀ extraction mode as a function of the excitation angle for the TE excitation of the PhC-A. The two PL signal maxima, one at around 22.5° and the other at 54.3°, occur at the similar angles as the leaky modes in the simulated curve of the transmission efficiency of the excitation laser, which implies that the enhancement of the signal is due to resonant in-coupling of the excitation laser into the structure. Similarly, the TM polarized excitation beam is coupled to TM₀ mode when incident at 42.9° (Figure 3C). Here the correspondence with the computed transmission spectrum is not perfect, which is caused by the inaccuracy of numerical simulation for TM₀ mode as explained in Suppl. info (Figure S12).

As a next step, the performance of the PhCs with respect to the light emission enhancement was evaluated via an enhancement factor, which we define as a ratio of the PL intensity measured on the PhC (I_PhC) to the PL intensity measured on the unpatterned diamond layer (I_ref) with thickness h. Figure 3D and E shows the dependence of the enhancement factor on the emission wavelength for the resonant excitation via TE₀ and TM₀, respectively, in comparison to the nonresonant excitation for the PhC-A. The total enhancement factor (EF_tot) can be written as

(2)EFtot(λ)=IPhC(λ)Iref(λ)=EFleaky(λ)+EFLamb−1

where the EF_leaky is the contribution of leaky modes to the PL and the EF_Lamb is the spectrally independent enhancement of the Lambertian radiation (further denoted as a Lambertian enhancement factor) being simply the enhancement of the radiation not coupled to guided or leaky modes. The correction −1 must be added so that the total enhancement remains 1 if both the EF_Lamb and EF_leaky are equal to 1 (i.e. the PL is not enhanced). Numerical values of the PL enhancement factors at the peak wavelengths of the extraction modes are summarized in Table 1. For the PhC-A, various combinations of the extraction and excitation leaky modes were evaluated, whereas for the PhC-B, only the combination relevant for the discussion is listed.

Table 1:

Enhancement factors for the photonic crystal (PhC)-A and PhC-B samples (for detailed explanation see the main text).

			PhC-A				PhC-B
Extraction mode			TE0	TM0	TE0	TM0	TE0
Excitation mode			TE0	TE0	TM0	TM0	TE0
Total enhancement factor			114.7	71.9	62.9	67.6	67.7
	Lambertian enh.a		6.1	6.1	4.8	4.8	7.6
	Leaky mode enh.		109.6	66.8	58.8	63.8	61.1
		Extraction enh.	17.4	13.4	17.7	14.4	21.5
		Excitation enh.	6.3	5.0	3.3	4.4	2.8

1. Various combinations of excitation/extraction modes were measured for PhC-A. Note that the excitation enhancement factor includes both, the in-coupling (Q-factor related) and field overlap (between excitation/extraction leaky modes) effects. ^aLambertian enhancement factor under resonant excitation.

As Table 1 shows for the PhC-A, the listed values of the Lambertian enhancement factor depend on the polarization of the excitation beam mainly because they reflect the enhancement with the resonant excitation. The radiation resonantly coupled to the TE₀ excitation leaky mode has higher spatial overlap with the emitters than the TM₀ mode and thus it provides higher excitation efficiency and subsequently the increase of the overall PL. The EF_Lamb values then naturally remain approximately constant over the whole PL spectrum (we have observed only small variations due to the Fabry-Pérot resonances). The Lambertian enhancement factor is much smaller for nonresonant excitation, where it may be caused by several factors: (1) diffraction of light on the PhC into the first real diffraction order, which changes the electric field distribution of excitation beam inside the sample, (2) different volume and surface of the PhC with respect to the reference layer, and (3) Fabry-Pérot resonances. Overall, the Lambertian enhancement factor presents only about 5% of the total PL enhancement (Table 1). The remaining 95% of the PL enhancement is due to leaky modes enhancement.

The leaky modes enhancement factor (at the wavelength of the leaky mode λ₀) can be divided into (1) pure extraction enhancement factor (EF_Extr) measured under nonresonant excitation angle and (2) resonant excitation enhancement factor (EF_Excit):

(3)EFleaky(λ0)=EFExtr⋅EFExcit

The highest, 110-fold leaky mode enhancement was obtained for the TE₀ resonant excitation and the TE₀ extraction leaky mode of the PhC-A (Figure 3D), which is six times more than for the nonresonant excitation (Table 1). For the TM₀ leaky extraction mode, the enhancement is around 67× when excited with TE₀ mode. On the other hand, for the TM₀ resonant excitation (Figure 3E), the PL enhancement at the TE₀ extraction mode is only around 59× whereas it is higher for the TM₀ extraction (64×). Clearly, the overlap of the excitation and the extraction modes (both TM₀) outweighs the fact that the structure is optimized for the extraction via the TE₀ mode. However, in overall the enhancement factor is much smaller than that obtained at this sample with TE₀ resonant excitation and extraction (Table 1), because the spatial overlap of the TM₀ mode with diamond and hence with the light-emitters is smaller than for the TE₀ mode (Figure 1B). These experimental results confirm our hypothesis that the PL emission can be significantly enhanced when coupling and out-coupling is realized via the photonic modes of the same type and order.

Furthermore, the extraction enhancement factors for a single type of the extraction mode are (within the error of the measurements) similar for both polarizations of the excitation beam, for example 17.4× and 17.7× (Table 1) for the TE₀ extraction mode. This is due to the fact that the diamond light-emitters do not possess any preferential orientation in the layer and thus respond similarly to both polarizations of the excitation beam.

For the case of PhC-B, the total enhancement factor is around 61, which is approximately three times more than for the nonresonant excitation (Table 1). The effect of resonant excitation is significantly lower when compared to PhC-A sample because the thickness of the waveguiding layer (h_w) is not optimized for resonant excitation and extraction scheme. On the other hand, as designed, the sample has higher extraction enhancement factor than PhC-A due to higher spatial overlap of the TE₀ with the PhC structure.

3.2 Q-factor analysis

The excitation and extraction enhancement can be contrasted with the Q-factor analysis. The Q-factors in Table 2 were extracted from measured and simulated band diagrams (Figure 4) and their computation is described in Suppl. info (Section 4, Experimental). The main cause of losses for TE₀ leaky mode is absorption (low Q_abs) because this mode is localized in the material and has thus high overlap with the lossy material. On the other hand, the losses of TM₀ mode are caused primarily by Bragg diffraction (low Q_dif) and scattering on surface defects (low Q_scat) as this mode is localized on the edge of the structure, where the PhC and fabrication defects are located.

Table 2:

The total Q-factor (Q) of leaky modes, which we determined from transmission measurement, is divided according to the type of losses: diffraction losses Q_dif, absorption losses Q_abs, and scattering losses Q_scat.

Leaky mode	PhC-A				PhC-B
		TE0		TM0		TE0
Wavelength (nm)	658	442	596	442	631	442
Q	82		61		36
Qdif	344	340	187	114	67	29
Qabs	142	116	207	130	242	315
Qscat	445		161		115

1. The relationship between Q-factors is given by (1).

Figure 4:

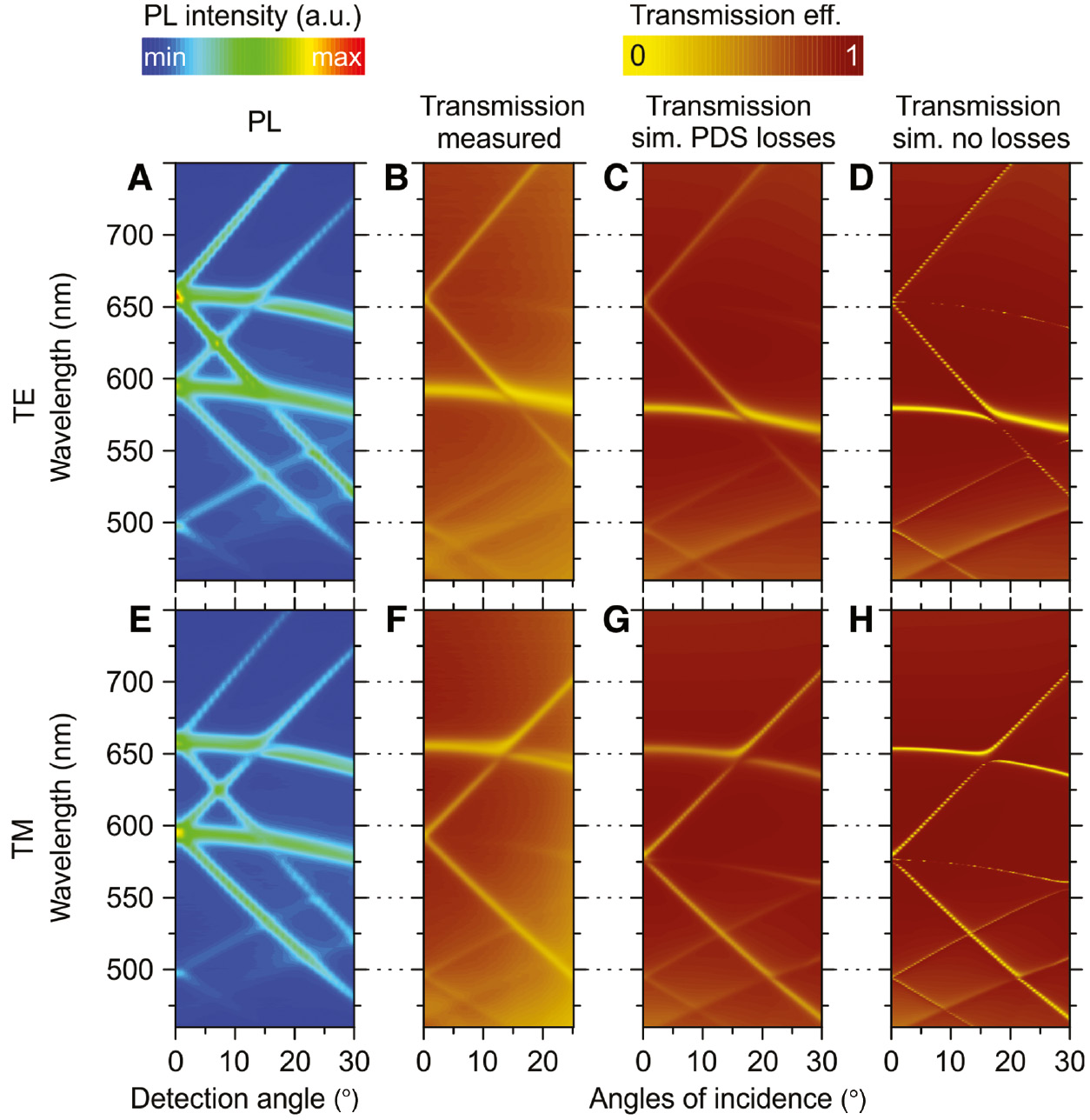
Measured PL spectra (PhC-A) as a function of the extraction angle, and transmission band diagrams.

(A) Angle-resolved PL spectra excited by TE-polarized laser beam incident at the resonant angle of 54.3° and (E) excited by the TM-polarized laser beam incident at the resonant angle of 42.9°. Measured (B), RCWA simulated with losses (C), and simulated without losses (D) transmission efficiency as a function of the angle of incidence (along the Γ-X direction of high symmetry) for the TE-polarized light. (F–H) Same for the TM-polarized light.

For the efficient out-coupling of the leaky modes high Q_abs and Q_scat, and low Q_dif is desirable. This assures that the PL coupled to the leaky mode is diffracted into the desired (normal) direction instead of being absorbed or scattered into random direction on material inhomogeneities and structural defects. When the Q-factors of TE₀ and TM₀ leaky modes of PhC-A are compared (Table 2), the TM₀ mode should work better for out-coupling. However, the highest extraction (i.e. under nonresonant excitation) enhancement factor around 17.5× was obtained with the TE₀ extraction mode (Table 1). The reason is that the Q-factor describes only the out-coupling of leaky modes from the structure and not the initial coupling of the PL to leaky modes, which was optimized for the TE₀ mode via the optimal thickness. Here the higher SM-LDOS of TE₀ mode plays more significant role than the better out-coupling of the TM₀ leaky mode from the structure. This clearly manifests the importance of both the spatial overlap between the extraction mode profile with the distribution of the excited light-emitters and the optimized thickness of the layer for coupling to this TE₀ mode.

In the case of excitation efficiency, the high Q_dif and Q_scat, and low Q_abs are desirable. In such a case the excitation beam stays long in the PhC and is simultaneously efficiently absorbed. Based on the Q-factors (Table 2) the TE₀ mode works best for the excitation efficiency, which is in accordance with the measured excitation enhancement factor (Table 1). Nevertheless, in the value of the excitation enhancement factor, also the overlap between the excitation and extraction mode plays an important role, which is evidenced by dependence of the excitation enhancement (Table 1) on the extraction leaky mode. Note, that although the thickness of the layer is optimized to achieve highest SM-LDOS for TE₀ mode at wavelengths around 650 nm, the excitation TE₀ leaky mode is even more localized in the layer because of shorter wavelength. The reduced SM-LDOS is not important for the absorption efficiency.

The in-coupling of excitation beam into structure is affected not only by the diffraction Q-factor but also by the monochromacy and directivity of light. The high Q_dif is advantageous only for monochromatic and highly directional light in this respect. The total excitation enhancement (absorbed energy) can be partially simulated by rigorous coupled-wave analysis (RCWA) simulations (see Figure 1D). Nevertheless, it does not count with the scattering of light and fabrication imperfections, which decrease the overall performance.

For the case of PhC-B the diamond layer is thinner (h_w) than for the PhC-A, whereas the PhC columns are higher (h_PhC). The TE₀ mode is thus more spread outside diamond layer, which decreases its single-mode local density of optical states in the diamond and increases its interaction with PhC structure that causes faster diffraction. The effect on Q-factors is that Q_dif is low and Q_abs high. As a result, the PhC-B should work better for extraction and worse for excitation when compared to the PhC-A sample, which we observed (Table 1).

4 Discussion and conclusion

The importance of spatial overlap of the extraction and excitation leaky mode may be manifested by considering the competition in PL extraction between the supported modes. The 78–124 nm thick diamond layer supports both TE₀ and TM₀ modes at all wavelengths. Each mode is diffracted into vertical direction at different extraction wavelength. The other mode also exists for these wavelengths, but it is extracted into different direction, e.g., the steep TM₀ band crossing the TE₀ extraction wavelength at around 17° (Figure 4A). Nevertheless, Figure 4A clearly shows that the steep TM₀ extraction band is weaker for resonant excitation with TE₀ mode when compared to the resonant excitation with TM₀ mode (Figure 4E). Similarly, the steep TE₀ extraction band is weaker in Figure 4E.

A significant portion of PL intensity coupled to TE₀ (or TM₀) mode is lost due to diffraction into nonvertical angles (flat bands in Figure 4A,E). The light diffracted into these directions can be collected by placing the optical fiber closer to the sample or by using objectives with higher numerical aperture. Nevertheless, it leads to the loss of spectral selectivity of leaky modes, because other wavelengths are also diffracted into these directions. Note that the spectral selectivity is especially important for sensing applications.

Figure 4 also compares the simulated and measured transmission efficiency. The most prominent difference between the simulated and measured transmission efficiency lies in the shift of the TM₀ mode spectral position. The difference originates from localization of electric field of this mode near the diamond surface as described in Suppl. info (Section 6, TM-polarized excitation).

The PhC structures under the study were designed to obtain high vertical PL enhancement in the red part of the visible spectrum. This is spectrally near to zero phonon spectral lines of negatively charged nitrogen vacancy (637 nm) or silicon vacancy (738 nm) color centers [2], [38], [39], which are potential single photon sources [3] and sensing components [40], [41]. Even though there were no (or very few) color centers in the present samples, they can be introduced into the diamond using ion implantation technique or directly during fabrication of new samples [42], [43]. The spectral position of the leaky modes may be shifted to the emission peak of the color center by adjusting the lattice constant [24]. However, due to the fabrication imperfections, tuning of the PhC structures to an exact a priori selected wavelength is not possible. Nevertheless, fine tuning of the extraction resonance spectral position can be done by postprocessing: overgrowth of the PhC structures with thin diamond layer to increase layer height or sample etching to reduce the layer height. The former was used for fabrication and spectral tuning of leaky resonances by bottom-up approach [28]. Also note that the spectral shift of resonances is not detrimental for excitation in-coupling as it only requires slight adjustment of the excitation beam angle of incidence. Furthermore, Figure 1C shows that the same TE₀ excitation mode can be excited also by other wavelengths if the resonant angle is shifted appropriately. Moreover, other resonant angles exist also for the excitation in the other direction of high symmetry, the Γ-M direction. Finally, the TM₀ leaky mode has high field intensity located on the PhC surface (Figure 1B). Combination of near-surface color centers sensitive to the changes of surroundings with a photonic crystal tuned at the TM₀ resonance is, therefore, promising for increased optical sensor sensitivity.

To conclude, we have shown that the resonant excitation/extraction scheme can be used to achieve 115-fold enhancement of PL intensity originating from light-emitters in nanocrystalline diamond-based photonic crystals. Even though that the nanocrystalline diamond possesses relatively high optical losses, the achieved enhancement is comparable to that obtained for a material with negligible losses [30]. In order to reach such enhancement, we have shown that both the spatial overlap between the excitation and the extraction leaky mode, and the spatial overlap between the light-emitters and the extraction leaky mode must be maximized. This condition is fulfilled for the TE₀ leaky mode used both for the excitation in-coupling and for the extraction of PL in the case of nanocrystalline diamond PhCs. The usage of the same mode for both excitation and extraction is more important than tuning of the Q-factors of excitation and extraction leaky modes individually. Moreover, the Q-factor must be separated into the effect of Bragg diffraction, absorption, and scattering in order to reasonably explain the excitation/extraction efficiency of the leaky modes. Our results, even though obtained on a specific material, can be extended towards any dielectric material with optical losses.