Home Polaritonics: from microcavities to sub-wavelength confinement
Article Open Access

Polaritonics: from microcavities to sub-wavelength confinement

  • Dario Ballarini and Simone De Liberato ORCID logo EMAIL logo
Published/Copyright: February 12, 2019
Download Article (PDF)
Become an author with De Gruyter Brill
Submit Manuscript Author Information
Nanophotonics
From the journal Nanophotonics Volume 8 Issue 4

Abstract

Following the initial success of cavity quantum electrodynamics in atomic systems, strong coupling between light and matter excitations is now achieved in several solid-state set-ups. In those systems, the possibility to engineer quantum emitters and resonators with very different characteristics has allowed access to novel nonlinear and non-perturbative phenomena of both fundamental and applied interest. In this article, we will review some advances in the field of solid-state cavity quantum electrodynamics, focussing on the scaling of the relevant figures of merit in the transition from microcavities to sub-wavelength confinement.

Keywords: cavity quantum electrodynamics; polaritonics; ultrastrong coupling

1 Introduction

In an idealised cavity quantum electrodynamics (CQED) set-up, in which a collection of dipoles interact with the discrete resonant mode of a photonic cavity, the relevant dimensionless parameter quantifying the intensity of the light–matter interaction is the normalised coupling η [1]. If η, which is the vacuum Rabi frequency Ω divided by the bare transition frequency ωx, becomes larger than the inverse of the quality factors of the light and matter resonances, the system enters the strong coupling regime. In such a regime, its physics can be correctly described only in terms of the light–matter hybrid eigenmodes of the coupled system, often named polaritons [2]. Higher order effects will become observable when η becomes non-negligible, a regime usually referred to as the ultrastrong, or non-perturbative, regime [1], [3]. Note that the two conditions are a priori independent and, thus, notwithstanding its name, the set of systems exhibiting ultrastrong coupling is not a subset of the strong coupled ones [4]. It is worthwhile to point out that once into the non-perturbative regime, the parameter η defined in Eq. (1) loses some of its relevance, as the approximations to consider a single electronic transition [5], [6], [7] or a single resonant cavity mode [8], [9], [10] fail.

The intensity of the normalised coupling between an electronic dipolar-active transition and a resonant electromagnetic mode can be calculated to be of the order [11]

(1)η=Ωωx=O(α3NVλV),

where α≃1/137 is the fine structure constant, N is the number of effective dipoles coherently coupled to the photonic mode, V is its effective mode volume at the location of the dipoles, and Vλ is the diffraction-limited volume. For Haroche’s Rydberg atoms in a superconducting microwave cavity, η<10−6: a single atom interacts very weakly with the electromagnetic field. Lowest order perturbation theory is then fully justified, and the achievement of strong coupling is only due to the outstanding lifetimes of the photonic and atomic transitions, with quality factors Q>108 [12].

From Eq. (1) we see that, for a given electronic transition (i.e. fixed Vλ), larger couplings can be achieved only by increasing the density NV, which physically measures the overlap between light and matter fields. At a fixed density, instead, η can be increased going towards longer wavelengths, and thus larger Vλ. Apart from determining the intensity of the normalised coupling, photonic mode volume and dipole density play other important roles in determining the physics of the system, creating trade-offs between different figures of merit. Sub-wavelength confinement, which allows achieving V≪Vλ, leads to unavoidable losses and thus lowers the quality factor Q [13]. The number of involved dipoles can, instead, change the nature of the system’s response, which in the limit N→∞ is well described by a bosonised Dicke model [14], while nonlinearities appear as it approaches N=1 [15], [16], where it is described by a quantum Rabi model [17].

Using those simple figures of merit as a guide, in this article we will review different combinations of resonator technologies and CQED set-ups used in the literature to achieve strong and ultrastrong coupling. We do not aim at providing a comprehensive review of the developing field of polaritonics, but try to highlight the trade-offs between different design strategies. We will, in particular, highlight the impact of the transition between diffraction-limited cavities and plasmonic sub-wavelength resonators. Given their relevance for plasmonics, we will focus mainly on Wannier and Frankel excitons covering near-infrared and shorter wavelengths. Only in the last part of the article will we briefly consider longer wavelength CQED systems, in which sub-wavelength confinement can be provided either by plasmonic waveguides or by analogous phonon-based resonators. Given the very different physics involved, in this article we will focus on semiconductor-based systems, neglecting both superconducting [18] and magnetic systems [19].

The rest of this article is articulated as follows. In Sections 2 and 3 we will discuss in some further detail the link between sub-wavelength confinement and losses and the novel physics that can be observed in the few-dipoles-strong coupling limit. In Section 4 we briefly describe various excitonic resonances commonly used in CQED and in Section 5 the different kinds of resonators coupled with them. In Section 6 we will pass to review some solid-state CQED platforms working at longer wavelength, where plasmonic resonators effectively behave as waveguides and phonon-based resonators present an interesting dielectric alternative to metallic ones. Finally, in Section 7 we will briefly analyse the different data gathered in the rest of the review and comment on their relevance for the future development of polaritonic science and technology.

2 Sub-wavelength confinement and losses

The most important drawback of the use of plasmonic resonators in CQED is certainly their extremely small quality factor. Losses are seemingly unavoidable because the confinement of the electromagnetic field below the diffraction-limited volume is made possible by storing energy in the kinetic part of a dissipative free-electron gas [13], [20]. The frequency dependance of the interplay between confinement and losses can be understood by using the analytically solvable case of a metallic half-space. Maxwell boundary conditions ensure that a surface-bound solution has to satisfy the relation

(2)ε(ω)κvac=−κmet,

where κvac and κmet are the inverse extinction lengths on the vacuum and metallic side, respectively, and ε(ω) is the metal dielectric function. As the absolute value of the dielectric function of the Drude model increases at smaller frequencies, with a zero-crossing at the plasma frequency ωP, Eq. (2) then implies that the electromagnetic field in the lossy metal increases with frequency.

It has been recently shown by Khurgin that this result can be elegantly obtained purely from energy conservation arguments [20]. In particular, the fraction of the total energy that ends up being stored in kinetic form, and thus subject to collisional losses, can be written in terms of the plasma frequency as

(3)Pk≃11+2a2λ2ωP2ω2,

where the ratio between the confinement length a and the wavelength in the material λ is related to the normalised mode volume VVλ. Consistently with the previous argument, Pk varies from 0 (and thus no collisional losses) for ω≪ωP to 1 close the plasma frequency.

For metals, ωP is in the UV, and at mid-infrared and longer wavelengths there is thus very little plasmon left, and the resonators are better described as simple metallic waveguides. As we will briefly discuss in Section 6, at those wavelengths a more apt comparison is thus with non-metallic materials characterised by lower values of the plasma frequency.

3 From the Dicke to the Rabi model

In the dilute excitation regime, that is, when the number of dipoles coupled to light is much larger than the number of excitations, the optical response of a collection of dipoles can be described by a bosonic field. Although this could seem a truism in the linear regime, such a correspondence extends to the nonlinear regime, allowing the achievement of stimulated scattering and condensation of hybrid light–matter excitations [2], [21], [22], and more generally treating matter excitations, and a fortiori polaritons, as fully bosonic particles [23], [24], [25]. Saturation-induced effects are in those cases limited to highly excited regimes [26], [27] or to very large values of η [16], [28].

At the opposite end of the spectrum, a single dipole, described by the quantum Rabi model [17], provides the perfect nonlinear system, presenting saturation at the single-photon level [29], [30]. Reducing the number of dipoles involved in the formation of a polariton is not only a way to influence its optical spectrum though [15]. In the last decade, various workers have investigated the impact of strong coupling on chemistry and material science [31], [32], [33], [34], [35], noticing how certain degrees of freedom of the molecules coupled to the photonic field were affected by the single-molecule coupling strength [36], [37], [38], [39].

Moving towards fewer dipoles has thus been an important drive in the development of novel solid-state CQED systems, and probably the one most affected by concomitant advances in plasmonics, which only recently allowed achieving the milestone of single-molecule strong coupling [40]. Note that reducing the number of molecules is not the only way to transition between the Dicke and the Rabi models, which can also be effectively simulated by more complex set-ups [41], [42].

4 Excitons

There are two fundamentally different descriptions of excitons, representing limiting cases of semiconductors with localised or delocalised polarisability: Frenkel and Wannier–Mott [43], [44]. Frenkel excitons exist in materials with low dielectric constant (standard with organic compounds) and are localised on one (or a few) molecules. Wannier–Mott excitons are typical of semiconductors with larger dielectric constant such as III–V and II–VI crystals and are delocalised over hundreds of atomic sites. A visually clear representation of the localised–delocalised transition between the two types of excitons, shown in Figure 1, can be obtained by mapping the 3D exciton wavefunction in the bulk material Ψ(x, y, z) on the surface of a 4D sphere described by three hyperangles, Ψ(θ, ϕ, χ) [45].

Figure 1: Wavefunction of 3D excitons calculated in spherical coordinates on the surface of a 4D hypersphere (glome) [45].In the plot, ω is the angular separation between the electron and the hole, with ω≈0 for Frenkel excitons and, on the opposite limit, delocalised over the whole space for ε=∞. The radius of the glome is normalised to 1 for simplicity in both cases and it is related (inversely proportional) to the dielectric constant of the material and the reduced mass of the exciton. In the inset, pictorial representations of the 2D cross-sections of the Frenkel and Wannier–Mott wavefunctions on the glome are shown.
Figure 1:

Wavefunction of 3D excitons calculated in spherical coordinates on the surface of a 4D hypersphere (glome) [45].

In the plot, ω is the angular separation between the electron and the hole, with ω≈0 for Frenkel excitons and, on the opposite limit, delocalised over the whole space for ε=∞. The radius of the glome is normalised to 1 for simplicity in both cases and it is related (inversely proportional) to the dielectric constant of the material and the reduced mass of the exciton. In the inset, pictorial representations of the 2D cross-sections of the Frenkel and Wannier–Mott wavefunctions on the glome are shown.

The dimensionality of the system plays a crucial role on the optical properties of excitons, and strictly 2D structures (sub-nanometre thicknesses) such as van der Waals layered materials can combine the best properties of Frenkel and Wannier–Mott excitons. In Table 1, the relevant parameters for excitons in different materials are reported.

Table 1:

Excitonic properties in inorganic, organic, and hybrid semiconductors.

GaAs QWGaN QWOrganic (Lumogen)Organic (TDAF)WS2 (TMD)2D Perovskites
Bohr radius (nm)12.53.5111.74.5
Binding energy (meV)5–20408301000700370
Oscill. strength3×104 μm−23×105 μm−23×107 μm−37×108 μm−39×105 μm−25×105 μm−2
Hom. FWHM (meV)0.030.363333
Interactions (μeV μm2)1–100.510−210−46×10−21
Exciton resonance (eV)1.53.523.522.4
Background nb3.52.71.623.91.8

  1. For GaAs and GaN QWs, thicknesses of 7 and 2.7 nm and barriers of AlGaAs and AlGaN are considered, respectively. Organic molecules in the table are small dyes, a perylene derivative (Lumogen Red F305) and 2,7-bis[9,9-di(4-methylphenyl)-fluoren-2-yl]-9,9-di(4-methylphenyl)fluorene (TDAF). The monolayer of WS2 is measured without the cladding layer. The 2D perovskite is a large single crystal of phenethylammonium lead iodide (C6H5(CH2)2NH3)2PbI4 (PEAI) self-assembled by an anti-solvent-vapor-assisted crystallisation method and subsequent mechanically exfoliated to produce thin flakes of 100 nm. The oscillator strength of layered perovskites is normalised to the number of inorganic layers, in analogy to GaAs QWs. For a single monolayer of tungstene disulfide (WS2), the background refractive index is given as obtained from spectroscopic ellipsometry for completeness, but its role in the exciton formation is negligible since most of the field lies outside the monolayer.

In order to be able to compare the number of coupled dipoles in different CQED material systems, it is practical to introduce the concept of oscillator strength.

The oscillator strength f of a transition from the initial state g to a state x can be defined quite generally by a dimensionless quantity in terms of the transition dipole moment 〈x|ε^⋅r^|g〉, with ε^ the polarisation vector of light and ri the electron position, as

(4)fε^,x=2meωℏ|〈x|ε^⋅∑iri|g〉|2

with me the electron mass and ℏω the energy difference between the final and the initial state [46]. Physically, the oscillator strength of a transition is the ratio between the absorption rate of that transition and the absorption rate of a single-electron oscillator with the same oscillation frequency ω, thus providing an effective dipole number for many-body excitations.

For fully delocalised excitons, the dimensionless oscillator strength is proportional to the crystal volume, because the centre-of-mass wavefunction (Figure 1) extends over the whole crystal. However, in real systems, the sample size must be replaced by the exciton coherence length Lc, which describes how far the centre of mass of the exciton can move without losing coherence. Delocalised excitons in GaAs quantum well (QW) show coherence lengths of ≈200 nm, while organic excitons are, in the best case of J-aggregates, coherent over few nanometres [47], [48]. The exciton-polariton Rabi frequency is proportional to the exciton oscillator strength, to the total number of dipoles coupled to light, and to the spatial overlap between the material and light field. It follows that a simple reduction of the electromagnetic mode volume in Eq. (1) does not automatically increase the Rabi splitting unless the number N of dipoles is kept constant. The meaningful quantity is therefore the oscillator strength per unit volume f˜, that is, the oscillator strength of a single dipole times the number of excitons that can be filled in the unit volume.

For practical purposes, the oscillator strength per unit volume, f˜, is obtained from the absorption coefficient α(ω) integrated over the excitonic peak as [46], [49], [50]

(5)∫α(ω)dω=πe22ε0nbmecf˜,

where nb is the background refraction index, ε0 is the vacuum permittitivity, and c is the speed of light. In a QW, the oscillator strength is, instead, proportional to the considered surface, and it is thus expressed per unit area per QW. Typical values for excitons in GaAs QWs with thickness of 7 nm are of the order of f˜≈104 μm−2. In order to increase the coupling strength, multiple QWs can be embedded in the same planar resonator, leading to a total scaling

(6)η∝Nf˜L,

where N is the number of QWs and L is the effective cavity thickness.

On the opposite end of the spectrum, in organic compounds, an exciton is often localised on a single molecule (Figure 1) with f≈0.5–1.5. The oscillator strength is therefore measured per unit volume according to Eq. (5), with f˜=NV×f and NV the molecular density. As shown in Table 1, in the same volume of a microcavity (≈μm3) the equivalent number of oscillators is about three orders of magnitude larger for Frenkel excitons in organic molecules than for Wannier–Mott excitons in GaAs QWs. This allows the Rabi splitting in organic microcavities to reach hundreds of meV and, in some cases, to enter into the ultrastrong coupling regime in the visible range with η≈0.3 [51], [52].

Importantly, the photon–exciton interaction scales as an inverse power of the Bohr radius ab, while the Coulomb interaction between excitons roughly scale as Ebab2, where Eb is the exciton binding energy [53], [54], [55], [56], [57]. As such, the large ab of excitons in GaAs QWs makes it challenging to achieve ultrastrong coupling with these materials [58], but at the same time they are particularly suited for dressing the photons with nonlinearities three orders of magnitude higher than in standard optical crystals [59]. In the past decade, these have allowed the demonstration of a large number of active optical functionalities, from spin switches to all-optical logic gates, and from polariton multi-stability to polariton simulators of many-body Hamiltonians [60], [61], [62], [63], [64], [65]. This has been possible thanks to the high degree of control on the material purity and the advances in the deposition and processing techniques that have allowed GaAs/GaAlAs- and InGaAs/GaAs-based structures to lead the field. The exciton binding energy is, however, relatively low, of a few meV, limiting their operation to cryogenic temperatures, but also allowing the observation of other interesting interaction-induced phenomena [58], [66]. The strong coupling regime with higher band-gap semiconductors such as GaN and ZnO has been largely studied at room temperature [67], [68], [69]. Despite the fact that the optical quality is in general substantially lower than for GaAs-based structures, these materials hold a strong potential for technological applications and have shown room-temperature polariton lasing, under both optical and electrical injection in the case of GaN [70], [71], [72]. The huge binding energy of Frenkel excitons makes organic molecules a promising alternative for polaritons at room temperature [22], [73], [74], [75], and their smaller Bohr radius allows them to reach the ultrastrong light–matter coupling regime [51], [52]. Still, the smaller ab means as well much smaller exciton–exciton interactions, challenging the implementation of nonlinear optical effects in room-temperature polariton systems. However, new perspectives are opened by the peculiarities of strong coupling in organic materials, where the large energy splitting can alter the relaxation dynamics and optical efficiencies, but also can act as all-optical switching of the reaction dynamics [76], [77], [78]. Moreover, the synthetic versatility of organic molecules facilitates their integration in optical resonators with smaller modal volumes, such as plasmonic cavities, allowing increase of the normalised coupling η up to the ultrastrong regime with only a bunch of molecules. Relevant data for various excitonic resonances can be found in Table 1.

The best properties of Frenkel and Wannier–Mott excitons are mixed when the exciton is extremely confined on a lower dimensionality, such as in monolayers of transition-metal dichalcogenides (TMDs). In these 2D semiconductors, the electronic screening is reduced by dimensionality, and typical binding energies are hundreds of meV, allowing strong coupling to be observed at room temperature. In analogy to the strategy adopted with epitaxial QWs, stacking N monolayers increases the coupling by a factor N [79]. Interestingly, layered perovskites form naturally ordered structures of 2D inorganic layers separated by chains of organic molecules. These hybrid materials are excellent semiconductors in the visible range, and strong coupling with single crystals of 2D perovskites has shown comparable characteristics to GaAs QWs but working at room temperature [80], [81], [82]. The nonlinearities associated with these flat excitons are similar to those of Wannier–Mott excitons in GaAs QWs, including the spin-dependent strength of the interaction between excitons, opening the door to all-optical spin manipulation at room temperature [83], [84], [85].

5 Resonator technologies

In Figure 2, the strong coupling regime with organic and inorganic excitons is shown for different resonator technologies, going from dielectric cavities to surface evanescent modes and plasmonic cavities with ultrasmall mode volumes. The parabolic dispersion of a photon in a cavity is partially retained by the lower polariton branch (LPB), as shown in Figure 2D. The effective mass of polaritons close to the bottom of the LPB is only a tiny fraction of the exciton’s mass, enabling stimulated scattering to prevail over losses even at room temperature. Polariton condensation requires, however, long lifetimes to reach the critical density at the bottom of the LPB. The microcavities with the highest optical quality are obtained by epitaxial deposition of two dielectric mirrors (dielectric Bragg reflectors, DBRs) composed of alternating layers of GaAs and AlGaAs, and polariton condensation was initially demonstrated in a GaAs-based microcavity at 4 K with CdTe QWs [89], [90]. After the observation of polariton condensation, out-of-equilibrium quantum fluids have been largely explored in these solid-state systems [2]. Among other results, superfluidity, Josephson oscillations, quantised vorticity, and optical spin-Hall effect are only some examples of the rich physics that can be investigated with microcavity polaritons [91], [92], [93], [94], [95], [96], [97], [98]. Recently, GaAs microcavities with extremely long polariton lifetimes ≈200 ps have allowed approaching the physics of equilibrium quantum fluids, opening new possibilities for the manipulation of large polariton condensates [99], [100], [101], [102], [103]. Moreover, the fine control over the lithographic patterning of these structures has prompted the realisation of topological structures, with promising results recently reported [104], [105], [106].

Figure 2: Photonic structures showing strong coupling with a matter resonance in the visible range.(A) Cavity made of two DBR mirrors with the exciton dipole represented by the red sphere. (B) Bloch surface wave (BSW) sustained on the top of a single DBR, with the thin active layer deposited at the maximum enhancement of the electromagnetic field. (C) Spatial distribution of the electromagnetic field (numerically simulated by FDTD) at resonance with a gap-plasmon, with the maximum enhancement localised within the two metallic nanoparticles. (D) Dispersion of the microcavity polariton associated with the structure in (A): the parabolic dispersion of a photon in a cavity (red dashed line) and the flat dispersion of the exciton (black dashed line) in this angular range show a clear anti-crossing with vacuum Rabi energy ℏΩ=4 meV and exciton-cavity detuning δ=–3 meV [86]. (E) Dispersion of organic BSW polaritons. The light line is defined by the interface between the heterostructure and air (blue line). The Rabi energy anti-crossing between the the BSW (red dashed line) and the exciton (black dashed line) is Ω=ℏ50 meV [87]. (F) SEM image of an array of plasmonic nanoparticle dimers as in (C), where hybridisation can occur between the localised plasmons, the surface modes associated with the lattice, and the organic molecular exciton of the deposited material. (G) Dispersion of the structure in (F), with an organic molecular layer deposited on top of the array of coupled nanoparticles. The anti-crossing is small compared to the line width but still visible [88]. Additional details on the parameter structures can be found in Refs [86], [87], [88].
Figure 2:

Photonic structures showing strong coupling with a matter resonance in the visible range.

(A) Cavity made of two DBR mirrors with the exciton dipole represented by the red sphere. (B) Bloch surface wave (BSW) sustained on the top of a single DBR, with the thin active layer deposited at the maximum enhancement of the electromagnetic field. (C) Spatial distribution of the electromagnetic field (numerically simulated by FDTD) at resonance with a gap-plasmon, with the maximum enhancement localised within the two metallic nanoparticles. (D) Dispersion of the microcavity polariton associated with the structure in (A): the parabolic dispersion of a photon in a cavity (red dashed line) and the flat dispersion of the exciton (black dashed line) in this angular range show a clear anti-crossing with vacuum Rabi energy ℏΩ=4 meV and exciton-cavity detuning δ=–3 meV [86]. (E) Dispersion of organic BSW polaritons. The light line is defined by the interface between the heterostructure and air (blue line). The Rabi energy anti-crossing between the the BSW (red dashed line) and the exciton (black dashed line) is Ω=ℏ50 meV [87]. (F) SEM image of an array of plasmonic nanoparticle dimers as in (C), where hybridisation can occur between the localised plasmons, the surface modes associated with the lattice, and the organic molecular exciton of the deposited material. (G) Dispersion of the structure in (F), with an organic molecular layer deposited on top of the array of coupled nanoparticles. The anti-crossing is small compared to the line width but still visible [88]. Additional details on the parameter structures can be found in Refs [86], [87], [88].

The DBR technology, while ensuring high quality factors and long polariton lifetimes, is limited to mode volumes comparable to the cubic wavelength of light in the material. In these structures, the normalised coupling with embedded GaAs QW excitons can reach values η≃0.1–1%, allowing the strong coupling regime to be measured only with relatively high quality factors Q>103. Strong coupling with a single quantum dot (QD) has been observed in a high-Q micropillar and photonic crystal cavities at low temperatures [107], [108], [109], [110], [111], [112]. More recently, attempts to use polariton nonlinearities to realise squeezed light or polariton blockade have been reported [113], [114], [115], [116], [117], [118]. It has been shown also that single and entangled photons can be injected from outside into the polariton mode and quantum correlations deployed by the coupling with a condensate [119]. On the opposite side, with many millions of dipoles coupled to the electromagnetic field, DBRs with lower quality factors (Q≈600) already show polariton condensation at room temperature [22], [120], [121]. Note that, despite that polariton nonlinearities associated with molecular excitons have been measured to be two to three orders of magnitude weaker than for inorganic excitons, the large density of oscillators has enabled the observation of collective effects such as superfluid flow across a defect [122]. An alternative to full microcavities are waveguide modes and evanescent modes at the interface between a metal and a dielectric or at the interface between a DBR and air [123], [124], [125], [126], [127]. These structures are particularly suited for in-plane propagation and are useful when the realisation of the top DBR in standard cavities may damage the active material. Strong coupling with a Bloch surface wave (BSW) has allowed the measurement of nonlinearities with organic molecules and TMD monolayers in propagating polariton fluids [87], [128]. Strong coupling involving both GaAs QWs and TMD monolayers has also been demonstrated in hybrid structures [129], [130]. When strong coupling involves a surface plasmon (SP), the mode volume is reduced with respect to optical microcavities and BSW, reaching sub-wavelength values at the price of much smaller quality factors [131], [132], [133], [134], [135], [136]. This trends is evident in Figure 3, where the effective volumes are shown as a function of the quality factor for several of the works discussed in this section and reported in Table 2.

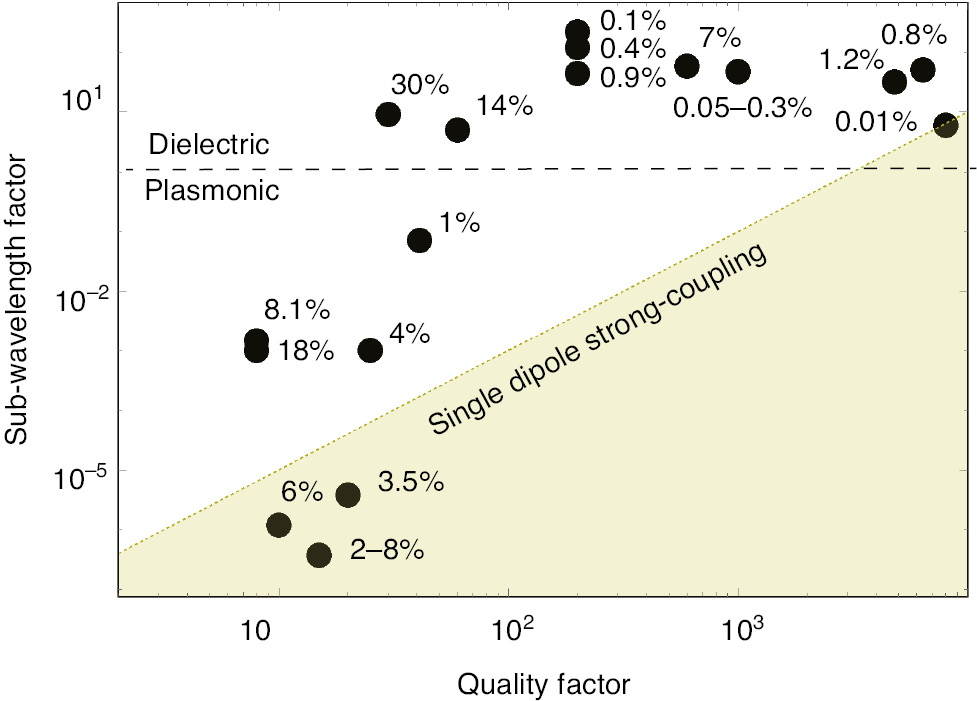
Figure 3: Sub-wavelength factor VVλ${V \over {{V_\lambda }}}$ versus the quality factor of the photonic resonators for the works in Table 2.The normalised coupling η is shown as well for each point. The horizontal line indicates the minimum sub-wavelength factor achievable with dielectric structures (≈1). The dashed line represents the scaling of V in order to keep the condition of strong coupling with a single dipole (N=1) for a given f≈1. Note that, at the top-right corner, the small η of InGaAs QD is compared with the almost ultrastrong coupling regime of single molecule at the left-bottom corner.
Figure 3:

Sub-wavelength factor VVλ versus the quality factor of the photonic resonators for the works in Table 2.

The normalised coupling η is shown as well for each point. The horizontal line indicates the minimum sub-wavelength factor achievable with dielectric structures (≈1). The dashed line represents the scaling of V in order to keep the condition of strong coupling with a single dipole (N=1) for a given f≈1. Note that, at the top-right corner, the small η of InGaAs QD is compared with the almost ultrastrong coupling regime of single molecule at the left-bottom corner.

Table 2:

Estimated figures of merit for representative exciton–polariton systems, from dielectric DBR microcavities to plasmonic arrays and localised plasmonic cavities.

ResonatorExcitonMaterialV/VλNQℏωx (meV)η (%)Room temp.Ref.
NPoMOMMethylene blue4×10−71151.92Y[40]
NPoMOMMethylene blue4×10−710151.98Y[40]
LPOMCyanine dye10−36×10381.5518Y[137]
LPOMHITC molecules10−318881.678.1Y[138]
SMOMSquaraine dye91.4×108301.8530Y[51]
SMOMTDAF51.9×107603.514Y[52]
DBROMTDAF303.2×1076003.57Y[22]
MDQDInGaAs610080001.670.01N[107]
LPQDZnS3.8×10−63201.553.5Y[139]
GPQDCdS1.2×10−68101.96Y[140]
DBR28 QWGaAs477.8×10510001.610.3N[58]
DBRQWGaAs472.8×10410001.610.05N[58]
DBRBulkGaAs2188.4×1032001.50.1N[141]
DBRBulkGaN1199×1032003.50.4Y[141]
DBRBulkZnO442×1042003.30.9Y[141]
OCTMDMoSe2518.4×10563751.660.8Y[142]
NPoMTMDWSe210−3182251.634Y[79]
LPTMDMoS20.07232411.971Y[143]
DBRTMDMoS2317.8×10448001.871.2Y[144]

  1. MD, MicroDisk; DBR, DBR microcavities; OC, open DBR microcavity; SM, microcavity with semitransparent silver mirrors; LS, localised plasmon array; GP, gap-plasmon; NPoM, nanoparticle on mirror; OM, organic molecules, TMD, monolayer of transition-metal dichalcogenide; QW, quantum well; QD, quantum dot.

To allow comparison between different resonator technologies, the confinement for planar optical cavities is considered only in the direction perpendicular to the cavity plane, while taking a conventional surface area given by S=πλ02 for the resonant wavelength in air λ0, as the minimal diffraction-limited surface of the pump. Note that, in the case of DBR structures, the effective mode volume, which has to include the penetration length in the dielectric mirrors, is usually not explicitly reported in the literature, and it has thus to be estimated from available data. The number of dipoles is meant as the equivalent number of electron oscillators as obtained directly from the measured oscillator strengths.

Even with sub-wavelength volumes and strong oscillator strengths, the limit for achieving strong coupling with a single dipole at room temperature is stringent. At room temperature, thermal fluctuations reduce the maximum quality factor, meaning that strong coupling can be achieved only by reducing the mode volume. As η∝1V and in the strong coupling regime η>1Q, in Figure 3 the scaling of the maximum volume for strong coupling with a single molecule is drawn as V∝Q2. The extreme localisation of the electromagnetic field is achieved with plasmonic cavities. Metallic nanoparticles sustain highly localised plasmonic modes with mode volumes of few hundreds of nanometre cubes, leading to extremely small sub-wavelength confinement. Ultrastrong coupling with localised plasmons and organic excitons has been theoretically investigated [145] and recently demonstrated with normalised coupling η≃0.18 [137].

The interaction between different localised plasmons can be handled following different strategies. In arrays of metallic nanoparticles, hybridisation between the diffracted modes of the array and localised plasmons allow the reduction of the losses inherent in the metallic absorption while keeping a relatively small mode volume, allowing strong coupling to be obtained with organic molecules and TMD monolayers [88], [143], [146], [147]. Recently, interaction and coherence of polariton condensates have been shown in such structures at room temperature [148]. To further reduce the field volume, two metallic nanoparticles (or a nanoparticle on a flat metallic mirror) can be brought close enough to allow direct hybridisation of the localised plasmon modes, boosting the electric field in the inter-particle gap by several orders of magnitude. Gap-plasmon cavities have the lowest mode volume, and strong coupling with a single molecule has been recently demonstrated at room temperature using such plasmonic resonators [40]. This is possible thanks to the relatively high normalised coupling, arising from the highly confined electromagnetic field and despite the low dipole density (see Figure 3). This result opens broad fundamental and technological perspectives spanning from quantum plasmonics to photochemistry and suggests that the ultrastrong coupling regime could be achieved in such resonators with a relatively small number of dipoles.

6 Long-wavelength polaritonics

At longer wavelengths, the distinction between plasmonic and standard resonators loses some of its relevance, because, as visible from Eq. (3), only a limited portion of the field energy is stored in kinetic form. Nevertheless, in the field of mid-infrared and terahertz polaritons, the use of sub-wavelength resonators, which still have limited quality factors when compared with DBR, has led to important results which we will briefly examine for the two most relevant cases of intersubband and Landau polaritons. We will finally mention recent advances in phonon-polariton resonators, which, due to their longer lifetimes and lower plasma frequencies, provide an interesting analogue to plasmonic resonators at longer wavelengths.

6.1 Intersubband polaritons

Intersubband polaritons are hybrid quasi-particles resulting from the strongly coupled transition between multiple conduction subbands in doped QWs. The schematic of a simple two-subband intersubband transition is sketched in Figure 4A. Easily tunable though the terahertz and mid-infrared portions of the spectrum by engineering the QW design, those excitations are the object of intense research interest due to their potential as a novel platform for mid-infrared and terahertz nanophotonics [149], [150], [151], [152], [153], [154], [155]. Moreover, the vacuum Rabi frequency in those systems is proportional to the square root of the electron density, allowing for a conceptually and technologically straightforward way to access the ultrastrong coupling regime [156] and to modify the coupling on-site [157].

Figure 4: Sketch of the three different long-wavelength polaritonic platforms discussed in the main text.(A) Intersubband transition between two conduction subbands in a doped quantum well. (B) Transition between different Landau levels in a 2D electron gas under applied magnetic field. (C) Surface phonon–polariton resonance ℏωSPhP at the interface between a polar dielectric and vacuum. In the figure, EF is the Fermi energy, B is the applied magnetic field, and ℏωPh, ℏωLO, and ℏωTO are, respectively, the energies of the photon and of the longitudinal and transverse optical phonons.
Figure 4:

Sketch of the three different long-wavelength polaritonic platforms discussed in the main text.

(A) Intersubband transition between two conduction subbands in a doped quantum well. (B) Transition between different Landau levels in a 2D electron gas under applied magnetic field. (C) Surface phonon–polariton resonance ℏωSPhP at the interface between a polar dielectric and vacuum. In the figure, EF is the Fermi energy, B is the applied magnetic field, and ℏωPh, ℏωLO, and ℏωTO are, respectively, the energies of the photon and of the longitudinal and transverse optical phonons.

Because of their TM selection rule and their comparatively long wavelength, DBRs are not viable alternatives in those systems, which led to the exploration of a number of different designs. Intersubband polaritons were observed for the first time in 2003 [158] using doped GaAs QWs and confining the electromagnetic field exploiting total internal reflection. Using, instead, a top metallic mirror, this was also first system in which the ultrastrong coupling regime was observed, with η≃0.11 [159].

Sub-wavelength cavities are often employed in intersubband polaritons, using either sub-wavelength metallic patches over a metal ground [154], [160], 3D nanoantennas [161], or LC meta-material resonators [162], [163]. In Table 3 we provide the parameters for some representative intersubband polariton experiments using different resonator technologies.

Table 3:

Figures of merit for representative intersubband polariton samples using different resonators.

ResonatorV/VλNQℏωx (meV)η (%)Ref.
Planar11081515211[159]
Nanopatch10−4107121224[160]
LC Metamaterial10−52400101258[162]

6.2 Landau polaritons

Landau polaritons exploit as matter component the transitions between Landau levels in charged gases under applied magnetic fields, as sketched in Figure 4B [164]. On the photonic side, various kinds of both diffraction-limited and sub-wavelength resonators have been used, including stripline resonators [165], split-ring resonator metamaterials [166], [167], [168], and DBR resonators [169], [170].

According to the different resonators employed, Landau polaritons have achieved the record normalised coupling between present CQED systems (η≃1.43 [168]) and also remarkable results in terms of the number of electrons coupled to the resonator (N≃90 [171]) and quality factors at long wavelengths (Q≃183 [169]). Parameters for those three samples are collected in Table 4.

Table 4:

Figures of merit for representative Landau polariton resonators.

ResonatorV/VλNQℏωx (meV)η (%)Ref.
DBR11081831.69[169]
LC Metamaterial2×10−62×10732.0143[168]
LC Metamaterial6×10−109081.236[171]

6.3 Phonon-polaritons

Phonon-polaritons are essentially mid-infrared analogues of plasmons, which exploit the movement of ions in the crystal lattice to confine the electromagnetic field instead of the movement of free charges in a metal. Such phonon-polaritons exist only at longer wavelengths, in the Reststrahlen band of polar dielectics, and are characterised by much longer lifetimes, not being subject to Ohmic losses. Although those excitations lead to smaller field enhancement because a part of the electric energy ends up as potential ionic deformation energy [20], they can still provide comparable sub-wavelength confinement and tunability [172], [173], [174], [175], [176], [177]. Moreover, thanks to phonon anharmonicity, they can provide polaritons with large nonlinear interactions [178], [179].

A relatively recent addition to the catalogue of CQED technologies, surface phonon-polaritons, whose dispersion is shown in Figure 4C, have been strongly coupled to a number of other excitations, including plasmonic nanorods [180], graphene plasmons [181], localised phonon-polariton modes [182], and ENZ (epsilon-near-zero) modes [183]. Localised phonon-polaritons have also been coupled to intersubband transition in a quantum cascade laser architecture [184], [185] although without achieving strong coupling.

7 Conclusions

Data reported in Tables 2–4 are represented in Figures 3 and 5 along multiple dimensions. Spanning multiple orders of magnitudes along dipole number, confinement factor, wavelength, and normalised coupling strength, polaritonic platforms have pushed to the extreme different boundaries of light–matter interaction.

Figure 5: Number of effective dipoles (N×f) vs sub-wavelength confinement factor as reported in Tables 2–4.The normalised coupling η is shown in the label on each point. The vertical shaded regions indicate the sub-wavelength range for dielectric microcavities (purple), plasmonic surface modes (yellow), and extremely localised plasmonic nanoantennas (green). The energy of the electronic resonance is shown for each point by the color code on the right of the figure. The grey lines represent the scaling of volume and dipole number, at a given frequency and constant η. Given that the dipole density is roughly constant for each materials, each line represents increasing light–matter interaction going from the bottom-left corner to the top-right corner. The horizontal line indicates the unitary strength of an ideal single electronic oscillator, N×f=1.
Figure 5:

Number of effective dipoles (N×f) vs sub-wavelength confinement factor as reported in Tables 2–4.

The normalised coupling η is shown in the label on each point. The vertical shaded regions indicate the sub-wavelength range for dielectric microcavities (purple), plasmonic surface modes (yellow), and extremely localised plasmonic nanoantennas (green). The energy of the electronic resonance is shown for each point by the color code on the right of the figure. The grey lines represent the scaling of volume and dipole number, at a given frequency and constant η. Given that the dipole density is roughly constant for each materials, each line represents increasing light–matter interaction going from the bottom-left corner to the top-right corner. The horizontal line indicates the unitary strength of an ideal single electronic oscillator, N×f=1.

Although any simple heuristic is bound to be inaccurate when used to analyse such a heterogeneous set, we can see that expected patterns emerge. In Figure 3, the trade-off between sub-wavelength confinement and losses, described by Eq. (3), is apparent. From the same image we can see that, even though strong coupling with single emitters can be a priori achieved with different resonator technologies, only in deeply sub-wavelength plasmonic resonators the coupling strength can be made large enough to be useful for proposed applications in chemistry and modification of electronic properties [36], [37], [38], [39]. In Figure 5, the different samples, including mid-infrared ones, are represented as a function of their sub-wavelength factor, dipole number, and normalised coupling. Diagonal lines represent ideal N∝VVλ dependencies at equal η for different representative resonances, from Eq. (1). Even though the ultrastrong coupling regime has been achieved in planar microcavities using organic molecules, it is clear how going towards lower frequencies, thus reducing the denominator of η=Ωωx, allows us to achieve coupling well beyond of what possible at shorter wavelengths.

In this article we have provided a cursory look at recent developments in the field of solid-state CQED, paying particular attention to figures of merit and trade-offs relevant for different optically active transitions in diffraction-limited and sub-wavelength resonators. We discussed the design choices required to access the scientifically and technologically interesting regimes of ultrastrong and single-molecule strong coupling and hopefully provided useful tools for the design of future CQED platforms.

Acknowledgements

SDL is a University Research Fellow of the Royal Society and acknowledges support from the Innovation Fund of the EPSRC Programme EP/M009122/1. DB acknowledges the ERC project ElecOpteR grant number 780757. The authors are grateful to C. Gubbin, D. Gerace, and D. Sanvitto for fruitful discussions, and to F. Riminucci for FTDT calculations.

References

[1] Kockum AF, Miranowicz A, De Liberato S, Savasta S, Nori F. Ultrastrong coupling between light and matter. Nat Rev Phys 2019;1:19–40.10.1038/s42254-018-0006-2Search in Google Scholar

[2] Carusotto I, Ciuti C. Quantum fluids of light. Rev Mod Phys 2013;85:299–366.10.1103/RevModPhys.85.299Search in Google Scholar

[3] Forn-Díaz P, Lamata L, Rico E, Kono J, Solano E. Ultrastrong coupling regimes of light-matter interaction. 2018;arXiv:1804.09275.10.1103/RevModPhys.91.025005Search in Google Scholar

[4] De Liberato S. Virtual photons in the ground state of a dissipative system. Nat Commun 2017;8:1465.10.1038/s41467-017-01504-5Search in Google Scholar PubMed PubMed Central

[5] De Bernardis D, Jaako T, Rabl P. Daniele De Bernardis, Tuomas Jaako, Peter Rabl. Cavity quantum electrodynamics in the nonperturbative regime. Phys Rev A 2018;97:043820.10.1103/PhysRevA.97.043820Search in Google Scholar

[6] De Bernardis D, Pilar P, Jaako T, De Liberato S, Rabl P. Breakdown of gauge invariance in ultrastrong-coupling cavity QED. Phys Rev A 2018;98:053819.10.1103/PhysRevA.98.053819Search in Google Scholar

[7] Di Stefano O, Settineri A, Macrì V, Garziano L, Stassi R, Savasta S, Nori F. Resolution of Gauge Ambiguities in Ultrastrong-Coupling Cavity QED. 2018;arXiv:1809.08749.10.1038/s41567-019-0534-4Search in Google Scholar

[8] Sundaresan NM, Liu Y, Sadri D, et al. Beyond strong coupling in a multimode cavity. Phys Rev X 2015;5:021035.10.1103/PhysRevX.5.021035Search in Google Scholar

[9] George J, Chervy T, Shalabney A, et al. Multiple rabi splittings under ultrastrong vibrational coupling. Phys Rev Lett 2016;117:153601.10.1103/PhysRevLett.117.153601Search in Google Scholar PubMed

[10] Sánchez Muñoz C, Nori F, De Liberato S. Resolution of superluminal signalling in non-perturbative cavity quantum electrodynamics. Nat Commun 2018;9:1924.10.1038/s41467-018-04339-wSearch in Google Scholar PubMed PubMed Central

[11] Devoret MH, Girvin S, Schoelkopf R. Circuit-QED: Howstrong can the coupling between a Josephson junction atom and a transmission line resonator be? Ann Phys 2007;16:767–9.10.1002/andp.200710261Search in Google Scholar

[12] Haroche S, Raimond JM. Exploring the quantum: atoms, cavities, and photons. Oxford: Oxford University Press, 2006.10.1093/acprof:oso/9780198509141.001.0001Search in Google Scholar

[13] Khurgin JB. How to deal with the loss in plasmonics and metamaterials. Nat Nanotechnol 2015;10:2 EP.10.1038/nnano.2014.310Search in Google Scholar PubMed

[14] Kirton P, Roses MM, Keeling J, Dalla Torre EG. Introduction to the Dicke model: from equilibrium to nonequilibrium, and vice versa. 2018:arXiv:1805.09828.10.1002/qute.201800043Search in Google Scholar

[15] Todorov Y, Sirtori C. Few-electron ultrastrong light-matter coupling in a quantum LC circuit yanko todorov and carlo sirtori. Phys Rev X 2014;4:041031.10.1103/PhysRevX.4.041031Search in Google Scholar

[16] Cortese E, Garziano L, De Liberato S. Polariton spectrum of the Dicke-Ising model Erika Cortese, Luigi Garziano, and Simone De Liberato. Phys Rev A 2017;96:053861.10.1103/PhysRevA.96.053861Search in Google Scholar

[17] Rossatto DZ, Villas-Bôas CJ, Sanz M, Solano E. Cooling by heating in the quantum optics domain. Phys Rev A 2017;96:013849.10.1103/PhysRevA.86.035802Search in Google Scholar

[18] Yoshihara F, Fuse T, Ashhab S, Kakuyanagi K, Saito S, Semba K. Superconducting qubit-oscillator circuit beyond the ultrastrong-coupling regime. Nat Phys 2016;13:44 EP.10.1038/nphys3906Search in Google Scholar

[19] Zhang X, Zou C-L, Jiang L, Tang HX. Strongly coupled magnons and cavity microwave photons. Phys Rev Lett 2014;113:156401.10.1103/PhysRevLett.113.156401Search in Google Scholar PubMed

[20] Khurgin J. Relative merits of phononics vs. plasmonics: the energy balance approach. Nanophotonics 2017;7:305.10.1515/nanoph-2017-0048Search in Google Scholar

[21] Kéna-Cohen S, Forrest SR. Room-temperature polariton lasing in an organic single-crystal microcavity. Nat Photonics 2010;4:371 EP.10.1038/nphoton.2010.86Search in Google Scholar

[22] Daskalakis KS, Maier SA, Murray R, Kéna-Cohen S. Nonlinear interactions in an organic polariton condensate. Nat Mater 2014;13:271–8.10.1038/nmat3874Search in Google Scholar PubMed

[23] De Liberato S, Ciuti C. Stimulated scattering and lasing of intersubband cavity polaritons. Phys Rev Lett 2009;102:136403.10.1103/PhysRevLett.102.136403Search in Google Scholar PubMed

[24] Shammah N, Lambert N, Nori F, De Liberato S. Superradiance with local phase-breaking effects. Phys Rev A 2017;96:023863.10.1103/PhysRevA.96.023863Search in Google Scholar

[25] Dominici L, Colas D, Donati S, et al. Ultrafast control and rabi oscillations of polaritons. Phys Rev Lett 2014;113:226401.10.1103/PhysRevLett.113.226401Search in Google Scholar PubMed

[26] Deng H, Weihs G, Snoke D, Bloch J, Yamamoto Y. Polariton lasing vs. photon lasing in a semiconductor microcavity. Proc Natl Acad Sci 2003;100:15318–23.10.1073/pnas.2634328100Search in Google Scholar PubMed PubMed Central

[27] Zanotto S, Degl’Innocenti R, Xu J-H, Sorba L, Tredicucci A, Biasiol G. Ultrafast optical bleaching of intersubband cavity polaritons. Phys Rev B 2012;86:201302.10.1103/PhysRevB.86.201302Search in Google Scholar

[28] Di Stefano O, Stassi R, Garziano L, Kockum AF, Savasta S, Nori F. Feynman-diagrams approach to the quantum Rabi model for ultrastrong cavity QED: stimulated emission and reabsorption of virtual particles dressing a physical excitation. New J Phys 2017;19:053010.10.1088/1367-2630/aa6cd7Search in Google Scholar

[29] Birnbaum KM, Boca A, Miller R, Boozer AD, Northup TE, Kimble HJ. Photon blockade in an optical cavity with one trapped atom. Nature 2005;436:87–90.10.1038/nature03804Search in Google Scholar PubMed

[30] Ridolfo A, Leib M, Savasta S, Hartmann MJ. Photon blockade in the ultrastrong coupling regime. Phys Rev Lett 2012;109:193602.10.1103/PhysRevLett.109.193602Search in Google Scholar PubMed

[31] Ebbesen TW. Hybrid light–matter states in a molecular and material science perspective. Acc Chem Res 2016;49:2403–12.10.1021/acs.accounts.6b00295Search in Google Scholar PubMed

[32] Thomas A, George J, Shalabney A, et al. Ground-state chemical reactivity under vibrational coupling to the vacuum electromagnetic field. Angew Chem Int Ed 2016;55:11462–6.10.1002/anie.201605504Search in Google Scholar PubMed PubMed Central

[33] Galego J, Garcia-Vidal FJ, Feist J. Many-molecule reaction triggered by a single photon in polaritonic chemistry. Phys Rev Lett 2017;119:136001.10.1103/PhysRevLett.119.136001Search in Google Scholar PubMed

[34] Ribeiro RF, Martãnez-martãnez LA, Du M, Campos-Gonzalez-Angulo J, Yuen-Zhou J. Polariton chemistry: controlling molecular dynamics with optical cavities. Chem Sci 2018;9:6325–39.10.1039/C8SC01043ASearch in Google Scholar PubMed

[35] Feist J, Galego J, Garcia-Vidal FJ. Polaritonic chemistry with organic molecules. ACS Photonics 2018;5:205–16.10.1021/acsphotonics.7b00680Search in Google Scholar

[36] Galego J, Garcia-Vidal FJ, Feist J. Cavity-induced modifications of molecular structure in the strong-coupling regime. Phys Rev X 2015;5:041022.10.1103/PhysRevX.5.041022Search in Google Scholar

[37] Cwik JA, Kirton P, De Liberato S, Keeling J. Excitonic spectral features in strongly-coupled organic polaritons. Phys Rev A 2016;93:033840.10.1103/PhysRevA.93.033840Search in Google Scholar

[38] Cortese E, Lagoudakis PG, De Liberato S. collective optomechanical effects in cavity quantum electrodynamics. Phys Rev Lett 2017;119:043604.10.1103/PhysRevLett.119.043604Search in Google Scholar PubMed

[39] Martínez-Martínez LA, Ribeiro RF, Campos-González-Angulo J, Yuen-Zhou J. Polariton chemistry: controlling molecular dynamics with optical cavities. Chem Sci 2018;9:6325–39.10.1039/C8SC01043ASearch in Google Scholar PubMed

[40] Chikkaraddy R, de Nijs B, Benz F, et al. Single-molecule strong coupling at room temperature in plasmonic nanocavities. Nature 2016;535:127–30.10.1038/nature17974Search in Google Scholar PubMed PubMed Central

[41] Crespi A, Longhi S, Osellame R. Photonic realization of the quantum rabi model. Phys Rev Lett 2012;108:163601.10.1103/PhysRevLett.108.163601Search in Google Scholar PubMed

[42] De Liberato S, Ciuti C. Quantum phases of a multimode bosonic field coupled to flat electronic bands. Phys Rev Lett 2013;110:133603.10.1103/PhysRevLett.110.133603Search in Google Scholar PubMed

[43] Yu P, Cardona M. Fundamentals of semiconductors. Berlin, Springer, 1996.10.1007/978-3-662-03313-5Search in Google Scholar

[44] Weisbuch C, Vinter B. Quantum semiconductor structures. Boston, Academic Press, 1991.10.1016/B978-0-08-051557-1.50009-3Search in Google Scholar

[45] Loos P-F. Understanding excitons using spherical geometry. Phys Lett A 2012;376:1997.10.1016/j.physleta.2012.05.010Search in Google Scholar

[46] Andreani LC. Confined electrons and photons. In: Burstein E, Weisbuch C, eds. New York: Plenum, 1995, p. 57.Search in Google Scholar

[47] Deveaud B, Clérot F, Roy N, Satzke K, Sermage B, Katzer DS. Enhanced radiative recombination of free excitons in GaAs quantum wells. Phys Rev Lett 1991;67:2355.10.1103/PhysRevLett.67.2355Search in Google Scholar PubMed

[48] De Boer S, Wiersma DA. Dephasing-induced damping of superradiant emission in J-aggregates. Chem Phys Lett 1990;165:45–53.10.1016/0009-2614(90)87010-OSearch in Google Scholar

[49] Weisbuch C, Benisty H, Houdré R. Overview of fundamentals and applications of electrons, excitons and photons in confined structures. J Lumin 2000;85:271–93.10.1016/S0022-2313(99)00194-5Search in Google Scholar

[50] Hoffmann M, Schmidt K, Fritz T, Hasche T, Agranovich V, Leo K. The lowest energy Frenkel and charge-transfer excitons in quasi-one-dimensional structures: application to MePTCDI and PTCDA crystals. Chem Phys 2000;258:73–96.10.1016/S0301-0104(00)00157-9Search in Google Scholar

[51] Gambino S, Mazzeo M, Genco A, et al. Exploring Light–Matter Interaction Phenomena under Ultrastrong Coupling Regime. ACS Photonics 2014;1:1042–8.10.1021/ph500266dSearch in Google Scholar

[52] Kéna-Cohen S, Maier SA, Bradley DDC. Ultrastrongly Coupled Exciton–Polaritons in Metal-Clad Organic Semiconductor Microcavities. Adv Opt Mater 2013;1:827–33.10.1002/adom.201300256Search in Google Scholar

[53] Weisbuch C, Houdré R, Stanley RP. Spontaneous emission and laser oscillation in microcavities. In: Yokoyama H, Ujihara K, eds. USA, CRC Press, 1995, Chapter 4, pp. 109–150.Search in Google Scholar

[54] Chemla D. Quasi-two-dimensional excitations in GaAs/Al_xGa_1-xAs semiconductor multiple quantum well structures Helv Phys Acta 1983;6:607–37.Search in Google Scholar

[55] Ciuti C, Savona V, Piermarocchi C, Quattropani A, Schwendimann P. Role of the exchange of carriers in elastic exciton-exciton scattering in quantum wells. Phys Rev B 1998;58:7926.10.1103/PhysRevB.58.7926Search in Google Scholar

[56] Tassone F, Yamamoto Y. Exciton-exciton scattering dynamics in a semiconductor microcavity and stimulated scattering into polaritons. Phys Rev B 1999;59:10830.10.1103/PhysRevB.59.10830Search in Google Scholar

[57] Andreani LC, Panzarini G, Gérard J-M. Strong-coupling regime for quantum boxes in pillar microcavities: Theory. Phys Rev B 1999;60:13276.10.1103/PhysRevB.60.13276Search in Google Scholar

[58] Brodbeck S, De Liberato S, Amthor M, et al. Experimental verification of the very strong coupling regime in a gaas quantum well microcavity. Phys Rev Lett 2017;119:027401.10.1103/PhysRevLett.119.027401Search in Google Scholar PubMed

[59] Snoke D. Polariton condensation and lasing. Exciton polaritons in microcavities, Springer series in solid state sciences. Berlin, Springer, 2012, Chapter 12.10.1007/978-3-642-24186-4_12Search in Google Scholar

[60] Amo A, Liew TCH, Adrados C, et al. Exciton-polariton spin switches. Nat Photonics 2010;4:361.10.1038/nphoton.2010.79Search in Google Scholar

[61] De Giorgi M, Ballarini D, Cancellieri E, et al. Control and ultrafast dynamics of a two-fluid polariton switch. Phys Rev Lett 2012;109:266407.10.1103/PhysRevLett.109.266407Search in Google Scholar PubMed

[62] Ballarini D, De Giorgi M, Cancellieri E, et al. All-optical polariton transistor. Nat Commun 2013;4:1778.10.1038/ncomms2734Search in Google Scholar PubMed

[63] Paraïso TK, Wouters M, Léger Y, Morier-Genoud F, Deveaud-Plédran B. Multistability of a coherent spin ensemble in a semiconductor microcavity. Nat Mater 2010;9:655–60.10.1038/nmat2787Search in Google Scholar PubMed

[64] Berloff NG, Silva M, Kalinin K, et al. Realizing the classical XY Hamiltonian in polariton simulators. Nat Mater 2017;16:1120–6.10.1038/nmat4971Search in Google Scholar PubMed

[65] Dreismann A, Ohadi H, del Valle-Inclan Redondo Y, et al. A sub-femtojoule electrical spin-switch based on optically trapped polariton condensates. Nat Mater 2016;15:1074–8.10.1038/nmat4722Search in Google Scholar PubMed

[66] Khurgin JB. Excitonic radius in the cavity polariton in the regime of very strong coupling. Solid State Commun 2001;117:307.10.1016/S0038-1098(00)00469-5Search in Google Scholar

[67] Christmann G, Simeonov D, Butté R, Feltin E, Carlin J-F, Grandjean N. Impact of disorder on high quality factor III-V nitride microcavities. Appl Phys Lett 2006;89:261101.10.1063/1.2420788Search in Google Scholar

[68] Christopoulos S, von Högersthal GBH, Grundy AJD, et al. Room-temperature polariton lasing in semiconductor microcavities. Phys Rev Lett 2007;98:126405.10.1103/PhysRevLett.98.126405Search in Google Scholar PubMed

[69] Christmann G, Butté R, Feltin E, Carlin J-F, Grandjean N. Room temperature polariton lasing in a GaNAlGaN multiple quantum well microcavity. Appl Phys Lett 2008;93:051102.10.1063/1.2966369Search in Google Scholar

[70] Das A, Heo J, Jankowski M, et al. Room temperature ultralow threshold gan nanowire polariton laser. Phys Rev Lett 2011;107:066405.10.1103/PhysRevLett.107.066405Search in Google Scholar PubMed

[71] Li F, Orosz L, Kamoun O, et al. From excitonic to photonic polariton condensate in a zno-based microcavity. Phys Rev Lett 2013;110:196406.10.1103/PhysRevLett.110.196406Search in Google Scholar PubMed

[72] Bhattacharya P, Frost T, Deshpande S, Baten MZ, Hazari A, Das A. Room temperature electrically injected polariton laser. Phys Rev Lett 2014;112:236802.10.1103/PhysRevLett.112.236802Search in Google Scholar PubMed

[73] Michetti P, Mazza L, La Rocca G. in Organic nanophotonics. Nano-optics and nanophotonics (ed Zhao Y). Berlin: Springer, 2015, pp. 39–68.10.1007/978-3-662-45082-6_2Search in Google Scholar

[74] Agranovich VM, Litinskaia M, Lidzey DG. Cavity polaritons in microcavities containing disordered organic semiconductors. Phys Rev B 2003;67:085311.10.1103/PhysRevB.67.085311Search in Google Scholar

[75] Scafirimuto F, Urbonas D, Scherf U, Mahrt RF, Stöferle T. Room-temperature exciton-polariton condensation in a tunable zero-dimensional microcavity. ACS Photonics 2018;5:85–9.10.1021/acsphotonics.7b00557Search in Google Scholar

[76] Du M, Ribeiro RF, Yuen-Zhou J. Remote control of chemistry in optical cavities. 2018;arXiv:1810.10083 [quant-ph].Search in Google Scholar

[77] Ballarini D, De Giorgi M, Gambino S, et al. polariton induced enhanced emission from an organic dye under strong coupling regime. Adv Opt Mater 2014;2:1076.10.1002/adom.201400226Search in Google Scholar

[78] Schwartz T, Hutchison JA, Genet C, Ebbesen TW. Reversible switching of ultrastrong light-molecule coupling. Phys Rev Lett 2011;106:196405.10.1103/PhysRevLett.106.196405Search in Google Scholar PubMed

[79] Kleemann M-E, Chikkaraddy R, Alexeev EM, et al. Strong-coupling of WSe2 in ultra-compact plasmonic nanocavities at room temperature. Nat Commun 2017;8:1296.10.1038/s41467-017-01398-3Search in Google Scholar PubMed PubMed Central

[80] D’Innocenzo V, Grancini G, Alcocer MJP, et al. Excitons versus free charges in organo-lead tri-halide perovskites. Nat Commun 2014;5:3586.10.1038/ncomms4586Search in Google Scholar PubMed

[81] Su R, Diederichs C, Wang J, et al. Room-temperature polariton lasing in all-inorganic perovskite nanoplatelets. Nano Lett 2017;17:3982–8.10.1021/acs.nanolett.7b01956Search in Google Scholar PubMed

[82] Fieramosca A, De Marco L, Passoni M, et al. Tunable out-of-plane excitons in 2D single crystal perovskites. ACS Photonics 2018;5:4179.10.1021/acsphotonics.8b00984Search in Google Scholar

[83] Ballarini D, Amo A, Viña L, Sanvitto D, Skolnick MS, Roberts JS. Transition from the strong- to the weak-coupling regime in semiconductor microcavities: polarization dependence. Appl Phys Lett 2007;90:201905.10.1063/1.2739370Search in Google Scholar

[84] Vladimirova M, Cronenberger S, Scalbert D, et al. Polarization controlled nonlinear transmission of light through semiconductor microcavities. Phys Rev B 2009;79:115325.10.1103/PhysRevB.79.115325Search in Google Scholar

[85] Fieramosca A, Polimeno L, Ardizzone V, et al. Phys Opt 2018;arXiv:1811.04041.Search in Google Scholar

[86] Gianfrate A, Dominici L, Voronych O, et al. Superluminal X-waves in a polariton quantum fluid. Light Sci Appl 2018;7:17119.10.1038/lsa.2017.119Search in Google Scholar PubMed PubMed Central

[87] Lerario G, Ballarini D, Fieramosca A, et al. High-speed flow of interacting organic polaritons. Light Sci Appl 2017;6:e16212.10.1038/lsa.2016.212Search in Google Scholar PubMed PubMed Central

[88] Todisco F, Esposito M, Panaro S, et al. Toward Cavity Quantum Electrodynamics with Hybrid Photon Gap-Plasmon States. ACS Nano 2016;10:11360–8.10.1021/acsnano.6b06611Search in Google Scholar PubMed

[89] Deng H, Weihs G, Santori C, Bloch J, Yamamoto Y. Condensation of semiconductor microcavity exciton polaritons. Science 2002;298:199–202.10.1126/science.1074464Search in Google Scholar PubMed

[90] Kasprzak J, Richard M, Kundermann S, et al. Bose-Einstein condensation of exciton polaritons. Nature 2006;443:449–14.10.1038/nature05131Search in Google Scholar PubMed

[91] Amo A, Sanvitto D, Laussy FP, et al. Collective fluid dynamics of a polariton condensate in a semiconductor microcavity. Nature 2009;457:291–5.10.1038/nature07640Search in Google Scholar PubMed

[92] Amo A, Lefrére J, Pigeon S, et al. Superfluidity of polaritons in semiconductor microcavities. Nat Phys 2009;5:805–10.10.1038/nphys1364Search in Google Scholar

[93] Abbarchi M, Amo A, Sala VG, et al. Macroscopic quantum self-trapping and Josephson oscillations of exciton polaritons. Nat Phys 2013;9:275–9.10.1038/nphys2609Search in Google Scholar

[94] Lagoudakis KG, Pietka B, Wouters M, André R, Deveaud-Plédran B. Coherent oscillations in an exciton-polariton Josephson junction. Phys Rev Lett 2010;105:120403.10.1103/PhysRevLett.105.120403Search in Google Scholar PubMed

[95] Sanvitto D, Pigeon S, Amo A, et al. All-optical control of the quantum flow of a polariton condensate. Nat Photonics 2011;5:610–4.10.1038/nphoton.2011.211Search in Google Scholar

[96] Lagoudakis KG, Wouters M, Richard M, et al. Quantized vortices in an exciton-polariton condensate. Nat Phys 2008;4:706–10.10.1038/nphys1051Search in Google Scholar

[97] Dominici L, Dagvadorj G, Fellows JM, et al. Vortex and half-vortex dynamics in a nonlinear spinor quantum fluid. Sci Adv 2015;1: e1500807.10.1126/sciadv.1500807Search in Google Scholar PubMed PubMed Central

[98] Kavokin A, Malpuech G, Glazov M. Optical spin Hall effect. Phys Rev Lett 2005;95:136601.10.1103/PhysRevLett.95.136601Search in Google Scholar PubMed

[99] Steger M, Liu G, Nelsen B, et al. Long-range ballistic motion and coherent flow of long-lifetime polaritons. Phys Rev B 2013;88:235314.10.1103/PhysRevB.88.235314Search in Google Scholar

[100] Nelsen B, Liu G, Steger M, et al. Dissipationless flow and sharp threshold of a polariton condensate with long lifetime. Phys Rev X 2013;3:041015.10.1103/PhysRevX.3.041015Search in Google Scholar

[101] Sun Y, Wen P, Yoon Y, et al. Bose-einstein condensation of long-lifetime polaritons in thermal equilibrium. Phys Rev Lett 2017;118:016602.10.1103/PhysRevLett.118.016602Search in Google Scholar PubMed

[102] Caputo D, Ballarini D, Dagvadorj G, et al. Topological order and thermal equilibrium in polariton condensates. Nat Mater 2018;17:145–51.10.1038/nmat5039Search in Google Scholar PubMed

[103] Ballarini D, Caputo D, Sánchez Muñoz C, et al. Macroscopic two-dimensional polariton condensates. Phys Rev Lett 2017;118:215301.10.1103/PhysRevLett.118.215301Search in Google Scholar PubMed

[104] Karzig T, Bardyn C-E, Lindner NH, Refael G. Topological polaritons. Phys Rev X 2015;5:031001.10.1103/PhysRevX.5.031001Search in Google Scholar

[105] Baboux F, Ge L, Jacqmin T, et al. Bosonic condensation and disorder-induced localization in a flat band. Phys Rev Lett 2016;116:066402.10.1103/PhysRevLett.116.066402Search in Google Scholar PubMed

[106] Klembt S, Harder TH, Egorov OA, et al. Exciton-polariton topological insulator. Nature 2018;562:552–6.10.1038/s41586-018-0601-5Search in Google Scholar PubMed

[107] Peter E, Senellart P, Martrou D, et al. Exciton-photon strong-coupling regime for a single quantum dot embedded in a microcavity. Phys Rev Lett 2005;95:067401.10.1103/PhysRevLett.95.067401Search in Google Scholar PubMed

[108] Reithmaier JP, Sek G, Löffler A, et al. Strong coupling in a single quantum dot–semiconductor microcavity system. Nature 2004;432:126405.10.1038/nature02969Search in Google Scholar PubMed

[109] Yoshie T, Scherer A, Hendrickson J, et al. Vacuum Rabi splitting with a single quantum dot in a photonic crystal nanocavity. Nature 2004;432:200–3.10.1038/nature03119Search in Google Scholar PubMed

[110] Hennessy K, Badolato A, Winger M, et al. Quantum nature of a strongly coupled single quantum dot–cavity system. Nature 2007;445:896–9.10.1038/nature05586Search in Google Scholar PubMed

[111] Press D, Götzinger S, Reitzenstein S, et al. Strong coupling of single quantum dots to micropillars. Phys Rev Lett 2007;98:117402.10.1103/PhysRevLett.98.117402Search in Google Scholar PubMed

[112] Schneider C, Gold P, Reitzenstein S, Höfling S, Kamp M. Quantum dot micropillar cavities with quality factors exceeding 250,000. Appl Phys B 2016;122:19.10.1007/s00340-015-6283-xSearch in Google Scholar

[113] Boulier T, Bamba M, Amo A, et al. Polariton-generated intensity squeezing in semiconductor micropillars. Nat Commun 2014;5:3260.10.1038/ncomms4260Search in Google Scholar PubMed

[114] Adiyatullin AF, Anderson MD, Flayac H, et al. Periodic squeezing in a polariton Josephson junction. Nat Commun 2017;8:1329.10.1038/s41467-017-01331-8Search in Google Scholar PubMed PubMed Central

[115] Verger A, Ciuti C, Carusotto I. Polariton quantum blockade in a photonic dot. Phys Rev B 2006;73:193306.10.1103/PhysRevB.73.193306Search in Google Scholar

[116] Snijders HJ, Frey JA, Norman J, et al. Observation of the unconventional photon blockade. Phys Rev Lett 2018;121:043601.10.1103/PhysRevLett.121.043601Search in Google Scholar PubMed

[117] Delteil A, Fink T, Schade A, Hofling S, Schneider C, Imamoglu A. Quantum correlations of confined exciton-polaritons. 2018;arXiv:1805.04020 [cond-mat.mes-hall].Search in Google Scholar

[118] Muñoz-Matutano G, Wood A, Johnson M, et al. 2017;arXiv:1712.05551 [cond-mat.mes-hall].Search in Google Scholar

[119] Cuevas Á, López Carreño JC, Silva B, et al. First observation of the quantized exciton-polariton field and effect of interactions on a single polariton. Sci Adv 2018;4:eaao6814.10.1126/sciadv.aao6814Search in Google Scholar PubMed PubMed Central

[120] Lidzey DG, Bradley DDC, Virgili T, Armitage A, Skolnick MS, Walker S. Room temperature polariton emission from strongly coupled organic semiconductor microcavities. Phys Rev Lett 1999;82:3316–9.10.1103/PhysRevLett.82.3316Search in Google Scholar

[121] Plumhof JD, Stöferle T, Mai L, Scherf U, Mahrt RF. Room-temperature Bose–Einstein condensation of cavity exciton–polaritons in a polymer. Nat Mater 2014;13:247–52.10.1038/nmat3825Search in Google Scholar PubMed

[122] Lerario G, Fieramosca A, Barachati F, et al. Room-temperature superfluidity in a polariton condensate. Nat Phys 2017;13:837–41.10.1038/nphys4147Search in Google Scholar

[123] Tinkler L, Walker P, Skryabin D, et al. Ultra-low-power hybrid light–matter solitons. Nat Commun 2014;6:9317.10.1038/ncomms9317Search in Google Scholar

[124] Lerario G, Cannavale A, Ballarini D, et al. Room temperature Bloch surface wave polaritons. Opt Lett 2014;39:2068.10.1364/OL.39.002068Search in Google Scholar PubMed

[125] Pirotta S, Patrini M, Liscidini M, et al. Strong coupling between excitons in organic semiconductors and Bloch surface waves. Appl Phys Lett 2014;104:051111.10.1063/1.4863853Search in Google Scholar

[126] Liscidini M, Gerace D, Sanvitto D, Bajoni D. Guided Bloch surface wave polaritons. Appl Phys Lett 2011;98:121118.10.1063/1.3571285Search in Google Scholar

[127] Kaliteevski M, Iorsh I, Brand S, et al. Tamm plasmon-polaritons: Possible electromagnetic states at the interface of a metal and a dielectric Bragg mirror. Phys Rev B 2007;76:165415.10.1103/PhysRevB.76.165415Search in Google Scholar

[128] Barachati F, Fieramosca A, Hafezian S, et al. Interacting polariton fluids in a monolayer of tungsten disulfide. Nat Nanotechnol 2018;13:906–9.10.1038/s41565-018-0219-7Search in Google Scholar PubMed

[129] Wurdack M, Lundt N, Klaas M, et al. Observation of hybrid Tamm-plasmon exciton- polaritons with GaAs quantum wells and a MoSe2 monolayer. Nat Commun 2017;8:259.10.1038/s41467-017-00155-wSearch in Google Scholar PubMed PubMed Central

[130] Lundt N, Klembt S, Cherotchenko E, et al. Room-temperature Tamm-plasmon exciton-polaritons with a WSe2 monolayer. Nat Commun 2016;7:13328.10.1038/ncomms13328Search in Google Scholar PubMed PubMed Central

[131] Kristensen PT, Hughes S. Modes and mode volumes of leaky optical cavities and plasmonic nanoresonators. ACS Photonics 2014;1:2.10.1021/ph400114eSearch in Google Scholar

[132] Törmä P, Barnes W. Strong coupling between surface plasmon polaritons and emitters: a review. Rep Prog Phys 2015;78:013901.10.1088/0034-4885/78/1/013901Search in Google Scholar PubMed

[133] Bellessa J, Bonnand C, Plenet JC, Mugnier J. Strong coupling between surface plasmons and excitons in an organic semiconductor. Phys Rev Lett 2004;93:036404.10.1103/PhysRevLett.93.036404Search in Google Scholar PubMed

[134] Symonds C, Bonnand C, Plenet JC, et al. Particularities of surface plasmon–exciton strong coupling with large Rabi splitting. New J Phys 2008;10:065017.10.1088/1367-2630/10/6/065017Search in Google Scholar

[135] Hakala TK, Toppari JJ, Kuzyk A, et al. Vacuum rabi splitting and strong-coupling dynamics for surface-plasmon polaritons and rhodamine 6G molecules. Phys Rev Lett 2009;103:053602.10.1103/PhysRevLett.103.053602Search in Google Scholar PubMed

[136] Aberra Guebrou S, Symonds C, Homeyer E, et al. Coherent emission from a disordered organic semiconductor induced by strong coupling with surface plasmons. Phys Rev Lett 2012;108:066401.10.1103/PhysRevLett.108.066401Search in Google Scholar PubMed

[137] Todisco F, De Giorgi M, Esposito M, et al. Ultrastrong plasmon–exciton coupling by dynamic molecular aggregation. ACS Photonics 2018;5:143–50.10.1021/acsphotonics.7b00554Search in Google Scholar

[138] Kato F, Minamimoto H, Nagasawa F, Yamamoto YS, Itoh T, Murakoshi K. Active tuning of strong coupling states between dye excitons and localized surface plasmons via electrochemical potential control. ACS Photonics 2018;5:788–96.10.1021/acsphotonics.7b00841Search in Google Scholar

[139] Groß H, Hamm JM, Tufarelli T, Hess O, Hecht B. Near-field strong coupling of single quantum dots. Sci Adv 2018;4:eaar4906.10.1126/sciadv.aar4906Search in Google Scholar PubMed PubMed Central

[140] Leng H, Szychowski B, Daniel M-C, Pelton M. Strong coupling and induced transparency at room temperature with single quantum dots and gap plasmons. Nat Commun 2018;9:4012.10.1038/s41467-018-06450-4Search in Google Scholar PubMed PubMed Central

[141] Faure S, Guillet T, Lefebvre P, Bretagnon T, Gil B. Comparison of strong coupling regimes in bulk GaAs, GaN, and ZnO semiconductor microcavities. Phys Rev B 2008;78:235323.10.1103/PhysRevB.78.235323Search in Google Scholar

[142] Dufferwiel S, Schwarz S, Withers F, et al. Exciton–polaritons in van der Waals heterostructures embedded in tunable microcavities. Nat Commun 2015;6:8579.10.1038/ncomms9579Search in Google Scholar PubMed PubMed Central

[143] Liu W, Lee B, Naylor CH, et al. Strong Exciton–plasmon coupling in MoS2 coupled with plasmonic lattice. Nano Lett 2016;16:1262–9.10.1021/acs.nanolett.5b04588Search in Google Scholar PubMed

[144] Liu X, Galfsky T, Sun Z, et al. Strong light–matter coupling in two-dimensional atomic crystals. Nat Phys 2015;9:30–4.10.1038/nphoton.2014.304Search in Google Scholar

[145] Cacciola A, Di Stefano O, Stassi R, Saija R, Savasta S. Ultrastrong coupling of plasmons and excitons in a nanoshell. ACS Nano 2014;8:11483. pMID: 25337782.10.1021/nn504652wSearch in Google Scholar PubMed

[146] Vasa P, Pomraenke R, Schwieger S, et al. Coherent exciton–surface-plasmon-polariton interaction in hybrid metal-semiconductor nanostructures. Phys Rev Lett 2008;101:116801.10.1103/PhysRevLett.101.116801Search in Google Scholar PubMed

[147] Väkeväinen AI, Moerland RJ, Rekola HT, et al. Plasmonic surface lattice resonances at the strong coupling regime. Nano Lett 2014;14:1721–7.10.1021/nl4035219Search in Google Scholar PubMed

[148] De Giorgi M, Ramezani M, Todisco F, et al. Interaction and coherence of a plasmon–exciton polariton condensate. ACS Photonics 2018;5:3666–72.10.1021/acsphotonics.8b00662Search in Google Scholar

[149] De Liberato S, Ciuti C. Quantum model of microcavity intersubband electroluminescent devices. Phys Rev B 2008;77:155321.10.1103/PhysRevB.77.155321Search in Google Scholar

[150] De Liberato S, Ciuti C, Phillips CC. Terahertz lasing from intersubband polariton-polariton scattering in asymmetric quantum wells. Phys Rev B 2013;87:241304.10.1103/PhysRevB.87.241304Search in Google Scholar

[151] Zanotto S, Mezzapesa FP, Bianco F, et al. Perfect energy-feeding into strongly coupled systems and interferometric control of polariton absorption. Nat Phys 2014;10:830–4.10.1038/nphys3106Search in Google Scholar

[152] Alpeggiani F, Andreani LC. Quantum theory of surface plasmon polaritons: planar and spherical geometries. Plasmonics 2014;9:965.10.1007/s11468-014-9703-6Search in Google Scholar

[153] Colombelli R, Manceau J-M. Perspectives for intersubband polariton lasers. Phys Rev X 2015;5:011031.10.1364/CLEO_SI.2015.STu4G.5Search in Google Scholar

[154] Askenazi B, Vasanelli A, Todorov Y, et al. Midinfrared ultrastrong Light–matter coupling for THz thermal emission. ACS Photonics 2017;4:2550.10.1021/acsphotonics.7b00838Search in Google Scholar

[155] Manceau J-M, Tran N-L, Biasiol G, et al. Resonant intersubband polariton-LO phonon scattering in an optically pumped polaritonic device. Appl Phys Lett 2018;112:191106.10.1063/1.5029893Search in Google Scholar

[156] Ciuti C, Bastard G, Carusotto I. Quantum vacuum properties of the intersubband cavity polariton field. Phys Rev B 2005;72:115303.10.1103/PhysRevB.72.115303Search in Google Scholar

[157] Günter G, Anappara AA, Hees J, et al. Sub-cycle switch-on of ultrastrong light–matter interaction. Nature 2009;458:178.10.1038/nature07838Search in Google Scholar PubMed

[158] Dini D, Köhler R, Tredicucci A, Biasiol G, Sorba L. Microcavity polariton splitting of intersubband transitions. Phys Rev Lett 2003;90:116401.10.1103/PhysRevLett.90.116401Search in Google Scholar PubMed

[159] Anappara AA, De Liberato S, Tredicucci A, et al. Signatures of the ultrastrong light-matter coupling regime. Phys Rev B 2009;79:201303.10.1103/PhysRevB.79.201303Search in Google Scholar

[160] Todorov Y, Andrews AM, Colombelli R, et al. Ultrastrong light-matter coupling regime with polariton dots. Phys Rev Lett 2010;105:196402.10.1103/PhysRevLett.105.196402Search in Google Scholar PubMed

[161] Malerba M, Ongarello T, Paulillo B, et al. Towards strong light-matter coupling at the single-resonator level with sub-wavelength mid-infrared nano-antennas. Appl Phys Lett 2016;109:021111.10.1063/1.4958330Search in Google Scholar

[162] Benz A, Campione S, Liu S, et al. Strong coupling in the sub-wavelength limit using metamaterial nanocavities. Nat Commun 2013;4:2882.10.1038/ncomms3882Search in Google Scholar PubMed PubMed Central

[163] Benz A, Campione S, Klem JF, Sinclair MB, Brener I. Control of strong light–matter coupling using the capacitance of metamaterial nanocavities. Nano Lett 2015;15:1959–66.10.1021/nl504815cSearch in Google Scholar PubMed

[164] Hagenmüller D, De Liberato S, Ciuti C. Ultrastrong coupling between a cavity resonator and the cyclotron transition of a two-dimensional electron gas in the case of an integer filling factor. Phys Rev B 2010;81:235303.10.1103/PhysRevB.81.235303Search in Google Scholar

[165] Muravev VM, Andreev IV, Kukushkin IV, Schmult S, Dietsche W. Observation of hybrid plasmon-photon modes in microwave transmission of coplanar microresonators. Phys Rev B 2011;83:075309.10.1103/PhysRevB.83.075309Search in Google Scholar

[166] Scalari G, Maissen C, Turcinkova D, et al. Ultrastrong coupling of the cyclotron transition of a 2D electron Gas to a THz metamaterial. Sci 2012;335:1323.10.1126/science.1216022Search in Google Scholar PubMed

[167] Scalari G, Maissen C, Hagenmüller D, et al. Ultrastrong light-matter coupling at terahertz frequencies with split ring resonators and inter-Landau level transitions. J Appl Phys 2013;113:136510.10.1063/1.4795543Search in Google Scholar

[168] Bayer A, Pozimski M, Schambeck S, et al. Terahertz light–matter interaction beyond unity coupling strength. Nano Lett 2017;17:6340–4.10.1021/acs.nanolett.7b03103Search in Google Scholar PubMed

[169] Zhang Q, Lou M, Li X, et al. Collective non-perturbative coupling of 2D electrons with high-quality-factor terahertz cavity photons. Nat Phys 2016;12:1005–11.10.1038/nphys3850Search in Google Scholar

[170] Li X, Bamba M, Zhang Q, et al. Vacuum Bloch–Siegert shift in landau polaritons with ultra-high cooperativity. Nat Photonics 2018;12:324.10.1038/s41566-018-0153-0Search in Google Scholar

[171] Keller J, Scalari G, Cibella S, et al. Few-Electron ultrastrong light-matter coupling at 300 GHz with nanogap hybrid LC microcavities. Nano Lett 2017;17:7410–5.10.1021/acs.nanolett.7b03228Search in Google Scholar PubMed

[172] Hillenbrand R, Taubner T, Keilmann F. Phonon-enhanced light–matter interaction at the nanometre scale. Nature 2002;418:159–62.10.1038/nature00899Search in Google Scholar PubMed

[173] Wang T, Li P, Hauer B, Chigrin DN, Taubner T. Optical properties of single infrared resonant circular microcavities for surface phonon polaritons. Nano Lett 2013;13:5051–5.10.1021/nl4020342Search in Google Scholar PubMed

[174] Caldwell JD, Glembocki OJ, Francescato Y, et al. Low-loss, extreme sub-diffraction photon confinement via silicon carbide surface phonon polariton nanopillar resonators. Nano Lett 2013;13:3690–7.10.1021/nl401590gSearch in Google Scholar PubMed

[175] Caldwell JD, Lindsay L, Giannini V et al. Low-loss, infrared and terahertz nanophotonics using surface phonon polaritons. Nanophotonics 2015;4:44.10.1515/nanoph-2014-0003Search in Google Scholar

[176] Gubbin CR, Maier SA, De Liberato S. Theoretical investigation of phonon polaritons in SiC micropillar resonators. Phys Rev B 2017;95:035313.10.1103/PhysRevB.95.035313Search in Google Scholar

[177] Wang T, Li P, Chigrin DN, et al. Phonon-Polaritonic bowtie nanoantennas: Controlling infrared thermal radiation at the nanoscale. ACS Photonics 2017;4:1753–60.10.1021/acsphotonics.7b00321Search in Google Scholar

[178] Gubbin CR, De Liberato S. Theory of Four-Wave-Mixing in phonon polaritons. ACS Photonics 2018;5:284.10.1021/acsphotonics.7b00863Search in Google Scholar

[179] Razdolski I, Passler NC, Gubbin CR, et al. Second harmonic generation from strongly coupled localized and propagating phonon-polariton modes. Phys Rev B 2018;98:125425.10.1103/PhysRevB.98.125425Search in Google Scholar

[180] Huck C, Vogt J, Neuman T, et al. Strong coupling between phonon-polaritons and plasmonic nanorods. Opt Express 2016;24:25528.10.1364/OE.24.025528Search in Google Scholar PubMed

[181] Li K, Fitzgerald JM, Xiao X, et al. Graphene plasmon cavities made with silicon carbide. ACS Omega 2017;2:3640–6.10.1021/acsomega.7b00726Search in Google Scholar PubMed PubMed Central

[182] Gubbin CR, Martini F, Politi A, Maier SA, De Liberato S. Strong and coherent coupling between localized and propagating phonon polaritons. Phys Rev Lett 2016;116:246402.10.1103/PhysRevLett.116.246402Search in Google Scholar PubMed

[183] Passler NC, Gubbin CR, Folland TG, et al. Strong coupling of Epsilon-Near-Zero phonon polaritons in polar dielectric heterostructures. Nano Lett 2018;18:4285–92.10.1021/acs.nanolett.8b01273Search in Google Scholar PubMed

[184] Othani K, Meng B, Franckié M, et al. Raman emission from an electrically pumped phonon polariton laser. 2018;arXiv:1808.09844.10.1364/CLEO_SI.2018.SF3G.5Search in Google Scholar

[185] Franckié M, Ndebeka-Bandou C, Ohtani K, Faist J. Quantum model of gain in phonon-polariton lasers. Phys Rev B 2018;97:075402.10.1103/PhysRevB.97.075402Search in Google Scholar

Received: 2018-11-05
Revised: 2019-01-08
Accepted: 2019-01-10
Published Online: 2019-02-12

©2019 Simone De Liberato et al., published by De Gruyter, Berlin/Boston

This work is licensed under the Creative Commons Attribution 4.0 Public License.

Articles in the same Issue

  1. Editorial
  2. Plasmon-exciton coupling
  3. Special Issue Articles
  4. Preparation and properties of plasmonic-excitonic nanoparticle assemblies
  5. High optical magnetism of dodecahedral plasmonic meta-atoms
  6. Quantum dot plasmonics: from weak to strong coupling
  7. Enhancing functionalities of atomically thin semiconductors with plasmonic nanostructures
  8. Six-fold plasmonic enhancement of thermal scavenging via CsPbBr3 anti-Stokes photoluminescence
  9. Phase-matched nonlinear second-harmonic generation in plasmonic metasurfaces
  10. Prospects and applications of plasmon-exciton interactions in the near-field regime
  11. Pliable polaritons: Wannier exciton-plasmon coupling in metal-semiconductor structures
  12. Polaritonics: from microcavities to sub-wavelength confinement
https://doi.org/10.1515/nanoph-2018-0188
Keywords for this article
cavity quantum electrodynamics; polaritonics; ultrastrong coupling
Creative Commons
BY 4.0

Articles in the same Issue

  1. Editorial
  2. Plasmon-exciton coupling
  3. Special Issue Articles
  4. Preparation and properties of plasmonic-excitonic nanoparticle assemblies
  5. High optical magnetism of dodecahedral plasmonic meta-atoms
  6. Quantum dot plasmonics: from weak to strong coupling
  7. Enhancing functionalities of atomically thin semiconductors with plasmonic nanostructures
  8. Six-fold plasmonic enhancement of thermal scavenging via CsPbBr3 anti-Stokes photoluminescence
  9. Phase-matched nonlinear second-harmonic generation in plasmonic metasurfaces
  10. Prospects and applications of plasmon-exciton interactions in the near-field regime
  11. Pliable polaritons: Wannier exciton-plasmon coupling in metal-semiconductor structures
  12. Polaritonics: from microcavities to sub-wavelength confinement
Sign up now to receive a 20% welcome discount
Institutional Access
How does access work?
Have an idea on how to improve our website?
Please write us.
© 2025 De Gruyter Brill
Downloaded on 7.9.2025 from https://www.degruyterbrill.com/document/doi/10.1515/nanoph-2018-0188/html
Scroll to top button