Coupling single emitters to quantum plasmonic circuits

1 Introduction

When directing a photon towards a single emitter [e.g. an atom, a quantum dot (QD), or a defect center], the probability that the photon being absorbed (or emitted in a single mode) is typically very low due to the small cross-section of the emitter [1]. By strongly focusing the photon, the absorption probability can be largely improved [2–4] particularly if the photon is radially polarized [5], but reaching high probabilities is highly challenging particularly if the emitter is inhomogeneously broadened [6]. Another common approach to enhance the photon-emitter interaction strength is to place the emitter inside a cavity in which the photon bounces back and forth several times, thereby increasing the probability for absorption [7]. This approach, which is related to the Purcell effect [8], however, can be only used for narrowband emitters and photons due to the small bandwidth of the cavity. Finally, strong absorption can be attained by placing the emitter at an optimal position in the confined field of the plasmonic mode propagating along a small waveguide made of metal. As a plasmon mode, the propagating eigenmode of a waveguide made of metal can be tightly confined to below the optical diffraction limit [9], and the waveguide acts as an ultrastrong lens that focuses the light down to a few nanometers in the transverse dimension. Due to this exceptionally strong focusing capability, the emitter can interact with the photon with an extraordinary strength and thus absorb the photon with unit probability or, equivalently, a photon emitted from the dipole can be directed into a single plasmonic mode of the wire with unit probability [10].

Surface plasmon polaritons are electromagnetic excitations of charge density waves at the interface between a conductor and a dielectric medium, and as mentioned above, they can be confined to transverse dimensions much smaller than what is possible with conventional optics [11, 12]. Applying Fermi’s golden rule to evaluate the interaction strength between a dipole transition and such a surface plasmon mode, the coupling strength g is found to scale with the local electric field per photon, E₀(r₀), which is higher when the field confinement increases [10]. About a decade ago, it was theoretically suggested that the resulting coupling rate to propagating surface plasmon modes, Γ_pl, can largely exceed the spontaneous emission rate to the radiation field, Γ_rad, and that nonradiative decay rates, Γ_nonrad, are negligible for the considered parameter space [10].¹ For a schematic illustration of the system, as an example, we chose a nanowire plasmon waveguide, and the rates are illustrated in Figure 1. These findings stimulated an enormous interest and triggered experimental efforts in using surface plasmon modes for enhanced light-matter interaction and device applications. It is worth mentioning that propagating surface plasmons are different from localized surface plasmons. In contrast to localized plasmons, propagating plasmons are traveling in a well-defined direction as the real part of their wavevectors is nonzero. This basically means that the propagating plasmon can be guided through metallic circuits much like optical beams in photonic circuits. The difference between the photonic and plasmonic guiding, however, is that the transverse dimension of the latter guiding can go below the diffraction limit and thus interact strongly with single emitters. The vision is therefore to build arbitrarily complex plasmonic circuits with metallic waveguides in which the plasmons can strongly interact with emitters and thereby enable classical and quantum information processing with a very small footprint. In addition to information processing, a scalable plasmonic platform of strongly interacting emitters and photons might be a promising system for investigating out-of-equilibrium many-body physics.

Figure 1

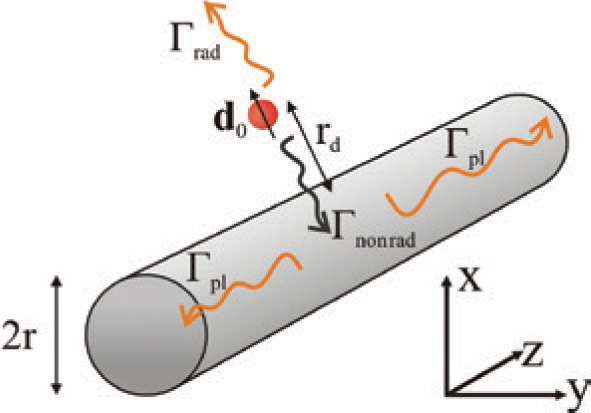
Schematic illustration of the individual decay channels of a dipole emitter d₀ located at a distance r_d next to a metallic nanowire. The emitter (orange sphere with black arrow) decays by emitting a single photon, which is directed into free space, into ohmic losses of the metallic wire, or into the single plasmonic mode propagating along wire. Γ_rad, Γ_pl, and Γ_nonrad denote the decay rates to the radiation field, the propagating surface plasmon mode, and the metallic loss channels, respectively. The ratio between the different rates is determined by the distance between the dipole emitter and the wire, r_d.

In this review, we will describe experimental efforts towards the realization of an efficient interaction between a single optical dipole emitter and propagating surface plasmon modes supported by metallic waveguides. There exists a vast literature on plasmonics systems and circuits, which have been discussed in a number of review articles [12–17]. In this review, however, we mainly focus on quantum plasmonic circuits in which quantum states, and in particular single plasmonic states, are propagating. We thus focus on reviewing work on which single propagating plasmons are generated by a single emitter. We start by discussing the definition of “quantum plasmonics” and subsequently summarize different potential applications of the plasmon-emitter platform. Then, we discuss the various experimental activities solely focusing on the coupling between a “single emitter” and a propagating plasmon supported by a metallic waveguide. We conclude with an outlook in which we summarize a number of challenges that have to be solved for further progress and new directions of the field.

2 Quantum plasmonics

The property of strong confinement of the electromagnetic field has opened a new world of opportunities in both classical and quantum optics. Applications in the latter field have triggered the new field of quantum plasmonics [13]. But what is “quantum” in quantum plasmonics? Before answering this question, let us briefly review some of the first experiments carried out at the interface between quantum optics and plasmonics.

The experiment reported by Altewischer et al. [18] originally triggered the curiosity of the quantum optics community in the field of plasmonics. They have shown that the entanglement present in the polarization degree of freedom of two spatially separated optical modes survived after one of the photons passed through a gold film perforated with nanometer-sized holes. In the holes, photons excite surface plasmon resonances and thus enhance the total transmission through the gold film [19]. Later experiments reported by Fasel et al. [20] confirmed these findings by demonstrating that also time-energy entanglement was preserved after a photon-surface plasmon-photon conversion process. The survival of quadrature squeezing after surface plasmon excitation demonstrated that the phase coherence is also not affected by surface plasmon excitations [21, 22] and that linear propagation losses can be modeled by an effective beam splitter interaction. Together with the demonstration of Hong-Ou-Mandel interference of identical photons (produced externally by spontaneous parametric down-conversion) on a surface plasmon-based beam splitter [23–25], this series of experiments leaves little doubt that surface plasmon modes are well described by bosonic field operators.

These experiments suggest that plasmons behave similarly to bosonic electromagnetic fields. This is also what is expected from theory derived by Pines in the 1950s [26], establishing the quantization of collective electron oscillations that have bosonic properties. Due to the large number of electrons, a macroscopic collective excitation is formed and can be described by the macroscopic permittivity ∈ of the materials. This permittivity determines the mode profile and their guidance along a waveguide [9], and in a modern context, the quantization of surface plasmon modes has been addressed by Tame et al. [27], taking metal losses into account.

The aforementioned experiments are referred to as being “quantum plasmonics” experiments due to the fact that the statistics of the propagating plasmons cannot be described by a well-behaving Glauber-Sudharshan P-function. This function is defined as a weight function, P(α), in the coherent state basis |α〉, where α is the complex coherent state amplitude. The density matrix ρ̂ of a single mode state can then be written as ρ̂ = ∫ p(α)∣α〉〈α∣d²α [28, 29]. Quadrature squeezed states, single-photon states, and other non-Gaussian pure states do not possess a well behaving P-function and are thus often considered as nonclassical states. Therefore, the excitation of plasmonic modes in such nonclassical bosonic modes are often coined “quantum plasmonics” [13].

However, there exists also another definition of quantum plasmonics, which is relevant when the structures are reduced to very small dimensions of about a few nanometers. In this regime, the standard assumption of a continuous energy spectrum of the electrons might break down as the electrons become bounded and thus exhibit a quantized energy spectrum [30]. Furthermore, if very short length scales are considered, the quantum delocalization nature of electrons might be relevant and should be taken into account [31]. Due to this possible need for taking into account the energy quantization and the nonlocal nature of the electrons, the plasmonic behavior can only be described by a full quantum model; thus, it is referred to as “quantum plasmonics” [13]. However, all experiments to date on propagating plasmons have not been affected by these quantum phenomena (to the best of our knowledge); thus, the “quantum” in quantum plasmonics in previous experiments simply refers to the quantum statistics of the propagating bosonic mode. In addition to the entangled and squeezed plasmonic states discussed above, there have been a number of activities devoted to the generation of single plasmonic states by coupling single emitters to metallic waveguides. This will now be discussed in greater detail.

3 Emitter coupling to surface plasmons

In this section, we first consider the coupling of an emitter to a plasmonic mode supported by a metallic waveguide, as illustrated in Figure 1. The emitter with an angular transition frequency ω and dipole moment d₀ is positioned a distance r_d away from the surface of the waveguide. The one-dimensional waveguide is considered to have finite dimensions in the transverse (x, y)-plane and to be infinite in the longitudinal z-direction. The original framework for emitter-waveguide mode coupling was set by Klimov and Ducloy [32]. Using the quasi-static approximation, they derived an analytical expressions for the spontaneous emission rate into the guided mode, Γ_pl, radiation field, Γ_rad, and nonradiative emission due to dissipation of the fiber, Γnonrad, which is related to the imaginary part of the permittivity, 𝔍𝔪(∈). This work was later extended by Chang et al. [10] on the case of metallic nanowires supporting propagating surface plasmon modes [9]. It was found that, for an optimal dipole orientation parallel to the electric field component of the radially polarized surface plasmon mode, d₀||E_r, the decay rate into the plasmon mode Γ_pl (the guided mode in the dielectric nanofiber case) can largely exceed the sum of all other decay channels, i.e. Γ_pl≫Γ_rad+Γ_nonrad. This results in a β-factor very close to 1, where the β-factor is defined as the ratio of emission going into the guided modes to the total decay rate, β = Γ_pl/(Γ_pl+Γ_rad+Γ_nonrad). This result is the central motivation for the experimental investigations discussed in the following sections. The strong Γ_pl component, relative to all other decay channels, effectively originates from the tight mode confinement associated with the fundamental surface plasmon mode. For small r_d, the Γ_nonrad component dominates, as it scales with 1/rd3, reflecting the near field of the emitter [10].

If the plasmon mode cannot be described analytically, for example, when the nanowire is placed on a substrate or in the case of other waveguides, such as grooves or wedges, the total decay rate Γ_tot and the individual decay channels (Γ_pl, Γ_nonrad, and Γ_rad) can only be obtained numerically using a finite-element method [33] or a finite difference time domain method [34]. Although, for the normalized plasmonic decay channel Γ_pl/Γ₀, it is sufficient to know the electric E(x,y) and magnetic H(x,y) field distributions in the transverse (x,y)-plane, a rigorous modeling in three dimensions is required to obtain the total decay rate Γ_tot and to estimate the β-factor.

One may also obtain the decay rate of a dipole emitter at a position r using the proportionality Γ(r)∝𝔍𝔪TrG(r,r), where G(r,r) is the three-dimensional Green’s tensor [35]. In the vicinity to a two-dimensional, infinitely long waveguide with arbitrary shape, G(r,r), can be expressed in a Fourier series of two-dimensional Green’s tensors G^2D(r_∥,r_∥,k_z), where k_z is the longitudinal wavenumber, as done by Barthes et al. [36]. The two-dimensional Green’s tensor is then further separated as G2D=Gref2D+ΔG2D, where Gref2D accounts for the contribution from the reference system, such as the homogeneous background or the substrate, and ∆G^2D describes the contribution from the waveguide structure. The waveguide contribution to the modification of the decay rate, expressed as a function of k_z, is then obtained btained as Δρu2D(r||,  kz)∞ℑm{∈(r||)Tr[u⋅ΔG2D⋅u]}, where u is a unit vector along the direction of the dipole. Δρu2D is referred to as the modified two-dimensional local density of states and plotted in Figure 2 as a function of k_z for a cylindrically shaped nanowire made of silver and a radially oriented dipole. Partial integrations of Δρu2D then yield the contributions from the total emission rate to the radiation field, guided plasmonic mode, and lossy plasmonic modes (the nonradiative channel), as indicated in Figure 2.

Figure 2

Plot of the modified two-dimensional density of states, Δρu2D, as a function of normalized longitudinal wavenumber k_z/k₀, where k₀ is the wavenumber of the surrounding, for a dipole located a distance d from a cylindrically shaped silver nanowire with a radius of 20 nm [36]. The dipole is radially oriented with respect to the wire surface and located in a homogeneous material with ε = 2. The contributions of ∆ρ to γ_rad, γ_pl, and the nonradiative mode γ_NR are indicated at the bottom of the figure. The large contribution of the guided plasmon mode is highlighted by the peak centered around the effective mode index n_eff = 2.28 of the plasmon mode.

4 Experimental approaches

4.3 Statistical coupling of single emitters to nanowire waveguides

The dipole emitter-surface plasmon excitation is an optical near-field coupling process that scales as ∼1/r³ for cylindrically shaped nanowires, where r is the nanowire radius. Silver nanowires synthesized with the wet-chemical process typically have a radius in the range of 10–500 nm in which case surface plasmons are most efficiently excited for r_d between 10 and 50 nm. For very short distances r_d of a few nanometers, Γ_nonrad becomes the dominant decay channel independent of the wire diameter [10]. In the present context, Γ_nonrad refers to the emitter coupling to lossy plasmon modes [44]. In some context, this is called quenching and is not to be mistaken with nonradiative decay processes intrinsic to some emitters.

The first groundbreaking result on single-emitter surface plasmon coupling was obtained by Akimov et al. [45] (Figure 3A). In their study, the samples were prepared by spin-casting colloidal CdSe QDs on glass substrates followed by a layer of poly(methyl methacrylate) (PMMA) with thicknesses in the range of 30–100 nm acting as a separation layer to the silver nanowires, subsequently deposited using a stamp. Afterwards, the samples were covered with another layer of PMMA ensuring a symmetric optical environment and preventing the silver from corrosion. Single QDs, identified by second-order correlation function measurements g⁽²⁾(τ) on the emitted photon statistics, were at random found to be coupled to the silver nanowire surface plasmon mode. For nanowires with a diameter of ∼102±24 nm, they observed a mean total decay rate enhancement of up to 1.7 compared to uncoupled QDs for a separation of r_d = 30 nm. The excitation of the surface plasmon mode was further verified by the observation of photon reemission from the distant nanowire end, which was anticorrelated with direct QD emission as witnessed by a cross-correlation measurement between direct radiative emission, corresponding to Γ_rad, and the distant nanowire end, corresponding to excitations of the propagating plasmonic mode, Γ_pl. Due to an inhomogeneous distribution of the QD spontaneous emission rate, only statistical estimates on the decay rate enhancement and the resulting coupling to surface plasmons could be provided, which is an intrinsic limitation of the spin-casting and random assembly approach. In a related experiment, Fedutik et al. [46] (Figure 3C) separated an ensemble of CdSe colloidal QDs from silver nanowires by coating the wires with a thin SiO₂ spacer layer and verified the plasmon excitation by observing scattered surface plasmons from the wire ends.

Figure 3

Experimental approaches on random single emitter surface plasmon coupling. (A) Single CdSe colloidal QDs are placed next to single silver nanowires, separated by a PMMA spacer layer from the nanowire [45]. (B) AFM image of a silver nanowire with adhered nanodiamonds containing single NV centers [41]. (C) CdSe colloidal QDs placed on a silver nanowire, separated by a SiO₂ spacer layer [46].

The first related experiment with diamond nanocrystals containing single nitrogen-vacancy (NV) centers was reported by Kolesov et al. [41] (Figure 3B). They attached the diamond nanocrystals in solution to the silver nanow-ires by making use of the adhesive polymer layer surrounding the silver nanowires. Using the broad NV center optical emission spectrum of t100 nm and the single- photon statistics, Kolesov et al. could verify the wave- particle duality of surface plasmon polaritons by observing a strong modulation in the resulting nanowire spectrum (the plasmonic decay channel _pl) and antibunching in the photon number statistics. Li et al. [47] deposited silver nanowires on a glass substrate and covered the wires with a 10 nm thin layer of Al₂O₃ using an atomic layer deposition technique. For CdSe/ZnS core/shell QDs spin casted on the sample and thereby deposited next to a nanowire, they reported surface plasmon excitation with an efficiency up to 40%.

4.5 Controlled coupling to a plasmon gap mode

Due to the finite size of the diamond crystals and the limitation in fabricating thinner single silver nanowires, the possibility to excite the highly confined surface plasmon gap modes occurring between two parallel silver nanow-ires was explored [55]. In parallel configuration of two nanowires with a small gap, the single modes cease to exit and two hybrid modes form. These hybrid modes can be understood as an in-phase and out-of-phase superposition of the single modes and are referred to as symmetric (+,+) or antisymmetric (+,-) modes depending on the transverse charge/phase distribution. The improved field confinement and the increased coupling rates of the gap plasmon mode compared to a single nanowire mode are summarized in Figure 4. It is the large mode confinement in the gap region and the smaller propagation losses κ compared to a single silver nanowire that make this structure attractive for emitter plasmon coupling. The antisymmetric (+,-) mode facilitates a large plasmonic decay rate Γ_pl when the emitter is placed at the mode field maximum in the gap region, which is about one order of magnitude larger compared to maximum achievable decay rates to single nanowires with similar linear propagation losses κ (Figure 4C).

Figure 4

Pointing vector of the guided surface plasmon mode on (A) a single nanowire and (B) the antisymmetric gap mode with a separation of 9 nm between the wires. (C) Comparison of the normalized decay rate into the plasmon mode Γ_pl/Γ₀ between the single and the dual nanowire configuration, parameterized as a function of linear propagation loss κ. All graphs are taken from Ref. [55].

The experiment reported by Kumar et al. [55] directly demonstrates the dual nanowire advantage by selecting an NV center with a relatively long intrinsic lifetime of 45.2 ns, which was reduced to 11.9 ns after coupling to a single nanowire and further down to 5.4 ns when a second nanowire was placed nearby (Figure 5). The diamond nanocrystal was measured with a height of 27 nm, which is significantly smaller than the nanowire radius of 55 nm. Hence, the NV center was not located at the maximum electric field, max{E(r)}, in the gap region. An optical image of the final structures highlights that the integrated photon count rate from the nanowire ends exceeded the collected radiative emission from the NV center.

Figure 5

(A) Lifetime measurements of one NV center when located on the glass substrate (black) after coupling to a single nanowire (red) and after locating in the gap between two nanowires (blue). (B) AFM topography image of two parallel nanowires (the black arrow indicates the location of the NV center) and sketch of the system in the transverse plane. (C) Fluorescence image of the dual wire structure when the NV center is continuously excited. All graphs are taken from Ref. [55].

4.6 NV center coupling to a channel plasmons in a V-groove

Recently, Bermúdez-Ureña et al. coupled single NV centers to the channel plasmon mode of a V-groove waveguide [56] (Figure 6). V-grooves with a width −315 nm and a height −510 nm were milled with a focused ion beam into a gold film of 1.2 μm total thickness [53]. On their ends, the V-grooves were terminated with tapered nanomirrors [57], as shown in Figure 6B. After depositing an array of nanodiamonds with a controlled electron-beam lithography method nearby the V-groove, a suitable NV center with a long lifetime (−26 ns) and high count rate was selected and placed in the groove by the aid of an AFM tip. The channel plasmon propagation length was measured to be 4.65±0.48 μm using the NV center coupling to the plasmon mode, matching the theoretically expected value of 4.56 μm obtained by averaging over the broad NV center spectrum. Comparing the NV center lifetimes before and after coupling yields a total decay rate enhancement of 2.3, and together with an estimate of the propagation losses and coupling efficiency to the radiation field at the groove end, a β-factor of 0.42-0.03 was estimated, which is in good agreement with simulations indicating a value of 00.56 for this structure.

Figure 6

(A) Illustration of the approach for NV center channel plasmon coupling: a green laser excites the NV center, which decays by exciting channel plasmons along the V-groove and subsequently scatter to the far field at the ends. (B) Scanning electron microscope image of a V-groove fabricated in gold, illustrating the groove profile and a mirrors. (C) Total electric field profile of the supported channel plasmon mode. The field polarization is indicated by an arrow. Images taken from Ref. [56].

4.8 Plasmonic resonators

A nanoscale plasmonic resonator based on synthetic silver nanowires was proposed and demonstrated by de Leon et al. [61]. The silver nanowires were embedded in PMMA, and a cavity resonance was achieved by defining distributed bragg reflectors (DBRs) at the nanowire ends with electron-beam lithography (see Figure 7A). The achieved DBR plasmon reflection was in the range of 90%–95%, resulting in a measured Q-value of 58 (the highest value they reported is 94) at a vacuum wavelength of 638 nm for a nanowire with a diameter of -100 nm, close to the theoretical expectation of Q = 100. Together with a small effective mode of V_eff 0.04(λ₀/n)³, they expect a Purcell factor up to 200 and measure F 75 with CdSe colloidal QDs by comparing the lifetimes of coupled and uncoupled QDs. For NV centers in diamond nanocrystals, a Purcell factor of 735 is reported, exceeding the value of dielectric cavities [62, 63].

Figure 7

Plasmon resonators made (A) on a silver colloidal nanowire by defining DBR mirrors on the surrounding PMMA medium [61] and (B) by adding block reflectors confining a plasmon mode propagating along the wedge [64]. The scale bars in (A) and (B) both correspond to 1 m.

Wedge waveguides and resonators, made with template stripping for achieving long propagation [42], have recently been investigated by Kress et al. [64] for enhanced light-matter interaction at the single emitter level. Normalized to ohmic propagation losses, wedge waveguides show the highest field confinement [65, 66] compared to other structures such as channels [53], nanowires [9], and hybrid plasmonic waveguides [67]. The resonators were made by adding block reflectors across the wedge having a reflectivity of u93% (see Figure 7B). With the long propagation length of 19 9m (at a vacuum wavelength of 630 nm), they measured a Q-value of -191 with a 10-1m-long resonator. Using a modified electrostatic printing technique [68], they deposited core/shell/shell CdSe/CdS/ ZnS colloidal QDs on the wedge [69] and the lifetime was reduced by a factor of 22.6 compared to emitters dispersed in liquid.

5 Quantum applications of strongly confined propagating plasmons

Systems of propagating photons in plasmonic structures with single emitters open the potential for efficient single-photon generation, single-photon absorption, and strong photon-photon interaction mediated by a strong nonlinearity. As a result of the potentially large Purcell effect of a single emitter coupled to a plasmonic wire, photons spontaneously emitted from the dipole emitter will be harvested by the propagating plasmon mode of the wire and thus directed into a single well-defined spatial mode. By coupling this plasmonic mode to the mode of a dielectric waveguide, it has been shown theoretically that single photons can be generated with high efficiency and high speed [10].

An even more appealing application of the plasmon-emitter system is the promise of a giant nonlinearity that enables a strong interaction between individual plasmons [70]. This may impact the fields of nonlinear optics and quantum optics. For example, the strong interaction may lead to the realization of an optical switch at the single photon level [71]. The basic idea is to make use of the saturation nonlinearity of a two-level emitter: The emitter will absorb and thus scatter off a single photon while it will be invisible to the next photon (as it has been excited by the first one). This makes up the single-photon switch. A similar strategy using a three-level system in replacement of the two-level system may lead to the realization of a single-photon transistor, which might have important usage in quantum information processing and quantum networks [72].

On the more exotic side, it has been predicted that the combination of strong nonlinear interaction and directional coupling between a larger number of emitters may lead to multipartite entanglement as well as to new quantum phase transitions of light [73–75] or photon crystallization [76, 77]. Originally, such proposals have envisioned the use of cavity quantum electrodynamics in high-finesse cavities [78, 79], but more recently the ideas have been formulated also in the context of propagating modes coupled to emitters in one-dimensional waveguides [76]. In addition to using plasmonic waveguides [80, 81], there have been proposals on using atomic clouds coupled to guided modes of photonic waveguides such as tapered fibers [82, 83], photonic crystal fibers [84], or photonic crystal waveguides [85]. The ideas have been also translated into systems based on superconducting qubits coupled to microwave waveguides [86, 87].

6 Outlook

Most of the experiments on a plasmonic platform exhibiting true quantum properties have been based on simple circuitry such as a single wire, two coupled wires, V-grooves, or wedges. However, to make the platform attractive for quantum applications, it is important to be able to make more sophisticated plasmonic circuits that include the plasmon generation process, the linear and nonlinear interaction, and potentially also the detection process on-chip. As we have seen above, relatively efficient generation of single photons have been demonstrated, beam-splitting and interference have been shown, and on-chip detection has been realized [88, 89]. However, the complete demonstration of all three stages on a single chip has not been realized yet.

An important first test towards quantum physics in a plasmonic system is the observation of Hong-Ou-Mandel interference between two single photons generated on-chip from two independent single-photon emitters and with two on-chip detectors. Initial steps towards such a landmarking experiment have been performed where the plasmonic interference was observed between two externally generated photons that were coupled onto the chip for interference and outcoupled again for detection [23, 25]. Another experiment with an external source but with on-chip detection has shown indication of Hong-Ou-Mandel interference [24]. However, the plasmonic circuitry for all these demonstrations are not optimized for coupling to single emitters and thus for a complete demonstration where all components are on-chip will require the design and development of a new system. A first critical step is to demonstrate plasmon-plasmon interference with two on-chip emitters but using external detectors. This can, for example, be carried out using two silicon-vacancy (SiV) centers in diamond, which have been shown to exhibit quantum photon interference without the need for special filtering or frequency control [90]. After such a milestone demonstration, the next step would be full integration with emitters, manipulation, and detection, paving the way for more complex nanoscale quantum plasmonic devices.

The construction of such a plasmonic quantum chip is fraught with technical challenges associated with fabrication and integration. However, one of the biggest challenges that we are faced with when trying to scale the circuits is loss. The loss problem simply has to be solved to make it a viable platform for scalable quantum information processing, as propagation loss limits the capabilities in carrying out fault-tolerant quantum information processing. In classical information processing, losses can be overcome by the insertion of on-chip amplifiers that compensate for the losses [91, 92] and are demonstrated by Noginov et al. for propagating surface plasmon modes [93]. Such amplification processes [94] cannot be used in quantum information processing, as it inevitably will add noise to the plasmonic quantum states [95–97], thereby destroying the quantum information. As an alternative, one needs to devise alternative designs that minimize the losses. Above we discussed a couple of systems based on gap plasmons in which the loss rate could be reduced, whereas the high coupling strength remained at the same level. To reduce the loss rate even further, hybrid approaches have been introduced. Such approaches are combined systems of plasmonic and photonic waveguides, where one tries to make use of the low-loss properties of the photonic waveguides and the strong confinement properties of the metallic waveguides [67]. Yet another alternative is to replace the noble metal structures with other materials, for example, ceramic compounds [98], which relative to silver and gold have shown reduced losses in the near- and mid-infrared regimes where several semiconductor systems are active. Further development of these and similar ideas will be critical to the success of building up larger quantum plasmonic circuits for quantum information processing. However, quantum plasmonic circuitry is still in its infancy and it can be expected that new discoveries might be uncovered and lead to new key turning points in the engineering of low-loss plasmonic circuits.