Optical Yagi-Uda nanoantennas

3.1. Plasmonic nanoantennas

Metals at RF are highly conductive, and, thus, can be considered as nearly perfect reflectors. The penetration length of the fields (the skin depth) is negligible compared with the dimensions of the antenna elements. At optical frequencies, however, the skin depth is of the order of 10 nm, and, thus, is comparable with the dimensions of the nanoantenna elements. As a consequence, losses in metals are not negligible any more, and they depend both on the type of metal used and on the operation wavelength of the nanoantenna application. Gold, for example, which is most commonly used for nanoantenna fabrication because it does not oxidize on air, can only be used in the near-infrared and in the red part of the visible spectral region, while it exhibits huge losses at smaller wavelengths due to interband transitions [16]. For nanoantenna applications in the visible silver has more favorable optical properties [16].

The increased skin depth also requires revising the basic principles of RF antenna design. Indeed, while the dimensions of RF antennas are determined by an incident wavelength λ [11], the dimensions of optical nanoantennas must also take into account optical properties of metals. It changes the standard procedure to determine the optimal length of the feeding element for optical Yagi-Uda antennas (see Figure 2), making it rely on the reduced effective wavelength λ_eff. Direct numerical calculations demonstrate a simple relation between λ_eff and λ [1, 2, 17]:

Figure 2

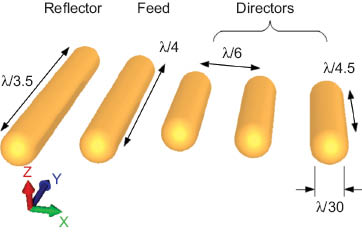
Schematic of an optical Yagi-Uda antenna consisting of gold nanorods used for the feed, reflector and directors with the possible dimensions in comparison with the incident wavelength λ. At the typical telecommunication wavelength of λ=1550 nm the area occupied by the nanoantenna is ~400×400 nm and its weight is ~70 femtogrammes.

where a and b are some coefficients with dimensions of length that depend on geometry and material properties [17], and λ_p is the plasma wavelength. According to this wavelength scaling rule, an optical half-wave nanoantenna is not λ/2 in length but is of a shorter length λ_eff/2. Difference between the length of the optical and RF dipolar antennas depends on the antenna geometry and is usually in the range of 2–6 for gold and silver nanoparticles [1, 17].

The choice of the cross-sectional dimensions of optical nanoantenna elements and internal edge-to-edge spacing between them also differs from the standard RF procedure. In the RF regime, the inter-element spacing typically ranges between 0.1λ and 0.315λ and is conditioned by practical rather than physical considerations such as the simplicity and stability of the antenna construction. As a rule, the diameter of RF antenna elements is small compared to the spacing between the elements. At optical wavelengths, however, the antenna element diameter becomes a crucial parameter because the inevitable absorption losses in metals can be reduced by making the volume of the elements larger [18].

Another difference between optical and RF antennas is the excitation of the feeding element. In RF region, Yagi-Uda antennas are locally driven at the feed-gap by electrically connecting the feed, which is typically aλ/2 dipole, to the feed-line. However, most of the optical nanoantennas investigated so far have been driven from the far-field [2]. Such excitation scheme is not optimal for the Yagi-Uda design because the feed is surrounded by other elements placed at small distances as compared with the operating wavelength. Therefore, it would be advantageous to place the light source in the near-field region of the feed. It makes the optical Yagi-Uda nanoantennas perfect candidates for controlling emission of isolated quantum nanoemitters, such as, e.g., quantum dots [19] and color centers in nanodiamonds [20].

In order to obtain a strong near-field coupling of an isolated emitter to the fundamental mode of the feed, it is critical to place the emitter at a high electric mode density point. For the nanoantenna geometry shown in Figure 2 this point corresponds to one of the ends of the feeding element. A judicious engineering of the feed, such as, e.g., the introduction of a small (30–50 nm in width) gap in the center of the feed, can further increase the coupling strength by exploiting the Purcell effect [21].

The effective wavelength design principle was used for the fabrication and experimental demonstration of highly unidirectional emission of a quantum dot coupled to an optical Yagi-Uda nanoantenna [12] shown in Figure 3A. One of the most important antenna characteristics – the angular emission diagram – was calculated from the experimental Fourier-plane image and agrees well with the result of numerical simulations (Figure 3B): the nanoantenna emits in a narrow cone in the forward direction, mainly into the medium which is optically denser. This result is in good agreement with the prediction that emitters at the surface between two interfaces emit mainly into the medium which is optically denser in the case that the emission direction is close to the critical angle [12].

Figure 3

Optical Yagi-Uda nanoantenna driven by a quantum dot. (A) Scanning electron microscopy image of the fabricated 5-element Yagi-Uda nanoantenna. (B) Angular radiation diagram for the fabricated Yagi-Uda nanoantenna (black line) vs. theoretical prediction (red line). Adapted with permission [12]. Copyright 2010, American Association for the Advancement of Science.

In an earlier experimental study of plasmonic Yagi-Uda nanoantennas [13], the local emission from an emitter arranged at the feeding point was emulated by using the polarization dependence of the nanorod response to an external driving field. The nanoantenna array investigated in [13] is depicted in Figure 4A. It consists of a feeding element, a reflector and three directors, all of which were fabricated lithographically on a glass substrate and embedded in a sputter-deposited SiO_x film to suppress the effects of a varying refractive index on the coupling between array elements. The distance between the feeding element and the reflector is 125 nm, that between the feeding element and the directors 150 nm, which corresponds to parameters from a previous theoretical study [18]. The feeding element was tilted by 45° towards the nanoantenna axis (x) and driven by light polarized parallel to the x-coordinate. Owing to its diagonal alignment, the feeding element converts a part of the driving light into light polarized along the major axis of the passive elements (y). As was confirmed in a separate test measurement, the passive elements emit only a negligibly small amount of light polarized perpendicular to the driving field. It was therefore concluded that almost all of the y-polarized light originates from the plasma oscillations of the feeding element. Thus, the emission patterns obtained by detecting only the y-polarization correspond to the emission patterns of radiation from just the feeding element, modified by the passive response of the other nanoantenna elements.

Figure 4

Optical Yagi-Uda nanoantenna with a rotated feeding element driven by a laser beam. (A) Scanning electron microscopy image of the nanoantenna. (B) Measured (solid circles) and theoretically predicted (open circles) radiation patterns of the nanoantenna. Adapted with permission [13]. Copyright 2010, Nature Publishing Group.

In the measurement of the radiation pattern, the sample was set on a prism and covered by a hemispherical lens with index-matching oil to avoid refraction and total reflection. The feeding element was driven by a laser diode at a wavelength of 662 nm through a polarizer. The emission was detected in the plane that is orthogonal to the substrate and includes the nanoantenna main axis. The result for a five-element Yagi-Uda antenna is shown in Figure 4B. The radiation pattern of the nanoantenna shows directional behavior with the emission concentrated around angles close to the region around 0–20°, where the small mismatch of the refractive index suppresses the emission. Taking into account this suppression of a significant part of the forward emission, one observes fairly good qualitative agreement between the experimental results (red solid dots) and the theoretical prediction from the dipole model (circles). In particular, the experimental data clearly show a side lobe around 70° and a small backward emission separated by a minimum at 110°. These features of the emission pattern originate from the characteristic interferences between radiation from different array elements, indicating that the directionality of the emission is indeed obtained from the coupling of the array elements.

The results presented in Figures 3 and 4 demonstrate the realization of plasmonic Yagi-Uda nanoantennas composed of arrays of appropriately tuned metal nanoparticles. Most importantly, they clearly show that the basic principles of RF antenna design can be applied successfully to obtain the same kind of directivity in the optical regime. It is worth noting that, in contrast to the nanoantenna excited by a laser beam [13], the nanoantenna demonstrated in ref. [12] ensures full control of the direction of light emission from single quantum emitters. It represents a decisive step toward the development of subwavelength quantum light sources [22] with directive properties of RF antennas not attainable with optical cavities [19, 21]. Such sources will make it possible to transmit and receive single and entangled photons [19] at subwavelength scale, which is an essential feature for quantum cryptography, communication and computing [23].

The near-field excitation design of Yagi-Uda nanoantennas also opens up new ways for the implementation of more complicated RF antenna concepts at the nanoscale. Recently, arrays of three-dimensional (3D) optical Yagi-Uda nanoantennas (Figure 5), fabricated using top-down fabrication techniques combined with layer-by-layer processing, have been suggested [14]. The creation of optical nanoantenna arrays brings the concept of RF phased antenna arrays to the nanoscale, where each antenna is driven independently with a defined phase and amplitude. It considerably widens the applicability range of optical Yagi-Uda nanoantennas, making it possible to steer the direction of the emitted light beam by addressing each nanoantenna independently and controlling the phase of the feeding circuit by means of phase modulators [14].

Figure 5

Phased array of optical Yagi-Uda nanoantennas. (A) Artists view of a 3×3 Yagi-Uda nanoantenna array fed by phase modulating feeding circuits. (B) Scanning electron microscopy image of an optical Yagi-Uda nanoantenna array. The gold structure is fabricated on a glass substrate. The nanorods are embedded in photopolymer. Scale bar is 500 nm. Adapted with permission [14]. Copyright 2011, Nature Publishing Group.

It is also worth mentioning the efforts targeted to reduce absorption losses in Yagi-Uda nanoantennas by modifying the geometry and the arrangement of the nanoparticles composing the Yagi-Uda architectures [24–28]. These ultracompact nanoantennas look like a Yagi-Uda structure without either reflector or directors. Interestingly, a construction that would lead to a poor performance in RF region not only works well at the nanoscale, but also opens up novel opportunities not possible at larger scales, such as a very high front-to-back ratio attainable with only two coupled nanoparticles separated by a distance as small as ∼1/65 of the operating wavelength. Another extreme case of a Yagi-Uda structure is represented by nanoantenna arrays consisting of equally spaced metal nanoparticles of the same size [29]. These arrays possess Bragg modes allowing for long-range and large area emission enhancement even if the nanoantenna is excited by an emitter with unfavorable dipole moment orientation [30].

3.2. All-dielectric nanoantennas

Another way for reducing losses and thereby increasing the antenna efficiency is to utilize high-permittivity low-loss dielectric nanoparticles instead of metallic ones [31]. This approach has been already used in RF region [32] where Yagi-Uda dielectric resonator antennas are known to have a larger operation band width as compared with all-metal constructions.

However, in the optical region, the use of dielectric materials promises great advantage over highly absorptive metals. Many studies concentrate on the nanoparticles made of silicon – one of the key materials of integrated photonics. The real part of the permittivity of the silicon is about 16 whereas the imaginary part, indicating dissipative losses, is up to two orders of magnitude smaller than that of silver or gold [33].

It has recently been suggested to make optical Yagi-Uda nanoantennas of all-dielectric elements (A.E. Krasnok et al., Unpublished). All-dielectric Yagi-Uda nanoantennas are a promising alternative to their metallic counterparts because of low losses and, as was suggested earlier [34], single spherical nanoparticles made of high-permittivity dielectrics may support both electric and magnetic resonant modes, which is not attainable with single spherical metal nanoparticles. This feature may greatly expand the applicability of optical nanoantennas for, e.g., detection of magnetic dipole transitions of molecules.

Figure 6A shows an example of all-dielectric Yagi-Uda nanoantenna consisting of four directors and one reflector made of silicon (without effective feed). The optimal performance of the nanoantenna at one operating wavelength can be achieved when the director nanoparticles sustain a magnetic resonance and the reflector nanoparticle sustains an electric resonance. Thus, the radii of the directors should be smaller than the radius of the reflector because the positions of the magnetic and electric resonances shift linearly with the radius of the nanoparticle (A.E. Krasnok et al., Unpublished). Consequently, the nanoantenna investigated (A.E. Krasnok et al., Unpublished) consists of nanoparticles with the radii of 70 nm and 75 nm used for directors and reflector, respectively.

Figure 6

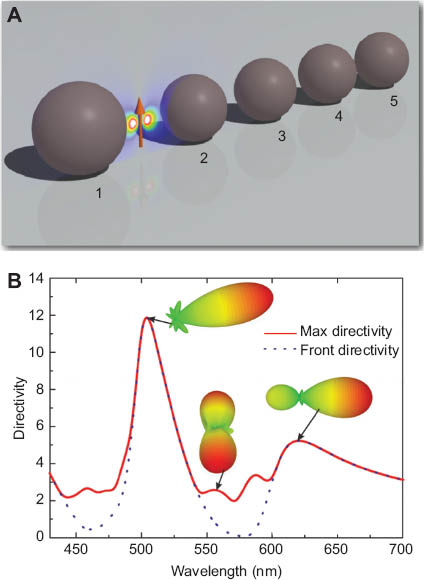
(A) All-dielectric optical Yagi-Uda nanoantenna, consisting of the reflector (sphere 1) of the radius of 75 nm, and smaller directors (spheres 2–5) of the radii of 70 nm. The dipole source is placed equidistantly between the reflector and the first director at the distance D. The separation between the neighboring directors is also D. (B) Directivity of the all-dielectric Yagi-Uda nanoantenna as a function of the wavelength for the separation distance D=70 nm. Insets show radiation pattern diagrams at particular wavelengths.

Figure 6B shows the directivity spectrum of the all-dielectric Yagi-Uda nanoantenna excited by a dipole source placed equidistantly between the reflector and the first director surfaces at the distance D=70 nm. The insets in Figure 6B show the radiation patterns at particular wavelengths. One observes a strong maximum at λ≈500 nm. The main lobe of the emission pattern at this operating wavelength is extremely narrow with the beam-width about 40° and negligible backscattering.

However, the radiation efficiencies of both all-dielectric and plasmonic Yagi-Uda nanoantennas are nearly the same for D=70 nm with the averaged value 70%. Although dissipation losses of silicon are much smaller than those of silver or gold, the dielectric particles absorb the electromagnetic energy by the whole spherical volume, while the metallic particles do it at the surface only. As a result, there is no substantial difference in the overall performance of these two types of nanoantennas for relatively large distances between the elements.

The difference between all-dielectric and plasmonic nanoantennas becomes very strong for smaller spacings between the elements: the radiation efficiency of all-dielectric nanoantennas is insensitive to the separation distance whereas the radiation efficiency of plasmonic nanoantennas drops significantly. This is caused by local field enhancement between two adjacent metallic surfaces, which leads to effectively larger absorption of the whole structure. Thus, the use of all-dielectric nanoparticles without the field enhancement allows making more compact nanoantennas e.g., for on-chip wireless communication. However, in contrast to plasmonic nanoantennas, all-dielectric nanoantennas do not provide large spontaneous emission enhancement, which is extremely important for emerging applications such as energy conversion, sensing and quantum information.

4.1. Tapered nanoantennas

Hereafter, we discuss emerging strategies for the development of optical Yagi-Uda nanoantennas able to receive and emit light waves of different lengths with nearly the same efficiency. As in the preceding sections, we will use and extend ideas known from RF antenna technology.

In order to fully explore the potential of the Yagi-Uda architecture one increases the length of the antenna by incrementing the number of directors. The additional directors help to keep an antenna focused on what is in front of it only. It increases the antenna efficiency when the antenna looks toward the transmitter and ignores signals coming from other directions.

While the use of this method does not present significant difficulties at RF frequencies, at optical frequencies absorption losses impose severe restrictions on the length of the antenna. Luckily, this restriction can be overcome by slowly tapering the length of the directors. The improvement of the directivity of RF Yagi-Uda antennas by slowly varying the length of directors was suggested by Sengupta [38] in 1959. His idea was abandoned in the modern RF antenna technique because the suggested tapering can be applied to long Yagi-Uda antennas only and results in heavy and unstable constructions. Conversely, at optical frequencies tapering of the plasmonic waveguides [39] and metamaterials [40] is a very efficient way for nanofocusing of light. The effect of the taper shape and the optimal taper angle on nanofocusing has been discussed actively in the literature (see, e.g., ref. [41]).

Recently, it has been demonstrated that tapering of a plasmonic Yagi-Uda nanoantenna (see Figure 7A) not only serves to focus light and to increase the overall efficiency, but also allows for shrinking down the nanoantenna longitudinal dimension by decreasing the spacing between the elements by a factor of 10. A pronounced improvement has been found for a particular configuration with 42 nanorods and the tapering angle α=6.6° (see the inset in Figure 7A for the definition of α) at the principal design wavelength 1.515 μm [43–45].

Figure 7

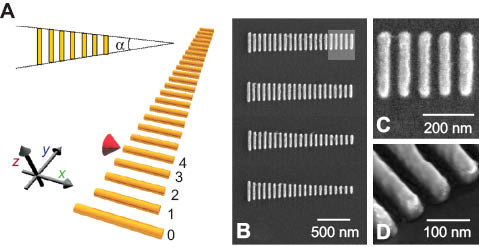
(A) Schematic of tapered Yagi-Uda nanoantenna excited by an emitter via one of the possible excitation sites. The inset shows the definition of the tapering angle α. (B) Scanning electron microscopy images of the fabricated nanoantennas with different nanorod length variations. (C, D) Close-ups of the highlighted region of one of the nanoantennas.

Figures 7B–D show experimental tapered Yagi-Uda nanoantennas consisting of 21 nanorods with different length variations [42]. The nanoantennas were fabricated on a glass substrate covered by 5 nm of indium tin oxide (ITO) using electron-beam lithography followed by evaporation of 50 nm of gold and a lift-off procedure (see the discussion in the “Fabrication and Characterization” section). With lateral nanorod diameters of ≈45 nm and inter-element spacings of ≈35 nm the dimensions of the experimentally realized structures come very close to theoretical design parameters [43–45], rendering them suitable for optical near-field and far-field characterization.

Each nanorod can be used for the excitation of the tapered Yagi-Uda nanoantenna by quantum emitters matched spectrally with the nanorod resonant frequency and placed in the nanorod near-field region [44, 45]. Multifrequency broadband operation of the nanoantenna resulting from an overlap of the spontaneous emission spectra for different emitter positions (Figure 8A) opens up novel opportunities for broadband emission enhancement, spectroscopy and sensing. A collective excitation with narrow emission linewidth emitters converts the nanoantenna into an efficient multifrequency plasmon-enhanced light “super-emitter” with a discrete spectrum (Figure 8B). Due to the reciprocity principle, the same tapered nanoantenna can be used both as a transmitter and/or as a receiver, thus being useful for creating a broadband wireless communication system.

Figure 8

(A) Spontaneous emission enhancement spectra of the tapered Yagi-Uda nanoantenna excited with an x-polarized emitter via different excitation sites (see Figure 7A) for the definition of the polarization and excitation site numbers. The dashed line, a guide to the eye, connects the maxima of the spectra. (B) Spontaneous emission enhancement spectra of the nanoantenna excited simultaneously by 10 narrowband x-polarized nanoemitters. Adapted with permission [44]. Copyright 2012, Elsevier.

4.2. Log-periodic nanoantennas

Tapered Yagi-Uda nanoantennas are conceptually similar to log-periodic optical nanoantennas inspired by RF log-periodic architectures [11]. The original idea of optical log-periodic antennas probably belongs to Gonzalez and Boreman [46] who used a lithographic antenna to couple infrared radiation into a bolometer with submicron dimensions (Figure 9). The excitation of an optical log-periodic antenna with quantum dots has recently been demonstrated theoretically and experimentally [47, 48]. In analogy to RF antennas [11], different log-periodic architectures have been considered including arrays of nanorods, nanodipoles and zig-zags [47–49].

Figure 9

Log-periodic optical antenna coupled to a microbolometer. Adapted with permission [46]. Copyright 2005, Elsevier.

However, optical log-periodic antennas demonstrated so far just mimic the possible geometries of RF log-periodic antennas such as the length and the spacings of the elements. What has not been achieved yet in the optical range is the excitation of alternating elements with 180° of phase shift from one another. In RF region, it is normally done by connecting individual elements to alternating wires of a balanced transmission line in order to ensure that the phasing of the elements is correct. Furthermore, as compared with tapered designs, the realization of optical log-periodic nanoantennas requires higher fabrication precision because both the length and the spacings of the elements shrink toward the nanoantenna front-end.

6.1. Fabrication

Optical Yagi-Uda nanoantennas are commonly fabricated by standard electron-beam lithography (EBL) followed by metal evaporation and a liftoff procedure [12–14]. In this way fabrication accuracies below 50 nm can be obtained. However, this method only allows for the realization of planar antenna geometries. In order to obtain stacked structures like the three-element Yagi-Uda antenna arrays shown in Figure 5B [14], a multi-step EBL process has to be applied, where several functional layers of metal nanostructures are processed on top of each other. For the success of this method accurate planarization and alignment procedures are crucial. In ref. [14], as a first step, gold alignment markers with a thickness of 250 nm are fabricated on a quartz substrate. Next, a first planar 30-nm gold nanorod layer is processed using the standard fabrication procedure for in-plane nanostructures. Afterwards, a 100-nm thick spacer layer consisting of the solidifiable photo polymer PC403 (JCR) is spin-coated on top of this layer, followed by a pre- and a hard-bake. In the next step, the alignment markers are used for accurately stacking a second nanorod layer on top of the first one. Finally, the planarization, alignment, and in-plane fabrication steps are repeated in order to obtain a third stacked layer.

Similarly, a two step EBL process enables the controlled placement of quantum emitters at defined positions with respect to the nanoantenna as demonstrated in ref. [12]. In the first lithography step Yagi-Uda nanoantennas are defined on a glass substrate, followed by thermal evaporation of a 30-nm gold layer and lift-off. Next, a second lithography step is used to define 70-nm square areas at the hot spots of the antenna feed elements for the formation of a self-assembled monolayer of mercaptoundecanoic acid. Core-shell quantum dots can then be immobilized on these functionalized areas, and in a last step the unexposed resist is removed. The overall result of this procedure is displayed in Figure 3A.

Other top-down techniques which have been employed for nanoantenna fabrication include focused ion beam (FIB) milling [69], nanoimprint lithography [70], and nanostencil lithography [71]. While FIB stands out by its versatility to allow for high-precision structuring of almost any conductive substrate, the latter two techniques aim at large-area high-throughput fabrication [4].

Linear plasmonic nanoantenna arrays, which closely resemble the Yagi-Uda geometry, have furthermore been obtained by the controlled assembly of chemically synthesized gold nanocubes using a nanomanipulator [72, 73]. Similar approaches rely on nanomanipulation of plasmonic particles with an atomicforce microscope tip [74, 75]. The growing interest in such bottom-up techniques is justified by the purity and well-defined crystallinity of chemically grown nanoparticles, by the wide range of different nanoparticle shapes and materials/composites available, as well as by the good control of inter-particle distance [4].

6.2. Characterization

6.2.1. Classically designed Yagi-Uda nanoantennas

In analogy to RF antennas, optical nanoantennas can serve both as transmitters and receivers. Because of the reciprocity principle, the emitted radiation pattern of an antenna is equal to its receiving pattern. Experimentally, in RF region it is common to determine the directive properties of antennas by measuring the load current of an antenna receiving radiation from a remote electromagnetic wave source [11]. As this technique cannot be used in optical region, several near- and far-field spectroscopic techniques have been developed for the characterization of optical Yagi-Uda nanoantennas [12–15].

A straightforward way of measuring the optical properties of Yagi-Uda nanoantenna arrays is linear-optical reflectance and transmittance spectroscopy [14]. While the antenna array’s angular radiation pattern cannot be accessed directly this way, the spectral positions of the plasmonic antenna resonances are identified and evidence for directional behavior is given by differences between reflectance spectra in forward direction, i.e., for light incident from the director side, and backward direction, i.e., for light incident from the reflector side.

A very elegant method of actually measuring a nanoantenna’s angular radiation pattern is to characterize the antenna in emission mode by back-focal-plane imaging within a confocal microscope [12, 76]. To this end, emission from the antenna into the substrate is collected with a high-NA objective, and the intensity distribution on the objective’s back focal plane or Fourier-plane, which contains the directions of emission towards the substrate, is imaged on an electron-multiplying CCD camera.

In order to characterize the nanoantenna’s directive properties in emission mode it is crucial to implement a mechanism ensuring that the antenna is only driven at its feeding element, while the reflector and director elements are only excited in a passive manner through coupling to the feed. In ref. [13] this is accomplished by tilting the feeding element by 45°, making it possible to couple to it with light polarized perpendicular to the emitted polarization of the Yagi-Uda nanoantenna. An alternative route is to drive the feed via carefully aligned quantum dots. In ref. [12] quantum dots are placed exclusively in the high-field regions of the feed element. They are excited far off resonance with respect to other antenna elements, thereby again leading to a selective excitation of the feed element. Both of these techniques furthermore offer the advantage to allow for separating the fields emitted by the antenna from the exciting fields by means of additional polarization or color filters brought in front of the detector.

Yagi-Uda nanoantennas in receiving mode have just recently been investigated experimentally using cross-polarization apertureless near-field optical microscopy [15]. The local out-of-plane electric field components of the sample are imaged by raster-scanning it underneath the tip. Furthermore, the optical amplitude as well as the optical phase are detected using a homodyne amplification scheme, which allows for visualizing the temporal evolution and the dynamics of the reception process.

Figure 11A shows the 3D topography of the investigated optical Yagi-Uda nanoantenna fabricated on a glass substrate and illuminated by a weakly focused s-polarized (green arrow) laser beam (λ=1064 nm) under an oblique incident angle (gray arrow) [15]. Panels B–D in Figure 11 show the real part of the E-fields measured above the nanoantenna at different snapshots in time denoted as 0° phase, 64° phase and 128° phase, respectively.

Figure 11

(A) 3D topography of the optical Yagi-Uda nanoantenna. (B–D) Real part of the measured optical signal superimposed onto the topography at different incidents of time: (B) 0° phase, (C) 64° phase, and (D) 128° phase. Adapted with permission [15]. Copyright 2011, American Chemical Society.

When the phase is of 0° (Figure 11B), the two directors show one positive and one negative field lobe with a field node in between them. The feed element shows a weak amplitude, and the reflector shows a dipole pointing in the opposite direction with respect to the directors. When the phase is of 64° (Figure 11C), all nanoantenna elements show the same color scheme corresponding to the same dipole moment orientations. Notice that the feed element is at its maximum field, brighter than all the other elements at any time. At 128° phase (Figure 11D) the reflector reaches its maximum, but the feed is already declining and the dipole moments of the directors have already flipped.

Thus, the directionality of optical Yagi-Uda nanoantennas manifests itself by the dependence of the local field enhancement at the feeding element on the illumination direction. This effect is similar to the increase in the power measured in experiments with RF antennas receiving signals from a test antenna [11].

Near-field optical measurement of a rotated (backward illuminated) nanoantenna with the same dimensions demonstrated that the change of the illumination direction leads to a destructive interference suppressing the resonance of the feeding element. Therefore, the difference between near-field images for forward and backward illumination of the same antenna structure is also a clear proof of the antenna directionality.

Another experimental technique offering a ∼10 nm spatial resolution using a 30 keV focused electron beam as broad-band point dipole source of visible radiation has been recently presented and applied to study the emission properties of an optical Yagi-Uda antenna composed of a linear array of gold nanoparticles [77]. Angle-resolved spectra for different wavelengths shown in ref. [77] reveal evidence for directional emission of light that depends strongly on where the nanoantenna is excited. These experimental results are explained by a simple and intuitive coupled point dipole model, which includes the effect of the dielectric substrate. In overall, the work establishes angle-resolved cathodoluminescence spectroscopy as a powerful tool to characterize single optical nanoantennas.

7.1. Wireless optical communication

The objective of optical antenna design is equivalent to that of classical antenna design: to optimize the energy transfer between a localized source or receiver and the free-radiation field [2]. In telecommunication, an antenna can be used both as a receiver and as a transmitter. By utilizing two identical RF antennas, the first one operating as a transmitter and the second one as a receiver, one can create an RF wireless communication system. The same concept can also be used in optics where an on-chip integrated optical wireless system, suggested theoretically in ref. [79], might provide an alternative to subwavelength plasmonic waveguides [6], which suffer from absorption losses during light transmission. In analogy to waveguides, nanoantennas confine light below the diffraction limit but, in contrast to waveguides, they transmit it through a channel with relatively low losses.

As the transmitter and the receiver of a wireless system should both have a high directivity, one can envision an optical interconnect consisting of two (or more) optical Yagi-Uda nanoantennas looking one toward another [80] (Figure 12). However, one needs to take into account that in practice the nanoantennas will be fabricated on a substrate. As was demonstrated in ref. [12], the presence of the substrate leads to a deflection of the main lobe of the nanoantenna emission pattern toward the medium with a higher refractive index (Figure 3B).

Figure 12

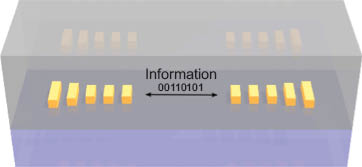
Two optical Yagi-Uda nanoantennas embedded into an optically homogeneous medium can be configured as an on-chip optical interconnect.

While the deflection of the main lobe toward the substrate is not inconvenient when using, for example, a direct emission pattern imaging technique [76], the emission in the forward direction is crucial for many other applications including on-chip horizontal wireless transmission sketched in Figure 12. This aim can be accomplished by embedding the nanoantennas into an optically homogeneous medium as attempted in ref. [13]. The formation of a directive emission pattern above a high-index silicon substrate was also observed in ref. [77]. Although this is a very challenging numerical problem, a reasonable description can be obtained by using an analytical coupled dipole method, which includes the effect of the silicon substrate. It was shown that ∼90% of light was scattered into the substrate. On the other hand, it was demonstrated that the substrate also significantly enhanced the local density of optical states at the position of the dipole, increasing the excitation probability.

The aforementioned techniques can be used to control the emission patterns of the Yagi-Uda nanoantennas configured as an on-chip optical interconnect. A quantum dot can be placed in the near field of the nanoantenna-transmitter so that it drives its resonant feeding element. The resulting quantum-dot luminescence will be strongly polarized and highly directed into a narrow forward angular cone, and then received by the nanoantenna-receiver. By placing another nanoemitter near the resonant feed of the nanoantenna-receiver, one can communicate energy to, from, and between nanoemitters taking into consideration a Stokes shift between excitation and emission wavelengths. Using a tapered Yagi-Uda [43, 45] or a log-periodic [47] nanoantenna one can envision novel schemes of energy transmission to, from and between many nanoemitters at different frequencies simultaneously by precisely placing them near individual nanoantenna elements.

Furthermore, tunable Yagi-Uda nanoantennas with a semiconductor loading of the feeding element [67] can perform as active components of optical wireless communication systems. They can perform not only as frequency selective transmitters or receivers, but also as an all-optical bistable switching device [81] exhibiting emission properties not attainable with actively tunable dipole or bow-tie plasmonic nanoantennas [61, 82, 83].

7.2. Nanoscale spectroscopy

Nanoscale field confinement by optical nanoantennas offers remarkable opportunities for single molecule detection [84–86] and nanospectroscopy [87]. Yagi-Uda nanoantennas can perform as an optical spectrum analyzer at the nanometer scale that is able to distribute different frequency contents of the radiation of an optical dipole source into different directions in space [88]. The feasibility of this concept has been demonstrated theoretically based on optical Yagi-Uda nanoantennas composed of plasmonic core-shell nanoparticles [89]. Core-shell plasmonic nanoparticles with the core made of an ordinary dielectric and the shell of a plasmonic material, or vice versa, are ideal for this purpose because their resonant frequencies can be adjusted in a broad range by varying the ratio of the core radius b to the outer radius a. Specifically, b=a of each particle can be designed deliberately to “detune” its resonance so that they may play the role of the “reflectors” or the “directors” in a conventional RF Yagi-Uda antenna.

The beam pattern of a core-shell Yagi-Uda nanoantenna is sensitive to the variation of the operating wavelength for two reasons. Firstly, the relative permittivities of the plasmonic materials forming the nanoparticles, and the resulting electric polarizability of these particles, are wavelength dependent. Secondly, when the sizes of the nanoparticles and their relative positions are decided and then kept fixed, different operating wavelengths would lead to different relative electrical sizes and relative distances, which causes variation in coupling among particles. Therefore, optical nanoantennas composed of plasmonic particles are intrinsically sensitive to wavelength variation. Using this unique property, one can envision an innovative nanoscale “Yagi-Uda” spectrum analyzer in which the absorption and emission of a fluorescent molecule can be separated away both spectrally and spatially.

7.3. Photovoltaic devices

Photovoltaics, a promising technology relying on the conversion of sunlight to electricity, may allow for the generation of electrical power on a very large scale. It could thus make a considerable contribution to solving the energy problem faced by our society. Plasmonic excitation and light localization can be used advantageously in high-efficient photovoltaics [90].

Conventionally, photovoltaic absorbers are optically thick in order to allow better light absorption and photocarrier current collection. However, a large portion of the solar spectrum, especially in the 600–1100 nm spectral range, is poorly absorbed (Figure 13). The use of plasmonic nanoantennas of subwavelength dimensions can reduce the physical thickness of photovoltaic absorber layers while keeping their optical thickness constant. These nanoantenna-receivers can trap and couple freely propagating sunlight into an absorbing semiconductor thin film, increasing the effective absorption cross-section.

Figure 13

AM1.5 solar spectrum, together with a graph that indicates the solar energy absorbed in a 2-μm-thick crystalline Si film. Adapted with permission [90]. Copyright 2010, Nature Publishing Group.

Broadband tapered Yagi-Uda nanoantennas extend the list of advantages of plasmonic nanoantennas for photovolatics because they can be designed to absorb sunlight in a very broad spectral range. In order to achieve this specific goal, the number of nanorods and the nanorod length variation can be chosen [44, 45] such that the antenna spectrum covers the AM1.5 solar spectrum including the “problematic” spectral range of 600–1100 nm. Since the reception characteristics of the nanoantenna are nearly constant at all operating wavelengths, it is expected that all fractions of the solar spectrum would be absorbed almost equally.

7.4. Nanosensing

The scientific advances of recent years have recognized optical nanoantennas as a technology that could make possible a range of innovations. One of the important areas where the nanoantennas have immediate implications are plasmon mediated chemistry [91] and sensing [92–97].

Tapered Yagi-Uda nanoantennas can develop significantly the idea of the nanoantenna-enhanced gas sensing [97]. In order to achieve this goal, single nanoparticles made of gas-sensitive active materials such as platinum (Pt), palladium (Pd) or iridium (Ir) can be precisely placed in the near-field region of individual nanorods of nanoantennas as shown in Figure 14 [98]. Alternatively, Pt, Pd or Ir can be deposited on the top of the nanoantenna elements. Yet another configuration is a tapered array of elements made of different metals.

Figure 14

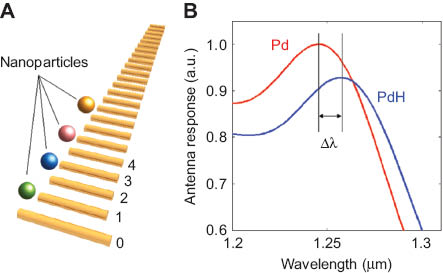
(A) Schematic of a broadband plasmonic array Yagi-Uda nanoantenna consisting of metal nanorods of varying length. Active nanoparticles are placed in close vicinity of the nanorods. (B) Optical sensing principle using the nanoantenna interacting with only one active palladium nanoparticle placed at the excitation site n=1. A change in the optical properties of the nanoparticle on exposure to hydrogen (Pd to PdH) causes a resonance shift (Δλ) in the optical response of the nanoantenna.

When exposed to the gas, a change in the size and optical properties of the active nanoparticles will influence the resonances of the individual nanorods, which in turn inevitably changes the far-field characteristics of the nanoantenna at different operating wavelengths. Thanks to a high sensitivity of the Yagi-Uda architecture, the expected spectral shift will be larger as compared with a several nanometers shift observed with single bow-tie nanoantennas [97, 99]. Furthermore, as shown in Figure 8B, the separation between the peaks in the nanoantenna spectra is large enough to allow for easy reading of data from different nanoparticles.

Any change in the far-field response of the nanoantenna can be detected using conventional far-field spectroscopy techniques [2] or with another broadband Yagi-Uda nanoantenna employed as a receiver. The latter configuration is attractive for application to horizontal on-chip plasmonic wireless signal-transmission circuits, which can be used for real-time transmission of data monitored by the nanosensor. Since the data on different monitored chemical substances can be transmitted simultaneously at different wavelengths, the suggested nanoantenna-based sensors can be used in the development of nanoscale optical nose devices that can be tuned both geometrically and dynamically to monitor different gases at different operating wavelengths.

7.5. Quantum communication and information

Efficient sources of single and entangled photons are crucial for the development of quantum information technology [23]. Single semiconductor quantum dots can emit single photons and degenerate polarization entangled photon pairs consisting of photons with the horizontal and vertical polarizations [19]. In order to collect the emitted photons, the quantum dot spontaneous emission can be controlled and funnelled in an optical cavity mode. When a quantum dot is spatially and spectrally coupled to a cavity mode, its emission rate into the mode is increased by the Purcell factor, which opens up a possibility of a high collection efficiency of the emitted photons.

Yagi-Uda nanoantennas can be used for the emission of single photons with a high efficiency as compared with optical cavities because they provide a large and broadband Purcell factor accompanied by a high directivity [12]. Moreover, using broadband tapered [43, 45] and log-periodic [47] nanoantennas one can generate single photons at different frequencies at the same time. However, the implementation of Yagi-Uda nanoantennas to the extraction of polarization entangled photon pairs is challenging because of two different spontaneous emission enhancement rates for the different photon polarizations that eventually erases the entanglement. One of the possible solutions to this problem can be found by fabricating 3D Yagi–Uda nanoantennas one in close proximity to another. This arrangement also known as photonic molecule [100] can offer identical emission conditions for different photon polarizations.

7.6. Optical metamaterials

In the previous sections we have demonstrated that arrays of plasmonic particles forming Yagi-Uda nanoantennas are able to precisely manipulate light in the same way as arrays of metal bars manipulate radio waves. Nowadays, a large and growing body of research investigates novel artificial materials – metamaterials [101] able to manipulate light in new ways not existing in nature. Metamaterials could make possible a range of optical innovations such as, e.g., more powerful microscopes, telecommunications and computers.

One of the approaches for creating metamaterials is to abruptly change the phase of light, which dramatically modifies how light propagates. However, this concept is not new. Indeed, the idea of controlling the phase was used by Uda and Yagi in their famous antenna 85 years ago. We remind that the reflector of a Yagi-Uda antenna is longer than its resonant length, its impedance is inductive and thus the current on the reflector lags the voltage induced on the reflector. The director elements are shorter than the resonant length, which makes them capacitive, so that the current leads the voltage. This causes a phase distribution to occur across the elements, simulating the phase progression of a plane wave across the array of elements.

However, Uda and Yagi could not know that a long-held Snell’s law, used to describe how light reflects and refracts while passing from one material into another, would be generalized 85 years after their invention. It has been shown in ref. [102] that the phase of light and the propagation direction can be changed dramatically by using metamaterials based on an array of V-shaped plasmonic nanoparticles. Very recently, this idea has been extended to the near infrared, which is essential for telecommunications, and more importantly applied to a broad spectral range from 1 to 1.9 mm [103]. The resulting nanoantenna array (see Figure 15A,B) offers an unparalleled control of anomalous reflection and refraction, including negative refraction (Figure 15C,D). This could lead to a variety of applications such as spatial phase modulation, beam shaping, beam steering, and plasmonic lenses, and it could also have an impact on transformation optics and on-chip optics.

Figure 15

(A) Schematic view of the metamaterial nanoantenna array. The unit cell of the plasmonic interface (in blue) consists of eight gold V-shaped nanoparticles of 40-nm arm width and 30-nm thickness, repeated with a periodicity of Λ in the x direction and λ/8 in the y direction. The phase delay for cross–polarized light increases along the x axis from right to left. (B) Scanning electron microscope images of the unit cells of four antenna arrays with different periodicities fabricated on a single silicon wafer. (C, D) The false-color maps indicate the experimentally measured relative intensity profiles for the antenna array labeled (1) (see panel (B), Λ=1440 nm) with x-polarized excitation. The dashed line shows the theoretical prediction of the peak position using the generalized Snell’s law. (C) Refraction angle vs. wavelength for cross-polarized light with 30° incidence angle. (D) Reflection angle vs. wavelength for cross-polarized light with 65° incidence angle. Adapted with permission [103]. Copyright 2011, American Association for the Advancement of Science.