The impact of imbalanced groups in UEFA Euro 1980–2024 and comparison with the FIFA World Cup

3.1 Group strength

To assess imbalance in groups at the Euro, we follow the method Lapré and Palazzolo (2023) used to assess imbalance in groups at the World Cup. Consequently, this section draws heavily from Lapré and Palazzolo (2023). First, for each Euro, we use World Football Elo Ratings (eloratings.net) to assess the strength for the participating teams at the time of the draw. As Elo ratings use a low volatility index, Elo ratings are well suited to assess team strength in empirical analysis over long periods of time (Gásquez and Royuela 2016). Scholars have extensively used Elo ratings (Cea et al. 2020; Csató 2022, 2023a,b; Gásquez and Royuela 2016; Lapré and Palazzolo 2023; Lasek et al. 2013; Lasek et al. 2016). Gomes de Pinho Zanco et al. (2024) provide a comprehensive analysis of the Elo method. Szczecinski and Djebbi (2020) improve on the Elo algorithm by modeling draws. Szczecinski (2022) further generalizes the Elo algorithm by modeling the margin of victory. FIFA has also adopted the Elo method since 2018 in their FIFA Men’s World Ranking, but Szczecinski and Roatis (2022) note that FIFA’s method can be improved by taking home advantage and goal difference into account.

Let r i ′ and r _i be the updated rating after a match and the old (pre-match) rating for team i respectively. K is a weight constant ranging from 20 for friendly matches to 60 for World Cup matches. After each match, the update formula adjusts the rating for team i by comparing the actual match outcome against team j with the expected outcome:

where W is the actual match outcome from team i’s perspective (1 for a win, 0.5 for a draw, and 0 for a loss) and the win expectancy on a neutral field is:

Win expectancy is modified if one team is playing at home by adding 100 points to the rating for the home team (eloratings.net/about).

For each of the 12 Euro tournaments since 1980, we collected Elo ratings for all participating teams at the time of the draw from international-football.net. Let r _it be the Elo rating for team i on the date of the draw for Euro t. To incorporate home advantage, we increase the rating for the host team by 100 (Csató 2023a, 2025c; Lapré and Palazzolo 2023). Next, we use the team ratings to calculate group strength. For each group G _t in Euro t, we calculate group strength g s G t as the average of the team ratings: g s G t = 1 4 ∑ i ∈ G t r i t . Guyon (2015) and Laliena and López (2019) note that a group can be tough when three teams are strong even if the fourth team is much weaker. This observation is particularly relevant if only two teams advance out of the group as is the case for the 16-team Euros (1996–2012) in our dataset. Therefore, we also calculate an alternative measure for group strength as the average of the team ratings of the three strongest teams in a group: g s G t ′ = 1 3 ∑ i ∈ G t r i t − min i ∈ G t r i t . Figure 1A and B show g s G t and g s G t ′ for all groups. Figure 2 shows the range in both measures of group strength for the 12 Euro tournaments since 1980. Higher variation in g s G t implies more competitive imbalance across groups, whereas no variation in g s G t would imply perfect balance across groups.

Figure 1:

Group strength. Number of groups in 1980–1992: 2, 1996–2012: 4, 2016–2024: 6. A: Group strength calculated as the average Elo rating of all four teams in the group. B: Group strength calculated as the average Elo rating of the best three teams in the group.

Figure 2:

Range in group strength. Number of groups in 1980–1992: 2, 1996–2012: 4, 2016–2024: 6.

To interpret Elo ratings for Euro teams we calculate several averages. During 1996–2024 (the years which featured quarterfinals), the average Elo rating for all quarterfinalists is 1,931 compared to 1,870 for all teams. So, the difference between an average Euro participant and an average quarterfinalist is 61 Elo rating points. Euro 1980 resulted in a top 4. Euro 1984 was the first tournament to feature semifinals. During 1980–2024, the average Elo rating for all semifinalists (or top 4) is 1,968 compared to 1,881 for all teams. Hence, the difference between an average Euro team and an average semifinalist is 87 Elo rating points. The range in group strength varies from 20 points in 1984 to 170 points in 2012. For seven of the eight tournaments with quarterfinals (1996–2024), the range in group strength is more than the 61-point difference between an average team and an average quarterfinalist. The extent of competitive imbalance has grown since the expansion to 16 teams in 1996 but shrank somewhat with the expansion to 24 teams in 2016. Our observations are similar when we consider g s G t ′ instead of g s G t .

3.2 Group opponents rating

Following Lapré and Palazzolo (2023), we calculate group opponents rating for team i in Euro t as g o p p r i t = 1 3 ∑ j ∈ G i t r j t , where G _it is the set of three opponents for team i in the group stage of Euro t. We also calculate an alternative measure for group opponents rating by averaging the ratings of the two strongest opponents: g o p p r i t ′ = 1 2 ∑ j ∈ G i t r j t − min j ∈ G i t r j t . Figure 3 shows the range in both measures of group opponents rating for each Euro. For both measures, the range in group opponents rating is large – it exceeds the 87-point difference between an average team and an average semifinalist in every Euro since 1996.

Figure 3:

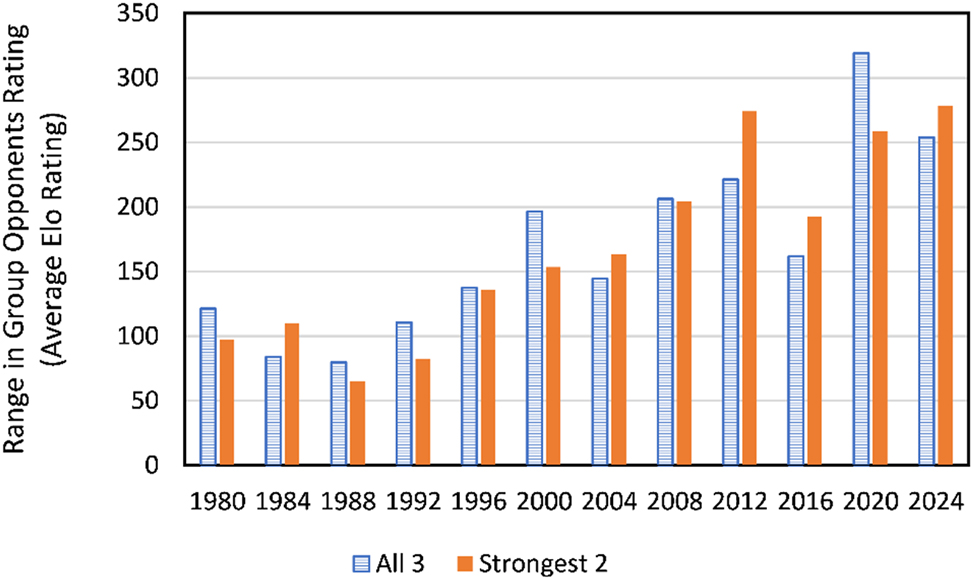
Range in group opponents rating. Number of groups in 1980–1992: 2, 1996–2012: 4, 2016–2024: 6.

3.3 Comparison of imbalance with FIFA World Cup

How does the variation in group strength for the Euro compare with the FIFA World Cup? We use the data on the 1954–2022 FIFA World Cup tournaments from Lapré and Palazzolo (2023). We perform several robust tests for the equality of variances in group strength across the World Cup and the Euro. Levene introduced a robust W ₀ test statistic that does not assume that the underlying populations are from a Gaussian distribution (Brown and Forsythe 1974). Brown and Forsythe (1974) proposed alternative formulations for Levene’s test statistic that use more robust estimators of central tendency instead of the mean. The first alternative (W ₅₀) replaces the mean with the median, while the second alternative replaces the mean with the 10 % trimmed mean (W ₁₀). Table 3 reports all three robust tests of the equality of variance in group strength between the World Cup sample and the Euro sample. Clearly, all p-values are greater than 0.05. So, we cannot reject the null hypothesis that the variance in group strength is equal across the World Cup and the Euro. We arrive at the same conclusion for the group strength based on all four teams in the group or the strongest three teams in the group.

Our conclusion is robust for different subsamples as well. If we compare group strength for the 16-team World Cups (1954–1978) and the 16-team Euros (1996–2012), the variances are not statistically significantly different. We reach the same conclusion comparing the 24-team World Cups (1982–1994) and the 24-team Euros (2016–2024). Lastly, we also reach the same conclusion if we compare recent World Cups and Euros since 1998.

Next, we compare the variance in group opponents rating between the World Cup and the Euro. Table 4 shows that variances are not statistically significantly different regardless of whether we consider all three opponents or only the strongest two opponents in the group. In conclusion, the competitive imbalance in the Euro is just as large as it is in the World Cup.

4.1 Impact of group opponents rating on reaching the quarterfinals

The first dependent variable is QF _it = 1 if team i reached the quarterfinals in Euro t, and 0 otherwise. Several factors can influence a team’s probability to reach the quarterfinals. First, we control for the number of teams, N _t , in Euro t. Second, seeded teams are supposed to be the stronger teams. Seeded teams avoid playing each other in the group stage. We control for the potential benefit of being seeded (Monks and Husch 2009) with S _it = 1 if team i was a seeded team in Euro t. Third, we control for the strength of team i in Euro t with r _it . As mentioned in Section 3, home advantage for the host is included in the host rating. However, to test if there is an effect not captured by the extra 100 Elo points, we also include a host dummy H _it = 1 if team i was a (co-)host for Euro t. For our key independent variable of interest, group opponents rating for team i in Euro t, we use both goppr _it and g o p p r i t ′ . We use logistic regression to estimate the probability of reaching the quarterfinals as follows:

A negative value for β ₁ means that a team playing in a Euro with more teams has a lower probability of reaching the quarterfinals. A positive value for β ₂ means that a seeded team has a higher probability of reaching the quarterfinals. A positive value for β ₃ means that a higher quality team has a higher probability of reaching the quarterfinals. A significant estimate for β ₄ means that there is a home advantage effect not captured by the extra 100 Elo points included in the team rating. A negative value for β ₅ implies that a team playing against higher quality opponents in the group stage has a lower probability of reaching the quarterfinals.

To avoid overfitting in logistic regression, Hosmer et al. (2013) recommend at least 10 observed events per independent variable. For the 8 Euros in years 1996–2024, we have 8 × 8 = 64 quarterfinal observations. Following the rule of 10 events per variable, we can include at most 6 independent variables. As we include only 5 independent variables in the full model, we are not at risk of overfitting.

Table 5 shows the results of the logistic regression for reaching the quarterfinals. In Model (1), the negative and statistically significant estimate for β ₁ indicates that more teams in a tournament reduces the probability of reaching the quarterfinals. The insignificant estimate for β ₂ means that seeded teams do not have a higher probability of reaching the quarterfinals. The positive and statistically significant estimate for β ₃ indicates that stronger teams have a higher probability of reaching the quarterfinals. The insignificant estimate for β ₄ means that any home advantage effect is not statistically significantly different from the extra 100 Elo points included in the team rating. The negative and statistically significant estimate for β ₅ means that playing against stronger opponents in the group reduces the probability of reaching the quarterfinals. Model (2) shows that the impact of group opponents rating is robust if we measure group opponents ratings by averaging the ratings of the two strongest opponents in the group.

Next, we quantify the impact of group opponents rating on the probability of reaching the quarterfinals. In Model (3) in Table 5, we re-estimate Model (1) without the insignificant seed and host variables. Let β ^ i be the estimate for β _i for variable i from Model (3) in Table 5. We rewrite the estimated logistic regression model to determine the estimated probability of reaching the quarterfinals, Pr Q F i t ^ = 1 :

In Section 3, we calculated that an average team for the 1996–2024 Euros has an Elo rating of 1,870 and the difference between an average team and an average quarterfinalist is 61 points. Note that 61 points is smaller than the observed ranges in Figure 3 for 1996–2024. Next, we compare an average team facing average opponents versus average quarterfinalists in the group, i.e., an increase in group opponents rating of 61 points. A change in group opponents rating from 1,870 to 1,931 drastically decreases the probability of reaching the quarterfinals. In a 16-team Euro, we find that an increase in group opponents rating from 1,870 to 1,931 decreases Pr Q F i t ^ = 1 from 0.50 to 0.38. In a 24-team Euro, an increase in group opponents rating from 1,870 to 1,931 decreases Pr Q F i t ^ = 1 from 0.28 to 0.19. Hence, an increase in group opponents rating by only 61 points decreases the probability of reaching the quarterfinals by 12 and 9 percentage points depending on the number of teams in the Euro.

The estimates in Table 5 for the Euro are similar to the estimates for the FIFA World Cup obtained by Lapré and Palazzolo (2023). We formally test whether the impact of group opponents rating on the probability of reaching the quarterfinals is the same across the World Cup and the Euro. First, we pool the observations from the Euro with the observations from the World Cup 1954–2022 (Lapré and Palazzolo 2023). We estimate Models (3) and (4) in Table 5 for the pooled dataset. (The seed variable was not significant for the World Cup. If we include the host variable, it is not significant either.) Models (1) and (2) in Table 6 report the results. Second, we define D _Euro = 1 if an observation was from the Euro, 0 if the observation was from the World Cup. We test for a change in slope parameters for the Euro observations by estimating:

The results in Models (3) and (4) in Table 6 show that none of the interaction terms with D _Euro are statistically significantly different from zero. Consequently, the impact of group opponents rating on the probability of reaching the quarterfinals is the same across the World Cup and the Euro.

4.2 Impact of group opponents rating on reaching the semifinals

Our second dependent variable is SF _it = 1 if team i reached the semifinals in Euro t, and 0 otherwise. Table 7 shows the logistic regression results. For the 12 Euros from 1980 through 2024, we have 12 × 4 = 48 semifinal observations. Applying the rule of 10 events per variable, we can include at most 4 independent variables. In Model (1), the estimate for β ₅ is not significant. So, in contrast to the quarterfinal analysis, a higher group opponents rating does not reduce the probability of reaching the semifinals. This finding is robust in Model (2) when we use only the two strongest opponents in the group to calculate group opponents rating. Seeding information is available since 1992. When we include Seed and Host in Models (3) and (4) in Table 7, neither variable is significant; none of our conclusions change. The findings in Table 7 for the Euro match the findings for the World Cup in Lapré and Palazzolo (2023). In the World Cup, group opponents rating did not significantly affect the probability of reaching the semifinals either.

5.1 Predictive accuracy: UEFA ranking versus Elo rating

Next, we verify that the Elo rating is a more accurate predictor of success at the Euro than the UEFA ranking. We follow an approach similar to Csató (2024) who compares the predictive accuracy of UEFA club coefficients and football club Elo ratings in UEFA Champions League games. In the Euro, except for games featuring a (co-)host, both teams play on a neutral field. Therefore, we remove games featuring (co-)hosts in our prediction study. The 2020 Euro (held in 2021 because of the COVID-19 pandemic) was unusual as it featured 9 co-hosts (as opposed to the usual one host or two co-hosts). We also remove the 2020 Euro games in our prediction study. Lastly, following Csató (2024), we remove games that resulted in a draw in the group stage.

UEFA started ranking teams in 2000. So, we focus on 6 Euro tournaments: 2000–2016 and 2024. These tournaments had 226 games combined, of which 38 games featured a (co-)host. Of the remaining 188 games played on a neutral field, 40 games were group games that ended in a draw. Thus, our sample consists of 148 games played on a neutral field won by one team. For each game, by convention, we label the first team listed as the “home” team and the second team listed as the “away” team. The dependent variable is 1 if the home team won the game, 0 if the away team won the game. The first independent variable – UEFA ranking predicts win – is 1 if the UEFA ranking for the home team is higher than for the away team, 0 otherwise. The second independent variable – Elo rating predicts win – is 1 if the Elo rating for the home team is higher than for the away team, 0 otherwise.

Models (1) and (2) in Table 8 show that the prediction based on the Elo rating has a higher McFadden Pseudo R ², higher percentage correctly classified, and a higher area under ROC. Furthermore, if we include both independent variables in Model (3), the prediction based on the UEFA ranking is not significant whereas the prediction based on the Elo rating is significant. Together, Models (1)–(3) suggest that the Elo rating is a more accurate predictor of success at the Euro than the ranking used by UEFA.

As rankings are based on ratings, the difference in Elo ratings for two teams contains additional information beyond merely noting which team has the highest Elo rating. In Model (4), we use the difference in Elo ratings as the independent variable. Similar to Model (2), Model (4) outperforms Model (1). Compared to Model (2), Model (4) has a higher Pseudo R ² (0.136 vs. 0.116) and a higher area under ROC (0.741 vs. 0.697), but a lower percentage correctly classified (66.9 % vs. 69.6 %). We cannot perform a similar analysis for UEFA ratings, because the 2024 UEFA rankings do not monotonically increase with the points in the qualifying groups as UEFA has ranked first the group winners and subsequently the group runners-up. Hence, some group winners are ranked higher than some group runners-up even though they obtained fewer points in the qualifying groups. Appendix A.1 shows that the findings in Table 8 are robust if we (i) split the sample into three periods corresponding to the UEFA ranking methods: 2000–2008, 2012–2016, and 2024, (ii) include the 21 games from the 2020 Euro played on a neutral field that did not end in a draw, and (iii) omit the 11 knockout-stage games decided by a penalty shootout.

5.2 UEFA versus FIFA progress

As mentioned in Section 3, scholars have extensively used World Elo Ratings to rank soccer teams. Next, we evaluate the gap between FIFA and UEFA ranking mechanisms on the one hand, and World Elo Ratings on the other hand. For each World Cup and Euro since 1998, we rank participating teams from 1 through N _t using (i) the organizer’s ranking mechanism, and (ii) the World Elo ratings. Figure 4 shows the correlation between the organizer’s rank and the World Elo rank. The correlation between the FIFA rank and the World Elo rank has increased over time. While FIFA rankings were flawed for a long time (Lapré and Palazzolo 2023), FIFA adopted an Elo method for their World ranking in 2018. The 2022 World Cup was the first World Cup for which FIFA used their Elo method. This change likely contributed to the highest correlation of 91 % observed in Figure 4. UEFA improved the correlation between the UEFA rank and the World Elo rank in 2012 and 2016, but with the switch to an inferior ranking method, the correlation in 2024 was as low as 57 %.

Figure 4:

Correlation between World Elo Rank and organizer’s rank of participating teams by tournament at the time of the draw. Squares indicate FIFA, diamonds indicate UEFA. Lines indicate one standard error below and above the Pearson correlation coefficient. The 2000 correlation is not significant. All other correlations are significant at 0.05.

To visualize what these correlations mean, Figure 5 shows scatterplots of the organizer’s rank against the World Elo rank for the 2022 World Cup and the Euro 2024. Even a correlation of 91 % is far from perfect (when all points fall on the 45-degree line). Indeed, as Szczecinski and Roatis (2022) point out, FIFA could still improve the predictive capacity of their Elo algorithm by taking home advantage and goal differential into account. The correlation of 57 % for the Euro 2024 is terrible. Group D (France, Netherlands, Austria, Poland) were all above the 45-degree line, meaning that UEFA underrated the strength of all four teams in group D. Indeed, group D was the toughest group (average Elo rating of 1,906), and two teams (France and Netherlands) reached the semifinals. Group E (Belgium, Ukraine, Romania, Slovakia) was the weakest group (average Elo rating of 1,794). Romania and Slovakia were severely overrated by UEFA whereas Ukraine was underrated. None of the teams from group E won a single game in the knockout stage.

Figure 5:

Correlation between World Elo Rank and organizer’s rank of participating teams in the 2022 FIFA World Cup (0.91) versus the UEFA Euro 2024 (0.57) at the time of the draw. For Euro 2024, squares denote teams in group D; triangles denote teams in group E.

In Table 9, we list the seven policy recommendations Lapré and Palazzolo (2023) proposed for FIFA to avoid substantial competitive imbalance in the World Cup. Table 9 compares the progress FIFA and UEFA have made so far. Both FIFA and UEFA still make the host a seed. Both organizers have also recently started to perform the draw when not all participating teams are known. We recommend abolishing this practice. If, however, FIFA and UEFA continue with this practice, they should at least adopt Csató’s (2023a) solution.

For the 2024 Euro, Table 15 in Appendix A.2 shows a comparison of the composition of the pots from the official UEFA regime with the composition of the pots formed strictly based on Elo ratings. Figure 6 shows the average pot strength for these two regimes. The Elo regime creates pots which are monotonically decreasing in strength. Under the UEFA regime, however, Pot 2 was even weaker than Pots 3 and 4!

Figure 6:

Strength of pots according to the official UEFA seeding regime and a seeding regime based on World Elo Ratings for the 2024 Euro.

The greatest contributing factor to creating competitive imbalance at the World Cup is FIFA’s allocation of confederation slots. UEFA does not have to deal with this complication. So, it is even more surprising that (i) competitive imbalance at the Euro is just as bad as at the World Cup, and (ii) the impact of competitive imbalance is the same across the Euro and the World Cup. The main culprit is the poor rating mechanism UEFA uses to rank participating teams. UEFA club competitions suffer from a similar shortcoming (Csató 2024). Just like Csató (2024) recommends UEFA to adopt an Elo method to rate clubs, the fix for the Euro is easy: UEFA should adopt an Elo rating system for national teams, preferably the World Elo rating system, but even the current FIFA ranking would likely be an improvement.