Abstract
In this paper, we present and analyze a mathematical programming approach to expansion draft optimization in the context of the 2017 NHL expansion draft involving the Vegas Golden Knights, noting that this approach can be generalized to future NHL expansions and to those in other sports leagues. In particular, we present a novel mathematical optimization approach, consisting of two models, to optimize expansion draft protection and selection decisions made by the various teams. We use this approach to investigate a number of expansion draft scenarios, including the impact of “collaboration” between existing teams, the trade-off between team performance and salary cap flexibility, as well as opportunities for Vegas to take advantage of side agreements in a “leverage” experiment. Finally, we compare the output of our approach to what actually happened in the expansion draft, noting both similarities and discrepancies between our solutions and the actual outcomes. Overall, we believe our framework serves as a promising foundation for future expansion draft research and decision-making in hockey and in other sports.
Appendix: Point shares background
Here, we provide some additional insight into the PS metric. First, we show in Figure 5 that team PS is a relatively good surrogate for overall team performance, using regular season team points and team PS for all teams from 2014–2015 to 2016–2017.
To get a sense of the typical range of PS values for a player, Figure 6 shows the distribution of player PS for 2016–2017.
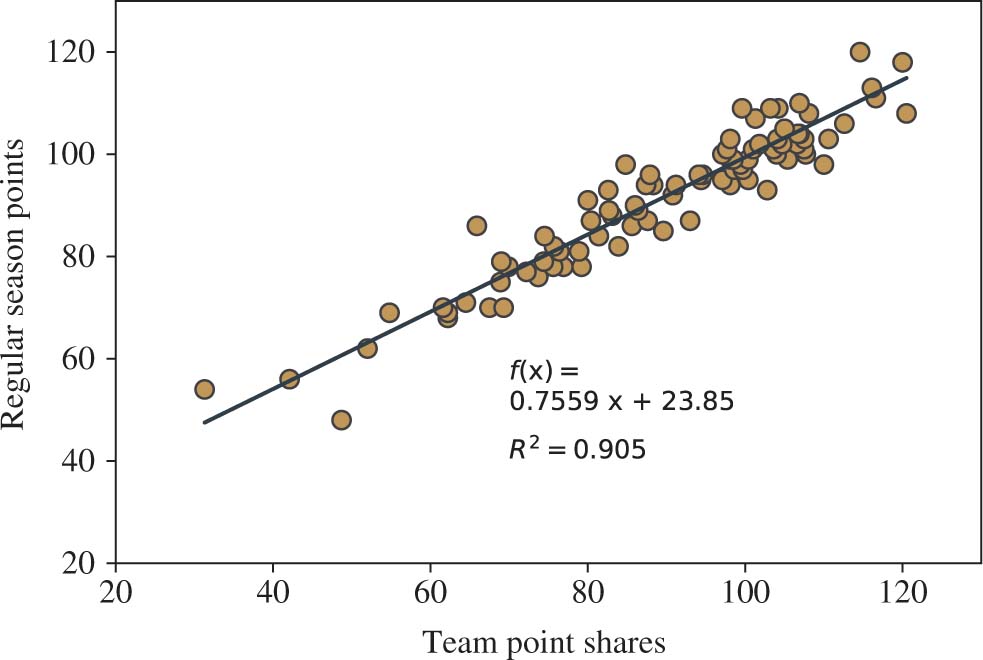
The relationship between regular season team points and team PS.
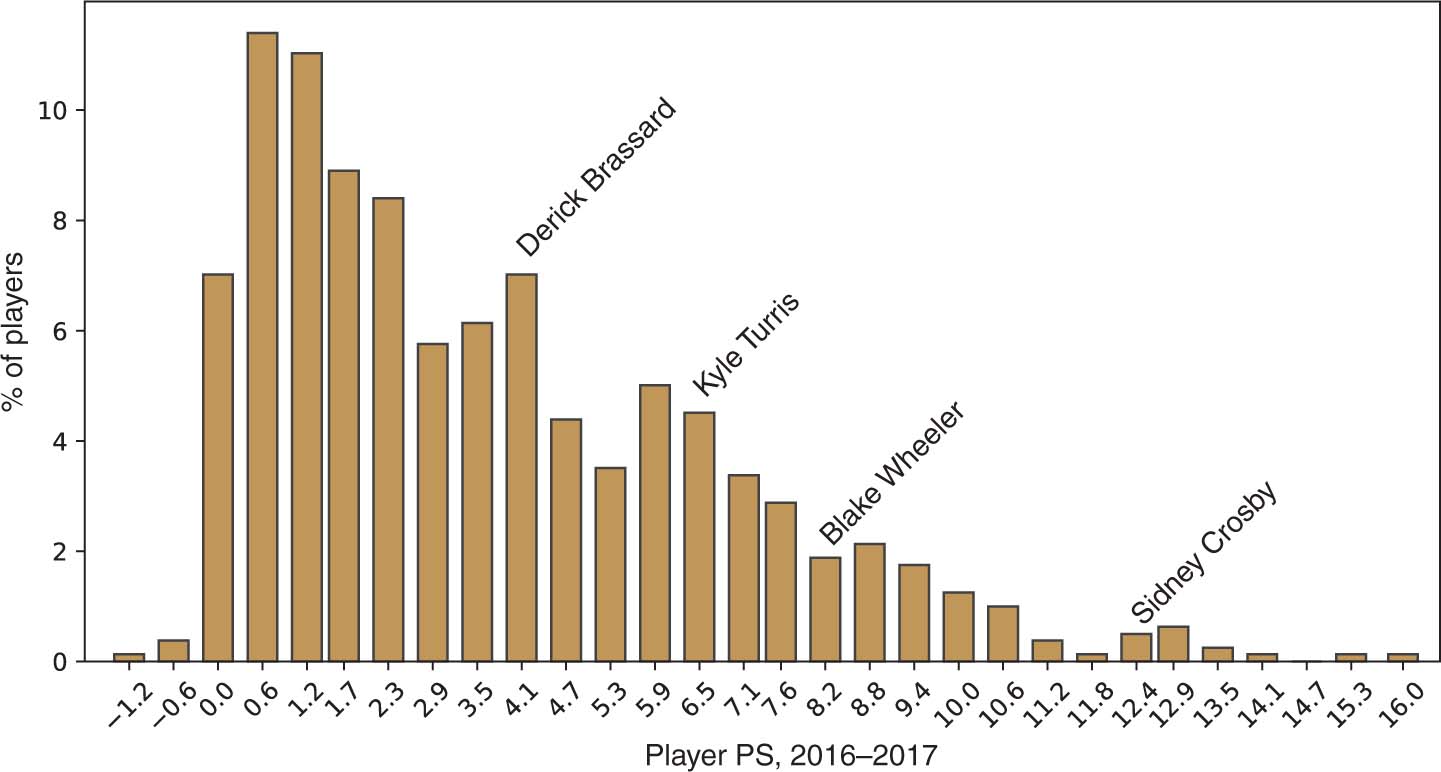
Point Share distribution for 2016–2017 players with at least ten games played. Min = −1.2, max = 16.0, 10th percentile = 0.2, 90th percentile = 7.8.
References
Amoros, J., L. F. Escudero, J. F. Monge, J. V. Segura, and O. Reinoso. 2011. “Team Aspar Uses Binary Optimization to Obtain Optimal Gearbox Ratios in Motorcycle Racing.” Interfaces 42:191–198.10.1287/inte.1110.0580Search in Google Scholar
Beaudoin, D. and T. B. Swartz. 2010. “Strategies for Pulling the Goalie in Hockey.” The American Statistician 64:197–204.10.1198/tast.2010.09147Search in Google Scholar
Becker, A. and X. A. Sun. 2016. “An Analytical Approach for Fantasy Football Draft and Lineup Management.” Journal of Quantitative Analysis in Sports 12:17–30.10.1515/jqas-2013-0009Search in Google Scholar
Bonami, P., A. Lodi, A. Tramontani, and S. Wiese. 2015. “On Mathematical Programming with Indicator Constraints.” Mathematical programming 151:191–223.10.1007/s10107-015-0891-4Search in Google Scholar
Boon, B. H. and G. Sierksma. 2003. “Team Formation: Matching Quality Supply and Quality Demand.” European Journal of Operational Research 148:277–292.10.1016/S0377-2217(02)00684-7Search in Google Scholar
Chan, T. C. Y., J. A. Cho, and D. C. Novati. 2012. “Quantifying the Contribution of NHL Player Types to Team Performance.” Interfaces 42:131–145.10.1287/inte.1110.0612Search in Google Scholar
Chan, T. C. Y. and D. Fearing. 2017. “Process Flexibility in Baseball: the Value of Positional Flexibility.” forthcoming in Management Science. https://doi.org/10.1287/mnsc.2017.3004.10.1287/mnsc.2017.3004Search in Google Scholar
Chan, T. C. Y. and R. Singal. 2016. “A Markov Decision Process-Based Handicap System for Tennis.” Journal of Quantitative Analysis in Sports 12:179–188.10.1515/jqas-2016-0057Search in Google Scholar
Dawson, D. and L. Magee. 2001. “The National Hockey League Entry Draft, 1969-1995: An Application of a Weighted Pool-Adjacent-Violators Algorithm.” The American Statistician 55:194–199.10.1198/000313001317098158Search in Google Scholar
Dickson, G., T. Arnold, and L. Chalip. 2005. “League Expansion and Interorganisational Power.” Sport Management Review 8:145–165.10.1016/S1441-3523(05)70037-1Search in Google Scholar
Duran, G., M. Guajardo, and D. Saure. 2017. “Scheduling the South American Qualifiers to the 2018 FIFA World Cup by Integer Programming.” European Journal of Operational Research 262:1109–1115.10.1016/j.ejor.2017.04.043Search in Google Scholar
Franks, A. M., A. D’Amour, D. Cervone, and L. Bornn. 2016. “Meta-Analytics: Tools for Understanding the Statistical Properties of Sports Metrics.” Journal of Quantitative Analysis in Sports 12:151–165.10.1515/jqas-2016-0098Search in Google Scholar
Fry, M. J., A. W. Lundberg, and J. W. Ohlmann. 2007. “A Player Selection Heuristic for a Sports League Draft.” Journal of Quantitative Analysis in Sports 3, doi:10.2202/1559-0410.1050.10.2202/1559-0410.1050Search in Google Scholar
Gibson, M. R., J. W. Ohlmann, and M. J. Fry. 2010. “An Agent-Based Stochastic Ruler Approach for Stochastic Knapsack Problem with Sequential Competition.” Computers and Operations Research 37:598–609.10.1016/j.cor.2009.02.028Search in Google Scholar
Gramacy, R. B., S. T. Jensen, and M. Taddy. 2013. “Estimating Player Contribution in Hockey with Regularized Logistic Regression.” Journal of Quantitative Analysis in Sports 9:97–111.10.1515/jqas-2012-0001Search in Google Scholar
James, B. and J. Henzler. 2002. Win Shares. Stats Inc.Search in Google Scholar
Kaplan, E. H., K. Mongeon, and J. T. Ryan. 2014. “A Markov Model for Hockey: Manpower Differential and Win Probability Added.” INFOR: Information Systems and Operational Research 52:39–50.10.3138/infor.52.2.39Search in Google Scholar
Kubatko, J. 2011. “Calculating Point Shares.” https://www.hockey-reference.com/about/point_shares.html, [Online; accessed 12-December-2017].Search in Google Scholar
Light, J., A. Chernin, and J. M. Heffernan. 2016. “NHL Expansion and Fan Allegiance: A Mathematical Modelling Study.” Mathematics-in-Industry Case Studies 7.10.1186/s40929-016-0009-0Search in Google Scholar
Macdonald, B. 2011. “A Regression-Based Adjusted Plus-Minus Statistic for NHL Players.” Journal of Quantitative Analysis in Sports 7, doi:10.2202/1559-0410.1284.10.2202/1559-0410.1284Search in Google Scholar
Macdonald, B. 2012. “Adjusted Plus-Minus for NHL Players Using Ridge Regression with Goals, Shots, Fenwick, and Corsi.” Journal of Quantitative Analysis in Sports 8, doi:10.1515/1559-0410.1447.10.1515/1559-0410.1447Search in Google Scholar
MacDonald, B. and W. Pulleyblank. 2014. “Realignment in the NHL, MLB, NFL, and NBA.” Journal of Quantitative Analysis in Sports 10:225–240.10.1515/jqas-2013-0070Search in Google Scholar
Mason, D. S. and W. M. Foster. 2007. “Putting Moneyball on Ice?” International Journal of Sport Finance 2:206.Search in Google Scholar
NHL. 2016a. “Hockey Operations Guidelines.” http://www.nhl.com/ice/page.htm?id=26377, [Online; accessed 30-November-2016].Search in Google Scholar
NHL. 2016b. “Rules for 2017 NHL Expansion Draft.” https://www.nhl.com/news/nhl-expansion-draft-rules/c-281010592, [Online; accessed 28-November-2016].Search in Google Scholar
Pantuso, G. 2017. “The Football Team Composition Problem: A Stochastic Programming Approach.” Journal of Quantitative Analysis in Sports 13:113–129.10.1515/jqas-2017-0030Search in Google Scholar
Pettigrew, S. 2015. “Assessing the Offensive Productivity of NHL Players Using in-Game Win Probabilities.” in Proceedings of 2015 Sloan Sports Analytics Conference.Search in Google Scholar
Quinn, K. G. and P. B. Bursik. 2007. “Growing and Moving the Game: Effects of MLB Expansion and Team Relocation 1950-2004.” Journal of Quantitative Analysis in Sports, 3, doi:10.2202/1559-0410.1054.10.2202/1559-0410.1054Search in Google Scholar
Rigdon, S. E. 2011. “The Penalty Shot/Optional Minor Choice in Ice Hockey.” Journal of Quantitative Analysis in Sports 7, doi:10.2202/1559-0410.1271.10.2202/1559-0410.1271Search in Google Scholar
Riley, S. N. 2017. “Investigating the Multivariate Nature of NHL Player Performance with Structural Equation Modeling.” PloS One 12:e0184346.10.1371/journal.pone.0184346Search in Google Scholar PubMed PubMed Central
Schmidt, M. B. 2001. “Competition in Major League Baseball: The Impact Expansion.” Applied Economics Letters 8:21–26.10.1080/135048501750041231Search in Google Scholar
Schuckers, M. and J. Curro. 2015. “Total Hockey Rating (THoR): A Comprehensive Statistical Rating of National Hockey League Forwards and Defensemen Based Upon All on-Ice Events.” in Proceedings of 2015 Sloan Sports Analytics Conference.Search in Google Scholar
Schulte, O., M. Khademi, S. Gholami, Z. Zhao, M. Javan, and P. Desaulniers. 2017. “A Markov Game Model for Valuing Actions, Locations, and Team Performance in Ice Hockey.” Data Mining and Knowledge Discovery 31:1735–1757.10.1007/s10618-017-0496-zSearch in Google Scholar
Seravalli, F. 2016a. “Vegas isn’t Getting a Lot for $500M.” http://www.tsn.ca/vegas-isn-t-getting-a-lot-for-500m-1.615117, [Online; accessed 30-November-2016].Search in Google Scholar
Seravalli, F. 2016b. “Viva Las Vegas! TSN Hockey’s Early Expansion Team Lineup.” https://www.tsn.ca/viva-las-vegas-tsn-hockey-s-early-expansion-team-lineup-1.614039, [Online; accessed 01-December-2016].Search in Google Scholar
Shea, S. M. and C. E. Baker. 2012. “Calculating Wins Over Replacement Player (WORP) for NHL Goaltenders.” Journal of Quantitative Analysis in Sports 8, doi:10.1515/1559-0410.1358.10.1515/1559-0410.1358Search in Google Scholar
Thomas, A. C. 2006. “The Impact of Puck Possession and Location on Ice Hockey Strategy.” Journal of Quantitative Analysis in Sports 2, doi:10.2202/1559-0410.1007.10.2202/1559-0410.1007Search in Google Scholar
Thomas, A. C., S. L. Ventura, S. T. Jensen, and S. Ma. 2013. “Competing Process Hazard Function Models for Player Ratings in Ice Hockey.” The Annals of Applied Statistics 7:1497–1524.10.1214/13-AOAS646Search in Google Scholar
Trick, M. A., H. Yildiz, and T. Yunes. 2011. “Scheduling Major League Baseball Umpires and the Traveling Umpire Problem.” Interfaces 42:232–244.10.1287/inte.1100.0514Search in Google Scholar
Van Voorhis, T. 2002. “Highly Constrained College Basketball Scheduling.” Journal of the Operational Research Society 53:603–609.10.1057/palgrave.jors.2601356Search in Google Scholar
Vincent, C. B. and B. Eastman. 2009. “Defining the Style of Play in the NHL: An Application of Cluster Analysis.” Journal of Quantitative Analysis in Sports 5, doi:10.2202/1559-0410.1133.10.2202/1559-0410.1133Search in Google Scholar
Washburn, A. 1991. “Still more on Pulling the Goalie.” Interfaces 21:59–64.10.1287/inte.21.2.59Search in Google Scholar
©2019 Walter de Gruyter GmbH, Berlin/Boston
Articles in the same Issue
- Frontmatter
- The advantage of lefties in one-on-one sports
- A mathematical optimization framework for expansion draft decision making and analysis
- Analysis of a constructive matheuristic for the traveling umpire problem
- A Bayesian method for computing intrinsic pitch values using kernel density and nonparametric regression estimates
- The probabilities of winning a racquetball doubles match motivate a fairer side-out scoring scheme for singles and team events
Articles in the same Issue
- Frontmatter
- The advantage of lefties in one-on-one sports
- A mathematical optimization framework for expansion draft decision making and analysis
- Analysis of a constructive matheuristic for the traveling umpire problem
- A Bayesian method for computing intrinsic pitch values using kernel density and nonparametric regression estimates
- The probabilities of winning a racquetball doubles match motivate a fairer side-out scoring scheme for singles and team events

