Challenges and Present Fields of Action at Laser Scanner Based Deformation Analyses

2.1 Type of Deformation

Generally, deformations describe either geometrical changes in shape and dimension, i. e., relative movements inside the object’s surface, as well as rigid body movements ([11], pp. 92; [3]). Analyzing the first category of deformations is more common at laser scanner based deformation analyses since a laser scanner is perfectly suited to acquire surfaces, their geometries and potential changes in geometry nearly continuously in space.

To analyze rigid body movements, collecting the deformation of some selected object points representing the complete rigid object is sufficient usually. Hence, if an object is assumed to move only as a rigid body, laser scanners are used only seldom for deformation analysis.

Consequently, not the position and orientation of the scanned surface is of main interest at most laser scanner applications, but inner geometrical changes of the surface itself due to relative movements. This increases the demands on a suited surface representation being able to detect even small geometrical, inner deformations.

This differentiation between rigid body movements and relative movements inside the object’s surface is straightforward when analyzing the deformations of man-made structures. However, this is not the case when dealing with natural phenomena. E. g., judging whether a landslide only moves (rigid body movement) or also changes its shape and dimension (relative movement) is not a trivial task. This is, amongst others, based on the fact that natural phenomena cannot be distinguished from the environment easily as, e. g., a man-made dam can.

2.2 Type of Reference Surface

At the first type of reference surface, the deformation analysis is based on one single epoch. Here, areal deformations of the surface are defined as deviations from a given reference surface where the parameter values of this surface can either be also given or their estimation is part of the deformation analysis. Examples are the deformation analysis of a cooling tower with given hyperbolic parameterization [17] or the deformation analysis of the main reflector of a radio telescope with a given paraboloid parameterization [15].

In the second scenario, surfaces are scanned in at least two epochs: deformations equal deviations between the surfaces of different epochs. Hence, the reference surface is not given but has been determined in a previous epoch. For the deformation analysis of a dam, see Alba et al. [1] or Eling [5].

When analyzing the deformation of man-made structures, a combination of both scenarios is usually performed: Since the surface is constructed, it follows certain physical rules like smoothness or straightness that are known priori due to construction plans. Consequently, reference parameterizations might exist.

Contrary, when analyzing natural surfaces, e. g., like landslides, rocks or solifluction processes – where no reference parameterization can be given due to lack of knowledge –, two or more epochs are needed to discover deformations.

2.3 Type of Surface Representation

To compare the scanned point cloud to a reference surface or to the surface of a previous epoch, a surface representation is needed. Dependent on the choice of surface representation and the aim of the deformation analysis, the comparison is point-based, point cloud-based, surface-based, geometry-based or parameter-based [29].

Either the complexity of the underlying representation as well as the expressiveness increases from the first type to the latter one: While the point- and point cloud-based approaches do not consider any surface or other connection between neighbouring points of a surface, the surface-based approach only connects neighbouring points by a mesh or other parameter-free representations. Hence, all sorts of measurement errors degrade the outcome of these three types of surface representations.

Only at the geometry- and parameter-based approach, the surface is represented based on parameters and an adjustment. While the geometry-based approach only analyzes areal deviations from the reference, the parameter-based approach explicitly analyzes the estimated parameters. Examples for each representation can be found in Ohlmann-Lauber and Schäfer [29] and Kuhlmann and Holst [21].

Similar to Section 2.1 and 2.2, a division between man-made structures and natural surfaces is appropriate: Man-made structures can, usually, more easily be parameterized than natural surfaces. Thus, natural surfaces are often represented only point-, point cloud- or surface-based. Since these approaches are not based on an adjustment, the spatial point distribution and the measurement noise directly impact the quality of the deformation analysis. This problem is also addressed in Dupuis et al. [4] for the deformation analysis of leafs.

3.1 Calibration of Laser Scanners

The technology of laser scanning has not yet been subjected to a quality management as is had been done for other geodetic instruments like levels, total stations or GPS-antennas. The complexity of performing a quality assessment of a terrestrial laser scanner arises out of the fact that laser scanners appear as a black-box [36]: their internal error sources and the pre-processing steps of the measurements are hidden from the operator.

A panoramic laser scanner is constructed by three main axes (Figure 1), i. e., primary and secondary rotation axes and collimation axis. The first and second one are similar to the trunnion axis and the vertical axis, respectively, of a total station. The collimation axis is defined by the laser beam vector after reflection at the mirror.

Figure 1

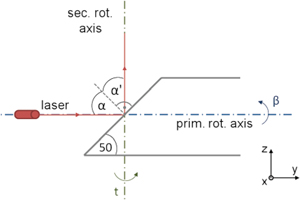
Internal construction of a panoramic terrestrial laser scanner.

For scanning, a laser beam generated by a diode is aligned to the center of a mirror whose reflecting surface is inclined to the laser beam axis by 50 gon. The primary rotation axis is defined by the longitudinal axis of this mirror whose rotation around this axis leads to the vertical deflection β of the laser beam. Due to this parallelism of laser beam vector and primary rotation axis, the laser beam is deflected by an angle of 100 gon following the equality of incidence angle α and emergent angle α’. This whole construction rotates around the secondary rotation axis that deflects the laser beam horizontally by the angle t. Similar to the construction of a total station, the three axes – i. e., primary rotation axis, secondary rotation axis, collimation axis – are assumed to be orthogonal to each other and to coincide in one point.

All of these physical assumptions can only be met to a certain level of accuracy. Hence, deviations from these assumptions lead to systematic measurement errors. These can be grouped in four categories [16]:

1. Laser: horizontal and vertical eccentricities, horizontal and vertical inorthogonalities, etc.

2. Mirror: inclination error, etc.

3. Axes: vertical index error, horizontal and vertical eccentricities of secondary rotation axis, horizontal and vertical inorthogonalities of primary rotation axis, etc.

4. Electrooptical distance measurement: zero error, scale factor, etc.

While the first three groups of error sources are due to misconstruction of the deflection unit, the latter one describes errors of the distance measurements. As indicated in the enumeration, the list of error sources is not exhaustive [16].

Figure 2 exemplarily shows the effect of the inclination error of the mirror: Due to the error of Δφ, the laser beam vector is deflected by an error of 2 ⋅ Δφ leading to errors in the horizontal direction. For the scanning of a plane in 10 m distance, the resulting systematic error of the horizontal angle t when simulating an inclination error of Δφ = 2.5 mgon is shown in Figure 3.

Figure 2

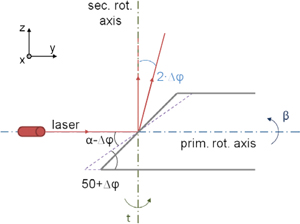
Effect on the beam deflection due to a inclination error of the mirror Δφ.

Figure 3

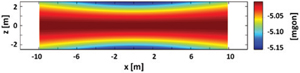
Error of horizontal angle t due to an inclination error of the mirror of Δφ = 2.5 mgon when scanning a plane in 10 m distance where the laser scanner is stationed symmetrically in front of the plane.

As can be seen, this error is not negligible. This especially holds for areal deformation analyses since these systematic measurement errors need to be isolated from the areal deformations. Otherwise, it is hardly possible to distinguish between deformation and measurement errors. However, this isolation is a hard task as both, the areal deformations and also the measurements errors, lead to areal deviations from the reference surface.

The isolation of the systematic errors during the regular deformation analyses only succeeds in exceptional applications, e. g, at the deformation analysis of the 100 m radio telescope in Effelberg, Germany [14, 15]. However, this isolation only worked since the deformed object was sampled in two faces, the object covered nearly the whole field of vision of the laser scanner and the object is known very accurately [14].

These matters of fact explain the necessity of calibrating a laser scanner before using it for deformation analyses. This calibration of terrestrial laser scanners is based on two steps:

1. Defining the calibration parameters that have to be estimated and assessing of the corresponding equations. These differ partially from the ones of a total station, as has already been shown by the previous categorization and the view in the inside of a panoramic laser scanner (see Figures 2–3).

2. Developing a calibration field that can be used to estimate the calibration parameters with high accuracy and low correlation.

Both steps are presently fields of action at research institutions, which can be seen by the great amount of publications where only a short selection can be named here: Gordon [6], Holst und Kuhlmann [14], Holst et al. [16], Lichti et al. [25], Reshetyuk [31], Rietdorf [32]. For further discussion, see Kuhlmann and Holst [21].

3.2 Spatial Correlations of Scan Points

The stochastic model of terrestrial laser scans is often limited to assuming variances for the measured polar elements: horizontal angle, vertical angle and distance. Correlations either between these polar elements of one scan point as well as the ones between the polar elements of different points are neglected. This fact is reasoned by the lack of knowledge about the correlations. However, it represents the reality only insufficiently which can be specified in the following.

When sampling an object by a terrestrial laser scanner, four error sources degrade the accuracy of the scan points: the internal errors due to misconstruction (see Subsection 3.1), the measurement configuration (i. e., incidence angle; [38]), metrological conditions and the object itself [35, 39]. While the first category affects all measured polar elements of a laser scanner, the other ones affect only the electro-optical distance measurements. The error sources of each category lead to stochastic (random) as well as to deterministic (systematic) errors that can only be identified and eliminated to a certain amount. This especially holds for the object errors that are mainly due to the material of the object, its color and reflectivity.

The systematic errors being not eliminated correlate the measurements as they are not normally-distributed. Since most of these errors only vary slowly along the surface of the measured object (i. e., the ones due to similar angles of impact, object characteristics and metrological conditions), one can assume the correlation to be proportional to the distance between scan points. Hence, neighbored points are correlated very high whereas the correlation converges to zero with increasing point distance.

However, neither the correlations’ magnitude nor their spatial decrease is known. Hence, by neglecting these correlations in the stochastic model of the deformation analysis, the estimated covariances are far too optimistic. Consequently, parameters and corresponding areal deformations are assumed to be significant because it is implied by the high parameter accuracy [13, 14].

This can be emphasized by simulations: A plane is scanned in 10 m distance where the measured distances are correlated between neighbored scan points. In real applications, this correlation would not be known. Hence, the covariance matrix would only consider variances of the polar elements. The global test of the approximation [26] is declined in this case. Contrary, if the correlation between the scan points had been known and, thus, had been integrated in the stochastic model, the global test would have been accepted.

In the first case, this global test, thus, indicates that observations, functional and stochastic model are not consistent. Since the observations are simulated, the decline of this global test can be reasoned by the neglect of correlations in the stochastic model. However, when performing real scans, this discovered inconsistency in the approximation could most probably not be related directly to the neglected spatial correlations of the scan points. Hence, due to the lack of information about spatial correlations, the non-deformed plane might be assumed to be deformed.

While the existence of correlations could have been proven in some studies [18, 19] general strategies for revealing and assessing correlations are not at hand. This is challenging since these correlations presumably differ by a large amount between different measurement configurations and object properties.

Thus, estimating and including spatial correlations of scan points is a present field of action at laser scanner based deformation analyses. Prospective studies could focus on determining the effective number of measurements ([11], pp. 346) and the correlation structure dependent on different configurations and object properties. Similar investigations also helped to improve the stochastic model of the GPS [20].

3.3 Configuration of Surface Approximation

When approximating a scanned surface, the number of observations is usually sufficient regarding redundancy to estimate the surface parameters. The large number of scan points implies high accuracy and reliability of the derived results. However, both accuracy and reliability rather depend also on the regularity of the object sampling. At laser scanning, this object sampling is irregular due to the polar deflection.

Holst [12] and Holst and Kuhlmann [14] show that the network configuration of the surface approximation is a better indicator – compared to the absolute redundancy – for certifying the quality of the results of the surface approximation. For analyzing the network configuration, they use the partial redundancies combining functional model, stochastic model and sampling density. In this analysis, they reveal the large impact of the regularity of the object sampling. Here, not the absolute number of scan points is of interest but their spatial distribution.

At areal deformation analyses, the surface is not known completely. Instead, the surface may be affected by local, unknown deformations leading to arbitrary areal deviations from the reference surface. Their detection and quantification is one aim of the corresponding areal deformation analyses of the object. Consequently, the object knowledge – resulting in the associated surface parameterization – is only limited (see Section 3.5).

At laser scanner based deformation analyses, both aspects are combined: the sampling density is irregular and the object knowledge is incomplete. This results in a biased parameter estimation. Holst and Kuhlmann [14], Holst et al. [13, 15] and Holst [12] revealed these biases for different kinds of deformation analyses by investigating the network configuration. A reduction of this bias and its variation that depend on the station of the laser scanner can be obtained by (1) thinning the point cloud to a regular sampling, by (2) inserting spatial correlations between neighboring points or by (3) robust estimation [13]. However, each of these solutions bears disadvantages since (1) scan points are eliminated, (2) nearly completely filled covariance matrices need to be processed or (3) different kind of error models are used for approximation.

Hence, handling the irregular sampling in combination with the limited object knowledge is a present field of action for laser scanner based deformation analyses [12].

3.4 Surface Parameterization

The Introduction addresses the continualization of engineering geodesy which also strengthens the need of transforming point-wise methods used in deformation analyses to areal methods. This consideration can be highlighted by two selected aspects presented in the following.

3.5 Extended Uncertainty

At surface approximations, the functional model of the object, i. e., the surface parameterization, has to be defined priori. Thus, object knowledge has to be integrated. At some approaches, this object knowledge is given explicitly, e. g., at the deformation analysis of the main reflector of the 100 m radio telescope in Effelsberg: The main reflector equals a rotational paraboloid. Contrary, when approximating, e. g., a church’s vault or leafs [9], the object knowledge is only limited.

Independent from this general question whether the geometry of the object is known priori or is easy to parametrize, the object can only seldom be parameterized accurately. Hence, the surface parameterization is afflicted with uncertainty. However, previous studies about laser scanner based deformation analyses only consider metrological aspects affecting the uncertainty (see also Subsection 3.1–3.2). Consequently, these considerations should be extended by the object uncertainty leading to an extended uncertainty model. Extended uncertainty models have already been proposed by Kutterer [23, 24], Schön [34] and Neumann [28].

The metrological uncertainty arises out of deterministic and stochastic errors (see Section 3.1–3.2). Contrary, the object uncertainty arises out of imperfect knowledge and simplification: Imperfect knowledge describes the imprecise knowledge about the real object, simplification the generalized surface parameterization. The first aspect includes unknown deformations, the latter one object details being neglected in the surface parameterization.

Both types of object uncertainty affect the parameter estimation systematically and, thus, bias the deformation analysis (see also Section 3.3). While this bias cannot be reduced by including an extended uncertainty model, the inclusion of the object uncertainty would lead to more realistic parameter variances so that this bias would not be significant any more. Hence, an extended uncertainty model would save from misleadingly detected deformations.

Integrating an extended uncertainty model would be feasible within an interval approach [23, 34] or within the fuzzy-theory [28] which could both be used instead of least-squares estimation.

Altogether, these considerations need to be focused in future studies. An integration of object uncertainty seems to be unavoidable to deal with either limited object knowledge as well as with realistic estimates of the parameters’ uncertainties.

Only if this succeeds, a significant parameter test for detecting and analyzing areal deformations can be performed. Hence, the integration of an extended uncertainty model is a present field of action at laser scanner based deformation analyses.